Greedy Algorithms
Greedy Approach: A Deep Dive - Algorithms for Coding Interviews in Python
Greedy Algorithms | Interview Cake
Greedy Algorithm - InterviewBit
Basics of Greedy Algorithms Tutorials & Notes | Algorithms | HackerEarth
Introduction
A greedy algorithm, as the name suggests, always makes the choice that seems to be the best at that moment. This means that it makes a locally-optimal choice in the hope that this choice will lead to a globally-optimal solution. They never look backwards at what they’ve done to see if they could optimise globally. This is the main difference between Greedy and Dynamic Programming.
Greedy is an algorithmic paradigm in which the solution is built piece by piece. The next piece that offers the most obvious and immediate benefit is chosen. The greedy approach will always make the choice that will maximize the profit and minimize the cost at any given point. It means that a locally-optimal choice is made in the hope that it will lead to a globally-optimal solution.
A greedy algorithm builds up a solution by choosing the option that looks the best at every step.
Sometimes greedy algorithm fails to find the optimal solution because it does not consider all available data and make choices which seems best at that moment. A famous example for this limitation is searching the largest path in a tree.
The greedy algorithm fails to solve this problem because it makes decisions purely based on what the best answer at the time is:
at each step it did choose the largest number and solve the problem as
7 -> 12 -> 6 -> 9. Total is: 34.
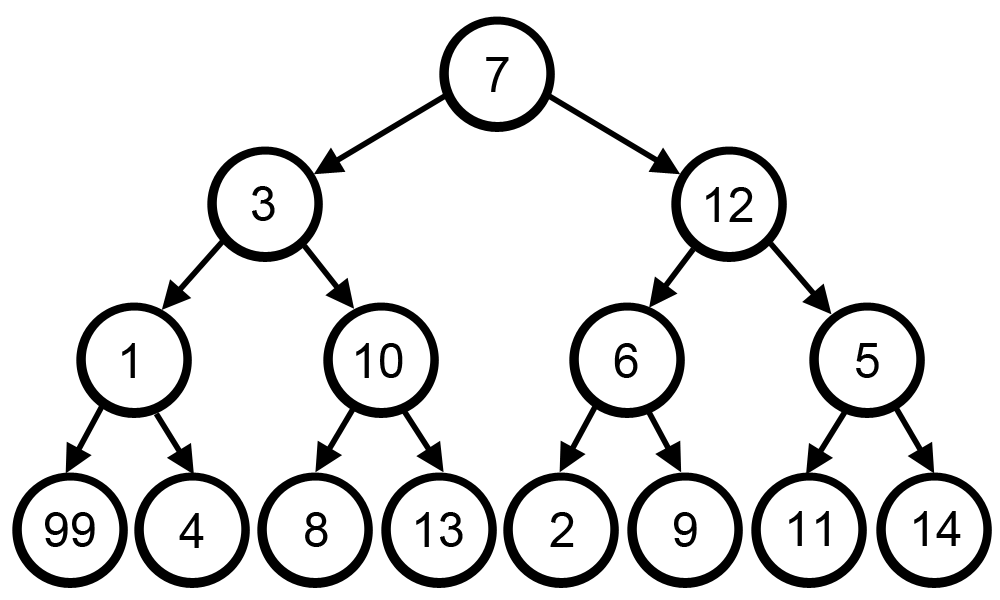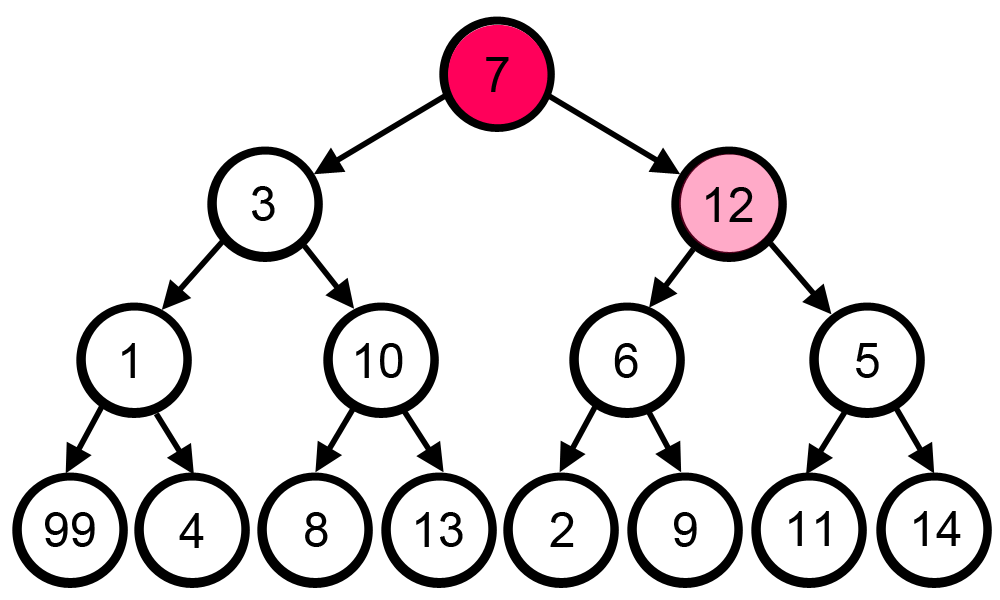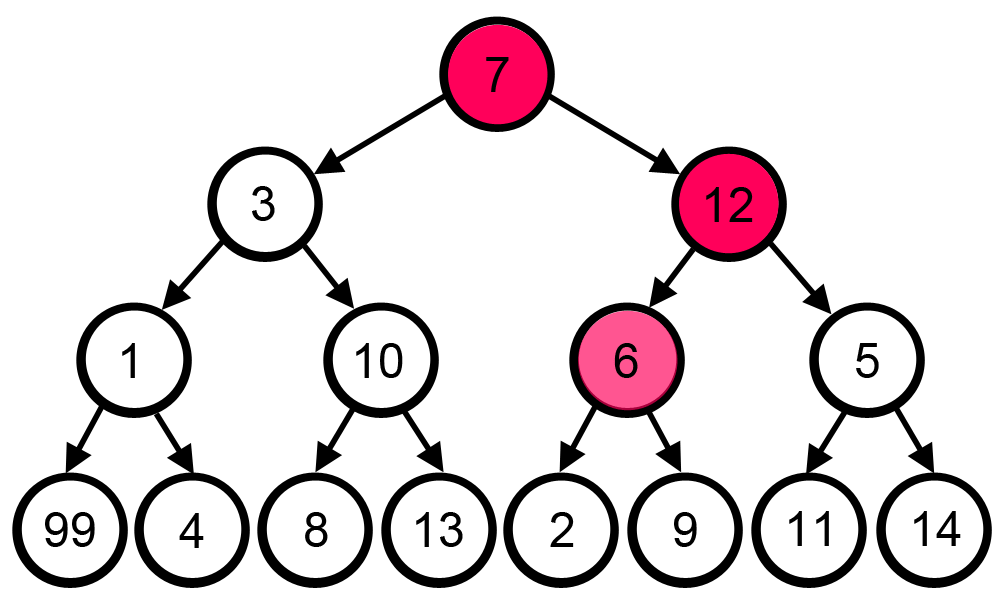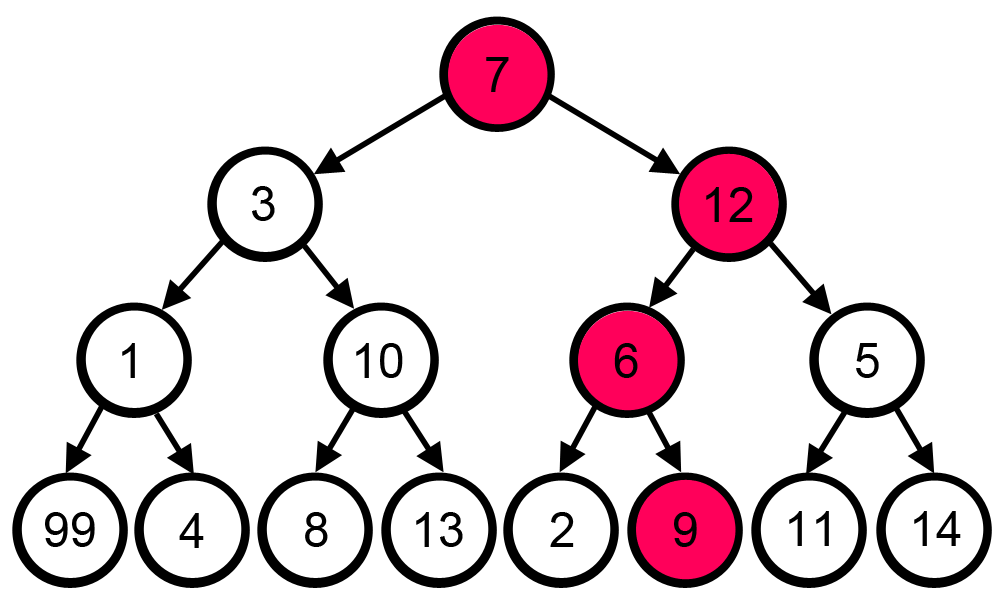
This is not the optimal solution. Correct solution to this problem is, 7 -> 3 -> 1 -> 99. Total is: 110.
A greedy algorithm works if a problem exhibits the following two properties:
- Greedy Choice Property*: A globally optimal solution can be reached at by creating a locally optimal solution. In other words, an optimal solution can be obtained by creating "greedy" choices.
- Optimal substructure: Optimal solutions contain optimal subsolutions. In other words, answers to subproblems of an optimal solution are optimal.
Examples
- Connect Ropes
-
Minimum Cost to Connect Sticks
""" 1167. Minimum Cost to Connect Sticks You have some number of sticks with positive integer lengths. These lengths are given as an array sticks, where sticks[i] is the length of the ith stick. You can connect any two sticks of lengths x and y into one stick by paying a cost of x + y. You must connect all the sticks until there is only one stick remaining. Return the minimum cost of connecting all the given sticks into one stick in this way. Example 1: Input: sticks = [2,4,3] Output: 14 Explanation: You start with sticks = [2,4,3]. 1. Combine sticks 2 and 3 for a cost of 2 + 3 = 5. Now you have sticks = [5,4]. 2. Combine sticks 5 and 4 for a cost of 5 + 4 = 9. Now you have sticks = [9]. There is only one stick left, so you are done. The total cost is 5 + 9 = 14. Example 2: Input: sticks = [1,8,3,5] Output: 30 Explanation: You start with sticks = [1,8,3,5]. 1. Combine sticks 1 and 3 for a cost of 1 + 3 = 4. Now you have sticks = [4,8,5]. 2. Combine sticks 4 and 5 for a cost of 4 + 5 = 9. Now you have sticks = [9,8]. 3. Combine sticks 9 and 8 for a cost of 9 + 8 = 17. Now you have sticks = [17]. There is only one stick left, so you are done. The total cost is 4 + 9 + 17 = 30. Example 3: Input: sticks = [5] Output: 0 Explanation: There is only one stick, so you don't need to do anything. The total cost is 0. https://leetcode.com/problems/minimum-cost-to-connect-sticks """ from typing import List from heapq import heapify, heappop, heappush # O(n log n) time class Solution: def connectSticks(self, sticks: List[int]): total = 0 heapify(sticks) while len(sticks) > 1: stick = heappop(sticks) + heappop(sticks) total += stick heappush(sticks, stick) return total -
Minimum Waiting Time
""" Minimum Waiting Time: You're given a non-empty array of positive integers representing the amounts of time that specific queries take to execute. Only one query can be executed at a time, but the queries can be executed in any order. A query's waiting time is defined as the amount of time that it must wait before its execution starts. In other words, if a query is executed second, then its waiting time is the duration of the first query; if a query is executed third, then its waiting time is the sum of the durations of the first two queries. Write a function that returns the minimum amount of total waiting time for all of the queries. For example, if you're given the queries of durations [1, 4, 5], then the total waiting time if the queries were executed in the order of [5, 1, 4] would be (0) + (5) + (5 + 1) = 11. The first query of duration 5 would be executed immediately, so its waiting time would be 0, the second query of duration 1 would have to wait 5 seconds (the duration of the first query) to be executed, and the last query would have to wait the duration of the first two queries before being executed. Note: you're allowed to mutate the input array. https://www.algoexpert.io/questions/Minimum%20Waiting%20Time """ """ ensure the longest waiting times are at the end """ def minimumWaitingTime(queries): queries.sort() total = 0 prev_time = 0 for time in queries: total += prev_time prev_time += time return total def minimumWaitingTime2(queries): queries.sort() total = 0 for idx, num in enumerate(queries): last_idx = len(queries)-1 # add waiting time for the elements to the right of the current element total += num * (last_idx - idx) return total -
Class Photos
""" Class Photos: It's photo day at the local school, and you're the photographer assigned to take class photos. The class that you'll be photographing has an even number of is students, and all these students are wearing red or blue shirts. In fact, exactlyhalf of the class is wearing red shirts, and the other half is wearing blue shirts. You're responsible for arranging the students in two rows before taking the photo. Each row should contain the same number of the students and shouldadhere to the following guidelines: All students wearing red shirts must be in the same row. All students wearing blue shirts must be in the same row. Each student in the back row must be strictly taller than the student directly in front of them in the front row. You're given two input arrays: one containing the heights of all the students with red shirts and another one containing the heights of all the students with blue shirts. These arrays will always have the same length, and each height will be a positive integer. Write a function that returns whether or not a class photo that follows the stated guidelines can be taken. Note: you can assume that each class has at least 2 students. https://www.algoexpert.io/questions/Class%20Photos """ """ Each student in the back row must be strictly taller than the student directly in front of them in the front row. """ def classPhotos(redShirtHeights, blueShirtHeights): redShirtHeights.sort() blueShirtHeights.sort() isRedTaller = redShirtHeights[0] > blueShirtHeights[0] for idx in range(len(redShirtHeights)): if isRedTaller: if redShirtHeights[idx] <= blueShirtHeights[idx]: return False else: if redShirtHeights[idx] >= blueShirtHeights[idx]: return False return True -
Two City Scheduling
""" 1029. Two City Scheduling A company is planning to interview 2n people. Given the array costs where costs[i] = [aCosti, bCosti], the cost of flying the ith person to city a is aCosti, and the cost of flying the ith person to city b is bCosti. Return the minimum cost to fly every person to a city such that exactly n people arrive in each city. Example 1: Input: costs = [[10,20],[30,200],[400,50],[30,20]] Output: 110 Explanation: The first person goes to city A for a cost of 10. The second person goes to city A for a cost of 30. The third person goes to city B for a cost of 50. The fourth person goes to city B for a cost of 20. The total minimum cost is 10 + 30 + 50 + 20 = 110 to have half the people interviewing in each city. Example 2: Input: costs = [[259,770],[448,54],[926,667],[184,139],[840,118],[577,469]] Output: 1859 Example 3: Input: costs = [[515,563],[451,713],[537,709],[343,819],[855,779],[457,60],[650,359],[631,42]] Output: 3086 Constraints: 2 * n == costs.length 2 <= costs.length <= 100 costs.length is even. 1 <= aCosti, bCosti <= 1000 https://leetcode.com/problems/two-city-scheduling """ from typing import List """""" class Solution: def twoCitySchedCost(self, costs: List[List[int]]): total_cost = 0 # sort be how much we save by going to city A costs.sort(key=lambda x: x[1]-x[0], reverse=True) for idx, cost_arr in enumerate(costs): if idx < len(costs)/2: # consider A: # the 1st half are best suited to traveling to A, saves us the most money total_cost += cost_arr[0] else: # consoder B total_cost += cost_arr[1] return total_cost -
Task Assignment
""" Task Assignment: You're given an integer k representing a number of workers and an array of positive integers representing durations of tasks that must be completed by the workers. Specifically, each worker must complete two unique tasks and can only work on one task at a time. The number of tasks will always be equal to 2k such that each worker always has exactly two tasks to complete. All tasks are independent of one another and can be completed in any order. Workers will complete their assigned tasks in parallel, and the time taken to complete all tasks will be equal to the time taken to complete the longest pair of tasks. Write a function that returns the optimal assignment of tasks to each worker such that the tasks are completed as fast as possible. Your function should return a list of pairs, where each pair stores the indices of the tasks that should be completed by one worker. The pairs should be in the following format: [task1, task2], where the order of task1 and task2 doesn't matter. Your function can return the pairs in any order. If multiple optimal assignments exist, any correct answer will be accepted. Note: you'll always be given at least one worker (i.e., k will always be greater than 0). https://www.algoexpert.io/questions/Task%20Assignment """ def taskAssignment(k, tasks): output = [] # add indices to tasks for idx in range(len(tasks)): tasks[idx] = [tasks[idx], idx] # sort by task duration tasks.sort(key=lambda x: x[0]) # add first half to output for idx in range(k): output.append([tasks[idx][1]]) # add second half: from largest task to smallest pos = 0 for idx in reversed(range(k, len(tasks))): output[pos] = output[pos] + [tasks[idx][1]] pos += 1 return output def taskAssignment1(k, tasks): output = [] # add indices to tasks for idx in range(len(tasks)): tasks[idx] = [tasks[idx], idx] # sort by task duration tasks.sort(key=lambda x: x[0]) tasks_length = len(tasks) # add largest and smallest task for idx in range(k): first_task = tasks[idx][1] second_task = tasks[(tasks_length - 1) - idx][1] output.append([first_task, second_task]) return output -
Valid Starting City
""" Valid Starting City: Imagine you have a set of cities that are laid out in a circle, connected by a circular road that runs clockwise. Each city has a gas station that provides gallons of fuel, and each city is some distance away from the next city. You have a car that can drive some number of miles per gallon of fuel, and your goal is to pick a starting city such that you can fill up your car with that city's fuel, drive to the next city, refill up your car with that city's fuel, drive to the next city, and so on and so forth until you return back to the starting city with 0 or more gallons of fuel left. This city is called a valid starting city, and it's guaranteed that there will always be exactly one valid starting city. For the actual problem, you'll be given an array of distances such that city i is distances[i] away from city i + 1. Since the cities are connected via a circular road, the last city is connected to the first city. In other words, the last distance in the distances array is equal to the distance from the last city to the first city. You'll also be given an array of fuel available at each city, where fuel[i] is equal to the fuel available at city i. The total amount of fuel available (from all cities combined) is exactly enough to travel to all cities. Your fuel tank always starts out empty, and you're given a positive integer value for the number of miles that your car can travel per gallon of fuel (miles per gallon, or MPG). You can assume that you will always be given at least two cities. Write a function that returns the index of the valid starting city. Sample Input distances = [5, 25, 15, 10, 15] fuel = [1, 2, 1, 0, 3] mpg = 10 Sample Output 4 https://www.algoexpert.io/questions/Valid%20Starting%20City """ def validStartingCity0(distances, fuel, mpg): start = 0 end = 0 miles_remaining = 0 visited = 1 while visited < len(distances): miles_if_move = miles_remaining - distances[end] + (fuel[end]*mpg) # is a valid move if miles_if_move >= 0: miles_remaining = miles_if_move visited += 1 end = movePointerForward(distances, end) # not a valid move -> move start forward else: if end == start: end += 1 # move to where start will be miles_remaining = 0 visited = 1 else: miles_remaining = miles_remaining + \ distances[start] - (fuel[start]*mpg) visited -= 1 start += 1 return start def movePointerForward(array, pointer): if pointer + 1 < len(array): return pointer + 1 return 0 """ [0,1,2,3] start = 0 # if we reach a point where we will have < 0 fuel when we move forward, # we pause and start += 1 and remove the effects of the starting point: # remove fuel added and add fuel spent """ """ ------------------------------------------------------------------------------------------------------------------------------------ start at city 0 and calculate the lowest amount of fuel you will ever have: - this will be the valid starting city (it is the furthest by mpg) - whatever city we start from, we will always reach there with a negative amount of fuel 10 mile = 1 gal (mpg) 5 miles = ? gal -> 5/10 """ class StartingCity: def __init__(self, index, fuel_remaining): self.index = index self.fuel_remaining = fuel_remaining def validStartingCity(distances, fuel, mpg): starting_city = StartingCity(-1, float('inf')) current_fuel = 0 for i in range(len(fuel)): # # the city with the lowest amount of fuel you will ever have is the valid starting city if current_fuel < starting_city.fuel_remaining: starting_city.index = i starting_city.fuel_remaining = current_fuel # # add fuel current_fuel += fuel[i] # # travel to next city fuel_consumed = distances[i]/mpg # 1 - 1.2 = -0.19999999999999996 # 0.1 + 0.2 = 0.30000000000000004 current_fuel = round(current_fuel - fuel_consumed, 10) return starting_city.index -
Two City Scheduling *
Two City Scheduling - LeetCode
class Solution: def twoCitySchedCost(self, costs: List[List[int]]): total_cost = 0 # sort be how much we save by going to city A costs.sort(key=lambda x: x[1]-x[0], reverse=True) for idx, cost_arr in enumerate(costs): if idx < len(costs)/2: # consider A: # the 1st half are best suited to traveling to A, saves us the most money total_cost += cost_arr[0] else: # consoder B total_cost += cost_arr[1] return total_cost -
Partition Labels

""" 763. Partition Labels You are given a string s. We want to partition the string into as many parts as possible so that each letter appears in at most one part. Return a list of integers representing the size of these parts. Example 1: Input: s = "ababcbacadefegdehijhklij" Output: [9,7,8] Explanation: The partition is "ababcbaca", "defegde", "hijhklij". This is a partition so that each letter appears in at most one part. A partition like "ababcbacadefegde", "hijhklij" is incorrect, because it splits s into less parts. Example 2: Input: s = "eccbbbbdec" Output: [10] https://leetcode.com/problems/partition-labels/ Prerequisite: https://leetcode.com/problems/merge-intervals """ """ Solution: find intervals - merge intervals Let's try to repeatedly choose the smallest left-justified partition. Consider the first label, say it's 'a'. The first partition must include it, and also the last occurrence of 'a'. However, between those two occurrences of 'a', there could be other labels that make the minimum size of this partition bigger. For example, in "abccaddbeffe", the minimum first partition is "abccaddb". This gives us the idea for the algorithm: For each letter encountered, process the last occurrence of that letter, extending the current partition [anchor, j] appropriately. """ # O(n) time | O(1) space class Solution: def partitionLabels(self, s: str): """ Divide string into intervals/partitions and merge overlapping intervals. """ result = [] # mark the last index of each character last_pos = {} for idx, char in enumerate(s): last_pos[char] = idx # divide the characters into partitions partition_start = 0 partition_end = 0 for idx, char in enumerate(s): # if outside the current partition, save the prev partition length & start a new one if idx > partition_end: result.append(partition_end-partition_start+1) # start new partition partition_end = idx partition_start = idx # update the end of the partition partition_end = max(last_pos[char], partition_end) # once we find a pertition that ends at the last character, save it if partition_end == len(s)-1: # save the last partition result.append(partition_end-partition_start+1) return result return result -
Jump Game
[Java] A general greedy solution to process similar problems - LeetCode Discuss
""" Jump Game You are given an integer array nums. You are initially positioned at the array's first index, and each element in the array represents your maximum jump length at that position. Return true if you can reach the last index, or false otherwise. Example 1: Input: nums = [2,3,1,1,4] Output: true Explanation: Jump 1 step from index 0 to 1, then 3 steps to the last index. Example 2: Input: nums = [3,2,1,0,4] Output: false Explanation: You will always arrive at index 3 no matter what. Its maximum jump length is 0, which makes it impossible to reach the last index. https://leetcode.com/problems/jump-game """ """ Top down: try every single jump pattern that takes us from the first position to the last. We start from the first position and jump to every index that is reachable. We repeat the process until last index is reached. When stuck, backtrack. One quick optimization we can do for the code above is to check the nextPosition from right to left. (jump furthest) The theoretical worst case performance is the same, but in practice, for silly examples, the code might run faster. Intuitively, this means we always try to make the biggest jump such that we reach the end as soon as possible Top-down Dynamic Programming can be thought of as optimized backtracking. It relies on the observation that once we determine that a certain index is good / bad, this result will never change. This means that we can store the result and not need to recompute it every time. Therefore, for each position in the array, we remember whether the index is good or bad. O(n^2) time | O(2n) == O(n) space """ class SolutionMEMO: def canJump(self, nums): return self.jump_helper(nums, [None]*len(nums), 0) def jump_helper(self, nums, cache, idx): if idx >= len(nums)-1: return True if cache[idx] is not None: return cache[idx] for i in reversed(range(idx+1, idx+nums[idx]+1)): if self.jump_helper(nums, cache, i): cache[idx] = True return cache[idx] cache[idx] = False return cache[idx] """ Bottom up: Top-down to bottom-up conversion is done by eliminating recursion. In practice, this achieves better performance as we no longer have the method stack overhead and might even benefit from some caching. More importantly, this step opens up possibilities for future optimization. The recursion is usually eliminated by trying to reverse the order of the steps from the top-down approach. The observation to make here is that we only ever jump to the right. This means that if we start from the right of the array, every time we will query a position to our right, that position has already be determined as being GOOD or BAD. This means we don't need to recurse anymore, as we will always hit the memo/cache table. O(n^2) time | O(n) space ------------------------------------------------------------------------------------------------------------------------- Greedy Once we have our code in the bottom-up state, we can make one final, important observation. From a given position, when we try to see if we can jump to a GOOD position, we only ever use one - the first one. In other words, the left-most one. If we keep track of this left-most GOOD position as a separate variable, we can avoid searching for it in the array. Not only that, but we can stop using the array altogether. O(n) time | O(1) space """ class SolutionBU: def canJump(self, nums): dp = [None]*len(nums) dp[-1] = True for idx in reversed(range(len(nums)-1)): for idx_2 in range(idx+1, idx+nums[idx]+1): if dp[idx_2] == True: dp[idx] = True break return dp[0] class Solution: def canJump(self, nums): last_valid = len(nums)-1 for idx in reversed(range(len(nums)-1)): if idx+nums[idx] >= last_valid: last_valid = idx return last_valid == 0 -
Jump Game II
Jump Game II - Greedy - Leetcode 45 - Python
[Java] A general greedy solution to process similar problems - LeetCode Discuss
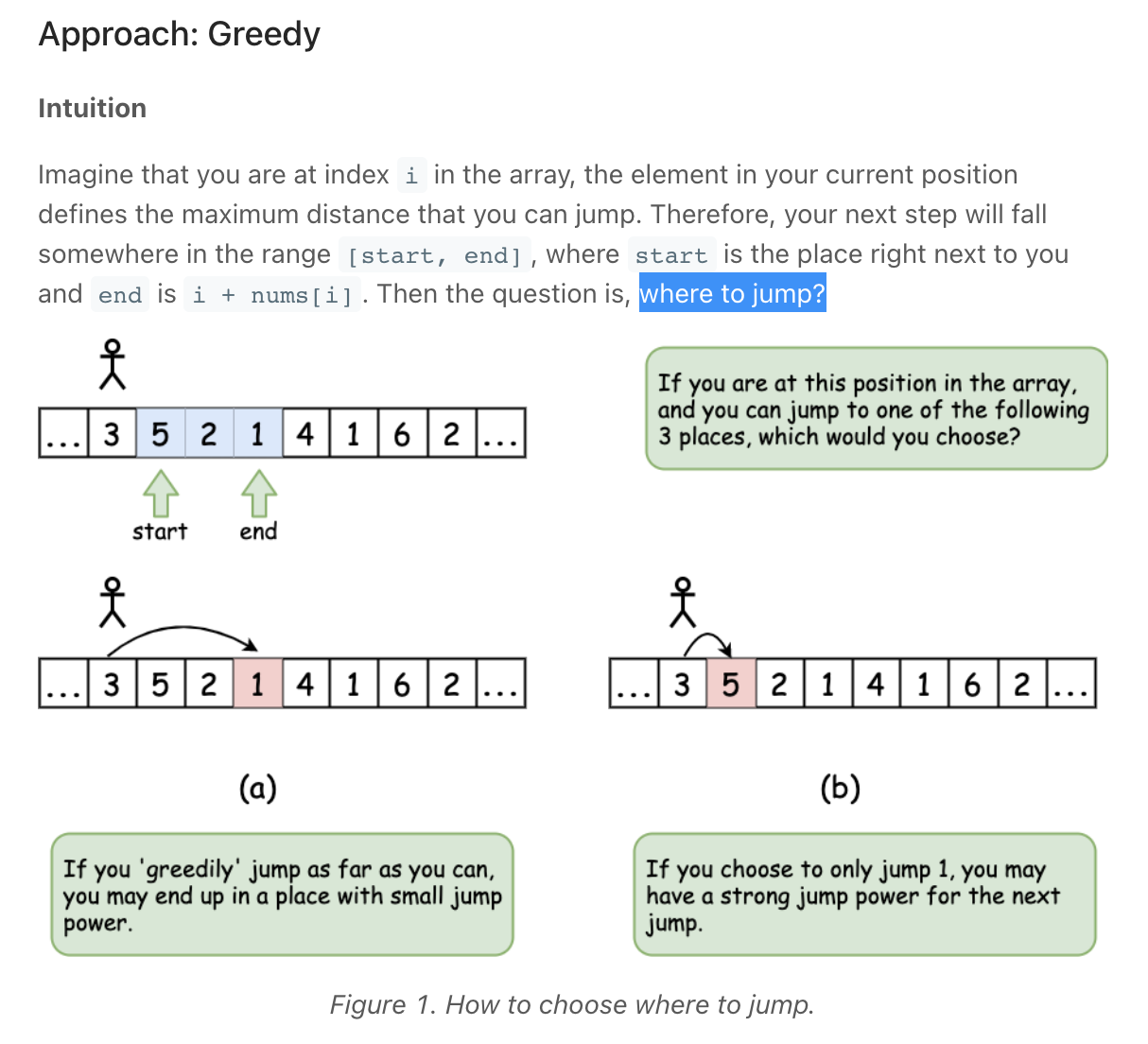
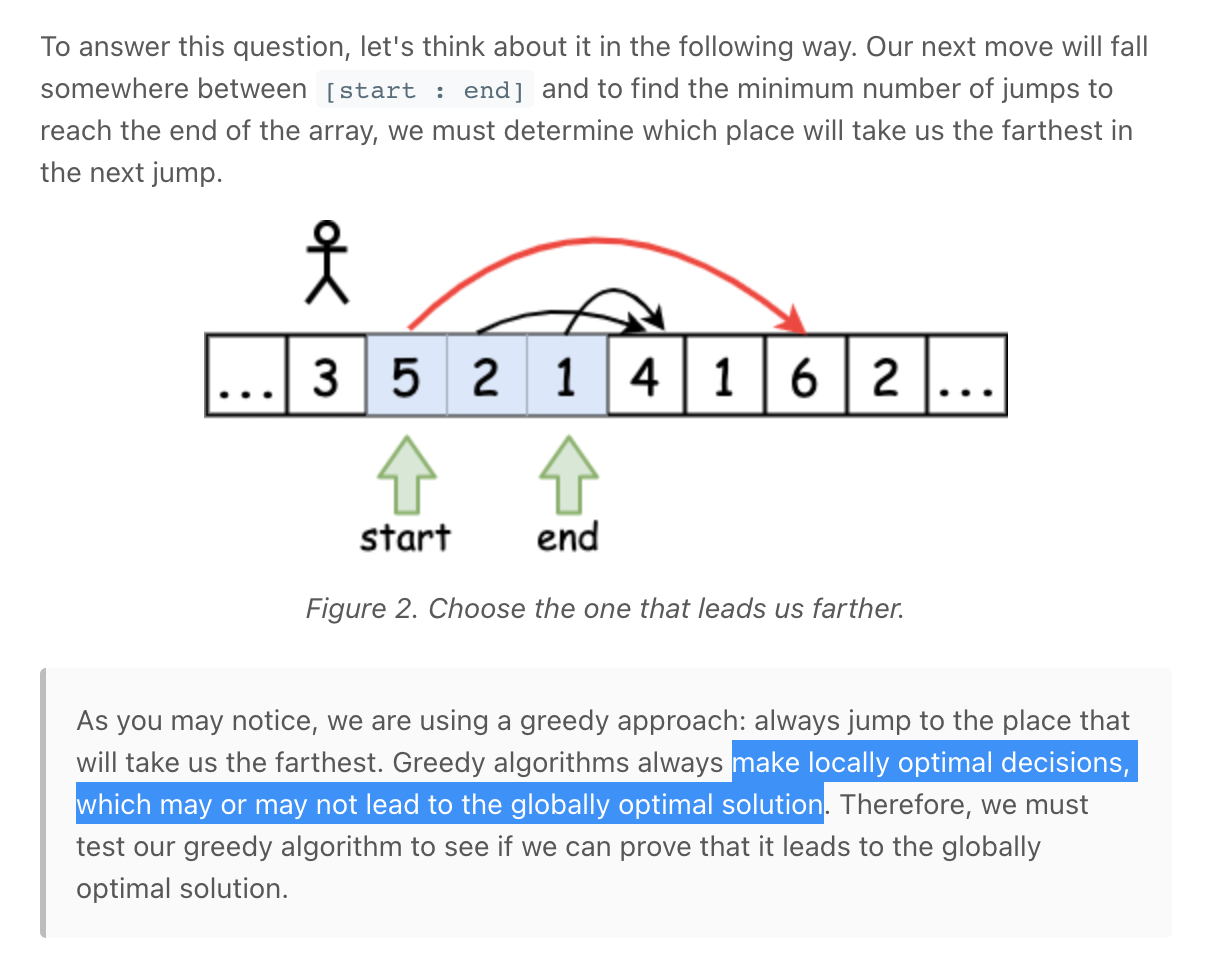
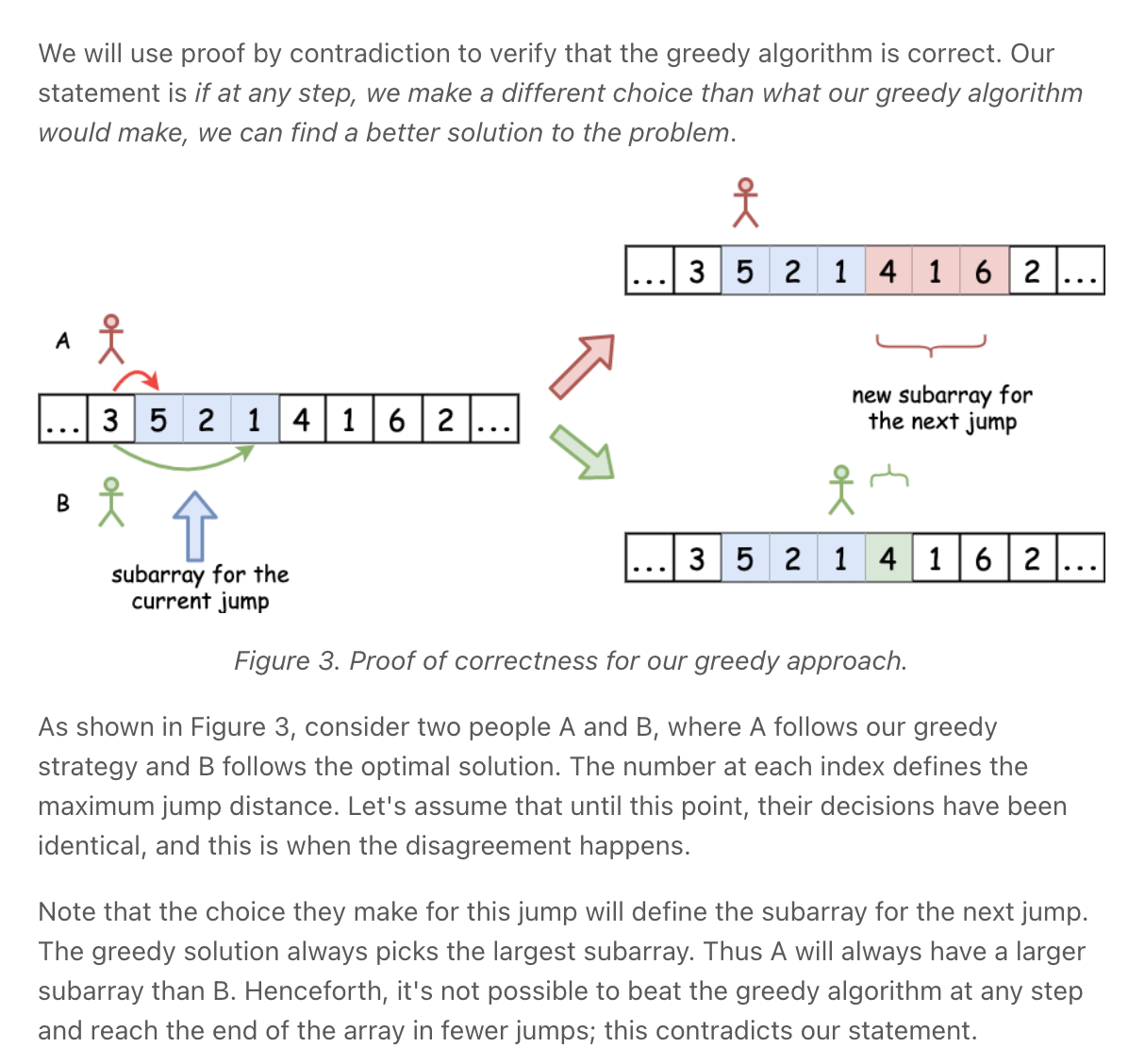
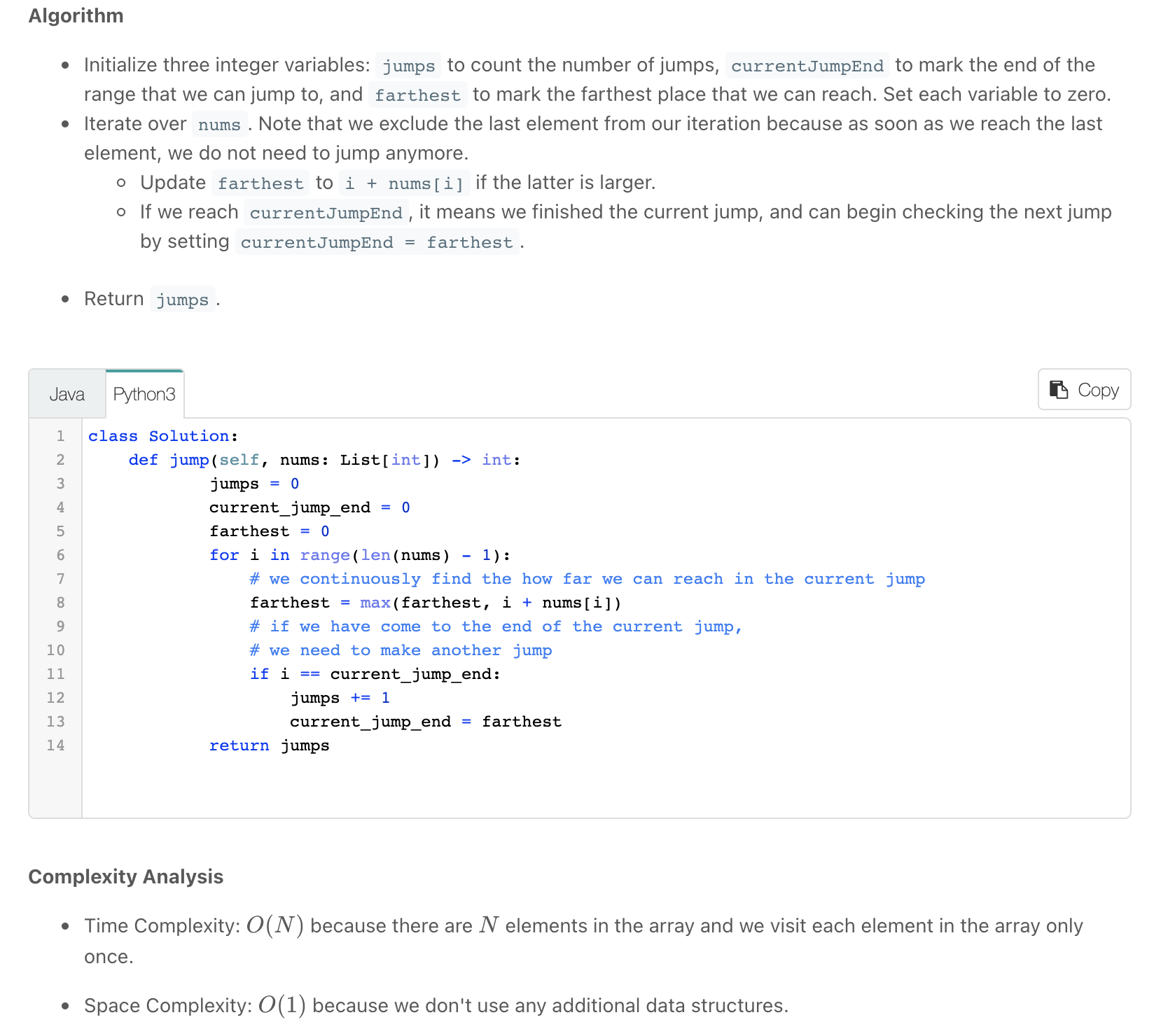
""" 45. Jump Game II Given an array of non-negative integers nums, you are initially positioned at the first index of the array. Each element in the array represents your maximum jump length at that position. Your goal is to reach the last index in the minimum number of jumps. You can assume that you can always reach the last index. Example 1: Input: nums = [2,3,1,1,4] Output: 2 Explanation: The minimum number of jumps to reach the last index is 2. Jump 1 step from index 0 to 1, then 3 steps to the last index. Example 2: Input: nums = [2,3,0,1,4] Output: 2 https://leetcode.com/problems/jump-game-ii Prerequisites: - https://leetcode.com/problems/jump-game """ """ DP Memoization """ class SolutionMEMO: def jump(self, nums): cache = [None]*len(nums) cache[-1] = 0 self.jump_helper(nums, 0, cache) return cache[0] def jump_helper(self, nums, idx, cache): if idx >= len(nums): return 0 if cache[idx] is not None: return cache[idx] result = float('inf') for i in range(idx+1, idx+nums[idx]+1): result = min(result, self.jump_helper(nums, i, cache)) result += 1 # add current jump cache[idx] = result return cache[idx] """ DP Bottom up """ class Solution: def jump(self, nums): cache = [None]*len(nums) cache[-1] = 0 for idx in reversed(range(len(nums)-1)): if nums[idx] != 0: cache[idx] = min(cache[idx+1:idx+nums[idx]+1]) + 1 else: cache[idx] = float('inf') return cache[0] """ Greedy https://www.notion.so/paulonteri/Greedy-Algorithms-b9b0a6dd66c94e7db2cbbd9f2d6b50af#255fab0c8c0242df8f7e53d9ec2a83b8 https://leetcode.com/problems/minimum-number-of-taps-to-open-to-water-a-garden/discuss/506853/Java-A-general-greedy-solution-to-process-similar-problems """ class Solution_: def jump(self, nums): result = 0 current_jump_end = 0 farthest_possible = 0 # furthest jump we made/could have made for i in range(len(nums) - 1): # we continuously find the how far we can reach in the current jump # record the futhest point accessible in our current jump farthest_possible = max(farthest_possible, i + nums[i]) # if we have come to the end of the current jump, we need to make another jump if i == current_jump_end: result += 1 # move to the furthest possible point current_jump_end = farthest_possible return result class Solution: def jump(self, nums): result = 0 i = 0 farthest_possible = 0 # furthest jump we made/could have made while i < len(nums) - 1: # # create new jump & move to the furthest possible point farthest_possible = max(farthest_possible, i + nums[i]) # new jump - jump furthest result += 1 current_jump_end = farthest_possible # next i += 1 # # move to end of current jump while i < len(nums) - 1 and i < current_jump_end: # we continuously find the how far we can reach in the current jump # record the futhest point accessible in our current jump farthest_possible = max(farthest_possible, i + nums[i]) i += 1 return result -
Video Stitching
""" Video Stitching You are given a series of video clips from a sporting event that lasted time seconds. These video clips can be overlapping with each other and have varying lengths. Each video clip is described by an array clips where clips[i] = [starti, endi] indicates that the ith clip started at starti and ended at endi. We can cut these clips into segments freely. For example, a clip [0, 7] can be cut into segments [0, 1] + [1, 3] + [3, 7]. Return the minimum number of clips needed so that we can cut the clips into segments that cover the entire sporting event [0, time]. If the task is impossible, return -1. Example 1: Input: clips = [[0,2],[4,6],[8,10],[1,9],[1,5],[5,9]], time = 10 Output: 3 Explanation: We take the clips [0,2], [8,10], [1,9]; a total of 3 clips. Then, we can reconstruct the sporting event as follows: We cut [1,9] into segments [1,2] + [2,8] + [8,9]. Now we have segments [0,2] + [2,8] + [8,10] which cover the sporting event [0, 10]. Example 2: Input: clips = [[0,1],[1,2]], time = 5 Output: -1 Explanation: We can't cover [0,5] with only [0,1] and [1,2]. Example 3: Input: clips = [[0,1],[6,8],[0,2],[5,6],[0,4],[0,3],[6,7],[1,3],[4,7],[1,4],[2,5],[2,6],[3,4],[4,5],[5,7],[6,9]], time = 9 Output: 3 Explanation: We can take clips [0,4], [4,7], and [6,9]. Example 4: Input: clips = [[0,4],[2,8]], time = 5 Output: 2 Explanation: Notice you can have extra video after the event ends. https://leetcode.com/problems/video-stitching """ class SolutionDP: def videoStitching(self, clips, time): clips.sort() dp = [float('inf')] * (time+1) dp[0] = 0 for left, right in clips: # ignore ranges that will be greater than the time if left > time: continue # reach every point possible for idx in range(left, min(right, time)+1): # steps to reach idx = min((prevoiusly recorded), (steps to reach left + the one step to idx)) dp[idx] = min(dp[idx], dp[left]+1) if dp[-1] == float('inf'): return -1 return dp[-1] class Solution: def videoStitching(self, clips, T): result = 0 # # Save the right-most possible valid jump for each left most index max_jumps = [-1]*(T+1) for left, right in clips: if left > T: continue if right-left <= 0: continue max_jumps[left] = max(max_jumps[left], min(right, T)) # Jump Game II: it is then a jump game idx = 0 current_jump_end = 0 furthest_jump = 0 # furthest jump we made/could have made while idx < T: # # create a new jump furthest_jump = max(max_jumps[idx], furthest_jump) # check if we can make a valid jump if max_jumps[idx] == -1 and furthest_jump <= idx: # if we cannot make a jump and we need to make a jump to increase the furthest_jump return -1 # make jump - move end to the furthest possible point result += 1 current_jump_end = furthest_jump idx += 1 # # reach end of jump while idx <= T and idx < current_jump_end: # we continuously find the how far we can reach in the current jump # record the futhest point accessible in our current jump furthest_jump = max(max_jumps[idx], furthest_jump) idx += 1 return result -
Minimum Number of Taps to Open to Water a Garden
""" Minimum Number of Taps to Open to Water a Garden There is a one-dimensional garden on the x-axis. The garden starts at the point 0 and ends at the point n. (i.e The length of the garden is n). There are n + 1 taps located at points [0, 1, ..., n] in the garden. Given an integer n and an integer array ranges of length n + 1 where ranges[i] (0-indexed) means the i-th tap can water the area [i - ranges[i], i + ranges[i]] if it was open. Return the minimum number of taps that should be open to water the whole garden, If the garden cannot be watered return -1. Example 1: Input: n = 5, ranges = [3,4,1,1,0,0] Output: 1 Explanation: The tap at point 0 can cover the interval [-3,3] The tap at point 1 can cover the interval [-3,5] The tap at point 2 can cover the interval [1,3] The tap at point 3 can cover the interval [2,4] The tap at point 4 can cover the interval [4,4] The tap at point 5 can cover the interval [5,5] Opening Only the second tap will water the whole garden [0,5] Example 2: Input: n = 3, ranges = [0,0,0,0] Output: -1 Explanation: Even if you activate all the four taps you cannot water the whole garden. Example 3: Input: n = 7, ranges = [1,2,1,0,2,1,0,1] Output: 3 Example 4: Input: n = 8, ranges = [4,0,0,0,0,0,0,0,4] Output: 2 Example 5: Input: n = 8, ranges = [4,0,0,0,4,0,0,0,4] Output: 1 https://leetcode.com/problems/minimum-number-of-taps-to-open-to-water-a-garden """ """ Prerequisites: - https://leetcode.com/problems/jump-game - https://leetcode.com/problems/jump-game-ii - https://leetcode.com/problems/video-stitching https://www.notion.so/paulonteri/Greedy-Algorithms-b9b0a6dd66c94e7db2cbbd9f2d6b50af#d7578cbb76c7423d9c819179fc749be5 https://leetcode.com/problems/minimum-number-of-taps-to-open-to-water-a-garden/discuss/506853/Java-A-general-greedy-solution-to-process-similar-problems """ class Solution_: def minTaps(self, n, ranges): taps = 0 # # Save the right-most possible jump for each left most index jumps = [-1]*(n) for idx, num in enumerate(ranges): if num == 0: continue left_most = max(0, idx-num) right_most = min(n, idx+num) jumps[left_most] = max(jumps[left_most], right_most) # # Jump Game II current_jump_end = 0 furthest_can_reach = -1 # furthest jump we made/could have made for idx, right_most in enumerate(jumps): # we continuously find the how far we can reach in the current jump # record the futhest point accessible in our current jump furthest_can_reach = max(right_most, furthest_can_reach) # if we have come to the end of the current jump, we need to make another jump # the new jump should start immediately after the old jump if idx == current_jump_end: # if we cannot make a jump and we need to make a jump to increase the furthest_can_reach if right_most == -1 and furthest_can_reach <= idx: return -1 # move end to the furthest possible point current_jump_end = furthest_can_reach taps += 1 if furthest_can_reach == n: return taps return -1 class Solution: def minTaps(self, n, ranges): taps = 0 # # Save the right-most possible jump for each left most index jumps = [-1]*(n) for idx, num in enumerate(ranges): if num == 0: continue left_most = max(0, idx-num) right_most = min(n, idx+num) jumps[left_most] = max(jumps[left_most], right_most) # # Jump Game II idx = 0 furthest_can_reach = -1 # furthest jump we made/could have made while idx < n: # # create a new jump furthest_can_reach = max(jumps[idx], furthest_can_reach) # check if we can make a valid jump if jumps[idx] == -1 and furthest_can_reach <= idx: # if we cannot make a jump and we need to make a jump to increase the furthest_can_reach return -1 # make jump - move end to the furthest possible point taps += 1 current_jump_end = furthest_can_reach idx += 1 # # reach end of jump while idx < n and idx < current_jump_end: # we continuously find the how far we can reach in the current jump # record the futhest point accessible in our current jump furthest_can_reach = max(jumps[idx], furthest_can_reach) idx += 1 if furthest_can_reach == n: return taps return -1
Honourable mentions
- 0/1 Knapsack
Find the original version of this page (with additional content) on Notion here.
Created: December 13, 2021 16:05:48