Bit Manipulation
Introduction
Bit Manipulation - InterviewBit
Basics of Bit Manipulation Tutorials & Notes | Basic Programming | HackerEarth
Binary Computation and Bitwise Operators
Binary | Tech Interview Handbook
📌 TIPS | HACKS WHICH YOU CAN'T IGNORE AS A CODER ✨🎩 - LeetCode Discuss
Bitwise Operators in Python - Real Python
XOR is a logical bitwise operator that returns 0 (false) if both bits are the same and returns 1 (true) otherwise. In other words, it only returns 1 if exactly one bit is set to 1 out of the two bits in comparison.
Conversion to binary and back
>>> bin(5)
'0b101'
>>> int('101',2)
5
Important properties of XOR to remember
Following are some important properties of XOR to remember:
- Taking XOR of a number with itself returns 0, e.g.,
1 ^ 1 = 029 ^ 29 = 0
- Taking XOR of a number with 0 returns the same number, e.g.,
1 ^ 0 = 131 ^ 0 = 31
- XOR is Associative & Commutative, which means:
(a ^ b) ^ c = a ^ (b ^ c)a ^ b = b ^ a
Check if right most bit is a one
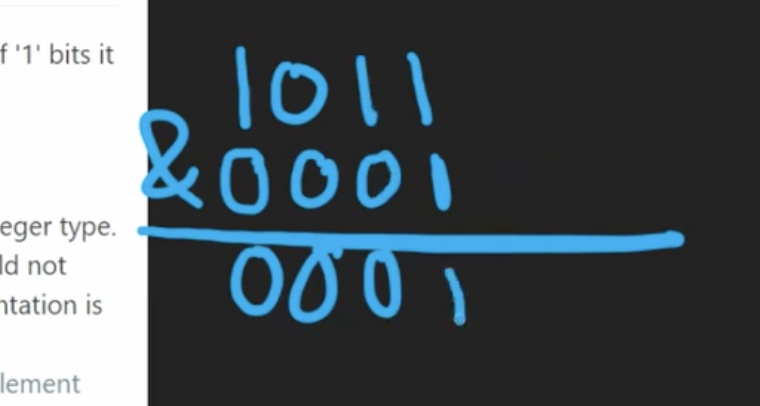
Remember that a single one can be assumed to have zeros till the left end
Screen Recording 2021-11-11 at 15.40.32.mov
Examples:
-
Number of 1 Bits
Number of 1 Bits
""" 191. Number of 1 Bits Write a function that takes an unsigned integer and returns the number of '1' bits it has (also known as the Hamming weight). Note: Note that in some languages, such as Java & Python, there is no unsigned integer type. In this case, the input will be given as a signed integer type. It should not affect your implementation, as the integer's internal binary representation is the same, whether it is signed or unsigned. In Java, the compiler represents the signed integers using 2's complement notation. Therefore, in Example 3, the input represents the signed integer. -3. Example 1: Input: n = 00000000000000000000000000001011 Output: 3 Explanation: The input binary string 00000000000000000000000000001011 has a total of three '1' bits. Example 2: Input: n = 00000000000000000000000010000000 Output: 1 Explanation: The input binary string 00000000000000000000000010000000 has a total of one '1' bit. Example 3: Input: n = 11111111111111111111111111111101 Output: 31 Explanation: The input binary string 11111111111111111111111111111101 has a total of thirty one '1' bits. https://leetcode.com/problems/number-of-1-bits """ from collections import Counter """ https://youtu.be/5Km3utixwZs """ # O(1) time | O(1) space # It will run a maximum of 32 times, since the input is 32 bits long. class Solution: def hammingWeight(self, n: int): count = 0 while n: # check if right most number is 1 by running an & operation with 1 if n & 1 == 1: count += 1 # logical right shift to remove the right-most 1 n = n >> 1 return count class Solution_: def hammingWeight(self, n: int): # convert to binary string and count the number of 1's return Counter(bin(n))['1'] -
Counting Bits
Counting Bits
""" 338. Counting Bits Given an integer n, return an array ans of length n + 1 such that for each i (0 <= i <= n), ans[i] is the number of 1's in the binary representation of i. Example 1: Input: n = 2 Output: [0,1,1] Explanation: 0 --> 0 1 --> 1 2 --> 10 Example 2: Input: n = 5 Output: [0,1,1,2,1,2] Explanation: 0 --> 0 1 --> 1 2 --> 10 3 --> 11 4 --> 100 5 --> 101 Constraints: 0 <= n <= 105 https://leetcode.com/problems/counting-bits Prerequisites: - https://leetcode.com/problems/number-of-1-bits """ class Solution: def countBits(self, n: int): bits = [None] * (n+1) bits[0] = 0 for num in range(1, n+1): bits[num] = self.get_bits(bits, num) return bits def get_bits(self, bits, num): count = 0 # # check if has 1 at right end if num & 1: count += 1 # #right shift: # remove the number at the right end num = num >> 1 # # get the number of ones remaining after shifting # right shift == floor dividing by two, so will be smaller & have been precalculated return count + bits[num]
Numbers used in examples in binary form
>>> bin(2)
'0b10'
>>> bin(3)
'0b11'
>>> bin(4)
'0b100'
>>> bin(5)
'0b101'
>>> 2 & 1
Examples
>>> 2 & 1 # 10 & 01
0
>>> 3 & 1
1
>>> 4 & 1
0
>>> 5 & 1
1
Bit shifting
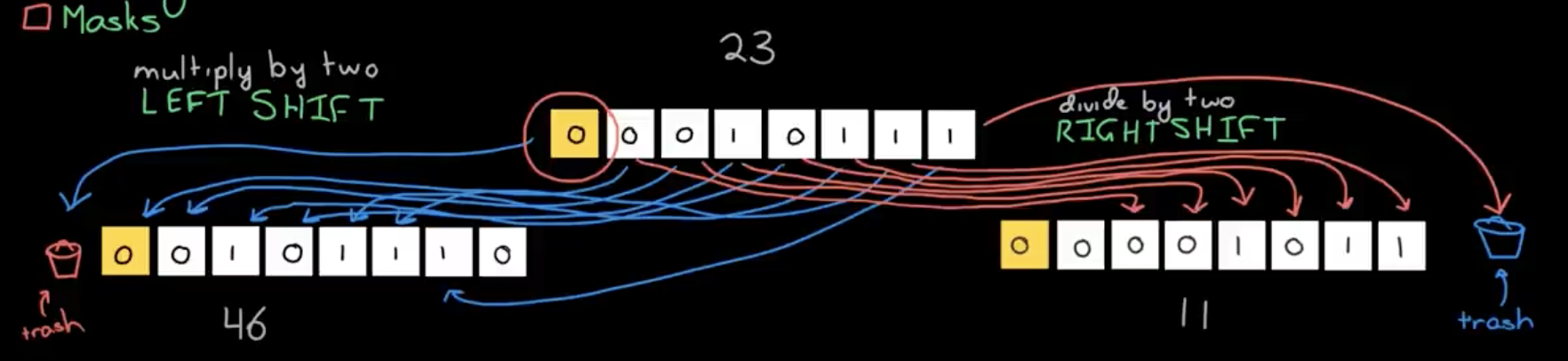
A bit shift moves each digit in a number's binary representation left or right. There are three main types of shifts:
Left Shifts
When shifting left, the most-significant bit is lost, and a 0 bit is inserted on the other end.
The left shift operator is usually written as "<<". **0010 << 1 → 0100**
0010 << 1 → 0100
0010 << 2 → 1000
A single left shift multiplies a binary number by 2:
0010 << 1 → 0100
0010 is 2
0100 is 4
Logical Right Shifts
This does not exist in python!
How to get the logical right binary shift in python
When shifting right with a logical right shift, the least-significant bit is lost and a 0 is inserted on the other end.
1011 >>> 1 → 0101
1011 >>> 3 → 0001
For positive numbers, a single logical right shift divides a number by 2, throwing out any remainders.
0101 >>> 1 → 0010
0101 is 5
0010 is 2
Arithmetic Right Shifts
Examples
-
Number of 1 Bits
Number of 1 Bits
""" 191. Number of 1 Bits Write a function that takes an unsigned integer and returns the number of '1' bits it has (also known as the Hamming weight). Note: Note that in some languages, such as Java & Python, there is no unsigned integer type. In this case, the input will be given as a signed integer type. It should not affect your implementation, as the integer's internal binary representation is the same, whether it is signed or unsigned. In Java, the compiler represents the signed integers using 2's complement notation. Therefore, in Example 3, the input represents the signed integer. -3. Example 1: Input: n = 00000000000000000000000000001011 Output: 3 Explanation: The input binary string 00000000000000000000000000001011 has a total of three '1' bits. Example 2: Input: n = 00000000000000000000000010000000 Output: 1 Explanation: The input binary string 00000000000000000000000010000000 has a total of one '1' bit. Example 3: Input: n = 11111111111111111111111111111101 Output: 31 Explanation: The input binary string 11111111111111111111111111111101 has a total of thirty one '1' bits. https://leetcode.com/problems/number-of-1-bits """ from collections import Counter """ https://youtu.be/5Km3utixwZs """ # O(1) time | O(1) space # It will run a maximum of 32 times, since the input is 32 bits long. class Solution: def hammingWeight(self, n: int): count = 0 while n: # check if right most number is 1 by running an & operation with 1 if n & 1 == 1: count += 1 # logical right shift to remove the right-most 1 n = n >> 1 return count class Solution_: def hammingWeight(self, n: int): # convert to binary string and count the number of 1's return Counter(bin(n))['1'] -
Counting Bits
Counting Bits
""" 338. Counting Bits Given an integer n, return an array ans of length n + 1 such that for each i (0 <= i <= n), ans[i] is the number of 1's in the binary representation of i. Example 1: Input: n = 2 Output: [0,1,1] Explanation: 0 --> 0 1 --> 1 2 --> 10 Example 2: Input: n = 5 Output: [0,1,1,2,1,2] Explanation: 0 --> 0 1 --> 1 2 --> 10 3 --> 11 4 --> 100 5 --> 101 Constraints: 0 <= n <= 105 https://leetcode.com/problems/counting-bits Prerequisites: - https://leetcode.com/problems/number-of-1-bits """ class Solution: def countBits(self, n: int): bits = [None] * (n+1) bits[0] = 0 for num in range(1, n+1): bits[num] = self.get_bits(bits, num) return bits def get_bits(self, bits, num): count = 0 # # check if has 1 at right end if num & 1: count += 1 # #right shift: # remove the number at the right end num = num >> 1 # # get the number of ones remaining after shifting # right shift == floor dividing by two, so will be smaller & have been precalculated return count + bits[num]
When shifting right with an arithmetic right shift, the least-significant bit is lost and the most-significant bit is copied. Languages handle arithmetic and logical right shifting in different ways. Java provides two right shift operators: >> does an arithmetic right shift and >>> does a logical right shift. **1011 >> 1 → 1101**
1011 >> 1 → 1101
1011 >> 3 → 1111
0011 >> 1 → 0001
0011 >> 2 → 0000
The first two numbers had a 1 as the most significant bit, so more 1's were inserted during the shift. The last two numbers had a 0 as the most significant bit, so the shift inserted more 0's. If a number is encoded using two's complement, then an arithmetic right shift preserves the number's sign, while a logical right shift makes the number positive.
Python uses this by default
# Arithmetic shift
1011 >> 1 → 1101
1011 is -5
1101 is -3
# Logical shift
1111 >>> 1 → 0111
1111 is -1
0111 is 7
Simple problems
todo:
Single Number
"""
Single Number:
Given a non-empty array of integers nums, every element appears twice except for one. Find that single one.
You must implement a solution with a linear runtime complexity and use only constant extra space.
https://leetcode.com/problems/single-number/
"""
"""
4^4=0 -> cancel out each other
4^0=4
4^7^6^6^4^7=0 -> contains all the pairs
4^7^6^4^7=6 -> missing pair of 6
"""
class Solution:
def singleNumber(self, nums):
res = 0
for num in nums:
res ^= num
return res
Missing Number
"""
Missing Number:
Given an array nums containing n distinct numbers in the range [0, n], return the only number in the range that is missing from the array.
Follow up: Could you implement a solution using only O(1) extra space complexity and O(n) runtime complexity?
Example 1:
Input: nums = [3,0,1]
Output: 2
Explanation: n = 3 since there are 3 numbers, so all numbers are in the range [0,3]. 2 is the missing number in the range since it does not appear in nums.
Example 2:
Input: nums = [0,1]
Output: 2
Explanation: n = 2 since there are 2 numbers, so all numbers are in the range [0,2]. 2 is the missing number in the range since it does not appear in nums.
Example 3:
Input: nums = [9,6,4,2,3,5,7,0,1]
Output: 8
Explanation: n = 9 since there are 9 numbers, so all numbers are in the range [0,9]. 8 is the missing number in the range since it does not appear in nums.
Example 4:
Input: nums = [0]
Output: 1
Explanation: n = 1 since there is 1 number, so all numbers are in the range [0,1]. 1 is the missing number in the range since it does not appear in nums.
https://leetcode.com/problems/missing-number/
"""
"""
Sum formulae:
(sum of all possible numbers) - (sum of given number) = missing_number
"""
class Solution0:
def missingNumber(self, nums):
possible = sum(range(len(nums)+1))
given = sum(nums)
return possible - given
"""
Bitwise XOR
4^4=0 -> cancel out each other
4^0=4
4^7^6^6^4^7=0 -> contains all the pairs
4^7^6^4^7=6 -> missing pair of 6
- XOR all the possible numbers with the given numbers,
the result will be the missing as it won't have a partner to cancel it out
example: [3,0,1]
- > all possible: 0^1^2^3
- > given: 3^0^1
- > 0^1^2^3 ^ 3^0^1 = 2 (it won't be canceled out)
"""
class Solution:
def missingNumber(self, nums):
res = 0
for i in range(1, len(nums)+1):
res ^= i
for num in nums:
res ^= num
return res
Number of 1 Bits
"""
191. Number of 1 Bits
Write a function that takes an unsigned integer and returns the number of '1' bits it has (also known as the Hamming weight).
Note:
Note that in some languages, such as Java & Python, there is no unsigned integer type.
In this case, the input will be given as a signed integer type. It should not affect your implementation, as the integer's internal binary representation is the same, whether it is signed or unsigned.
In Java, the compiler represents the signed integers using 2's complement notation.
Therefore, in Example 3, the input represents the signed integer. -3.
Example 1:
Input: n = 00000000000000000000000000001011
Output: 3
Explanation: The input binary string 00000000000000000000000000001011 has a total of three '1' bits.
Example 2:
Input: n = 00000000000000000000000010000000
Output: 1
Explanation: The input binary string 00000000000000000000000010000000 has a total of one '1' bit.
Example 3:
Input: n = 11111111111111111111111111111101
Output: 31
Explanation: The input binary string 11111111111111111111111111111101 has a total of thirty one '1' bits.
https://leetcode.com/problems/number-of-1-bits
"""
from collections import Counter
"""
https://youtu.be/5Km3utixwZs
"""
# O(1) time | O(1) space
# It will run a maximum of 32 times, since the input is 32 bits long.
class Solution:
def hammingWeight(self, n: int):
count = 0
while n:
# check if right most number is 1 by running an & operation with 1
if n & 1 == 1:
count += 1
# logical right shift to remove the right-most 1
n = n >> 1
return count
class Solution_:
def hammingWeight(self, n: int):
# convert to binary string and count the number of 1's
return Counter(bin(n))['1']
Counting Bits
"""
338. Counting Bits
Given an integer n, return an array ans of length n + 1 such that for each i (0 <= i <= n),
ans[i] is the number of 1's in the binary representation of i.
Example 1:
Input: n = 2
Output: [0,1,1]
Explanation:
0 --> 0
1 --> 1
2 --> 10
Example 2:
Input: n = 5
Output: [0,1,1,2,1,2]
Explanation:
0 --> 0
1 --> 1
2 --> 10
3 --> 11
4 --> 100
5 --> 101
Constraints:
0 <= n <= 105
https://leetcode.com/problems/counting-bits
Prerequisites:
- https://leetcode.com/problems/number-of-1-bits
"""
class Solution:
def countBits(self, n: int):
bits = [None] * (n+1)
bits[0] = 0
for num in range(1, n+1):
bits[num] = self.get_bits(bits, num)
return bits
def get_bits(self, bits, num):
count = 0
# # check if has 1 at right end
if num & 1:
count += 1
# #right shift:
# remove the number at the right end
num = num >> 1
# # get the number of ones remaining after shifting
# right shift == floor dividing by two, so will be smaller & have been precalculated
return count + bits[num]
Sum of Two Integers
-
https://leetcode.com/problems/sum-of-two-integers
Blind-75 - Sum of Two Integers - Leetcode 371 - Java





Find the original version of this page (with additional content) on Notion here.
Created: December 13, 2021 16:05:48