Merge Intervals
Introduction
Interval | Tech Interview Handbook
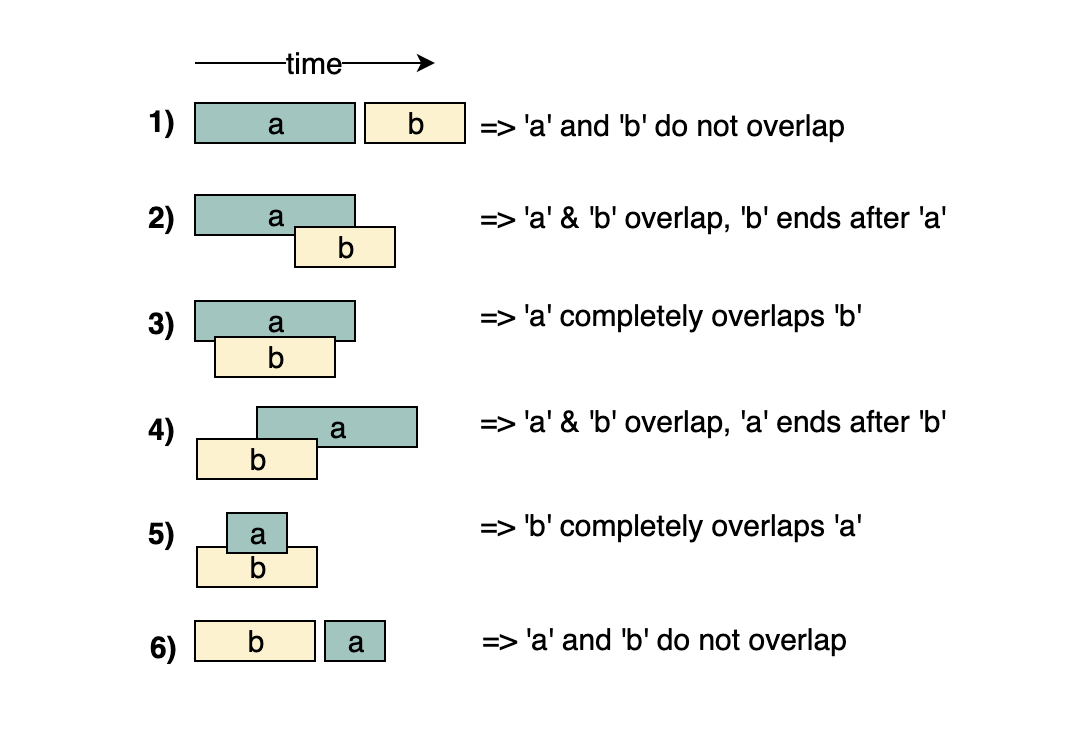
This pattern describes an efficient technique to deal with overlapping intervals. In a lot of problems involving intervals, we either need to find overlapping intervals or merge intervals if they overlap.
Given two intervals (‘a’ and ‘b’), there will be six different ways the two intervals can relate to each other:
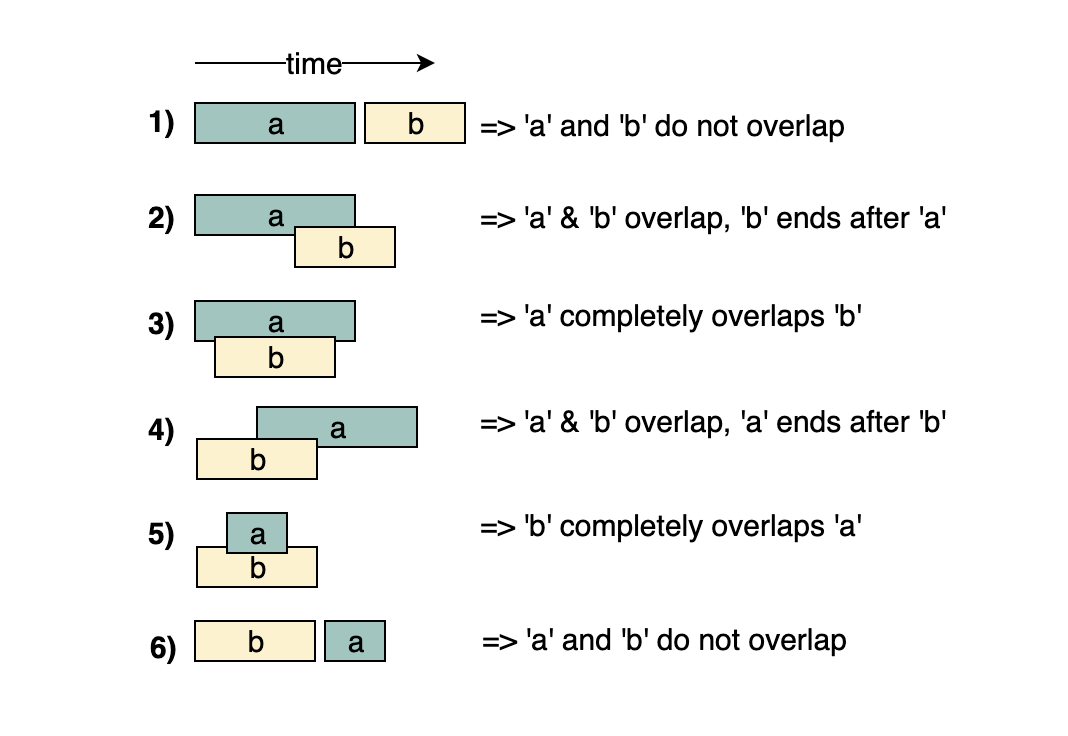
Understanding the above six cases will help us in solving all intervals related problems.
Helpers
- Draw number line
- Sort the intervals
Simple examples
Conflicting Appointments
"""
Given an array of intervals representing ‘N’ appointments, find out if a person can attend all the appointments.
Example 1:
Appointments: [[1,4], [2,5], [7,9]]
Output: false
Explanation: Since [1,4] and [2,5] overlap, a person cannot attend both of these appointments.
Example 2:
Appointments: [[6,7], [2,4], [8,12]]
Output: true
Explanation: None of the appointments overlap, therefore a person can attend all of them.
Example 3:
Appointments: [[4,5], [2,3], [3,6]]
Output: false
Explanation: Since [4,5] and [3,6] overlap, a person cannot attend both of these appointments.
"""
def can_attend_all_appointments(intervals):
intervals.sort(key=lambda x: x[0])
start, end = 0, 1
for i in range(1, len(intervals)):
if intervals[i][start] < intervals[i-1][end]:
# please note the comparison above, it is "<" and not "<="
# while merging we needed "<=" comparison, as we will be merging the two
# intervals having condition "intervals[i][start] == intervals[i - 1][end]" but
# such intervals don't represent conflicting appointments as one starts right
# after the other
return False
return True
Merge Intervals
Problem
"""
Merge Intervals:
Given a list of intervals, merge all the overlapping intervals to produce a list that has only mutually exclusive intervals.
Example 1:
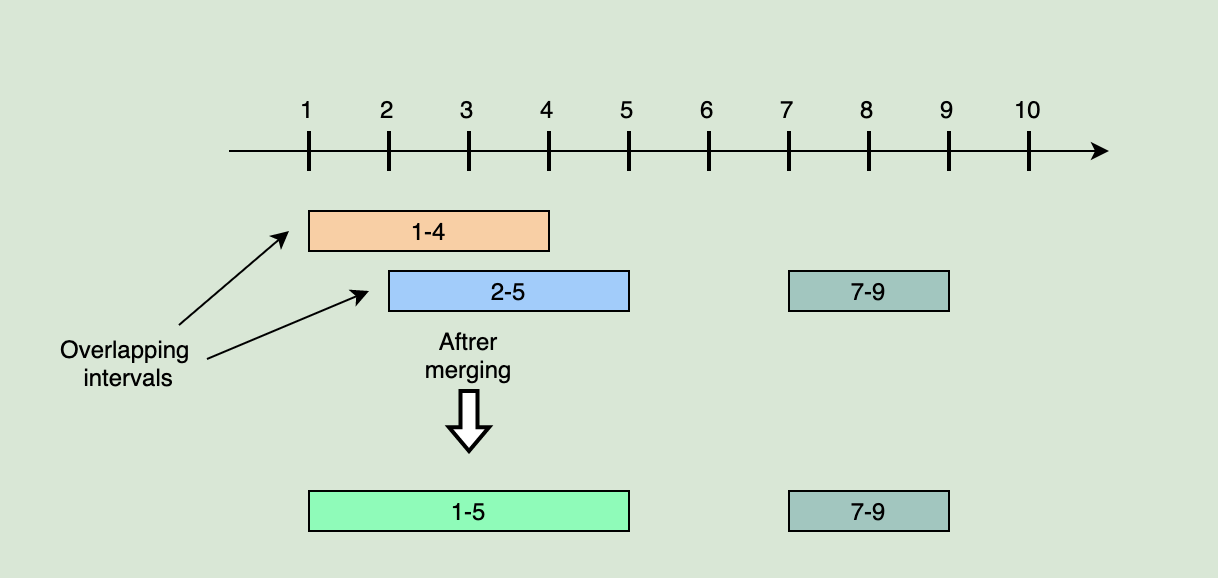
Intervals: [[1,4], [2,5], [7,9]]
Output: [[1,5], [7,9]]
Explanation: Since the first two intervals [1,4] and [2,5] overlap, we merged them into one [1,5].
Example 2:
Intervals: [[6,7], [2,4], [5,9]]
Output: [[2,4], [5,9]]
Explanation: Since the intervals [6,7] and [5,9] overlap, we merged them into one [5,9].
Example 3:
Intervals: [[1,4], [2,6], [3,5]]
Output: [[1,6]]
Explanation: Since all the given intervals overlap, we merged them into one.
"""
Solution
Let’s take the example of two intervals (‘a’ and ‘b’) such that a.start <= b.start. There are four possible scenarios:
Our goal is to merge the intervals whenever they overlap. For the above-mentioned three overlapping scenarios (2, 3, and 4), this is how we will merge them:
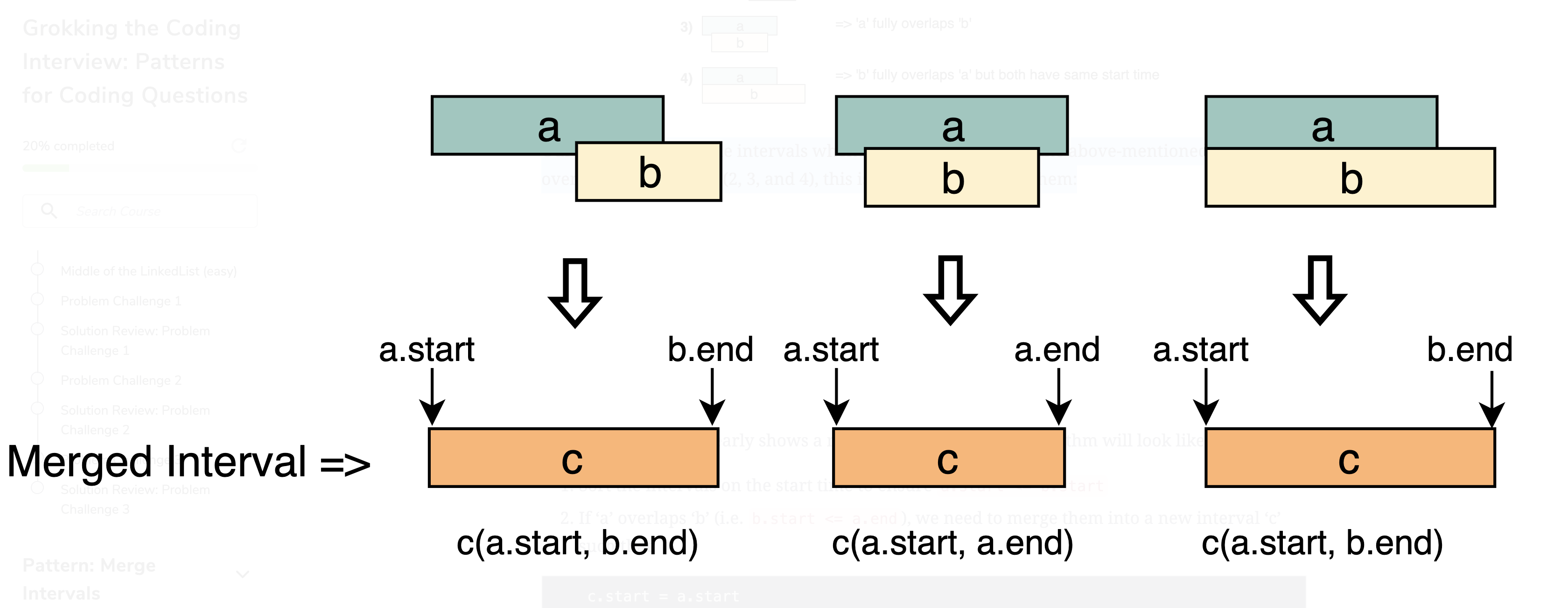
Earliest end vs latest end
The diagram above clearly shows a merging approach. Our algorithm will look like this:
- Sort the intervals on the start time to ensure
a.start <= b.start - If ‘a’ overlaps ‘b’ (i.e.
b.start <= a.end), we need to merge them into a new interval ‘c’ such that: - We will keep repeating the above two steps to merge ‘c’ with the next interval if it overlaps with ‘c’.
c.start = a.start
c.end = max(a.end, b.end)
"""
Solution:
[[6,7], [2,4], [5,9]]
sort
[[2,4], [5,9], [6,7]]
merge
[[2,4], [5,9]]
- so that its easier to know what comes b4 what, we should ***sort the intervals by their starting interval***
- we can then check if a particular interval overlaps the next ones by checking if its ***ending interval > the next's starting interval***
- the new merged interval will have the start as the first's starting interval and the ending to be the max(the next's ending interval, the first's starting interval)
"""
class Interval:
def __init__(self, start, end):
self.start = start
self.end = end
def merge(intervals):
merged = []
intervals.sort(key=lambda x: x.start)
i = 0
while i < len(intervals)-1:
start = intervals[i].start
end = intervals[i].end
while i < len(intervals)-1 and end >= intervals[i+1].start:
i += 1
end = max(end, intervals[i].end)
merged.append(Interval(start, end))
return merged
"""
Leetcode 56: Merge Intervals
Given a collection of intervals, merge all overlapping intervals.
Example:
Input:
[[8,10],[15,18], [1,3],[2,6]]
[[1,3],[2,6],[8,10],[15,18]]
[[1,3]]
[]
[[1,4],[4,5]]
[[1,4],[2,3]]
Output:
[[1,6],[8,10],[15,18]]
[[1,6],[8,10],[15,18]]
[[1,3]]
[]
[[1,5]]
[[1,4]]
https://leetcode.com/problems/merge-intervals
"""
from typing import List
"""
[[6,7], [2,4], [5,9]]
**0 1 2 3 4 5 6 7 8 9
2---4
5-------9
6-7**
- have a res arrray
- sort the intervals by their start value:
- for each interval (curr_interval):
- if it overlaps the next, merge the next into it (update the curr_intervals end)
- skip the next (move the index forward)
- repeat this until we no longer find an overlap
- add it to res
- return res
"""
class Solution:
def merge(self, intervals: List[List[int]]):
merged = []
intervals.sort(key=lambda x: x[0])
i = 0
while i < len(intervals):
start = intervals[i][0]
end = intervals[i][1]
while i < len(intervals)-1 and end >= intervals[i+1][0]:
i += 1
end = max(end, intervals[i][1])
merged.append([start, end])
i += 1
return merged
class Solution2:
def merge(self, intervals: List[List[int]]):
# sort
intervals.sort(key=lambda item: item[0])
i = 0
# no need to check the last array
while (i + 1) < len(intervals):
curr_a = intervals[i]
next_a = intervals[i+1]
# check for overlap
if curr_a[1] >= next_a[0]:
# merge
# we use max coz of such a case: [[1,4],[2,3]]
# make the last element of the first array be the furthest(largest value)
intervals[i][1] = max(curr_a[1], next_a[1])
# delete the second array
intervals.pop(i+1)
else:
i += 1
return intervals
Time & Space complexity
The time complexity of the above algorithm is O(N ∗ log N), where ‘N’ is the total number of intervals. We are iterating the intervals only once which will take O(N), in the beginning though, since we need to sort the intervals, our algorithm will take O(N ∗ log N).
The space complexity of the above algorithm will be O(N) as we need to return a list containing all the merged intervals.
Intervals Intersection *
Problem
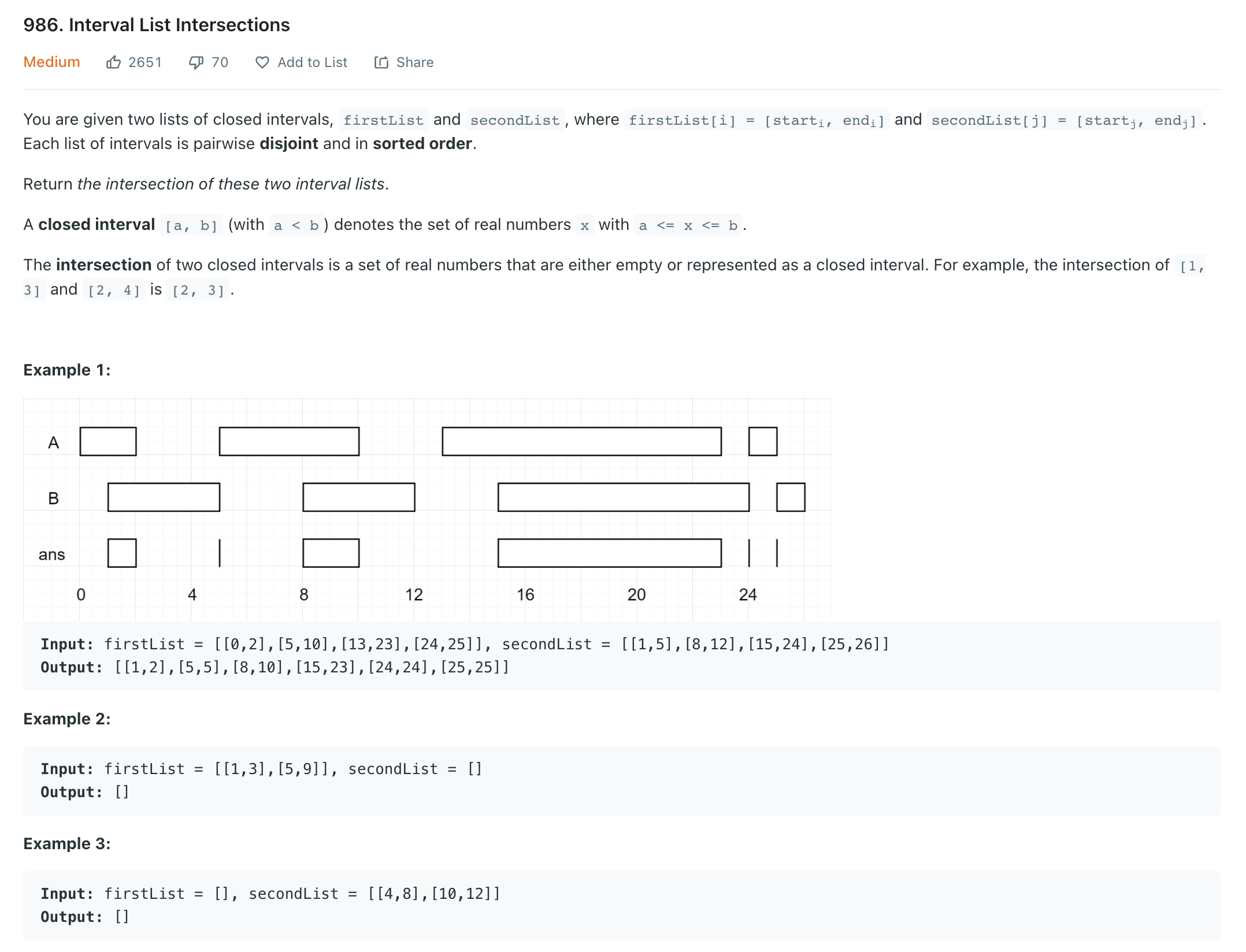
"""
Interval List Intersections:
You are given two lists of closed intervals, firstList and secondList,
where firstList[i] = [starti, endi] and secondList[j] = [startj, endj].
Each list of intervals is pairwise disjoint and in sorted order.
Return the intersection of these two interval lists.
A closed interval [a, b] (with a < b) denotes the set of real numbers x with a <= x <= b.
The intersection of two closed intervals is a set of real numbers that are either empty or represented as a closed interval.
For example, the intersection of [1, 3] and [2, 4] is [2, 3].
Example:
Input: arr1=[[1, 3], [5, 6], [7, 9]], arr2=[[2, 3], [5, 7]]
Output: [2, 3], [5, 6], [7, 7]
Explanation: The output list contains the common intervals between the two lists.
Example:
Input: arr1=[[1, 3], [5, 7], [9, 12]], arr2=[[5, 10]]
Output: [5, 7], [9, 10]
Explanation: The output list contains the common intervals between the two lists.
Example 1:
Input: firstList = [[0,2],[5,10],[13,23],[24,25]], secondList = [[1,5],[8,12],[15,24],[25,26]]
Output: [[1,2],[5,5],[8,10],[15,23],[24,24],[25,25]]
Example 2:
Input: firstList = [[1,3],[5,9]], secondList = []
Output: []
Example 3:
Input: firstList = [], secondList = [[4,8],[10,12]]
Output: []
Example 4:
Input: firstList = [[1,7]], secondList = [[3,10]]
Output: [[3,7]]
"""
"""
Intervals Intersection:
Given two lists of intervals, find the intersection of these two lists.
Each list consists of disjoint intervals sorted on their start time.
Example 1:
Input: arr1=[[1, 3], [5, 6], [7, 9]],
arr2=[[2, 3], [5, 7]]
Output: [2, 3], [5, 6], [7, 7]
Explanation: The output list contains the common intervals between the two lists.
Example 2:
Input: arr1=[[1, 3], [5, 7], [9, 12]], arr2=[[5, 10]]
Output: [5, 7], [9, 10]
Explanation: The output list contains the common intervals between the two lists.
https://leetcode.com/problems/interval-list-intersections/
https://www.educative.io/courses/grokking-the-coding-interview/JExVVqRAN9D
"""
Solution
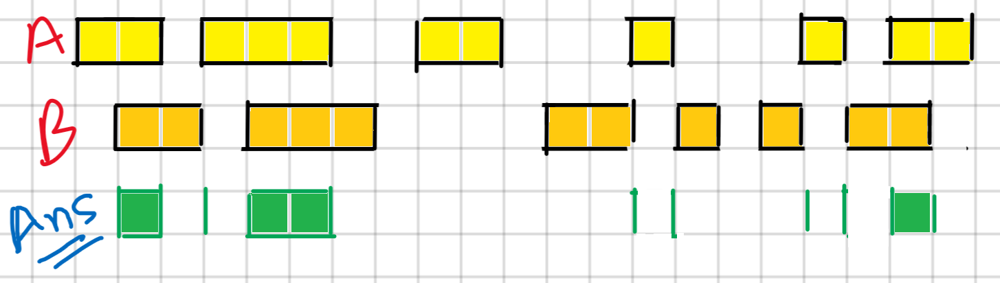
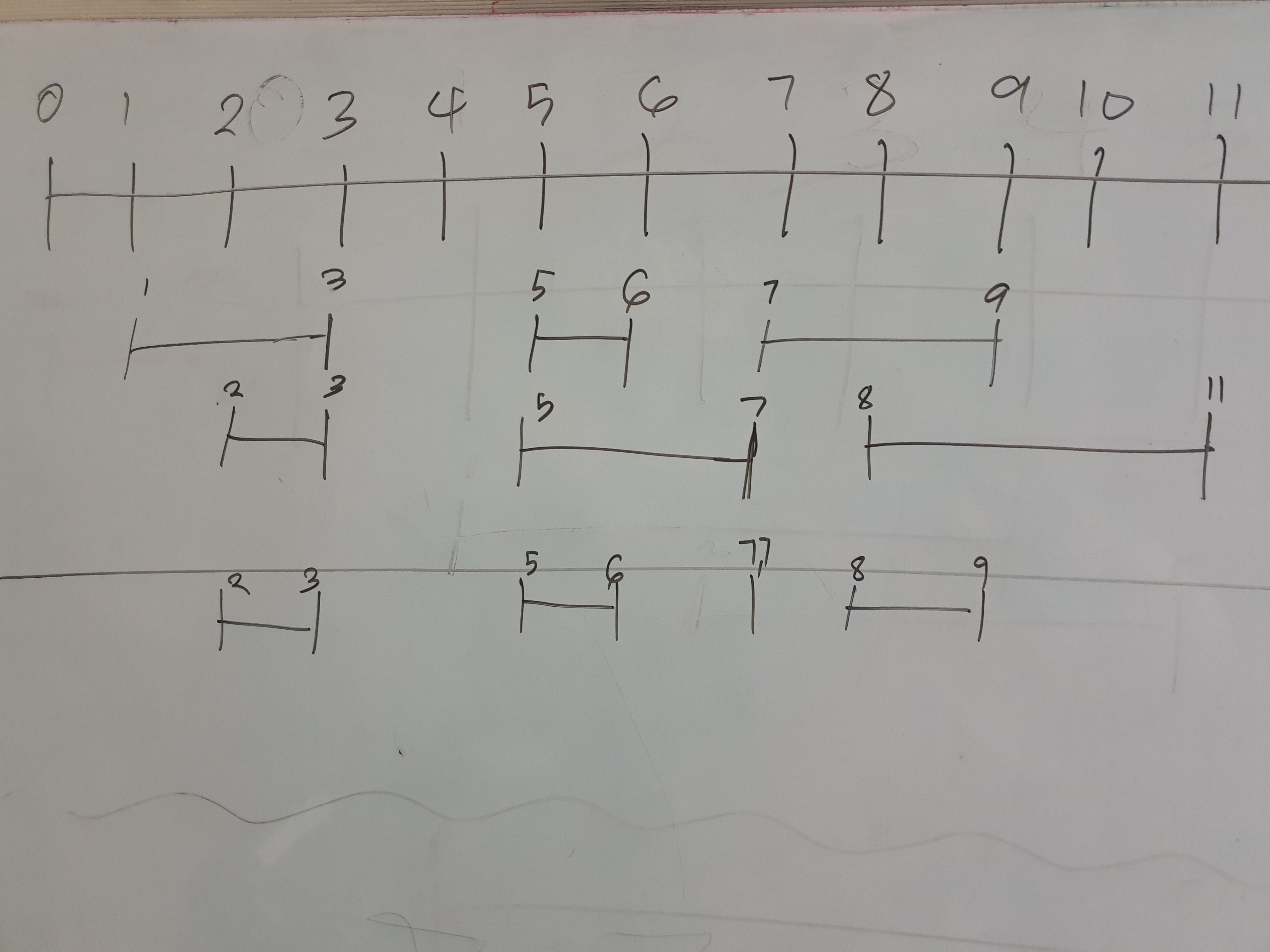
"""
Solution:
---
# Note: Each list of intervals is pairwise disjoint and in sorted order.
- check if start of two <= end of one and end of two >= start of one: => ensure they are together (are not before or after each other)
- if so:
***intersection = [max(start_one, start_two), min(end_one, end_two)]***
- futhest start, first end (end that is in both intervals)
- move the pointer of the interval with the ***least ending forward***
- list with the smaller might have another intersection in the current bigger intersection
- because the bigger one might still be in another intersection
firstList = [[0,2],[5,10],[13,23],[24,25]],
secondList = [[1,5],[8,12],[15,24],[25,26]]
one,two,res
0,0,[] => intersection = [max(0,1), min(2,5)]
1,0,[[1,2], ] => intersection = [max(5,1), min(10,5)]
1,1,[[1,2],[5,5] ] => intersection = [max(5,8), min(10,12)]
2,1,[[1,2],[5,5],[8,10] ] => intersection = None
2,2,[[1,2],[5,5],[8,10] ] => intersection = [max(13,15), min(23,24)]
3,2,[[1,2],[5,5],[8,10],[15,23] ] => intersection = [max(24,15), min(25,24)]
3,3,[[1,2],[5,5],[8,10],[15,23],[24,24] ] => intersection = [max(24,25), min(25,26)]
3,3,[[1,2],[5,5],[8,10],[15,23],[24,24],[25,25] ]
"""
class Solution:
def getIntersection(self, l_one, l_two):
# futhest start, first end -> ensures interval is in both intervals
return [max(l_one[0], l_two[0]), min(l_one[1], l_two[1])]
def intervalIntersection(self, firstList, secondList):
if not firstList or not secondList:
return []
res = []
one = 0
two = 0
while one <= len(firstList)-1 and two <= len(secondList)-1:
l_one = firstList[one]
l_two = secondList[two]
if l_two[0] <= l_one[1] and l_two[1] >= l_one[0]: # if has interval
res.append(self.getIntersection(l_one, l_two))
# move forward the pointer of list with the least ending
# so that we can continue evaluating the one with the furthest end in the next loop
if two == len(secondList)-1 or l_one[1] < l_two[1]:
one += 1
else:
two += 1
return res
[Python] Two Pointer Approach + Thinking Process Diagrams - LeetCode Discuss
Partition Labels
Find the original version of this page (with additional content) on Notion here.
Created: December 13, 2021 16:05:48