Hare & Tortoise Algorithm
Fast & Slow pointers introduction
The Fast & Slow pointer approach, also known as the Hare & Tortoise algorithm, is a pointer algorithm that uses two pointers which move through the array (or sequence/LinkedList) at different speeds. This approach is quite useful when dealing with cyclic LinkedLists or arrays.
By moving at different speeds (say, in a cyclic LinkedList), the algorithm proves that the two pointers are bound to meet. The fast pointer should catch the slow pointer once both the pointers are in a cyclic loop.
One of the famous problems solved using this technique was Finding a cycle in a LinkedList.
Simple problems
LinkedList Cycle
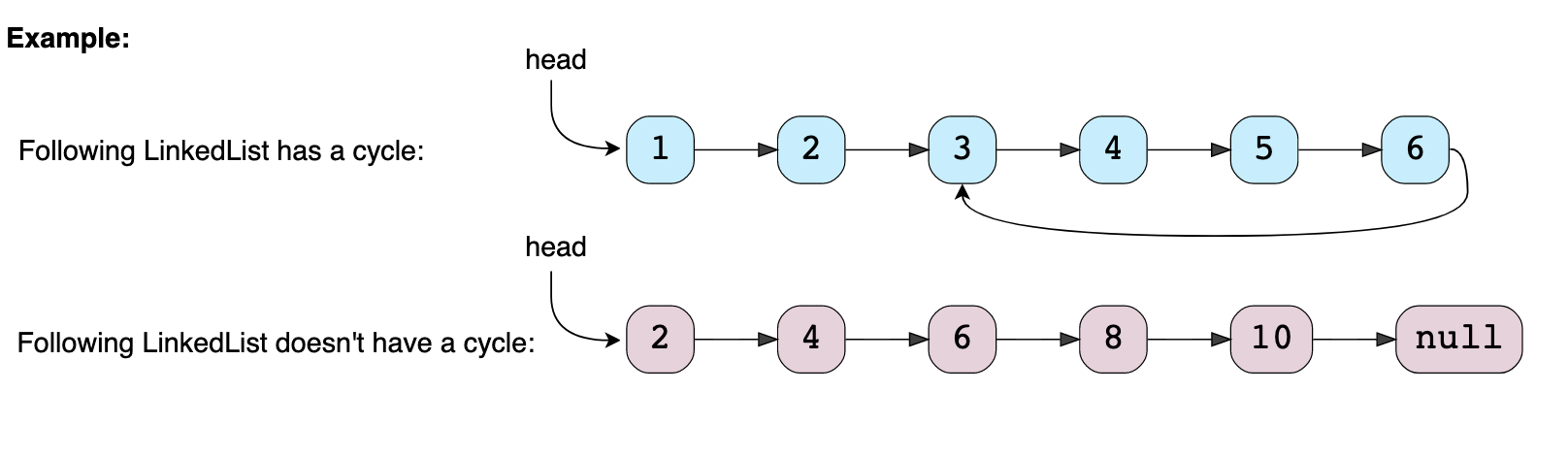
Given the head of a Singly LinkedList, write a function to determine if the LinkedList has a cycle in it or not.
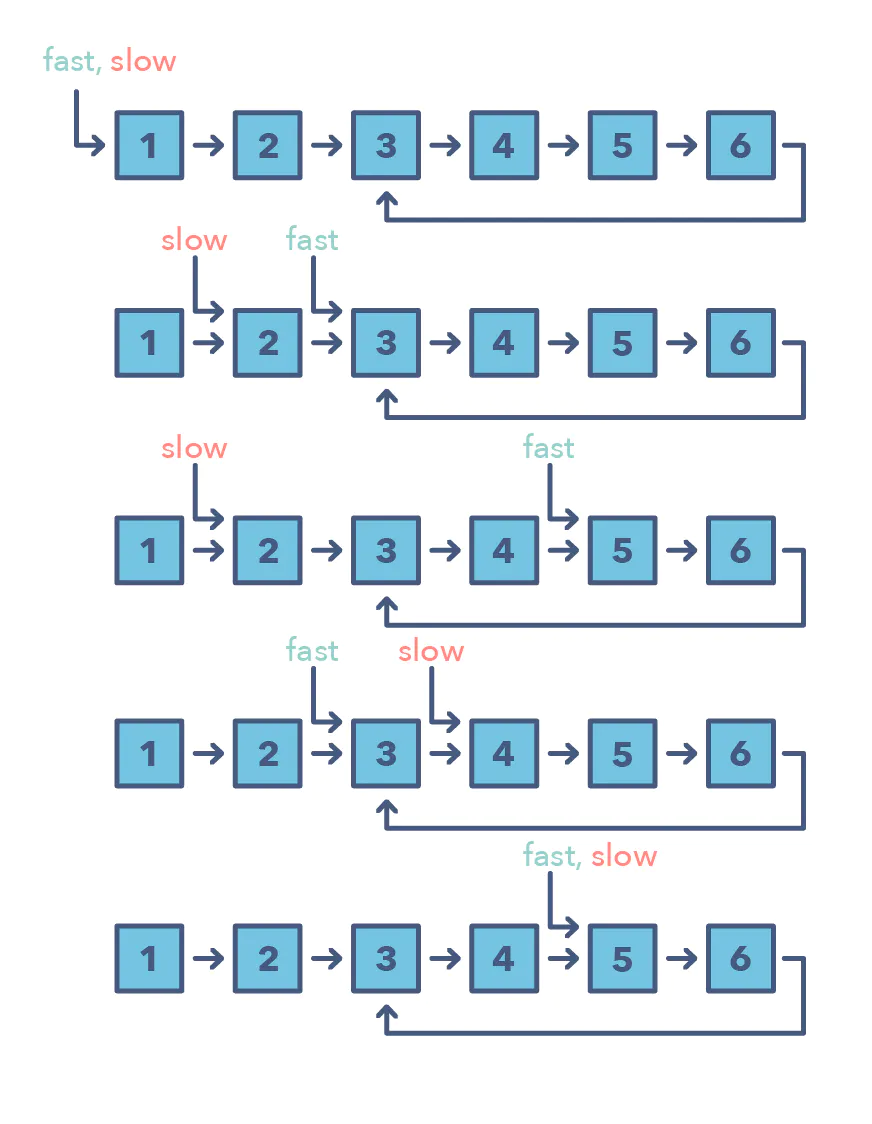
Imagine two racers running on a circular racing track. If one racer is faster than the other, the faster racer is bound to catch up and cross the slower racer from behind. We can use this fact to devise an algorithm to determine if a LinkedList has a cycle in it or not.
Imagine we have a slow and a fast pointer to traverse the LinkedList. In each iteration, the slow pointer moves one step and the fast pointer moves two steps. This gives us two conclusions:
- If the LinkedList doesn’t have a cycle in it, the fast pointer will reach the end of the LinkedList before the slow pointer to reveal that there is no cycle in the LinkedList.
- The slow pointer will never be able to catch up to the fast pointer if there is no cycle in the LinkedList.
If the LinkedList has a cycle, the fast pointer enters the cycle first, followed by the slow pointer. After this, both pointers will keep moving in the cycle infinitely. If at any stage both of these pointers meet, we can conclude that the LinkedList has a cycle in it.
why will they meet?
https://youtu.be/gBTe7lFR3vc?t=446
"""
Linked List Cycle:
Given head, the head of a linked list, determine if the linked list has a cycle in it
There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer.
Internally, pos is used to denote the index of the node that tail's next pointer is connected to.
Note that pos is not passed as a parameter.
Return true if there is a cycle in the linked list. Otherwise, return false.
https://leetcode.com/problems/linked-list-cycle
https://www.notion.so/paulonteri/Hare-Tortoise-Algorithm-1020d217ffb54e47b7aea3c175d75618#0f0930e961414b1e90871b4efbe3d1b6
"""
# Definition for singly-linked list.
class ListNode:
def __init__(self, x):
self.val = x
self.next = None
class Solution:
def hasCycle(self, head: ListNode):
if head is None:
return False
# move to initial positions
slow = head
fast = head.next
if fast is None:
return False
fast = fast.next
while fast != None:
if fast == slow:
return True
slow = slow.next
fast = fast.next
if fast:
fast = fast.next
return False
Length of LinkedList Cycle
Given the head of a LinkedList with a cycle, find the length of the cycle.
"""
Once the fast and slow pointers meet,
we can save the slow pointer and iterate the whole cycle with another pointer
until we see the slow pointer again to find the length of the cycle.
"""
class Node:
def __init__(self, value, next=None):
self.value = value
self.next = next
def find_cycle_length(head):
slow, fast = head, head
while fast is not None and fast.next is not None:
fast = fast.next.next
slow = slow.next
if slow == fast: # found the cycle
return calculate_cycle_length(slow)
return 0
def calculate_cycle_length(slow):
current = slow
cycle_length = 0
while True:
current = current.next
cycle_length += 1
if current == slow:
break
return cycle_length
Start of LinkedList Cycle
Problem
Given the head of a Singly LinkedList that contains a cycle, write a function to find the starting node of the cycle.
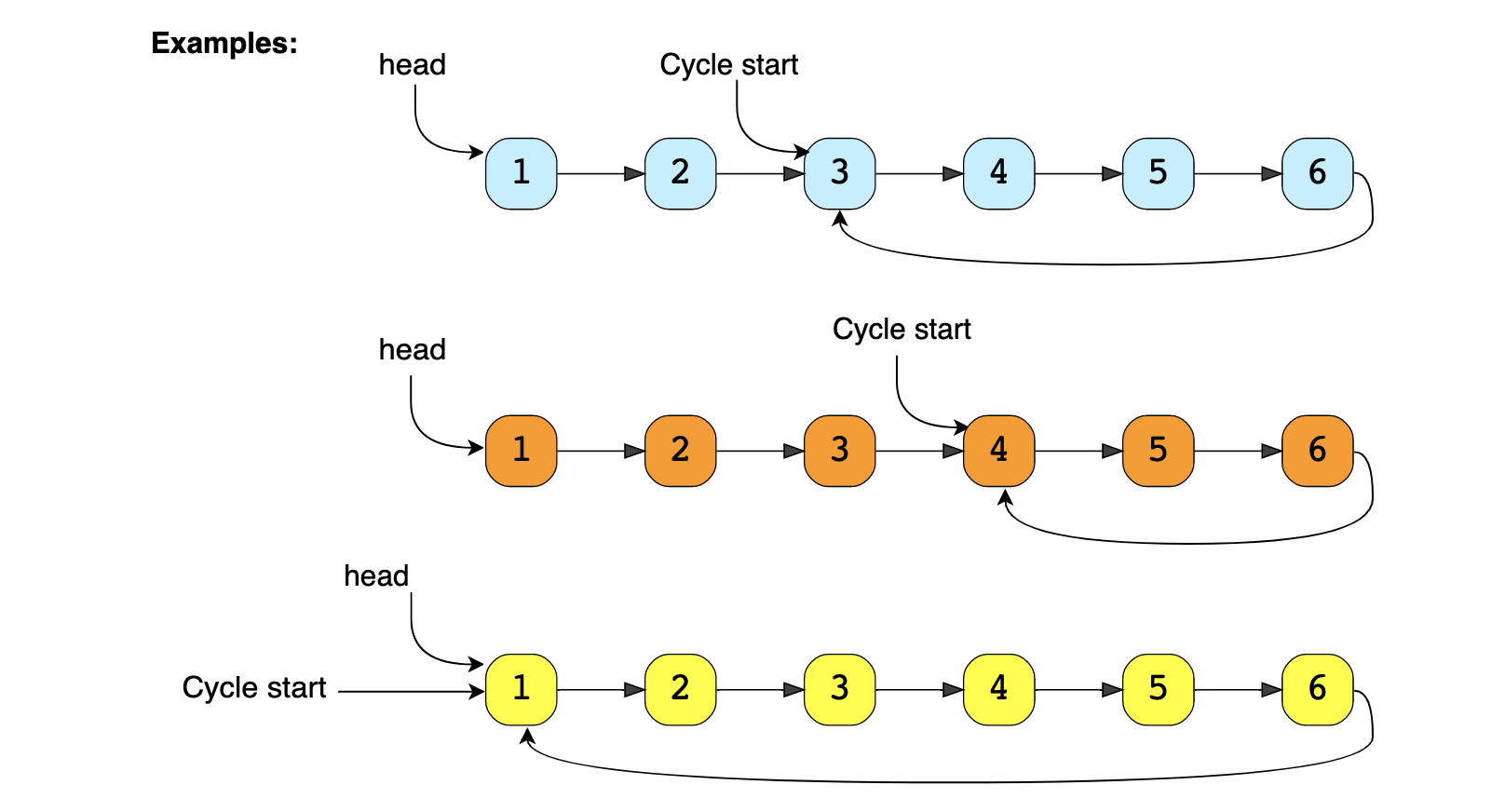
Solution
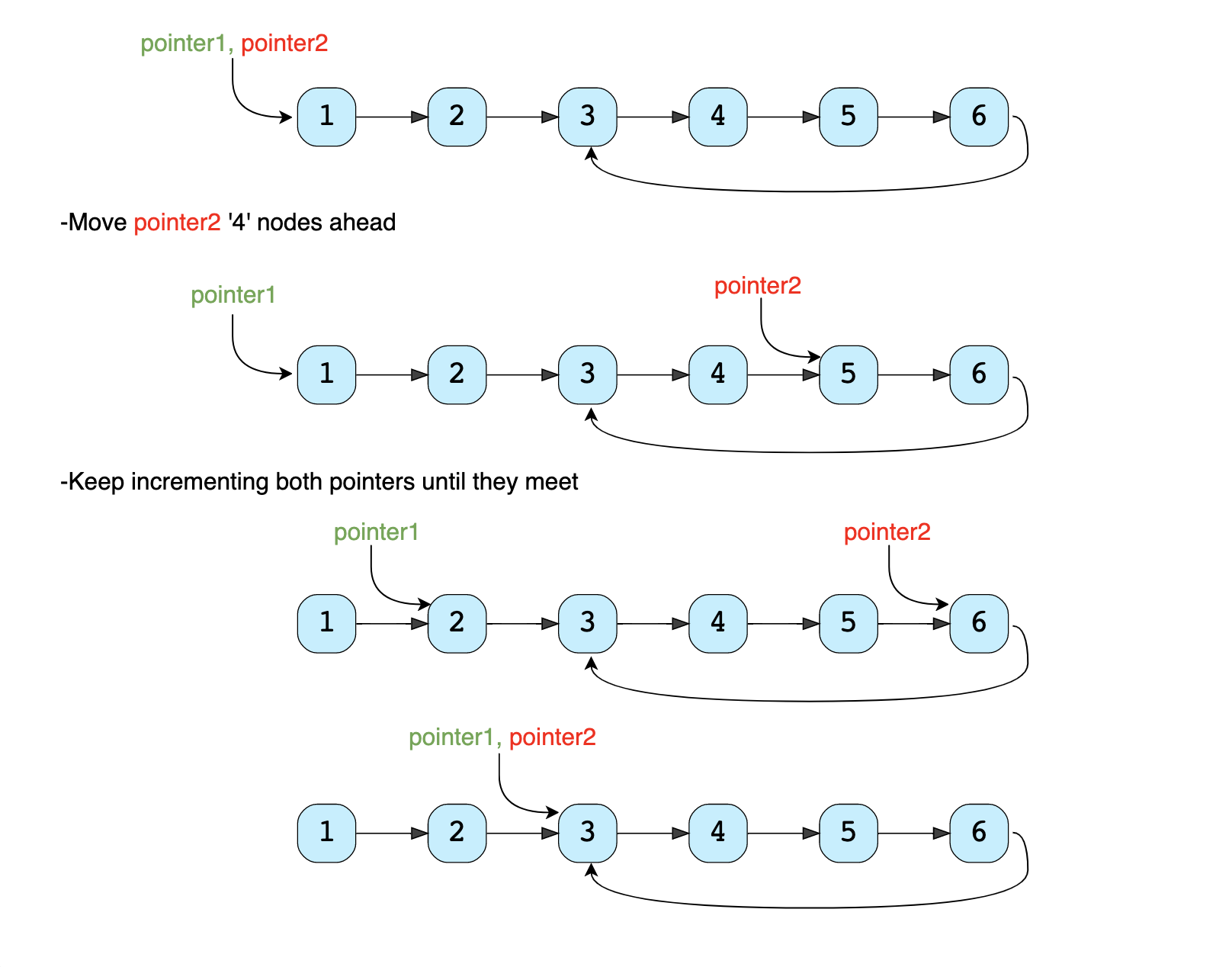
If we know the length of the LinkedList cycle, we can find the start of the cycle through the following steps:
- Take two pointers. Let’s call them
pointer1andpointer2. - Initialize both pointers to point to the start of the LinkedList.
- We can find the length of the LinkedList cycle using the approach discussed in Length of LinkedList Cycle. Let’s assume that the length of the cycle is ‘K’ nodes.
- Move
pointer2ahead by ‘K’ nodes. - Now, keep incrementing
pointer1andpointer2until they both meet. - Imagine the cycle as a circular track: As
pointer2is ‘K’ nodes ahead ofpointer1, which means,pointer2must have completed one loop in the cycle when both pointers meet. Their meeting point will be the start of the cycle.- if
pointer2is ‘K’ nodes ahead ofpointer1, it means that whenpointer1will be at the start of the cycle,pointer2two will be at the end - they are the same node
- if
Code
"""
Find start of linked list cycle:
Given the head of a Singly LinkedList that contains a cycle, write a function to find the starting node of the cycle.
https://www.educative.io/courses/grokking-the-coding-interview/N7pvEn86YrN
https://www.notion.so/paulonteri/Hare-Tortoise-Algorithm-1020d217ffb54e47b7aea3c175d75618#0f0930e961414b1e90871b4efbe3d1b6
"""
"""
Linked List Cycle II
Given a linked list, return the node where the cycle begins. If there is no cycle, return null.
There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer.
Internally, pos is used to denote the index of the node that tail's next pointer is connected to. Note that pos is not passed as a parameter.
Notice that you should not modify the linked list
https://leetcode.com/problems/linked-list-cycle-ii/
https://www.algoexpert.io/questions/Find%20Loop
https://www.notion.so/paulonteri/Hare-Tortoise-Algorithm-1020d217ffb54e47b7aea3c175d75618#0f0930e961414b1e90871b4efbe3d1b6
"""
class Node:
def __init__(self, value, next=None):
self.value = value
self.next = next
def find_cycle_start(head):
cycle_length = 0
# find the LinkedList cycle
slow, fast = head, head
while (fast is not None and fast.next is not None):
fast = fast.next.next
slow = slow.next
if slow == fast: # found the cycle
cycle_length = calculate_cycle_length(slow)
break
return find_start(head, cycle_length)
def calculate_cycle_length(slow):
current = slow
cycle_length = 0
while True:
current = current.next
cycle_length += 1
if current == slow:
break
return cycle_length
def find_start(head, cycle_length):
pointer1 = head
pointer2 = head
# move pointer2 ahead 'cycle_length' nodes
while cycle_length > 0:
pointer2 = pointer2.next
cycle_length -= 1
# increment both pointers until they meet at the start of the cycle
while pointer1 != pointer2:
pointer1 = pointer1.next
pointer2 = pointer2.next
return pointer1
class Solution:
def detectCycle(self, head):
if not head:
return None
# # find cycle
fast = head
slow = head
while True:
if fast is None or fast.next is None: # find invalid
return None
slow = slow.next
fast = fast.next.next
if slow == fast:
break
# # find start of cycle
# the (dist) head to the start of the cycle ==
# the (dist) meeting point to the start of the cycle
one = head
two = fast
while one != two:
one = one.next
two = two.next
return one
"""
Find Loop:
Write a function that takes in the head of a Singly Linked List that contains a loop
(in other words, the list's tail node points to some node in the list instead of None / null).
The function should return the node (the actual node--not just its value) from which the loop originates in constant space.
Each LinkedList node has an integer value as well as a next node pointing to the next node in the list.
Sample Input
head = 0 -> 1 -> 2 -> 3 -> 4 -> 5 -> 6 // the head node with value 0
^ v
9 <- 8 <- 7
Sample Output
4 -> 5 -> 6 // the node with value 4
^ v
9 <- 8 <- 7
https://www.algoexpert.io/questions/Find%20Loop
"""
# This is an input class. Do not edit.
class LinkedList:
def __init__(self, value):
self.value = value
self.next = None
def findLoop(head):
# .next to allow the first loop to work
p_one = head.next
p_two = head.next.next
# find meeting point
while p_two != p_one:
p_one = p_one.next
p_two = p_two.next.next
# # find start of cycle
# the (dist) head to the start of the cycle ==
# the (dist) meeting point to the start of the cycle
p_one = head
while p_two != p_one:
p_one = p_one.next
p_two = p_two.next
return p_one
Time & Space complexity
As we know, finding the cycle in a LinkedList with ‘N’ nodes and also finding the length of the cycle requires O(N). Also, as we saw in the above algorithm, we will need O(N) to find the start of the cycle. Therefore, the overall time complexity of our algorithm will be O(N).
Happy Number
Problem
Try doing it in constant space
"""
Happy Number:
Any number will be called a happy number if,
after repeatedly replacing it with a number equal to the sum of the square of all of its digits, leads us to number ‘1’.
All other (not-happy) numbers will never reach ‘1’. Instead, they will be stuck in a cycle of numbers which does not include ‘1’.
Example 1:
Input: n = 19
Output: true
Explanation:
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1
Example 2:
Input: n = 2
Output: false
Example 3:
Input: 23
Output: true (23 is a happy number)
Explanations: Here are the steps to find out that 23 is a happy number:
Example 4:
Input: 12
Output: false (12 is not a happy number)
Explanations: Here are the steps to find out that 12 is not a happy number:
"""
Solution
The process, defined above, to find out if a number is a happy number or not, always ends in a cycle. If the number is a happy number, the process will be stuck in a cycle on number ‘1,’ and if the number is not a happy number then the process will be stuck in a cycle with a set of numbers.
We saw in the LinkedList Cycle problem that we can use the Fast & Slow pointers method to find a cycle among a set of elements. As we have described above, each number will definitely have a cycle. Therefore, we will use the same fast & slow pointer strategy to find the cycle and once the cycle is found, we will see if the cycle is stuck on number ‘1’ to find out if the number is happy or not.
Brute force
def square_of_digits(num):
res = 0
while num > 0:
res += (num % 10) * (num % 10)
num = num // 10
return res
# using memory
def find_happy_number_01(num):
store = set()
store.add(num)
while num != 1:
num = square_of_digits(num)
if num in store:
return False
store.add(num)
return True
Optimal
def square_of_digits(num):
res = 0
while num > 0:
res += (num % 10) * (num % 10)
num = num // 10
return res
def find_happy_number(num):
fast = num
slow = num
loop_started = False
while slow != fast or not loop_started:
loop_started = True
fast = square_of_digits(square_of_digits(fast))
slow = square_of_digits(slow)
if slow == 1 or fast == 1:
return True
return False
Find the original version of this page (with additional content) on Notion here.
Created: December 13, 2021 16:05:48