Heaps & Priority Queues
Heaps
Implement A Binary Heap - An Efficient Implementation of The Priority Queue ADT (Abstract Data Type)
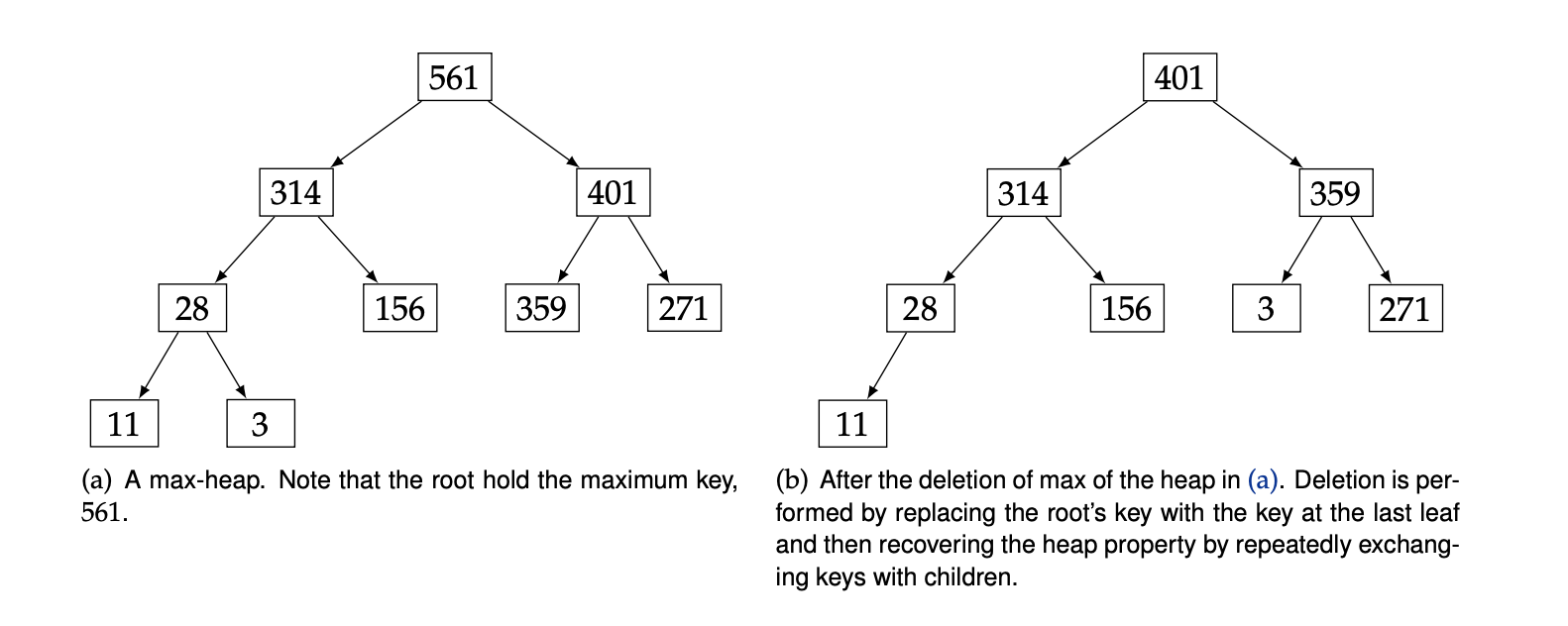
A heap is a specialized binary tree. Specifically, it is a complete binary tree. The keys must satisfy the heap property — the key at each node is at least as great as the keys stored at its children. (Min and Max heaps are complete binary trees with some unique properties)
A max-heap can be implemented as an array; the children of the node at index i are at indices 2i + 1 and 2i + 2. The array representation for the max-heap in Figure [561, 314, 401, 28, 156, 359, 271, 11, 3].
A max-heap supports O(log n) insertions, O(1) time lookup for the max element, and O(log n) deletion of the max element. The extract-max operation is defined to delete and return the maximum element. Searching for arbitrary keys has O(n) time complexity.
A heap is sometimes referred to as a priority queue because it behaves like a queue, with one difference: each element has a “priority” associated with it, and deletion removes the element with the highest priority.
The min-heap is a completely symmetric version of the data structure and supports O(1) timelookups for the minimum element.
A heap, as an implementation of a priority queue, is a good tool for solving problems that involve extremes, like the most or least of a given metric.
There are other words that indicate a heap might be useful:
- Largest
- Smallest
- Biggest
- Smallest
- Best
- Worst
- Top
- Bottom
- Maximum
- Minimum
- Optimal
Whenever a problem statement indicates that you’re looking for some extreme element, it’s worthwhile to think about whether a priority queue would be useful.
Representation as an array
- Root node, i = 0 is the first item of the array
- A left child node, left(i) = 2i + 1
- A right child node, right(i) = 2i + 2
- A parent node, parent(i) = (i-1) / 2

Time complexity
- Get Max or Min Element
- The Time Complexity of this operation is O(1).
- Remove Max or Min Element
- The time complexity of this operation is O(Log n) because we need to maintain the max/mix at their root node, which takes Log n operations.
- Insert an Element
- Time Complexity of this operation is O(Log n) because we insert the value at the end of the tree and traverse up to remove violated property of min/max heap.
Heap Sorted array
Average Worst case Average Worst case
Space O(n) O(n) O(n) O(n)
Search O(n) O(n) O(log n) O(log n)
Insert* O(1) **O(log n)** O(n) O(n)
Delete* O(log n) **O(log n)** O(n) O(n)
Examples:
🌳 Prim's Minimum Spanning Tree Algorithm *
-
n smallest value → min heap, n largest value → max heap
-
Kth Largest Number in a Stream
-
Continuous Median
-
Meeting Rooms II/Laptop Rentals
""" Meeting Rooms II Given an array of meeting time intervals consisting of start and end times: [[s1,e1],[s2,e2],...] (si < ei), find the minimum number of conference rooms required. Input: [[0,30],[5,10],[15,20]] [[0,30]] [[0,30],[5,10],[1,20],[7,30],[50,10],[15,20],[0,30],[5,10],[15,20]] Output: 2 1 6 https://leetcode.com/problems/meeting-rooms-ii/ """ from typing import List import heapq """ Laptop Rentals: You're given a list of time intervals during which students at a school need a laptop. These time intervals are represented by pairs of integers [start, end], where 0 <= start < end. However, start and end don't represent real times; therefore, they may be greater than 24. No two students can use a laptop at the same time, but immediately after a student is done using a laptop, another student can use that same laptop. For example, if one student rents a laptop during the time interval [0, 2], another student can rent the same laptop during any time interval starting with 2. Write a function that returns the minimum number of laptops that the school needs to rent such that all students will always have access to a laptop when they need one. Sample Input times = [ [0, 2], [1, 4], [4, 6], [0, 4], [7, 8], [9, 11], [3, 10], ] Sample Output 3 https://www.algoexpert.io/questions/Laptop%20Rentals """ # this can be optimized futher plus variables have been overused: # this is to help in undertanding the solution # time O(n log(n)) | space O(n) class Solution: def minMeetingRooms(self, intervals: List[List[int]]): if not intervals: return 0 # sort meetings by starting time intervals.sort(key=lambda x: x[0]) # # Logic: # if the next meeting is earlier than the earliest ending time, then no room will be free for it. # Otherwise, update the ending time (for the room) # # (ending_times heap) used to store the ending times of all meeting rooms # if a second meeting is held in a room, we replace the 1st's ending time, # we delete the 1st meeting ending time and add the 2nd's # create ending times heap # the heap will help us in keep the earliest ending time per room 'on top, [0]' ending_times = [intervals[0][1]] i = 1 while i < len(intervals): # in any case, we will add the meeting's ending time to the ending_times, # however, if the earliest ending time is less than it's starting, it means those two can share a room # so we remove the earlier one's ending time # # check if (curr starting time) overlaps earliest ending time curr_meeting = intervals[i] # cannot share room if curr_meeting[0] < ending_times[0]: # similar to adding another meeting room heapq.heappush(ending_times, curr_meeting[1]) # can share room # meeting starts later than the earliest ending # free room -> not overlap else: # remove the first room's ending time from the count # similar to updating meeting room's earliest ending heapq.heappop(ending_times) heapq.heappush(ending_times, curr_meeting[1]) i += 1 # we always added rooms to the heap and: # whenever we found conflicts in times we didn't remove from the heap but, # we removed when we were reusing the same room # the meeting ending times that were not replaced return len(ending_times) """ ----------------------------------------------------------------------------------------------------------------------------------------------- [[0, 2], [0, 4], [1, 4], [3, 10], [4, 6], [7, 8], [9, 11]] [9,7,10] [[0, 10], [0, 20], [1, 9], [2, 8], [3, 7], [4, 6], [5, 6], [10, 15], [11, 12]] [15, 20, 12, 8, 7, 6, 6] """ # time O(n^2) time | space O(n) def laptopRentalsBF(times): times.sort() # will record when the currently borrowed laptop will be free (end time) needed = [] for time in times: added = False # check if we can find a laptop that we will use once it is free for idx in range(len(needed)): if needed[idx] <= time[0]: # use laptop when it gets free needed[idx] = time[1] added = True break if not added: # no free laptop -> we need another one needed.append(time[1]) return len(needed) """ ----------------------------------------------------------------------------------------------------------------------------------------------- use a min-heap to get the earliest time a laptop will be free sort the input array to ensure the ones with the earliest times come first """ def laptopRentals(times): times.sort() # will record when the currently borrowed laptop will be free (end time) needed = [] for time in times: # # check if we can find a laptop that we will use once it is free if needed and needed[0] <= time[0]: # replace the earliest free laptop heapq.heappop(needed) heapq.heappush(needed, time[1]) else: # no free laptop -> we need another one heapq.heappush(needed, time[1]) return len(needed) -
Path With Maximum Minimum Value *
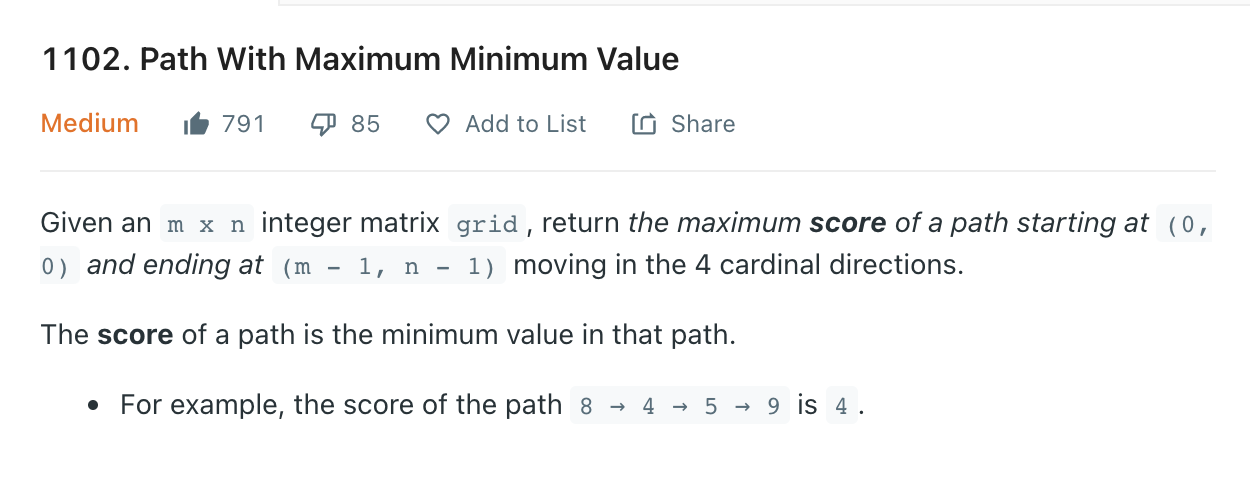

Uses: reversed Prim's Minimum Spanning Tree Algorithm
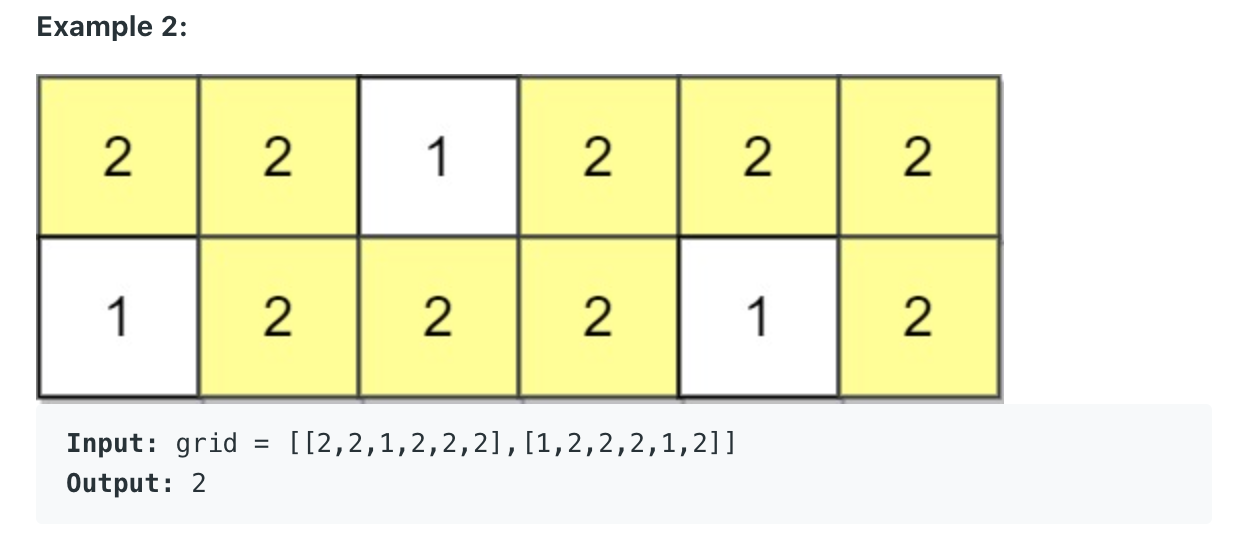
""" Path With Maximum Minimum Value: Given an m x n integer matrix grid, return the maximum score of a path starting at (0, 0) and ending at (m - 1, n - 1) moving in the 4 cardinal directions. The score of a path is the minimum value in that path. For example, the score of the path 8 → 4 → 5 → 9 is 4. Example 1: Input: grid = [[5,4,5],[1,2,6],[7,4,6]] Output: 4 Explanation: The path with the maximum score is highlighted in yellow. Example 2: Input: grid = [[2,2,1,2,2,2],[1,2,2,2,1,2]] Output: 2 Example 3: Input: grid = [[3,4,6,3,4],[0,2,1,1,7],[8,8,3,2,7],[3,2,4,9,8],[4,1,2,0,0],[4,6,5,4,3]] Output: 3 https://leetcode.com/problems/path-with-maximum-minimum-value/ https://leetcode.com/problems/path-with-maximum-minimum-value/discuss/457525/JAVA-A-Summery-of-All-Current-Solutions https://www.notion.so/paulonteri/Heaps-Priority-Queues-bb4a8de1dbe54089854d8d03c833126c#a8a0e9b8526c4b42a37090b4df52ed3a """ import heapq """ To prune our search tree, we take a detailed look at our problem. Since we have no need to find the shortest path, we could only focus on how to find a path avoiding small values. To do so, we could sort adjacents of our current visited vertices to find the maximum, and always choose the maximum as our next step. To implement, we could use a heap to help us maintaining all adjacents and the top of the heap is the next candidate. Time: O(Vlog(V) + E). Because the maximum number of element in the queue cannot be larger than V so pushing and popping from queue is O(log(V)). Also we only push each vertex to the queue once, so at maximum we do it V times. Thats Vlog(V). The E bit comes from the for loop inside the while loop. Space: O(V) where V is the maximum depth of our search tree. Uses: reversed Prim's Minimum Spanning Tree Algorithm https://www.notion.so/paulonteri/Trees-Graphs-edc3401e06c044f29a2d714d20ffe185#596bc798759a4edabe22a895aadeb12c """ class Solution(object): def maximumMinimumPath(self, A): """ ensure we always visit the larger neighbours the max_heap will ensure that the smallest neighbours are not visited Even if we took a wrong path, we can always take the right path again because the max_heap will return us to the next valid large spot/neighbour """ DIRS = [[0, 1], [1, 0], [0, -1], [-1, 0]] maxscore = A[0][0] max_heap = [] # negate element to simulate max heap heapq.heappush(max_heap, (-A[0][0], 0, 0)) while len(max_heap) != 0: val, row, col = heapq.heappop(max_heap) # update max maxscore = min(maxscore, -val) # reached last node if row == len(A) - 1 and col == len(A[0]) - 1: break for d in DIRS: new_row, new_col = d[0] + row, d[1] + col is_valid_row = new_row >= 0 and new_row < len(A) is_valid_col = new_col >= 0 and new_col < len(A[0]) if is_valid_row and is_valid_col and A[new_row][new_col] >= 0: heapq.heappush( max_heap, (-A[new_row][new_col], new_row, new_col) ) # mark as visited A[new_row][new_col] = -1 return maxscore -
Task Scheduler *
""" 621. Task Scheduler Given a characters array tasks, representing the tasks a CPU needs to do, where each letter represents a different task. Tasks could be done in any order. Each task is done in one unit of time. For each unit of time, the CPU could complete either one task or just be idle. However, there is a non-negative integer n that represents the cooldown period between two same tasks (the same letter in the array), that is that there must be at least n units of time between any two same tasks. Return the least number of units of times that the CPU will take to finish all the given tasks. Example 1: Input: tasks = ["A","A","A","B","B","B"], n = 2 Output: 8 Explanation: A -> B -> idle -> A -> B -> idle -> A -> B There is at least 2 units of time between any two same tasks. Example 2: Input: tasks = ["A","A","A","B","B","B"], n = 0 Output: 6 Explanation: On this case any permutation of size 6 would work since n = 0. ["A","A","A","B","B","B"] ["A","B","A","B","A","B"] ["B","B","B","A","A","A"] ... And so on. Example 3: Input: tasks = ["A","A","A","A","A","A","B","C","D","E","F","G"], n = 2 Output: 16 Explanation: One possible solution is A -> B -> C -> A -> D -> E -> A -> F -> G -> A -> idle -> idle -> A -> idle -> idle -> A Constraints: 1 <= task.length <= 104 tasks[i] is upper-case English letter. The integer n is in the range [0, 100]. https://leetcode.com/problems/task-scheduler """ from typing import List from collections import Counter from heapq import heapify, heappop, heappush """ tasks = ["A","A","A","B","B","B"], n = 2 A B A B ,n=2 -> A,B,ID,A,B A A B A ,n=2 -> A,B,ID,A,ID,A A A B B ,n=2 -> A,B,ID,A,B ["A","A","A","A","A","A","B","C","D","E","F","G"], n = 2 Counter({'A': 6, 'B': 1, 'C': 1, 'D': 1, 'E': 1, 'F': 1, 'G': 1}) [A, , ,A, , ,A, , ,A, , ,A, , ,A] [A,B, ,A, , ,A, , ,A, , ,A, , ,A] [A,B,C,A, , ,A, , ,A, , ,A, , ,A] [A,B,C,A,D, ,A, , ,A, , ,A, , ,A] [A,B,C,A,D,E,A,F,G,A, , ,A, , ,A] ... quickly fill [A,B,C, A,D,E, A,F,G, A,idle,idle, A,idle,idle, A] => length 16 """ class Solution: def leastInterval(self, tasks: List[str], n: int): """ Steps: - `time_taken` = 0 - Have a `max_heap` that contains the counts of each task - Have a while loop: - takes at most n+1 tasks from the `max_heap` - processes them (reduce count by one) - records how many tasks it has processed ( add them to `time_taken`) - if not at the end of the task queue / max_heap is not empty: - the minimum time taken is n+1 `{tasks processed + waiting time(if any)} == n+1` - else: time taken is the number of tasks done Video tutorials: - https://youtu.be/Z2Plc8o1ld4 - https://youtu.be/ySTQCRya6B0 """ if n == 0: return len(tasks) time_taken = 0 # create max_heap (negate values added to simulate max_heap) max_heap = [-count for count in Counter(tasks).values()] heapify(max_heap) while max_heap: curr_processing = [] # # get tasks to be processed for _ in range(n+1): if not max_heap: continue curr_processing.append(-heappop(max_heap)) # # process tasks and return to heap if not yet done with task for task_count in curr_processing: if task_count-1 > 0: heappush(max_heap, -(task_count-1)) # # record how many tasks we processed if not max_heap: # if we reached the end, (no more tasks) # we might have processed less than n+1 items as there is no waiting time after each time_taken += len(curr_processing) else: # if not at the end, # always, (tasks processed + waiting time(if any)) == n+1 time_taken += n+1 return time_taken -
Reorganize String **
""" Reorganize String Given a string s, rearrange the characters of s so that any two adjacent characters are not the same. Return any possible rearrangement of s or return "" if not possible. Example 1 Input: s = "aab" Output: "aba" Example 2: Input: s = "aaab" Output: "" 3: "aaaabbbbbccd" "babababcabcd" Constraints: 1 <= s.length <= 500 s consists of lowercase English letters. https://leetcode.com/problems/reorganize-string """ from collections import Counter from heapq import heapify, heappush, heappop class Solution: def reorganizeString(self, s: str): """ The goal is to first exhaust the most-frequent chars. We build a frequency dict of the letters in the string. We push all the letters into a max heap together with their frequencies We pop two letters at a time from the heap, add them to our result string, decrement their frequencies and push them back into heap. Why do we have to pop two items/letters at a time you're wondering? Because if we only pop one at a time, we will keep popping and pushing the same letter over and over again if that letter has a freq greater than 1. Hence by popping two at time, adding them to result, decrementing their freq and finally pushing them back into heap, we guarantee that we are always alternating between letters. https://leetcode.com/problems/reorganize-string/discuss/492827/Python-Simple-heap-solution-with-detailed-explanation """ res = [] character_count = [(-count, char) for char, count in Counter(s).items()] heapify(character_count) while len(res) < len(s): # # add most frequent # 1 count_1, char_1 = heappop(character_count) count_1 *= -1 res.append(char_1) # 2 count_2 = 0 if character_count: count_2, char_2 = heappop(character_count) count_2 *= -1 res.append(char_2) # # return into heap if count_1 > 1: count_1 -= 1 heappush(character_count, (-count_1, char_1)) if count_2 > 1: count_2 -= 1 heappush(character_count, (-count_2, char_2)) for idx in range(1, len(s)): if res[idx-1] == res[idx]: return "" return "".join(res)
Heap sort
Priority Queue
heapq
heapq.heapify(a)
import heapq
a = [3, 5, 1, 2, 6, 8, 7]
heapq.heapify(a)
a
# [1, 2, 3, 5, 6, 8, 7]
heapify() modifies the list in place but doesn’t sort it. A heap doesn’t have to be sorted to satisfy the heap property. However, since every sorted list does satisfy the heap property, running heapify() on a sorted list won’t change the order of elements in the list.
The first element, a[0], will always be the smallest element.
heapq.heappop(a)
To pop the smallest element while preserving the heap property, the Python heapq module defines heappop().
import heapq
a = [1, 2, 3, 5, 6, 8, 7]
heapq.heappop(a)
# 1
a
# [2, 5, 3, 7, 6, 8]
heapq.heappush(a, 4)
The Python heapq module also includes heappush() for pushing an element to the heap while preserving the heap property.
import heapq
a = [2, 5, 3, 7, 6, 8]
heapq.heappush(a, 4)
a
# [2, 5, 3, 7, 6, 8, 4]
heapq.heappop(a)
# 2
heapq.heappop(a)
# 3
heapq.heappop(a)
# 4
With miltidementional arrays
import heapq
arr = [[2, 1], [1, 1], [1, 2]]
heapq.heappop(arr)
# [1, 1]
heapq.heappop(arr)
# [1, 2]
heapq.heappop(arr)
# [2, 1]
🌳 Prim's Minimum Spanning Tree Algorithm *
Find the original version of this page (with additional content) on Notion here.
Created: December 13, 2021 16:05:48