Searching
Searching Algorithms - Algorithms for Coding Interviews in Python
Search
General search
Examples
https://leetcode.com/discuss/interview-question/373202
-
Search a 2D Matrix
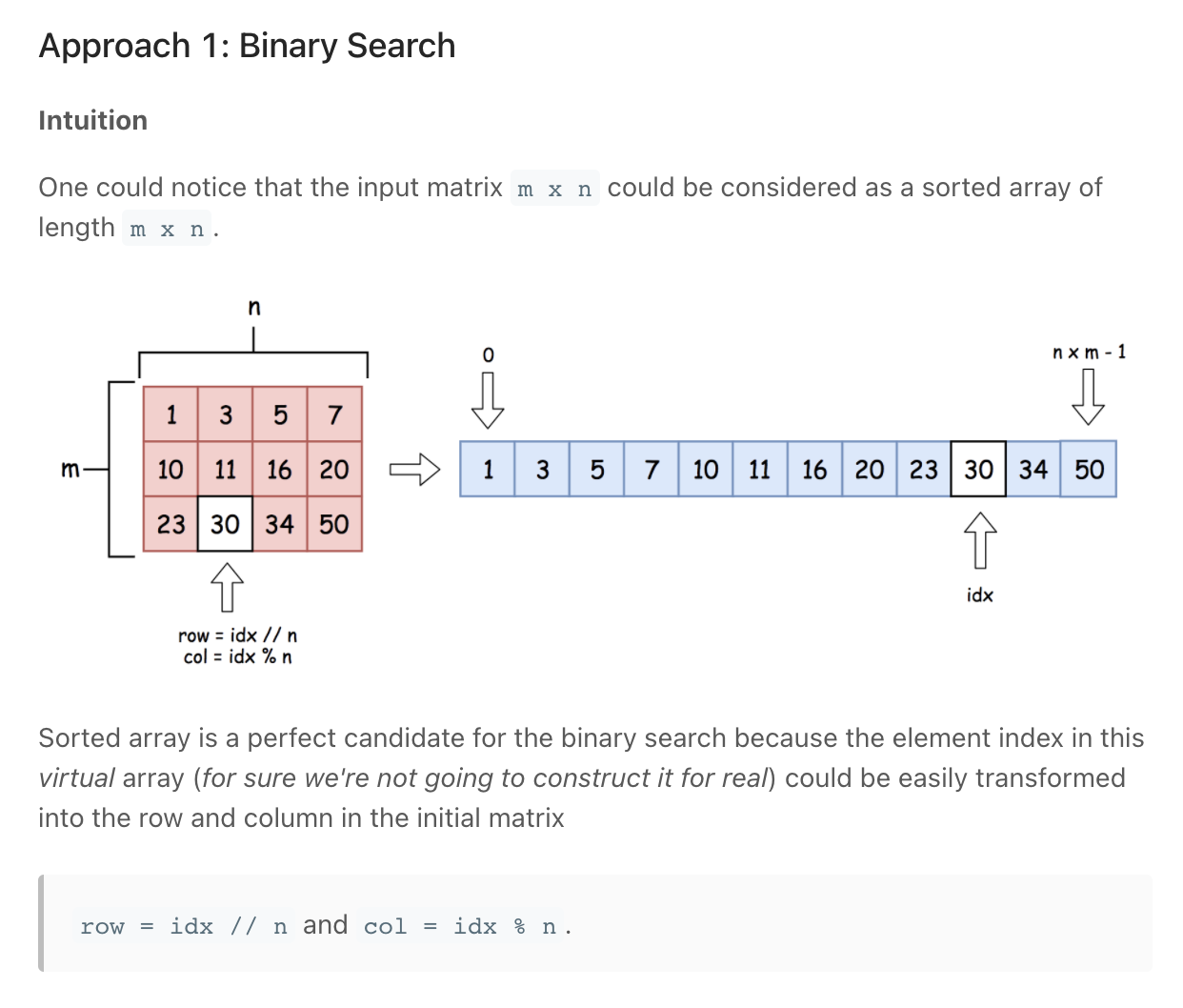
Treat is as one long 1D array



""" Search a 2D Matrix: Write an efficient algorithm that searches for a value in an m x n matrix. This matrix has the following properties: Integers in each row are sorted from left to right. The first integer of each row is greater than the last integer of the previous row. https://leetcode.com/problems/search-a-2d-matrix/ """ from typing import List """ Search In Sorted Matrix: You're given a two-dimensional array (a matrix) of distinct integers and a target integer. Each row in the matrix is sorted, and each column is also sorted; the matrix doesn't necessarily have the same height and width. Write a function that returns an array of the row and column indices of the target integer if it's contained in the matrix, otherwise [-1, -1]. Sample Input: matrix = [ [1, 4, 7, 12, 15, 1000], [2, 5, 19, 31, 32, 1001], [3, 8, 24, 33, 35, 1002], [40, 41, 42, 44, 45, 1003], [99, 100, 103, 106, 128, 1004], ] target = 44 Sample Output: [3, 3] https://www.algoexpert.io/questions/Search%20In%20Sorted%20Matrix """ class Solution0: def binarySearch(self, target, array): left = 0 right = len(array)-1 while left <= right: mid = (right + left) // 2 if array[mid] == target: return True if array[mid] < target: left = mid + 1 else: right = mid - 1 return False def searchMatrix(self, matrix: List[List[int]], target: int): for row in matrix: if row[0] <= target and row[-1] >= target: return self.binarySearch(target, row) return False """ matrix = [ [1, 3, 5, 7], [10,11,16,20], [23,30,34,60] ] target = 13 Output: false target = 16 Output: true target = 16 --- if we start at 0,0 - we do not know if it is in current row, or those below --- if we start at 0,4 - we are sure it isn't in current row, we move down - at 1,4: - we are sure it is in this row or none other """ class Solution: def searchMatrix(self, matrix: List[List[int]], target: int): row = 0 while row < len(matrix): # # check rows # check last item in row if matrix[row][len(matrix[0])-1] < target: # move to next row row += 1 elif matrix[row][0] > target: return False # # found correct row # Binary Search on Row else: left = 0 right = len(matrix[0])-1 while left <= right: mid = (right + left) // 2 if matrix[row][mid] == target: return True if matrix[row][mid] < target: left = mid + 1 else: right = mid - 1 return False return False def searchInSortedMatrix(matrix, target): # start at top right row = 0 col = len(matrix[0]) - 1 while row < len(matrix) and col >= 0: if matrix[row][col] > target: col -= 1 # move left elif matrix[row][col] < target: row += 1 # move down else: return[row, col] return[-1, -1] """ matrix = [ [1, 4, 7, 12, 15, 1000], [2, 5, 19, 31, 32, 1001], [3, 8, 24, 33, 35, 1002], [40, 41, 42, 44, 45, 1003], [99, 100, 103, 106, 128, 1004], ] target = 44 - Start curr at the top right corner - Check wether you should increase or decrease curr's value Move sideways(decrease), downwards (increase) - """ -
Intersection of Two Arrays
""" Intersection of Two Arrays Given two integer arrays nums1 and nums2, return an array of their intersection. Each element in the result must be unique and you may return the result in any order. Example 1: Input: nums1 = [1,2,2,1], nums2 = [2,2] Output: [2] Example 2: Input: nums1 = [4,9,5], nums2 = [9,4,9,8,4] Output: [9,4] Explanation: [4,9] is also accepted. https://leetcode.com/problems/intersection-of-two-arrays """ """ Alternative approach: sort the input arrays and use two pointers """ class Solution: def intersection(self, nums1, nums2): result = set() one = set(nums1) two = set(nums2) for num in one: if num in two: result.add(num) return list(result) class Solution_: def intersection(self, nums1, nums2): """ :type nums1: List[int] :type nums2: List[int] :rtype: List[int] """ set1 = set(nums1) set2 = set(nums2) return list(set2 & set1) -
Intersection of Two Arrays II
""" Intersection of Two Arrays II Given two integer arrays nums1 and nums2, return an array of their intersection. Each element in the result must appear as many times as it shows in both arrays and you may return the result in any order. Example 1: Input: nums1 = [1,2,2,1], nums2 = [2,2] Output: [2, 2] Example 2: Input: nums1 = [4,9,5], nums2 = [9,4,9,8,4] Output: [9,4] Explanation: [4,9] is also accepted. 3: [4,9,5] [9,4,9,8,4] => [4,9] https://leetcode.com/problems/intersection-of-two-arrays-ii """ """ Alternative: use hashmap/collections.Counter """ class Solution: def intersect(self, nums1, nums2): result = [] nums1.sort() nums2.sort() one, two = 0, 0 while one < len(nums1) and two < len(nums2): if nums1[one] == nums2[two]: result.append(nums1[one]) one += 1 two += 1 elif nums1[one] < nums2[two]: one += 1 else: two += 1 return result -
Search Suggestions System
""" 1268. Search Suggestions System Given an array of strings products and a string searchWord. We want to design a system that suggests at most three product names from products after each character of searchWord is typed. Suggested products should have common prefix with the searchWord. If there are more than three products with a common prefix return the three lexicographically minimums products. Return list of lists of the suggested products after each character of searchWord is typed. Example 1: Input: products = ["mobile","mouse","moneypot","monitor","mousepad"], searchWord = "mouse" Output: [ ["mobile","moneypot","monitor"], ["mobile","moneypot","monitor"], ["mouse","mousepad"], ["mouse","mousepad"], ["mouse","mousepad"] ] Explanation: products sorted lexicographically = ["mobile","moneypot","monitor","mouse","mousepad"] After typing m and mo all products match and we show user ["mobile","moneypot","monitor"] After typing mou, mous and mouse the system suggests ["mouse","mousepad"] Example 2: Input: products = ["havana"], searchWord = "havana" Output: [["havana"],["havana"],["havana"],["havana"],["havana"],["havana"]] Example 3: Input: products = ["bags","baggage","banner","box","cloths"], searchWord = "bags" Output: [["baggage","bags","banner"],["baggage","bags","banner"],["baggage","bags"],["bags"]] Example 4: Input: products = ["havana"], searchWord = "tatiana" Output: [[],[],[],[],[],[],[]] Constraints 1 <= products.length <= 1000 There are no repeated elements in products. 1 <= Σ products[i].length <= 2 * 10^4 All characters of products[i] are lower-case English letters. 1 <= searchWord.length <= 1000 All characters of searchWord are lower-case English letters. https://leetcode.com/problems/search-suggestions-system/ """ """ - given: products, searchword - suggests at most 3 (common prefix) - after each character is typed BF: (P.W + P log P) * S - search arr, get all words with prefix - sort by lexographic order, return top 3 SOL 1: - we can store words in trie P*S get_words(pref, trie): - heap - for each word, add it to a heap, of max size 3 - return heap Input ["havana"] "tatiana" Output: [] Expected [[],[],[],[],[],[],[]] """ from typing import List import heapq class Word: def __init__(self, word): self.word = word def __gt__(self, other): return other.word > self.word class Trie: def __init__(self): self.store = {} self.end_char = "*" def add(self, word): curr_store = self.store for char in word: if char not in curr_store: curr_store[char] = {} curr_store = curr_store[char] curr_store[self.end_char] = word def search_prefix(self, prefix): curr_store = self.store for char in prefix: if char not in curr_store: return [] curr_store = curr_store[char] res = [] self._get_all_words(curr_store, res) return res def _get_all_words(self, curr_store, result): """dfs""" for key, value in curr_store.items(): if key == self.end_char: heapq.heappush(result, Word(value)) if len(result) > 3: heapq.heappop(result) else: self._get_all_words(value, result) class Solution: def suggestedProducts(self, products: List[str], searchWord: str): result = [] trie = Trie() for word in products: trie.add(word) for i in range(len(searchWord)): search_results = trie.search_prefix(searchWord[:i+1]) if search_results: res = [item.word for item in search_results] res.sort() result.append(res) else: result.append([]) return result -
Kth Largest Element in an Array
""" Kth Largest Element in an Array Given an integer array nums and an integer k, return the kth largest element in the array. Note that it is the kth largest element in the sorted order, not the kth distinct element. Example 1: Input: nums = [3,2,1,5,6,4], k = 2 Output: 5 Example 2: Input: nums = [3,2,3,1,2,4,5,5,6], k = 4 Output: 4 https://leetcode.com/problems/kth-largest-element-in-an-array """ class Solution: def findKthLargest(self, array, k): return self.quick_select(array, len(array)-k, 0, len(array)-1) def quick_select(self, array, idx, start, end): if start == end: return array[start] # # pick pivot and sort numbers relative to it (like quick sort) pivot = start # # sort numbers with respect to pivot then put pivot between the large and small numbers # left and right to stop at a place where: left >= pivot & right <= pivot left = start + 1 right = end while left <= right: # check if can be swapped if array[left] > array[pivot] and array[right] < array[pivot]: array[left], array[right] = array[right], array[left] if array[left] <= array[pivot]: # no need to swap left += 1 if array[right] >= array[pivot]: # no need to swap right -= 1 # place pivot at correct position # # place the pivot at correct position (right) # # place pivot at correct position # we know that once the sorting is done, the number at left >= pivot & right <= pivot # smaller values go to the left of array[pivot] # # right is at a value < pivot, so ot should be moved left array[pivot], array[right] = array[right], array[pivot] # after swapping right is the only number we are sure is sorted # check if we are at the idx being looked for if right == idx: return array[right] # # proceed search elif right < idx: return self.quick_select(array, idx, right+1, end) else: return self.quick_select(array, idx, start, right-1) x = Solution() x.findKthLargest([5, 6, 4], 2) -
Word Search
""" Word Search Given a 2D board and a word, find if the word exists in the grid. The word can be constructed from letters of sequentially adjacent cells, where "adjacent" cells are horizontally or vertically neighboring. The same letter cell may not be used more than once. Constraints: board and word consists only of lowercase and uppercase English letters. 1 <= board.length <= 200 1 <= board[i].length <= 200 1 <= word.length <= 10^3 https://leetcode.com/problems/word-search/ """ from typing import List # O(n) time | O(n) space -> because of the recursion call stack | class Solution: def exist(self, board: List[List[str]], word: str): # Iterate over each character h = 0 while h < len(board): w = 0 while w < len(board[0]): # stop iteration if we find the word if board[h][w] == word[0] and self.searchWordOutward(board, word, h, w, 0): return True w += 1 h += 1 return False def searchWordOutward(self, board, word, h, w, word_pos): # check if past end of word (found all characters) if word_pos >= len(word): return True if h < 0 or h >= len(board) or \ w < 0 or w >= len(board[0]): return False if board[h][w] != word[word_pos]: return False # remove seen character seen_char = board[h][w] board[h][w] = '' # Expand: move on to next character (word_pos + 1) -> in the order right, left, top, bottom found = self.searchWordOutward(board, word, h, w+1, word_pos+1) or \ self.searchWordOutward(board, word, h, w-1, word_pos+1) or \ self.searchWordOutward(board, word, h+1, w, word_pos+1) or \ self.searchWordOutward(board, word, h-1, w, word_pos+1) # return seen character board[h][w] = seen_char return found """ Input: [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]] "ABCCED" [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]] "SEE" [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]] "ABCB" Output: true true false """
Linear/Sequential Search
Go through each element one by one. When the element you are searching for is found, return its index.
Binary Search
Binary-search Interview Questions - LeetCode Discuss
Requires a sorted array.
The terminology used in Binary Search:
- Target - the value that you are searching for
- Index - the current location that you are searching
- Left, Right - the indices from which we use to maintain our search Space
- Mid - the index that we use to apply a condition to determine if we should search left or right

How does it work?
In its simplest form, Binary Search operates on a contiguous sequence with a specified left and right index. This is called the Search Space. Binary Search maintains the left, right, and middle indices of the search space and compares the search target or applies the search condition to the middle value of the collection; if the condition is unsatisfied or values unequal, the half in which the target cannot lie is eliminated and the search continues on the remaining half until it is successful. If the search ends with an empty half, the condition cannot be fulfilled and the target is not found.
Common types of Binary Search
Simple Binary Search
This is the most basic and elementary form of Binary Search. It is the standard Binary Search Template that most high schools or universities use when they first teach students computer science. It is used to search for an element or condition which can be determined by accessing a single index in the array.
Basic logic:
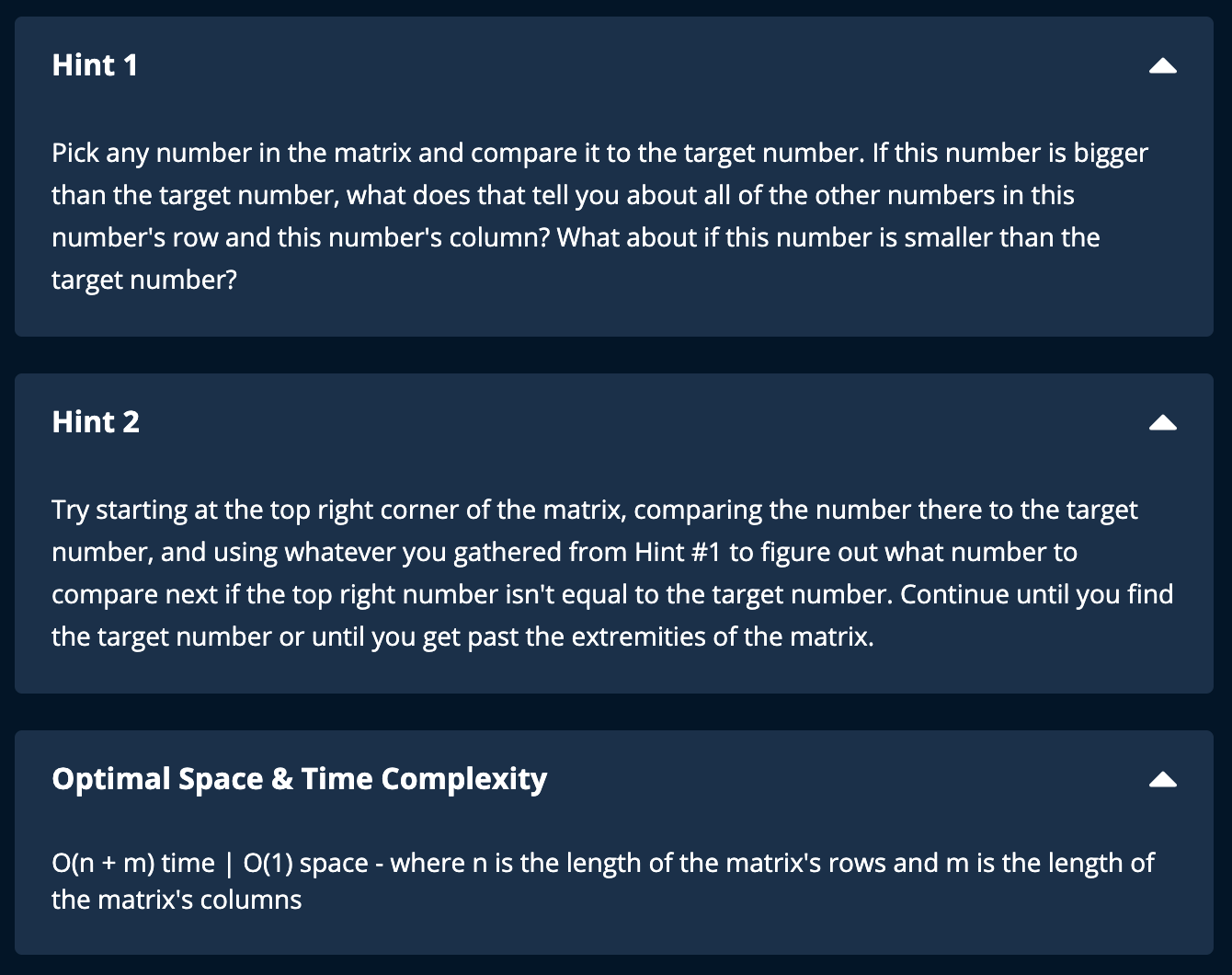
# Binary Search
# -1 means not found
def search(self, nums, target):
if not nums:
return -1
if len(nums) == 1 and nums[0] == target:
return 0
left, right = 0, len(nums) - 1
# not while left < right: because of cases where the target is on the right pointer
# like ([1,2,5], 5)
# the mid can be on the left pointer but never on the right pointer because of the,
# the floor division -> rounds down results
while left <= right:
mid = (left+right) // 2
if nums[mid] == target:
return mid
# # check which half is invalid. Note that mid is already invalid
# left is invalid (all the numbers to the left are smaller than target)
elif target > nums[mid]:
# move left pointer
# skip mid & all the numbers to the left of it
left = mid + 1
else:
# skip mid & all the numbers to the right of it
right = mid - 1
return -1
Key attributes:
- Search condition can be determined without comparing to the element's neighbours
- No post-processing is required because at each step, you are checking to see if the element has been found. If you reach the end, then you know the element is not found
- We allow the right & left pointer be on the same index
Distinguishing Syntax:
- Termination:
left > rightThe while loop looks similar towhile left <= right: - Searching Left:
right = mid-1 - Searching Right:
left = mid+1 - Initial Condition:
left = 0, right = length-1
Examples
-
Guess Number Higher or Lower
""" Guess Number Higher or Lower: (Binary Search) We are playing the Guess Game. The game is as follows: I pick a number from 1 to n. You have to guess which number I picked. Every time you guess wrong, I will tell you whether the number I picked is higher or lower than your guess. You call a pre-defined API int guess(int num), which returns 3 possible results: -1: The number I picked is lower than your guess (i.e. pick < num). 1: The number I picked is higher than your guess (i.e. pick > num). 0: The number I picked is equal to your guess (i.e. pick == num). Return the number that I picked. https://leetcode.com/problems/guess-number-higher-or-lower/ """ # # # The guess API is already defined for you. # @param num, your guess # @return -1 if my number is lower, 1 if my number is higher, otherwise return 0 # def guess(num: int) -> int: def guess(num: int): pass # # class Solution: def guessNumber(self, n): if n < 2: return n left = 1 right = n # we don't use left < right because: the middle pointer will never be at the right pointer, # so if the the number we are guessing == n, the right pointer will never be checked (right = n) and, # hence never find the guess number while left <= right: mid = (left+right) // 2 guess_res = guess(mid) if guess_res == 0: return mid # lower elif guess_res == 1: left = mid + 1 else: right = mid - 1 class Solution00: def guessNumber(self, x: int): left = 1 right = x while left <= right: mid = (left+right) // 2 res = guess(mid) # print(left, right, mid, res) if res == 0: return mid elif res == -1: right = mid - 1 else: left = mid + 1 """ [0,1,2,3,4,5,6,7,8] [1,2,3,4,5,6,7,8,9] 6 r = 9 l = 1 m = 5 r = 9 l = 1 m = 5 """ -
Sqrt(x) *
""" Sqrt(x): (Binary Search) Given a non-negative integer x, compute and return the square root of x. Since the return type is an integer, the decimal digits are truncated, and only the integer part of the result is returned. Example 1: Input: x = 4 Output: 2 Example 2: Input: x = 8 Output: 2 Explanation: The square root of 8 is 2.82842..., and since the decimal part is truncated, 2 is returned. https://leetcode.com/problems/sqrtx/ """ class Solution: def mySqrt(self, x: int): left = 1 right = x while left <= right: mid = (left+right) // 2 mid_sq = mid * mid if mid_sq == x: return mid elif mid_sq > x: right = mid - 1 else: left = mid + 1 return right # return (left+right) // 2 """ [0,1,2,3,4,5,6,7,8] [1,2,3,4,5,6,7,8,9] 9 l = 1,0 r = 9,8 mid = 5,4 l = 1,0 r = 4,3 mid = 3,2 [0,1,2,3,4,5,6,7] [1,2,3,4,5,6,7,8] 8 l = 1,0 r = 8,7 mid = 4,3 l = 1,0 r = 3,2 mid = 2,1 """ def mySqrt(self, x): if x < 2: return x left = 1 right = x while left <= right and left ** 2 <= x: # Remember: # the mid can be on the left pointer, never on the right: floor division -> rounds down results # we want to push left as far up as possible: # then we can do some rounding down logic later mid = (left+right) // 2 mid_squared = mid ** 2 if mid_squared == x: return mid elif mid_squared > x: right = mid - 1 else: left = mid + 1 # from the prompt, we are allowed to round down for example, the square root of 8 is 2.82842..., we return 2 # this means that the first val we find where (val**2 <= x) is the correct result # left will always be larger or equal to the sq root because of the logic in the above while loop while left ** 2 > x: left -= 1 return left # # Also works # mid = (left + right) // 2 # while mid ** 2 > x: # mid -= 1 # return mid # this would have worked if we were rounding up # while not right ** 2 >= x: # right += 1 # return right # 2147395599 # without comments def mySqrtWC(self, x: int): if x < 2: return x left = 1 right = x while left <= right and left ** 2 <= x: mid = (left+right) // 2 mid_squared = mid ** 2 if mid_squared == x: return mid elif mid_squared > x: right = mid - 1 else: left = mid + 1 # Also works mid = (left + right) // 2 while mid ** 2 > x: mid -= 1 return mid # while left ** 2 > x: # left -= 1 # return left -
Root of Number
""" Root of Number: Many times, we need to re-implement basic functions without using any standard library functions already implemented. For example, when designing a chip that requires very little memory space. In this question we’ll implement a function root that calculates the n’th root of a number. The function takes a nonnegative number x and a positive integer n, and returns the positive n’th root of x within an error of 0.001 (i.e. suppose the real root is y, then the error is: |y-root(x,n)| and must satisfy |y-root(x,n)| < 0.001). Don’t be intimidated by the question. While there are many algorithms to calculate roots that require prior knowledge in numerical analysis, there is also an elementary method which doesn’t require more than guessing-and-checking. Try to think more in terms of the latter. Make sure your algorithm is efficient, and analyze its time and space complexities. Examples: input: x = 7, n = 3 output: 1.913 input: x = 9, n = 2 output: 3 """ """ ----------------- PROBLEM ----------------- : calculates the n’th root of a number takes in nonnegative number x and a positive integer n, and returns the positive n’th root of x within an error of 0.001 suppose the real root is y, then the error is: |y-root(x,n)| and must satisfy |y-root(x,n)| < 0.001). ----------------- EXAMPLES ----------------- : x = 7, n = 3 1.913 x = 9, n = 2 3 x = 8, n = 3 2 x = 4, n = 2 2 x = 3, n = 2 1.732 r^n = x 0.001 - 8 for each of them ^n ----------------- BRUTE FORCE ----------------- : Time complexity : O(1000x) -> O(x) Space complexity: O(1) x = 4, n = 2 (0.001, 0.002,.... 1 => 1000) * 4 x = 8, n = 3 (0.001, 0.002,.... 1 => 1000) * 8 ----------------- OPTIMAL ----------------- : x = 4, n = 2 left right mid 0.001 - 4.000 2 x = 8, n = 3 left right mid 0.001 - 8.000 4 0.001 - 4.000 2 x = 3, n = 2 left right mid 0.001 - 3.000 1.5 1.5 - 3.00 1.5+0.75 = 2.25 1.5 - 2.25 --- x = 1.1, n = 2 1.04 left right mid mid^n 0 1.1 0.55 0.3 --- x = 9.1, n = 2 3.01 --- Special case: x = 0.9, n = 2 0.949 x = 0.5, n = 2 0.707 left right mid mid^n 0.5 1 .75 .5625 break condition: - abs(mid^n - x) < 0.001 """ def root(x, n): left = 0 right = x # special condition if x < 1: left = x right = 1 while left < right: mid = (left+right)/2 mid_power_n = mid ** n # found answer if abs(mid_power_n - x) < 0.001: return round(mid, 3) # is smaller elif mid_power_n < x: left = mid # is larger else: right = mid print(root(7, 3)) print(root(3, 2)) print(root(160, 3)) print(root(0.9, 2)) print(root(0.5, 3)) -
Pow(x, n) **
Pow(x, n) - X to the power of N - Leetcode 50 - Python
""" Pow(x, n) Implement pow(x, n), which calculates x raised to the power n (i.e., xn). Example 1: Input: x = 2.00000, n = 10 Output: 1024.00000 Example 2: Input: x = 2.10000, n = 3 Output: 9.26100 Example 3: Input: x = 2.00000, n = -2 Output: 0.25000 Explanation: 2-2 = 1/22 = 1/4 = 0.25 https://leetcode.com/problems/powx-n https://youtu.be/g9YQyYi4IQQ """ """ 2 ** 6 2*2*2*2*2*2 2**3 * 2**3 (2**2 * 2**1) * (2**2 * 2**1) (2**1 * 2**1 * 2**1) * (2**1 * 2**1 * 2**1) 2^12 => (2^6)^2 2^6 => (2^3)^2 2^3 => (2^1)^2 * 2 2^10 => (2^5)^2 2^5 => (2^2)^2 * 2 2^2 => (2^1)^2 """ class Solution: def myPow(self, x: float, n: int): res = self.my_pow_helper(x, abs(n)) if n < 0: return 1/res return res def my_pow_helper(self, x, n): if x == 0: return 0 if n == 0: return 1 if n == 1: return x half_n = n // 2 n_is_odd = n % 2 != 0 # calculate power half_power = self.my_pow_helper(x, half_n) if n_is_odd: return half_power * half_power * x return half_power * half_power -
Divide Two Integers ***
Divide Two Integers | Live Coding with Explanation | Leetcode -29

Screen Recording 2021-11-29 at 19.50.23.mov
""" Divide Two Integers: Given two integers dividend and divisor, divide two integers without using multiplication, division, and mod operator. Return the quotient after dividing dividend by divisor. The integer division should truncate toward zero, which means losing its fractional part. For example, truncate(8.345) = 8 and truncate(-2.7335) = -2. Note: Assume we are dealing with an environment that could only store integers within the 32-bit signed integer range: [−231, 231 − 1]. For this problem, assume that your function returns 231 − 1 when the division result overflows. Example 1: Input: dividend = 10, divisor = 3 Output: 3 Explanation: 10/3 = truncate(3.33333..) = 3. Example 2: Input: dividend = 7, divisor = -3 Output: -2 Explanation: 7/-3 = truncate(-2.33333..) = -2. Example 3: Input: dividend = 0, divisor = 1 Output: 0 Example 4: Input: dividend = 1, divisor = 1 Output: 1 https://leetcode.com/problems/divide-two-integers """ class SolutionBF: def divide(self, dividend: int, divisor: int): is_neg = False if divisor < 0: divisor = abs(divisor) is_neg = not is_neg if dividend < 0: dividend = abs(dividend) is_neg = not is_neg count = 0 while dividend >= divisor: dividend -= divisor count += 1 if is_neg: return -count return count """ dividend = 28, divisor = 3 Repeated Exponential Searches - Keep on doubling divisor till it cannot be doubled more 3 =3 =3*2^0 6 =3*2 =3*2^1 12 =3*2*2 =3*2^2 24 =3*2*2*2 =3*2^3 => 8 threes we remained with 28-4 - repeat the above process for """ class Solution: def divide(self, dividend: int, divisor: int): # Special case: overflow MAX_INT = 2147483647 # 2**31 - 1 MIN_INT = -2147483648 # -2**31 if dividend == MIN_INT and divisor == -1: return MAX_INT # handle negatives is_neg = False if divisor < 0: divisor = abs(divisor) is_neg = not is_neg if dividend < 0: dividend = abs(dividend) is_neg = not is_neg result = 0 # quotient # # actual division ---------------------------------------------------- while dividend >= divisor: curr_divisor = divisor two_power = 0 while curr_divisor+curr_divisor <= dividend: curr_divisor += curr_divisor # (double divisor) two_power += 1 # record that we doubled the divisor result += 2**two_power # we used the divisor 2**two_power times dividend -= curr_divisor # remaining # # ---------------------------------------------------- if is_neg: return -result return result -
Random Pick with Weight *
""" Random Pick with Weight: (answers are so random) You are given an array of positive integers w where w[i] describes the weight of ith index (0-indexed). We need to call the function pickIndex() which randomly returns an integer in the range [0, w.length - 1]. pickIndex() should return the integer proportional to its weight in the w array. For example, for w = [1, 3], the probability of picking the index 0 is 1 / (1 + 3) = 0.25 (i.e 25%) while the probability of picking the index 1 is 3 / (1 + 3) = 0.75 (i.e 75%). More formally, the probability of picking index i is w[i] / sum(w). Example 1: Input ["Solution","pickIndex"] [[[1]],[]] Output [null,0] Explanation Solution solution = new Solution([1]); solution.pickIndex(); // return 0. Since there is only one single element on the array the only option is to return the first element. Example 2: Input ["Solution","pickIndex","pickIndex","pickIndex","pickIndex","pickIndex"] [[[1,3]],[],[],[],[],[]] Output [null,1,1,1,1,0] Explanation Solution solution = new Solution([1, 3]); solution.pickIndex(); // return 1. It's returning the second element (index = 1) that has probability of 3/4. solution.pickIndex(); // return 1 solution.pickIndex(); // return 1 solution.pickIndex(); // return 1 solution.pickIndex(); // return 0. It's returning the first element (index = 0) that has probability of 1/4. Since this is a randomization problem, multiple answers are allowed so the following outputs can be considered correct : [null,1,1,1,1,0] [null,1,1,1,1,1] [null,1,1,1,0,0] [null,1,1,1,0,1] [null,1,0,1,0,0] ...... and so on. https://leetcode.com/problems/random-pick-with-weight """ import random """ Example: [1,2,3] [1/5, 2/5, 3/5] 1 2 3 |-|--|---| => 5 [1,3] 1 3 |-|---| [1,1,2] 1 1 2 |-|-|--| [0-0.25, 0.25-0.5, 0.5-1] """ # Your Solution object will be instantiated and called as such: # obj = Solution(w) # param_1 = obj.pickIndex() class Solution: def __init__(self, w): self.w = w self.total = sum(w) self.probability_range = [] prev_probability = 0 for num in self.w: curr = prev_probability + num/self.total self.probability_range.append(curr) prev_probability = curr # print(self.probability_range) def pickIndex(self): pick = random.random() # binary search left = 0 right = len(self.probability_range) while left < right: mid = (left+right) // 2 if self.probability_range[mid] > pick: right = mid else: left = mid + 1 return left -
Find Peak Element
""" Find Peak Element A peak element is an element that is strictly greater than its neighbors. Given an integer array nums, find a peak element, and return its index. If the array contains multiple peaks, return the index to any of the peaks. You may imagine that nums[-1] = nums[n] = -∞. You must write an algorithm that runs in O(log n) time. Example 1: Input: nums = [1,2,3,1] Output: 2 Explanation: 3 is a peak element and your function should return the index number 2. Example 2: Input: nums = [1,2,1,3,5,6,4] Output: 5 Explanation: Your function can return either index number 1 where the peak element is 2, or index number 5 where the peak element is 6. https://leetcode.com/problems/find-peak-element/ """ """ [1,2,3,1] => 2 [1,2,3,4,5] => 4 [5,4,3,2,1] => 0 Binary search: - if the element at mid is in an increasing order: - if we move to the right, we might find a peak(decreases) or the array end which are both valid answers - the opposite is also True """ class Solution: def findPeakElement(self, nums): if len(nums) == 1: return 0 left = 0 right = len(nums)-1 while left <= right: mid = (left+right) // 2 # ends (also is peak) if mid == 0: if nums[mid+1] < nums[mid]: return mid left = mid + 1 elif mid == len(nums)-1: if nums[mid-1] < nums[mid]: return mid right = mid # is peak but not on ends elif nums[mid-1] < nums[mid] and nums[mid+1] < nums[mid]: return mid # is increasing elif nums[mid-1] < nums[mid]: left = mid + 1 # is increasing else: right = mid -
Search a 2D Matrix

Treat is as one long 1D array




""" Search a 2D Matrix: Write an efficient algorithm that searches for a value in an m x n matrix. This matrix has the following properties: Integers in each row are sorted from left to right. The first integer of each row is greater than the last integer of the previous row. https://leetcode.com/problems/search-a-2d-matrix/ """ from typing import List """ Search In Sorted Matrix: You're given a two-dimensional array (a matrix) of distinct integers and a target integer. Each row in the matrix is sorted, and each column is also sorted; the matrix doesn't necessarily have the same height and width. Write a function that returns an array of the row and column indices of the target integer if it's contained in the matrix, otherwise [-1, -1]. Sample Input: matrix = [ [1, 4, 7, 12, 15, 1000], [2, 5, 19, 31, 32, 1001], [3, 8, 24, 33, 35, 1002], [40, 41, 42, 44, 45, 1003], [99, 100, 103, 106, 128, 1004], ] target = 44 Sample Output: [3, 3] https://www.algoexpert.io/questions/Search%20In%20Sorted%20Matrix """ class Solution0: def binarySearch(self, target, array): left = 0 right = len(array)-1 while left <= right: mid = (right + left) // 2 if array[mid] == target: return True if array[mid] < target: left = mid + 1 else: right = mid - 1 return False def searchMatrix(self, matrix: List[List[int]], target: int): for row in matrix: if row[0] <= target and row[-1] >= target: return self.binarySearch(target, row) return False """ matrix = [ [1, 3, 5, 7], [10,11,16,20], [23,30,34,60] ] target = 13 Output: false target = 16 Output: true target = 16 --- if we start at 0,0 - we do not know if it is in current row, or those below --- if we start at 0,4 - we are sure it isn't in current row, we move down - at 1,4: - we are sure it is in this row or none other """ class Solution: def searchMatrix(self, matrix: List[List[int]], target: int): row = 0 while row < len(matrix): # # check rows # check last item in row if matrix[row][len(matrix[0])-1] < target: # move to next row row += 1 elif matrix[row][0] > target: return False # # found correct row # Binary Search on Row else: left = 0 right = len(matrix[0])-1 while left <= right: mid = (right + left) // 2 if matrix[row][mid] == target: return True if matrix[row][mid] < target: left = mid + 1 else: right = mid - 1 return False return False def searchInSortedMatrix(matrix, target): # start at top right row = 0 col = len(matrix[0]) - 1 while row < len(matrix) and col >= 0: if matrix[row][col] > target: col -= 1 # move left elif matrix[row][col] < target: row += 1 # move down else: return[row, col] return[-1, -1] """ matrix = [ [1, 4, 7, 12, 15, 1000], [2, 5, 19, 31, 32, 1001], [3, 8, 24, 33, 35, 1002], [40, 41, 42, 44, 45, 1003], [99, 100, 103, 106, 128, 1004], ] target = 44 - Start curr at the top right corner - Check wether you should increase or decrease curr's value Move sideways(decrease), downwards (increase) - """
Advanced Binary Search I
This is an advanced form of binary search that is used to search for an element or condition which requires accessing the current index & its right neighbour's index.
Basic logic:
check out the examples
def search(self, nums, target):
if not nums or len(nums) < 1:
return -1
left, right = 0, len(nums) -1
while left < right:
mid = (left+right) // 2
if nums[mid] == target:
return mid
elif target > nums[mid]:
left = mid + 1
else:
right = mid
# because of left < right : the middle pointer will never be at the right pointer,
# so if the the target is at the end of the array,
# the right pointer will never be checked (right = nums[-1]) and, hence never find the target
# example: search([1,2,3], 3) -> will return -1
if left < len(nums) and nums[left] == target:
return left
return -1
Key Attributes:
- Most of the time Post-processing required. Loop/Recursion ends when you have 1 element left. Need to assess if the remaining element meets the condition.
This is because the
while left < rightinstead ofwhile left <= right* If the target is at the right index, it won't have been found in the initial search(while loop). - Search Condition needs to access the element's immediate right/left neighbour
- Use the element's right/left neighbour to determine if the condition is met and decide whether to go left or right
- Guarantees Search Space is at least 2 in size at each step
- An advanced way to implement Binary Search.
Distinguishing Syntax:
- Initial Condition:
left = 0, right = length - Termination:
left == right - Searching Left:
right = mid - Searching Right:
left = mid+1
Examples
-
Find Minimum in Rotated Sorted Array
""" Find Minimum in Rotated Sorted Array: Suppose an array of length n sorted in ascending order is rotated between 1 and n times. For example, the array nums = [0,1,2,4,5,6,7] might become: [4,5,6,7,0,1,2] if it was rotated 4 times. [0,1,2,4,5,6,7] if it was rotated 7 times. Notice that rotating an array [a[0], a[1], a[2], ..., a[n-1]] 1 time results in the array [a[n-1], a[0], a[1], a[2], ..., a[n-2]]. Given the sorted rotated array nums, return the minimum element of this array. https://leetcode.com/problems/find-minimum-in-rotated-sorted-array/ After this: Search in Rotated Sorted Array https://leetcode.com/problems/search-in-rotated-sorted-array/ """ class Solution: # search for the beginning of the unsorted part def findMin(self, nums): if not nums: return None left, right = 0, len(nums) - 1 while left < right: mid = (right + left) // 2 # look for the beginning of the unsorted part if nums[mid] > nums[mid+1]: return nums[mid+1] if nums[mid - 1] > nums[mid]: return nums[mid] # Binary Search if nums[mid] > nums[right]: # check if right side is unsorted left = mid + 1 else: right = mid - 1 # return smallest number return nums[left] """ [3,4,5,1,2] [4,5,6,7,0,1,2] [11,13,15,17] [11,13,15,17,10] [1] [3,1,2] """ -
Search in Rotated Sorted Array
""" Search in Rotated Sorted Array: There is an integer array nums sorted in ascending order (with distinct values). Prior to being passed to your function, nums is rotated at an unknown pivot index k (0 <= k < nums.length) such that the resulting array is [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]] (0-indexed). For example, [0,1,2,4,5,6,7] might be rotated at pivot index 3 and become [4,5,6,7,0,1,2]. Given the array nums after the rotation and an integer target, return the index of target if it is in nums, or -1 if it is not in nums. You must write an algorithm with O(log n) runtime complexity. Example 1: Input: nums = [4,5,6,7,0,1,2], target = 0 Output: 4 Example 2: Input: nums = [4,5,6,7,0,1,2], target = 3 Output: -1 Example 3: Input: nums = [1], target = 0 Output: -1 https://leetcode.com/problems/search-in-rotated-sorted-array/ https://www.algoexpert.io/questions/Shifted%20Binary%20Search Prerequisite: Find Minimum in Rotated Sorted Array https://leetcode.com/problems/find-minimum-in-rotated-sorted-array/ """ class Solution_: def search(self, nums, target): start_idx = self.get_smallest_num_idx(nums) if target >= nums[start_idx] and target <= nums[-1]: return self.binary_search(nums, target, start_idx, len(nums)-1) return self.binary_search(nums, target, 0, start_idx) def get_smallest_num_idx(self, nums): left = 0 right = len(nums)-1 while left <= right: mid = (left+right)//2 if mid > 0 and nums[mid-1] > nums[mid]: return mid if mid < len(nums)-1 and nums[mid+1] < nums[mid]: return mid+1 # if right is unsorted if nums[mid] > nums[right]: left = mid + 1 else: right = mid - 1 return left def binary_search(self, nums, target, left, right): while left <= right: mid = (left+right) // 2 if nums[mid] == target: return mid elif target > nums[mid]: left = mid + 1 else: right = mid - 1 return -1 """ - we know that: - If a section (left-mid or mid-right) is unsorted then the other must be sorted """ class Solution: def search(self, nums, target): left = 0 right = len(nums)-1 while left <= right: mid = (left+right)//2 if nums[mid] == target: return mid if nums[left] <= nums[mid]: # left is sorted if target >= nums[left] and target <= nums[mid]: # in left right = mid else: left = mid + 1 else: # right is sorted if target >= nums[mid] and target <= nums[right]: # in right left = mid else: right = mid - 1 return -1 -
First Bad Version
""" First Bad Version: You are a product manager and currently leading a team to develop a new product. Unfortunately, the latest version of your product fails the quality check. Since each version is developed based on the previous version, all the versions after a bad version are also bad. Suppose you have n versions [1, 2, ..., n] and you want to find out the first bad one, which causes all the following ones to be bad. You are given an API bool isBadVersion(version) which returns whether version is bad. Implement a function to find the first bad version. You should minimize the number of calls to the API. Example 1: Input: n = 5, bad = 4 Output: 4 Explanation: call isBadVersion(3) -> false call isBadVersion(5) -> true call isBadVersion(4) -> true Then 4 is the first bad version. Example 2: Input: n = 1, bad = 1 Output: 1 https://leetcode.com/problems/first-bad-version/ """ # The isBadVersion API is already defined for you. # @param version, an integer # @return an integer # def isBadVersion(version): def isBadVersion(mid): pass class Solution: def firstBadVersion(self, n): first_bad = n-1 left = 1 right = n while left <= right: mid = (left+right) // 2 if isBadVersion(mid): first_bad = mid right = mid - 1 else: left = mid + 1 return first_bad class Solution_: def firstBadVersion(self, n): left = 1 right = n while left < right: mid = (left+right) // 2 if isBadVersion(mid): # in the next loop, this will result in left being brought closer to the bad versions # [1,2,3] if bv=2, l=0, r=2, in the next, l=2 # avoid skipping bad versions right = mid else: # only move left if mid version is good # this ensures left never skips any bad version, it will always land on the first bad version # skip all good versions left = mid + 1 return left """ try to move left to the first bad version - make sure not to pass it (bad version) with right """ """ // [1,2,3] [0,1,2,3,4,5,6,7,8] [1,2,3,4,5,6,7,8,9] 6 and above r = 9 l = 1 m = 5 r = 9 l = 6 m = 7 [0,1,2,3,4,5,6,7,8] [1,2,3,4,5,6,7,8,9] 2 and above r = 9 l = 1 m = 5 r = 5 l = 1 m = 2 r = 2 l = 1 m = 1 r = 2 l = 2 m = 2 break """ class Solution00: def firstBadVersion(self, n): left = 1 right = n while left < right: mid = (left+right) // 2 # only move left if mid version is good # this ensures left never skips any bad version, it will always land on the first bad version if not isBadVersion(mid): left = mid + 1 # try and move right closer and closer to the first bad version else: right = mid return left -
Find First and Last Position of Element in Sorted Array/Search For Range
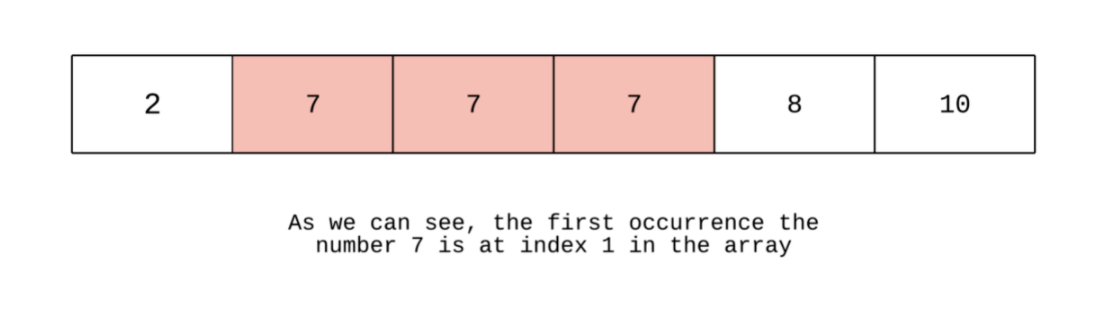
""" Find First and Last Position of Element in Sorted Array/Search For Range: Given an array of integers nums sorted in ascending order, find the starting and ending position of a given target value. If target is not found in the array, return [-1, -1]. You must write an algorithm with O(log n) runtime complexity. Example 1: Input: nums = [5,7,7,8,8,10], target = 8 Output: [3,4] Example 2: Input: nums = [5,7,7,8,8,10], target = 6 Output: [-1,-1] Example 3: Input: nums = [], target = 0 Output: [-1,-1] https://leetcode.com/problems/find-first-and-last-position-of-element-in-sorted-array/ https://www.algoexpert.io/questions/Search%20For%20Range """ """ - find the number using binary search - find start of range using binary search - find end of range using binary search [0,1,2,3,4,5] [5,7,7,8,8,10] 8 [0, 1, 2, 3, 4, 5 6, 7 8 9 10 11 12] [0, 1, 21, 33, 45, 45, 45, 45, 45, 45, 61, 71, 73] 45 # find end l, r m 6, 12 9 10,12 11 10,10 10 """ """ Simplest using pointers to remember last seen """ class Solution_P: def searchRange(self, nums, target): return [ self.find_start(nums, target), self.find_end(nums, target) ] def find_start(self, nums, target): last_seen = -1 left = 0 right = len(nums)-1 while left <= right: mid = (left+right)//2 if nums[mid] > target: right = mid - 1 elif nums[mid] < target: left = mid + 1 else: # record that we have seen it & # ignore everything to the right last_seen = mid right = mid - 1 return last_seen def find_end(self, nums, target): last_seen = -1 left = 0 right = len(nums)-1 while left <= right: mid = (left+right)//2 if nums[mid] > target: right = mid - 1 elif nums[mid] < target: left = mid + 1 else: # record that we have seen it & # ignore everything to the left last_seen = mid left = mid + 1 return last_seen """ """ class Solution00: def searchRange(self, nums, target): # # find target left = 0 right = len(nums)-1 while left <= right: mid = (left+right)//2 if nums[mid] < target: left = mid + 1 elif nums[mid] > target: right = mid - 1 else: break mid = (left+right)//2 if mid < 0 or mid >= len(nums) or nums[mid] != target: return [-1, -1] # # find start of range start_left = 0 start_right = mid while start_left < start_right: start_mid = (start_left+start_right)//2 # ensure start_right's value always == target, # when start_left == start_right, that will be the leftmost value with a value of target if nums[start_mid] == target: start_right = start_mid else: start_left = start_mid + 1 # # find end of range end_left = mid end_right = len(nums)-1 while end_left <= end_right: # print(end_left, end_right) end_mid = (end_right+end_left)//2 # ensure end_left's value always == target, # when end_right == end_left, that will be the rightmost value with a value of target if nums[end_mid] == target: end_left = end_mid + 1 else: end_right = end_mid - 1 # # return [start_left, end_right] """ improvement of above, same time complexity """ class Solution: def searchRange(self, nums, target): # # find start of range start_left = 0 start_right = len(nums)-1 while start_left < start_right: start_mid = (start_left+start_right)//2 # 1. place start_right in the target subarray if nums[start_mid] > target: start_right = start_mid continue # 2. ensure start_right's value always == target, # when start_left == start_right, that will be the leftmost value with a value of target if nums[start_mid] == target: start_right = start_mid else: start_left = start_mid + 1 # # find end of range end_left = 0 end_right = len(nums)-1 while end_left <= end_right: end_mid = (end_right+end_left)//2 # 1. place end_left in the target subarray if nums[end_mid] < target: end_left = end_mid + 1 continue # 2. find the first value not equal to target on the end_left pointer # then move the end_right - 1 coz end_left will be +1 position ahead of the last correct value if nums[end_mid] == target: end_left = end_mid + 1 else: end_right = end_mid - 1 if end_right < 0 or start_left >= len(nums) or nums[start_left] != target or nums[end_right] != target: return [-1, -1] # # return [start_left, end_right] -
Leftmost Column with at Least a One


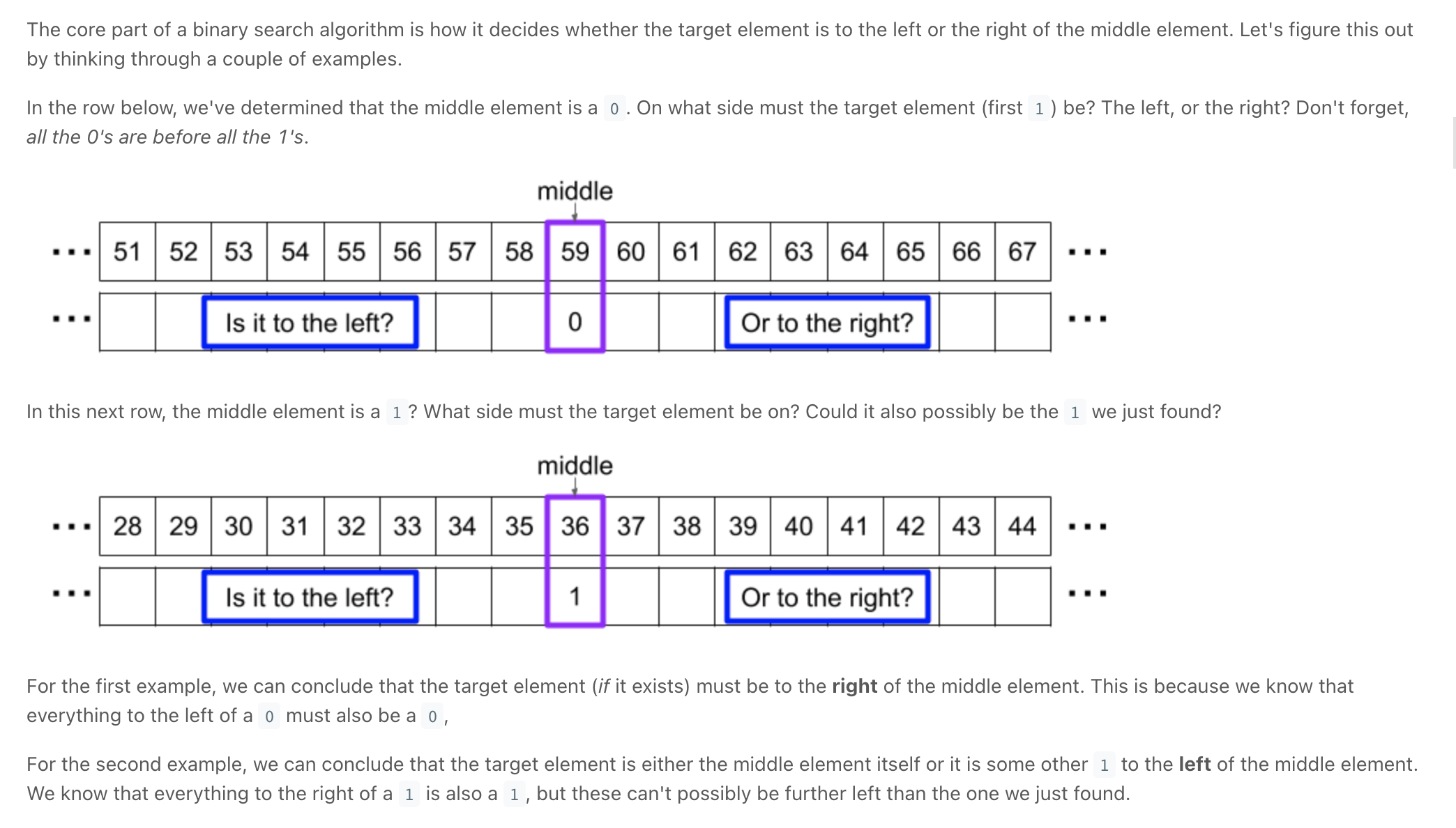

Screen Recording 2021-11-02 at 19.43.05.mov
""" Leftmost Column with at Least a One: A row-sorted binary matrix means that all elements are 0 or 1 and each row of the matrix is sorted in non-decreasing order. Given a row-sorted binary matrix binaryMatrix, return the index (0-indexed) of the leftmost column with a 1 in it. If such an index does not exist, return -1. You can't access the Binary Matrix directly. You may only access the matrix using a BinaryMatrix interface: BinaryMatrix.get(row, col) returns the element of the matrix at index (row, col) (0-indexed). BinaryMatrix.dimensions() returns the dimensions of the matrix as a list of 2 elements [rows, cols], which means the matrix is rows x cols. Submissions making more than 1000 calls to BinaryMatrix.get will be judged Wrong Answer. Also, any solutions that attempt to circumvent the judge will result in disqualification. For custom testing purposes, the input will be the entire binary matrix mat. You will not have access to the binary matrix directly. Example 1: Input: mat = [[0,0],[1,1]] Output: 0 Example 2: Input: mat = [[0,0],[0,1]] Output: 1 Example 3: Input: mat = [[0,0],[0,0]] Output: -1 Example 4: Input: mat = [[0,0,0,1],[0,0,1,1],[0,1,1,1]] Output: 1 https://leetcode.com/problems/leftmost-column-with-at-least-a-one Prerequisite: - https://leetcode.com/problems/first-bad-version """ # This is BinaryMatrix's API interface. # You should not implement it, or speculate about its implementation class BinaryMatrix(object): def get(self, row: int, col: int): pass def dimensions(self): pass """ Binary search every row: Let N be the number of rows, and M be the number of columns. Time complexity : O(NlogM). Start at the top right: similar to Search In Sorted Matrix https://leetcode.com/problems/search-a-2d-matrix Using the information that the rows are sorted, if we start searching from the right top corner(1st row, last column) and every time when we get a 1, as the row is sorted in non-decreasing order, there is a chance of getting 1 in the left column, so go to previous column in the same row. And if we get 0, there is no chance that in that row we can find a 1, so go to next row. """ class Solution: def leftMostColumnWithOne(self, binaryMatrix: 'BinaryMatrix'): left_most = -1 rows, cols = binaryMatrix.dimensions() row = 0 col = cols-1 while row < rows and col >= 0: # find left most at each row while col >= 0 and binaryMatrix.get(row, col) == 1: left_most = col col -= 1 row += 1 return left_most
BFS + DFS == 25% of the problems
Articles:
- Leetcode Pattern 1 | BFS + DFS == 25% of the problems — part 1 → DFS
- Leetcode Pattern 1 | DFS + BFS == 25% of the problems — part 2 → BFS
Most graph, tree and string problems simply boil down to a DFS (Depth-first search) / BFS (Breadth-first search)
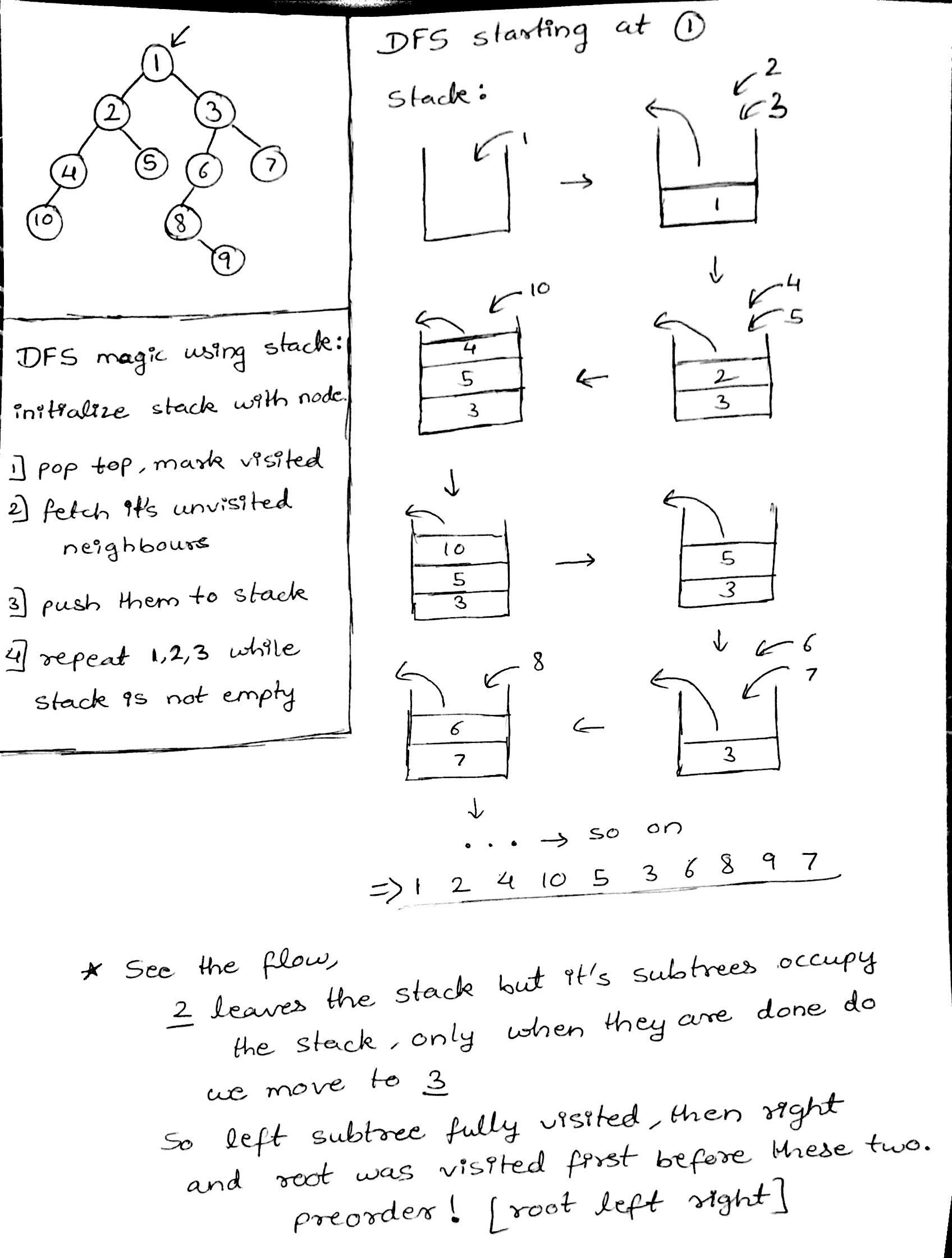
Have you ever wondered why we don’t use a queue for dfs or stack for bfs? questions like these really give us some insights into the difference between stacks and queues.
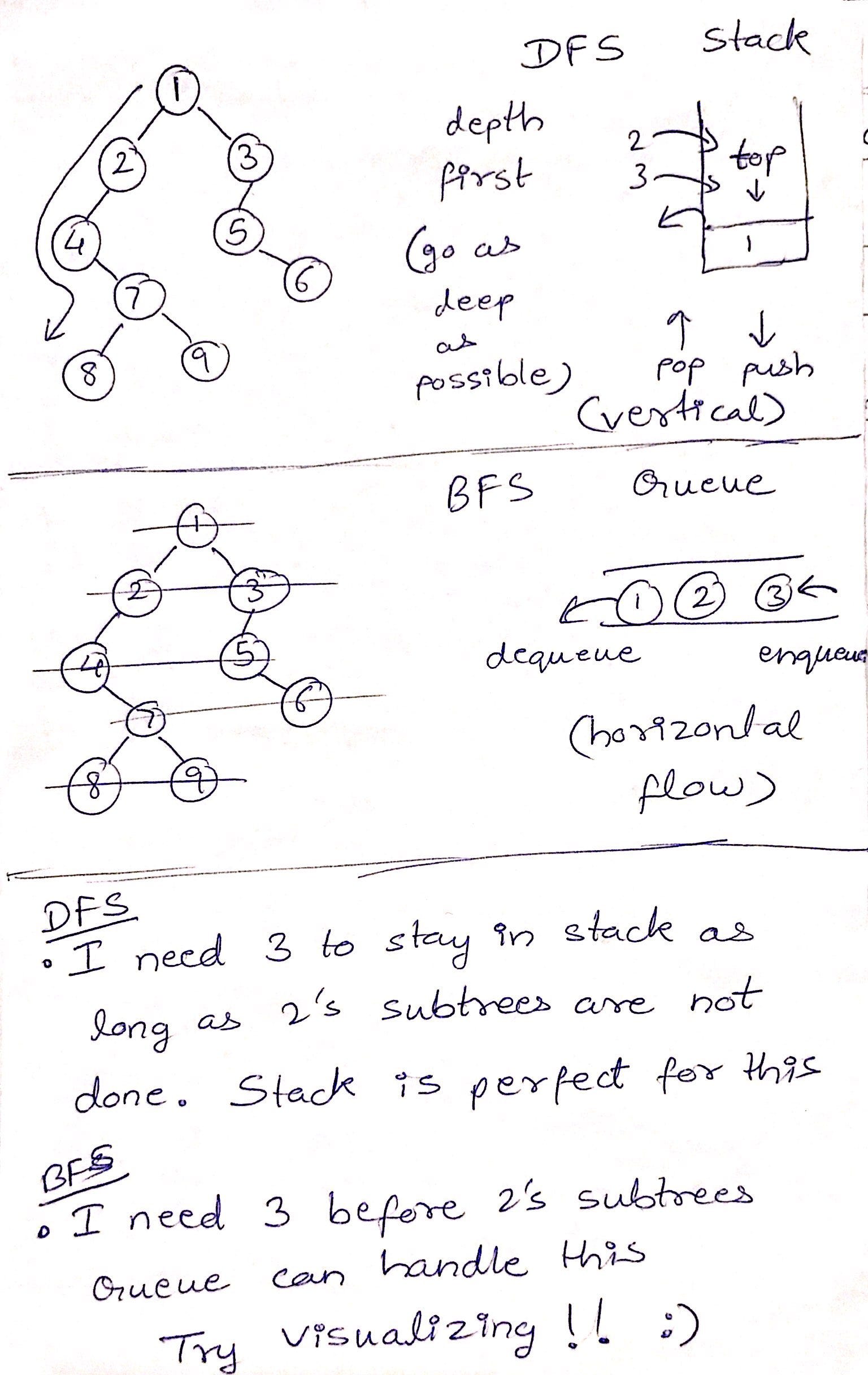
So using a stack I could pop 2 and push its kids and keep doing so eventually exhausting 2’s subtrees, 3 stays calmly in the stack just below the part where the real push-pop action is going, we pop 3 when all subtrees of 2 are done. This feature of the stack is essential for DFS.
While in a queue, I could dequeue 2 and enqueue its subtrees which go behind 3 as it was already sitting in the queue. So the next time I dequeue I get 3 and only after that do I move on to visiting 2’s subtrees, this is essentially a BFS!
For me this revelation was pure bliss. Take a moment to celebrate the history of Computer Science and the geniuses behind these simple yet powerful ideas.
Time Complexity
DFS:
Coding Patterns: Depth First Search (DFS)
DFS → diving as deep as possible before coming back to take a dive again: can use stack
Examples:
-
Course Schedule/Tasks Scheduling
-
Alien Dictionary
Basic DFS (use stack)
With recursion
class Node:
def __init__(self, name):
self.children = []
self.name = name
def depthFirstSearch(self, array):
self._depthFirstSearchHelper(array)
return array
def _depthFirstSearchHelper(self, array):
array.append(self.name)
for child in self.children:
child._depthFirstSearchHelper(array)
With stack
class Node:
def __init__(self, name):
self.children = []
self.name = name
def depthFirstSearch(self, array):
stack = [self]
while len(stack) > 0:
curr = stack.pop()
array.append(curr.name)
for idx in reversed(range(len(curr.children))):
stack.append(curr.children[idx])
return array
DFS on graph
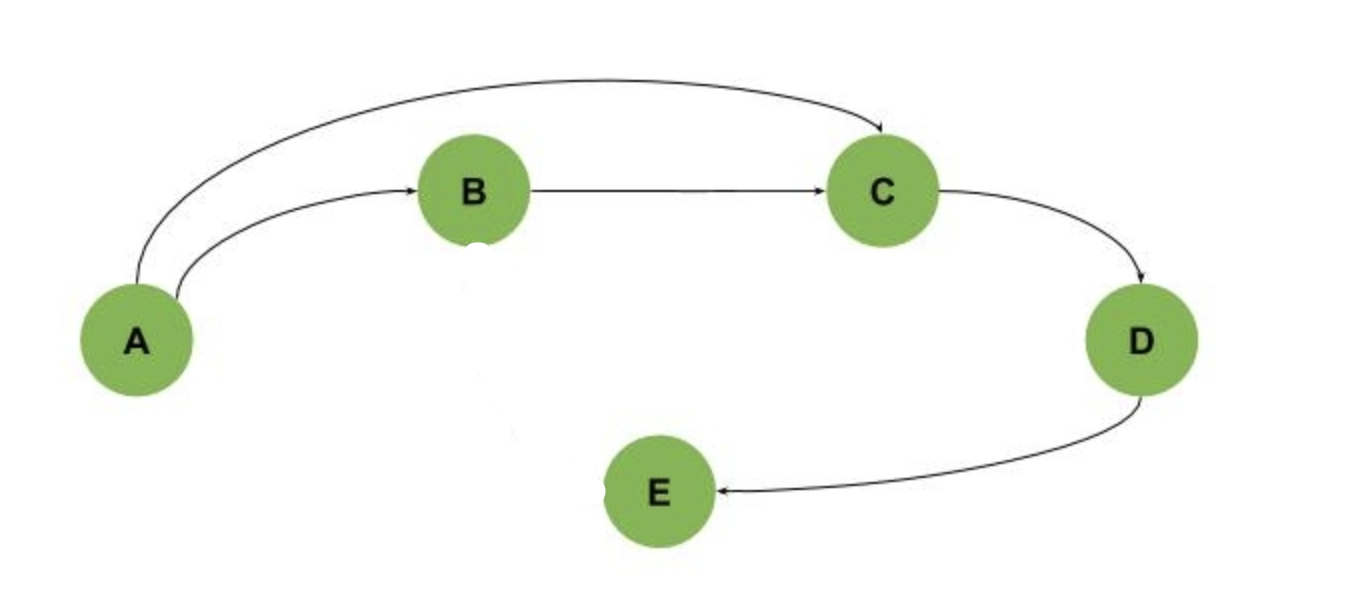
look carefully at C
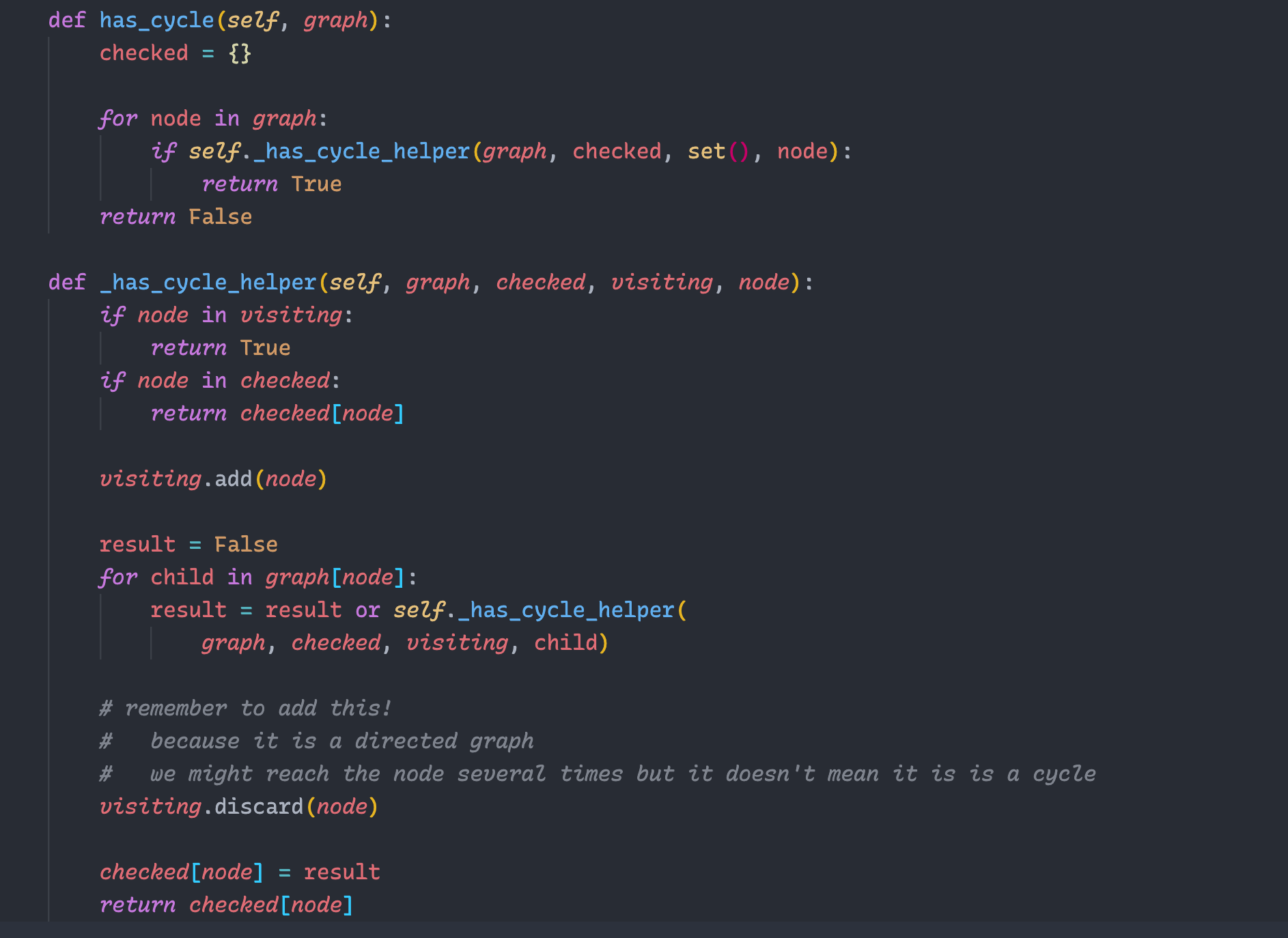
DFS on an adjacency list
With Preorder Traversal
BFS:
Coding Patterns: Breadth First Search (BFS)
Breadth First Search Algorithm | Shortest Path | Graph Theory

These are basically level order traversals.
BFS can be used to find a single-source shortest path in an unweighted graph because, in BFS, we reach a vertex with a minimum number of edges from a source vertex.
Thoughts on BFS:
- Problems in which you have to find the shortest path are most likely calling for a BFS.
- For graphs having unit edge distances, shortest paths from any point is just a BFS starting at that point, no need for Dijkstra’s algorithm.
- Maze solving problems are mostly shortest path problems and every maze is just a fancy graph so you get the flow.
Examples
🌳 Prim's Minimum Spanning Tree Algorithm *
-
Rotting Oranges
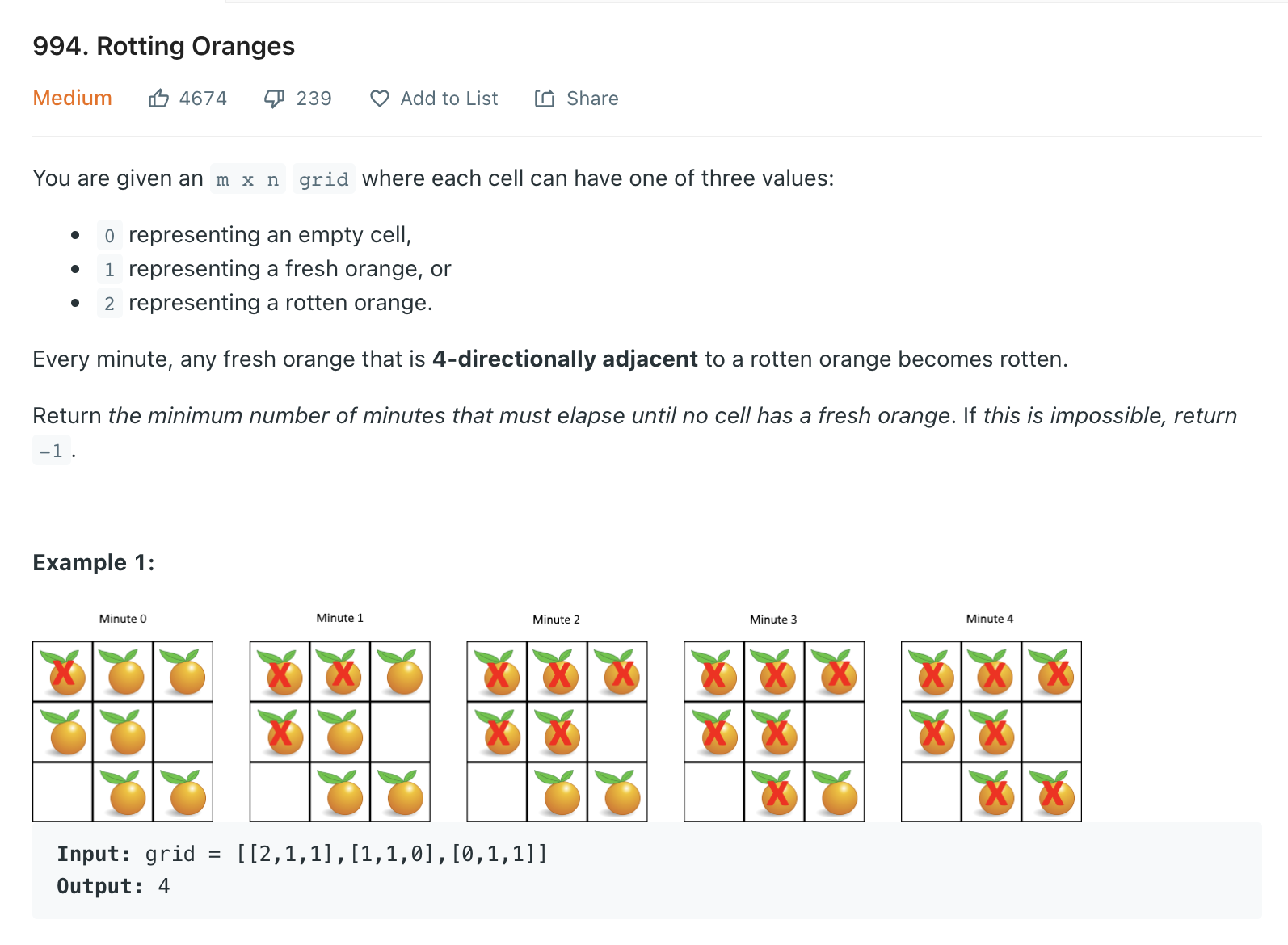
""" Rotting Oranges You are given an m x n grid where each cell can have one of three values: 0 representing an empty cell, 1 representing a fresh orange, or 2 representing a rotten orange. Every minute, any fresh orange that is 4-directionally adjacent to a rotten orange becomes rotten. Return the minimum number of minutes that must elapse until no cell has a fresh orange. If this is impossible, return -1. Example 1: Input: grid = [[2,1,1],[1,1,0],[0,1,1]] Output: 4 Example 2: Input: grid = [[2,1,1],[0,1,1],[1,0,1]] Output: -1 Explanation: The orange in the bottom left corner (row 2, column 0) is never rotten, because rotting only happens 4-directionally. Example 3: Input: grid = [[0,2]] Output: 0 Explanation: Since there are already no fresh oranges at minute 0, the answer is just 0. https://leetcode.com/problems/rotting-oranges """ from typing import List import collections """ BFS One of the most distinguished code patterns in BFS algorithms is that often we use a queue data structure to keep track of the candidates that we need to visit during the process. The main algorithm is built around a loop iterating through the queue. At each iteration, we pop out an element from the head of the queue. Then we do some particular process with the popped element. More importantly, we then append neighbors of the popped element into the queue, to keep the BFS process running. O(N) time | O(N) space """ class Solution: def orangesRotting(self, grid: List[List[int]]): minutes_needed = 0 rotten = collections.deque() # # scan the grid to find the initial values for the queue for row in range(len(grid)): for col in range(len(grid[0])): if grid[row][col] == 2: rotten.append((row, col)) # # run the BFS process on the queue, while rotten: found_fresh = False # empty rotten queue for _ in range(len(rotten)): rotten_row, rotten_col = rotten.popleft() for row, col in self.get_neighbours(grid, rotten_row, rotten_col): # if fresh if grid[row][col] == 1: grid[row][col] = 2 rotten.append((row, col)) found_fresh = True if found_fresh: minutes_needed += 1 for row in range(len(grid)): for col in range(len(grid[0])): if grid[row][col] == 1: return -1 return minutes_needed def get_neighbours(self, grid, row, col): neighbours = [] if row-1 >= 0: neighbours.append((row-1, col)) if row+1 < len(grid): neighbours.append((row+1, col)) if col-1 >= 0: neighbours.append((row, col-1)) if col+1 < len(grid[0]): neighbours.append((row, col+1)) return neighbours -
Word Search
""" Word Search Given a 2D board and a word, find if the word exists in the grid. The word can be constructed from letters of sequentially adjacent cells, where "adjacent" cells are horizontally or vertically neighboring. The same letter cell may not be used more than once. Constraints: board and word consists only of lowercase and uppercase English letters. 1 <= board.length <= 200 1 <= board[i].length <= 200 1 <= word.length <= 10^3 https://leetcode.com/problems/word-search/submissions/ """ from typing import List # O(n) time | O(n) space -> because of the recursion call stack | class Solution: def exist(self, board: List[List[str]], word: str): # Iterate over each character h = 0 while h < len(board): w = 0 while w < len(board[0]): # stop iteration if we find the word if board[h][w] == word[0] and self.searchWordOutward(board, word, h, w, 0): return True w += 1 h += 1 return False def searchWordOutward(self, board, word, h, w, word_pos): # check if past end of word (found all characters) if word_pos >= len(word): return True if h < 0 or h >= len(board) or \ w < 0 or w >= len(board[0]): return False if board[h][w] != word[word_pos]: return False # remove seen character seen_char = board[h][w] board[h][w] = '' # Expand: move on to next character (word_pos + 1) -> in the order right, left, top, bottom found = self.searchWordOutward(board, word, h, w+1, word_pos+1) or \ self.searchWordOutward(board, word, h, w-1, word_pos+1) or \ self.searchWordOutward(board, word, h+1, w, word_pos+1) or \ self.searchWordOutward(board, word, h-1, w, word_pos+1) # return seen character board[h][w] = seen_char return found """ Input: [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]] "ABCCED" [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]] "SEE" [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]] "ABCB" Output: true true false """ -
https://leetcode.com/problems/shortest-path-in-a-grid-with-obstacles-elimination/
Coding Interview Problem - Shortest Path With Obstacle Elimination
Leetcode - Shortest Path in a Grid with Obstacles Elimination (Python)
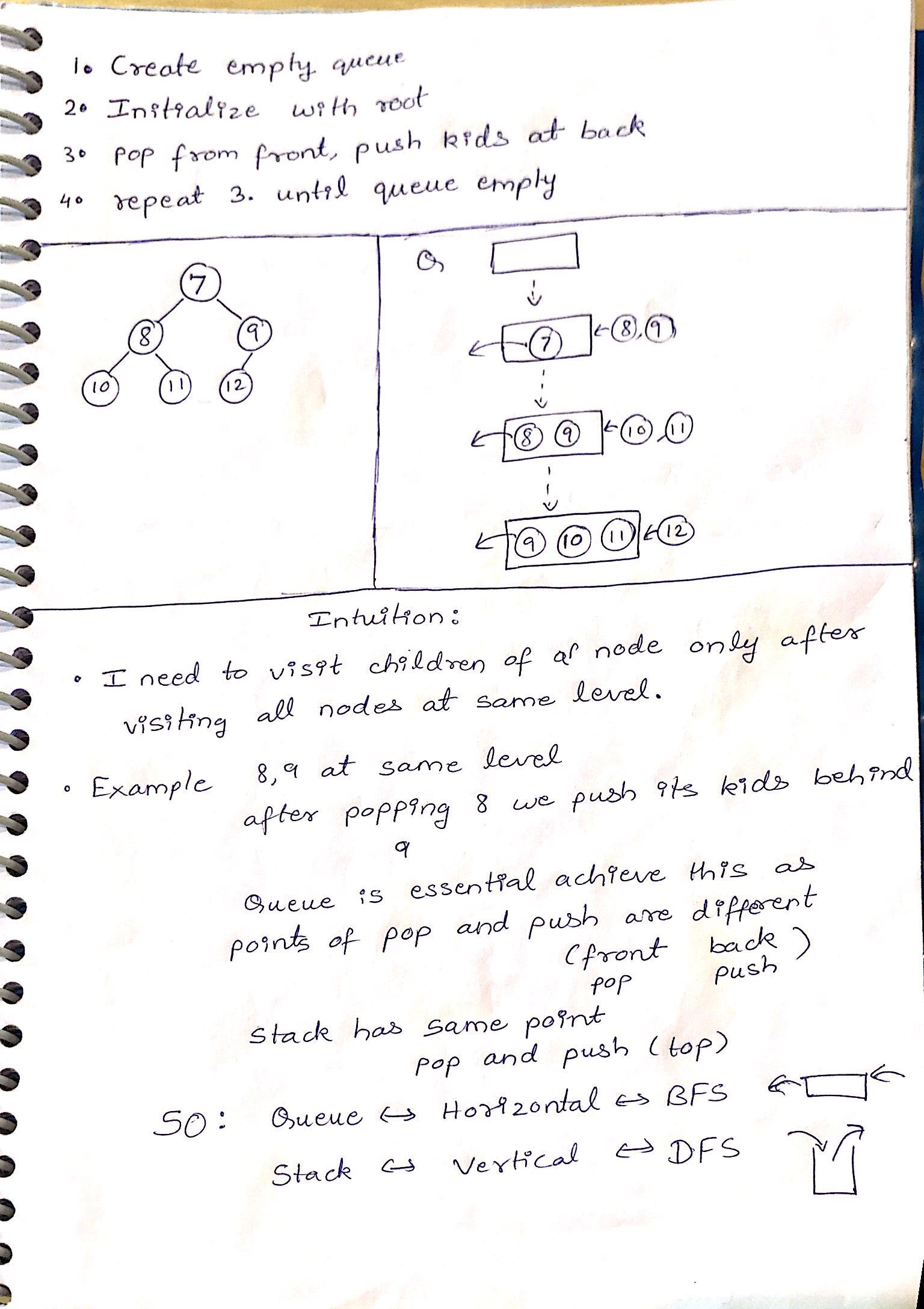
Basic BFS (uses queue)
With queue
class Node:
def __init__(self, name):
self.children = []
self.name = name
def breadthFirstSearch(self, array):
queue = [self]
while len(queue) > 0:
curr = queue.pop(0)
array.append(curr.name)
for child in curr.children:
queue.append(child)
return array
With Level order traversal:
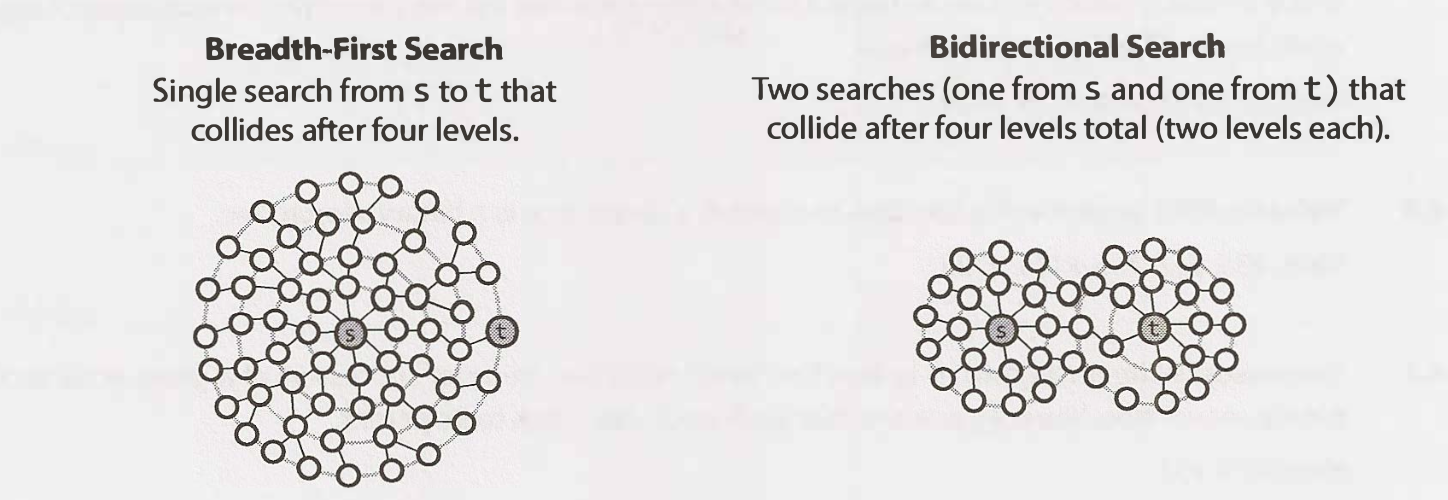
Bidirectional Search *
Bidirectional search is used to find the shortest path between a source and destination node. It operates by essentially running two simultaneous breadth-first searches, one from each node. When their searches collide, we have found a path.

BFS vs Dijkstra's?
Both are used to find the shortest path
Dijkstra's is only used on positively weighted graphs
Quick Select (used to select index)
Based on Quick Sort. The QuickSort sorting algorithm works by picking a "pivot" number from an array, positioning every other number in the array in sorted order with respect to the pivot (all smaller numbers to the pivot's left; all bigger numbers to the pivot's right), and then repeating the same two steps on both sides of the pivot until the entire array is sorted. Apply the technique used in Quick Sort until the pivot element gets positioned in the kth place in the array, at which point you'll have found the answer to the problem.
- Quicksort
Pick a random number from the input array (the first number, for instance) and let that number be the pivot. Iterate through the rest of the array using two pointers, one starting at the left extremity of the array and progressively moving to the right, and the other one starting at the right extremity of the array and progressively moving to the left.
As you iterate through the array, compare the left and right pointer numbers to the pivot. If the left number is greater than the pivot and the right number is less than the pivot, swap them; this will effectively sort these numbers with respect to the pivot at the end of the iteration. If the left number is ever less than or equal to the pivot, increment the left pointer; similarly, if the right number is ever greater than or equal to the pivot, decrement the right pointer. Do this until the pointers pass each other, at which point swapping the pivot with the right number should position the pivot in its final, sorted position, where every number to its left is smaller and every number to its right is greater.
If the pivot is in the kth position, you're done; if it isn't, figure out if the kth smallest number is located to the left or to the right of the pivot.
Repeat the process on the side of the kth smallest number, and keep on repeating the process thereafter until you find the answer.
Time Complexity
"""
Best: O(n) time | O(1) space - where n is the length of the input array
Average: O(n) time | O(1) space
Worst: O(n^2) time | O(1) space
"""
"""
Quick Select:
Pick a random number from the input array (the first number, for instance) and let that number be the pivot.
Iterate through the rest of the array using two pointers, one starting at the left extremity of the array and progressively moving to the right,
and the other one starting at the right extremity of the array and progressively moving to the left.
As you iterate through the array, compare the left and right pointer numbers to the pivot.
If the left number is greater than the pivot and the right number is less than the pivot, swap them; this will effectively sort these numbers with respect to the pivot at the end of the iteration.
If the left number is ever less than or equal to the pivot, increment the left pointer; similarly, if the right number is ever greater than or equal to the pivot, decrement the right pointer.
Do this until the pointers pass each other, at which point swapping the pivot with the right number should position the pivot in its final, sorted position,
where every number to its left is smaller and every number to its right is greater.
If the pivot is in the kth position, you're done; if it isn't, figure out if the kth smallest number is located to the left or to the right of the pivot.
Repeat the process on the side of the kth smallest number, and keep on repeating the process thereafter until you find the answer.
https://www.algoexpert.io/questions/Quickselect
https://leetcode.com/problems/kth-largest-element-in-an-array
"""
def quickselect(array, k):
return quick_select_helper(array, k-1, 0, len(array)-1)
def quick_select_helper(array, idx, start, end):
if start == end:
return array[start]
pivot = start
# # sort numbers with respect to pivot then put pivot between the large and small numbers
# left and right to stop at a place where: left >= pivot & right <= pivot
left = pivot+1
right = end
while left <= right:
# can be swapped
if array[left] > array[pivot] and array[right] < array[pivot]:
array[left], array[right] = array[right], array[left]
if array[left] <= array[pivot]: # no need to swap
left += 1
if array[right] >= array[pivot]: # no need to swap
right -= 1
# # place the pivot at correct position (right)
# # place pivot at correct position
# we know that once the sorting is done, the number at left >= pivot & right <= pivot
# smaller values go to the left of array[pivot]
array[pivot], array[right] = array[right], array[pivot]
if right == idx:
return array[right]
# # proceed search
if idx < right:
return quick_select_helper(array, idx, start, right-1)
else:
return quick_select_helper(array, idx, right+1, end)
Examples
-
Kth Largest Element in an Array
""" Kth Largest Element in an Array Given an integer array nums and an integer k, return the kth largest element in the array. Note that it is the kth largest element in the sorted order, not the kth distinct element. Example 1: Input: nums = [3,2,1,5,6,4], k = 2 Output: 5 Example 2: Input: nums = [3,2,3,1,2,4,5,5,6], k = 4 Output: 4 https://leetcode.com/problems/kth-largest-element-in-an-array """ class Solution: def findKthLargest(self, array, k): return self.quick_select(array, len(array)-k, 0, len(array)-1) def quick_select(self, array, idx, start, end): if start == end: return array[start] # # pick pivot and sort numbers relative to it (like quick sort) pivot = start # # sort numbers with respect to pivot then put pivot between the large and small numbers # left and right to stop at a place where: left >= pivot & right <= pivot left = start + 1 right = end while left <= right: # check if can be swapped if array[left] > array[pivot] and array[right] < array[pivot]: array[left], array[right] = array[right], array[left] if array[left] <= array[pivot]: # no need to swap left += 1 if array[right] >= array[pivot]: # no need to swap right -= 1 # place pivot at correct position # # place the pivot at correct position (right) # # place pivot at correct position # we know that once the sorting is done, the number at left >= pivot & right <= pivot # smaller values go to the left of array[pivot] # # right is at a value < pivot, so ot should be moved left array[pivot], array[right] = array[right], array[pivot] # after swapping right is the only number we are sure is sorted # check if we are at the idx being looked for if right == idx: return array[right] # # proceed search elif right < idx: return self.quick_select(array, idx, right+1, end) else: return self.quick_select(array, idx, start, right-1) x = Solution() x.findKthLargest([5, 6, 4], 2)
More Reading
https://emre.me/algorithms/search-algorithms/
Find the original version of this page (with additional content) on Notion here.
Created: December 13, 2021 16:05:48