Sliding Window
Introduction
Related
How to Solve Sliding Window Problems
Basic concept
Your window represents the current section of the string/array that you are “looking at” and usually there is some information stored along with it in the form of constants. At the very least it will have 2 pointers, one indicating the index corresponding beginning of the window, and one indicating the end of the window.
In many problems dealing with an array (or a LinkedList), we are asked to find or calculate something among all the contiguous subarrays of a given size.
Given an array, find the average of all contiguous subarrays of size ‘K’ in it.
Let’s understand this problem with a real input:
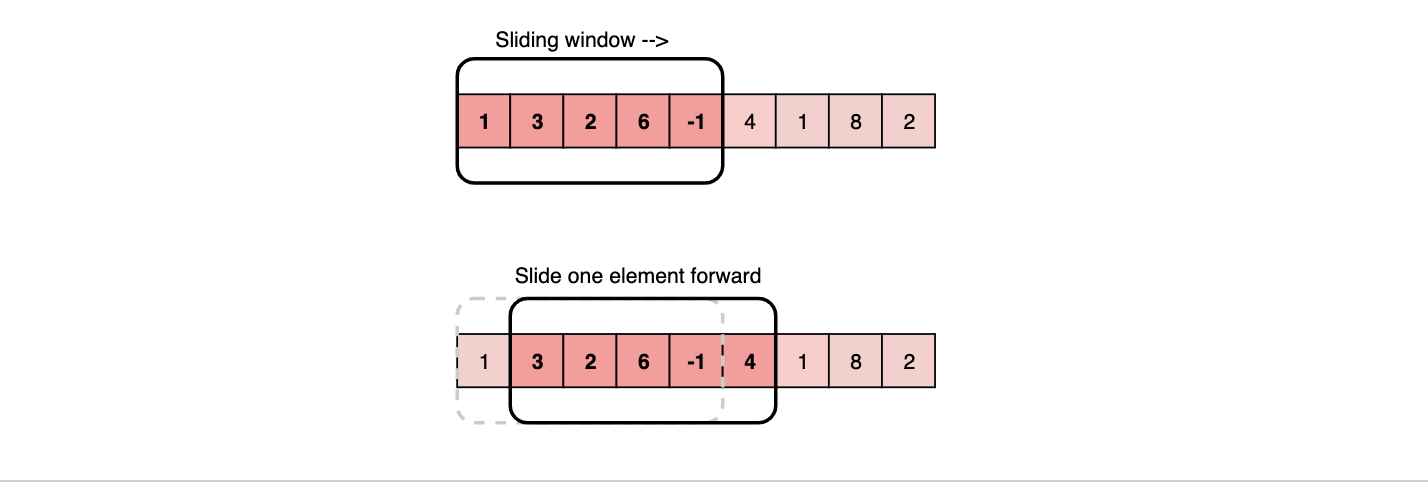
Array: [1, 3, 2, 6, -1, 4, 1, 8, 2], K=5
Here is the final output containing the averages of all contiguous subarrays of size 5:
Output: [2.2, 2.8, 2.4, 3.6, 2.8]
A brute-force algorithm will calculate the sum of every 5-element contiguous subarray of the given array and divide the sum by ‘5’ to find the average. Since for every element of the input array, we are calculating the sum of its next ‘K’ elements, the time complexity of the above algorithm will be O(N*K) where ‘N’ is the number of elements in the input array.
Do you see any inefficiency? The inefficiency is that for any two consecutive subarrays of size ‘5’, the overlapping part (four elements) will be evaluated twice. For example, take the above-mentioned input: As you can see, there are four overlapping elements between the subarray (indexed from 0-4) and the subarray (indexed from 1-5).

Can we somehow reuse the sum we have calculated for the overlapping elements?
Can we somehow reuse the sum we have calculated for the overlapping elements?
The efficient way to solve this problem would be to visualize each contiguous subarray as a sliding window of ‘5’ elements. This means that we will slide the window by one element when we move on to the next subarray. To reuse the sum from the previous subarray, we will subtract the element going out of the window and add the element now being included in the sliding window. This will save us from going through the whole subarray to find the sum and, as a result, the algorithm complexity will reduce to O(N).
How do you identify them?
There are some common giveaways:
- The problem will involve a data structure that is ordered and iterable like an array or a string
- You are looking for some subrange in that array/string, like a longest, shortest or target value.
- There is an apparent naive or brute force solution that runs in O(N²), O(2^N) or some other large time complexity.
Why is this dynamic programming?
They are a subset of dynamic programming problems, though the approach to solving them is quite different from the one used in solving tabulation or memoization problems. So different in fact, that to a lot of engineers it isn’t immediately clear that there even is a connection between the two at all.
Not that important btw...
This search for an optimum hints at the relationship between sliding window problems and other dynamic problems. You are using the optimal substructure property of the problem to guarantee that an optimal solution to a subproblem can be reused to help you find the optimal solution to a larger problem.
You are also using the fact that there are overlapping subproblems in the naive approach, to reduce the amount of work you have to do. Take the Minimum Window Substring problem. You are given a string, and a set of characters you need to look for in that string. There might be multiple overlapping substrings that contain all the characters you are looking for, but you only want the shortest one. These characters can also be in any order.
Implementation
One amazing thing about sliding window problems is that most of the time they can be solved in O(N) time and O(1) space complexity.
Example:
# find characters in string
String = 'ADOBECODEBANC'
Characters = 'ABC'
The naive way to approach this would be to first, scan through the string, looking at ALL the substrings of length 3, and check to see if they contain the characters you’re looking for. If you can’t find any of length 3, then try all substrings of length 4, and 5, and 6, and 7 and so on until you reach the length of the string. If you reach that point, you know that those characters are not in there.
This is really inefficient and runs in O(N²) time. And what’s happening is that you are missing out a lot of good information on each pass by constraining yourself to look at fixed length windows, and you’re re-examining a lot of parts of the string that don’t need to be re-examined.
You’re throwing out a lot of good work, and you’re redoing a lot of useless work.
Different Kinds of Windows
There are several kinds of sliding window problems.

1st pointer/2nd pointer
1) Fast/Slow
These ones have a fast pointer that grows your window under a certain condition. So for Minimum Window Substring, you want to grow your window until you have a window that contains all the characters you’re looking for. It will also have a slow pointer, that shrinks the window. Once you find a valid window with the fast pointer, you want to start sliding the slow pointer up until you no longer have a valid window.
For example, in the Minimum Window Substring problem, once you have a substring that contains all the characters you’re looking for, then you want to start shrinking it by moving the slow pointer up until you no longer have a valid substring (meaning you no longer have all the characters you’re looking for)
2) Fast/Catchup
This is very similar to the first kind, except, instead of incrementing the slow pointer up, you simply move it up the fast pointer’s location and then keep moving the fast pointer up. It sort of jumps or catches up to the index of the fast pointer when a certain condition is met.
This is apparent in the Max Consecutive Sum problem. Here you’re given a list of integers, positive and negative, and you are looking for a consecutive sequence that sums to the largest amount. Key insight: The slow pointer “jumps” to the fast pointer’s index when the current sum ends up being negative. More on how this works later.
For example, in the array: [1, 2, 3, -7, 7, 2, -12, 6] the result would be: 9 (7 + 2)
Again, you’re looking for some kind of optimum (ie the maximum sum).
3) Fast/Lagging
This one is a little different, but essentially the slow pointer is simply referencing one or two indices behind the fast pointer and it’s keeping track of some choice you’ve made.
For example, in the House Robber problem you are trying to see what the maximum amount of gold you can steal from houses that are not next door to each other. Here the choice is whether or not you should steal from the current house, given that you could instead have stolen from the previous house.The optimum you are looking for is the maximum amount of gold you can steal.
4) Front/Back
These ones are different because instead of having both pointers traveling from the front, you have one from the front, and the other from the back. An example of this is the Rainwater Problem where you are calculating the maximum amount of rainwater you can capture in a given terrain. Again, you are looking for a maximum value, though the logic is slightly different, you are still optimizing a brute force O(N²) solution.
These four patterns should come as no surprise. After all, there are only so many ways you can move two pointers through an array or string in linear time.

Look for “Key Insights”
One final thing to think about with these problems is the key insight that “unlocks” the problem. It usually involves deducing some fact based on the constraints of the problem that helps you look at it in a different way.
For example, in the House Robber problem, you can’t rob adjacent houses, but all houses have a positive amount of gold (meaning you can’t rob a house and have less gold after robbing it). The key insight here is that the maximum distance between any two houses you rob will be two. If you had three houses between robberies, you could just rob the one in the center of the three and you will be guaranteed to increase the amount of gold you steal.
For the Bit Flip problem, you don’t need to actually mutate the array in the problem, you just need to keep track of how many flips you have remaining. As you grow your window, you subtract from that number until you’ve exhausted all your flips, and then you shrink your window until you encounter a zero and gain a flip back.
Maximum Sum Subarray of Size K
"""
Maximum Sum Subarray of Size K (easy):
Given an array of positive numbers and a positive number ‘k,’ find the maximum sum of any contiguous subarray of size ‘k’.
Example 1:
Input: [2, 1, 5, 1, 3, 2], k=3
Output: 9
Explanation: Subarray with maximum sum is [5, 1, 3].
Example 2:
Input: [2, 3, 4, 1, 5], k=2
Output: 7
Explanation: Subarray with maximum sum is [3, 4].
https://www.educative.io/courses/grokking-the-coding-interview/JPKr0kqLGNP
"""
Solution
If has negative numbers:
A basic brute force solution will be to calculate the sum of all ‘k’ sized subarrays of the given array to find the subarray with the highest sum. We can start from every index of the given array and add the next ‘k’ elements to find the subarray’s sum.
If you observe closely, you will realize that to calculate the sum of a contiguous subarray, we can utilize the sum of the previous subarray. For this, consider each subarray as a Sliding Window of size ‘k.’ To calculate the sum of the next subarray, we need to slide the window ahead by one element. So to slide the window forward and calculate the sum of the new position of the sliding window, we need to do two things:
- Subtract the element going out of the sliding window, i.e., subtract the first element of the window.
- Add the new element getting included in the sliding window, i.e., the element coming right after the end of the window.
This approach will save us from re-calculating the sum of the overlapping part of the sliding window. Here is what our algorithm will look like:
Code
"""
Maximum Sum Subarray of Size K (easy):
Given an array of positive numbers and a positive number ‘k,’
find the maximum sum of any contiguous subarray of size ‘k’.
Example 1:
Input: [2, 1, 5, 1, 3, 2], k=3
Output: 9
Explanation: Subarray with maximum sum is [5, 1, 3].
Example 2:
Input: [2, 3, 4, 1, 5], k=2
Output: 7
Explanation: Subarray with maximum sum is [3, 4].
https://www.educative.io/courses/grokking-the-coding-interview/JPKr0kqLGNP
"""
"""
## Q
Given array, find the max contiguous array of size k
"""
"""
## SOLUTION
# Brute force
- create all contiguous subarrays of size k possible & find each of their sums then return the max
- this can be done by iterating k-1 steps forward at each point in the array
# Optimal
- create a window of size k, and record its sum
- iterate through the array,
adding the next element to the window (adding it to the sum), & at the same time
remove the 1st element in the window (remove its value from the sum),
record the sum if it is larger than the prev recorded sum
- repeat the step above till each subarray is considered
[0,1,2,3,4], k=3 +> 9
"""
# l=0, r=2 c=6, m=3
# l=1, r=3, c=6, m=6
# l=2, r=4, c=9, m=9
def max_sub_array_of_size_k(k, arr):
if len(arr) < k:
return -1
curr_sum = 0
maximum = -1
# first subarray -> create window
for idx in range(k):
curr_sum += arr[idx]
maximum = curr_sum
# other subarrays
for idx in range(1, len(arr)-(k-1)):
curr_sum -= arr[idx-1] # remove from window
curr_sum += arr[idx+(k-1)] # add to window
maximum = max(curr_sum, maximum)
return maximum
Time & space complexity
O(N) time | O(1) space
Smallest Subarray with a given sum
Problem
"""
Smallest Subarray with a given sum:
Given an array of positive numbers and a positive number ‘S,’
find the length of the smallest contiguous subarray whose sum is greater than or equal to ‘S’.
Return 0 if no such subarray exists.
Example 1:
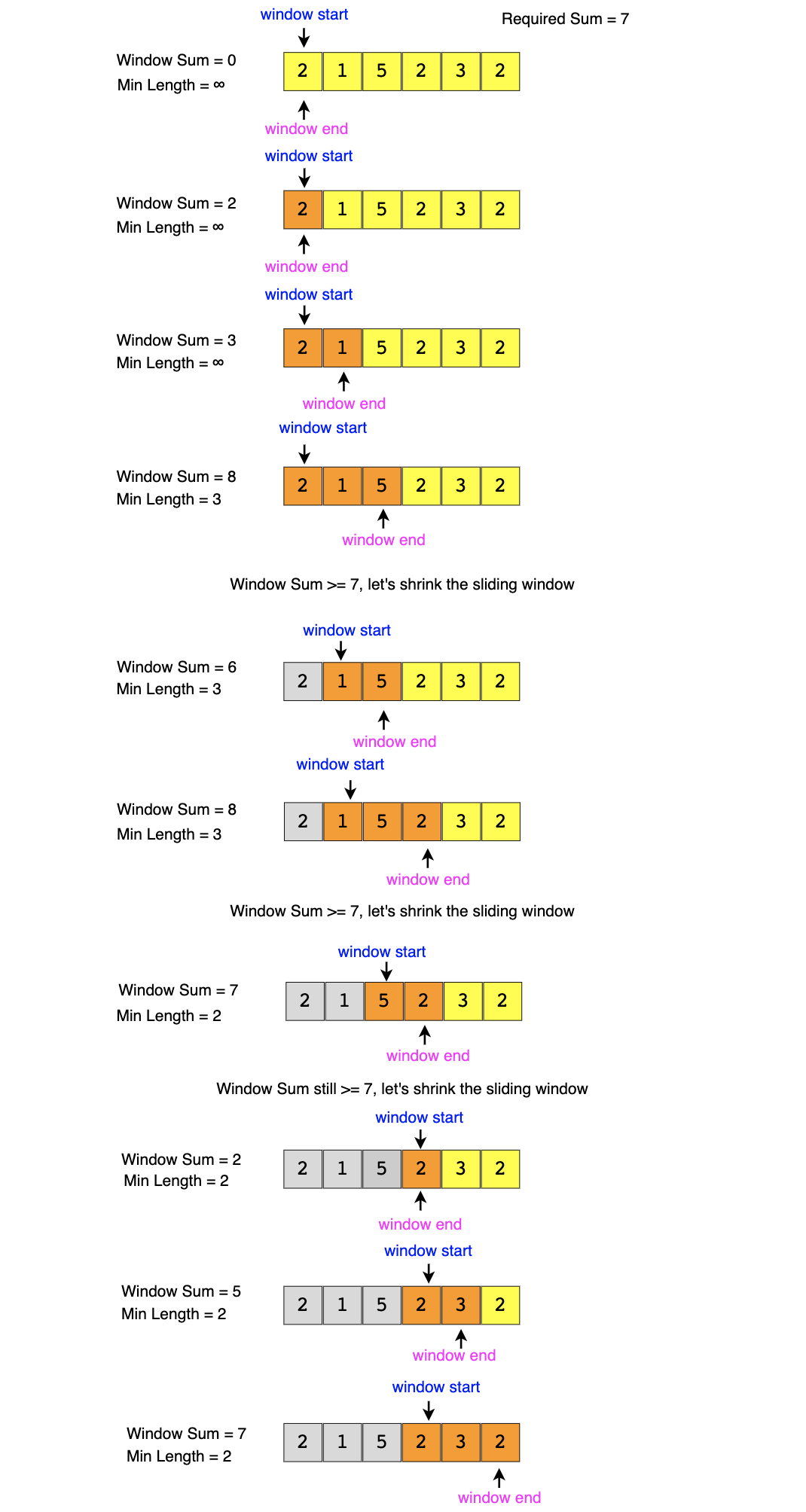
Input: [2, 1, 5, 2, 3, 2], S=7
Output: 2
Explanation: The smallest subarray with a sum greater than or equal to '7' is [5, 2].
Example 2:
Input: [2, 1, 5, 2, 8], S=7
Output: 1
Explanation: The smallest subarray with a sum greater than or equal to '7' is [8].
Example 3:
Input: [3, 4, 1, 1, 6], S=8
Output: 3
Explanation: Smallest subarrays with a sum greater than or equal to '8' are [3, 4, 1]
or [1, 1, 6].
https://www.educative.io/courses/grokking-the-coding-interview/7XMlMEQPnnQ
"""
Solution
if has negative numbers
Other
Solution 1
def decrease_window(curr_sum, arr, left):
curr_sum -= arr[left]
left += 1
return left, curr_sum
def increase_window(curr_sum, arr, right):
right += 1
curr_sum += arr[right]
return right, curr_sum
def smallest_subarray_with_given_sum_01(s, arr):
if not arr or len(arr) < 1:
return -1
smallest_len = float('inf')
# window boundary
left = 0
right = 0
curr_sum = arr[0]
while left < len(arr):
if curr_sum >= s:
smallest_len = min(smallest_len, (right-left)+1)
# cannot increase window
if right >= len(arr)-1:
left, curr_sum = decrease_window(curr_sum, arr, left)
# cannot decrease window
elif right == left:
right, curr_sum = increase_window(curr_sum, arr, right)
elif curr_sum >= s:
left, curr_sum = decrease_window(curr_sum, arr, left)
else:
right, curr_sum = increase_window(curr_sum, arr, right)
if smallest_len == float('inf'):
return -1
return smallest_len
Solution 2
"""
Explanation 2:
---
- first, we sum up elements from the beginning of the array until their sum becomes >= s
These elements will constitute our sliding window.
We will remember the length of this window as the smallest window so far.
- after this we keep adding one element to the window at every loop
- at each step, we try to shrink the window,
we shrink the window till its sum is < s to find the smallest window
- as we do this we try to keep updating the smallest length we have seen soo far
---
- increase the window till you get a sum >= s
- then decrease the window till your sum becomes < s (while keeping track of the smallest lengths)
- repeat till the end of the array
"""
def smallest_subarray_with_given_sum(s, arr):
if not arr or len(arr) < 1:
return -1
smallest_len = float('inf')
left = 0
curr_sum = 0
for right in range(len(arr)):
curr_sum += arr[right]
while left <= right and curr_sum >= s:
smallest_len = min(smallest_len, (right-left)+1)
# decrease window
curr_sum -= arr[left]
left += 1
if smallest_len == float('inf'):
return -1
return smallest_len
Longest Substring with K Distinct Characters
Problem
"""
Longest Substring with K Distinct Characters:
Given a string, find the length of the longest substring in it with no more than K distinct characters.
You can assume that K is less than or equal to the length of the given string.
Example 1:
Input: String="araaci", K=2
Output: 4
Explanation: The longest substring with no more than '2' distinct characters is "araa".
Example 2:
Input: String="araaci", K=1
Output: 2
Explanation: The longest substring with no more than '1' distinct characters is "aa".
Example 3:
Input: String="cbbebi", K=3
Output: 5
Explanation: The longest substrings with no more than '3' distinct characters are "cbbeb" & "bbebi".
"""
Solution
"""
Solution:
- Basics
we'll have a left, right pointer that will mark the current substring we are looking at
we'll have a store (a HashMap), that stores the characters in the substring with their count
- we will iterate through the string with the right pointer till we have a string with k distinct characters
- while we have a string with k distinct characters:
- then we we try to increase the substring length, by checking if the next char is in the store, then increase
- if we cannot increase, we decrease it by removing the first character in the substring
012345
araaci K=2
l,r,max,store
l=0,r=0,0,{a:1,}
# have to increase
l=0,r=1,2,{a:1,r:1}
# can increase
l=0,r=2,3,{a:2,r:1}
l=0,r=3,4,{a:3,r:1}
# have to decrease
l=1,r=3,4,{a:2,r:1}
l=2,r=3,4,{a:2,}
# have to increase
l=2,r=4,4,{a:2,c:1}
# have to decrease
l=3,r=4,4,{a:1,c:1}
l=4,r=4,4,{c:1,}
# have to increase
l=4,r=4,4,{c:1,}
l=4,r=5,4,{c:1,r:5}
"""
from collections import defaultdict
# O(N+N) time | O(K) space ==
# O(N) time | O(K) space
def longest_substring_with_k_distinct(str1, k):
if len(str1) <= 0:
return -1
longest = float('-inf')
left = 0
right = 0
store = defaultdict(int)
store[str1[0]] = 1
while right < len(str1)-1:
if len(store) < k:
right += 1
store[str1[right]] += 1
continue
# # we have k dist characters
longest = max(longest, (right-left)+1)
# can increase length of substring
if right < len(str1)-1 and str1[right+1] in store:
right += 1
store[str1[right]] += 1
# cannot increase length
else:
store[str1[left]] -= 1
if store[str1[left]] <= 0:
store.pop(str1[left])
left += 1
if longest == float('-inf'):
return -1
return longest
Fruits into Baskets
Problem
"""
Fruits into Baskets:
Given an array of characters where each character represents a fruit tree,
you are given two baskets, and your goal is to put maximum number of fruits in each basket.
The only restriction is that each basket can have only one type of fruit.
You can start with any tree, but you can’t skip a tree once you have started.
You will pick one fruit from each tree until you cannot, i.e., you will stop when you have to pick from a third fruit type.
Write a function to return the maximum number of fruits in both baskets.
Example 1:
Input: Fruit=['A', 'B', 'C', 'A', 'C']
Output: 3
Explanation: We can put 2 'C' in one basket and one 'A' in the other from the subarray ['C', 'A', 'C']
Example 2:
Input: Fruit=['A', 'B', 'C', 'B', 'B', 'C']
Output: 5
Explanation: We can put 3 'B' in one basket and two 'C' in the other basket.
This can be done if we start with the second letter: ['B', 'C', 'B', 'B', 'C']
https://www.educative.io/courses/grokking-the-coding-interview/Bn2KLlOR0lQ
"""
Solution
Very similar to Longest Substring with K Distinct Characters
"""
Solution:
- we need to find the longest subarray with a max of two distinct characters
- create a subarray with two distinct characters & once we have this,
- check if lengthening the array will not break the 2 dist char rule, if so, increase the length otherwise,
- decrease the subarray length by removing the first character in the subarray
['0', '1', '2', '3', '4', '5'] 6
['A', 'B', 'C', 'B', 'B', 'C']
left,right,store
l=0,r=0,{A:1,}
# increase size: we need to have a subarray with two distinct characters
l=0,r=1,{A:1,B:1}
# decrease size: we cannot increase, adding c will break the 2 dist characters rule
l=1,r=1,{B:1,}
# increase size
l=1,r=2,{B:1,C:1}
l=1,r=3,{B:2,C:1}
l=1,r=4,{B:3,C:1}
l=1,r=5,{B:3,C:2}
res = 3 # => {B:3,C:2}
"""
# from collections import defaultdict
def fruits_into_baskets(fruits):
if not fruits or len(fruits) < 2:
return -1
most_fruits = float('-inf')
left = right = 0
store = defaultdict(int)
store[fruits[0]] = 1
while right < len(fruits):
if len(store) < 2:
right += 1
if right < len(fruits) - 1:
store[fruits[right]] += 1
continue
most_fruits = max(most_fruits, (right-left)+1)
# can add one more
if right < len(fruits) - 1 and fruits[right+1] in store:
right += 1
store[fruits[right]] += 1
# can add: so remove one
else:
store[fruits[left]] -= 1
if store[fruits[left]] <= 0:
store.pop(fruits[left])
left += 1
if most_fruits == float('-inf'):
return -1
return most_fruits
Dutch National Flag Problem
Problem
"""
Dutch National Flag Problem/Three Number Sort:
Given an array containing 0s, 1s and 2s, sort the array in-place.
You should treat numbers of the array as objects, hence, we can’t count 0s, 1s, and 2s to recreate the array.
The flag of the Netherlands consists of three colors: red, white and blue;
and since our input array also consists of three different numbers that is why it is called Dutch National Flag problem.
Example 1:
Input: [1, 0, 2, 1, 0]
Output: [0 0 1 1 2]
Example 2:
Input: [2, 2, 0, 1, 2, 0]
Output: [0 0 1 2 2 2 ]
"""
Solution
def dutch_flag_sort(arr):
next_zero = 0
next_two = len(arr)-1
idx = 0
while idx < (len(arr)):
# swap values to their correct place
if arr[idx] == 0 and idx >= next_zero:
arr[idx], arr[next_zero] = arr[next_zero], arr[idx]
next_zero += 1
elif arr[idx] == 2 and idx <= next_two:
arr[idx], arr[next_two] = arr[next_two], arr[idx]
next_two -= 1
# only leave idx if value is in correct place
else:
idx += 1
Find All Anagrams in a String *
-
Permutation in String
""" Permutation in String Given two strings s1 and s2, return true if s2 contains a permutation of s1, or false otherwise. In other words, return true if one of s1's permutations is the substring of s2. Example 1: Input: s1 = "ab", s2 = "eidbaooo" Output: true Explanation: s2 contains one permutation of s1 ("ba"). Example 2: Input: s1 = "ab", s2 = "eidboaoo" Output: false Constraints: 1 <= s1.length, s2.length <= 104 s1 and s2 consist of lowercase English letters https://leetcode.com/problems/permutation-in-string Do after this: - https://leetcode.com/problems/find-all-anagrams-in-a-string/ """ from collections import Counter # Note: we can compare p_count and window_count in constant time because they are both at most size 26 # Space complexity: O(1) because p_count and window_count contain not more than 26 elements. class Solution: def checkInclusion(self, s1: str, s2: str): # # create counters window_counter = [0] * 26 s1_counter = [0] * 26 for char, count in Counter(s1).items(): s1_counter[self.char_idx(char)] = count # # look for permutations using a sliding window pattern for idx in range(len(s2)): # # create first window if idx < (len(s1)): window_counter[self.char_idx(s2[idx])] += 1 # # move window forward else: window_counter[self.char_idx(s2[idx-len(s1)])] -= 1 window_counter[self.char_idx(s2[idx])] += 1 # # check for result if s1_counter == window_counter: return True def char_idx(self, char): return ord(char) - ord('a') -
Find All Anagrams in a String *
""" Find All Anagrams in a String Given two strings s and p, return an array of all the start indices of p's anagrams in s. You may return the answer in any order. An Anagram is a word or phrase formed by rearranging the letters of a different word or phrase, typically using all the original letters exactly once. Example 1: Input: s = "cbaebabacd", p = "abc" Output: [0,6] Explanation: The substring with start index = 0 is "cba", which is an anagram of "abc". The substring with start index = 6 is "bac", which is an anagram of "abc". Example 2: Input: s = "abab", p = "ab" Output: [0,1,2] Explanation: The substring with start index = 0 is "ab", which is an anagram of "ab". The substring with start index = 1 is "ba", which is an anagram of "ab". The substring with start index = 2 is "ab", which is an anagram of "ab". Constraints: 1 <= s.length, p.length <= 3 * 104 s and p consist of lowercase English letters. https://leetcode.com/problems/find-all-anagrams-in-a-string/ Prerequisite: - https://leetcode.com/problems/permutation-in-string """ import collections # Time complexity: O(S) + O(P) since it's one pass along both strings. # Note: we can compare p_count and window_count in constant time because they are both at most size 26 # Space complexity: O(1) because p_count and window_count contain not more than 26 elements. class Solution: def findAnagrams(self, s: str, p: str): if len(p) > len(s): return[] anagrams = [] # an array of length 26 can be used instead (with the ASCII values of the chracters) p_count = collections.Counter(p) window_count = collections.Counter() for idx, char in enumerate(s): # # create window if idx < len(p): window_count[char] += 1 # # move window forward else: # remove char at left end left_end_char = s[idx-(len(p))] window_count[left_end_char] -= 1 if window_count[left_end_char] == 0: window_count.pop(left_end_char) # add char to right end window_count[char] += 1 # # check if anagrams if p_count == window_count: anagrams.append(idx-(len(p)-1)) return anagrams
Permutation in String
-
Permutation in String
""" Permutation in String Given two strings s1 and s2, return true if s2 contains a permutation of s1, or false otherwise. In other words, return true if one of s1's permutations is the substring of s2. Example 1: Input: s1 = "ab", s2 = "eidbaooo" Output: true Explanation: s2 contains one permutation of s1 ("ba"). Example 2: Input: s1 = "ab", s2 = "eidboaoo" Output: false Constraints: 1 <= s1.length, s2.length <= 104 s1 and s2 consist of lowercase English letters https://leetcode.com/problems/permutation-in-string Do after this: - https://leetcode.com/problems/find-all-anagrams-in-a-string/ """ from collections import Counter # Note: we can compare p_count and window_count in constant time because they are both at most size 26 # Space complexity: O(1) because p_count and window_count contain not more than 26 elements. class Solution: def checkInclusion(self, s1: str, s2: str): # # create counters window_counter = [0] * 26 s1_counter = [0] * 26 for char, count in Counter(s1).items(): s1_counter[self.char_idx(char)] = count # # look for permutations using a sliding window pattern for idx in range(len(s2)): # # create first window if idx < (len(s1)): window_counter[self.char_idx(s2[idx])] += 1 # # move window forward else: window_counter[self.char_idx(s2[idx-len(s1)])] -= 1 window_counter[self.char_idx(s2[idx])] += 1 # # check for result if s1_counter == window_counter: return True def char_idx(self, char): return ord(char) - ord('a') -
Find All Anagrams in a String *
""" Find All Anagrams in a String Given two strings s and p, return an array of all the start indices of p's anagrams in s. You may return the answer in any order. An Anagram is a word or phrase formed by rearranging the letters of a different word or phrase, typically using all the original letters exactly once. Example 1: Input: s = "cbaebabacd", p = "abc" Output: [0,6] Explanation: The substring with start index = 0 is "cba", which is an anagram of "abc". The substring with start index = 6 is "bac", which is an anagram of "abc". Example 2: Input: s = "abab", p = "ab" Output: [0,1,2] Explanation: The substring with start index = 0 is "ab", which is an anagram of "ab". The substring with start index = 1 is "ba", which is an anagram of "ab". The substring with start index = 2 is "ab", which is an anagram of "ab". Constraints: 1 <= s.length, p.length <= 3 * 104 s and p consist of lowercase English letters. https://leetcode.com/problems/find-all-anagrams-in-a-string/ Prerequisite: - https://leetcode.com/problems/permutation-in-string """ import collections # Time complexity: O(S) + O(P) since it's one pass along both strings. # Note: we can compare p_count and window_count in constant time because they are both at most size 26 # Space complexity: O(1) because p_count and window_count contain not more than 26 elements. class Solution: def findAnagrams(self, s: str, p: str): if len(p) > len(s): return[] anagrams = [] # an array of length 26 can be used instead (with the ASCII values of the chracters) p_count = collections.Counter(p) window_count = collections.Counter() for idx, char in enumerate(s): # # create window if idx < len(p): window_count[char] += 1 # # move window forward else: # remove char at left end left_end_char = s[idx-(len(p))] window_count[left_end_char] -= 1 if window_count[left_end_char] == 0: window_count.pop(left_end_char) # add char to right end window_count[char] += 1 # # check if anagrams if p_count == window_count: anagrams.append(idx-(len(p)-1)) return anagrams
Minimum Window Substring *
Continuous Subarray Sum **
Trapping rain water
Sliding Window Maximum
More examples
Facebook | SWE New Grad | London | January 2019 [Reject] - LeetCode Discuss
Max Consecutive Ones III - LeetCode
Find the original version of this page (with additional content) on Notion here.
Created: December 13, 2021 16:05:48