Recursion, DP & Backtracking
Dynamic Programming, Recursion, & Backtracking
![]()
Recursion
Thinking Recursively in Python - Real Python
5 Simple Steps for Solving Any Recursive Problem
Recursion is an approach to solving problems using a function that calls itself as a subroutine.
Recursion,%20DP%20&%20Backtracking%20525dddcdd0874ed98372518724fc8753/fixing_problems.webp
When do you use recursion? making one choice, then one after that, on and on. Or in hierarchies, networks and graphs.
![]()
Recursive strategy:
-
Order your data (not necessarily via code - just conceptually)
Helps in identifying the base case
Decompose the original problem into simpler instances of the same problem. This is the recursive case:
# Factorial n! = n x (n−1) x (n−2) x (n−3) ⋅⋅⋅⋅ x 3 x 2 x 1 n! = n x (n−1)! # Fibonacci Fn = Fn-1 + Fn-2

Whatever data we are operating on, whether it is numbers, strings, lists, binary trees or people, it is necessary to explicitly find an appropriate ordering that gives us a direction to move in to make the problem smaller. This ordering depends entirely on the problem, but a good start is to think of the obvious orderings: numbers come with their own ordering, strings and lists can be ordered by their length, binary trees can be ordered by depth.
Once we’ve ordered our data, we can think of it as something that we can reduce. In fact, we can write out our ordering as a sequence:
- 0, 1, 2, …, n for integers (i.e. for integer data d, degree(d) = d) Moving from right to left we move through the general (‘big’) cases, to the base (‘little’) cases
- [], [■], [■, ■], …, [■, … , ■] for lists(notice len = 0, len = 1, …, len = n i.e. for list data d, degree(d) = len(d))
-
Solve the Little Cases & identify Base cases

elf delivering presents for santa
Identifying the base cases, which are to be solved directly
The case for which the solution can be stated non-recursively.
As the large problem is broken down into successively less complex ones, those subproblems must eventually become so simple that they can be solved without further subdivision.
n! = n x (n−1)! n! = n x (n−1) x (n−2)! n! = n x (n−1) x (n−2) x (n−3)! ⋅ ⋅ n! = n x (n−1) x (n−2) x (n−3) ⋅⋅⋅⋅ x 3! n! = n x (n−1) x (n−2) x (n−3) ⋅⋅⋅⋅ x 3 x 2! n! = n x (n−1) x (n−2) x (n−3) ⋅⋅⋅⋅ x 3 x 2 x 1!
we have the correct ordering, we need to look at the smallest elements in our ordering, and decide how we are going to handle them.
Once we have solved our base cases, and we know our ordering, then solving the general case is as simple as reducing the problem in such a way that the degree of the data we’re operating on moves towards the base cases.
find a general case
-
Solve the Big Cases - General (recursive) case
Ensuring progress, that is the recursion converges to the solution.
case for which the solution to a problem is expressed in terms of a smaller version of itself.

Here, we handle the data rightwards in our ordering, that is, data of high degree. Usually, we consider data of arbitrary degree and aim to find a way to solve the problem by reducing it to an expression containing the same problem of lesser degree, e.g. in our Fibonacci example we started with arbitrary n and reduced fib(n) to fib(n-1) + fib(n-2) which is an expression containing two instances of the problem we started with, of lesser degree (n-1 and n-2, respectively).
-
Draw a recursion stack (tree) if you suspect it involves recursion - not necessarily at the last point in the strategy
Example:
""" Permutations: Leetcode 46 Given an array nums of distinct integers, return all the possible permutations. You can return the answer in any order. Example 1: Input: nums = [1,2,3] Output: [[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]] """ class Solution: def helper(self, permutations, curr_perm, elements): if len(elements) < 1: permutations.append(curr_perm) return for idx, num in enumerate(elements): self.helper(permutations, curr_perm+[num], elements[:idx]+elements[idx+1:]) def permute(self, nums: List[int]): permutations = [] self.helper(permutations, [], nums) return permutations """ [ [1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1] ] [] / | \ [1] [2] / \ / \ [1,2] [1,3] [2,1] [2,3] | | | | [1,2,3] [1,3,2] [2,1,3] [2,3,1] ([], [], [1,2,3]) ([], [1], [2,3]) ([], [2], [1,3]) ([], [3], [1,2]) ([], [1, 2], [3]) ([], [1, 3], [3]) perm(1,2) [][1,2] [1][2] [2][1] [1,2][] [2,1][] perm(1,2,3) [][1,2,3] / | \ [1][2,3] [2][1,3] [3][2,1] / \ / \ / \ [1,2][3] [1,3][2] [2,1][3] [2,3][1] [3,2][1] [3,1][2] | | | | | | [1,2,3] [1,3,2] [2,1,3] [2,3,1] [3,2,1] [3,1,2] """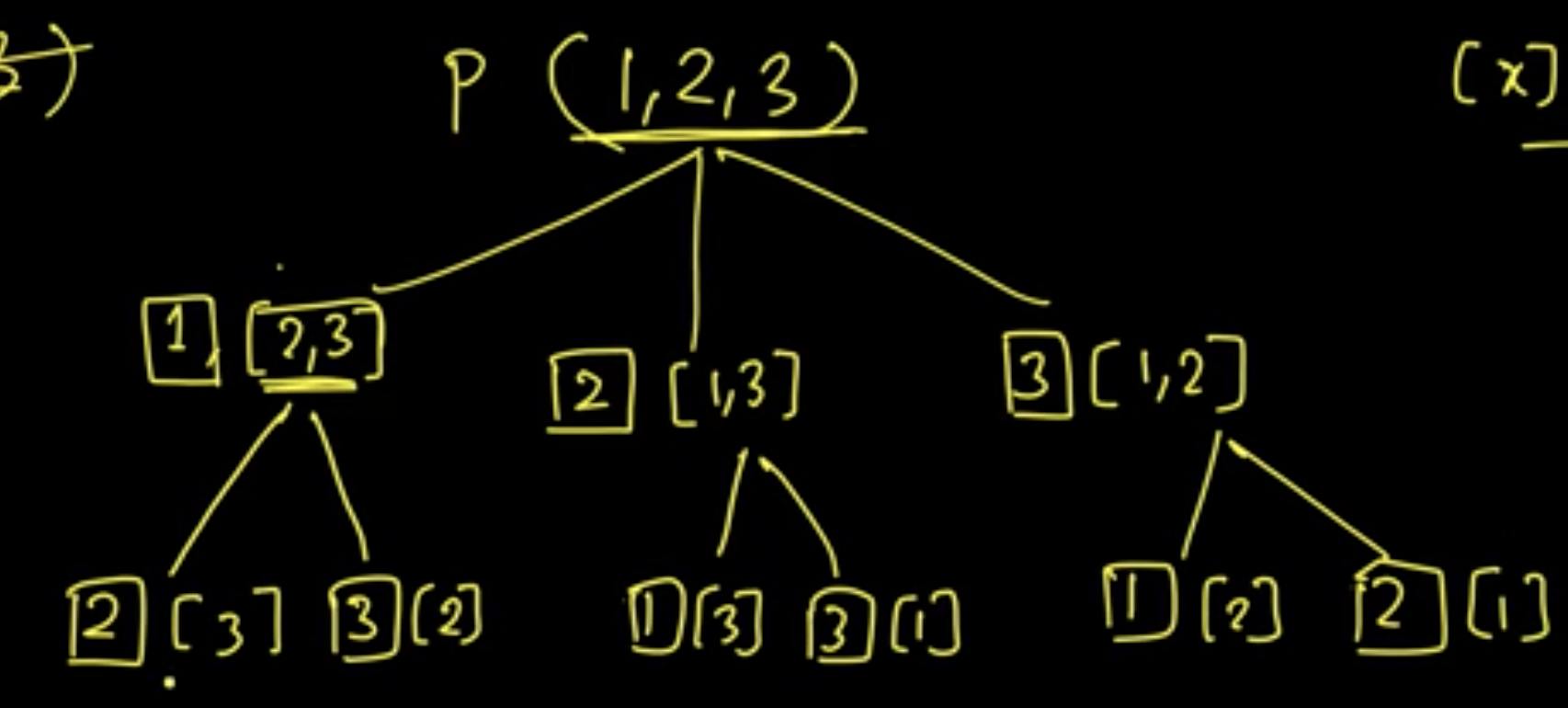
"""
order data:
find smaller/base cases:
solve little cases then big cases:
recursion stack:
"""
Examples
-
Tower of Hanoi
Towers of Hanoi: A Complete Recursive Visualization
5.10. Tower of Hanoi - Problem Solving with Algorithms and Data Structures

""" Tower of Hanoi https://youtu.be/rf6uf3jNjbo https://runestone.academy/runestone/books/published/pythonds/Recursion/TowerofHanoi.html https://leetcode.com/discuss/general-discussion/1517167/Tower-of-Hanoi-Algorithm-%2B-Python-code https://www.notion.so/paulonteri/Recursion-DP-Backtracking-525dddcdd0874ed98372518724fc8753#0fa86da6418247199688a4f435447d86 """ """ Here is a high-level outline of how to move a tower from the starting pole, to the goal pole, using an intermediate pole: 1. Move a tower of height-1 to an intermediate pole 2. Move the last/remaining disk to the final pole. 3. Move the disks height-1 to the first rod and repeat the above steps. Move the tower of height-1 from the intermediate pole to the final pole using the original pole. As long as we always obey the rule that the larger disks remain on the bottom of the stack, we can use the three steps above recursively, treating any larger disks as though they were not even there. The only thing missing from the outline above is the identification of a base case. The simplest Tower of Hanoi problem is a tower of one disk. In this case, we need move only a single disk to its final destination. A tower of one disk will be our base case. """ def tower_of_hanoi(n, from_rod="A", to_rod="C", aux_rod="B"): if n == 1: # The simplest Tower of Hanoi problem is a tower of one disk. # In this case, we need move only a single disk to its final destination. print("Move disk 1 from rod", from_rod, "to rod", to_rod) return # Move a tower of height-1 to an intermediate pole tower_of_hanoi(n-1, from_rod, aux_rod, to_rod) # Move the last/remaining disk to the final pole print("Move disk", n, "from rod", from_rod, "to rod", to_rod) # Move the disks height-1 to the first rod and repeat the above steps # Move the tower of height-1 from the intermediate pole to the final pole using the original pole. tower_of_hanoi(n-1, aux_rod, to_rod, from_rod) tower_of_hanoi(1) print("____________") tower_of_hanoi(2) print("____________") tower_of_hanoi(3) print("____________") tower_of_hanoi(4) print("____________") tower_of_hanoi(5)https://runestone.academy/runestone/books/published/pythonds/Recursion/TowerofHanoi.html
-
Recursive multiply
""" Recursive multiply """ def recursive_multiply(x, y): # reduce number of recursive calls - ensure y is smaller if y > x: return recursive_multiply(y, x) return recursive_multiply_helper(x, y) def recursive_multiply_helper(x, y): if y == 0: return 0 if y == 1: return x return x + recursive_multiply_helper(x, y-1) print(recursive_multiply(5, 4)) print(recursive_multiply(7, 3)) print(recursive_multiply(2, 2)) -
Subsets With Duplicates
-
Permutation
-
Letter Combinations of a Phone Number
""" Letter Combinations of a Phone Number: Given a string containing digits from 2-9 inclusive, return all possible letter combinations that the number could represent. Return the answer in any order. A mapping of digit to letters (just like on the telephone buttons) is given below. Note that 1 does not map to any letters. https://leetcode.com/problems/letter-combinations-of-a-phone-number/ """ """ Phone Number Mnemonics: If you open the keypad of your mobile phone, it'll likely look like this: ----- ----- ----- | | | | | 1 | 2 | 3 | | | abc | def | ----- ----- ----- | | | | | 4 | 5 | 6 | | ghi | jkl | mno | ----- ----- ----- | | | | | 7 | 8 | 9 | | pqrs| tuv | wxyz| ----- ----- ----- | | | 0 | | | ----- Almost every digit is associated with some letters in the alphabet; this allows certain phone numbers to spell out actual words. For example, the phone number 8464747328 can be written as timisgreat; similarly, the phone number 2686463 can be written as antoine or as ant6463. It's important to note that a phone number doesn't represent a single sequence of letters, but rather multiple combinations of letters. For instance, the digit 2 can represent three different letters (a, b, and c). A mnemonic is defined as a pattern of letters, ideas, or associations that assist in remembering something Companies oftentimes use a mnemonic for their phone number to make it easier to remember. Given a stringified phone number of any non-zero length, write a function that returns all mnemonics for this phone number, in any order. For this problem, a valid mnemonic may only contain letters and the digits 0 and 1. In other words, if a digit is able to be represented by a letter, then it must be. Digits 0 and 1 are the only two digits that don't have letter representations on the keypad. Note that you should rely on the keypad illustrated above for digit-letter associations. Sample Input phoneNumber = "1905" Sample Output [ "1w0j", "1w0k", "1w0l", "1x0j", "1x0k", "1x0l", "1y0j", "1y0k", "1y0l", "1z0j", "1z0k", "1z0l", ] // The mnemonics could be ordered differently. https://www.algoexpert.io/questions/Phone%20Number%20Mnemonics """ class Solution0: def letterCombinations(self, digits: str): if not digits: return [] key_map = { 2: ['a', 'b', 'c'], 3: ['d', 'e', 'f'], 4: ['g', 'h', 'i'], 5: ['j', 'k', 'l'], 6: ['m', 'n', 'o'], 7: ['p', 'q', 'r', 's'], 8: ['t', 'u', 'v'], 9: ['w', 'x', 'y', 'z'] } res = [''] for num in digits: new_res = [] for idx in range(len(res)): for letter in key_map[int(num)]: new_res.append(res[idx] + letter) res = new_res return res # ---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- key_map = { 0: ["0"], 1: ["1"], 2: ['a', 'b', 'c'], 3: ['d', 'e', 'f'], 4: ['g', 'h', 'i'], 5: ['j', 'k', 'l'], 6: ['m', 'n', 'o'], 7: ['p', 'q', 'r', 's'], 8: ['t', 'u', 'v'], 9: ['w', 'x', 'y', 'z'] } # # # # # def phoneNumberMnemonics00(phoneNumber): all_combinations = [] phoneNumberMnemonicsHelper00(phoneNumber, 0, all_combinations, []) return all_combinations def phoneNumberMnemonicsHelper00(phoneNumber, idx, all_combinations, curr_combination): if idx >= len(phoneNumber): all_combinations.append("".join(curr_combination)) return letters = key_map[int(phoneNumber[idx])] for letter in letters: phoneNumberMnemonicsHelper00( phoneNumber, idx + 1, all_combinations, curr_combination + [letter]) # ---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- # O(4^n * n) time | O(4^n * n) space - where n is the length of the phone number def phoneNumberMnemonics(phoneNumber): all_combinations = [] curr_combination_template = list(range(len(phoneNumber))) phoneNumberMnemonicsHelper( phoneNumber, 0, all_combinations, curr_combination_template) return all_combinations def phoneNumberMnemonicsHelper(phoneNumber, idx, all_combinations, curr_combination): if idx >= len(phoneNumber): all_combinations.append("".join(curr_combination)) return letters = key_map[int(phoneNumber[idx])] for letter in letters: # place current letter in curr_combination and go forward to other idxs # we will backtrack and place the other letters too curr_combination[idx] = letter phoneNumberMnemonicsHelper( phoneNumber, idx + 1, all_combinations, curr_combination) -
Interleaving String/Interweaving Strings
""" Interleaving String/Interweaving Strings: Given strings s1, s2, and s3, find whether s3 is formed by an interleaving of s1 and s2. An interleaving of two strings s and t is a configuration where they are divided into non-empty substrings such that: s = s1 + s2 + ... + sn t = t1 + t2 + ... + tm |n - m| <= 1 The interleaving is s1 + t1 + s2 + t2 + s3 + t3 + ... or t1 + s1 + t2 + s2 + t3 + s3 + ... Note: a + b is the concatenation of strings a and b. Example 1: Input: s1 = "aabcc", s2 = "dbbca", s3 = "aadbbcbcac" Output: true Example 2: Input: s1 = "aabcc", s2 = "dbbca", s3 = "aadbbbaccc" Output: false Example 3: Input: s1 = "", s2 = "", s3 = "" Output: true https://www.algoexpert.io/questions/Interweaving%20Strings https://leetcode.com/problems/interleaving-string/ https://leetcode.com/problems/interleaving-string/discuss/326347/C-dynamic-programming-practice-in-August-2018-with-interesting-combinatorics-warmup """ """ ------------------------------------------------------------------------------------------------------------------------------------------------------ """ def interweavingStringsBF_(one, two, three): if len(three) != len(one) + len(two): return False return interweavingStringsHelperBF_(one, two, three, 0, 0, 0) def interweavingStringsHelperBF_(one, two, three, one_idx, two_idx, three_idx): if three_idx == len(three): return True one_res = False two_res = False if one_idx < len(one) and one[one_idx] == three[three_idx]: one_res = interweavingStringsHelperBF_( one, two, three, one_idx+1, two_idx, three_idx+1) if two_idx < len(two) and two[two_idx] == three[three_idx]: two_res = interweavingStringsHelperBF_( one, two, three, one_idx, two_idx+1, three_idx+1) return one_res or two_res """ BF that can be cached """ def interweavingStringsBF(one, two, three): if len(three) != len(one) + len(two): return False return interweavingStringsHelperBF(one, two, three, 0, 0) def interweavingStringsHelperBF(one, two, three, one_idx, two_idx, ): three_idx = one_idx + two_idx if three_idx == len(three): return True one_res = False two_res = False if one_idx < len(one) and one[one_idx] == three[three_idx]: one_res = interweavingStringsHelperBF( one, two, three, one_idx+1, two_idx) if two_idx < len(two) and two[two_idx] == three[three_idx]: two_res = interweavingStringsHelperBF( one, two, three, one_idx, two_idx+1) return one_res or two_res """ ------------------------------------------------------------------------------------------------------------------------------------------------------ """ def interweavingStringsMEMO(one, two, three): if len(three) != len(one) + len(two): return False cache = [[None for _ in range(len(two)+1)] for _ in range(len(one)+1)] return interweavingStringsHelperMEMO(one, two, three, cache, 0, 0) def interweavingStringsHelperMEMO(one, two, three, cache, one_idx, two_idx, ): three_idx = one_idx + two_idx if three_idx == len(three): return True if cache[one_idx][two_idx] is not None: return cache[one_idx][two_idx] one_res = False two_res = False if one_idx < len(one) and one[one_idx] == three[three_idx]: one_res = interweavingStringsHelperMEMO(one, two, three, cache, one_idx+1, two_idx) if two_idx < len(two) and two[two_idx] == three[three_idx]: two_res = interweavingStringsHelperMEMO(one, two, three, cache, one_idx, two_idx+1) cache[one_idx][two_idx] = one_res or two_res return cache[one_idx][two_idx] """ ------------------------------------------------------------------------------------------------------------------------------------------------------ Bottom up: - for each char(in one or two) check if it matches what is in three: - if it does: if we had built the prev string up to that point == True ( one idx behind the curr idx in three (up or left depending on if the row or column matches) ) - then True # can be optimised to 1D array """ def interweavingStrings(one, two, three): if len(three) != len(one) + len(two): return False dp = [[False for _ in range(len(two)+1)] for _ in range(len(one)+1)] # # fill in the defaults that will be used to generate the next dp[0][0] = True for i in range(1, len(one)+1): # left column actual_idx = i-1 if one[actual_idx] == three[actual_idx] and dp[i-1][0] == True: dp[i][0] = True for i in range(1, len(two)+1): # top row actual_idx = i-1 if two[actual_idx] == three[actual_idx] and dp[0][i-1] == True: dp[0][i] = True # # fill in the rest for one_idx in range(1, len(one)+1): for two_idx in range(1, len(two)+1): actual_one_idx = one_idx-1 actual_two_idx = two_idx-1 actual_three_idx = one_idx + two_idx - 1 # # check if the string matches then check if we had built it successfully up to that point # check one if one[actual_one_idx] == three[actual_three_idx] and dp[one_idx-1][two_idx] == True: dp[one_idx][two_idx] = True # check two if two[actual_two_idx] == three[actual_three_idx] and dp[one_idx][two_idx-1] == True: dp[one_idx][two_idx] = True return dp[-1][-1] -
Magic Index

""" Magic Index: A magic index in an array A[ 0••• n -1] is defined to be an index such that A[ i] = i. Given a sorted array of distinct integers, write a method to find a magic index, if one exists, in array A. FOLLOW UP: What if the values are not distinct? """ """ What if the values are not distinct? - cannot use two pointers """ def magicIndex(array): return magicIndexHelper(array, 0, len(array)-1) def magicIndexHelper(array, left, right): if left > right: return -1 mid = (left+right) // 2 if array[mid] == mid: return mid left_side = magicIndexHelper(array, left, min(mid-1, array[mid])) right_side = magicIndexHelper(array, max(mid+1, array[mid]), right) if left_side >= 0: return left_side elif right_side >= 0: return right_side return -1 def FillArray(): array = [0] * 10 array[0] = -14 array[1] = -12 array[2] = 0 array[3] = 1 array[4] = 2 array[5] = 5 array[6] = 9 array[7] = 10 array[8] = 23 array[9] = 25 return array array = FillArray() print(magicIndex(array)) print(magicIndex([1, 3, 2, 4, 5])) print(magicIndex([0, 6, 6, 6, 6])) print(magicIndex([1, 4, 4, 4, 4])) -
Sort Stack *
""" Sort Stack Write a function that takes in an array of integers representing a stack, recursively sorts the stack in place (i.e., doesn't create a brand new array), and returns it. The array must be treated as a stack, with the end of the array as the top of the stack. Therefore, you're only allowed to: Pop elements from the top of the stack by removing elements from the end of the array using the built-in .pop() method in your programming language of choice. Push elements to the top of the stack by appending elements to the end of the array using the built-in .append() method in your programming language of choice. Peek at the element on top of the stack by accessing the last element in the array. You're not allowed to perform any other operations on the input array, including accessing elements (except for the last element), moving elements, etc.. You're also not allowed to use any other data structures, and your solution must be recursive. Sample Input stack = [-5, 2, -2, 4, 3, 1] Sample Output [-5, -2, 1, 2, 3, 4] https://www.algoexpert.io/questions/Sort%20Stack """ # # this will work by looping through all the elements of the stack # # a bottom-up recursion approach where we start by sorting a stack of len 0, len 1, then 2, then 3 # remove every element till we have an empty stack # then insert them one by one at their correct position # O(n^2) time | O(n) space - where n is the length of the stack def sortStack(stack): # base case if len(stack) == 0: return stack # remove element at the top (element top), # sort the rest of the stack, # insert top back to the stack but at its correct position # this will be work easily because the rest of the stack is sorted top = stack.pop() sortStack(stack) insertElementInCorrectPosition(stack, top) return stack # assumes stack is sorted or empty def insertElementInCorrectPosition(stack, num): # base cases # correct positions to insert num if len(stack) == 0 or stack[-1] <= num: stack.append(num) # remove the element at the top and try to insert num at a lower position # insert num at a lower position than top # return top once that is done else: top = stack.pop() insertElementInCorrectPosition(stack, num) stack.append(top) -
Regular Expression Matching
""" Regular Expression Matching Given an input string s and a pattern p, implement regular expression matching with support for '.' and '*' where: '.' Matches any single character. '*' Matches zero or more of the preceding element. The matching should cover the entire input string (not partial). Example 1: Input: s = "aa", p = "a" Output: false Explanation: "a" does not match the entire string "aa". Example 2: Input: s = "aa", p = "a*" Output: true Explanation: '*' means zero or more of the preceding element, 'a'. Therefore, by repeating 'a' once, it becomes "aa". Example 3: Input: s = "ab", p = ".*" Output: true Explanation: ".*" means "zero or more (*) of any character (.)". Example 4: Input: s = "aab", p = "c*a*b" Output: true Explanation: c can be repeated 0 times, a can be repeated 1 time. Therefore, it matches "aab". Example 5: Input: s = "mississippi", p = "mis*is*p*." Output: false https://leetcode.com/problems/regular-expression-matching/ """ """ Basic Regex Parser: Implement a regular expression function isMatch that supports the '.' and '*' symbols. The function receives two strings - text and pattern - and should return true if the text matches the pattern as a regular expression. For simplicity, assume that the actual symbols '.' and '*' do not appear in the text string and are used as special symbols only in the pattern string. In case you aren’t familiar with regular expressions, the function determines if the text and pattern are the equal, where the '.' is treated as a single a character wildcard (see third example), and '*' is matched for a zero or more sequence of the previous letter (see fourth and fifth examples). For more information on regular expression matching, see the Regular Expression Wikipedia page. Explain your algorithm, and analyze its time and space complexities. Examples: input: text = "aa", pattern = "a" output: false input: text = "aa", pattern = "aa" output: true input: text = "abc", pattern = "a.c" output: true input: text = "abbb", pattern = "ab*" output: true input: text = "acd", pattern = "ab*c." output: true https://www.pramp.com/challenge/KvZ3aL35Ezc5K9Eq9Llp """ class Solution: def isMatch(self, text, pattern): if len(text) == 0 and len(pattern) == 0: return True if len(pattern) == 0: return False return self.is_match_helper(text, pattern, 0, 0) def is_match_helper(self, text, pattern, text_idx, pattern_idx): # base cases if text_idx == len(text): if pattern_idx == len(pattern): return True if pattern_idx+1 < len(pattern) and pattern[pattern_idx+1] == '*': return self.is_match_helper(text, pattern, text_idx, pattern_idx+2) return False if pattern_idx == len(pattern): return False # '*' if pattern_idx < len(pattern)-1 and pattern[pattern_idx+1] == '*': prev_char = pattern[pattern_idx] # many of prev_char after_pattern = text_idx if prev_char == ".": after_pattern = len(text) else: while after_pattern < len(text) and text[after_pattern] == prev_char: after_pattern += 1 # try all possibilities for idx in range(text_idx, after_pattern+1): if self.is_match_helper(text, pattern, idx, pattern_idx+2): return True return False # '.' elif pattern[pattern_idx] == '.': return self.is_match_helper(text, pattern, text_idx+1, pattern_idx+1) # other characters else: if pattern[pattern_idx] != text[text_idx]: return False return self.is_match_helper(text, pattern, text_idx+1, pattern_idx+1) """ """ class Solution_: def isMatch(self, text, pattern): if len(text) == 0 and len(pattern) == 0: return True if len(pattern) == 0: return False cache = [[None for _ in range(len(pattern))] for _ in range(len(text))] return self.is_match_helper(text, pattern, cache, 0, 0) def is_match_helper(self, text, pattern, cache, text_idx, pattern_idx): # base cases if text_idx == len(text): if pattern_idx == len(pattern): return True if pattern_idx+1 < len(pattern) and pattern[pattern_idx+1] == '*': return self.is_match_helper(text, pattern, cache, text_idx, pattern_idx+2) return False if pattern_idx == len(pattern): return False if cache[text_idx][pattern_idx] is not None: return cache[text_idx][pattern_idx] # '*' if pattern_idx < len(pattern)-1 and pattern[pattern_idx+1] == '*': prev_char = pattern[pattern_idx] # many of prev_char after_pattern = text_idx if prev_char == ".": after_pattern = len(text) else: while after_pattern < len(text) and text[after_pattern] == prev_char: after_pattern += 1 # try all possibilities for idx in range(text_idx, after_pattern+1): if self.is_match_helper(text, pattern, cache, idx, pattern_idx+2): cache[text_idx][pattern_idx] = True return cache[text_idx][pattern_idx] cache[text_idx][pattern_idx] = False return cache[text_idx][pattern_idx] # '.' elif pattern[pattern_idx] == '.': cache[text_idx][pattern_idx] = self.is_match_helper( text, pattern, cache, text_idx+1, pattern_idx+1) return cache[text_idx][pattern_idx] # other characters else: if pattern[pattern_idx] != text[text_idx]: cache[text_idx][pattern_idx] = False else: cache[text_idx][pattern_idx] = self.is_match_helper( text, pattern, cache, text_idx+1, pattern_idx+1) return cache[text_idx][pattern_idx] -
Strobogrammatic Number II *
""" Strobogrammatic Number II Given an integer n, return all the strobogrammatic numbers that are of length n. You may return the answer in any order. A strobogrammatic number is a number that looks the same when rotated 180 degrees (looked at upside down). Example 1: Input: n = 2 Output: ["11","69","88","96"] Example 2: Input: n = 1 Output: ["0","1","8"] https://leetcode.com/problems/strobogrammatic-number-ii """ """ We realised that we have 2 base cases (simplest subproblems): - n=1 --> ['0', '1', '8'] - n=2 --> ['00', '11', '88', '69', '96'] The rest can be built around that: - n=3 --> ["101","808","609","906","111","818","619","916","181","888","689","986"] all w invalid --> ["000","101","808","609","906","010","111","818","619","916","080","181","888","689","986"] - n=4 --> ["1001","8008","6009","9006","1111","8118","6119","9116","1881","8888","6889","9886","1691","8698","6699","9696","1961","8968","6969","9966"] all w invalid --> ["0000","1001","8008","6009","9006","0110","1111","8118","6119","9116","0880","1881","8888","6889","9886","0690","1691","8698","6699","9696","0960","1961","8968","6969","9966"] Have a recursive function that builds from the base cases upwards: Example: ``` def helper(n): if n == 1: return ['0', '1', '8'] if n == 2: return ['00', '11', '88', '69', '96'] result = [] for base in helper(n-2): result.append('0' + base + '0') result.append('1' + base + '1') result.append('6' + base + '9') result.append('8' + base + '8') result.append('9' + base + '6') return result ``` then return the valid results """ class Solution_: def findStrobogrammatic(self, n: int): result = [] for num in self.findStrobogrammatic_helper(n): # remove leading zeros if str(int(num)) == num: result.append(num) return result def findStrobogrammatic_helper(self, n): # Base cases if n == 1: return ['0', '1', '8'] if n == 2: return ['00', '11', '88', '69', '96'] result = [] # this is the only way they can be expanded for base in self.findStrobogrammatic_helper(n-2): result.append('0' + base + '0') result.append('1' + base + '1') result.append('6' + base + '9') result.append('8' + base + '8') result.append('9' + base + '6') return result # Time complexity O(n). We iterate n//2 times in for _ in range(n//2). Within this, we iterate for num in output at most 5 times, since output has at most 5 numbers. # Space complexity O(n). class Solution: def findStrobogrammatic(self, n: int): result = [] # handle even or odd combinations = [''] if n % 2 == 0 else ['0', '1', '8'] for _ in range(n//2): temp = [] for num in combinations: temp.append('0' + num + '0') temp.append('1' + num + '1') temp.append('8' + num + '8') temp.append('6' + num + '9') temp.append('9' + num + '6') combinations = temp for num in combinations: # remove leading zeros if str(int(num)) == num: result.append(num) return result
How do you determine if there is a recursive solution to a problem?
- Base case question Is there a base case? Is there a way out of the function that does not require a recursive call and in which the function works correctly?
- Smaller caller question Does each recursive call result in a smaller version of the original problem which leads inescapably to the base case.
- General case question Assuming each recursive call works correctly, does this lead to the correct solution to the whole problem? The answer to this question can be shown through induction:
- Show that the solution works for the base case, i.e. SumOfSquares(n, n).
- Assume that the solution works for the case of SumOfSquares(n, n+1).
- Now to finish the proof show that the solution works for SumOfSquares(n, n+2):
- The return value from the first recursive call to the function would be n + SumOfSquares(n+1, n+2).
- This is just the results of a call to the base case SumOfSquares(n, n) which we have already shown to work, and a call to what is syntactically equivalent to SumOfSquares(n, n+1) which we have assumed works.
- Thus, by induction, we have shown that the function works for all values of m and n where m < n. - number of choices to make
Ways of dividing a problem into subproblems:
Recursive solutions, by definition, are built off of solutions to subproblems. Many times, this will mean simply to compute f(n) by adding something, removing something, or otherwise changing the solution for f(n-1). In other cases, you might solve the problem for the first half of the data set, then the second half, and then merge those results.
There are many ways you might divide a problem into subproblems. Three of the most common approaches to developing an algorithm are bottom-up, top-down, and half-and-half.
Top-down and bottom-up refer to two general approaches to dynamic programming. A top-down solution starts with the final result and recursively breaks it down into subproblems. The bottom-up method does the opposite. It takes an iterative approach to solve the subproblems first and then works up to the desired solution.
1. Top-Down Approach
The top-down approach can be more complex since it's less concrete. But sometimes, it's the best way to think about the problem. In these problems, we think about how we can divide the problem for case N into subproblems. Be careful of overlap between the cases.
Top-down with Memoization:
In this approach, we try to solve the bigger problem by recursively finding the solution to smaller sub-problems. Whenever we solve a sub-problem, we cache its result so that we don’t end up solving it repeatedly if it’s called multiple times. Instead, we can just return the saved result. This technique of storing the results of already solved subproblems is called Memoization.
2. Bottom-Up Approach
The bottom-up approach is often the most intuitive. We start with knowing how to solve the problem for a simple case, like a list with only one element. Then we figure out how to solve the problem for two elements, then for three elements, and so on. The key here is to think about how you can build the solution for one case off of the previous case (or multiple previous cases).
Bottom-up with Tabulation:
Tabulation is the opposite of the top-down approach and avoids recursion. In this approach, we solve the problem “bottom-up” (i.e. by solving all the related sub-problems first). This is typically done by filling up an n-dimensional table. Based on the results in the table, the solution to the top/original problem is then computed.
Tabulation is the opposite of Memoization, as in Memoization we solve the problem and maintain a map of already solved sub-problems. In other words, in memoization, we do it top-down in the sense that we solve the top problem first (which typically recurses down to solve the sub-problems).
Examples:
-
Sort stack
""" Sort Stack: (Under stacks) Write a function that takes in an array of integers representing a stack, recursively sorts the stack in place (i.e., doesn't create a brand new array), and returns it. The array must be treated as a stack, with the end of the array as the top of the stack. Therefore, you're only allowed to: Pop elements from the top of the stack by removing elements from the end of the array using the built-in .pop() method in your programming language of choice. Push elements to the top of the stack by appending elements to the end of the array using the built-in .append() method in your programming language of choice. Peek at the element on top of the stack by accessing the last element in the array. You're not allowed to perform any other operations on the input array, including accessing elements (except for the last element), moving elements, etc.. You're also not allowed to use any other data structures, and your solution must be recursive. Sample Input stack = [-5, 2, -2, 4, 3, 1] Sample Output [-5, -2, 1, 2, 3, 4] https://www.algoexpert.io/questions/Sort%20Stack """ # O(n^2) time | O(n) space - where n is the length of the stack # # this will work by looping through all the elements of the stack # # a bottom-up recursion approach where we start by sorting a stack of len 0, len 1, then 2, then 3 # remove every element till we have an empty stack # then insert them one by one at their correct position def sortStack(stack): # base case if len(stack) == 0: return stack # remove element at the top (element top), # sort the rest of the stack, # insert top back to the stack but at its correct position # this will be work easily because the rest of the stack is sorted top = stack.pop() sortStack(stack) insertElementInCorrectPosition(stack, top) return stack # requires a sorted stack def insertElementInCorrectPosition(stack, num): # base cases # correct positions to insert num if len(stack) == 0 or stack[-1] <= num: stack.append(num) # remove the element at the top and try to insert num at a lower position # return top once that is done else: top = stack.pop() insertElementInCorrectPosition(stack, num) stack.append(top)
3. Half-and-Half Approach
In addition to top-down and bottom-up approaches, it's often effective to divide the data set in half. For example, a binary search works with a "half-and-half" approach. When we look for an element in a sorted array, we first figure out which half of the array contains the value. Then we recurse and search for it in that half. Merge sort is also a "half-and-half" approach. We sort each half of the array and then merge together the sorted halves.
Maintaining State
When dealing with recursive functions, keep in mind that each recursive call has its own execution context, so to maintain state during recursion you have to either:
- Thread (pass down) the state through each recursive call so that the current state is part of the current call’s execution context
- Keep the state in the global scope
- eg: use nonlocal
Guides:
- Recursion is especially suitable when the input is expressed in recursive rules such as a computer grammar.
- Recursion is a good choice for search, enumeration, and divide-and-conquer.
- Use recursion as an alternative to deeply nested iteration loops. For example, recursion is much better when you have an undefined number of levels, such as the IP address problem generalized to k substrings.
- If you are asked to remove recursion from a program, consider mimicking call stack with the stack data structure.
- Recursion can be easily removed from a tail-recursive program by using a while-loop no stack is needed. (Optimizing compilers do this.)
- If a recursive function may end up being called with the same arguments more than once, cache the results-this is the idea behind Dynamic Programming
A divide-and-conquer algorithm works by repeatedly decomposing a problem into two or more smaller independent subproblems of the same kind until it gets to instances that are simple enough to be solved directly.
More explanation
A useful mantra to adopt when solving problems recursively is ‘fake it ’til you make it’, that is, pretend you’ve already solved the problem for a simpler case, and then try to reduce the larger problem to use the solution for this simpler case. If a problem is suited to recursion, there should actually only be a small number of simple cases which you need to explicitly solve, i.e. this method of reducing to a simpler problem can be used to solve every other case.
![]()
Suppose we are given some actual data of some data type, call it dₒ. The idea with recursion is to pretend that we have already solved the problem or computed the desired function f for all forms of this data type that are simpler than dₒ according to some degree of difficulty that we need to define. Then, if we can find a way of expressing f(dₒ) in terms of one or more f(d)s, where all of these d s are less difficult (have a smaller degree) than dₒ, then we have found a way to reduce and solve for f(dₒ). We repeat this process, and hopefully, at some point, the remaining f(d)s will get so simple that we can easily implement a fixed, closed solution to them. Then, our solution to the original problem will reveal itself as our solutions to progressively simpler problems aggregate and cascade back up to the top.
Honourable mentions
-
Use indexes to eliminate elements in an array instead of creating a new array all the time in recursion
Creating new array:
def getPermutationsHelper(res, curr_perm, array): if len(array) == 0: if len(curr_perm) > 0: res.append(curr_perm) return for i in range(len(array)): # add the number(array[i]), add it to the permutation and remove it from the array new_array = array[:i] + array[i+1:] # remove number form array new_perm = curr_perm + [array[i]] # add number to the permutation getPermutationsHelper(res, new_perm, new_array) def getPermutations(array): res = [] getPermutationsHelper(res, [], array) return resUsing indexes:
def swap(array, a, b): array[a], array[b] = array[b], array[a] def getPermutationsHelper(res, curr_perm, array, pos): if pos >= len(array): if len(curr_perm) > 0: res.append(curr_perm) return for i in range(pos, len(array)): # add the number(array[i]) to the permutation # place the element of interest at the first position (pos) # Example: for getPermutationsHelper(res, [], [1,2,3], 0), while in this for loop # when at value 1 (i=0), we want 1 to be at pos(0), so that we can iterate through [2,3,4] next without adding 1 again # when at 2, we want 2 to be at pos(0), so that we can iterate through [1,3,4] next ([2,1,3,4]) # when at 3, we want it to be at pos(0), so that we can iterate through [2,1,4] next ([3,2,1,4]) # so we have to manually place it there (via swapping with the element at pos), then we return it just before the loop ends # and move pos forward new_perm = curr_perm + [array[i]] # add number to the permutation # place the element of interest at the first position (pos) swap(array, pos, i) getPermutationsHelper(res, new_perm, array, pos+1) # return the element of interest to its original position swap(array, i, pos) def getPermutations(array): res = [] getPermutationsHelper(res, [], array, 0) return resEven better
def swap(array, a, b): array[a], array[b] = array[b], array[a] def getPermutationsHelper(res, array, pos): if pos == len(array) - 1: res.append(array[:]) return for i in range(pos, len(array)): # place the element of interest at the first position (pos) # Example: for getPermutationsHelper(res, [], [1,2,3], 0), while in this for loop # when at value 1 (i=0), we want 1 to be at pos(0), so that we can iterate through [2,3,4] next without adding 1 again # when at 2, we want 2 to be at pos(0), so that we can iterate through [1,3,4] next ([2,1,3,4]) # when at 3, we want it to be at pos(0), so that we can iterate through [2,1,4] next ([3,2,1,4]) # so we have to manually place it there (via swapping with the element at pos), then we return it just before the loop ends # and move pos forward # place the element of interest at the first position (pos) swap(array, pos, i) getPermutationsHelper(res, array, pos+1) # return the element of interest to its original position swap(array, i, pos) def getPermutations(array): res = [] getPermutationsHelper(res, array, 0) return res-
Combination Sum III




""" 216. Combination Sum III Find all valid combinations of k numbers that sum up to n such that the following conditions are true: Only numbers 1 through 9 are used. Each number is used at most once. Return a list of all possible valid combinations. The list must not contain the same combination twice, and the combinations may be returned in any order. Example 1: Input: k = 3, n = 7 Output: [[1,2,4]] Explanation: 1 + 2 + 4 = 7 There are no other valid combinations. Example 2: Input: k = 3, n = 9 Output: [[1,2,6],[1,3,5],[2,3,4]] Explanation: 1 + 2 + 6 = 9 1 + 3 + 5 = 9 2 + 3 + 4 = 9 There are no other valid combinations. Example 3: Input: k = 4, n = 1 Output: [] Explanation: There are no valid combinations. Using 4 different numbers in the range [1,9], the smallest sum we can get is 1+2+3+4 = 10 and since 10 > 1, there are no valid combination. Example 4: Input: k = 3, n = 2 Output: [] Explanation: There are no valid combinations. Example 5: Input: k = 9, n = 45 Output: [[1,2,3,4,5,6,7,8,9]] Explanation: 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45 There are no other valid combinations. https://leetcode.com/problems/combination-sum-iii/ Do after: - https://leetcode.com/problems/combination-sum """ # O(9! * K) time class Solution(object): def combinationSum3(self, k, n): res = [] self.helper(n, res, 1, 0, [0]*k, 0) return res def helper(self, n, res, start_num, curr_idx, curr, total): if total == n and curr_idx == len(curr): res.append(curr[:]) return if total >= n or start_num > 9 or curr_idx >= len(curr): return for number in range(start_num, 10): curr[curr_idx] = number self.helper(n, res, number+1, curr_idx+1, curr, total+number) curr[curr_idx] = 0 -
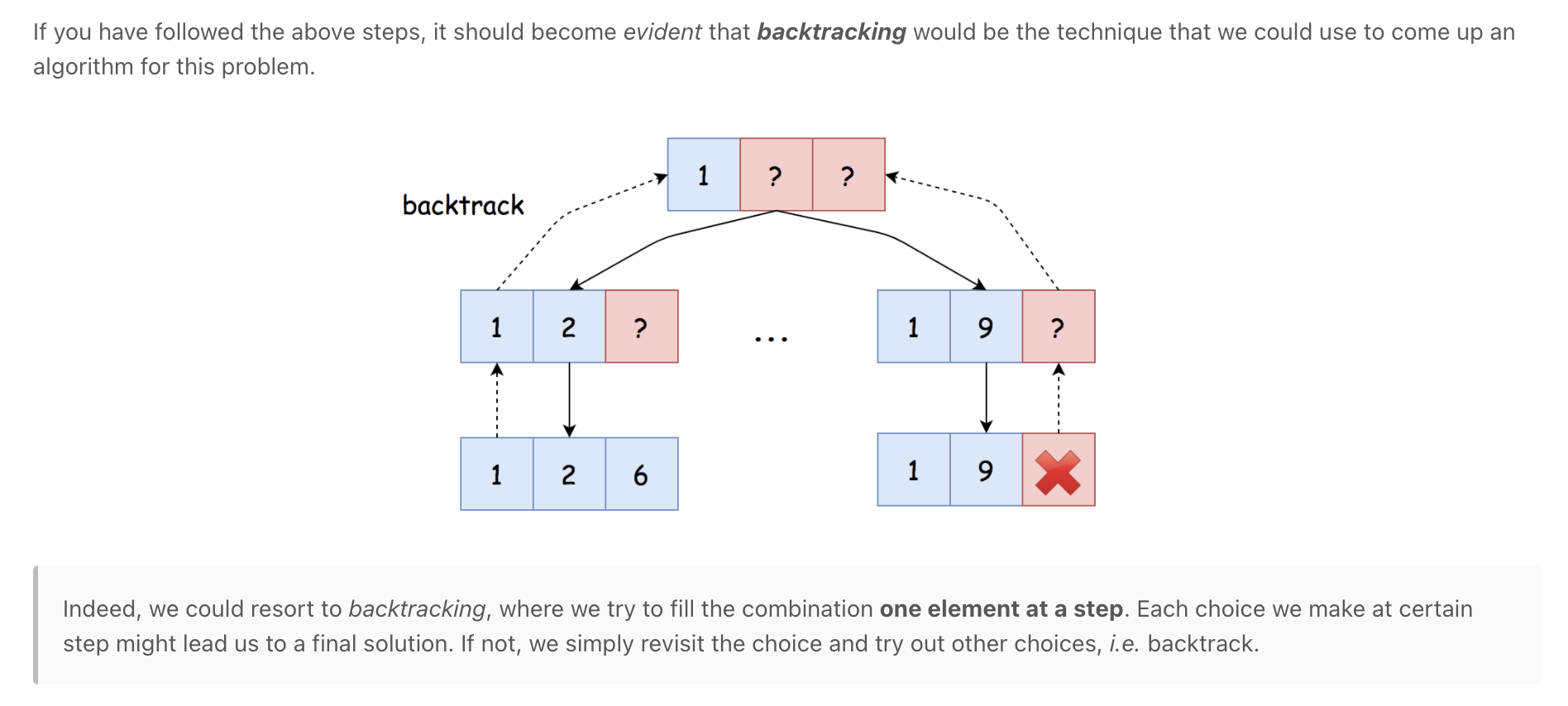
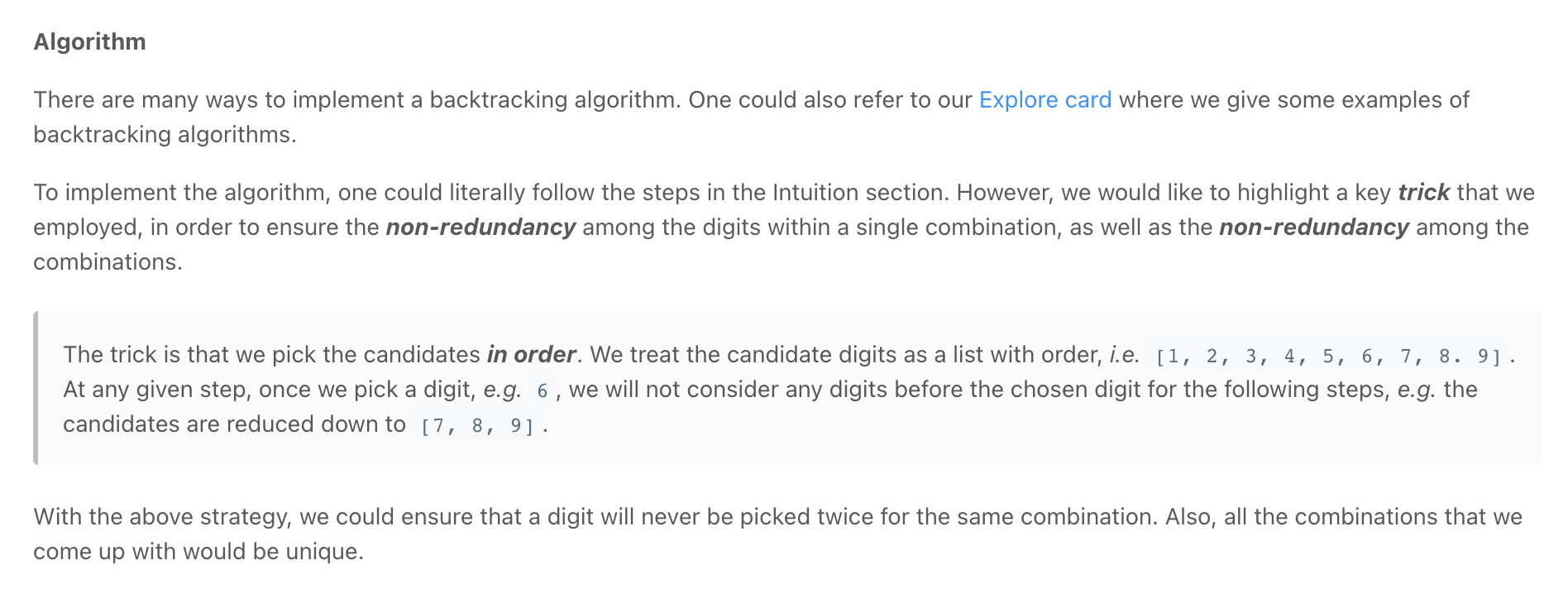
Combination Sum
Combination Sum - Backtracking - Leetcode 39 - Python
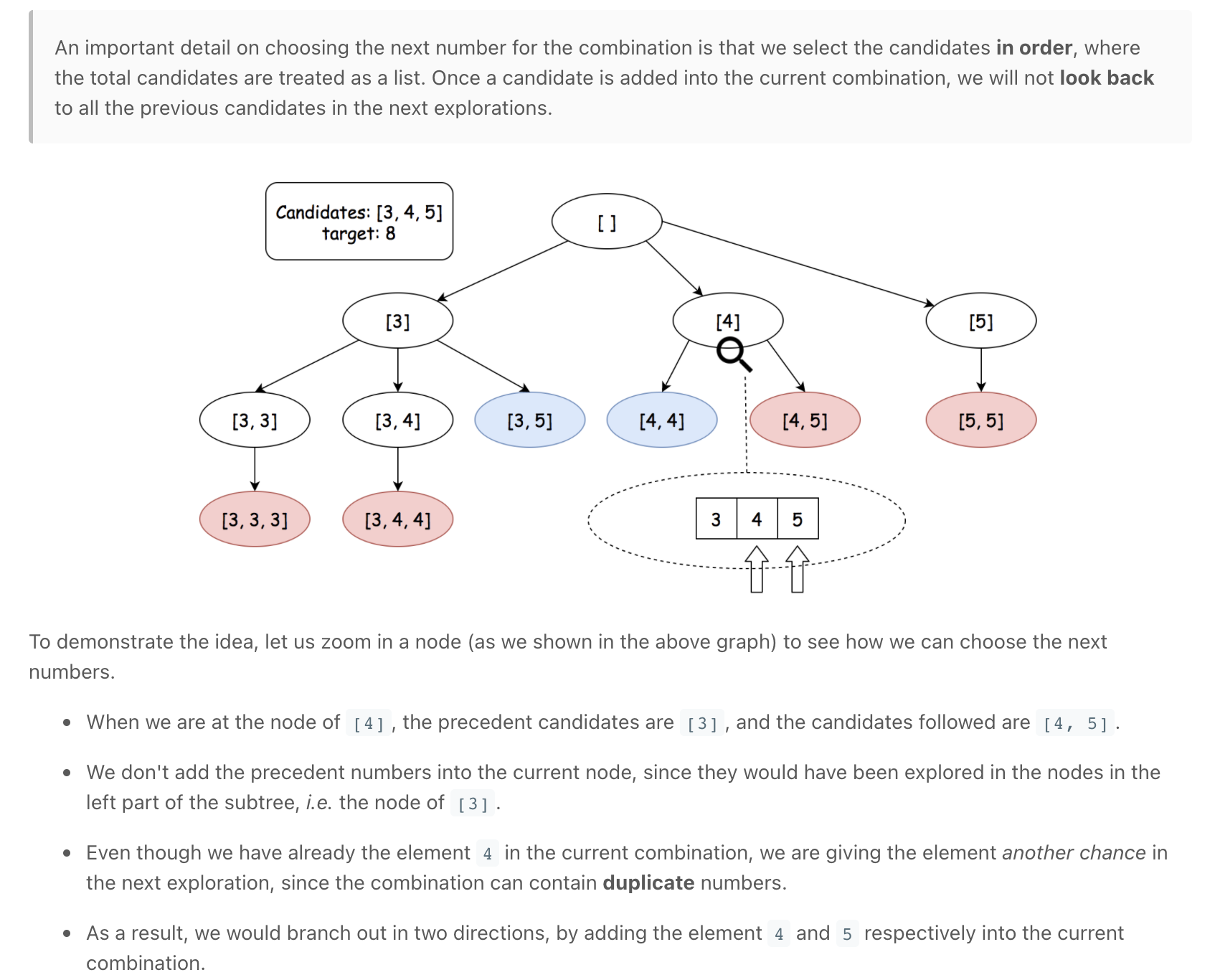

""" Combination Sum Given an array of distinct integers candidates and a target integer target, return a list of all unique combinations of candidates where the chosen numbers sum to target. You may return the combinations in any order. The same number may be chosen from candidates an unlimited number of times. Two combinations are unique if the frequency of at least one of the chosen numbers is different. It is guaranteed that the number of unique combinations that sum up to target is less than 150 combinations for the given input. Example 1: Input: candidates = [2,3,6,7], target = 7 Output: [[2,2,3],[7]] Explanation: 2 and 3 are candidates, and 2 + 2 + 3 = 7. Note that 2 can be used multiple times. 7 is a candidate, and 7 = 7. These are the only two combinations. Example 2: Input: candidates = [2,3,5], target = 8 Output: [[2,2,2,2],[2,3,3],[3,5]] Example 3: Input: candidates = [2], target = 1 Output: [] Example 4: Input: candidates = [1], target = 1 Output: [[1]] Example 5: Input: candidates = [1], target = 2 Output: [[1,1]] https://leetcode.com/problems/combination-sum Prerequisite: - https://leetcode.com/problems/combination-sum-iii """ """ candidates = [2,3,6,7], target = 7 7[] 5[2] 4[3] 3[2,2] 2[2,3] []rem_target / / \ \ [2]5 [3]4 [6]1 [7]0 / / [2,2]3 [2,3]2 | | [2,2,3]0 [2,3,2]0 """ class Solution(object): def combinationSum(self, candidates, target): return self.helper(candidates, 0, target) def helper(self, candidates, idx, target): # base cases if target == 0: return [[]] if target < 0 or idx >= len(candidates): return [] result = [] # add number # remember to give the current number another chance, rather than moving on (idx instead of idx+1) for arr in self.helper(candidates, idx, target-candidates[idx]): result.append(arr + [candidates[idx]]) # skip number result += self.helper(candidates, idx+1, target) return result """ Let N be the number of candidates, T be the target value, and M be the minimal value among the candidates. Time Complexity: O(N ^ T/M) Space Complexity: O(T/M) The execution of the backtracking is unfolded as a DFS traversal in a n-ary tree. The total number of steps during the backtracking would be the number of nodes in the tree. At each node, it takes a constant time to process, except the leaf nodes which could take a linear time to make a copy of combination. So we can say that the time complexity is linear to the number of nodes of the execution tree. Here we provide a loose upper bound on the number of nodes: First of all, the fan-out of each node would be bounded to N, i.e. the total number of candidates. The maximal depth of the tree, would be T/M, where we keep on adding the smallest element to the combination. As we know, the maximal number of nodes in N-ary tree of T/M, height would be : O(N ^ (T/M + 1)) Note that, the actual number of nodes in the execution tree would be much smaller than the upper bound, since the fan-out of the nodes are decreasing level by level. """ class Solution_: def combinationSum(self, candidates, target): results = [] def backtrack(remain, comb, start): if remain == 0: results.append(list(comb)) return elif remain < 0: return for i in range(start, len(candidates)): # add the number into the combination comb.append(candidates[i]) # give the current number another chance, rather than moving on (i instead of i+1) backtrack(remain - candidates[i], comb, i) # backtrack, remove the number from the combination comb.pop() backtrack(target, [], 0) return results
-
Dynamic programming
Dynamic Programming - 7 Steps to Solve any DP Interview Problem
Grokking Dynamic Programming Patterns for Coding Interviews - Learn Interactively
Fibonacci Numbers - Coderust: Hacking the Coding Interview
Demystifying Dynamic Programming
5 Simple Steps for Solving Dynamic Programming Problems
Calculating Fibonacci Numbers - Algorithms for Coding Interviews in Python
Memoization and Dynamic Programming | Interview Cake
Bottom-Up Algorithms and Dynamic Programming | Interview Cake
Introduction to Dynamic Programming 1 Tutorials & Notes | Algorithms | HackerEarth
leetcode/dynamic-programming-en.md at master · azl397985856/leetcode
Dynamic Programming - 7 Steps to Solve any DP Interview Problem
Dynamic programming is simple #3 (multi-root recursion) - LeetCode Discuss
Dynamic programming is basically, recursion plus using common sense. The intuition behind dynamic programming is that we trade space for time, i.e. to say that instead of calculating all the states taking a lot of time but no space, we take up space to store the results of all the sub-problems to save time later.
One can also think of dynamic programming as a table-filling algorithm: you know the calculations you have to do, so you pick the best order to do them in and ignore the ones you don't have to fill in.
DP is an optimisation technique → can reduce exponential to polynomial time
Common problems:
- Combinatory: Answer question... how many?
- Optimisation: maximises or minimises some function Examples: what is the minimum/maximum?
Dynamic programming is mostly just a matter of taking a recursive algorithm and finding the overlapping subproblems (that is, the repeated calls). You then cache those results for future recursive calls. Alternatively, you can study the pattern of the recursive calls and implement something iterative. You still "cache" previous work
Dynamic programming amounts to breaking down an optimization problem into simpler sub-problems and storing the solution to each sub-problem so that each sub-problem is only solved once. One of the simplest examples of dynamic programming is computing the nth Fibonacci number. A good way to approach such a problem is often to implement it as a normal recursive solution, and then add the caching part.
Every Dynamic Programming problem has a schema to be followed:
- Show that the problem can be broken down into optimal sub-problems.
- Recursively define the value of the solution by expressing it in terms of optimal solutions for smaller sub-problems.
- Compute the value of the optimal solution in a bottom-up fashion.
- Construct an optimal solution from the computed information.
The majority of the Dynamic Programming problems can be categorized into two types:
- Optimization problems The optimization problems expect you to select a feasible solution so that the value of the required function is minimized or maximized.
- Combinatorial problems expect you to figure out the number of ways to do something, or the probability of some event happening.
Examples
-
0/1 Knapsack
-
Levenshtein Distance
-
Coin Change 2 (Total Unique Ways To Make Change)
Problem
""" Coin Change 2/Total Unique Ways To Make Change: You are given an integer array coins representing coins of different denominations and an integer amount representing a total amount of money. Return the number of combinations that make up that amount. If that amount of money cannot be made up by any combination of the coins, return 0. You may assume that you have an infinite number of each kind of coin. The answer is guaranteed to fit into a signed 32-bit integer. Example 1: Input: amount = 5, coins = [1,2,5] Output: 4 Explanation: there are four ways to make up the amount: 5=5 5=2+2+1 5=2+1+1+1 5=1+1+1+1+1 Example 2: Input: amount = 3, coins = [2] Output: 0 Explanation: the amount of 3 cannot be made up just with coins of 2. Example 3: Input: amount = 10, coins = [10] Output: 1 https://leetcode.com/problems/coin-change-2/ https://www.algoexpert.io/questions/Number%20Of%20Ways%20To%20Make%20Change """Memoization
Coin Change 2 - Dynamic Programming Unbounded Knapsack - Leetcode 518 - Python

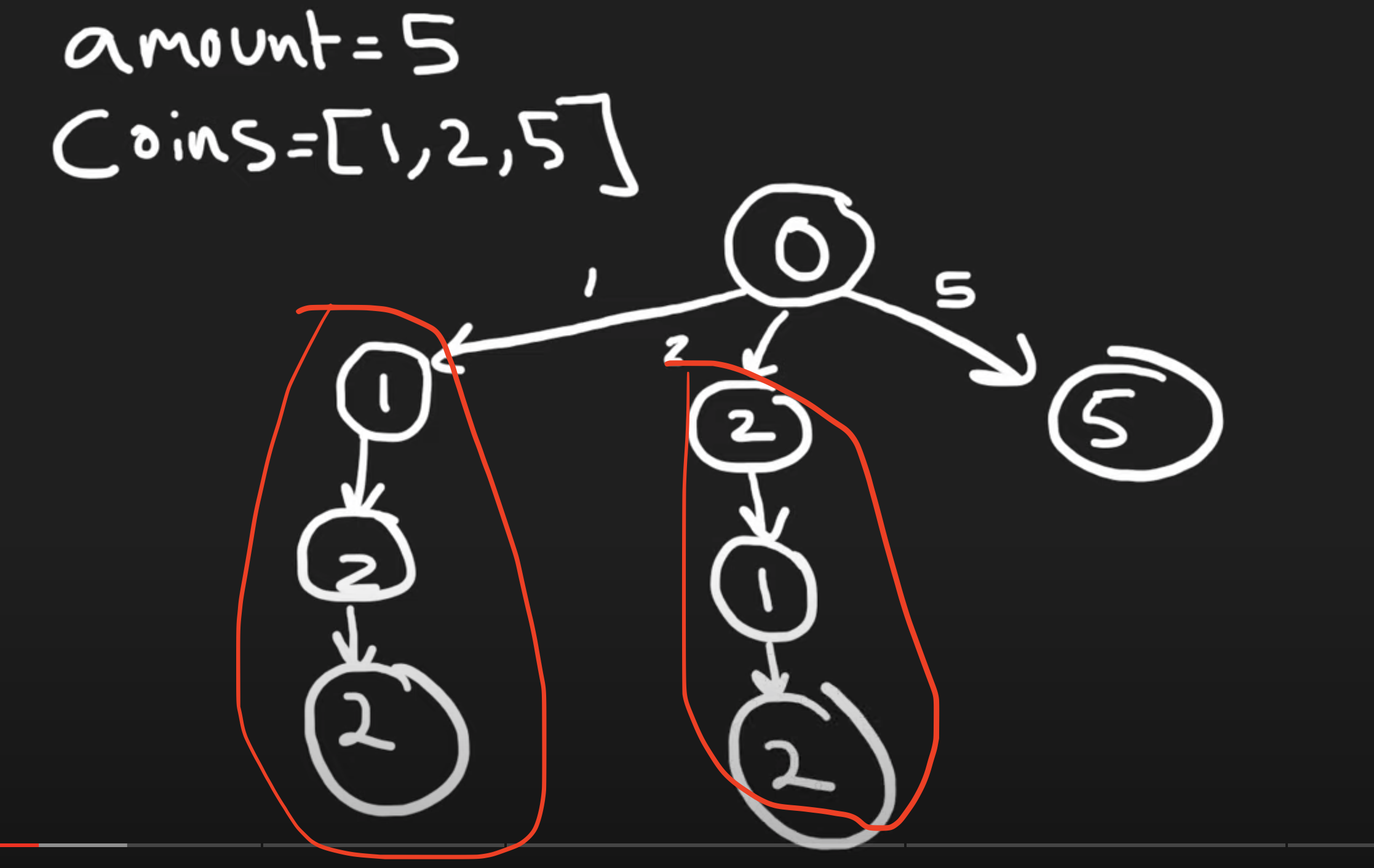
Duplicate recursive trees (we should avoid this)
""" - have a recursive function: - for each number in the array, choose to include it: - subtract the number from the amount and pass it down the recursive function - once you reach 0 return one of less than 0 return 0 - add up all the results - cache the total for each amount - ensure no duplicates by dividing the recursion trees by starting index - for examples for coins = [1,2,5] - index 0 tree: [1,2,5] - index 1 tree: [2,5] - index 2 tree: [5] """ class SolutionSLOW: # times out on leetcode def changeHelper(self, amount, coins, cache, idx): if amount == 0: return 1 if amount < 0: return 0 if (idx, amount) in cache: return cache[(idx, amount)] total = 0 for i in range(idx, len(coins)): total += self.changeHelper(amount-coins[i], coins, cache, i) cache[(idx, amount)] = total return cache[(idx, amount)] def change(self, amount, coins): return self.changeHelper(amount, coins, {}, 0) class SolutionSLOW2: # times out on leetcode def changeHelper(self, amount, coins, cache, idx): if amount == 0: return 1 if amount < 0 or idx == len(coins): return 0 if cache[idx][amount] != False: return cache[idx][amount] total = 0 # use it then next time we can decide to leave it out or use it again total += self.changeHelper(amount-coins[idx], coins, cache, idx) # not use coin and skip to the next total += self.changeHelper(amount, coins, cache, idx+1) cache[idx][amount] = total return cache[idx][amount] def change(self, amount, coins): cache = [[False for _ in range(amount+1)] for _ in range(len(coins))] return self.changeHelper(amount, coins, cache, 0) class Solution: def changeHelper(self, amount, coins, cache, idx): if amount == 0: return 1 if amount < 0 or idx == len(coins): return 0 if (idx, amount) in cache: return cache[(idx, amount)] total = 0 total += self.changeHelper(amount-coins[idx], coins, cache, idx) # use it then next time we can decide to leave it out or use it again total += self.changeHelper(amount, coins, cache, idx+1) # not use coin and skip to the next cache[(idx, amount)] = total return cache[(idx, amount)] def change(self, amount, coins): return self.changeHelper(amount, coins, {}, 0)Tabulation
coin change 2 | coin change 2 leetcode
Total Unique Ways To Make Change - Dynamic Programming ("Coin Change 2" on LeetCode)
Leetcode - Coin Change 2 (Python)
Coin Change 2 | LeetCode 518 | C++, Java, Python
Similar to knapsack

""" # if amount is zero you can always make that change with zero/no coins # if there are no coins there is no way to make change for amounts greater than zero number of ways = ( using the coin => reduce the amount by the coin's value (move left by the coin's value) + not using the coin => remove the coin (move up by one) ) 0 1 2 3 4 5 [] 1 0 0 0 0 0 [1] 1 1 1 1 1 1 [1,2] 1 [1,2,5] 1 """ class Solution: def change(self, amount, coins): dp = [[-1 for _ in range(amount+1)] for _ in range(len(coins)+1)] # Fill in defaults # if amount is zero you can always make that change with zero/no coins for i in range(len(coins)+1): dp[i][0] = 1 # if there are no coins there is no way to make change for amounts greater than zero for i in range(1, amount+1): dp[0][i] = 0 for coin in range(1, len(coins)+1): for amount in range(1, amount+1): actual_coin = coins[coin-1] total = 0 # not use coin => remove the coin (move up by one) total += dp[coin-1][amount] # use coin => reduce the amount by the coin's value (move left by the coin's value) if actual_coin <= amount: total += dp[coin][amount-actual_coin] # print(coin,actual_coin,amount,total) dp[coin][amount] = total return dp[-1][-1] # only keep needed fields in memory class Solution: def change(self, amount, coins): dp = [0 for _ in range(amount+1)] # if amount is zero you can always make that change with zero/no coins dp[0] = 1 for coin in coins: for amount in range(1, amount+1): total = dp[amount] # (ways_for_prev_coin) coin not added if coin <= amount: total += dp[amount-coin] # coin added dp[amount] = total return dp[-1] -
Coin Change
""" Coin Change: You are given an integer array coins representing coins of different denominations and an integer amount representing a total amount of money. Return the fewest number of coins that you need to make up that amount. If that amount of money cannot be made up by any combination of the coins, return -1. You may assume that you have an infinite number of each kind of coin. Example 1: Input: coins = [1,2,5], amount = 11 Output: 3 Explanation: 11 = 5 + 5 + 1 Example 2: Input: coins = [2], amount = 3 Output: -1 Example 3: Input: coins = [1], amount = 0 Output: 0 Example 4: Input: coins = [1], amount = 1 Output: 1 Example 5: Input: coins = [1], amount = 2 Output: 2 https://leetcode.com/problems/coin-change/ """ """ Min Number Of Coins For Change: Given an array of positive integers representing coin denominations and a single non-negative integer n representing a target amount of money, write a function that returns the smallest number of coins needed to make change for (to sum up to) that target amount using the given coin denominations. Note that you have access to an unlimited amount of coins. In other words, if the denominations are [1, 5, 10], you have access to an unlimited amount of 1s, 5s, and 10s. If it's impossible to make change for the target amount, return -1. https://www.algoexpert.io/questions/Min%20Number%20Of%20Coins%20For%20Change """ class SolutionMEM: def coinChange(self, coins, amount): cache = [[False for _ in range(amount+1)] for _ in range(len(coins))] res = self.coinChangeHelper(coins, 0, amount, cache) if res == float('inf'): return -1 return res def coinChangeHelper(self, coins, idx, amount, cache): if amount == 0: return 0 if amount < 0: return float('inf') if idx == len(coins): return float('inf') if cache[idx][amount]: return cache[idx][amount] # use it then next time we can decide to leave it out or use it again used = 1 + self.coinChangeHelper(coins, idx, amount-coins[idx], cache) # not use coin and skip to the next not_used = self.coinChangeHelper(coins, idx+1, amount, cache) cache[idx][amount] = min(used, not_used) return cache[idx][amount] """ ------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------ i = infinity 0 1 2 3 4 5 6 7 8 9 10 11 [] 0 i i i i i i i i i i i [1] 0 1 2 3 4 5 6 7 8 9 10 11 [1,2] 0 1 1 2 2 3 3 4 4 5 5 6 [1,2,5] 0 1 1 2 2 1 2 2 3 4 2 3 """ class SolutionDP: def coinChange(self, coins, amount): if amount == 0: return 0 if len(coins) == 0: return -1 dp = [ [float('inf') for _ in range(amount+1)] for _ in range(len(coins)+1)] for i in range(len(coins)+1): dp[i][0] = 0 for coin in range(1, len(coins)+1): for amount in range(1, amount+1): coin_val = coins[coin-1] not_use = dp[coin-1][amount] use = float('inf') if coin_val <= amount: use = 1 + dp[coin][amount-coin_val] dp[coin][amount] = min(use, not_use) if dp[-1][-1] == float('inf'): return -1 return dp[-1][-1] class SolutionDPImproved: def coinChange(self, coins, amount): if amount == 0: return 0 if len(coins) == 0: return -1 dp = [float('inf') for _ in range(amount+1)] dp[0] = 0 for amount in range(1, amount+1): for coin in coins: if coin > amount: continue use = 1 + dp[amount-coin] dp[amount] = min(use, dp[amount]) if dp[-1] == float('inf'): return -1 return dp[-1] -
Equal Subset Sum Partition
""" Equal Subset Sum Partition: Given a set of positive numbers, find if we can partition it into two subsets such that the sum of elements in both the subsets is equal. Example 1 Input: {1, 2, 3, 4} Output: True Explanation: The given set can be partitioned into two subsets with equal sum: {1, 4} & {2, 3} Example 2 Input: {1, 1, 3, 4, 7} Output: True Explanation: The given set can be partitioned into two subsets with equal sum: {1, 3, 4} & {1, 7} Example 3 Input: {2, 3, 4, 6} Output: False Explanation: The given set cannot be partitioned into two subsets with equal sum. https://leetcode.com/problems/partition-equal-subset-sum https://www.educative.io/courses/grokking-dynamic-programming-patterns-for-coding-interviews/3jEPRo5PDvx https://afteracademy.com/blog/partition-equal-subset-sum """ """ We know that if we can partition it into equal subsets that each set’s sum will have to be sum/2. If the sum is an odd number we cannot possibly have two equal sets. This changes the problem into finding if a subset of the input array has a sum of sum/2. We know that if we find a subset that equals sum/2, the rest of the numbers must equal sum/2 so we’re good since they will both be equal to sum/2. We can solve this using dynamic programming similar to the knapsack problem. We basically need to find two groups of numbers that will each be equal to sum(input_array) / 2 Finding one such group (with its sum = sum(input_array)/2) will imply that there will be another with a similar sum """ # ---------------------------------------------------------------------------------------------------------------------------------------------------------------- """ Brute Force 1: While using recursion, `iterate` through the input array, choosing whether to include each number in one of two arrays: "one" & "two" stop once the sum of elements in each of the arrays are equal to sum(input_array) / 2 """ def can_partition_helper_bf1(num, total, res, idx, one, two): # base cases if sum(one) == total/2 and sum(two) == total/2: res.append([one, two]) return if sum(one) > total/2 or sum(two) > total/2: return if idx >= len(num): return can_partition_helper_bf1(num, total, res, idx+1, one+[num[idx]], two) # one can_partition_helper_bf1(num, total, res, idx+1, one, two+[num[idx]]) # two def can_partition_bf1(num): res = [] total = sum(num) can_partition_helper_bf1(num, total, res, 0, [], []) return len(res) > 0 # ---------------------------------------------------------------------------------------------------------------------------------------------------------------- """ Brute Force 2: While using recursion, `iterate` through the input array, choosing whether to include each number in one of two sums: "one" & "two" stop once each of the sums are equal to sum(input_array) / 2 Basically Brute Force 1 without remembering the numbers """ def can_partition_helper_bf2(num, total, idx, one, two): # base cases if one == total/2 and two == total/2: return True if one > total/2 or two > total/2: return False if idx >= len(num): return False in_one = can_partition_helper_bf2(num, total, idx+1, one+num[idx], two) in_two = can_partition_helper_bf2(num, total, idx+1, one, two+num[idx]) return in_one or in_two def can_partition_bf2(num): total = sum(num) return can_partition_helper_bf2(num, total, 0, 0, 0) # ---------------------------------------------------------------------------------------------------------------------------------------------------------------- """ Brute Force 3: We basically need to find one group of numbers that will be equal to sum(input_array) / 2 Finding one such group (with its sum = sum(input_array)/2) will imply that there will be another with a similar sum While using recursion, `iterate` through the input array, choosing whether to include each number in the sum stop once the sum is equal to sum(input_array) / 2 Basically Brute Force 2 but dealing with one sum """ def can_partition_helper_bf3_0(num, total, idx, one): # base cases if one == total/2: return True if one > total/2: return False if idx >= len(num): return False included = can_partition_helper_bf3_0(num, total, idx+1, one+num[idx]) excluded = can_partition_helper_bf3_0(num, total, idx+1, one) return included or excluded # O(2^n) time | O(n) space def can_partition_bf3_0(num): total = sum(num) return can_partition_helper_bf3_0(num, total, 0, 0) # ----------------------------------- def can_partition_helper_bf3(num, total, idx): # base cases if total == 0: return True if total < 0: return False if idx >= len(num): return False included = can_partition_helper_bf3(num, total-num[idx], idx+1) excluded = can_partition_helper_bf3(num, total, idx+1) return included or excluded # O(2^n) time | O(n) space def can_partition_bf3(num): total = sum(num) return can_partition_helper_bf3(num, total/2, 0) # ---------------------------------------------------------------------------------------------------------------------------------------------------------------- """ Top-down Dynamic Programming with Memoization: We can use memoization to overcome the overlapping sub-problems. Since we need to store the results for every subset and for every possible sum, therefore we will be using a two-dimensional array to store the results of the solved sub-problems. The first dimension of the array will represent different subsets and the second dimension will represent different ‘sums’ that we can calculate from each subset. These two dimensions of the array can also be inferred from the two changing values (total and idx) in our recursive function. The above algorithm has time and space complexity of O(N*S), where ‘N’ represents total numbers and ‘S’ is the total sum of all the numbers. """ def can_partition_helper_memo(num, cache, total, idx): if total == 0: return True if total < 0 or idx >= len(num): return False if cache[idx][total] == True or cache[idx][total] == False: return cache[idx][total] included = can_partition_helper_memo(num, cache, total-num[idx], idx+1) excluded = can_partition_helper_memo(num, cache, total, idx+1) cache[idx][total] = included or excluded return cache[idx][total] # O(n*(s/2)) time & space -> where n represents total numbers & s is the total sum of all the numbers. def can_partition_memo(num): half_total = int(sum(num)/2) # convert to int for use in range if half_total != sum(num)/2: # ensure it wasn't a decimal number # if sum(num)/2 is an odd number, we can't have two subsets with equal sum return False cache = [[-1 for _ in range(half_total+1)] for _ in range(len(num))] # type: ignore return can_partition_helper_memo(num, cache, half_total, 0) # ---------------------------------------------------------------------------------------------------------------------------------------------------------------- """ Bottom-up Dynamic Programming: dp[n][total] means whether the specific sum 'total' can be gotten from the first 'n' numbers. If we can find such numbers from 0-'n' whose sum is total, dp[n][total] is true, otherwise it is false. dp[0][0] is true since with 0 elements a subset-sum of 0 is possible (both empty sets). dp[n][total] is true if dp[n-1][total] is true (meaning that we skipped this element, and took the sum of the previous result) or dp[n-1][total- element’s value(num[n])] assuming this isn’t out of range (meaning that we added this value to our subset-sum so we look at the sum — the current element’s value). This means, dp[n][total] will be ‘true’ if we can make sum ‘total’ from the first ‘n’ numbers. For each n and sum, we have two options: 1. Exclude the n. In this case, we will see if we can get total from the subset excluding this n: dp[n-1][total] 2. Include the n if its value is not more than ‘total’. In this case, we will see if we can find a subset to get the remaining sum: dp[n-1][total-num[n]] """ def can_partition_bu(num): half_total = int(sum(num)/2) # convert to int for use in range if half_total != sum(num)/2: # ensure it wasn't a decimal number # if its a an odd number, we can't have two subsets with equal sum return False dp = [[False for _ in range(half_total+1)] for _ in range(len(num))] # type: ignore for n in range(len(num)): for total in range(half_total+1): if total == 0: # '0' sum can always be found through an empty set dp[n][total] = True continue included = False excluded = False # # exclude if n-1 >= 0: excluded = dp[n-1][total] # # include if n <= total: rem_total = total - num[n] included = rem_total == 0 # fills the whole total if n-1 >= 0: # prev n can fill the remaining total included = included or dp[n-1][rem_total] dp[n][total] = included or excluded return dp[-1][-1] -
Maximum Subarray
-
Longest Common Subsequence **
DP pattern
""" Longest Common Subsequence Given two strings text1 and text2, return the length of their longest common subsequence. If there is no common subsequence, return 0. A subsequence of a string is a new string generated from the original string with some characters (can be none) deleted without changing the relative order of the remaining characters. For example, "ace" is a subsequence of "abcde". A common subsequence of two strings is a subsequence that is common to both strings. Example 1: Input: text1 = "abcde", text2 = "ace" Output: 3 Explanation: The longest common subsequence is "ace" and its length is 3. Example 2: Input: text1 = "abc", text2 = "abc" Output: 3 Explanation: The longest common subsequence is "abc" and its length is 3. Example 3: Input: text1 = "abc", text2 = "def" Output: 0 Explanation: There is no such common subsequence, so the result is 0. Constraints: 1 <= text1.length, text2.length <= 1000 text1 and text2 consist of only lowercase English characters. https://leetcode.com/problems/longest-common-subsequence """ class Solution: def longestCommonSubsequence(self, text1: str, text2: str): cache = [[None for _ in text2] for _ in text1] return self.lcs_helper(cache, text1, text2, 0, 0) def lcs_helper(self, cache, text1, text2, idx_1, idx_2): """ - base cases: - out of bounds - in cache - Check if characters match or not: - if match: move both idxs forwards and and add 1 to the result of that and return - else: try moving both idxs forward in separate function calls and return the longer one """ if idx_1 >= len(text1) or idx_2 >= len(text2): return 0 if cache[idx_1][idx_2]: return cache[idx_1][idx_2] if text1[idx_1] == text2[idx_2]: cache[idx_1][idx_2] = 1 + self.lcs_helper(cache, text1, text2, idx_1+1, idx_2+1) else: cache[idx_1][idx_2] = max( self.lcs_helper(cache, text1, text2, idx_1+1, idx_2), self.lcs_helper(cache, text1, text2, idx_1, idx_2+1) ) return cache[idx_1][idx_2] class Solution_: def longestCommonSubsequence(self, text1: str, text2: str): dp = [[0 for _ in range(len(text2)+1)] for _ in range(len(text1)+1)] for idx_1 in reversed(range(len(text1))): for idx_2 in reversed(range(len(text2))): # if match if text1[idx_1] == text2[idx_2]: dp[idx_1][idx_2] = 1 + dp[idx_1+1][idx_2+1] # add previous count else: dp[idx_1][idx_2] = max(dp[idx_1+1][idx_2], dp[idx_1][idx_2+1]) return dp[0][0] -
Longest Increasing Subsequence *
Longest Increasing Subsequence - Dynamic Programming - Leetcode 300

Tabulation_2
Tabulation_2
""" Longest Increasing Subsequence Given an integer array nums, return the length of the longest strictly increasing subsequence. A subsequence is a sequence that can be derived from an array by deleting some or no elements without changing the order of the remaining elements. For example, [3,6,2,7] is a subsequence of the array [0,3,1,6,2,2,7]. Example 1: Input: nums = [10,9,2,5,3,7,101,18] Output: 4 Explanation: The longest increasing subsequence is [2,3,7,101], therefore the length is 4. Example 2: Input: nums = [0,1,0,3,2,3] Output: 4 Example 3: Input: nums = [7,7,7,7,7,7,7] Output: 1 https://leetcode.com/problems/longest-increasing-subsequence/ """ """ [9] => 1 [8,9] => 2 [7,8,0,9] => 2 """ class Solution: def lengthOfLIS(self, nums): result = 0 cache = [None]*len(nums) # subsequence can start at any element for idx in range(len(nums)): result = max(self.helper(nums, idx, cache), result) return result def helper(self, nums, idx, cache): if cache[idx] is not None: return cache[idx] result = 1 # smallest subsequence for each number # next larger may be any larger element to the right for i in range(idx+1, len(nums)): if nums[i] > nums[idx]: result = max(1+self.helper(nums, i, cache), result) cache[idx] = result return cache[idx] # def lengthOfLIS(self, nums): # cache = [None]*len(nums) # for idx in range(len(nums)): # self.helper(nums, idx, cache) # return max(cache) class Solution_Tabulation_2: """ 1. Initialize an array dp with length nums.length and all elements equal to 1. - dp[i] represents the length of the longest increasing subsequence that ends with the element at index i. 2. Iterate from i = 1 to i = nums.length - 1. - At each iteration, use a second for loop to iterate from j = 0 to j = i - 1 (all the elements before i). - For each element before i, check if that element is smaller than nums[i]. - If so, set dp[i] = max(dp[i], dp[j] + 1). 3. Return the max value from dp. """ def lengthOfLIS(self, nums): dp = [0] * len(nums) for right in range(len(nums)): largest_prev_subs = 0 for left in range(right): if nums[right] > nums[left]: # largest_prev_subs = max( dp[left], largest_prev_subs) dp[right] = largest_prev_subs + 1 return max(dp) def lengthOfLIS_2(self, nums): dp = [1] * len(nums) for curr_idx in range(1, len(nums)): for prev_idx in range(curr_idx): if nums[curr_idx] > nums[prev_idx]: dp[curr_idx] = max( dp[curr_idx], dp[prev_idx] + 1 ) return max(dp) """ [10,9,2,5,3,7,101,18] [ 2,2,4,3,3,2, 1, 1] """ class Solution_Tabulation_1: def lengthOfLIS(self, nums): dp = [1]*len(nums) for idx in reversed(range(len(dp))): largest = 0 for i in range(idx+1, len(dp)): if nums[i] > nums[idx]: largest = max(dp[i], largest) dp[idx] = 1 + largest return max(dp) """ [10, 9, 2, 5, 3, 7, 101, 18] [ 0, 1, 2, 3, 4, 5, 6, 7] 0 [ 1, 1, 1, 1, 1, 1, 1, 1] 1 [ 1, 1, 1, 1, 1, 1, 1, 1] 2 [ 1, 1, 1, 1, 1, 1, 1, 1] 3 values smaller than 5 => 2 [ 1, 1, 1, 2, 1, 1, 1, 1] 4 values smaller than 3 => 2 [ 1, 1, 1, 2, 2, 1, 1, 1] 5 values smaller than 7 => 2,5,3 [ 1, 1, 1, 2, 2, 3, 1, 1] 6 values smaller than 101 => 2,5,3,7 [ 1, 1, 1, 2, 2, 3, 4, 1] 7 values smaller than 18 => 2,5,3,7 [ 1, 1, 1, 2, 2, 3, 4, 4] 1. Initialize an array dp with length nums.length and all elements equal to 1. dp[i] represents the length of the longest increasing subsequence that ends with the element at index i. 2. Iterate from i = 1 to i = nums.length - 1. At each iteration, use a second for loop to iterate from j = 0 to j = i - 1 (all the elements before i). For each element before i, check if that element is smaller than nums[i]. If so, set dp[i] = max(dp[i], dp[j] + 1). 3. Return the max value from dp. """ -
Longest Arithmetic Subsequence **
""" 1027. Longest Arithmetic Subsequence Given an array nums of integers, return the length of the longest arithmetic subsequence in nums. Recall that a subsequence of an array nums is a list nums[i1], nums[i2], ..., nums[ik] with 0 <= i1 < i2 < ... < ik <= nums.length - 1, and that a sequence seq is arithmetic if seq[i+1] - seq[i] are all the same value (for 0 <= i < seq.length - 1). Example 1: Input: nums = [3,6,9,12] Output: 4 Explanation: The whole array is an arithmetic sequence with steps of length = 3. Example 2: Input: nums = [9,4,7,2,10] Output: 3 Explanation: The longest arithmetic subsequence is [4,7,10]. Example 3: Input: nums = [20,1,15,3,10,5,8] Output: 4 Explanation: The longest arithmetic subsequence is [20,15,10,5]. Constraints: 2 <= nums.length <= 1000 0 <= nums[i] <= 500 https://leetcode.com/problems/longest-arithmetic-subsequence """ from collections import defaultdict from typing import List class Solution: def longestArithSeqLength(self, nums: List[int]): """ - have a `sequence_cache` hashmap for each element in the array with the keys and values: `{sequence_difference: count/length}` - iterate in reverse order - for each `element_1`: - iterate through all the elements to its right, and for each `element_2`: - get the `sequence difference`: (`element_1-element_2`) - check if staring a sequence with that sequence difference will be greater than what we have seen b4 for the same sequence difference - update the longest var to reflect the longest we have seen so far """ longest = 0 seq_cache = [defaultdict(lambda: 1) for num in nums] for idx_1 in reversed(range(len(nums))): for idx_2 in range(idx_1+1, len(nums)): seq_diff = nums[idx_2] - nums[idx_1] # current_seq_len = max(current_seq_len, seq_starting_at_idx_2_len+1) seq_cache[idx_1][seq_diff] = max(seq_cache[idx_1][seq_diff], seq_cache[idx_2][seq_diff]+1) longest = max(longest, seq_cache[idx_1][seq_diff]) return longest -
Russian Doll Envelopes **

""" Russian Doll Envelopes: You are given a 2D array of integers envelopes where envelopes[i] = [wi, hi] represents the width and the height of an envelope. One envelope can fit into another if and only if both the width and height of one envelope are greater than the other envelope's width and height. Return the maximum number of envelopes you can Russian doll (i.e., put one inside the other). Note: You cannot rotate an envelope. Example 1: Input: envelopes = [[5,4],[6,4],[6,7],[2,3]] Output: 3 Explanation: The maximum number of envelopes you can Russian doll is 3 ([2,3] => [5,4] => [6,7]). Example 2: Input: envelopes = [[1,1],[1,1],[1,1]] Output: 1 https://leetcode.com/problems/russian-doll-envelopes/ Based on: Longest Increasing Subsequence https://leetcode.com/problems/longest-increasing-subsequence """ class SolutionSLOW: # time limit exceeded def maxEnvelopes(self, envelopes): items = list({tuple(item) for item in envelopes}) items.sort(key=lambda x: x[0]+x[1]) return self.longest_increasing_subsequence(items) def longest_increasing_subsequence(self, envelopes): dp = [1]*len(envelopes) for idx in reversed(range(len(dp))): largest = 0 for i in range(idx+1, len(dp)): curr = envelopes[idx] nxt = envelopes[i] if curr[0] < nxt[0] and curr[1] < nxt[1]: largest = max(dp[i], largest) dp[idx] = 1 + largest return max(dp) """ """ class Solution: def maxEnvelopes(self, arr): arr.sort(key=lambda x: (x[0], -x[1])) # extract the second dimension and run the LIS # already sorted by width return self.length_of_longest_increasing_subsequence([i[1] for i in arr]) def length_of_longest_increasing_subsequence(self, nums): dp = [0] * len(nums) for right in range(len(nums)): largest_prev_subs = 0 for left in range(right): if nums[right] > nums[left]: # largest_prev_subs = max(dp[left], largest_prev_subs) dp[right] = largest_prev_subs + 1 return max(dp) -
Maximum Height by Stacking Cuboids *
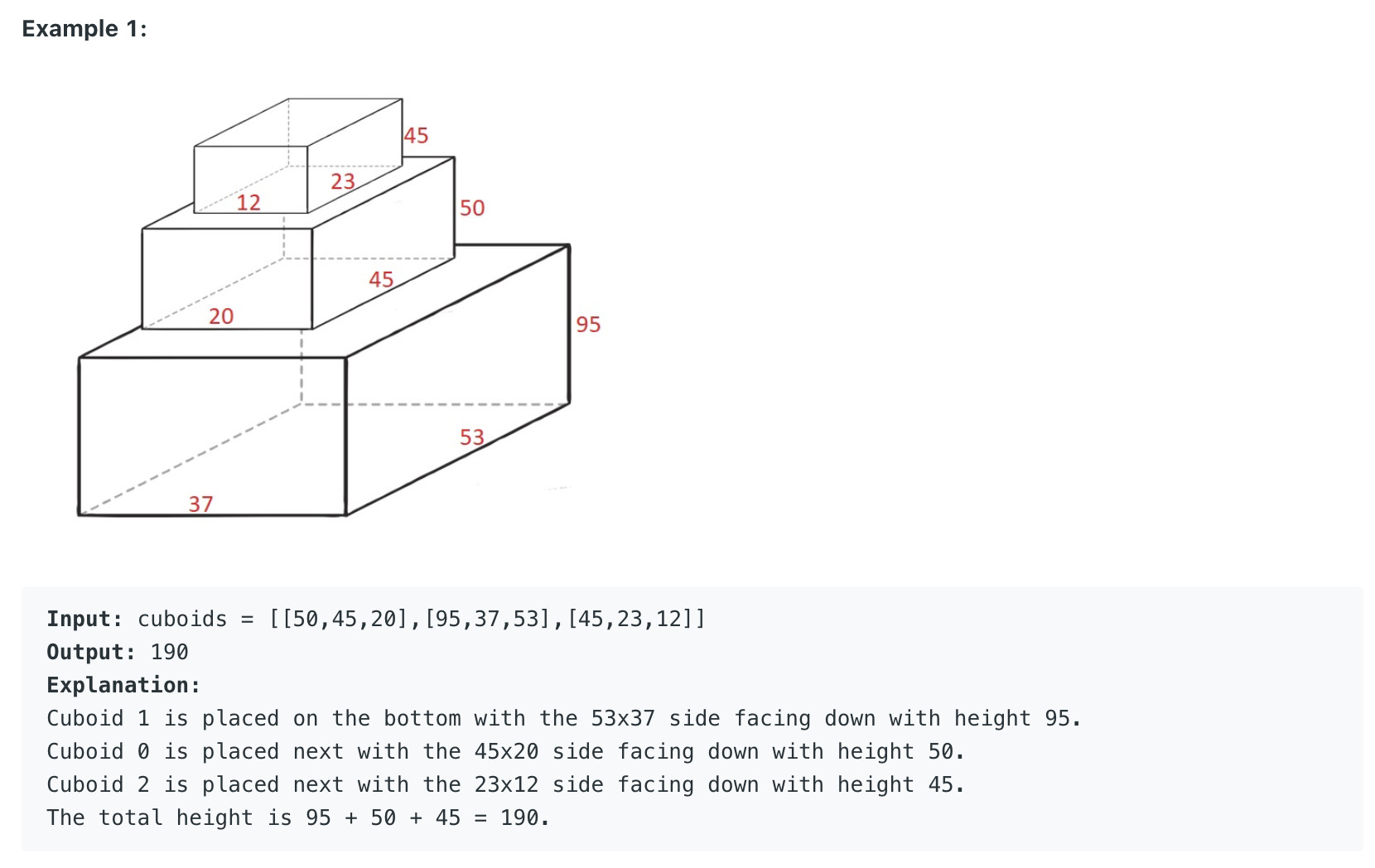
""" Maximum Height by Stacking Cuboids (Not worth your time lol) Given n cuboids where the dimensions of the ith cuboid is cuboids[i] = [widthi, lengthi, heighti] (0-indexed). Choose a subset of cuboids and place them on each other. You can place cuboid i on cuboid j if widthi <= widthj and lengthi <= lengthj and heighti <= heightj. You can rearrange any cuboid's dimensions by rotating it to put it on another cuboid. Return the maximum height of the stacked cuboids. https://leetcode.com/problems/maximum-height-by-stacking-cuboids/ Based on: Longest Increasing Subsequence: https://leetcode.com/problems/longest-increasing-subsequence Russian Doll Envelopes: https://leetcode.com/problems/russian-doll-envelopes/ """ """ https://leetcode.com/problems/maximum-height-by-stacking-cuboids/discuss/970364/Python-Top-Down-DP https://leetcode.com/problems/maximum-height-by-stacking-cuboids/discuss/970293/JavaC%2B%2BPython-DP-Prove-with-Explanation https://leetcode.com/problems/maximum-height-by-stacking-cuboids/discuss/971046/Formal-Proof-for-Greedy-Sorting-Dimensions """ class Solution: def maxHeight(self, cuboids): for cuboid in cuboids: cuboid.sort() return self.longest_increasing_subsequence(cuboids) def longest_increasing_subsequence(self, cuboids): result = 0 cuboids.sort() cache = [None]*len(cuboids) # subsequence can start at any element for idx in range(len(cuboids)): result = max(self.lis_helper(cuboids, idx, cache), result) return result def lis_helper(self, cuboids, idx, cache): if cache[idx] is not None: return cache[idx] result = cuboids[idx][2] for i in reversed(range(idx+1, len(cuboids))): curr = cuboids[idx] nxt = cuboids[i] if curr[0] <= nxt[0] and curr[1] <= nxt[1] and curr[2] <= nxt[2]: result = max( curr[2]+self.lis_helper(cuboids, i, cache), result ) cache[idx] = result return cache[idx] -
Longest Palindromic Subsequence **
""" 516. Longest Palindromic Subsequence Given a string s, find the longest palindromic subsequence's length in s. A subsequence is a sequence that can be derived from another sequence by deleting some or no elements without changing the order of the remaining elements. Example 1: Input: s = "bbbab" Output: 4 Explanation: One possible longest palindromic subsequence is "bbbb". Example 2: Input: s = "cbbd" Output: 2 Explanation: One possible longest palindromic subsequence is "bb". https://leetcode.com/problems/longest-palindromic-subsequence """ class Solution: def longestPalindromeSubseq(self, s: str): cache = [[None for _ in s] for _ in s] return self.lps_helper(s, cache, 0, len(s)-1) def lps_helper(self, s, cache, start, end): """ - if the characters at the ends match, we dive deeper and add 2 to the result of going deeper - if not: skip the start and the end and return the one with the highest result """ if start > end: return 0 if start == end: return 1 if cache[start][end]: return cache[start][end] if s[start] == s[end]: # dive deeper cache[start][end] = 2 + self.lps_helper(s, cache, start+1, end-1) else: # skip one character cache[start][end] = max(self.lps_helper(s, cache, start+1, end), self.lps_helper(s, cache, start, end-1)) return cache[start][end] -
https://leetcode.com/problems/valid-palindrome-iii/submissions/
-
Climbing Stairs / Triple Step
""" Climbing Stairs / Triple Step: You are climbing a staircase. It takes n steps to reach the top. Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top? https://leetcode.com/problems/climbing-stairs/ """ class Solution: def climbStairs(self, n): return self.helper(n) # in case we reach remaining=0, then we have found way (a correct set of steps) def helper(self, remaining, store={0: 1}): # store={0:1} is a base case if remaining < 0: return 0 if remaining in store: return store[remaining] total = self.helper(remaining-1, store) + \ self.helper(remaining-2, store) store[remaining] = total return store[remaining] """ Staircase Traversal: You're given two positive integers representing the height of a staircase and the maximum number of steps that you can advance up the staircase at a time. Write a function that returns the number of ways in which you can climb the staircase. For example, if you were given a staircase of height = 3 and maxSteps = 2 you could climb the staircase in 3 ways. You could take 1 step, 1 step, then 1 step, you could also take 1 step, then 2 steps, and you could take 2 steps, then 1 step. Note that maxSteps <= height will always be true. Sample Input: height = 4 maxSteps = 2 Sample Output: 5 // You can climb the staircase in the following ways: // 1, 1, 1, 1 // 1, 1, 2 // 1, 2, 1 // 2, 1, 1 // 2, 2 https://www.algoexpert.io/questions/Staircase%20Traversal """ # 0(k^n) time, 0(n) space - where k is the max steps, n - number of steps def staircaseTraversal00(height, maxSteps): return staircaseTraversalHelper00(height, maxSteps) def staircaseTraversalHelper00(height_remaining, max_steps): if height_remaining == 0: # if are exactly at the last step, we have found a way return 1 elif height_remaining < 0: # if we pass the last step, we made a mistake return 0 ways = 0 for step in range(1, max_steps+1): ways += staircaseTraversalHelper00(height_remaining - step, max_steps) return ways # memoization: # 0(k*n) time, 0(n) space - where k is the max steps, n - number of steps # for each call, we'll have to sum k elements together # for each of our n recursive calls, we have to do k work def staircaseTraversal(height, maxSteps): return staircaseTraversalHelper(height, maxSteps, {0: 1}) def staircaseTraversalHelper(height_remaining, max_steps, store): if height_remaining < 0: # if we pass the last step, we made a mistake return 0 # memoize if height_remaining in store: return store[height_remaining] ways = 0 for step in range(1, max_steps+1): ways += staircaseTraversalHelper(height_remaining - step, max_steps, store) store[height_remaining] = ways # memoize return store[height_remaining] """ ordering: legend=> [step][remaining] h=3 max_steps=2 [][3] [1][2] [2][1] [1][1] [2][0] [1][0] [1][0] h=4 max_steps=3 [][4] [1][3] [2][2] [3][1] [1][2] [2][1] [3][0] [1][1] [2][0] [1][0] h=0 max_steps=2 ways=1 h=1 max_steps=2 ways=1 h=2 max_steps=2 ways=2 h=3 max_steps=2 ways=3 h=4 max_steps=2 ways=5 we realise that: ways(n) = ways(n-1) + (n-2) .... + (n-max-steps) The number of ways to climb a staircase of height k with a max number of steps s is: numWays[k - 1] + numWays[k - 2] + ... + numWays[k - s]. This is because if you can advance between 1 and s steps, then from each step k - 1, k - 2, ..., k - s, you can directly advance to the top of a staircase of height k. By adding the number of ways to reach all steps that you can directly advance to the top step from, you determine how many ways there are to reach the top step. """ # <----------------------------------------------------------------------------------------------------------> # DP Solution # we will run the loop n times each with k work # O(k^n) time | O(n) space - where n is the height of the staircase and k is the number of allowed steps def staircaseTraversal04(height, maxSteps): # the indices represent the heights & the values the no. of ways max_ways = [0] * (height + 1) # base cases max_ways[0] = 1 max_ways[1] = 1 # try all steps: start from maxSteps, maxSteps-1, ..., 2 & 1 # ways(n) = ways(n-1) + (n-2) .... + (n-max-steps) for idx in range(2, height+1): ways = 0 start_idx = max(idx-maxSteps, 0) # prevent negatives for i in range(start_idx, idx): ways += max_ways[i] max_ways[idx] = ways return max_ways[-1] # <----------------------------------------------------------------------------------------------------------> # DP Solution improved # we will run the loop n times each with k work # O(n) time | O(n) space - where n is the height of the staircase and k is the number of allowed steps def staircaseTraversal05(height, maxSteps): # the indices represent the heights & the values the no. of ways max_ways = [0] * (height + 1) # base cases max_ways[0] = 1 max_ways[1] = 1 # # try all steps: start from maxSteps, maxSteps-1, ..., 2 & 1 # # ways(n) = ways(n-1) + (n-2) .... + (n-max-steps) # start with a window size of one window = max_ways[0] window_size = 1 # this cab be removed -> (idx == prev window_size) for idx in range(1, height+1): max_ways[idx] = window # manipulate window size window += max_ways[idx] if window_size == maxSteps: window -= max_ways[idx-maxSteps] else: window_size += 1 return max_ways[-1] -
Decode ways
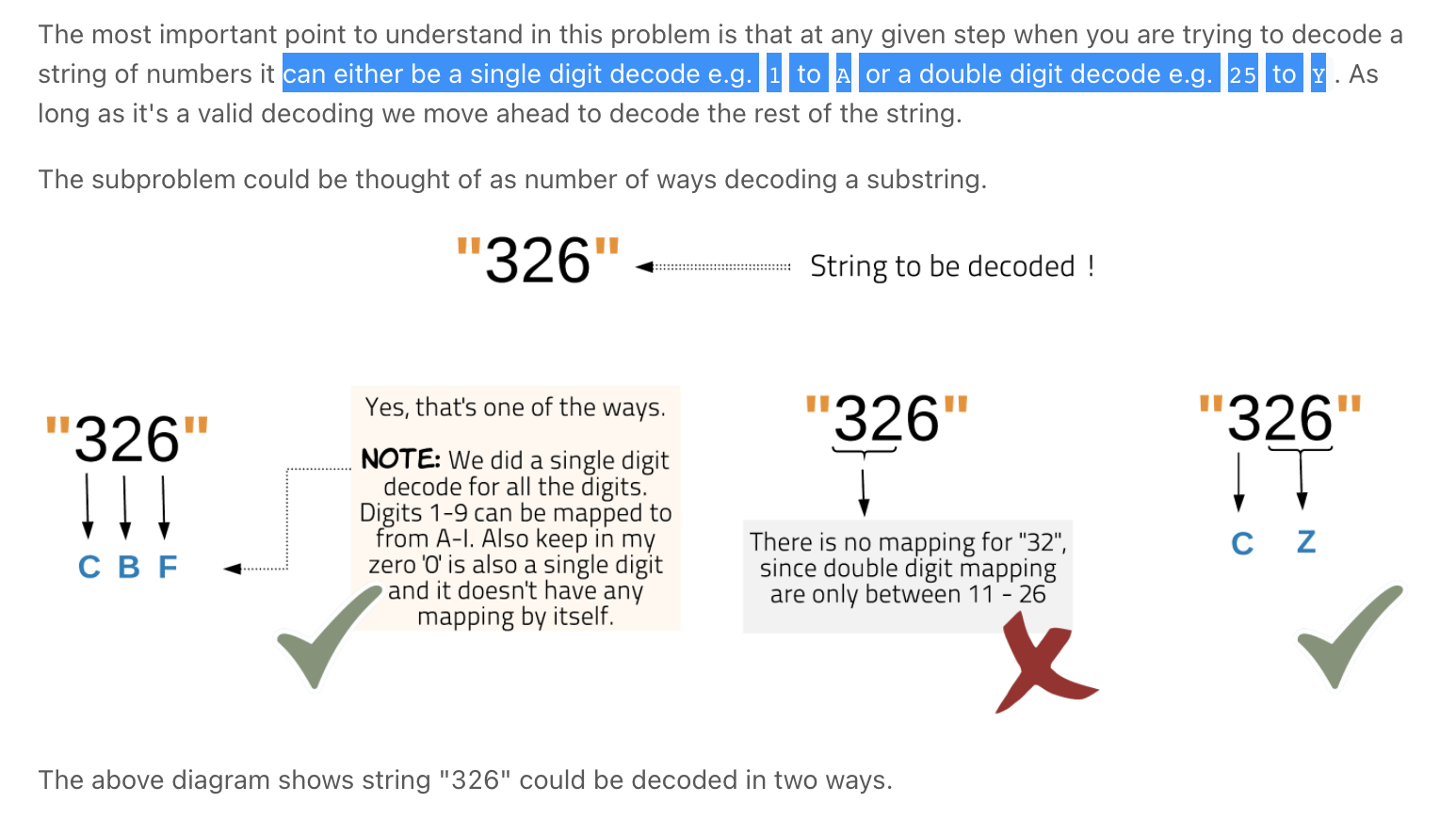
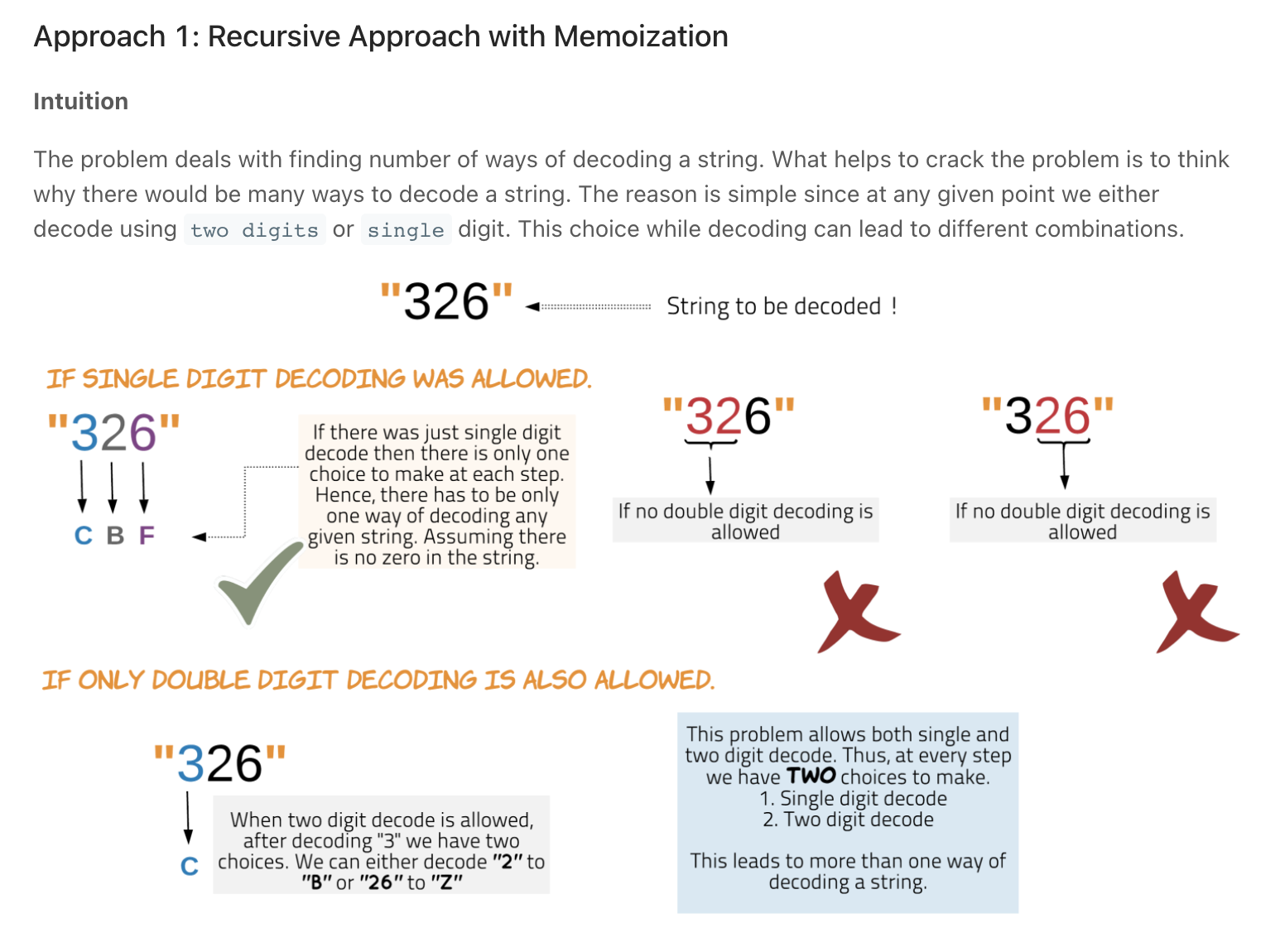
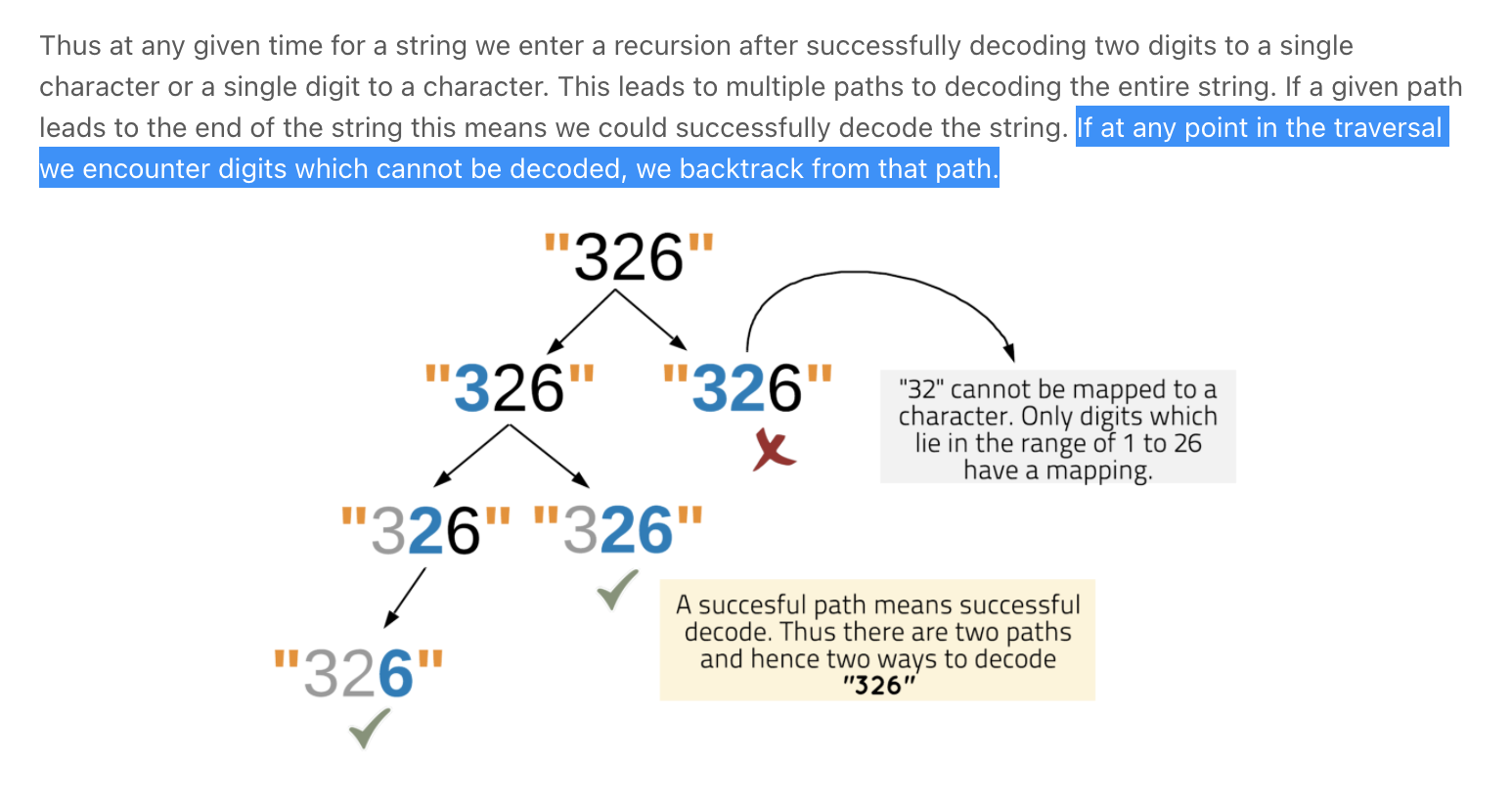
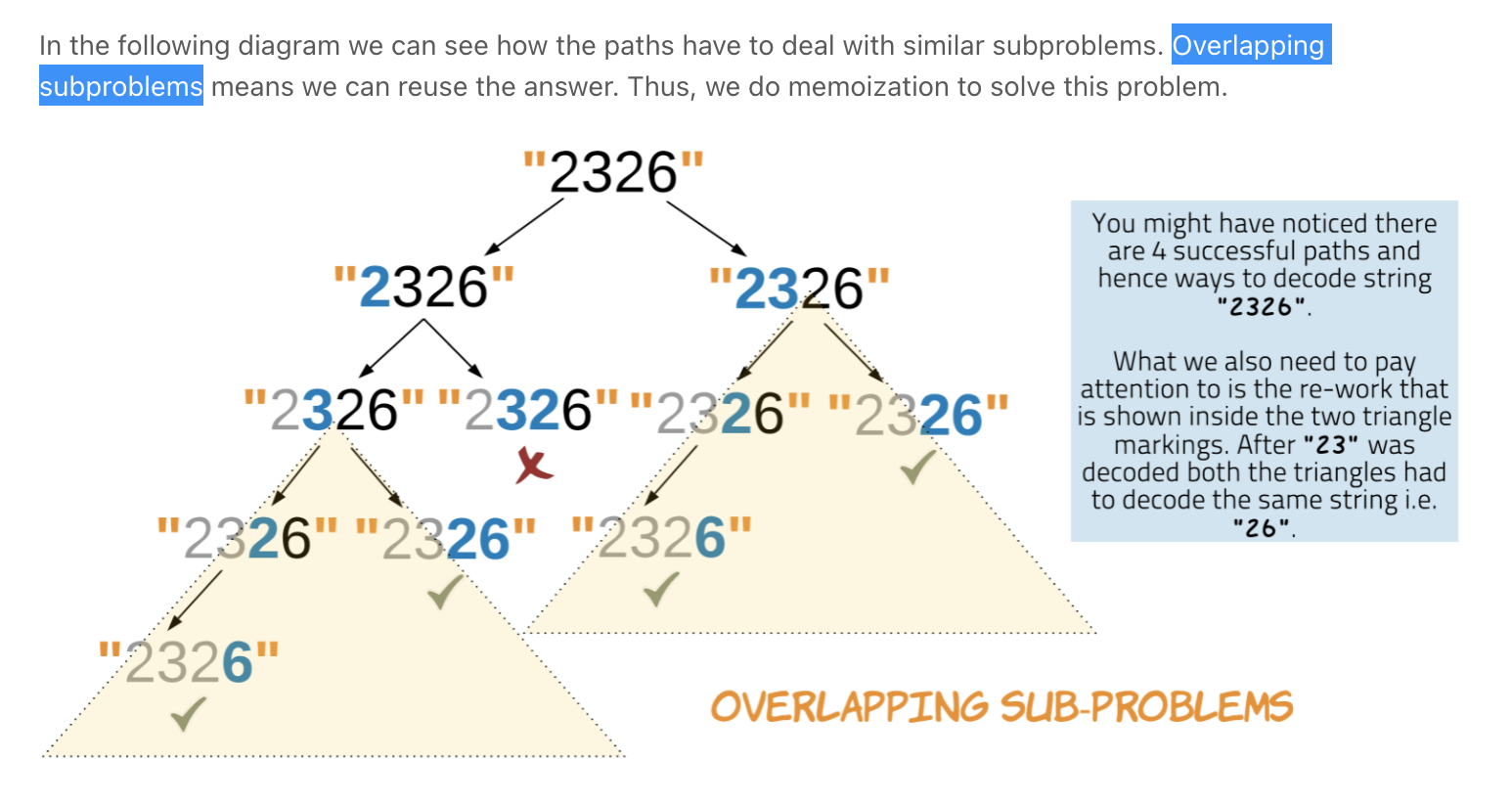
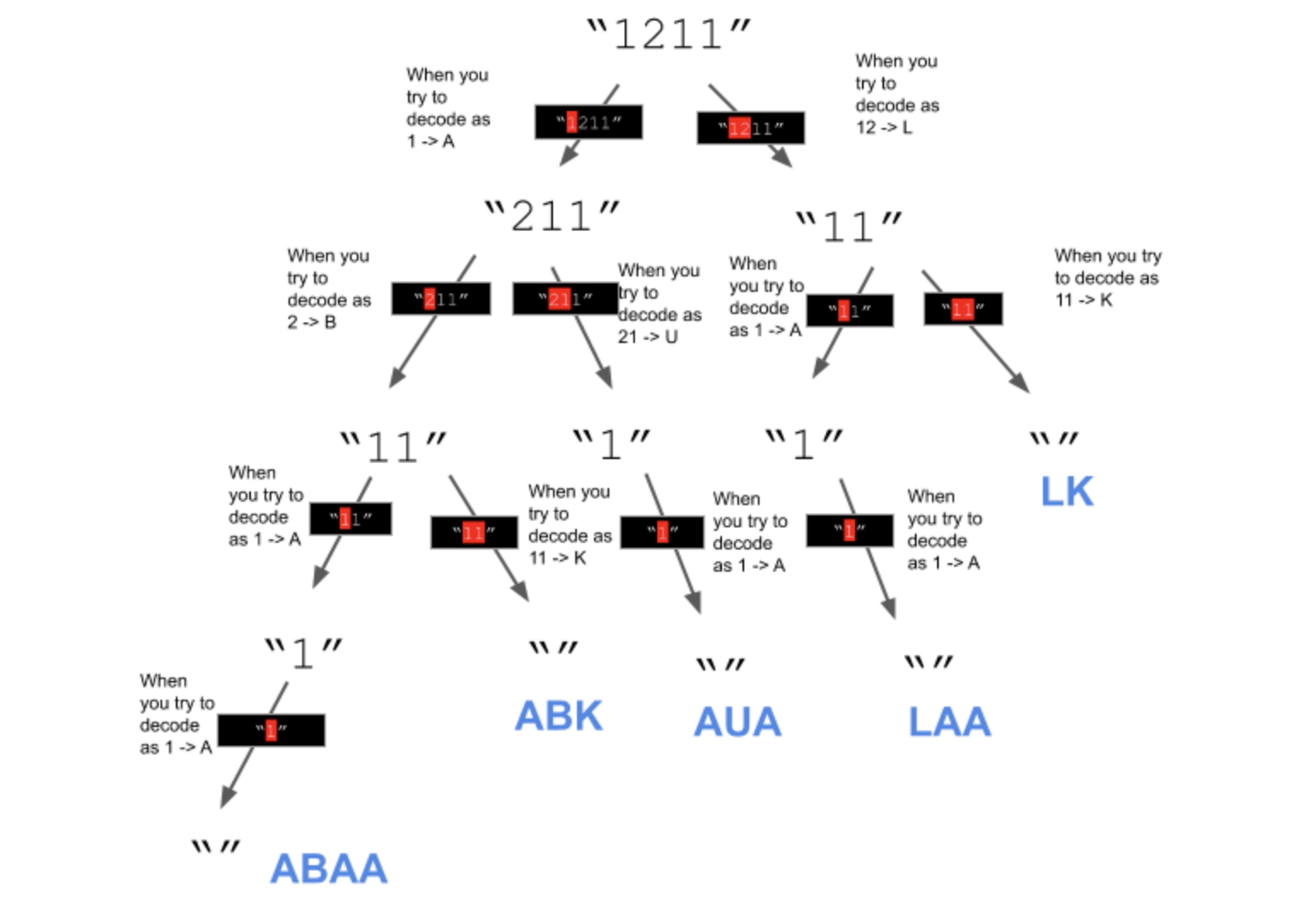
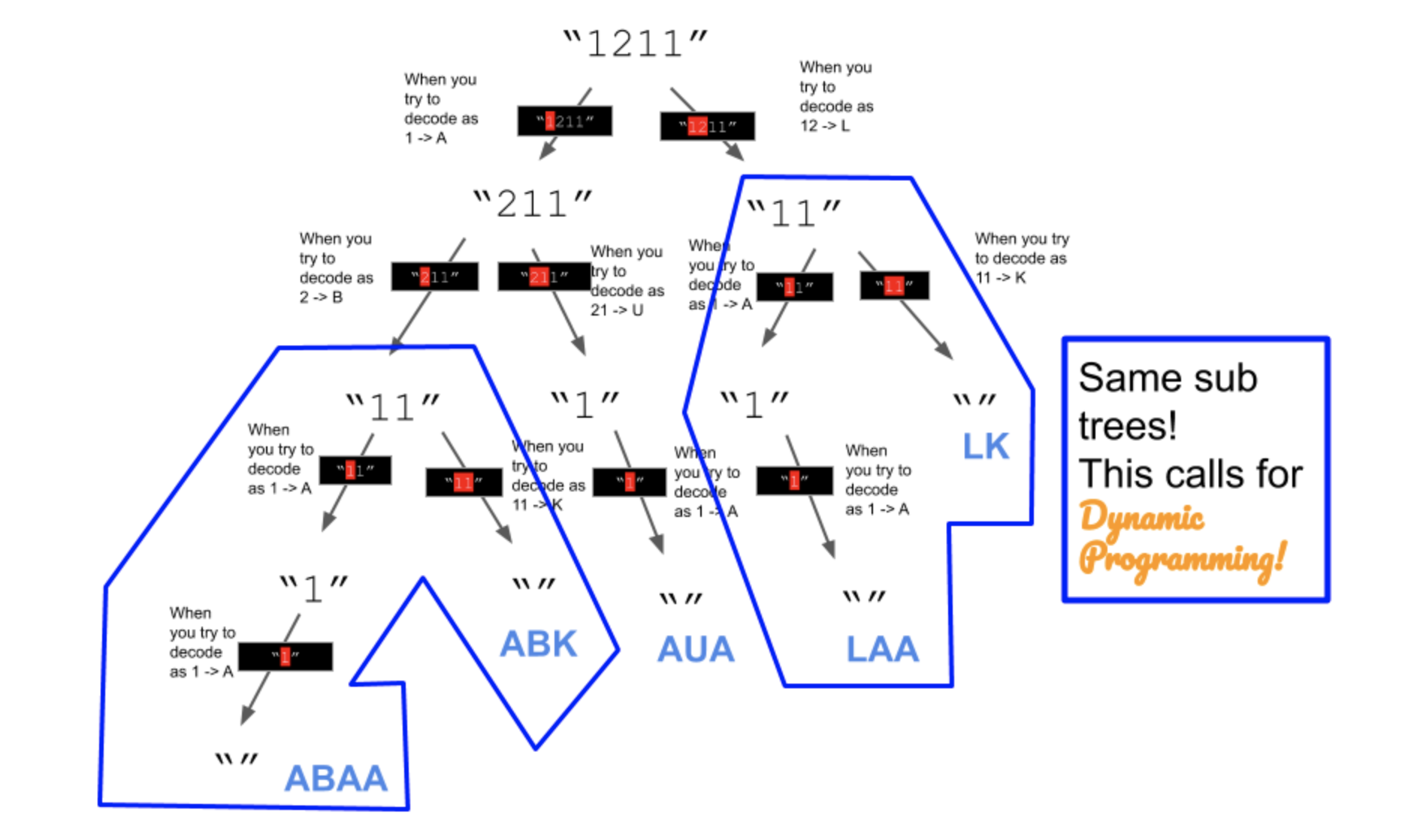



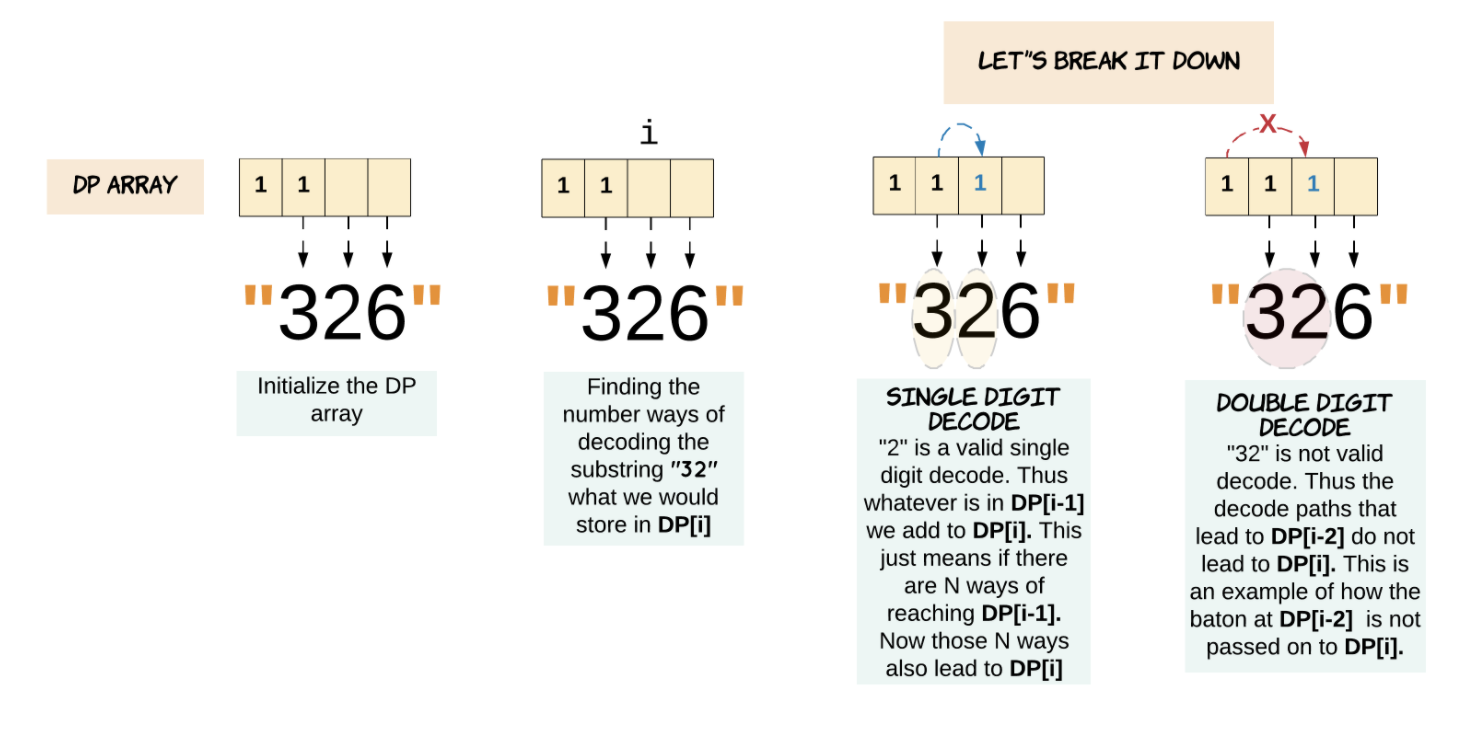


""" Decode Ways A message containing letters from A-Z can be encoded into numbers using the following mapping: 'A' -> "1" 'B' -> "2" ... 'Z' -> "26" To decode an encoded message, all the digits must be grouped then mapped back into letters using the reverse of the mapping above (there may be multiple ways). For example, "11106" can be mapped into: "AAJF" with the grouping (1 1 10 6) "KJF" with the grouping (11 10 6) Note that the grouping (1 11 06) is invalid because "06" cannot be mapped into 'F' since "6" is different from "06". Given a string s containing only digits, return the number of ways to decode it. The answer is guaranteed to fit in a 32-bit integer. Example 1: Input: s = "12" Output: 2 Explanation: "12" could be decoded as "AB" (1 2) or "L" (12). Example 2: Input: s = "226" Output: 3 Explanation: "226" could be decoded as "BZ" (2 26), "VF" (22 6), or "BBF" (2 2 6). Example 3: Input: s = "0" Output: 0 Explanation: There is no character that is mapped to a number starting with 0. The only valid mappings with 0 are 'J' -> "10" and 'T' -> "20", neither of which start with 0. Hence, there are no valid ways to decode this since all digits need to be mapped. Example 4: Input: s = "06" Output: 0 Explanation: "06" cannot be mapped to "F" because of the leading zero ("6" is different from "06"). Constraints: 1 <= s.length <= 100 s contains only digits and may contain leading zero(s). https://leetcode.com/problems/decode-ways """ """ https://www.notion.so/paulonteri/Recursion-DP-Backtracking-525dddcdd0874ed98372518724fc8753#fb64620280c74255982bb1d93455881b """ class Solution: def numDecodings(self, s: str): return self.helper(s, 0, [None]*len(s)) def helper(self, s, idx, cache): if idx == len(s): return 1 if cache[idx] is not None: return cache[idx] ways = 0 if s[idx] != "0": # length one ways += self.helper(s, idx+1, cache) # length two if idx < len(s)-1: num = int(s[idx:idx+2]) if num >= 1 and num <= 26: ways += self.helper(s, idx+2, cache) cache[idx] = ways return cache[idx] """ Bottom up DP """ class SolutionBU: def numDecodings(self, s: str): """ What if s was of length 1? 2? 3? 4? ... n? """ if not s or s[0] == "0": return 0 # # create array to store the subproblem results --------------------------------- dp = [0]*len(s) dp[0] = 1 # index 1: should handle 10, 11, 33, 30 if len(s) >= 2: # Check if successful single digit decode is possible. if s[1] != '0': dp[1] = 1 # Check if successful two digit decode is possible. two_digit = int(s[:2]) if two_digit >= 10 and two_digit <= 26: dp[1] += 1 # # fill in subproblem results ---------------------------------------------------------- for i in range(2, len(dp)): # Check if successful single digit decode is possible. if s[i] != '0': dp[i] = dp[i - 1] # Check if successful two digit decode is possible. two_digit = int(s[i-1: i+1]) if two_digit >= 10 and two_digit <= 26: # result: dp[i] = dp[i - 1] + dp[i - 2] dp[i] += dp[i - 2] return dp[-1] class SolutionBU2: def numDecodings(self, s: str): # Array to store the subproblem results dp = [0 for _ in range(len(s) + 1)] dp[0] = 1 # Ways to decode a string of size 1 is 1. Unless the string is '0'. # '0' doesn't have a single digit decode. dp[1] = 0 if s[0] == '0' else 1 for i in range(2, len(dp)): # Check if successful single digit decode is possible. if s[i - 1] != '0': dp[i] = dp[i - 1] # Check if successful two digit decode is possible. two_digit = int(s[i - 2: i]) if two_digit >= 10 and two_digit <= 26: dp[i] += dp[i - 2] return dp[len(s)] """ Iterative, Constant Space """ class SolutionITER: def numDecodings(self, s: str): if s[0] == "0": return 0 two_back = 1 one_back = 1 for i in range(1, len(s)): current = 0 if s[i] != "0": current = one_back two_digit = int(s[i - 1: i + 1]) if two_digit >= 10 and two_digit <= 26: current += two_back two_back = one_back one_back = current return one_back -
Interleaving String/Interweaving Strings
""" Interleaving String/Interweaving Strings: Given strings s1, s2, and s3, find whether s3 is formed by an interleaving of s1 and s2. An interleaving of two strings s and t is a configuration where they are divided into non-empty substrings such that: s = s1 + s2 + ... + sn t = t1 + t2 + ... + tm |n - m| <= 1 The interleaving is s1 + t1 + s2 + t2 + s3 + t3 + ... or t1 + s1 + t2 + s2 + t3 + s3 + ... Note: a + b is the concatenation of strings a and b. Example 1: Input: s1 = "aabcc", s2 = "dbbca", s3 = "aadbbcbcac" Output: true Example 2: Input: s1 = "aabcc", s2 = "dbbca", s3 = "aadbbbaccc" Output: false Example 3: Input: s1 = "", s2 = "", s3 = "" Output: true https://www.algoexpert.io/questions/Interweaving%20Strings https://leetcode.com/problems/interleaving-string/ https://leetcode.com/problems/interleaving-string/discuss/326347/C-dynamic-programming-practice-in-August-2018-with-interesting-combinatorics-warmup """ """ ------------------------------------------------------------------------------------------------------------------------------------------------------ """ def interweavingStringsBF_(one, two, three): if len(three) != len(one) + len(two): return False return interweavingStringsHelperBF_(one, two, three, 0, 0, 0) def interweavingStringsHelperBF_(one, two, three, one_idx, two_idx, three_idx): if three_idx == len(three): return True one_res = False two_res = False if one_idx < len(one) and one[one_idx] == three[three_idx]: one_res = interweavingStringsHelperBF_( one, two, three, one_idx+1, two_idx, three_idx+1) if two_idx < len(two) and two[two_idx] == three[three_idx]: two_res = interweavingStringsHelperBF_( one, two, three, one_idx, two_idx+1, three_idx+1) return one_res or two_res """ BF that can be cached """ def interweavingStringsBF(one, two, three): if len(three) != len(one) + len(two): return False return interweavingStringsHelperBF(one, two, three, 0, 0) def interweavingStringsHelperBF(one, two, three, one_idx, two_idx, ): three_idx = one_idx + two_idx if three_idx == len(three): return True one_res = False two_res = False if one_idx < len(one) and one[one_idx] == three[three_idx]: one_res = interweavingStringsHelperBF( one, two, three, one_idx+1, two_idx) if two_idx < len(two) and two[two_idx] == three[three_idx]: two_res = interweavingStringsHelperBF( one, two, three, one_idx, two_idx+1) return one_res or two_res """ ------------------------------------------------------------------------------------------------------------------------------------------------------ """ def interweavingStringsMEMO(one, two, three): if len(three) != len(one) + len(two): return False cache = [[None for _ in range(len(two)+1)] for _ in range(len(one)+1)] return interweavingStringsHelperMEMO(one, two, three, cache, 0, 0) def interweavingStringsHelperMEMO(one, two, three, cache, one_idx, two_idx, ): three_idx = one_idx + two_idx if three_idx == len(three): return True if cache[one_idx][two_idx] is not None: return cache[one_idx][two_idx] one_res = False two_res = False if one_idx < len(one) and one[one_idx] == three[three_idx]: one_res = interweavingStringsHelperMEMO(one, two, three, cache, one_idx+1, two_idx) if two_idx < len(two) and two[two_idx] == three[three_idx]: two_res = interweavingStringsHelperMEMO(one, two, three, cache, one_idx, two_idx+1) cache[one_idx][two_idx] = one_res or two_res return cache[one_idx][two_idx] """ ------------------------------------------------------------------------------------------------------------------------------------------------------ Bottom up: - for each char(in one or two) check if it matches what is in three: - if it does: if we had built the prev string up to that point == True ( one idx behind the curr idx in three (up or left depending on if the row or column matches) ) - then True # can be optimised to 1D array """ def interweavingStrings(one, two, three): if len(three) != len(one) + len(two): return False dp = [[False for _ in range(len(two)+1)] for _ in range(len(one)+1)] # # fill in the defaults that will be used to generate the next dp[0][0] = True for i in range(1, len(one)+1): # left column actual_idx = i-1 if one[actual_idx] == three[actual_idx] and dp[i-1][0] == True: dp[i][0] = True for i in range(1, len(two)+1): # top row actual_idx = i-1 if two[actual_idx] == three[actual_idx] and dp[0][i-1] == True: dp[0][i] = True # # fill in the rest for one_idx in range(1, len(one)+1): for two_idx in range(1, len(two)+1): actual_one_idx = one_idx-1 actual_two_idx = two_idx-1 actual_three_idx = one_idx + two_idx - 1 # # check if the string matches then check if we had built it successfully up to that point # check one if one[actual_one_idx] == three[actual_three_idx] and dp[one_idx-1][two_idx] == True: dp[one_idx][two_idx] = True # check two if two[actual_two_idx] == three[actual_three_idx] and dp[one_idx][two_idx-1] == True: dp[one_idx][two_idx] = True return dp[-1][-1] -
Unique Paths **
Unique Paths - Dynamic Programming - Leetcode 62
Unique Paths - Dynamic Programming - Leetcode 62
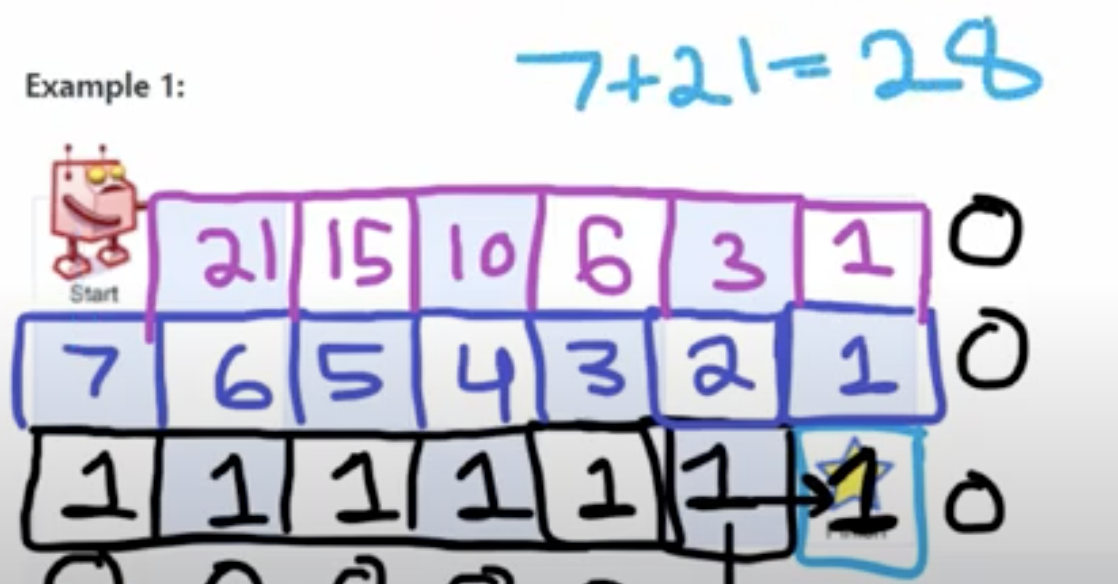


starting from end to beginning
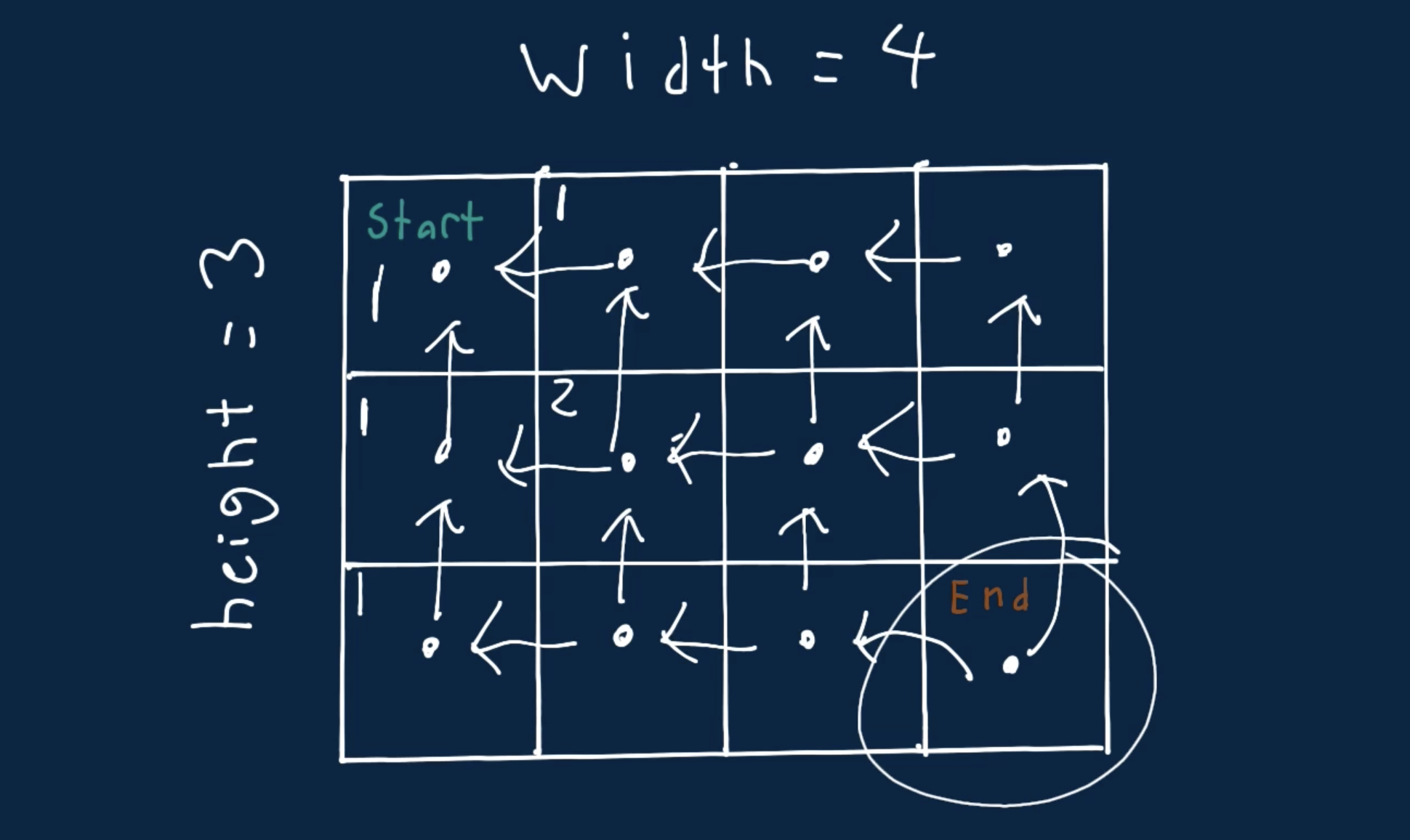
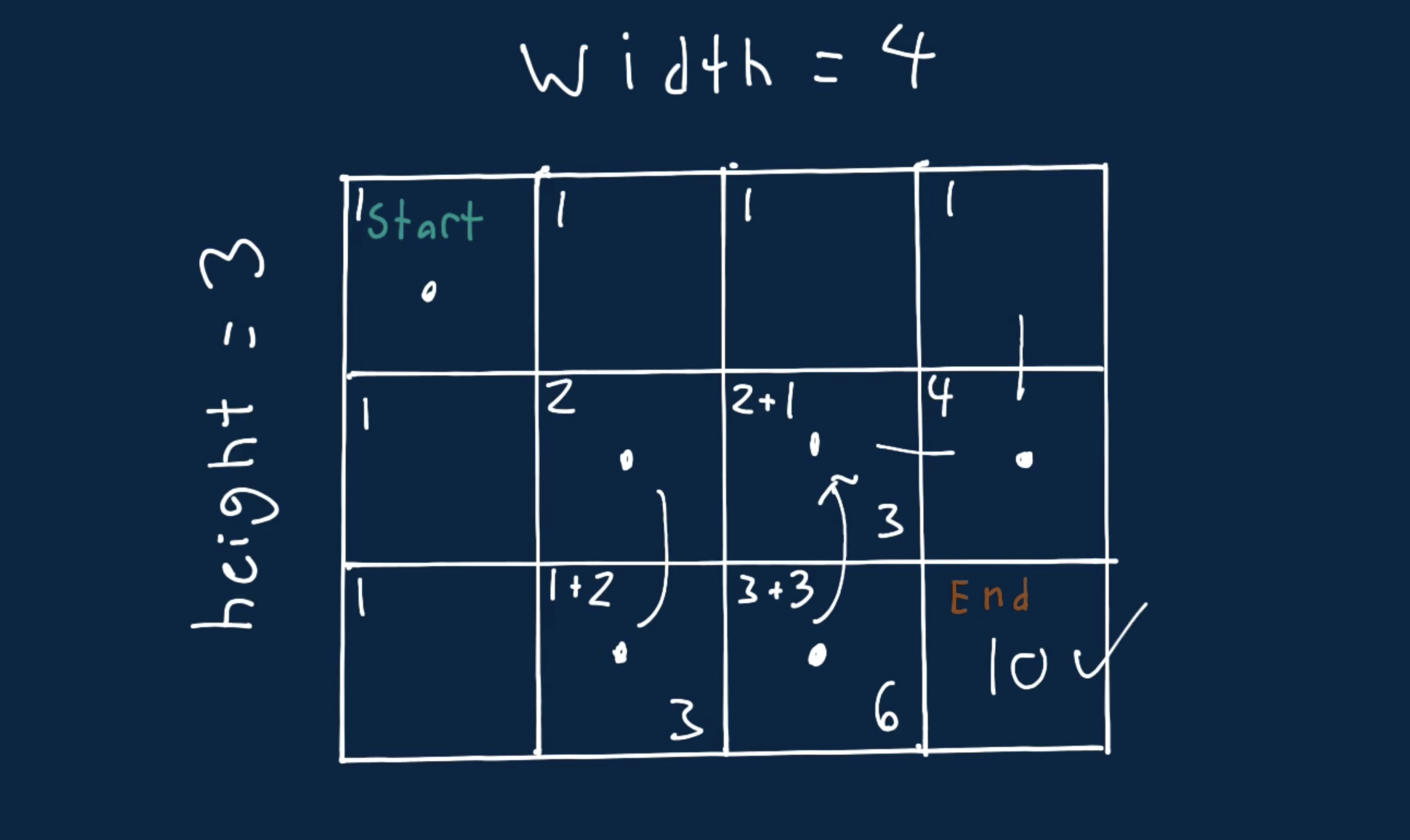

Screen Recording 2021-10-14 at 12.51.31.mov
""" Unique Paths: A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below). The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below). How many possible unique paths are there? Example 1: Input: m = 3, n = 7 Output: 28 Example 2: Input: m = 3, n = 2 Output: 3 Explanation: From the top-left corner, there are a total of 3 ways to reach the bottom-right corner: 1. Right -> Down -> Down 2. Down -> Down -> Right 3. Down -> Right -> Down Example 3: Input: m = 7, n = 3 Output: 28 Example 4: Input: m = 3, n = 3 Output: 6 Example: 99*1 => 1 Example 99*2 => 99 Number Of Ways To Traverse Graph: You're given two positive integers representing the width and height of a grid-shaped, rectangular graph. Write a function that returns the number of ways to reach the bottom right corner of the graph when starting at the top left corner. Each move you take must either go down or right. In other words, you can never move up or left in the graph. For example, given the graph illustrated below, with width = 2 and height = 3, there are three ways to reach the bottom right corner when starting at the top left corner: _ _ |_|_| |_|_| |_|_| Down, Down, Right Right, Down, Down Down, Right, Down Note: you may assume that width * height >= 2. In other words, the graph will never be a 1x1 grid. Sample Input width = 4 height = 3 Sample Output 10 https://leetcode.com/problems/unique-paths https://www.algoexpert.io/questions/Number%20Of%20Ways%20To%20Traverse%20Graph https://www.notion.so/paulonteri/Recursion-DP-Backtracking-525dddcdd0874ed98372518724fc8753#f980e95403a24443a371a10430a198ad Unique Paths II can help in understanding this """ """ Since robot can move either down or right, there is only one path to reach the cells in the first row: right->right->...->right. The same is valid for the first column, though the path here is down->down-> ...->down. """ """ [ 1 2 3 4 1[1, 1, 1, 1], 2[1, 2, 3, 4], 3[1, 3, 6, 10], 4[1, 4, 10, 20] ] """ # starting from end to beginning # note that the start is 1,1. 0,0 is out of bounds class SolutionMEMO: def uniquePaths(self, m, n): cache = [[False for _ in range(n+1)] for _ in range(m+1)] return self.uniquePathsHelper(m, n, cache) def uniquePathsHelper(self, m, n, cache): if m == 1 and n == 1: return 1 if m < 1 or n < 1: return 0 if cache[m][n]: return cache[m][n] total = 0 total += self.uniquePathsHelper(m, n-1, cache) total += self.uniquePathsHelper(m-1, n, cache) cache[m][n] = total return cache[m][n] """ ------------------------------------------------------------------------------------------------------------------------------------- what if the graph was: [ 1 1[1], ] [ 1 2 1[1, 1], 2[1, 2], ] [ 1 2 3 1[1, 1, 1], 2[1, 2, 3], 3[1, 3, 6] ] [ 1 2 3 4 1[1, 1, 1, 1], 2[1, 2, 3, 4], 3[1, 3, 6, 10], 4[1, 4, 10, 20] ] """ class Solution: def uniquePaths(self, m, n): if m == 1 and n == 1: return 1 cache = [[0 for _ in range(n+1)] for _ in range(m+1)] # fill in defaults for i in range(1, n+1): cache[1][i] = 1 for i in range(1, m+1): cache[i][1] = 1 for h in range(2, m+1): for w in range(2, n+1): # top + left cache[h][w] = cache[h-1][w] + cache[h][w-1] # print(cache) return cache[-1][-1] -
Unique Paths II
""" Unique Paths II / Robot in Grid: A robot is located at the top-left corner of a m x n grid. The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid. Now consider if some obstacles are added to the grids. How many unique paths would there be? An obstacle and space is marked as 1 and 0 respectively in the grid. https://leetcode.com/problems/unique-paths-ii/ """ class Solution: def uniquePathsWithObstacles(self, obstacleGrid): if obstacleGrid[len(obstacleGrid)-1][len(obstacleGrid[0])-1] == 1: return 0 return self.helper(obstacleGrid) def helper(self, obstacleGrid, row=0, col=0): # out of bounds if row >= len(obstacleGrid) or col >= len(obstacleGrid[0]): return 0 # reached end elif row == len(obstacleGrid)-1 and col == len(obstacleGrid[0])-1: return 1 # is occupied with obstacle elif obstacleGrid[row][col] == 1: return 0 # get cached result elif obstacleGrid[row][col] < 0: return -obstacleGrid[row][col] # move right right = self.helper(obstacleGrid, row, col+1) # move down down = self.helper(obstacleGrid, row+1, col) obstacleGrid[row][col] = -(right + down) # cache results return right + down
Honourable mentions
0/1 Knapsack (Dynamic Programming)
Characteristics of Dynamic Programming:
Before moving on to understand different methods of solving a DP problem, let’s first take a look at what are the characteristics of a problem that tells us that we can apply DP to solve it.
1. Optimal Substructure Property
02 - What is DP? (Dynamic Programming for Beginners)
Optimal substructure requires that you can solve a problem based on the solutions of subproblems. Any problem has optimal substructure property if its overall optimal solution can be constructed from the optimal solutions of its subproblems. For Fibonacci numbers, as we know,Fib(n) = Fib(n-1) + Fib(n-2). This clearly shows that a problem of size ‘n’ has been reduced to subproblems of size ‘n-1’ and ‘n-2’. Therefore, Fibonacci numbers have optimal substructure property.
A useful way to think about optimal substructure is whether a problem can be easily solved recursively. Recursive solutions inherently solve a problem by breaking it down into smaller subproblems. If you can solve a problem recursively, it most likely has an optimal substructure.
2. Overlapping Subproblems
02 - What is DP? (Dynamic Programming for Beginners)
Sub-problems are smaller versions of the original problem. In fact, sub-problems often look like a reworded version of the original problem. If formulated correctly, sub-problems build on each other in order to obtain the solution to the original problem. Any problem has overlapping sub-problems if finding its solution involves solving the same subproblem multiple times.
![]()
Take the example of the Fibonacci numbers; to find the fib(4), we need to break it down into the following sub-problems: fib(4)fib(3)fib(2)fib(2)fib(1)fib(1)fib(0)fib(0)fib(1)
We can clearly see the overlapping subproblem pattern here, as fib(2) has been evaluated twice and fib(1) has been evaluated three times.
Later we'll learn that: Whenever we solve a sub-problem, we cache its result so that we don’t end up solving it repeatedly if it’s called multiple times. Instead, we can just return the saved result. This technique of storing the results of already solved subproblems is called Memoization.
Dynamic Programming Methods
Memoization is the technique of writing a function that remembers the results of previous computations. Memoization ensures that a function doesn't run for the same inputs more than once by keeping a record of the results for the given inputs (usually in a dictionary).
Bottom-Up Algorithms: Going bottom-up is a way to avoid recursion, saving the memory cost that recursion incurs when it builds up the call stack. Put simply, a bottom-up algorithm "starts from the beginning," while a recursive algorithm often "starts from the end and works backwards."
1. Top-down with Memoization
In this approach, we try to solve the bigger problem by recursively finding the solution to smaller sub-problems. Whenever we solve a sub-problem, we cache its result so that we don’t end up solving it repeatedly if it’s called multiple times. Instead, we can just return the saved result. This technique of storing the results of already solved subproblems is called Memoization.
Fibonacci - This problem is normally solved with Divide and Conquer algorithm. There are 3 main parts in this technique:
- Divide: divide the problem into smaller sub-problems of same type
- Conquer: solve the sub-problems recursively
- Combine: combine all the sub-problems to create a solution to the original problem
![]()
def calculateFibonacci(n):
memoize = [-1 for x in range(n+1)]
return calculateFibonacciRecur(memoize, n)
def calculateFibonacciRecur(memoize, n):
if n < 2:
return n
if memoize[n] >= 0: # if we have already solved this subproblem, simply return the result from the cache
return memoize[n]
memoize[n] = calculateFibonacciRecur(memoize, n - 1) + calculateFibonacciRecur(memoize, n - 2)
return memoize[n]
2. Bottom-up with Tabulation
Tabulation is the opposite of the top-down approach and avoids recursion. In this approach, we solve the problem “bottom-up” (i.e. by solving all the related sub-problems first). This is typically done by filling up an n-dimensional table. Based on the results in the table, the solution to the top/original problem is then computed.
def calculateFibonacci(n):
dp = [0, 1]
for i in range(2, n + 1):
dp.append(dp[i - 1] + dp[i - 2])
return dp[n]
One can also think of dynamic programming as a table-filling algorithm: you know the calculations you have to do, so you pick the best order to do them in and ignore the ones you don't have to fill in.
Great explainer:
memoization: https://youtu.be/f2xi3c1S95M?t=596
tabulation: https://youtu.be/f2xi3c1S95M?t=893
Be careful while calculating DP's time complexities
The FAST method
The most successful interviewees are those who have developed a repeatable strategy to succeed. This is especially true for dynamic programming. This is the reason for the development of the FAST method.
There are four steps in the FAST method:
- First solution
- Analyze the first solution
- Identify the Subproblems
- Turn the solution around
1. First solution
This is an important step for any interview question but is particularly important for dynamic programming.
This step finds the first possible solution. This solution will be brute force and recursive. The goal is to solve the problem without concern for efficiency.
It means that if you need to find the biggest/smallest/longest/shortest something, you should write code that goes through every possibility and then compares them all to find the best one.
Your solution must also meet these restrictions:
- The recursive calls must be self-contained. That means no global variables.
- You cannot do tail recursion. Your solution must compute the results to each subproblem and then combine them afterwards.
-
Do not pass in unnecessary variables. Eg. If you can count the depth of your recursion as you return, don’t pass a count variable into your recursive function.
Once you’ve gone through a couple problems, you will likely see how this solution looks almost the same every time.
2. Analyze the first solution
In this step, we will analyze the first solution that you came upwith. This involves determining the time and space complexity of your first solution and asking whether there is obvious room for improvement.
As part of the analytical process, we need to ask whether the first solution fits our rules for problems with dynamic solutions:
- Does it have an optimal substructure? Since our solution’s recursive, then there is a strong likelihood that it meets this criteria. If we are recursively solving subproblems of the same problem, then we know that our substructure is optimal, otherwise our algorithm wouldn’t work.
- Are there overlapping subproblems? This can be more difficult to determine because it doesn’t always present itself with small examples. It may be necessary to try a medium-sized test case. This will enable you to see if you end up calling the same function with the same input multiple times.
3. Find the Subproblems
If our solution can be made dynamic, the exact subproblems to memoize must be codified. This step requires us to discover the high-level meaning of the subproblems. This will make it easier to understand the solution later. Our recursive solution can be made dynamic by caching the values. This top-down solution facilitates a better understanding of the subproblems which is useful for the next step.
4. Turn the solution around
We now have a top-down solution. This is fine and it would be possible to stop here. However, sometimes it is better to flip it around and to get a bottom-up solution instead. Since we understand our subproblems, we will do that. This involves writing a completely different function (without modifying the existing code). This will iteratively compute the results of successive subproblems until our desired result is reached.
In recursion for example for Fibonacci calculation, if the root node (in the recursion tree) has two children. Each of those children has two children (so four children total in the "grand children" level). Each of those grandchildren has two children, and so on. If we do this n times, we'll have roughlyO(2") nodes. This gives us a runtime of roughly 0(2").
Pro tips
How to avoid duplicates in recursion
![]()
Brute-force that can work with caching
Divide & Conquer
-
Tower of Hanoi
Towers of Hanoi: A Complete Recursive Visualization
5.10. Tower of Hanoi - Problem Solving with Algorithms and Data Structures

""" Tower of Hanoi https://youtu.be/rf6uf3jNjbo https://runestone.academy/runestone/books/published/pythonds/Recursion/TowerofHanoi.html https://leetcode.com/discuss/general-discussion/1517167/Tower-of-Hanoi-Algorithm-%2B-Python-code https://www.notion.so/paulonteri/Recursion-DP-Backtracking-525dddcdd0874ed98372518724fc8753#0fa86da6418247199688a4f435447d86 """ """ Here is a high-level outline of how to move a tower from the starting pole, to the goal pole, using an intermediate pole: 1. Move a tower of height-1 to an intermediate pole 2. Move the last/remaining disk to the final pole. 3. Move the disks height-1 to the first rod and repeat the above steps. Move the tower of height-1 from the intermediate pole to the final pole using the original pole. As long as we always obey the rule that the larger disks remain on the bottom of the stack, we can use the three steps above recursively, treating any larger disks as though they were not even there. The only thing missing from the outline above is the identification of a base case. The simplest Tower of Hanoi problem is a tower of one disk. In this case, we need move only a single disk to its final destination. A tower of one disk will be our base case. """ def tower_of_hanoi(n, from_rod="A", to_rod="C", aux_rod="B"): if n == 1: # The simplest Tower of Hanoi problem is a tower of one disk. # In this case, we need move only a single disk to its final destination. print("Move disk 1 from rod", from_rod, "to rod", to_rod) return # Move a tower of height-1 to an intermediate pole tower_of_hanoi(n-1, from_rod, aux_rod, to_rod) # Move the last/remaining disk to the final pole print("Move disk", n, "from rod", from_rod, "to rod", to_rod) # Move the disks height-1 to the first rod and repeat the above steps # Move the tower of height-1 from the intermediate pole to the final pole using the original pole. tower_of_hanoi(n-1, aux_rod, to_rod, from_rod) tower_of_hanoi(1) print("____________") tower_of_hanoi(2) print("____________") tower_of_hanoi(3) print("____________") tower_of_hanoi(4) print("____________") tower_of_hanoi(5)https://runestone.academy/runestone/books/published/pythonds/Recursion/TowerofHanoi.html
Backtracking
Boggle - Coderust: Hacking the Coding Interview
The Backtracking Blueprint: The Legendary 3 Keys To Backtracking Algorithms
Java: Backtracking Template -- General Approach - LeetCode Discuss
Backtracking Algorithm tries each possibility until they find the right one. It is a depth-first search of the set of possible solution. During the search, if an alternative doesn't work, then backtrack to the choice point, the place which presented different alternatives, and tries the next alternative.
Screen Recording 2021-10-25 at 18.50.53.mov
Backtracking is an algorithmic technique that involves trying possibilities along a "search path" and cutting off paths of search that will no longer yield a solution. Backtracking is an algorithmic technique for solving problems recursively by trying to build a solution incrementally, one piece at a time, removing those solutions that fail to satisfy the constraints of the problem at any point of time (by time, here, is referred to the time elapsed till reaching any level of the search tree).
![]()
Backtracking is an algorithmic technique that considers searching in every possible combination for solving a computational problem.
It is known for solving problems recursively one step at a time and removing those solutions that do not satisfy the problem constraints at any point in time. It is a refined brute force approach that tries out all the possible solutions and chooses the best possible ones out of them.
Examples:
-
All Paths From Source to Target
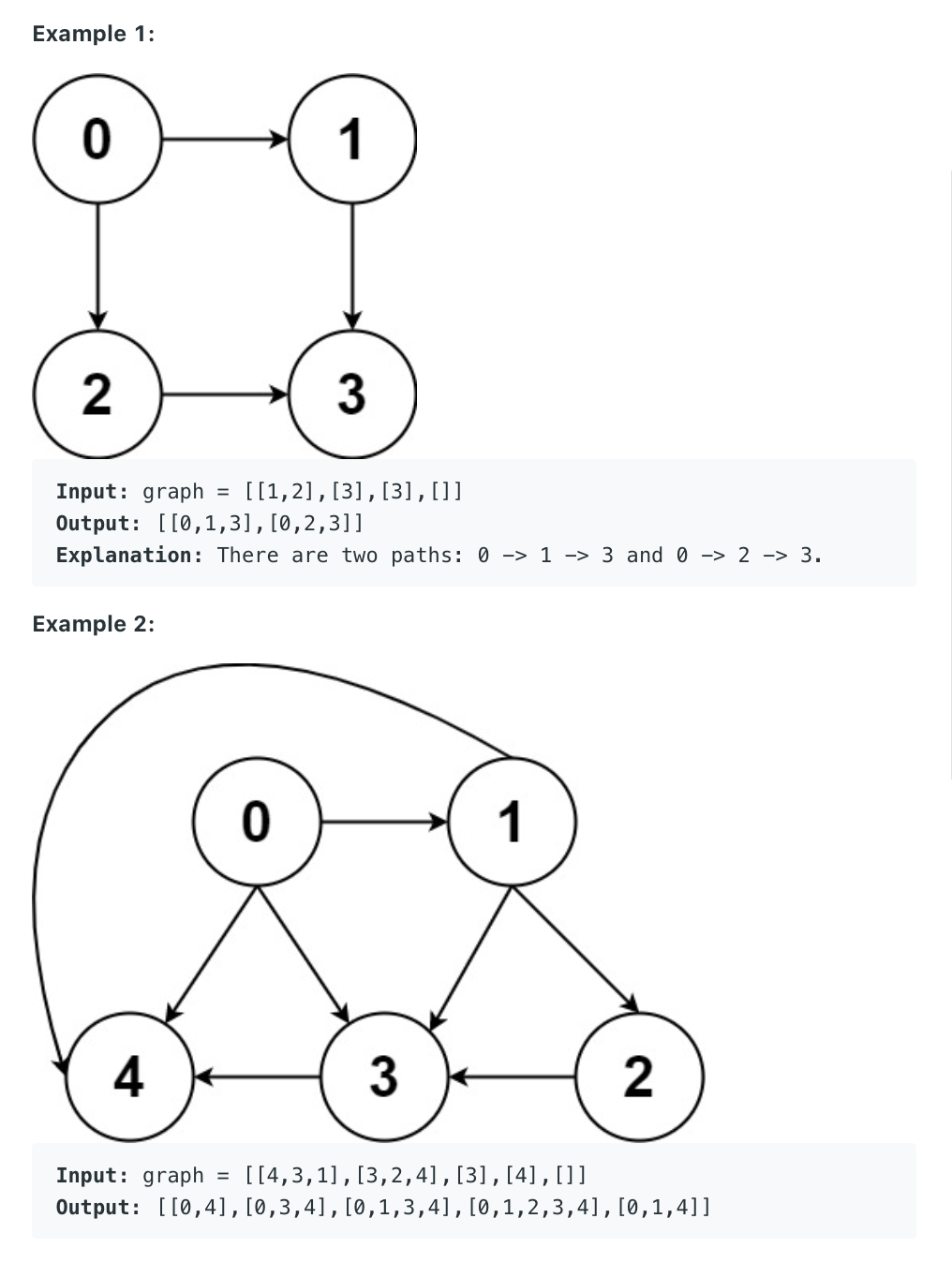

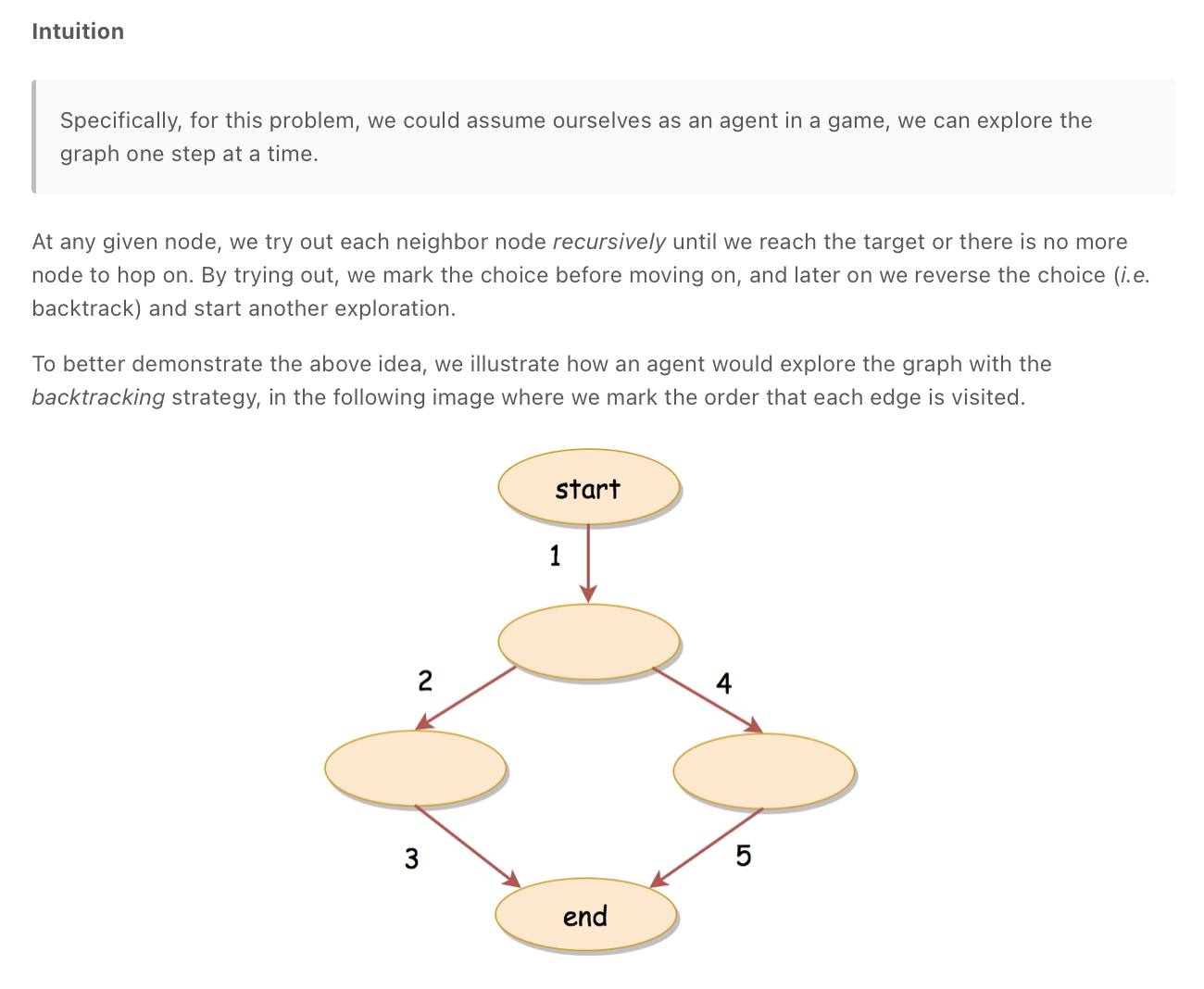



""" All Paths From Source to Target Given a directed acyclic graph (DAG) of n nodes labeled from 0 to n - 1, find all possible paths from node 0 to node n - 1 and return them in any order. The graph is given as follows: graph[i] is a list of all nodes you can visit from node i (i.e., there is a directed edge from node i to node graph[i][j]). Example 1: Input: graph = [[1,2],[3],[3],[]] Output: [[0,1,3],[0,2,3]] Explanation: There are two paths: 0 -> 1 -> 3 and 0 -> 2 -> 3. Example 2: Input: graph = [[4,3,1],[3,2,4],[3],[4],[]] Output: [[0,4],[0,3,4],[0,1,3,4],[0,1,2,3,4],[0,1,4]] Example 3: Input: graph = [[1],[]] Output: [[0,1]] Example 4: Input: graph = [[1,2,3],[2],[3],[]] Output: [[0,1,2,3],[0,2,3],[0,3]] Example 5: Input: graph = [[1,3],[2],[3],[]] Output: [[0,1,2,3],[0,3]] Constraints: n == graph.length 2 <= n <= 15 0 <= graph[i][j] < n graph[i][j] != i (i.e., there will be no self-loops). All the elements of graph[i] are unique. The input graph is guaranteed to be a DAG. https://leetcode.com/problems/all-paths-from-source-to-target """ from typing import List """ As a reminder, backtracking is a general algorithm that incrementally builds candidates to the solutions, and abandons a candidate ("backtrack") as soon as it determines that the candidate cannot possibly lead to a valid solution. Specifically, for this problem, we could assume ourselves as an agent in a game, we can explore the graph one step at a time. At any given node, we try out each neighbour node recursively until we reach the target or there is no more node to hop on. By trying out, we mark the choice before moving on, and later on we reverse the choice (i.e. backtrack) and start another exploration. """ # O(2^N) time | O(2^N) space # - every time we add a new node into the graph, the number of paths would double. # We have 2^N paths with building a path taking N time # We have 2^N paths with each path possibly containing N nodes class Solution: def allPathsSourceTarget(self, graph: List[List[int]]): """ - paths = [] - dfs(node, visiting, path): - if node is n-1: add the built path to the paths array - if node is in visiting set: return - (not needed because graph is acyclic) add node to visiting set - for all the child accessible to the node: - add node to path - dfs(child) - remove node from path - return paths """ paths = [] # backtracking def dfs(node, curr_path): if node == len(graph)-1: paths.append(curr_path[:]) for child in graph[node]: curr_path.append(child) dfs(child, curr_path) curr_path.pop() dfs(0, [0]) return paths -
Permutations II **




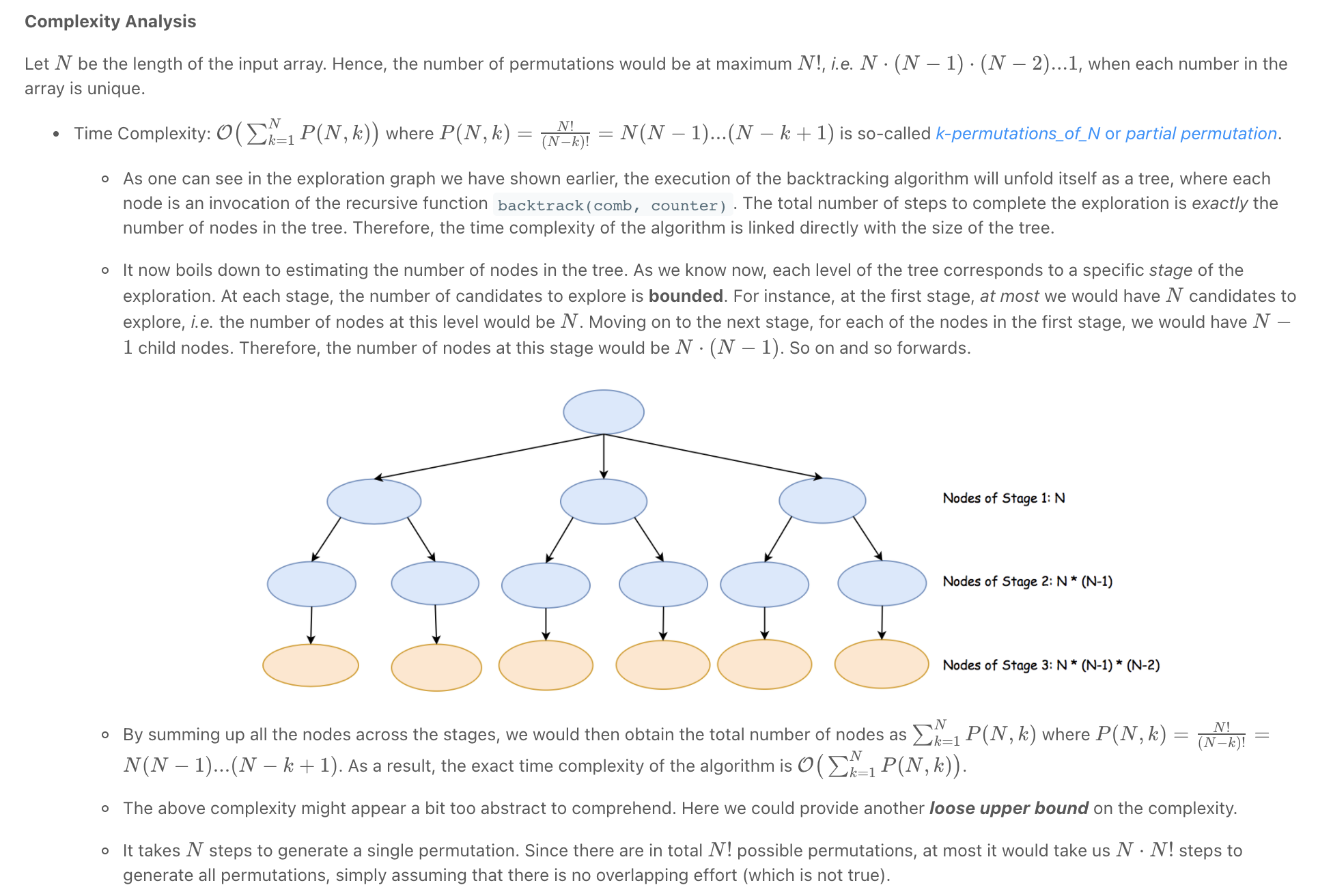

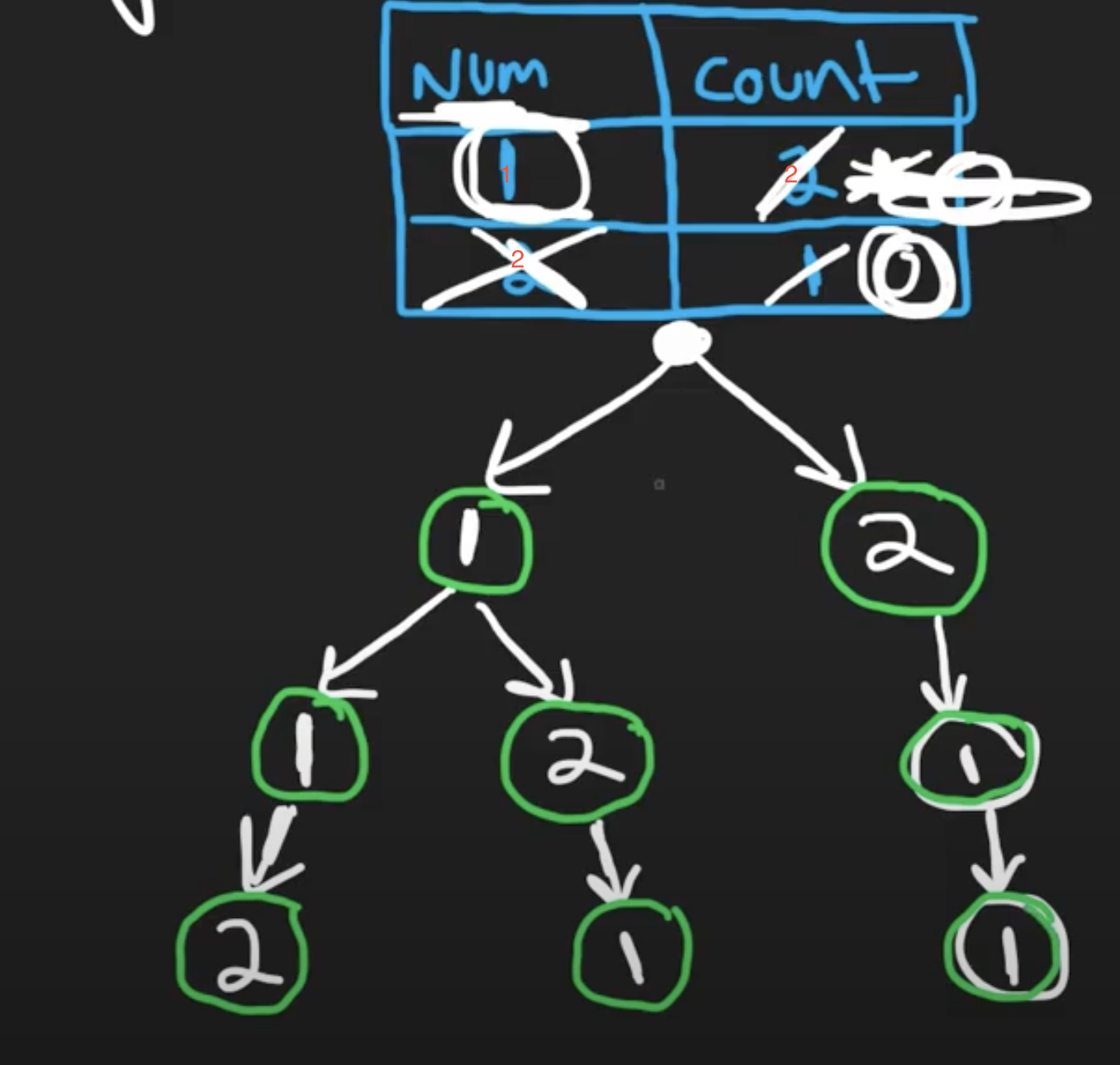
""" Permutations II Given a collection of numbers, nums, that might contain duplicates, return all possible unique permutations in any order. Example 1: Input: nums = [1,1,2] Output: [[1,1,2], [1,2,1], [2,1,1]] Example 2: Input: nums = [1,2,3] Output: [[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]] https://leetcode.com/problems/permutations-ii """ import collections class Solution: def permuteUnique(self, nums): result = [] # use a counter to ensure each number is considered only once for each position in the array self.dfs(collections.Counter(nums), len(nums), [], result) return result def dfs(self, numbers, length, curr, result): if len(curr) == length: result.append(curr) for num in numbers: if numbers[num] == 0: continue numbers[num] -= 1 self.dfs(numbers, length, curr+[num], result) # backtrack numbers[num] += 1 -
N-Queens
The N Queens Placement Problem Clear Explanation (Backtracking/Recursion)
Backtracking - N-Queens Problem
Clever way of dealing with diagonals


Alternatively
""" N-Queens The n-queens puzzle is the problem of placing n queens on an n x n chessboard such that no two queens attack each other. Given an integer n, return all distinct solutions to the n-queens puzzle. You may return the answer in any order. Each solution contains a distinct board configuration of the n-queens' placement, where 'Q' and '.' both indicate a queen and an empty space, respectively. https://leetcode.com/problems/n-queens/ https://www.algoexpert.io/questions/Non-Attacking%20Queens """ """ Time complexity: row: num of placements * time complexity for validating placement == n 0 : n * n 1 : n-2 (remove column & diagonal of prev) * n 2 : n-4 * n 3 : n-6 * n ... total => n! * n """ class Solution: def solveNQueens(self, n): result = [] self.solve_n_queens_helper(n, result, set(), 0) return result def solve_n_queens_helper(self, n, result, placed, row): if row == n: self.build_solution(n, placed, result) return for col in range(n): # place placed.add((row, col)) if self.is_valid_placement(n, placed): self.solve_n_queens_helper(n, result, placed, row+1) # remove placed.discard((row, col)) def is_valid_placement(self, n, placed): # check columns cols = set() for item in placed: cols.add(item[1]) if len(cols) < len(placed): return False # check positive diagonal # explanation: https://www.notion.so/paulonteri/Recursion-DP-Backtracking-525dddcdd0874ed98372518724fc8753#d51d8aa004ff49a4a0bf49c755fdf193 pos_diagonal = set() for item in placed: row, col = item pos_diagonal.add(row - col) if len(pos_diagonal) < len(placed): return False # check negative diagonal neg_diagonal = set() for item in placed: row, col = item neg_diagonal.add(row + col) if len(neg_diagonal) < len(placed): return False return True def build_solution(self, n, placed, result): # result.append(list(placed)) board = [["." for _ in range(n)]for _ in range(n)] for item in placed: row, col = item board[row][col] = "Q" for idx in range(n): board[idx] = "".join(board[idx]) result.append(board) """ """ class Solution_: def solveNQueens(self, n): result = [] board = [["." for _ in range(n)]for _ in range(n)] self.solve_n_queens_helper( n, board, result, set(), 0, set(), set(), set()) return result def solve_n_queens_helper(self, n, board, result, placed, row, cols_placed, pos_diagonal, neg_diagonal): if row == n: # print(board) board_copy = board[:] for idx in range(n): board_copy[idx] = "".join(board_copy[idx]) result.append(board_copy) return for col in range(n): # place added = self.add_placement_info( row, col, placed, cols_placed, pos_diagonal, neg_diagonal) if added: board[row][col] = "Q" self.solve_n_queens_helper( n, board, result, placed, row+1, cols_placed, pos_diagonal, neg_diagonal) # remove self.remove_placement_info( row, col, placed, cols_placed, pos_diagonal, neg_diagonal) board[row][col] = "." def add_placement_info(self, row, col, placed, cols_placed, pos_diagonal, neg_diagonal): # explanation: https://www.notion.so/paulonteri/Recursion-DP-Backtracking-525dddcdd0874ed98372518724fc8753#d51d8aa004ff49a4a0bf49c755fdf193 if col in cols_placed or row-col in pos_diagonal or row+col in neg_diagonal: return False placed.add((row, col)) cols_placed.add(col) pos_diagonal.add(row - col) neg_diagonal.add(row + col) return True def remove_placement_info(self, row, col, placed, cols_placed, pos_diagonal, neg_diagonal): # explanation: https://www.notion.so/paulonteri/Recursion-DP-Backtracking-525dddcdd0874ed98372518724fc8753#d51d8aa004ff49a4a0bf49c755fdf193 placed.discard((row, col)) cols_placed.discard(col) pos_diagonal.discard(row - col) neg_diagonal.discard(row + col) -
Sudoku
""" Sudoku Solver: Write a program to solve a Sudoku puzzle by filling the empty cells. A sudoku solution must satisfy all of the following rules: Each of the digits 1-9 must occur exactly once in each row. Each of the digits 1-9 must occur exactly once in each column. Each of the digits 1-9 must occur exactly once in each of the 9 3x3 sub-boxes of the grid. Example 1: Input: board = [["5","3",".",".","7",".",".",".","."],["6",".",".","1","9","5",".",".","."],[".","9","8",".",".",".",".","6","."],["8",".",".",".","6",".",".",".","3"],["4",".",".","8", ".","3",".",".","1"],["7",".",".",".","2",".",".",".","6"],[".","6",".",".",".",".","2","8","."],[".",".",".","4","1","9",".",".","5"],[".",".",".",".","8",".",".","7","9"]] Output: [["5","3","4","6","7","8","9","1","2"],["6","7","2","1","9","5","3","4","8"],["1","9","8","3","4","2","5","6","7"],["8","5","9","7","6","1","4","2","3"],["4","2","6","8", "5","3","7","9","1"],["7","1","3","9","2","4","8","5","6"],["9","6","1","5","3","7","2","8","4"],["2","8","7","4","1","9","6","3","5"],["3","4","5","2","8","6","1","7","9"]] https://leetcode.com/problems/sudoku-solver/ https://www.algoexpert.io/questions/Solve%20Sudoku """ def solveSudoku(board): solveSudokuHelper(board, 0, 0) return board def get_valid_nums(board, row, col): def get_all_in_3_by_three(board, row, col, invalid): end_row = end_col = 8 if row <= 2: end_row = 2 elif row <= 5: end_row = 5 if col <= 2: end_col = 2 elif col <= 5: end_col = 5 for i in range(end_row-2, end_row+1): for j in range(end_col-2, end_col+1): num = board[i][j] if num != 0: invalid.add(num) def get_all_in_row_and_col(board, row, col, invalid): for num in board[row]: if num != 0: invalid.add(num) for i in range(9): num = board[i][col] if num != 0: invalid.add(num) invalid = set() get_all_in_3_by_three(board, row, col, invalid) get_all_in_row_and_col(board, row, col, invalid) valid = [] for num in range(1, 10): if num not in invalid: valid.append(num) return valid def solveSudokuHelper(board, row, col): if row == 9: # Done return True # # calculate next next_row = row next_col = col + 1 if col == 8: next_col = 0 next_row += 1 # # fill board # check if prefilled if board[row][col] != 0: return solveSudokuHelper(board, next_row, next_col) # trial and error (backtracking) for num in get_valid_nums(board, row, col): board[row][col] = num # try with num # if we have correctly filled the table, there is no need to try out other nums if solveSudokuHelper(board, next_row, next_col): return True # backtrack: if the input was invalid (the else is not needed but it helps in understanding what is happening) else: board[row][col] = 0 -
Letter Case Permutations
-
Generate Parentheses *
""" 22. Generate Parentheses Given n pairs of parentheses, write a function to generate all combinations of well-formed parentheses. Example 1: Input: n = 3 Output: ["((()))","(()())","(())()","()(())","()()()"] Example 2: Input: n = 1 Output: ["()"] https://leetcode.com/problems/generate-parentheses """ class Solution: def generateParenthesis(self, n: int): all_parenthesis = [] def place_brackets(opening, closing, curr_par): """ - Only place opening if their count is less than n - Only place closing if their count is less than opening """ if opening == n and closing == n: all_parenthesis.append("".join(curr_par)) if opening < n: curr_par.append("(") place_brackets(opening+1, closing, curr_par) curr_par.pop() if closing < opening: curr_par.append(")") place_brackets(opening, closing+1, curr_par) curr_par.pop() place_brackets(0, 0, []) return all_parenthesis -
Word Break
Word Break | Dynamic Programming | Leetcode #139

""" Word Break: Given a string s and a dictionary of strings wordDict, return true if s can be segmented into a space-separated sequence of one or more dictionary words. Note that the same word in the dictionary may be reused multiple times in the segmentation. Example 1: Input: s = "leetcode", wordDict = ["leet","code"] Output: true Explanation: Return true because "leetcode" can be segmented as "leet code". Example 2: Input: s = "applepenapple", wordDict = ["apple","pen"] Output: true Explanation: Return true because "applepenapple" can be segmented as "apple pen apple". Note that you are allowed to reuse a dictionary word. Example 3: Input: s = "catsandog", wordDict = ["cats","dog","sand","and","cat"] Output: false abcde [a,b ab,cde, abc, abcde, e] => reason for DP https://leetcode.com/problems/word-break https://youtu.be/th4OnoGasMU """ """ ------------------------- Problem --------------------------------- string s dictionary of strings wordDict return true if s can be segmented into a space-separated sequence of one or more dictionary words. ------------------------- Examples --------------------------------- s = "applepenapple", wordDict = ["apple","pen"] True "apple pen apple" "bacbacbac" ["bacbac"] False "appleappapple" ["apple","app"] True "apple app apple" s = "catsandog", wordDict = ["cats","dog","sand","and","cat"] False "cats and og" ------------------------- Brute force --------------------------------- Backtracking O(2^n) idx = 0 find a word that starts with the char at idx: - in None return False - if we found one, try complete it (for all of them). If we can complete it, we move idx to the next index after the index at the end of the word repeat the above steps till the end of the end of the string and return True ------------------------- Optimal --------------------------------- ********* Look like a simple Trie problem but it's not ********* O(n^3) worst | O(n^2) average use the memoized brute force optimal substrcuture: small solutions add up to full """ class Solution: def wordBreak(self, s: str, wordDict): cache = [None] * len(s) return self.wordBreakHelper(s, wordDict, 0, cache) def wordBreakHelper(self, s, wordDict, idx, cache): if idx == len(s): return True if cache[idx] is not None: return cache[idx] for word in wordDict: if s[idx:idx+len(word)] == word: # if the word can be completed if self.wordBreakHelper(s, wordDict, idx+len(word), cache): cache[idx] = True return cache[idx] cache[idx] = False return cache[idx] -
Word Break II
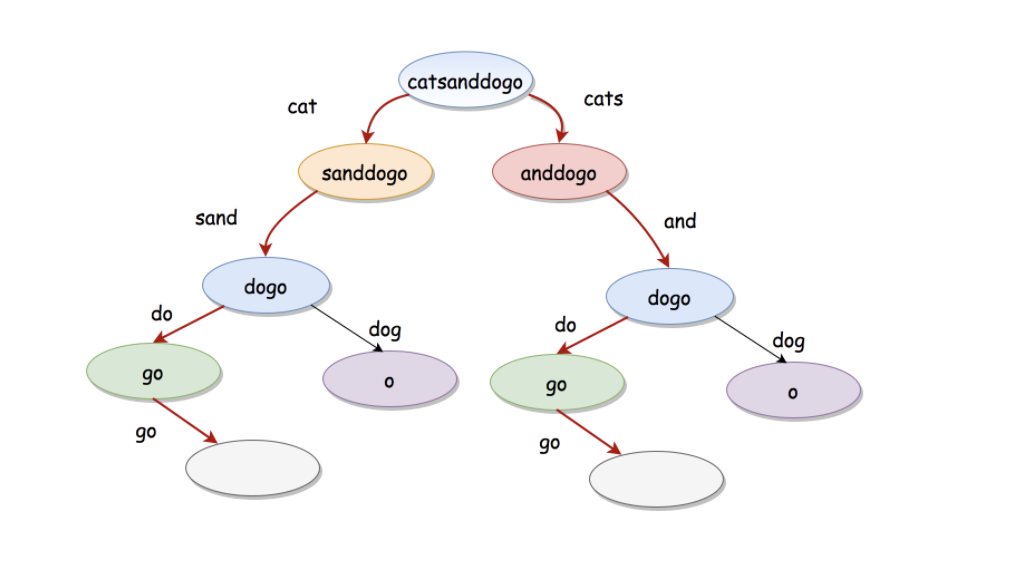
without caching
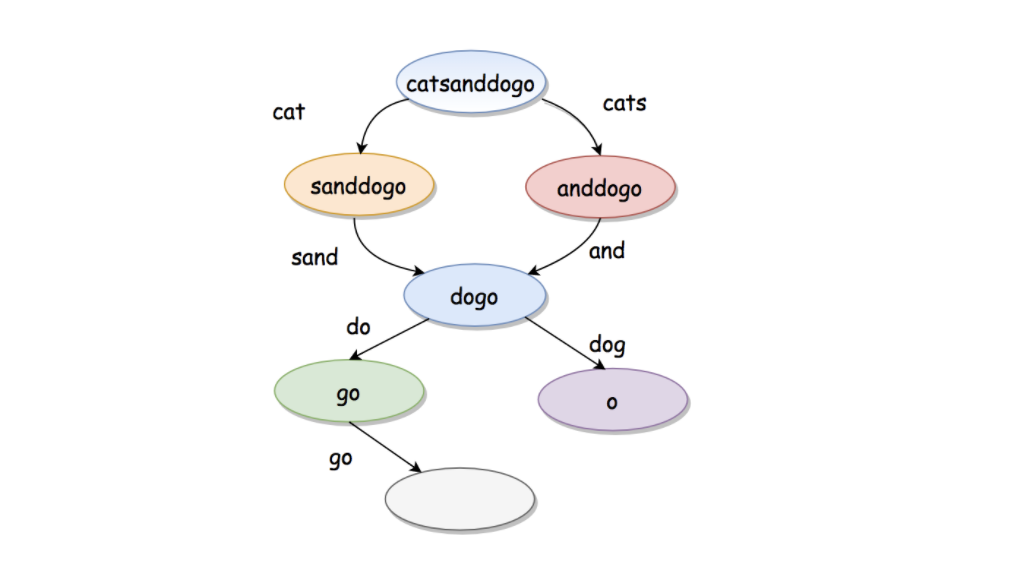
with caching

""" Word Break II Given a string s and a dictionary of strings wordDict, add spaces in s to construct a sentence where each word is a valid dictionary word. Return all such possible sentences in any order. Note that the same word in the dictionary may be reused multiple times in the segmentation. Example 1: Input: s = "catsanddog", wordDict = ["cat","cats","and","sand","dog"] Output: ["cats and dog","cat sand dog"] Example 2: Input: s = "pineapplepenapple", wordDict = ["apple","pen","applepen","pine","pineapple"] Output: ["pine apple pen apple","pineapple pen apple","pine applepen apple"] Explanation: Note that you are allowed to reuse a dictionary word. Example 3: Input: s = "catsandog", wordDict = ["cats","dog","sand","and","cat"] Output: [] https://leetcode.com/problems/word-break-ii """ from typing import List """ Time Complexity: O(n * 2^n), where n is the number of characters. In a worst case scenario Space Complexity: O(n * 2^n) There seems to be some disagreement online about the complexity of this problem; consider the following example to see the worst case scenario: s = aaaaaa wordDict = [a, aa, aaa, aaaa, aaaaa, aaaaaa] Our memo would look something like: { "a": ["a"] ----------------------------------------- 2^0 items, "aa": ["a a","aa"] ------------------------------ 2^1 items, "aaa": ["a a a", "aa a", "a aa", "aaa"] - 2^2 items, ... } That explains the space. The time could be explained by the number of executions of the subproblems. Namely, in the worst case we'd have to make n calls of the helper function, and each one of those calls would have 2^n append calls made, leaving us with O(n * 2^n) """ class Solution: def wordBreak(self, s: str, wordDict: List[str]): """ - try out all possible words at each index - cache the remaining substrings results - backtrack() - base cases - res [] - for each word check if it can start at the current index and end successfully - if so, call backtrack again - if it has results, merge the results of that with the current word - add the merged to res """ cache = {} def backtrack(idx): if idx == len(s): return [[]] if idx in cache: return cache[idx] res = [] for word in wordDict: # check if word can start at the current index and end successfully if not s[idx:idx+len(word)] == word: continue backtrack_res = backtrack(idx+len(word)) if not backtrack_res: continue # merge the results with the current word for sentence in backtrack_res: res.append([word]+sentence) cache[idx] = res return cache[idx] return [" ".join(sentence) for sentence in backtrack(0)] -
Remove Invalid Parentheses *


""" 301. Remove Invalid Parentheses Given a string s that contains parentheses and letters, remove the minimum number of invalid parentheses to make the input string valid. Return all the possible results. You may return the answer in any order.s Example 1: Input: s = "()())()" Output: ["(())()","()()()"] Example 2: Input: s = "(a)())()" Output: ["(a())()","(a)()()"] Example 3: Input: s = ")(" Output: [""] https://leetcode.com/problems/remove-invalid-parentheses https://youtu.be/cp0H_aR3OZo """ class Solution: def removeInvalidParentheses(self, s): result = set() invalid_opening, invalid_closing = self.count_invalid(s) self.valid_builder(s, result, [], 0, invalid_opening, invalid_closing) return list(result) def valid_builder(self, s, result, curr, idx, invalid_opening, invalid_closing): if idx == len(s): if invalid_opening == 0 and invalid_closing == 0 and self.is_valid(curr): result.add("".join(curr)) return char = s[idx] # can remove opening if char == "(" and invalid_opening > 0: self.valid_builder( s, result, curr, idx+1, invalid_opening-1, invalid_closing) # can remove closing if char == ")" and invalid_closing > 0: self.valid_builder( s, result, curr, idx+1, invalid_opening, invalid_closing-1) # add regardless self.valid_builder( s, result, curr+[char], idx+1, invalid_opening, invalid_closing) def count_invalid(self, s): invalid_closing = 0 invalid_opening = 0 # invalid closing opening_remaining = 0 for char in s: if char == "(": opening_remaining += 1 elif char == ")": if opening_remaining > 0: opening_remaining -= 1 else: invalid_closing += 1 # invalid closing closing_remaining = 0 for idx in reversed(range(len(s))): if s[idx] == ")": closing_remaining += 1 elif s[idx] == "(": if closing_remaining > 0: closing_remaining -= 1 else: invalid_opening += 1 return (invalid_opening, invalid_closing) def is_valid(self, s): opening_count = 0 for par in s: if par == "(": opening_count += 1 elif par == ")": if opening_count == 0: return False opening_count -= 1 return opening_count == 0 """ Time Complexity : O(2^N) Since in the worst case we will have only left parentheses in the expression and for every bracket we will have two options i.e. whether to remove it or consider it. Considering that the expression has N parentheses, the time complexity will be O(2^N) Space Complexity : O(N) because we are resorting to a recursive solution and for a recursive solution there is always stack space used as internal function states are saved onto a stack during recursion. The maximum depth of recursion decides the stack space used. Since we process one character at a time and the base case for the recursion is when we have processed all of the characters of the expression string, the size of the stack would be O(N). Note that we are not considering the space required to store the valid expressions. We only count the intermediate space here. """ class Solution_: def removeInvalidParentheses(self, s): result = set() inv_opening, inv_closing = self.count_invalid(s) self.valid_builder(result, list(s), 0, inv_opening, inv_closing) return list(result) def valid_builder(self, result, curr, idx, inv_opening, inv_closing): if idx == len(curr): if inv_opening == 0 and inv_closing == 0 and self.is_valid(curr): result.add("".join(curr)) return char = curr[idx] # can remove opening if char == "(" and inv_opening > 0: curr[idx] = "" self.valid_builder( result, curr, idx+1, inv_opening-1, inv_closing) curr[idx] = "(" # can remove closing if char == ")" and inv_closing > 0: curr[idx] = "" self.valid_builder( result, curr, idx+1, inv_opening, inv_closing-1) curr[idx] = ")" # leave it in / add regardless self.valid_builder( result, curr, idx+1, inv_opening, inv_closing) def count_invalid(self, s): inv_closing = 0 inv_opening = 0 # invalid closing opening_remaining = 0 for char in s: if char == "(": opening_remaining += 1 elif char == ")": if opening_remaining > 0: opening_remaining -= 1 else: inv_closing += 1 # invalid closing closing_remaining = 0 for idx in reversed(range(len(s))): if s[idx] == ")": closing_remaining += 1 elif s[idx] == "(": if closing_remaining > 0: closing_remaining -= 1 else: inv_opening += 1 return (inv_opening, inv_closing) def is_valid(self, s): opening_count = 0 for par in s: if par == "(": opening_count += 1 elif par == ")": if opening_count == 0: return False opening_count -= 1 return opening_count == 0 -
Combination Sum III






""" 216. Combination Sum III Find all valid combinations of k numbers that sum up to n such that the following conditions are true: Only numbers 1 through 9 are used. Each number is used at most once. Return a list of all possible valid combinations. The list must not contain the same combination twice, and the combinations may be returned in any order. Example 1: Input: k = 3, n = 7 Output: [[1,2,4]] Explanation: 1 + 2 + 4 = 7 There are no other valid combinations. Example 2: Input: k = 3, n = 9 Output: [[1,2,6],[1,3,5],[2,3,4]] Explanation: 1 + 2 + 6 = 9 1 + 3 + 5 = 9 2 + 3 + 4 = 9 There are no other valid combinations. Example 3: Input: k = 4, n = 1 Output: [] Explanation: There are no valid combinations. Using 4 different numbers in the range [1,9], the smallest sum we can get is 1+2+3+4 = 10 and since 10 > 1, there are no valid combination. Example 4: Input: k = 3, n = 2 Output: [] Explanation: There are no valid combinations. Example 5: Input: k = 9, n = 45 Output: [[1,2,3,4,5,6,7,8,9]] Explanation: 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45 There are no other valid combinations. https://leetcode.com/problems/combination-sum-iii/ Do after: - https://leetcode.com/problems/combination-sum """ # O(9! * K) time class Solution(object): def combinationSum3(self, k, n): res = [] self.helper(n, res, 1, 0, [0]*k, 0) return res def helper(self, n, res, start_num, curr_idx, curr, total): if total == n and curr_idx == len(curr): res.append(curr[:]) return if total >= n or start_num > 9 or curr_idx >= len(curr): return for number in range(start_num, 10): curr[curr_idx] = number self.helper(n, res, number+1, curr_idx+1, curr, total+number) curr[curr_idx] = 0 -
Combination Sum
Combination Sum - Backtracking - Leetcode 39 - Python


""" Combination Sum Given an array of distinct integers candidates and a target integer target, return a list of all unique combinations of candidates where the chosen numbers sum to target. You may return the combinations in any order. The same number may be chosen from candidates an unlimited number of times. Two combinations are unique if the frequency of at least one of the chosen numbers is different. It is guaranteed that the number of unique combinations that sum up to target is less than 150 combinations for the given input. Example 1: Input: candidates = [2,3,6,7], target = 7 Output: [[2,2,3],[7]] Explanation: 2 and 3 are candidates, and 2 + 2 + 3 = 7. Note that 2 can be used multiple times. 7 is a candidate, and 7 = 7. These are the only two combinations. Example 2: Input: candidates = [2,3,5], target = 8 Output: [[2,2,2,2],[2,3,3],[3,5]] Example 3: Input: candidates = [2], target = 1 Output: [] Example 4: Input: candidates = [1], target = 1 Output: [[1]] Example 5: Input: candidates = [1], target = 2 Output: [[1,1]] https://leetcode.com/problems/combination-sum Prerequisite: - https://leetcode.com/problems/combination-sum-iii """ """ candidates = [2,3,6,7], target = 7 7[] 5[2] 4[3] 3[2,2] 2[2,3] []rem_target / / \ \ [2]5 [3]4 [6]1 [7]0 / / [2,2]3 [2,3]2 | | [2,2,3]0 [2,3,2]0 """ class Solution(object): def combinationSum(self, candidates, target): return self.helper(candidates, 0, target) def helper(self, candidates, idx, target): # base cases if target == 0: return [[]] if target < 0 or idx >= len(candidates): return [] result = [] # add number # remember to give the current number another chance, rather than moving on (idx instead of idx+1) for arr in self.helper(candidates, idx, target-candidates[idx]): result.append(arr + [candidates[idx]]) # skip number result += self.helper(candidates, idx+1, target) return result """ Let N be the number of candidates, T be the target value, and M be the minimal value among the candidates. Time Complexity: O(N ^ T/M) Space Complexity: O(T/M) The execution of the backtracking is unfolded as a DFS traversal in a n-ary tree. The total number of steps during the backtracking would be the number of nodes in the tree. At each node, it takes a constant time to process, except the leaf nodes which could take a linear time to make a copy of combination. So we can say that the time complexity is linear to the number of nodes of the execution tree. Here we provide a loose upper bound on the number of nodes: First of all, the fan-out of each node would be bounded to N, i.e. the total number of candidates. The maximal depth of the tree, would be T/M, where we keep on adding the smallest element to the combination. As we know, the maximal number of nodes in N-ary tree of T/M, height would be : O(N ^ (T/M + 1)) Note that, the actual number of nodes in the execution tree would be much smaller than the upper bound, since the fan-out of the nodes are decreasing level by level. """ class Solution_: def combinationSum(self, candidates, target): results = [] def backtrack(remain, comb, start): if remain == 0: results.append(list(comb)) return elif remain < 0: return for i in range(start, len(candidates)): # add the number into the combination comb.append(candidates[i]) # give the current number another chance, rather than moving on (i instead of i+1) backtrack(remain - candidates[i], comb, i) # backtrack, remove the number from the combination comb.pop() backtrack(target, [], 0) return results -
Expression Add Operators ***





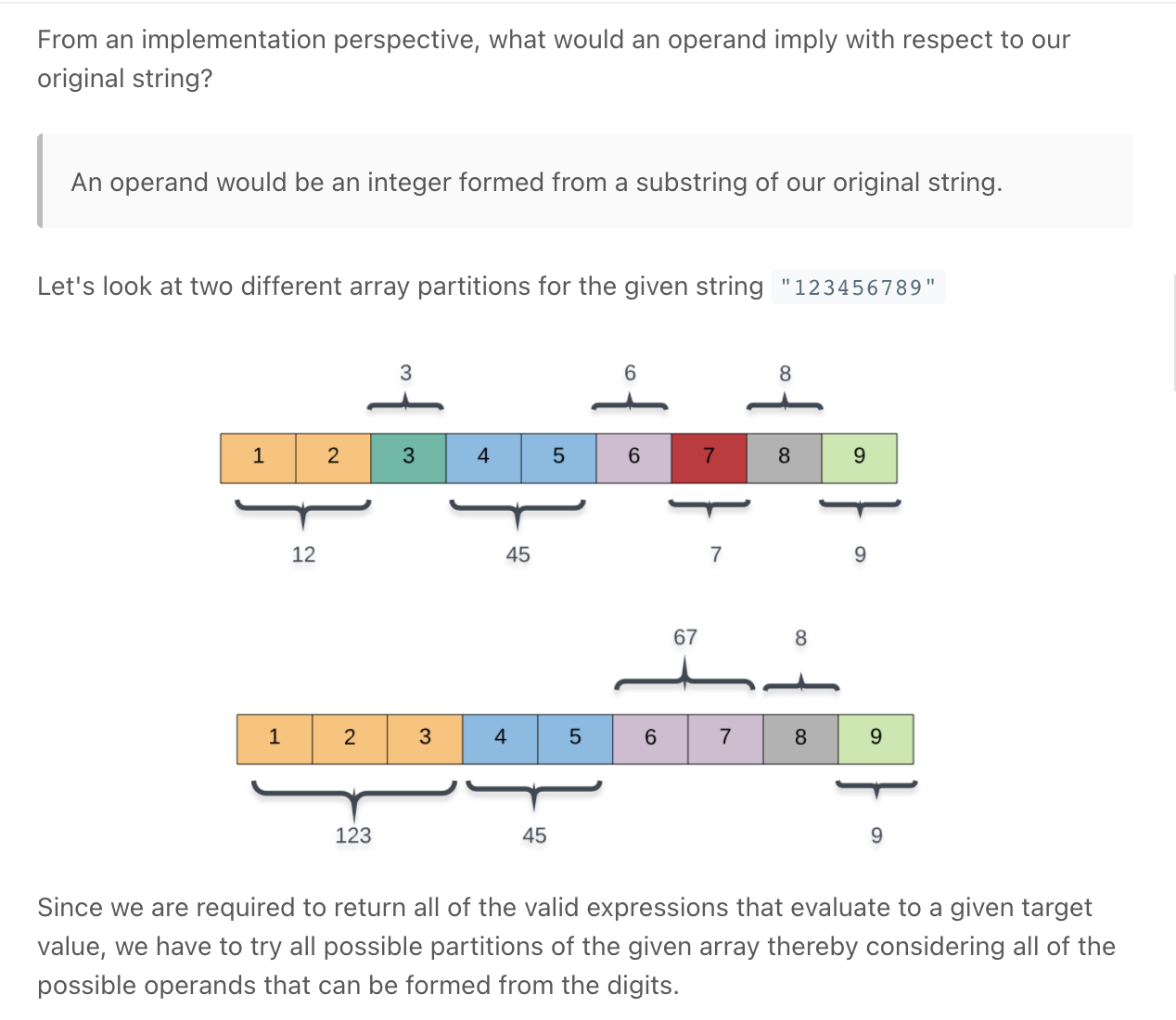





take note of the above ^

""" Expression Add Operators Given a string num that contains only digits and an integer target, return all possibilities to insert the binary operators '+', '-', and/or '*' between the digits of num so that the resultant expression evaluates to the target value. Note that operands in the returned expressions should not contain leading zeros. Example 1: Input: num = "123", target = 6 Output: ["1*2*3","1+2+3"] Explanation: Both "1*2*3" and "1+2+3" evaluate to 6. Example 2: Input: num = "232", target = 8 Output: ["2*3+2","2+3*2"] Explanation: Both "2*3+2" and "2+3*2" evaluate to 8. Example 3: Input: num = "105", target = 5 Output: ["1*0+5","10-5"] Explanation: Both "1*0+5" and "10-5" evaluate to 5. Note that "1-05" is not a valid expression because the 5 has a leading zero. Example 4: Input: num = "00", target = 0 Output: ["0*0","0+0","0-0"] Explanation: "0*0", "0+0", and "0-0" all evaluate to 0. Note that "00" is not a valid expression because the 0 has a leading zero. Example 5: Input: num = "3456237490", target = 9191 Output: [] Explanation: There are no expressions that can be created from "3456237490" to evaluate to 9191. https://leetcode.com/problems/expression-add-operators """ """ https://www.notion.so/paulonteri/Recursion-DP-Backtracking-525dddcdd0874ed98372518724fc8753#83d1fce1c9944b78a65a2c973be09e46 """ class Solution: def addOperators(self, num: str, target: int): answers = [] def dfs(idx, operand_left_section, prev_operation, total, string): """ Important info: - `operand_left_section` is used to recursively build operands. - Eg: for 123, it will grow as follows 1 => 12 => 123 \n - if its value is None it means there is no operand_left_section - `prev_operation`is used to store the results of the previous operation so that it can be undone in case we need to multiply \n - `total` is the result of the running calculation """ # # End (base cases) -------------------------------------------------------------------------------------- if idx == len(num): if total == target and operand_left_section == None: answers.append("".join(string[1:])) return # # Create operand -------------------------------------------------------------------------------------- # Extending the current operand by one digit operand = int(num[idx]) if operand_left_section: operand += (operand_left_section * 10) str_op = str(operand) # # Try out all(next) possible operands -------------------------------------------------------------------------------------- # To avoid cases where we have 1 + 05 or 1 * 05 since 05 won't be a valid operand. Hence this check if operand > 0: dfs(idx + 1, operand, prev_operation, total, string) # # Math ------------------------------------------------------------------------------------------------------------------- # remember to reset the operand_left_section to None (it is no longer needed, we will start a new one next time) # Can subtract or multiply only if there are some previous operations (will not happen at beginning) if string: # --- # Subtraction - negate operand (as prev_operation) so that we don't have to keep track of the signs string.append("-") string.append(str_op) dfs(idx+1, None, -operand, total-operand, string) string.pop() string.pop() # --- # Multiplication - undo last operation and multiply new_total = total - prev_operation # undo operation = prev_operation * operand # multiply new_total = new_total + operation # string.append("*") string.append(str_op) dfs(idx+1, None, operation, new_total, string) string.pop() string.pop() # --- # Addition - also used to handle index 0/starting out (no string) string.append("+") string.append(str_op) dfs(idx+1, None, operand, total+operand, string) string.pop() string.pop() dfs(0, None, 0, 0, []) return answersclass Solution: def addOperators(self, num: 'str', target: 'int') -> 'List[str]': N = len(num) answers = [] def recurse(index, prev_operand, current_operand, value, string): # Done processing all the digits in num if index == N: # If the final value == target expected AND # no operand is left unprocessed if value == target and current_operand == 0: answers.append("".join(string[1:])) return # Extending the current operand by one digit current_operand = current_operand*10 + int(num[index]) str_op = str(current_operand) # To avoid cases where we have 1 + 05 or 1 * 05 since 05 won't be a # valid operand. Hence this check if current_operand > 0: # NO OP recursion recurse(index + 1, prev_operand, current_operand, value, string) # ADDITION string.append('+'); string.append(str_op) recurse(index + 1, current_operand, 0, value + current_operand, string) string.pop();string.pop() # Can subtract or multiply only if there are some previous operands if string: # SUBTRACTION string.append('-'); string.append(str_op) recurse(index + 1, -current_operand, 0, value - current_operand, string) string.pop();string.pop() # MULTIPLICATION string.append('*'); string.append(str_op) recurse(index + 1, current_operand * prev_operand, 0, value - prev_operand + (current_operand * prev_operand), string) string.pop();string.pop() recurse(0, 0, 0, 0, []) return answers -
Partition to K Equal Sum Subsets *

O(N.N!) time
""" Partition to K Equal Sum Subsets Given an integer array nums and an integer k, return true if it is possible to divide this array into k non-empty subsets whose sums are all equal. Example 1: Input: nums = [4,3,2,3,5,2,1], k = 4 Output: true Explanation: It's possible to divide it into 4 subsets (5), (1, 4), (2,3), (2,3) with equal sums. Example 2: Input: nums = [1,2,3,4], k = 3 Output: false """ from typing import List """ Our goal is to break the given array into k subsets of equal sums. Firstly, we will check if the array sum can be evenly divided into k parts by ensuring that totalArraySum % k is equal to 0. Now, if the array sum can be evenly divided into k parts, we will try to build those k subsets using backtracking. O(N.N!) time | O(N) space: - The idea is that for each recursive call, we will iterate over N elements and make another recursive call. Assume we picked one element, then we iterate over the array and make recursive calls for the next N-1 elements and so on. Therefore, in the worst-case scenario, the total number of recursive calls will be N⋅(N−1)⋅(N−2)⋅...⋅2⋅1=N! and in each recursive call we perform an O(N) time operation. - Another way is to visualize all possible states by drawing a recursion tree. From root node we have NN recursive calls. The first level, therefore, has N nodes. For each of the nodes in the first level, we have (N-1) similar choices. As a result, the second level has N∗(N−1) nodes, and so on. The last level must have N⋅(N−1)⋅(N−2)⋅(N−3)⋅...⋅2⋅1 nodes. - make a subset with sum totalArraySum/k - reduce the needed(k) by one - start again with other numbers -repeat the above till the needed substets == 0 """ class Solution: def canPartitionKSubsets(self, nums: List[int], k: int): # get required subset size target_sum = sum(nums)/k if int(target_sum) != target_sum: return False # cannot have valid subsets # nums.sort(reverse=True) taken = [False]*len(nums) def backtracking(curr_sum, curr_k, idx): if curr_sum > target_sum: return False if curr_k == k: return True # When current subset sum reaches target sum then one subset is made. # Increment count and reset current subset sum to 0. if curr_sum == target_sum: return backtracking(0, curr_k+1, 0) # check if you starting to visit at a current index will give us the subsets for i in range(idx, len(nums)): # try not picked elements to make some combinations. if taken[i]: continue # visit (Include this element in current subset) taken[i] = True if backtracking(curr_sum+nums[i], curr_k, i+1): return True # if the current index works out, none other can # un-visit (Backtrack step) taken[i] = False # We were not able to make a valid combination after picking # each element from the array, hence we can't make k subsets. return False return backtracking(0, 0, 0) """ Memoization: O(N.2^N) time | O(N.2^N) space: - There will be N^2 unique combinations of the taken tuple, in which every combination of the given array will be linearly iterated. And if a combination occurs again then we just return the stored answer for it. - So for each subset, we are choosing the suitable elements from the array (basically iterate over nums and for each element either use it or skip it, which is O(N.2^N) operation) - The idea is that we have two choices for each element: include it in the subset OR not include it in the subset. We have N such elements. Therefore, the number of cases for events of including/excluding all numbers is: 2⋅2⋅2⋅...(N times)..⋅2 = 2^N - Another way is to visualize all possible states by drawing a recursion tree. In the first level, we have 2 choices for the first number, including the first number in the current subset or not. The second level, therefore, has 2 nodes. For each of the nodes in the second level, we have 2 similar choices. As a result, the third level has 2^2 nodes, and so on. The last level must have 2^N nodes. """ class Solution_: def canPartitionKSubsets(self, nums: List[int], k: int): # get required subset size target_sum = sum(nums)/k if int(target_sum) != target_sum: return False # cannot have valid subsets # nums.sort(reverse=True) taken = [False]*len(nums) cache = {} def backtracking(curr_sum, curr_k, idx): if curr_sum > target_sum: return False if curr_k == k: return True if tuple(taken) in cache: return cache[tuple(taken)] # When current subset sum reaches target sum then one subset is made. # Increment count and reset current subset sum to 0. if curr_sum == target_sum: cache[tuple(taken)] = backtracking(0, curr_k+1, 0) return cache[tuple(taken)] # check if you starting to visit at a current index will give us the subsets for i in range(idx, len(nums)): # try not picked elements to make some combinations. if not taken[i]: # visit (Include this element in current subset) taken[i] = True if backtracking(curr_sum+nums[i], curr_k, i+1): return True # if the current index works out, none other can # un-visit (Backtrack step) taken[i] = False # We were not able to make a valid combination after picking # each element from the array, hence we can't make k subsets. cache[tuple(taken)] = False return cache[tuple(taken)] return backtracking(0, 0, 0)
These "search paths" can manifest as:
- Actual search paths in a graph or searchable structure
- Chosen characters placed in a progress string
- Moves played in a puzzle, etc.
The 3 core ideas behind backtracking are:
- The Choice: What fundamental choice is being made at every step of the algorithm to advance to a solution?
- The Constraints: When is a path of decision no longer fruitful? When does the algorithm know for sure that it is wasting time following a certain path? If it is determined a path will no longer yield a solution an algorithm is said to "backtrack" when it returns control to a previous decision that can be advanced from.
- The Goal: When do we know that the solution has been found?
Backtracking algorithms are most naturally modeled recursively, though not all recursion is backtracking as backtracking is characterized by the actual act of backtracking when a path is no longer solvable. There must be an element of reflecting on the algorithm's state and deciding to backtrack.
More Reading
Find the original version of this page (with additional content) on Notion here.
Created: December 13, 2021 16:05:48