Levenshtein Distance *

Levenshtein Distance

Edit Distance | Dynamic Programming | LeetCode 72 | C++, Java, Python

Minimum edit distance | Dynamic programming | Backtracking

Edit Distance Between 2 Strings - The Levenshtein Distance ("Edit Distance" on LeetCode)

Introduction

Basic concept

""" 
Levenshtein Distance/Edit Distance:

Given two strings word1 and word2, return the minimum number of operations required to convert word1 to word2.
You have the following three operations permitted on a word:
    Insert a character
    Delete a character
    Replace a character


Example 1:
    Input: word1 = "horse", word2 = "ros"
    Output: 3
    Explanation: 
    horse -> rorse (replace 'h' with 'r')
    rorse -> rose (remove 'r')
    rose -> ros (remove 'e')
Example 2:
    Input: word1 = "intention", word2 = "execution"
    Output: 5
    Explanation: 
    intention -> inention (remove 't')
    inention -> enention (replace 'i' with 'e')
    enention -> exention (replace 'n' with 'x')
    exention -> exection (replace 'n' with 'c')
    exection -> execution (insert 'u')

https://leetcode.com/problems/edit-distance/
https://www.notion.so/paulonteri/Levenshtein-Distance-6eee820d93bb4de8a4be93cd42abd596#79d2868f016b40068d01c6a7b02c9c7c
"""

Solutions

Recursion (Brute force)

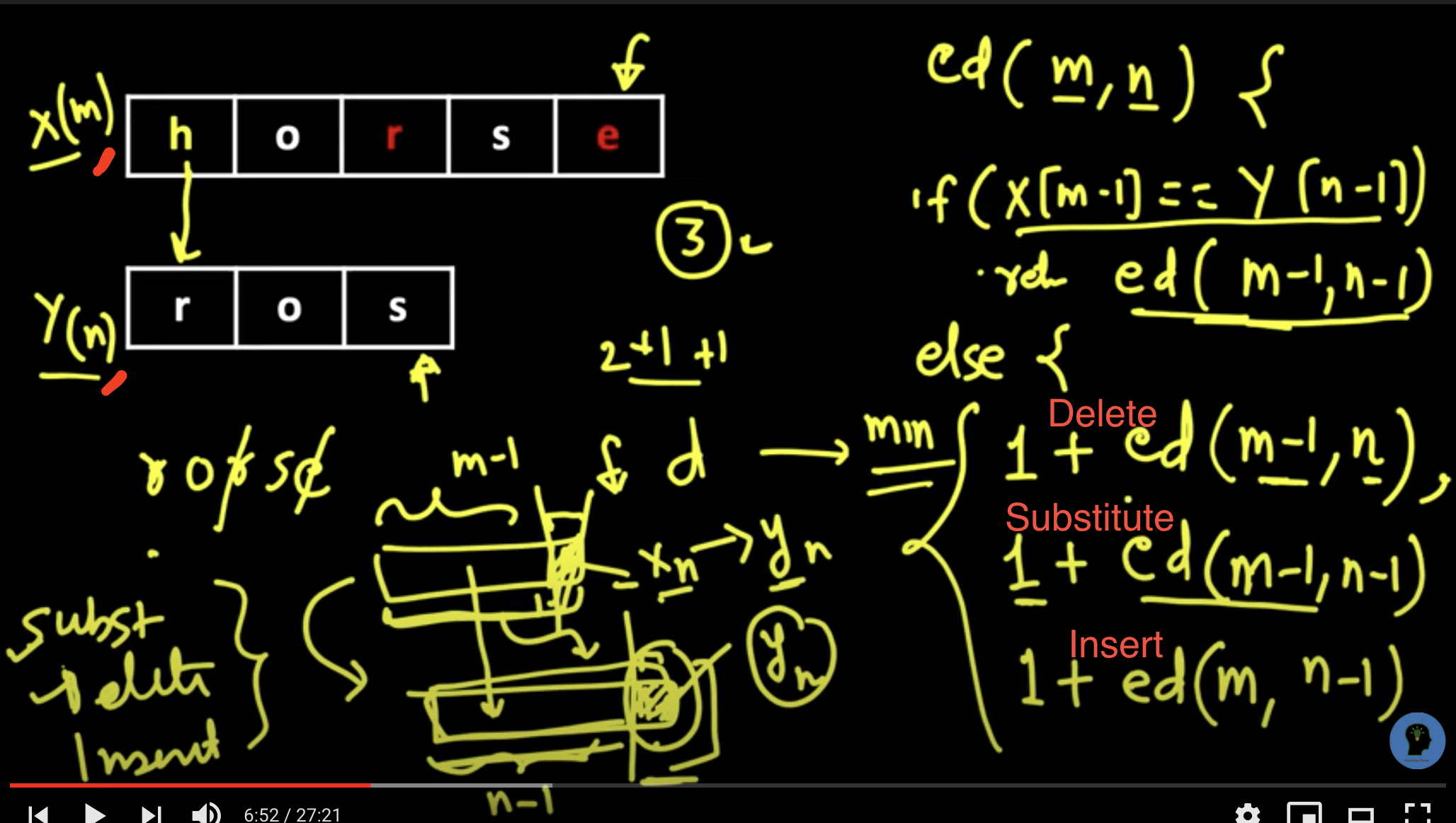
x to y https://youtu.be/ZkgBinDx9Kg

class Solution:
    def minDistanceHelper(self,  word1, word2, one, two, curr):
        # # base cases
        # end of both words
        if one == len(word1) and two == len(word2):
            return curr
        # end of any word
        if one == len(word1):
            return curr + len(word2) - two
        if two == len(word2):
            return curr + len(word1) - one

        # # operations required to convert word1 to word2
        # no operation needed
        if word1[one] == word2[two]:
            return self.minDistanceHelper(word1, word2, one+1, two+1, curr)

        # insert -> insert word2[two] into word1
        insert = self.minDistanceHelper(word1, word2, one, two+1, curr+1)
        # delete -> delete char at word1[one] (move to next char at word1)
        delete = self.minDistanceHelper(word1, word2, one+1, two, curr+1)
        # replace -> replace word1[one] with word2[two]
        replace = self.minDistanceHelper(word1, word2, one+1, two+1, curr+1)

        return min(insert, delete, replace)

    def minDistance(self, word1, word2):
        return self.minDistanceHelper(word1, word2, 0, 0, 0)

Brute-force that can work with caching

class Solution:
    def minDistanceHelper(self,  word1, word2, one, two):
        # # base cases
        # end of both words
        if one == len(word1) and two == len(word2):
            return 0
        # end of any word
        if one == len(word1):
            return len(word2) - two
        if two == len(word2):
            return len(word1) - one

        # # operations required to convert word1 to word2
        # no operation needed
        if word1[one] == word2[two]:
            return self.minDistanceHelper(word1, word2, one+1, two+1)

        # insert -> insert word2[two] into word1
        insert = self.minDistanceHelper(word1, word2, one, two+1)
        # delete -> delete char at word1[one] (move to next char at word1)
        delete = self.minDistanceHelper(word1, word2, one+1, two)
        # replace -> replace word1[one] with word2[two]
        replace = self.minDistanceHelper(word1, word2, one+1, two+1)
        return 1 + min(insert, delete, replace)

    def minDistance(self, word1, word2):
        return self.minDistanceHelper(word1, word2, 0, 0)

Memoization (Top Down Dynamic programming)

Improvement of the brute-force solution

class Solution:
    def minDistanceHelper(self, dp, word1, word2, one, two):
        # # base cases
        # end of both words
        if one == len(word1) and two == len(word2):
            return 0
        # end of any word
        if one == len(word1):
            return len(word2) - two
        if two == len(word2):
            return len(word1) - one

        # # check cache
        if dp[one][two]:
            return dp[one][two]

        # # operations required to convert word1 to word2
        # no operation needed
        if word1[one] == word2[two]:
            dp[one][two] = self.minDistanceHelper(dp, word1, word2, one+1, two+1)
        else:
            # insert -> insert word2[two] into word1
            insert = self.minDistanceHelper(dp, word1, word2, one, two+1)
            # delete -> delete char at word1[one] (move to next char at word1)
            delete = self.minDistanceHelper(dp, word1, word2, one+1, two)
            # replace -> replace word1[one] with word2[two]
            replace = self.minDistanceHelper(dp, word1, word2, one+1, two+1)
            dp[one][two] = 1 + min(insert, delete, replace)

        return dp[one][two]

    def minDistance(self, word1, word2):
        dp = [[False for _ in range(len(word2)+1)] for _ in range(len(word1)+1)]
        return self.minDistanceHelper(dp, word1, word2, 0, 0)

Tabulation (Bottom Up Dynamic programming)

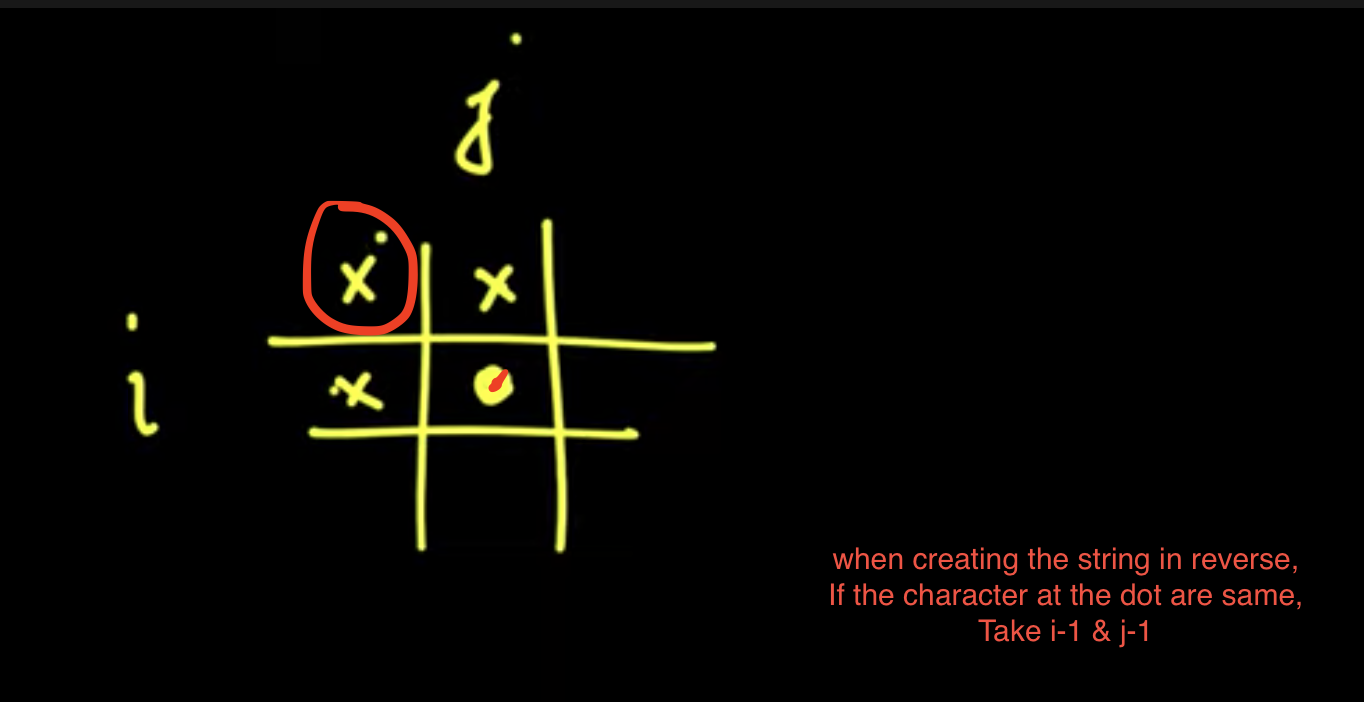
arrows show how to get results of certain actions

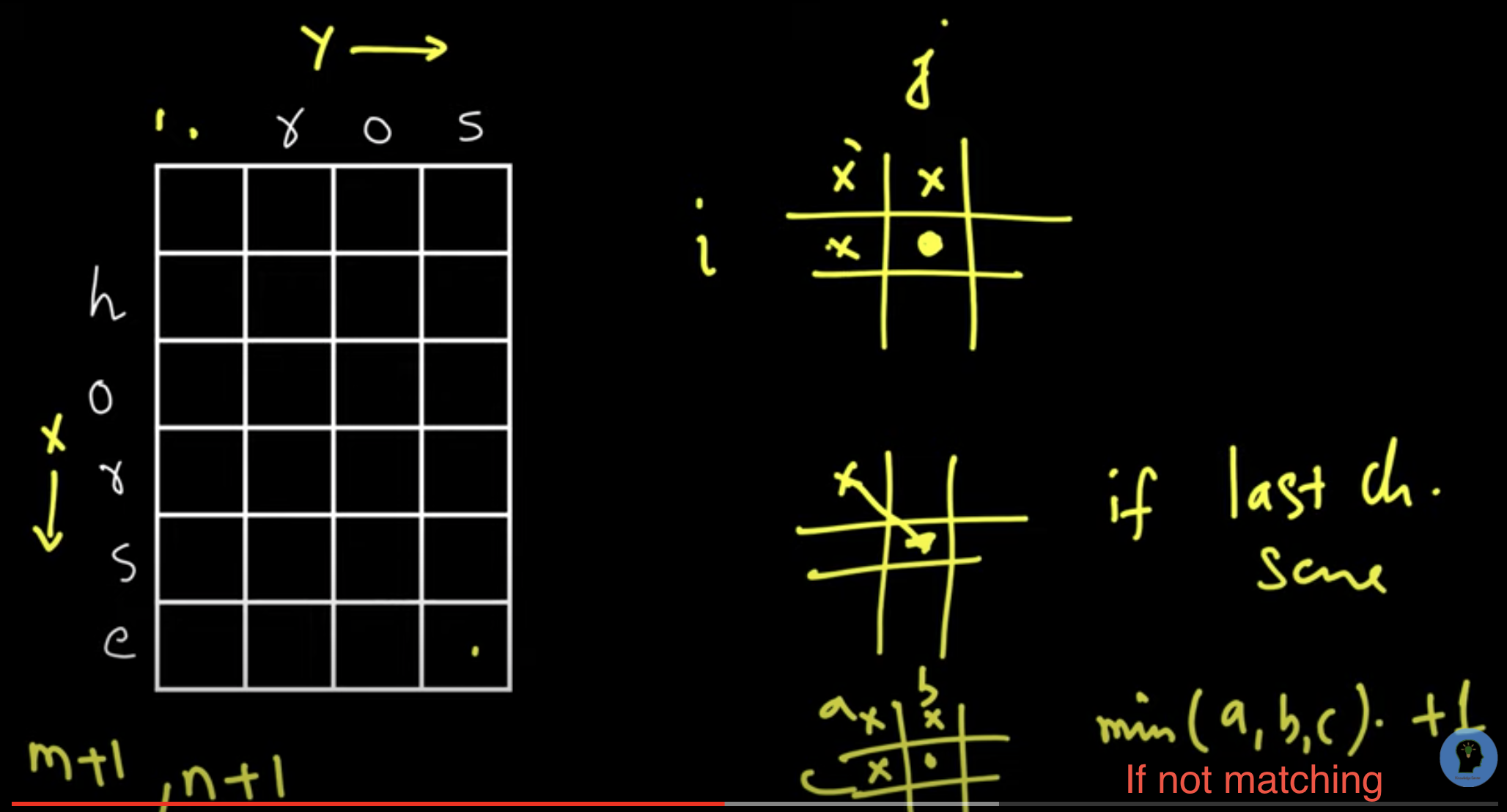
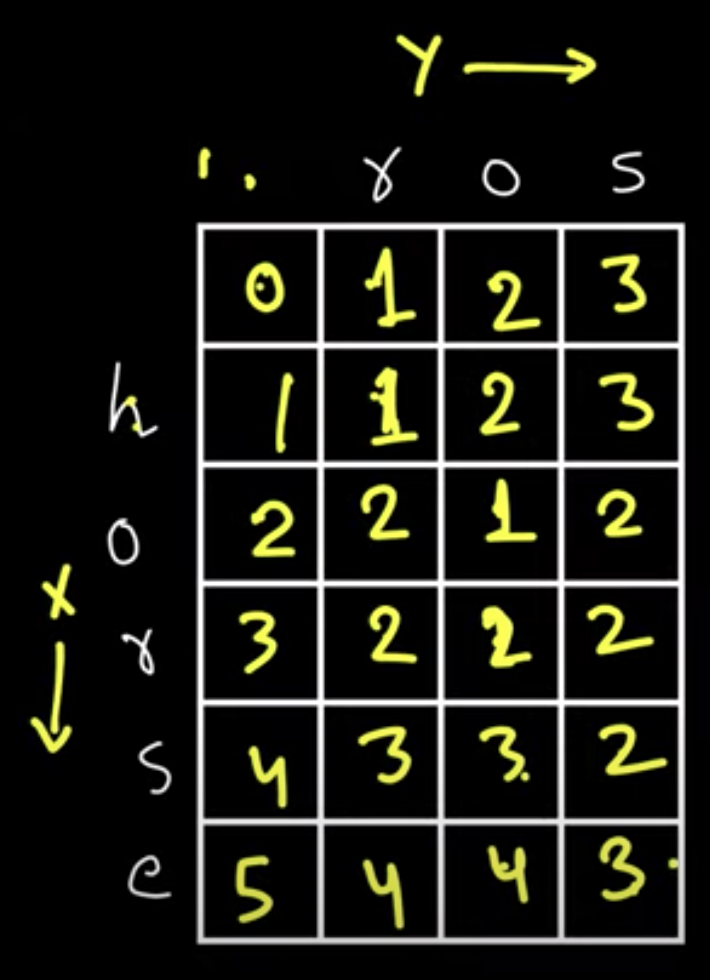
x to y

class Solution:
    def minDistance(self, word1, word2):

        dp = [[0 for _ in range(len(word1)+1)] for _ in range(len(word2)+1)]

        # # fill the values we know
        for i in range(len(dp[0])):
            dp[0][i] = i
        for i in range(len(dp)):
            dp[i][0] = i

        for two in range(1, len(dp)):
            for one in range(1, len(dp[0])):
                left = dp[two][one-1]  # delete
                top = dp[two-1][one]  # insert
                diagonal = dp[two-1][one-1]  # replace/skip

                if word1[one-1] == word2[two-1]:
                    dp[two][one] = dp[two-1][one-1]  # skip
                else:
                    dp[two][one] = min(left, top, diagonal) + 1

        return dp[-1][-1]

---

---

Find the original version of this page (with additional content) on Notion here.

---

---

Last update: December 13, 2021 16:05:48
Created: December 13, 2021 16:05:48

Authors: paulonteri (96.86%), Not Committed Yet (3.14%)