Two Heaps
Introduction
In many problems, where we are given a set of elements such that we can divide them into two parts. To solve the problem, we are interested in knowing the smallest element in one part and the biggest element in the other part. This pattern is an efficient approach to solve such problems.
This pattern uses two Heaps to solve these problems; A Min Heap to find the smallest element and a Max Heap to find the biggest element.
Ways to identify the Two Heaps pattern
- Useful in situations like Priority Queue, Scheduling
- If the problem states that you need to find the smallest/largest/median elements of a set
- Sometimes, useful in problems featuring a binary tree data structure
Find Median from Data Stream / Find the Median of a Number Stream
Problem
"""
Design a class to calculate the median of a number stream. The class should have the following two methods:
insertNum(int num): stores the number in the class
findMedian(): returns the median of all numbers inserted in the class
If the count of numbers inserted in the class is even, the median will be the average of the middle two numbers.
Example 1:
1. insertNum(3)
2. insertNum(1)
3. findMedian() -> output: 2
4. insertNum(5)
5. findMedian() -> output: 3
6. insertNum(4)
7. findMedian() -> output: 3.5
https://www.educative.io/courses/grokking-the-coding-interview/3Yj2BmpyEy4
https://www.algoexpert.io/questions/Continuous%20Median
"""
Solution


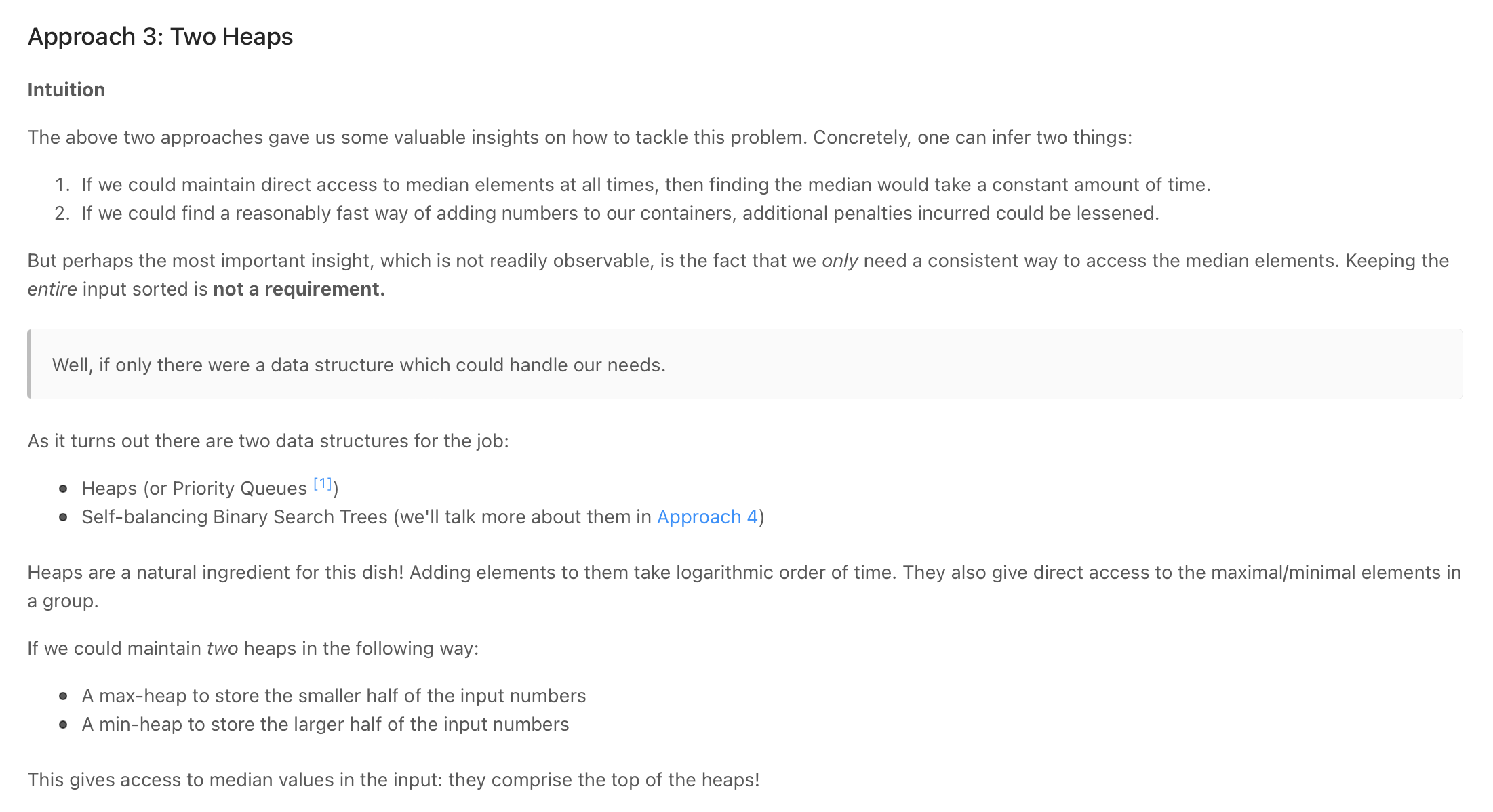
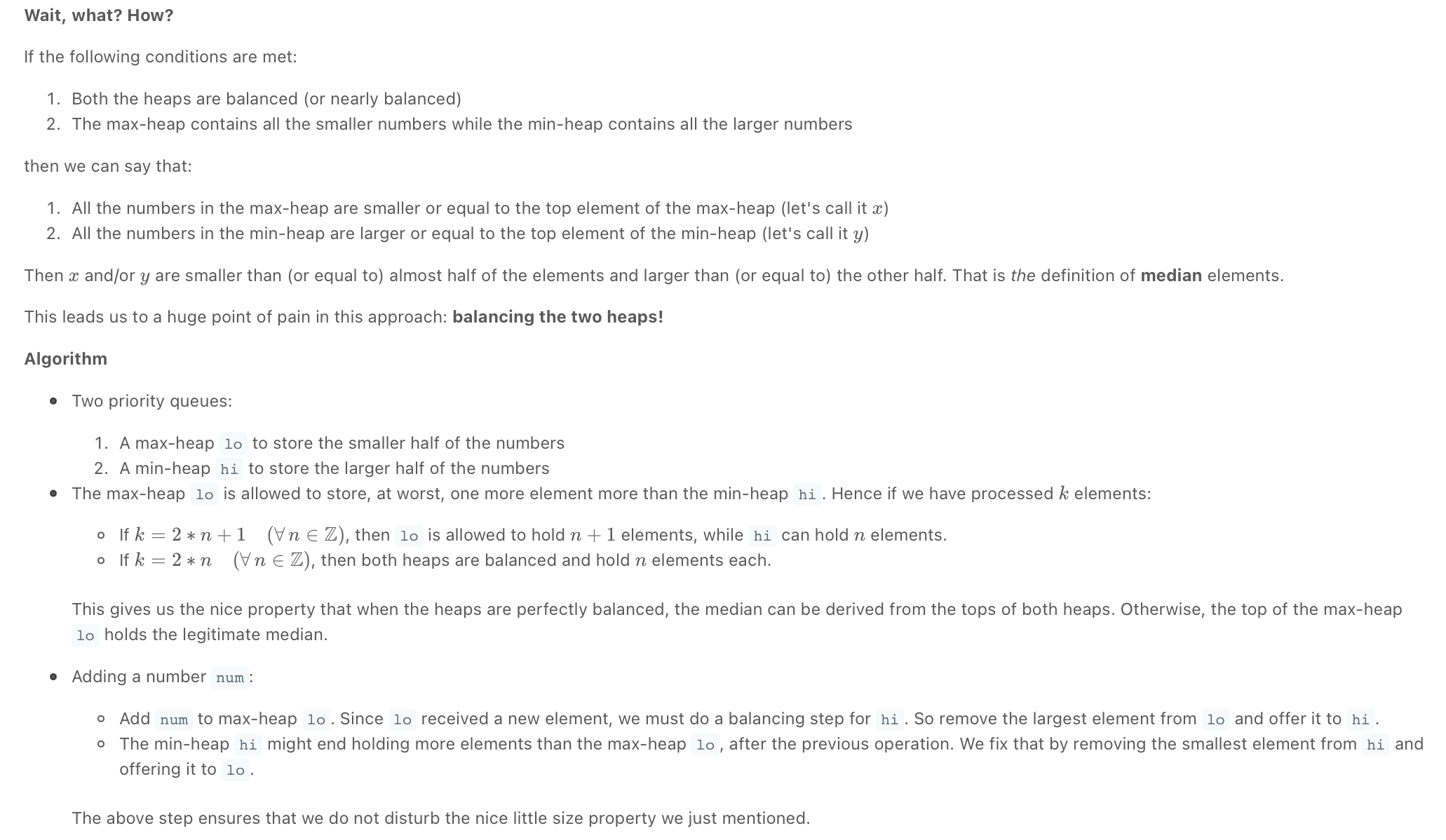
As we know, the median is the middle value in an ordered integer list. So a brute force solution could be to maintain a sorted list of all numbers inserted in the class so that we can efficiently return the median whenever required. Inserting a number in a sorted list will take O(N) time if there are ‘N’ numbers in the list. This insertion will be similar to the Insertion sort. Can we do better than this? Can we utilize the fact that we don’t need the fully sorted list - we are only interested in finding the middle element?
Assume ‘x’ is the median of a list. This means that half of the numbers in the list will be smaller than (or equal to) ‘x’ and half will be greater than (or equal to) ‘x’. This leads us to an approach where we can divide the list into two halves: one half to store all the smaller numbers (let’s call it smallNumList) and one half to store the larger numbers (let’s call it largNumList). The median of all the numbers will either be the largest number in the smallNumList or the smallest number in the largNumList. If the total number of elements is even, the median will be the average of these two numbers
The best data structure that comes to mind to find the smallest or largest number among a list of numbers is a Heap.
"""
Solution:
Assume ‘x’ is the median of a list. This means that half of the numbers in the list will be smaller than (or equal to) ‘x’ and half will be greater than (or equal to) ‘x’.
- we basically have to keep track of the middle number(s) at every point
- we can divide the set of numbers into two sorted halves (small & large numbers)
- the if total count of numbers is even, the median will be (the smallest large number + largest small number) / 2
- otherwise the median will be the middle number
larger = []
smaller = []
1. insertNum(3)
larger = [3]
smaller = []
2. insertNum(1)
larger = [3]
smaller = [1]
3. findMedian() -> output: 2
(3+1)/2
4. insertNum(5)
larger = [3,5]
smaller = [1]
5. findMedian() -> output: 3
(3)
6. insertNum(4)
larger = [3,4,5]
smaller = [1]
---
larger = [4,5]
smaller = [3,1]
7. findMedian() -> output: 3.5
(3+4)/2
"""
import heapq
class MedianOfAStream:
def __init__(self):
self.smaller = []
self.larger = []
def insert_num(self, num):
if len(self.larger) == 0 or num >= self.larger[0]:
heapq.heappush(self.larger, num)
else:
heapq.heappush(self.smaller, -num)
self.balance_heaps()
def find_median(self):
if len(self.larger) > len(self.smaller):
return self.larger[0]
else:
return (self.larger[0] + -self.smaller[0]) / 2
def balance_heaps(self):
while len(self.larger) > len(self.smaller) + 1:
heapq.heappush(self.smaller, -heapq.heappop(self.larger))
while len(self.larger) < len(self.smaller):
heapq.heappush(self.larger, -heapq.heappop(self.smaller))
Find the original version of this page (with additional content) on Notion here.
Created: December 13, 2021 16:05:48