Stacks & Queues

Stacks and Queues

Stacks

Stack data structure playlist

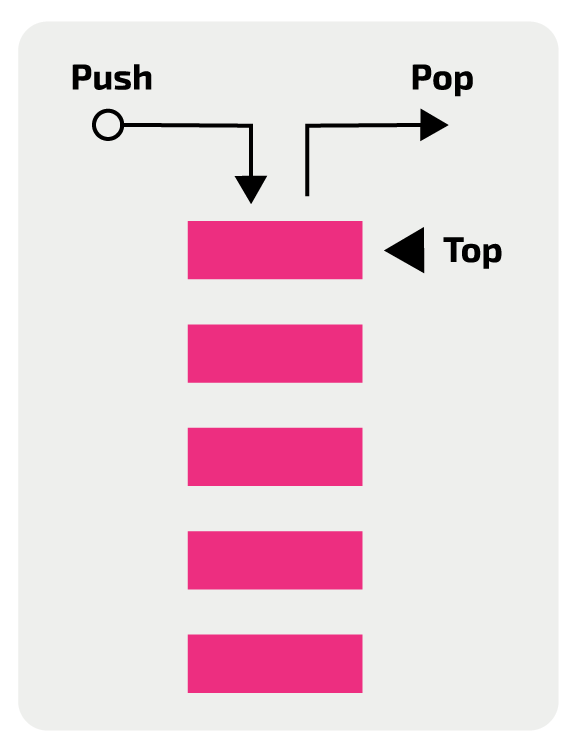
Stack is a linear data structure that follows a particular order in which the operations are performed. The order may be LIFO(Last In First Out).

Mainly the following three basic operations are performed in the stack:

• .push(): Adds an item in the stack. If the stack is full, then it is said to be an Overflow condition.
• .pop(): Removes an item from the stack. The items are popped in the reversed order in which they are pushed. If the stack is empty, then it is said to be an Underflow condition.
• .peek(): Returns top element of stack.
• **.is_empty():** Returns true if stack is empty, else false.

Often implemented as a linked list to give the above operations a time complexity of O(1)

The last-in, first-out semantics of a stack makes it very useful for creating reverse iterators for sequences that are stored in a way that would make it difficult or impossible to step back from a given element.

Some of the problems require you to implement your own stack class; for others, use the built-in list-type.

• s.append(e) pushes an element onto the stack. Not much can go wrong with a call to push.
• s[-1] will retrieve but does not remove, the element at the top of the stack.
• s.pop(0) will remove and return the element at the top of the stack.
• len(s) == 0 tests if the stack is empty.

Examples

DFS

• Min Max Stack Construction

  """
  Min Max Stack Construction:
  
  Write a MinMaxStack class for a Min Max Stack. The class should support:
  Pushing and popping values on and off the stack.
  Peeking at the value at the top of the stack.
  Getting both the minimum and the maximum values in the stack at any given point in time.
  All class methods, when considered independently, should run in constant time and with constant space.
  
  Sample Usage:
      // All operations below are performed sequentially.
      MinMaxStack(): - // instantiate a MinMaxStack
      push(5): -
      getMin(): 5
      getMax(): 5
      peek(): 5
      push(7): -
      getMin(): 5
      getMax(): 7
      peek(): 7
      push(2): -
      getMin(): 2
      getMax(): 7
      peek(): 2
      pop(): 2
      pop(): 7
      getMin(): 5
      getMax(): 5
      peek(): 5
  
  https://www.algoexpert.io/questions/Min%20Max%20Stack%20Construction
  """
  
  # all of the following will be called at valid times
  class MinMaxStack:
      def __init__(self):
          self.store = []
          # stores our min & max for every value in the stack
          self.min_max_store = []
  
      def peek(self):
          return self.store[-1]
  
      def pop(self):
          self.min_max_store.pop()
          return self.store.pop()
  
      def push(self, number):
          self.store.append(number)
  
          # store the current max & min
          max_value = number
          min_value = number
          if len(self.min_max_store) > 0:
              max_value = max(number, self.getMax())
              min_value = min(number, self.getMin())
          self.min_max_store.append({
              "max": max_value,
              "min": min_value
          })
  
      def getMin(self):
          return self.min_max_store[-1]['min']
  
      def getMax(self):
          return self.min_max_store[-1]['max']
  

• Decode String *

  

  Similar to what we have done

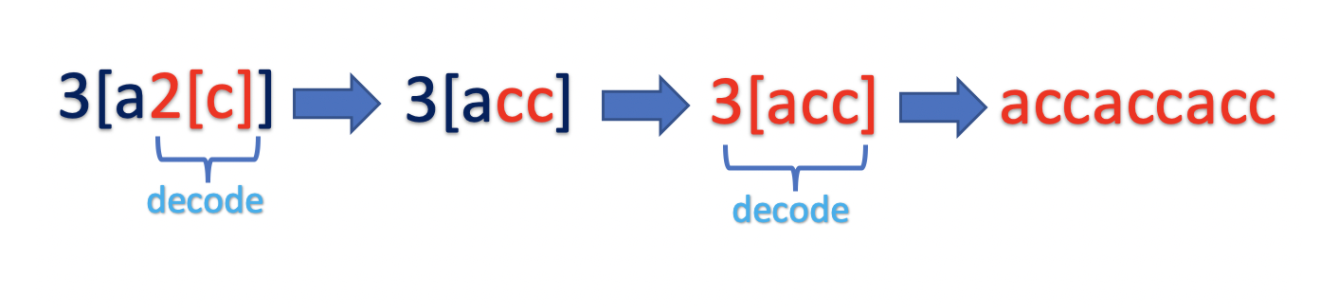
  Similar to what we have done

  

  

  """
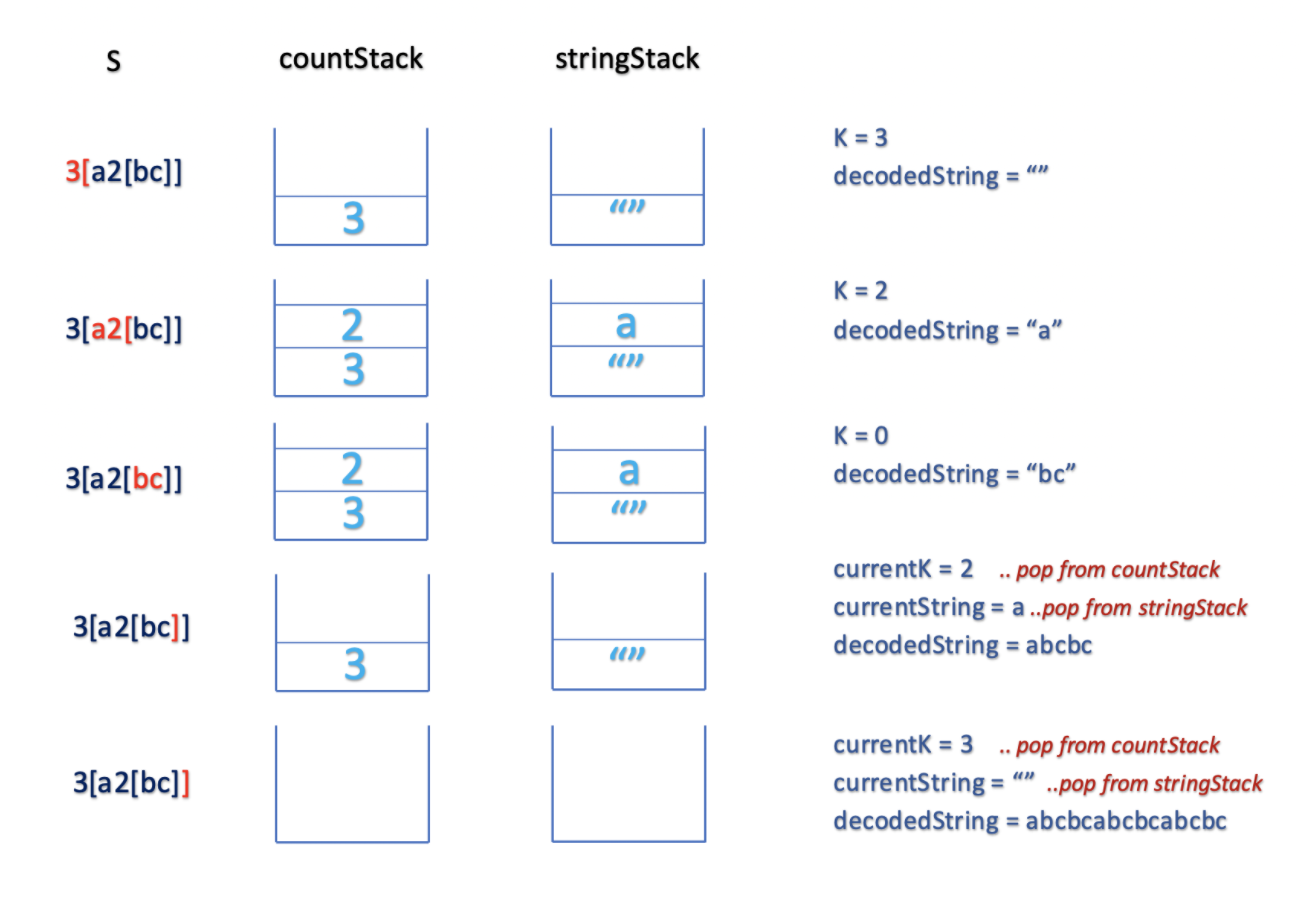
  Decode String
  
  Given an encoded string, return its decoded string.
  The encoding rule is: k[encoded_string], where the encoded_string inside the square brackets is being repeated exactly k times. 
  Note that k is guaranteed to be a positive integer.
  You may assume that the input string is always valid; No extra white spaces, square brackets are well-formed, etc.
  Furthermore, you may assume that the original data does not contain any digits and that digits are only for those repeat numbers, k.
  For example, there won't be input like 3a or 2[4].
  
  https://leetcode.com/problems/decode-string/
  """
  
  # O(n) time | O(n) space
  class Solution:
      def decodeString(self, s: str):
  
          if not s:
              return s
  
          # before we enter a bracket we store the current word in the prev_multiplier_stack,
          # so as to work on what is in the bracket only first, then
          #  we will restore it to ast it was after the closing bracket,
          #  and add the decoded content(decoded from in the brackets)
          prev_multiplier_stack = []  # add multipliers
          prev_str_stack = []
  
          current_str = ''
  
          i = 0
          while i < len(s):
              char = s[i]
  
              # handle multipliers
              if char.isnumeric():
                  # can be one didgit or many:
                  # Eg: '384[fsgs]asa'
                  num = ''
                  while s[i].isnumeric():
                      num += s[i]
                      i += 1
                  # store it for easy retrieval
                  prev_multiplier_stack.append(int(num))
  
              # open brackets
              elif char == "[":
                  # # we prepare to deal with what is in the brackets first
                  # store the current_str in the prev_str_stack
                  # will be undone once we hit a closing bracket
                  prev_str_stack.append(current_str)
                  current_str = ''  # we will now only deal with stuff that is in the brackets []
                  i += 1
  
              # close brackets
              elif char == "]":
                  # # leave bracket finally
                  # # decode then, return current_string as it was + decoded_chars
                  # get the prev(most recently added) multiplier
                  multiplier = prev_multiplier_stack.pop()
                  # decode
                  decoded_chars = current_str * multiplier
                  # return current_string as it was, + decoded_chars
                  current_str = prev_str_stack.pop() + decoded_chars
                  i += 1
                  #
                  # ignore
                  # # made this faster
                  # while multiplier > 0:
                  #     decoded_chars += current_str
                  #     multiplier -= 1
                  #
                  # # made this faster again
                  # decoded_chars = []
                  # while multiplier > 0:
                  #     decoded_chars.append(current_str)
                  #     multiplier -= 1
                  # return current_string as it was, + decoded_chars
                  # current_str = prev_str_stack.pop() + "".join(decoded_chars)
  
              # other characters
              else:
                  current_str += char
                  i += 1
  
          return current_str
  
  """
  Input:
      "3[a]2[bc]"
      "3[a2[c2[abc]3[cd]ef]]"
      "abc3[cd]xyz"
  Output:
      "aaabcbc"
      "acabcabccdcdcdefcabcabccdcdcdefacabcabccdcdcdefcabcabccdcdcdefacabcabccdcdcdefcabcabccdcdcdef"
      "abccdcdcdxyz"
  """
  
  class Solution00:
      def decodeString(self, s: str):
          res = ""
  
          multiplier_stack = []
          string_stack = []
  
          i = 0
          curr_string = ""
          while i < len(s):
  
              # handle numbers
              if s[i].isnumeric():
                  curr_num = ""
                  while s[i].isnumeric():
                      curr_num += s[i]
                      i += 1
  
                  multiplier_stack.append(int(curr_num))
                  continue
  
              # handle opening brackets
              elif s[i] == "[":
                  # # go into bracket
                  string_stack.append(curr_string)
                  curr_string = ""
  
              # handle closing brackets
              elif s[i] == "]":
                  # # get out of bracket
                  # multiply
                  prev_multiplier = multiplier_stack.pop()
                  multiplied_string = curr_string * prev_multiplier
                  # merge with outer bracket
                  prev_string = string_stack.pop()
                  curr_string = prev_string + multiplied_string
  
              # handle characters
              else:
                  curr_string += s[i]
  
              i += 1
  
          return curr_string
  

• Next Greater Element II *

  """
  Next Greater Element II 
  Given a circular integer array nums (i.e., the next element of nums[nums.length - 1] is nums[0]), 
      return the next greater number for every element in nums.
  The next greater number of a number x is the first greater number to its traversing-order next in the array, 
      which means you could search circularly to find its next greater number. If it doesn't exist, return -1 for this number.
  
  Example 1:
      Input: nums = [1,2,1]
      Output: [2,-1,2]
      Explanation: The first 1's next greater number is 2; 
          The number 2 can't find next greater number. 
          The second 1's next greater number needs to search circularly, which is also 2.
  Example 2:
      Input: nums = [1,2,3,4,3]
      Output: [2,3,4,-1,4]
  https://leetcode.com/problems/next-greater-element-ii
  """
  
  """
  Next Greater Element:
  
  Write a function that takes in an array of integers
   and returns a new array containing,at each index,
   the next element in the input array that's greater than the element at that index in the input array.
  In other words, your function should return a new array
   where outputArray[i] is the next element in the input array that's greater than inputArray[i].
  If there's no such next greater element for a particular index,
   the value at that index in the output array should be -1.
  
  For example, given array = [1, 2], your function should return [2, -1].
  Additionally, your function should treat the input array as a circular array.
   A circular array wraps around itself as if it were connected end-to-end.
   So the next index after the last index in a circular array is the first index.
   This means that, for our problem, given array = [0, 0, 5, 0, 0, 3, 0 0],
    the next greater element after 3 is 5, since the array is circular.
  
  Sample Input
      array = [2, 5, -3, -4, 6, 7, 2]
      Sample Output
      [5, 6, 6, 6, 7, -1, 5]
  
  https://www.algoexpert.io/questions/Next%20Greater%20Element
  """
  
  # O(n) time | O(n) space - where n is the length of the array
  def nextGreaterElement00(array):
      res = [-1] * len(array)
  
      # stack used to store the previous smaller numbers that haven't been replaced
      # stored in the form of {'idx': 0, 'val': 0}
      be_replaced_stack = []
  
      for i in range(len(array)*2):  # loop through twice because the array is circular
          array_idx = i % len(array)  # prevent out of bound errors
  
          # check if we have found some values in the be_replaced_stack stack
          #   that is smaller than the current array value array[array_idx]
          #   then replace them (their corresponding values in res)
          while len(be_replaced_stack) > 0 and be_replaced_stack[-1]['val'] < array[array_idx]:
  
              to_be_replaced = be_replaced_stack.pop()['idx']
              res[to_be_replaced] = array[array_idx]
  
          # add the current element to the be_replaced_stack so that it can be checked in the futere for replacement
          be_replaced_stack.append({'idx': array_idx, 'val': array[array_idx]})
  
      return res
  
  # O(n) time | O(n) space - where n is the length of the array
  def nextGreaterElement01(array):
      res = [-1] * len(array)
  
      # stack used to store the previous smaller numbers' indices that haven't been replaced
      be_replaced_stack = []
  
      for i in range(len(array)*2):  # loop through twice because the array is circular
          array_idx = i % len(array)  # prevent out of bound errors
  
          # check if we have found some values in the be_replaced_stack stack
          #   that is smaller than the current array value array[array_idx]
          #   then replace them (their corresponding values in res)
          while len(be_replaced_stack) > 0 and array[be_replaced_stack[-1]] < array[array_idx]:
              res[be_replaced_stack.pop()] = array[array_idx]
  
          # add the current element to the be_replaced_stack so that it can be checked in the futere for replacement
          be_replaced_stack.append(array_idx)
  
      return res
  
  """
  # we will use a stack to keep track of the past values that have not been replaced
  #  once we find a bigger element, we replace them and remove them from the stack
  #  then add the big element to the stack in the hope that it will be replaced
  
  array = [0, 1,  2,  3, 4, 5, 6] <= indices
  array = [2, 5, -3, -4, 6, 7, 2]
  
  ---
  num = 2 (index 0)
  res = [-1, -1, -1, -1, -1, -1, -1]
  stack = [2]
  
  num = 5 (index 1)
  res = [5, -1, -1, -1, -1, -1, -1]
  stack = [5] -> replaced all smaller values in res and the stack
  
  num = -3
  res = [5, -1, -1, -1, -1, -1, -1]
  stack = [5, -3]
  
  num = -4 (index 3)
  res = [5, -1, -1, -1, -1, -1, -1]
  stack = [5, -3, -4]
  
  num = 6 (index 4)
  res = [5, 6, 6, 6, -1, -1, -1]
  stack = [6] -> replaced all smaller values in res and the stack
  
  num = 7 (index 5)
  res = [5, 6, 6, 6, 7, -1, -1]
  stack = [7] -> replaced all smaller values in res and the stack
  
  num = 2 (index 6)
  res = [5, 6, 6, 6, 7, -1, -1]
  stack = [7,2]
  
  num = 2 (index 0)
  res = [5, 6, 6, 6, 7, -1, -1]
  stack = [7,2,2]
  ---
  
  """
  
  # O(n) time | O(n) space - where n is the length of the array
  def nextGreaterElement(array):
      res = [-1] * len(array)
  
      # stack used to store the previous smaller numbers that haven't been replaced
      next_nums_stack = []
  
      # loop through twice because the array is circular
      for i in reversed(range(len(array)*2)):
          array_idx = i % len(array)  # prevent out of bound errors
  
          while len(next_nums_stack) > 0:
              # if value at the top of the stack is smaller than the current value in the array,
              #   remove it from the stack till we find something larger
              if next_nums_stack[-1] <= array[array_idx]:
                  next_nums_stack.pop()
  
              # replace the value in the array by the
              #   value at the top of the stack (if stack[-1] is larger)
              else:
                  res[array_idx] = next_nums_stack[-1]
                  break
  
          # add the current element to the next_nums_stack so that it can be checked in the futere for replacement
          next_nums_stack.append(array[array_idx])
  
      return res
  

• Sunset views

  def sunsetViews(buildings, direction):
      stack = []
  
      # order of iteration
      order = range(len(buildings))
      if direction == "WEST":
          order = reversed(order)
  
      for i in order:
          # remove prev buildings that can be blocked by the current (shorter ones)
          while len(stack) > 0 and buildings[stack[-1]] <= buildings[i]:
              stack.pop()
  
          stack.append(i)
  
      if direction == "WEST":
          stack.reverse()
      return stack
  

• Three in One

  

  

• Simplify Path/Shorten Path

  """ 
  Simplify Path/Shorten Path:
  
  Given a string path, which is an absolute path (starting with a slash '/') to a file or directory in a Unix-style file system,
   convert it to the simplified canonical path.
  In a Unix-style file system, 
      a period '.' refers to the current directory, 
      a double period '..' refers to the directory up a level, 
      and any multiple consecutive slashes (i.e. '//') are treated as a single slash '/'. 
      For this problem, any other format of periods such as '...' are treated as file/directory names.
  The canonical path should have the following format:
      The path starts with a single slash '/'.
      Any two directories are separated by a single slash '/'.
      The path does not end with a trailing '/'.
      The path only contains the directories on the path from the root directory to the target file or directory (i.e., no period '.' or double period '..')
  Return the simplified canonical path.
  
  Example 1:
      Input: path = "/home/"
      Output: "/home"
      Explanation: Note that there is no trailing slash after the last directory name.
  Example 2:
      Input: path = "/../"
      Output: "/"
      Explanation: Going one level up from the root directory is a no-op, as the root level is the highest level you can go.
  Example 3:
      Input: path = "/home//foo/"
      Output: "/home/foo"
      Explanation: In the canonical path, multiple consecutive slashes are replaced by a single one.
  Example 4:
      Input: path = "/a/./b/../../c/"
      Output: "/c"
  
  https://leetcode.com/problems/simplify-path/
  https://www.algoexpert.io/questions/Shorten%20Path
  """
  
  """ 
  - have a stack and all all directories we find there
  - if we find a '..', remove the directory at the top of the stack
  - if we find a '//' or '.' skip it
  """
  
  class Solution0:
      def simplifyPath(self, path):
  
          stack = []
          start = 0
          end = 0
          while start < len(path):
              # cannot add to stack
              if not (end == len(path)-1 or path[end] == "/"):
                  end += 1
                  continue
  
              # # check logic
              substring = path[start:end]
              if end == len(path)-1 and path[end] != "/":
                  # deal with cases like "/home"
                  substring = path[start:end+1]
  
              # # path creation logic
              # if we find a '//' or '.' skip it
              if substring == '' or substring == '.':
                  pass
              # if we find a '..', remove the directory at the top of the stack
              elif substring == '..':
                  if stack:
                      stack.pop()
              # add directory
              else:
                  stack.append(substring)
  
              # # next
              start = end+1
              end = end+1
  
          return "/" + "/".join(stack)
  
  class Solution:
      def simplifyPath(self, path):
          stack = []
  
          paths = path.split("/")
          for substring in paths:
  
              # # path creation logic
              # if we find a '//' or '.' skip it
              if substring == '' or substring == '.':
                  pass
              # if we find a '..', remove the directory at the top of the stack
              elif substring == '..':
                  if stack:
                      stack.pop()
              # add directory
              else:
                  stack.append(substring)
  
          return "/" + "/".join(stack)
  

• Largest Rectangle in Histogram/Largest Rectangle Under Skyline *

  LARGEST RECTANGLE IN HISTOGRAM - Leetcode 84 - Python

  Screen Recording 2021-11-23 at 15.29.38.mov

  84. Largest Rectangle in a Histogram.mp4

  

  """ 
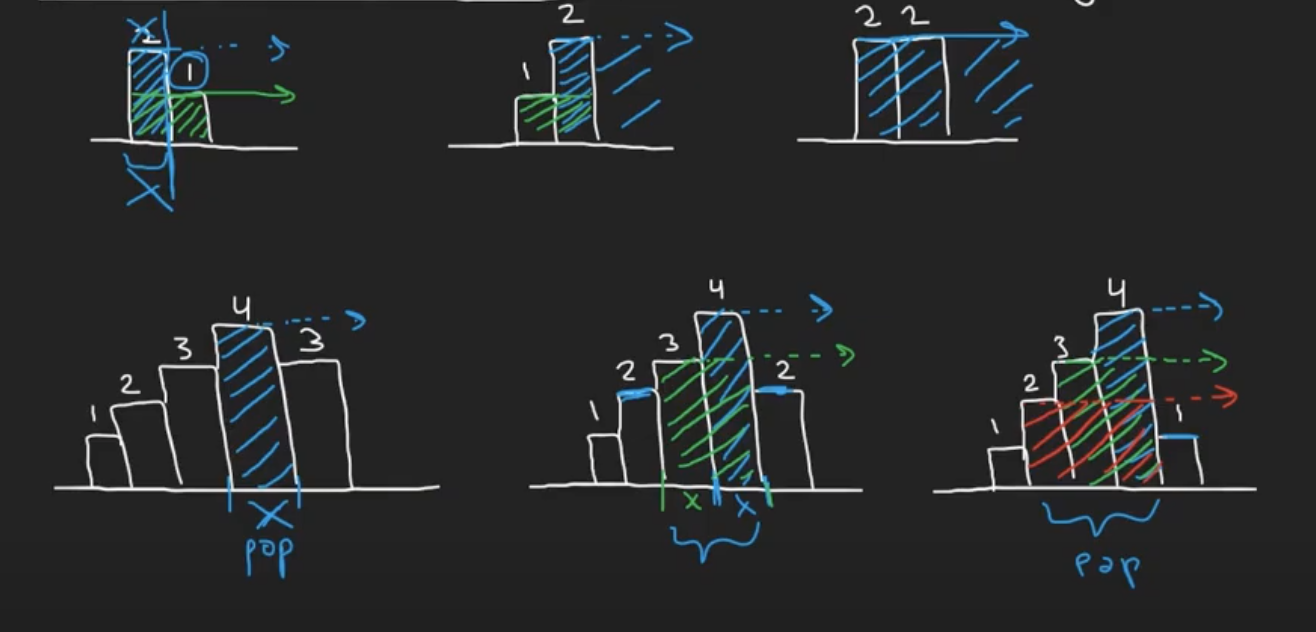
  Largest Rectangle in Histogram/Largest Rectangle Under Skyline:
  
  Given an array of integers heights representing the histogram's bar height where the width of each bar is 1, 
  return the area of the largest rectangle in the histogram.
  
  Example 1:
      Input: heights = [2,1,5,6,2,3]
      Output: 10
      Explanation: 5*2 The above is a histogram where width of each bar is 1.
      The largest rectangle is shown in the red area, which has an area = 10 units.
  Example 2:
      Input: heights = [2,4]
      Output: 4 => 2*2
  Example 3:
      heights = [1, 3, 3, 2, 4, 1, 5, 3, 2]
      9
  
      Below is a visual representation of the sample input.
                   _
               _  | |
         _ _  | | | |_
        | | |_| | | | |_
       _| | | | |_| | | |
      |_|_|_|_|_|_|_|_|_|
  
  https://leetcode.com/problems/largest-rectangle-in-histogram
  """
  
  #
  from collections import deque
  
  """
  Brute force:
  - for every building, expand outward
  """
  
  """
  - for each height try to find out where it started and calculate the height
  
  - keep track of the largest valid building up to that point:
      - that can still make rectangles
      - the stack will only conttain buildings that can continue expanding to the right
  
  [0,1,2,3,4,5]
  [2,1,5,6,2,3]
  
  stack = []
  
  n,  r,s(i,n)
  2,[(0,2)]2*1,
  1,[(0,1)] # one is in the prev two, 1*2,
  5,[(0,1),(2,5)],5*1,1*3
  6,[(0,1),(2,5),(3,6)],6*1,5*2,1*4
  2,[(0,1),(2,2)],2*3,1*5
  3,[(0,1),(2,2),(5,3)],3*1,1*5,2*4
  
  remaining in stack: [(0,1),(2,2),(5,3)]
  3*1
  2*4
  1*5
  
  """
  
  class RectangleInfo:
      def __init__(self, start_idx, height):
          self.start_idx = start_idx  # far right bound of building
          self.height = height
  
      def get_area(self, end_idx):
          return (end_idx-self.start_idx + 1) * self.height
  
  class Solution:
      def largestRectangleArea(self, heights):
          max_area = 0
          prev_valid_heights = deque()  # stack
  
          for idx, curr_height in enumerate(heights):
  
              # # determine left bound of curr height
              start_idx = idx
  
              # remove invalid buildings (that cannot be expanded to the right as they are taller than curr_height)
              # - also viewed as expanding as left as possible
              while prev_valid_heights and curr_height < prev_valid_heights[-1].height:
                  removed = prev_valid_heights.pop()
                  # calculate the area from when the removed was lat valid (using the last valid index)
                  max_area = max(max_area, removed.get_area(idx-1))
  
                  # our current rectangle can start from there
                  start_idx = removed.start_idx
  
              prev_valid_heights.append(RectangleInfo(start_idx, curr_height))
  
          # # empty stack
          while prev_valid_heights:
              removed = prev_valid_heights.pop()
              max_area = max(max_area, removed.get_area(len(heights)-1))
  
          return max_area
  

• Minimum Remove to Make Valid Parentheses

  

  Screen Recording 2021-11-03 at 13.53.53.mov

  """ 
  Minimum Remove to Make Valid Parentheses:
  
  Given a string s of '(' , ')' and lowercase English characters. 
  Your task is to remove the minimum number of parentheses ( '(' or ')', in any positions ) so that the resulting parentheses string is valid and return any valid string.
  
  Formally, a parentheses string is valid if and only if:
      It is the empty string, contains only lowercase characters, or
      It can be written as AB (A concatenated with B), where A and B are valid strings, or
      It can be written as (A), where A is a valid string.
  
  
  Example 1:
      Input: s = "lee(t(c)o)de)"
      Output: "lee(t(c)o)de"
      Explanation: "lee(t(co)de)" , "lee(t(c)ode)" would also be accepted.
  Example 2:
      Input: s = "a)b(c)d"
      Output: "ab(c)d"
  Example 3:
      Input: s = "))(("
      Output: ""
      Explanation: An empty string is also valid.
  Example 4:
      Input: s = "(a(b(c)d)"
      Output: "a(b(c)d)"
  
  https://leetcode.com/problems/minimum-remove-to-make-valid-parentheses
  """
  
  #
  
  """
  ---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
  ------------- PROBLEM --------------------
  - string will have  '(' , ')' and lowercase English characters
  
  - remove the minimum number of parentheses so that the resulting parentheses string is valid
  - return any valid string.
  
  ------------- EXAMPLES --------------------
  
  a(pp)l)e -> a(pp)le / a(ppl)e -> remove one closing  
  a(ppl)e  -> a(ppl)e           -> N/A
  a(pple   -> apple             -> remove one opening
  a(p(ple  -> apple             -> remove two opening
  
  a(pp()l)e     -> a(pp()l)e                                    -> N/A
  lee(t(c)o)de) -> lee(t(c)o)de / lee(t(c)ode)  / lee(t(co)de)  -> remove one closing
  a)b(c)d       -> ab(c)d                                       -> remove first closing
  
  a(pp()le 
  a(pp()l(e 
  
  "))(("
  
  ------------- BRUTE FORCE -------------------- O(n^2) time | O(n) space - where n = len(string)
  - count opening and closing then remove the larger randomly and see what works (validate)
  
  ------------- OPTIMAL --------------------
  ------------- 1: O(n) time | O(n) space - where n = len(string)
  Two Pass String Builder
  - remove any closing bracket that does not have a preceding opening bracket
  - remove any excess opening brackets starting at the end
  
  ------------- PSEUDOCODE --------------------
  ------------- 1:
  opening_running_count
      (how many unclosed opening brackets we have)
  
  - whenever we meet an opening bracket: opening_running_count += 1
  - whenever we meet a closing bracket:
      - if opening_running_count > 0: 
          opening_running_count -= 1
      - else:
          remove it
  - remove excess opening brackets starting at the end
  
  """
  
  class Solution:
      def minRemoveToMakeValid(self, s: str):
          opening_count = 0
  
          removed_closing = []
          for char in s:
              if char == "(":
                  opening_count += 1
                  removed_closing.append(char)
              elif char == ")":
                  # only add valid ones
                  if opening_count > 0:
                      removed_closing.append(char)
                      opening_count -= 1
              else:
                  removed_closing.append(char)
  
          # remove excess opening brackets
          output = [""] * (len(removed_closing) - opening_count)
  
          curr_idx = len(output) - 1
          for idx in reversed(range(len(removed_closing))):
              # remove
              if removed_closing[idx] == "(" and opening_count > 0:
                  opening_count -= 1
              else:
                  output[curr_idx] = removed_closing[idx]
                  curr_idx -= 1
  
          return "".join(output)
  
  class _Solution:
      def removeInvalidClosingbrackets(self, s, opening, closing):
          result = []
  
          opening_count = 0
          for char in s:
              if char == opening:
                  opening_count += 1
                  result.append(char)
              elif char == closing:
                  # only add valid ones
                  if opening_count > 0:
                      result.append(char)
                      opening_count -= 1
              else:
                  result.append(char)
  
          return result
  
      def minRemoveToMakeValid(self, s: str):
  
          # remove excess brackets
          removed_closing = self.removeInvalidClosingbrackets(s, "(", ")")
          removed_opening = reversed(self.removeInvalidClosingbrackets(reversed(removed_closing),
                                                                       ")", "("))
          return "".join(removed_opening)
  
  """ 
  ---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
  If we put the indexes of the "(" on the stack, then we'll know that all the indexes on the stack at the end are the indexes of the unmatched "(". 
  We should also use a set to keep track of the unmatched ")" we come across.
  """
  
  class Solution1:
      def minRemoveToMakeValid(self, s: str):
          indexes_to_remove = set()
          stack = []
          for i, c in enumerate(s):
              if c not in "()":
                  continue
              # opening brackets
              if c == "(":
                  stack.append(i)
  
              # closing brackets
              elif not stack:
                  indexes_to_remove.add(i)
              else:
                  stack.pop()
  
          # the union of two sets contains all the elements contained in either set (or both sets).
          indexes_to_remove = indexes_to_remove.union(set(stack))
  
          # build string with skipping invalid parenthesis
          string_builder = []
          for i, c in enumerate(s):
              if i not in indexes_to_remove:
                  string_builder.append(c)
          return "".join(string_builder)
  

• Exclusive Time of Functions

  

  """ 
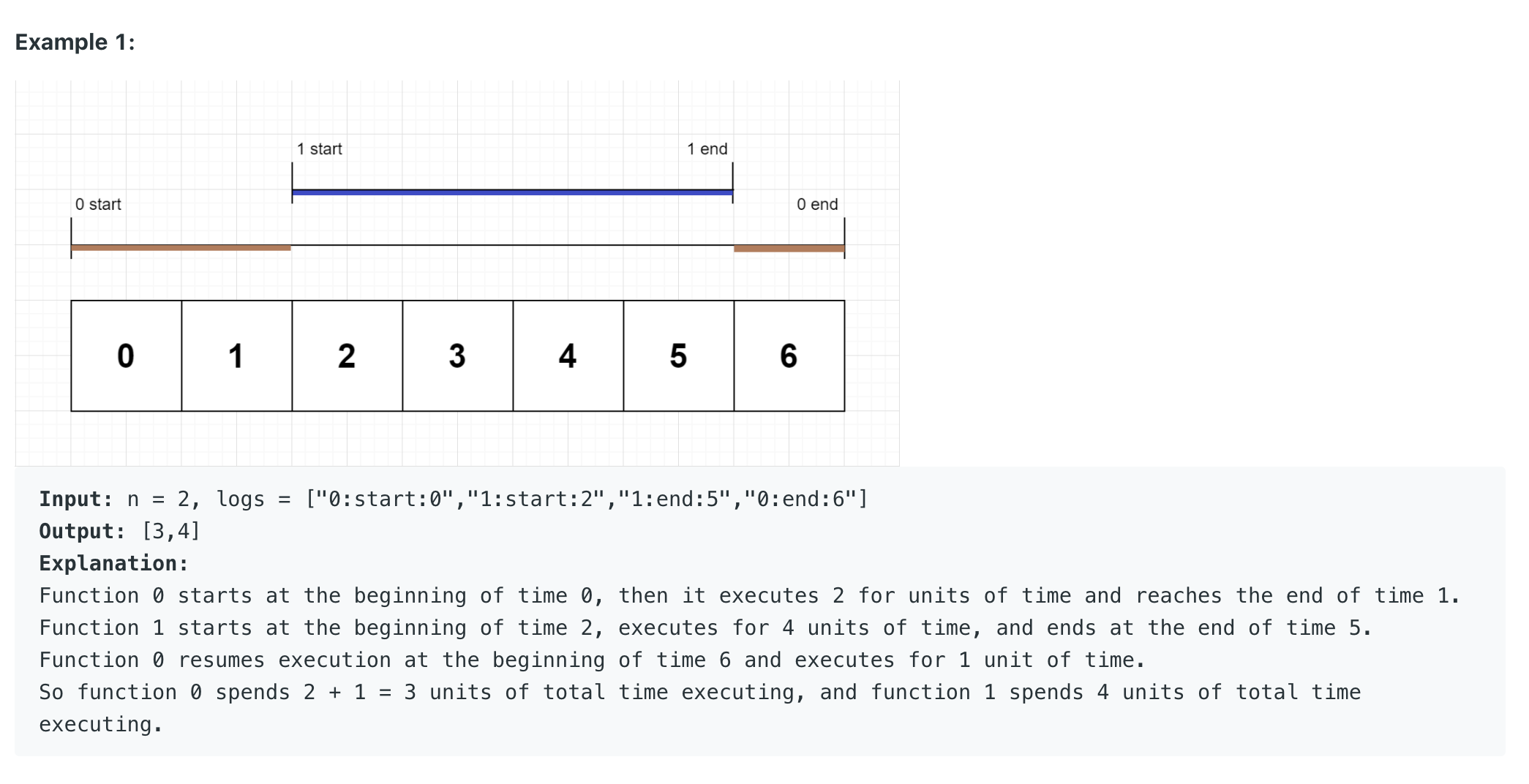
  Exclusive Time of Functions:
  
  On a single-threaded CPU, we execute a program containing n functions. 
  Each function has a unique ID between 0 and n-1.
  Function calls are stored in a call stack: when a function call starts, its ID is pushed onto the stack, and when a function call ends, its ID is popped off the stack. 
  The function whose ID is at the top of the stack is the current function being executed. 
  Each time a function starts or ends, we write a log with the ID, whether it started or ended, and the timestamp.
  You are given a list logs, where logs[i] represents the ith log message formatted as a string "{function_id}:{"start" | "end"}:{timestamp}". 
  For example, "0:start:3" means a function call with function ID 0 started at the beginning of timestamp 3, and "1:end:2" means a function call with function ID 1 ended at the end of timestamp 2. 
  Note that a function can be called multiple times, possibly recursively.
  A function's exclusive time is the sum of execution times for all function calls in the program. 
  For example, if a function is called twice, one call executing for 2 time units and another call executing for 1 time unit, the exclusive time is 2 + 1 = 3.
  Return the exclusive time of each function in an array, where the value at the ith index represents the exclusive time for the function with ID i.
  
  https://leetcode.com/problems/exclusive-time-of-functions/
  """
  
  import collections
  '''
  *** Fill array with current running job ***
  O(n+m) space | where m is the duration
  
  Input: 
      n = 2, 
      logs = ["0:start:0","0:start:2","0:end:5","1:start:6","1:end:6","0:end:7"]
  Output: 
      [7,1]
      [0, 1,  2, 3, 4,  5,  6,  0]
      [0, 0,  0, 0, 0,  0,  1,  0]
  Explanation:
  Function 0 starts at the beginning of time 0, executes for 2 units of time, and recursively calls itself.
  Function 0 (recursive call) starts at the beginning of time 2 and executes for 4 units of time.
  Function 0 (initial call) resumes execution then immediately calls function 1.
  Function 1 starts at the beginning of time 6, executes 1 units of time, and ends at the end of time 6.
  Function 0 resumes execution at the beginning of time 6 and executes for 2 units of time.
  So function 0 spends 2 + 4 + 1 = 7 units of total time executing, and function 1 spends 1 unit of total time executing.
  
  n = 2, logs = ["0:start:0","0:start:2","0:end:5","1:start:7","1:end:7","0:end:8"]
  
  ---
  prev_job = []
  curr_job = 0
  
  past_process
  [0, 1, 2, 3, 4, 5, 6, 7, 8]
  []
  
  ---
  
  "0:start:2"
  fill past_process with curr_job till idx 1
  add curr_job to prev_job
  change curr_job to 0
  
  prev_job = [0]
  curr_job = 0
  
  past_process
  [0,  1, 2, 3, 4, 5, 6, 7, 8]
  [0,  ]
  
  ---
  
  "0:end:5"
  fill past_process with curr_job till idx 5
  replace curr_job with prev_job.pop()
  
  prev_job = []
  curr_job = 0
  
  past_process
  [0,  1, 2, 3, 4, 5,  6, 7, 8]
  [0,  0, 0, 0, 0, 0,  ]
  
  ---
  
  "1:start:7"
  fill past_process with curr_job till idx 6
  add curr_job to prev_job
  change curr_job to 1
  
  prev_job = [0]
  curr_job = 1
  
  past_process
  [0,  1, 2, 3, 4, 5,  6,  7, 8]
  [0,  0, 0, 0, 0, 0,  0,  ]
  
  ---
  
  "1:end:7"
  fill past_process with curr_job till idx 7
  replace curr_job with prev_job.pop()
  
  prev_job = []
  curr_job = 0
  
  past_process
  [0,  1, 2, 3, 4, 5,  6,  7,  8]
  [0,  0, 0, 0, 0, 0,  0,  1,  ]
  
  ---
  
  "0:end:8"
  fill past_process with curr_job till idx 8
  replace curr_job with prev_job.pop()
  
  prev_job = []
  curr_job = None
  
  past_process
  [0,  1, 2, 3, 4, 5,  6,  7,  8]
  [0,  0, 0, 0, 0, 0,  0,  1,  0]
  
  n = 2, logs = ["0:start:0","1:start:2","1:end:5","0:end:6"]
  
  [0, 1,  2, 3, 4,  5, 6]
  [0, 0,  1, 1, 1,  0]
  --------------------------
  O(n) space
  without the space
  
  def time:
  
      result = [0] * len(n)
  
      stack = []
      last_job = 0
      for log in logs:
          if start:
              time
              job
              for _ in range((time-last_log)+1):
                  prev_job = stack[-1]
                  result[prev_job] += 1
  
              stack.append(job)
  
  
  
          elif end:
  
  '''
  
  """
  --------------------------------------------------------------------------------
  
  """
  
  class SolutionBF:
      def get_job_info(self, job_str):
          job, kind, time = job_str.split(":")
          return int(job), int(time), kind
  
      def exclusiveTime(self, n: int, logs):
          task_history = []
  
          stack = []
          next_placement = 0
          for log in logs:
              job, time, kind = self.get_job_info(log)
  
              if kind == "start":
                  # place last job
                  for _ in range((time-next_placement)):
                      prev_job = stack[-1]
                      task_history.append(prev_job)
  
                  # place current job
                  task_history.append(job)
                  next_placement = time+1
  
                  stack.append(job)
  
              elif kind == "end":
                  # place last job == current job
                  prev_job = stack.pop()
                  for _ in range((time-next_placement)+1):
                      task_history.append(prev_job)
                  next_placement = time+1
  
          task_counter = collections.Counter(task_history)
          result = [0] * n
          for key in task_counter:
              result[key] = task_counter[key]
          return result
  
  """
  --------------------------------------------------------------------------------
  
  """
  
  class Solution_:
      def get_job_info(self, job_str):
          job, kind, time = job_str.split(":")
          return int(job), int(time), kind
  
      def exclusiveTime(self, n: int, logs):
          result = [0] * n
  
          stack = []
          next_placement = 0
          for log in logs:
              job, time, kind = self.get_job_info(log)
  
              if kind == "start":
                  # place last job
                  for _ in range((time-next_placement)):
                      prev_job = stack[-1]
                      result[prev_job] += 1
  
                  # place current job
                  result[job] += 1
                  next_placement = time+1
  
                  # move to top of stack
                  stack.append(job)
  
              elif kind == "end":
                  # place last job == current job
                  prev_job = stack.pop()
                  for _ in range((time-next_placement)+1):
                      result[prev_job] += 1
                  next_placement = time+1
  
          return result
  
  """
  --------------------------------------------------------------------------------
  
  """
  
  class Solution:
      def get_job_info(self, job_str):
          job, kind, time = job_str.split(":")
          return int(job), int(time), kind
  
      def exclusiveTime(self, n: int, logs):
          result = [0] * n
  
          stack = []
          next_placement = 0
          for log in logs:
              job, time, kind = self.get_job_info(log)
  
              if kind == "start":
                  # place last job
                  # record how long the prev job ran (prev job should have continued running from next_placement)
                  if stack:
                      prev_job = stack[-1]
                      result[prev_job] += time-next_placement
  
                  # place current job
                  # start the current job with one run
                  result[job] += 1
                  next_placement = time+1
  
                  # move to top of stack
                  stack.append(job)
  
              elif kind == "end":
                  # place prev/last job == current job that has ended
                  stack.pop()
                  # record how long the prev job ran
                  result[job] += time-next_placement+1
                  next_placement = time+1
  
          return result
  

• Candy Crush 1D

  """ 
  1209. Remove All Adjacent Duplicates in String II/Candy Crush 1D
  
  You are given a string s and an integer k, a k duplicate removal consists of choosing k adjacent and equal letters from s and removing them, causing the left and the right side of the deleted substring to concatenate together.
  We repeatedly make k duplicate removals on s until we no longer can.
  Return the final string after all such duplicate removals have been made. It is guaranteed that the answer is unique.
  
  Example 1:
      Input: s = "abcd", k = 2
      Output: "abcd"
      Explanation: There's nothing to delete.
  Example 2:
      Input: s = "deeedbbcccbdaa", k = 3
      Output: "aa"
      Explanation: 
      First delete "eee" and "ccc", get "ddbbbdaa"
      Then delete "bbb", get "dddaa"
      Finally delete "ddd", get "aa"
  Example 3:
      Input: s = "pbbcggttciiippooaais", k = 2
      Output: "ps"
  
  
  Constraints:
      1 <= s.length <= 105
      2 <= k <= 104
      s only contains lower case English letters.
  
  
  https://leetcode.com/problems/remove-all-adjacent-duplicates-in-string-ii
  """
  
  class Solution:
      def removeDuplicates(self, s: str, k: int):
          """
          Add characters with their frequencies to a stack [(char, freq)]
          - b4 adding a charcater to the stack, check if the character at the top is similar
              - if so, let its frequency be that of the stack top + 1
              - else, add the character to the stack with a freq of 1
          - after adding, check if the next character is similar to the top of the stack
              - if so, add all similar characters to the stack to get the whole sequence of similar characters
  
          - Try to remove k characters from the stack:
              - if the top of the stack has a frequency of >= k:
                  - continue removing k characters from the stack till the above condition is False
  
          """
          stack = []
          idx = 0
          while idx < len(s):
              # add single character to stack
              self.add_to_stack(stack, s[idx])
              idx += 1
              # try to add similar characters to stack b4 crushing
              while idx < len(s) and stack and s[idx] == stack[-1][0]:
                  self.add_to_stack(stack, s[idx])
                  idx += 1
  
              # Candy Crush 1D
              self.remove_duplicates_from_stack(stack, k)
  
          # after loop
          self.remove_duplicates_from_stack(stack, k)
  
          return "".join([item[0] for item in stack])
  
      def remove_duplicates_from_stack(self, stack, k):
          """Candy Crush 1D"""
          while stack and stack[-1][1] >= k:
              # number_of_ks = stack[-1][1]//k
              for _ in range(k):
                  stack.pop()
  
      def add_to_stack(self, stack, char):
          """Add a single character to the stack"""
          if not stack or stack[-1][0] != char:
              stack.append((char, 1))
          else:
              stack.append((char, stack[-1][1]+1))
  

  # https://leetcode.com/discuss/interview-question/380650/Bloomberg-or-Phone-or-Candy-Crush-1D/1143991
  def add_to_stack(stack, char):
      if not stack or stack[-1][0] != char:
          stack.append((char, 1))
      else:
          stack.append((char, stack[-1][1]+1))
  
  def candy_crush_1d(s):
      stack = []
      idx = 0
      while idx < len(s):
          # add similar characters to stack b4 crushing
          while idx < len(s) and stack and s[idx] == stack[-1][0]:
              add_to_stack(stack, s[idx])
              idx += 1
  
          # crush
          if stack and stack[-1][1] >= 3:
              char = stack[-1][0]
              while stack and stack[-1][0] == char:
                  stack.pop()
  
          # add next
          if idx < len(s):
              add_to_stack(stack, s[idx])
              idx += 1
  
      return "".join([item[0] for item in stack])
  
  S = "aaabbbc"
  print(candy_crush_1d(S))
  
  S = "aabbbacd"
  print(candy_crush_1d(S))
  
  S = "aaabbbacd"
  print(candy_crush_1d(S))
  

• Remove All Adjacent Duplicates in String II/Candy Crush 1D

  """ 
  1209. Remove All Adjacent Duplicates in String II/Candy Crush 1D
  
  You are given a string s and an integer k, a k duplicate removal consists of choosing k adjacent and equal letters from s and removing them, causing the left and the right side of the deleted substring to concatenate together.
  We repeatedly make k duplicate removals on s until we no longer can.
  Return the final string after all such duplicate removals have been made. It is guaranteed that the answer is unique.
  
  Example 1:
      Input: s = "abcd", k = 2
      Output: "abcd"
      Explanation: There's nothing to delete.
  Example 2:
      Input: s = "deeedbbcccbdaa", k = 3
      Output: "aa"
      Explanation: 
      First delete "eee" and "ccc", get "ddbbbdaa"
      Then delete "bbb", get "dddaa"
      Finally delete "ddd", get "aa"
  Example 3:
      Input: s = "pbbcggttciiippooaais", k = 2
      Output: "ps"
  
  
  Constraints:
      1 <= s.length <= 105
      2 <= k <= 104
      s only contains lower case English letters.
  
  
  https://leetcode.com/problems/remove-all-adjacent-duplicates-in-string-ii
  """
  
  class Solution:
      def removeDuplicates(self, s: str, k: int):
          """
          Add characters with their frequencies to a stack [(char, freq)]
          - b4 adding a charcater to the stack, check if the character at the top is similar
              - if so, let its frequency be that of the stack top + 1
              - else, add the character to the stack with a freq of 1
          - after adding, check if the next character is similar to the top of the stack
              - if so, add all similar characters to the stack to get the whole sequence of similar characters
  
          - Try to remove k characters from the stack:
              - if the top of the stack has a frequency of >= k:
                  - continue removing k characters from the stack till the above condition is False
  
          """
          stack = []
          idx = 0
          while idx < len(s):
              # add single character to stack
              self.add_to_stack(stack, s[idx])
              idx += 1
              # try to add similar characters to stack b4 crushing
              while idx < len(s) and stack and s[idx] == stack[-1][0]:
                  self.add_to_stack(stack, s[idx])
                  idx += 1
  
              # Candy Crush 1D
              self.remove_duplicates_from_stack(stack, k)
  
          # after loop
          self.remove_duplicates_from_stack(stack, k)
  
          return "".join([item[0] for item in stack])
  
      def remove_duplicates_from_stack(self, stack, k):
          """Candy Crush 1D"""
          while stack and stack[-1][1] >= k:
              # number_of_ks = stack[-1][1]//k
              for _ in range(k):
                  stack.pop()
  
      def add_to_stack(self, stack, char):
          """Add a single character to the stack"""
          if not stack or stack[-1][0] != char:
              stack.append((char, 1))
          else:
              stack.append((char, stack[-1][1]+1)
  

Monotonic stack

Examples

• Next Greater Element II *

  """
  Next Greater Element II 
  Given a circular integer array nums (i.e., the next element of nums[nums.length - 1] is nums[0]), 
      return the next greater number for every element in nums.
  The next greater number of a number x is the first greater number to its traversing-order next in the array, 
      which means you could search circularly to find its next greater number. If it doesn't exist, return -1 for this number.
  
  Example 1:
      Input: nums = [1,2,1]
      Output: [2,-1,2]
      Explanation: The first 1's next greater number is 2; 
          The number 2 can't find next greater number. 
          The second 1's next greater number needs to search circularly, which is also 2.
  Example 2:
      Input: nums = [1,2,3,4,3]
      Output: [2,3,4,-1,4]
  https://leetcode.com/problems/next-greater-element-ii
  """
  
  """
  Next Greater Element:
  
  Write a function that takes in an array of integers
   and returns a new array containing,at each index,
   the next element in the input array that's greater than the element at that index in the input array.
  In other words, your function should return a new array
   where outputArray[i] is the next element in the input array that's greater than inputArray[i].
  If there's no such next greater element for a particular index,
   the value at that index in the output array should be -1.
  
  For example, given array = [1, 2], your function should return [2, -1].
  Additionally, your function should treat the input array as a circular array.
   A circular array wraps around itself as if it were connected end-to-end.
   So the next index after the last index in a circular array is the first index.
   This means that, for our problem, given array = [0, 0, 5, 0, 0, 3, 0 0],
    the next greater element after 3 is 5, since the array is circular.
  
  Sample Input
      array = [2, 5, -3, -4, 6, 7, 2]
      Sample Output
      [5, 6, 6, 6, 7, -1, 5]
  
  https://www.algoexpert.io/questions/Next%20Greater%20Element
  """
  
  # O(n) time | O(n) space - where n is the length of the array
  def nextGreaterElement00(array):
      res = [-1] * len(array)
  
      # stack used to store the previous smaller numbers that haven't been replaced
      # stored in the form of {'idx': 0, 'val': 0}
      be_replaced_stack = []
  
      for i in range(len(array)*2):  # loop through twice because the array is circular
          array_idx = i % len(array)  # prevent out of bound errors
  
          # check if we have found some values in the be_replaced_stack stack
          #   that is smaller than the current array value array[array_idx]
          #   then replace them (their corresponding values in res)
          while len(be_replaced_stack) > 0 and be_replaced_stack[-1]['val'] < array[array_idx]:
  
              to_be_replaced = be_replaced_stack.pop()['idx']
              res[to_be_replaced] = array[array_idx]
  
          # add the current element to the be_replaced_stack so that it can be checked in the futere for replacement
          be_replaced_stack.append({'idx': array_idx, 'val': array[array_idx]})
  
      return res
  
  # O(n) time | O(n) space - where n is the length of the array
  def nextGreaterElement01(array):
      res = [-1] * len(array)
  
      # stack used to store the previous smaller numbers' indices that haven't been replaced
      be_replaced_stack = []
  
      for i in range(len(array)*2):  # loop through twice because the array is circular
          array_idx = i % len(array)  # prevent out of bound errors
  
          # check if we have found some values in the be_replaced_stack stack
          #   that is smaller than the current array value array[array_idx]
          #   then replace them (their corresponding values in res)
          while len(be_replaced_stack) > 0 and array[be_replaced_stack[-1]] < array[array_idx]:
              res[be_replaced_stack.pop()] = array[array_idx]
  
          # add the current element to the be_replaced_stack so that it can be checked in the futere for replacement
          be_replaced_stack.append(array_idx)
  
      return res
  
  """
  # we will use a stack to keep track of the past values that have not been replaced
  #  once we find a bigger element, we replace them and remove them from the stack
  #  then add the big element to the stack in the hope that it will be replaced
  
  array = [0, 1,  2,  3, 4, 5, 6] <= indices
  array = [2, 5, -3, -4, 6, 7, 2]
  
  ---
  num = 2 (index 0)
  res = [-1, -1, -1, -1, -1, -1, -1]
  stack = [2]
  
  num = 5 (index 1)
  res = [5, -1, -1, -1, -1, -1, -1]
  stack = [5] -> replaced all smaller values in res and the stack
  
  num = -3
  res = [5, -1, -1, -1, -1, -1, -1]
  stack = [5, -3]
  
  num = -4 (index 3)
  res = [5, -1, -1, -1, -1, -1, -1]
  stack = [5, -3, -4]
  
  num = 6 (index 4)
  res = [5, 6, 6, 6, -1, -1, -1]
  stack = [6] -> replaced all smaller values in res and the stack
  
  num = 7 (index 5)
  res = [5, 6, 6, 6, 7, -1, -1]
  stack = [7] -> replaced all smaller values in res and the stack
  
  num = 2 (index 6)
  res = [5, 6, 6, 6, 7, -1, -1]
  stack = [7,2]
  
  num = 2 (index 0)
  res = [5, 6, 6, 6, 7, -1, -1]
  stack = [7,2,2]
  ---
  
  """
  
  # O(n) time | O(n) space - where n is the length of the array
  def nextGreaterElement(array):
      res = [-1] * len(array)
  
      # stack used to store the previous smaller numbers that haven't been replaced
      next_nums_stack = []
  
      # loop through twice because the array is circular
      for i in reversed(range(len(array)*2)):
          array_idx = i % len(array)  # prevent out of bound errors
  
          while len(next_nums_stack) > 0:
              # if value at the top of the stack is smaller than the current value in the array,
              #   remove it from the stack till we find something larger
              if next_nums_stack[-1] <= array[array_idx]:
                  next_nums_stack.pop()
  
              # replace the value in the array by the
              #   value at the top of the stack (if stack[-1] is larger)
              else:
                  res[array_idx] = next_nums_stack[-1]
                  break
  
          # add the current element to the next_nums_stack so that it can be checked in the futere for replacement
          next_nums_stack.append(array[array_idx])
  
      return res
  

---

---

Queues

https://leetcode.com/problems/shortest-subarray-with-sum-at-least-k/discuss/204290/Monotonic-Queue-Summary

To implement a queue, we again need two basic operations: enqueue() and dequeue()

enqueue() operation appends an element to the end of the queue and dequeue() operation removes an element from the beginning of the queue.

Examples

BFS

• Asteroid Collision

  """ 
  735. Asteroid Collision
  
  We are given an array asteroids of integers representing asteroids in a row.
  For each asteroid, the absolute value represents its size, and the sign represents its direction (positive meaning right, negative meaning left). 
  Each asteroid moves at the same speed.
  Find out the state of the asteroids after all collisions. 
  If two asteroids meet, the smaller one will explode. If both are the same size, both will explode. Two asteroids moving in the same direction will never meet.
  
  
  
  Example 1:
      Input: asteroids = [5,10,-5]
      Output: [5,10]
      Explanation: The 10 and -5 collide resulting in 10. The 5 and 10 never collide.
  Example 2:
      Input: asteroids = [8,-8]
      Output: []
      Explanation: The 8 and -8 collide exploding each other.
  Example 3:
      Input: asteroids = [10,2,-5]
      Output: [10]
      Explanation: The 2 and -5 collide resulting in -5. The 10 and -5 collide resulting in 10.
  Example 4:
      Input: asteroids = [-2,-1,1,2]
      Output: [-2,-1,1,2]
      Explanation: The -2 and -1 are moving left, while the 1 and 2 are moving right. Asteroids moving the same direction never meet, so no asteroids will meet each other.
  
  Constraints:
      2 <= asteroids.length <= 104
      -1000 <= asteroids[i] <= 1000
      asteroids[i] != 0
  
  https://leetcode.com/problems/asteroid-collision
  """
  
  from collections import deque
  from typing import List
  
  class Solution:
      def asteroidCollision(self, asteroids: List[int]):
  
          stack = deque()
          for asteroid in asteroids:
              if asteroid > 0:
                  stack.append(asteroid)
                  continue
  
              while asteroid and stack and stack[-1] > 0:
                  if abs(stack[-1]) > abs(asteroid):
                      asteroid = 0
                  elif abs(stack[-1]) == abs(asteroid):
                      stack.pop()
                      asteroid = 0
                  elif abs(stack[-1]) < abs(asteroid):
                      stack.pop()
  
              if asteroid and (not stack or stack[-1] < 0):
                  stack.append(asteroid)
                  asteroid = 0
  
          return list(stack)
  

• Implement Queue using Stacks

  """
  Implement Queue using Stacks:
  
  Implement a first in first out (FIFO) queue using only two stacks.
  The implemented queue should support all the functions of a normal queue (push, peek, pop, and empty).
  Implement the MyQueue class:
      void push(int x) Pushes element x to the back of the queue.
      int pop() Removes the element from the front of the queue and returns it.
      int peek() Returns the element at the front of the queue.
      boolean empty() Returns true if the queue is empty, false otherwise.
  Notes:
  You must use only standard operations of a stack, which means only push to top, peek/pop from top, size, and is empty operations are valid.
  Depending on your language, the stack may not be supported natively. 
  You may simulate a stack using a list or deque (double-ended queue) as long as you use only a stack's standard operations.
  Follow-up: 
  Can you implement the queue such that each operation is amortized O(1) time complexity? 
  In other words, performing n operations will take overall O(n) time even if one of those operations may take longer.
  
  https://leetcode.com/problems/implement-queue-using-stacks
  """
  
  class MyStack:
  
      def __init__(self):
          self.items = []
  
      def push(self, x: int):
          self.items.append(x)
  
      def pop(self):
          return self.items.pop()
  
      def peek(self):
          return self.items[-1]
  
      def empty(self):
          return len(self.items) == 0
  
  class MyQueue:
  
      def __init__(self):
          self.stack = MyStack()
          self.stack_reversed = MyStack()
  
      def push(self, x: int):
          # Push element x to the back of queue.
          self.stack.push(x)
  
      def pop(self):
          # Removes the element from in front of queue and returns that element.
          if self.stack_reversed.empty():
              self._reverse_stack()
  
          return self.stack_reversed.pop()
  
      def peek(self):
          # Get the front element.
          if self.stack_reversed.empty():
              self._reverse_stack()
  
          return self.stack_reversed.peek()
  
      def empty(self):
          # Returns whether the queue is empty.
          return self.stack.empty() and self.stack_reversed.empty()
  
      def _reverse_stack(self):
          # reverse stack one
          while not self.stack.empty():
              self.stack_reversed.push(self.stack.pop())
  
  # Your MyQueue object will be instantiated and called as such:
  # obj = MyQueue()
  # obj.push(x)
  # param_2 = obj.pop()
  # param_3 = obj.peek()
  # param_4 = obj.empty()
  

• Design Circular Queue

  """ 
  622. Design Circular Queue:
  
  Design your implementation of the circular queue. 
  The circular queue is a linear data structure in which the operations are performed based on FIFO (First In First Out) principle 
      and the last position is connected back to the first position to make a circle. 
  It is also called "Ring Buffer".
  
  One of the benefits of the circular queue is that we can make use of the spaces in front of the queue. 
  In a normal queue, once the queue becomes full, we cannot insert the next element even if there is a space in front of the queue. 
  But using the circular queue, we can use the space to store new values.
  
  Implementation the MyCircularQueue class:
      MyCircularQueue(k) Initializes the object with the size of the queue to be k.
      int Front() Gets the front item from the queue. If the queue is empty, return -1.
      int Rear() Gets the last item from the queue. If the queue is empty, return -1.
      boolean enQueue(int value) Inserts an element into the circular queue. Return true if the operation is successful.
      boolean deQueue() Deletes an element from the circular queue. Return true if the operation is successful.
      boolean isEmpty() Checks whether the circular queue is empty or not.
      boolean isFull() Checks whether the circular queue is full or not.
  
  You must solve the problem without using the built-in queue data structure in your programming language. 
  
  Example 1:
      Input
          ["MyCircularQueue", "enQueue", "enQueue", "enQueue", "enQueue", "Rear", "isFull", "deQueue", "enQueue", "Rear"]
          [[3], [1], [2], [3], [4], [], [], [], [4], []]
      Output
          [null, true, true, true, false, 3, true, true, true, 4]
      Explanation
          MyCircularQueue myCircularQueue = new MyCircularQueue(3);
          myCircularQueue.enQueue(1); // return True
          myCircularQueue.enQueue(2); // return True
          myCircularQueue.enQueue(3); // return True
          myCircularQueue.enQueue(4); // return False
          myCircularQueue.Rear();     // return 3
          myCircularQueue.isFull();   // return True
          myCircularQueue.deQueue();  // return True
          myCircularQueue.enQueue(4); // return True
          myCircularQueue.Rear();     // return 4
  """
  
  class MyCircularQueue:
  
      def __init__(self, k: int):
          self.store = [None] * k
          self.start = 0
          self.items_count = 0
  
      def enQueue(self, value: int):
          if self.isFull():
              return False
  
          if self.isEmpty():
              self.store[self.start] = value
          else:
              next_idx = self._getEndIdx() + 1
              next_idx %= len(self.store)
              self.store[next_idx] = value
  
          self.items_count += 1
          return True
  
      def deQueue(self):
          if self.isEmpty():
              return False
  
          self.store[self.start] = None
          self.start += 1
          self.start %= len(self.store)
  
          self.items_count -= 1
          return True
  
      def Front(self):
          if self.isEmpty():
              return -1
          return self.store[self.start]
  
      def Rear(self):
          if self.isEmpty():
              return -1
          return self.store[self._getEndIdx()]
  
      def isEmpty(self):
          return self.items_count == 0
  
      def isFull(self):
          return self.items_count == len(self.store)
  
      def _getEndIdx(self):
          return (self.start + self.items_count - 1) % len(self.store)
  
  # Your MyCircularQueue object will be instantiated and called as such:
  # obj = MyCircularQueue(k)
  # param_1 = obj.enQueue(value)
  # param_2 = obj.deQueue()
  # param_3 = obj.Front()
  # param_4 = obj.Rear()
  # param_5 = obj.isEmpty()
  # param_6 = obj.isFull()
  

• Animal Shelter

  

---

Monotonic Queue

Examples

• Sliding Window Maximum

  

  """ 
  239. Sliding Window Maximum
  
  You are given an array of integers nums, there is a sliding window of size k which is moving from the very left of the array to the very right. 
  You can only see the k numbers in the window. Each time the sliding window moves right by one position.
  Return the max sliding window.
  
  Example 1:
      Input: nums = [1,3,-1,-3,5,3,6,7], k = 3
      Output: [3,3,5,5,6,7]
      Explanation: 
          Window position                Max
          ---------------               -----
          [1  3  -1] -3  5  3  6  7       3
          1 [3  -1  -3] 5  3  6  7       3
          1  3 [-1  -3  5] 3  6  7       5
          1  3  -1 [-3  5  3] 6  7       5
          1  3  -1  -3 [5  3  6] 7       6
          1  3  -1  -3  5 [3  6  7]      7
  Example 2:
      Input: nums = [1], k = 1
      Output: [1]
  Example 3:
      Input: nums = [1,-1], k = 1
      Output: [1,-1]
  Example 4:
      Input: nums = [9,11], k = 2
      Output: [11]
  Example 5:
      Input: nums = [4,-2], k = 2
      Output: [4]
  
  https://leetcode.com/problems/sliding-window-maximum
  """
  
  from typing import List
  from collections import deque
  
  class Solution:
      def maxSlidingWindow(self, nums: List[int], k: int):
          """ 
          - have a double-ended-queue
          - for each element in the array:
              - clean deque
                  - remove the elements that are out of the window's bounds from the left of the deque
                  - remove all elements that are smaller than the element from the right of the deque
              - add the element to the deque
              - the largest element in this window is the leftmost element
          """
          result = []
  
          de_queue = deque()
          # add first k-1 elements
          for idx in range(k-1):
              while de_queue and nums[de_queue[-1]] <= nums[idx]:
                  de_queue.pop()
              de_queue.append(idx)
  
          for idx in range(k-1, len(nums)):
              # remove not in window
              if de_queue and de_queue[0] <= idx-k:
                  de_queue.popleft()
  
              # remove smaller
              while de_queue and nums[de_queue[-1]] <= nums[idx]:
                  de_queue.pop()
  
              # add the element to the deque & the largest element in this window is the left-most element
              de_queue.append(idx)
              result.append(nums[de_queue[0]])
  
          return result
  

---

collections.deque()

How to use a deque in Python

Can be used as both a stack and a queue:

• Stack: pop()
• Queue: popleft()

Here’s a summary of the main characteristics of deque:

• Stores items of any data type
• Is a mutable data type
• Supports membership operations with the in operator
• Supports indexing, like in a_deque[i]
• Doesn’t support slicing, like in a_deque[0:2]
• Supports built-in functions that operate on sequences and iterables, such as [len()](https://docs.python.org/3/library/functions.html#len), [sorted()](https://realpython.com/python-sort/), [reversed()](https://realpython.com/python-reverse-list/), and more
• Doesn’t support in-place sorting
• Supports normal and reverse iteration
• Supports pickling with [pickle](https://realpython.com/python-pickle-module/)
• Ensures fast, memory-efficient, and thread-safe pop and append operations on both ends

Creating deque instances is a straightforward process. You just need to import deque from collections and call it with an optional iterable as an argument:

>>> from collections import deque

>>> # Create an empty deque
>>> deque()
deque([])

>>> # Use different iterables to create deques
>>> deque((1, 2, 3, 4))
deque([1, 2, 3, 4])

>>> deque([1, 2, 3, 4])
deque([1, 2, 3, 4])

>>> deque(range(1, 5))
deque([1, 2, 3, 4])

>>> deque("abcd")
deque(['a', 'b', 'c', 'd'])

>>> numbers = {"one": 1, "two": 2, "three": 3, "four": 4}
>>> deque(numbers.keys())
deque(['one', 'two', 'three', 'four'])

>>> deque(numbers.values())
deque([1, 2, 3, 4])

>>> deque(numbers.items())
deque([('one', 1), ('two', 2), ('three', 3), ('four', 4)])

import collections

# Create a deque
DoubleEnded = collections.deque(["Mon","Tue","Wed"])
print(DoubleEnded)

# Append to the right
print("Adding to the right: ")
DoubleEnded.append("Thu")
print(DoubleEnded)

# append to the left
print("Adding to the left: ")
DoubleEnded.appendleft("Sun")
print(DoubleEnded)

# Remove from the right
print("Removing from the right: ")
DoubleEnded.pop()
print(DoubleEnded)

# Remove from the left
print("Removing from the left: ")
DoubleEnded.popleft()
print(DoubleEnded)

# Reverse the dequeue
print("Reversing the deque: ")
DoubleEnded.reverse()
print(DoubleEnded)

""" 
deque(['Mon', 'Tue', 'Wed'])

Adding to the right: 
deque(['Mon', 'Tue', 'Wed', 'Thu'])

Adding to the left: 
deque(['Sun', 'Mon', 'Tue', 'Wed', 'Thu'])

Removing from the right: 
deque(['Sun', 'Mon', 'Tue', 'Wed'])

Removing from the left: 
deque(['Mon', 'Tue', 'Wed'])

Reversing the deque: 
deque(['Wed', 'Tue', 'Mon'])
"""

If you instantiate deque without providing an iterable as an argument, then you get an empty deque. If you

---

---

Heaps

Priority queues

---

---

Find the original version of this page (with additional content) on Notion here.

---

---

Last update: December 13, 2021 16:05:48
Created: December 13, 2021 16:05:48

Authors: paulonteri (99.74%), Not Committed Yet (0.26%)