Trees & Graphs
General Trees
Tree question pattern ||2021 placement - LeetCode Discuss
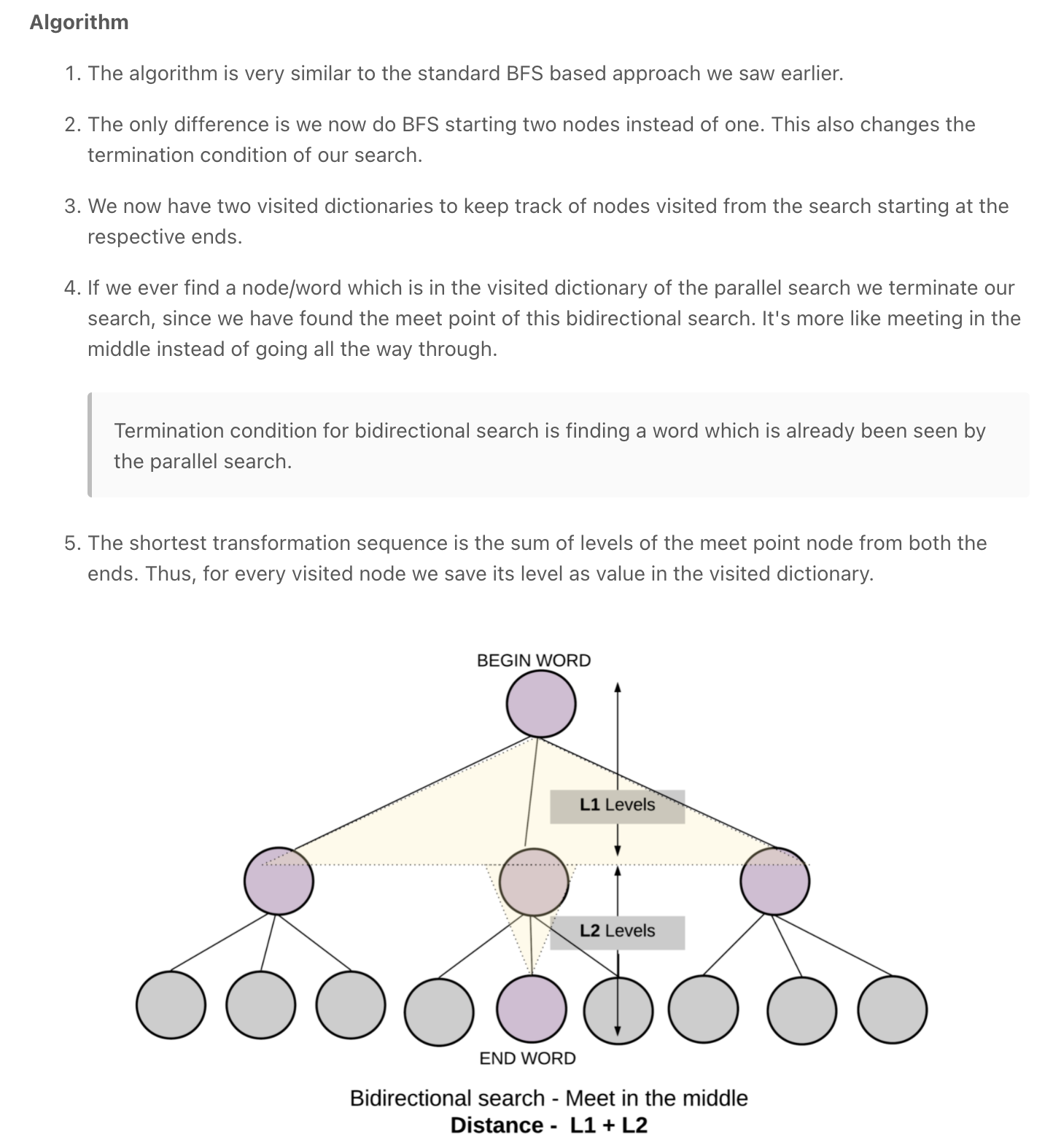
DFS, BFS & Bidirectional Search
Examples
-
Youngest Common Ancestor
""" Youngest Common Ancestor: You're given three inputs, all of which are instances of an AncestralTree class that have an ancestor property pointing to their youngest ancestor. The first input is the top ancestor in an ancestral tree (i.e., the only instance that has no ancestor--its ancestor property points to None / null), and the other two inputs are descendants in the ancestral tree. Write a function that returns the youngest common ancestor to the two descendants. Note that a descendant is considered its own ancestor. So in the simple ancestral tree below, the youngest common ancestor to nodes A and B is node A. https://www.algoexpert.io/questions/Youngest%20Common%20Ancestor """ # This is an input class. Do not edit. # class AncestralTree: # def __init__(self, name): # self.name = name # self.ancestor = None # O(d) time | O(d) space - where d is the depth (height) of the ancestral tree def getYoungestCommonAncestor00(topAncestor, descendantOne, descendantTwo): set_one = set() set_two = set() while descendantOne is not None or descendantTwo is not None: if descendantOne is not None: if descendantOne in set_two: return descendantOne # we do this before doing the two checks because any of them has to be ahead set_one.add(descendantOne) descendantOne = descendantOne.ancestor if descendantTwo is not None: if descendantTwo in set_one: return descendantTwo set_two.add(descendantTwo) descendantTwo = descendantTwo.ancestor # O(d) time | O(1) space - where d is the depth (height) of the ancestral tree def getYoungestCommonAncestor01(topAncestor, descendantOne, descendantTwo): depth_one = getNodeDepth(topAncestor, descendantOne) depth_two = getNodeDepth(topAncestor, descendantTwo) # put nodes at the same depth one = descendantOne two = descendantTwo if depth_one > depth_two: one = moveNodeUp(descendantOne, (depth_one-depth_two)) else: two = moveNodeUp(descendantTwo, (depth_two-depth_one)) # move nodes upward together while one != two: one = one.ancestor two = two.ancestor return one # or two (they are now equal) def getNodeDepth(topAncestor, node): depth = 0 while node is not topAncestor: depth += 1 node = node.ancestor return depth def moveNodeUp(node, dist): while dist > 0: node = node.ancestor dist -= 1 return node -
Lowest Common Manager
""" Lowest Common Manager: You're given three inputs, all of which are instances of an OrgChart class that have a directReports property pointing to their direct reports. The first input is the top manager in an organizational chart (i.e., the only instance that isn't anybody else's direct report), and the other two inputs are reports in the organizational chart. The two reports are guaranteed to be distinct. Write a function that returns the lowest common manager to the two reports. Sample Input // From the organizational chart below. topManager = Node A reportOne = Node E reportTwo = Node I A / \ B C / \ / \ D E F G / \ H I Sample Output Node B https://www.algoexpert.io/questions/Lowest%20Common%20Manager """ # This is an input class. Do not edit. class OrgChart: def __init__(self, name): self.name = name self.directReports = [] def getLowestCommonManager1(top_manager, report_one, report_two): common_manager = [None] getManagers(top_manager, report_one, report_two, common_manager) return common_manager[0] def getManagers(curr, report_one, report_two, common_manager): count = 0 # one of them is the common ancestor edge case if curr == report_one or curr == report_two: count = 1 for report in curr.directReports: count += getManagers(report, report_one, report_two, common_manager) if common_manager[0] == None and count == 2: common_manager[0] = curr return count """ """ class TreeInfo: def __init__(self, lowest_common_manager=None): self.lowest_common_manager = lowest_common_manager def getLowestCommonManager(topManager, reportOne, reportTwo): treeInfo = TreeInfo() getLowestCommonManagerHelper(topManager, reportOne, reportTwo, treeInfo) return treeInfo.lowest_common_manager def getLowestCommonManagerHelper(curr, reportOne, reportTwo, treeInfo): if not curr: return False found = curr == reportOne or curr == reportTwo for child in curr.directReports: child_found = getLowestCommonManagerHelper(child, reportOne, reportTwo, treeInfo) if found and child_found: treeInfo.lowest_common_manager = curr return False found = found or child_found return found
Bidirectional Search
Graphs/Networks
Graph Search Algorithms in 100 Seconds - And Beyond with JS
Graph Data Structure: Directed, Acyclic, etc | Interview Cake
List of graph algorithms for coding interview - LeetCode Discuss
Graph For Beginners [Problems | Pattern | Sample Solutions] - LeetCode Discuss
Topological Sort (for graphs) *
A tree is actually a type of graph, but not all graphs are trees. Simply put, a tree is a connected graph without cycles.
Examples
It can be helpful to go through 2D array problems
-
Accounts Merge
""" Accounts Merge: Given a list of accounts where each element accounts[i] is a list of strings, where the first element accounts[i][0] is a name, and the rest of the elements are emails representing emails of the account. Now, we would like to merge these accounts. Two accounts definitely belong to the same person if there is some common email to both accounts. Note that even if two accounts have the same name, they may belong to different people as people could have the same name. A person can have any number of accounts initially, but all of their accounts definitely have the same name. After merging the accounts, return the accounts in the following format: the first element of each account is the name, and the rest of the elements are emails in sorted order. The accounts themselves can be returned in any order. Example 1: Input: accounts = [["John","[email protected]","[email protected]"],["John","[email protected]","[email protected]"],["Mary","[email protected]"],["John","[email protected]"]] Output: [["John","[email protected]","[email protected]","[email protected]"],["Mary","[email protected]"],["John","[email protected]"]] Explanation: The first and second John's are the same person as they have the common email "[email protected]". The third John and Mary are different people as none of their email addresses are used by other accounts. We could return these lists in any order, for example the answer [['Mary', '[email protected]'], ['John', '[email protected]'], ['John', '[email protected]', '[email protected]', '[email protected]']] would still be accepted. Example 2: Input: accounts = [["Gabe","[email protected]","[email protected]","[email protected]"],["Kevin","[email protected]","[email protected]","[email protected]"],["Ethan","[email protected]","[email protected]","[email protected]"],["Hanzo","[email protected]","[email protected]","[email protected]"],["Fern","[email protected]","[email protected]","[email protected]"]] Output: [["Ethan","[email protected]","[email protected]","[email protected]"],["Gabe","[email protected]","[email protected]","[email protected]"],["Hanzo","[email protected]","[email protected]","[email protected]"],["Kevin","[email protected]","[email protected]","[email protected]"],["Fern","[email protected]","[email protected]","[email protected]"]] https://leetcode.com/problems/accounts-merge """ import collections """ -------------------- Problem -------------------- accounts[i][0] is a name, and the rest of the elements are emails Two accounts definitely belong to the same person if there is some common email to both accounts Note that even if two accounts have the same name, they may belong to different people as people could have the same name. A person can have any number of accounts initially, but all of their accounts definitely have the same name. -------------------- Examples -------------------- accounts = [ ["John","[email protected]","[email protected]"], ["John","[email protected]","[email protected]"], ["Mary","[email protected]"], ["John","[email protected]"]] Output: [ ["John","[email protected]","[email protected]","[email protected]"], ["Mary","[email protected]"], ["John","[email protected]"]] -------------------- Brute force -------------------- O(n^2) time | O(n) space - for every account, look for duplicates -------------------- Optimal -------------------- - build undirected cyclic graph of the emails - dfs/bfs returning all connected emails - add name to connected emails [["D","[email protected]","[email protected]","[email protected]","[email protected]"],["D","[email protected]","[email protected]"],["D","[email protected]","[email protected]"],["D","[email protected]","[email protected]"],["D","[email protected]","[email protected]"]] [ ["D","[email protected]","[email protected]","[email protected]","[email protected]"], ["D","[email protected]","[email protected]"], ["D","[email protected]","[email protected]"], ["D","[email protected]","[email protected]"] ["D","[email protected]","[email protected]"], ["D","[email protected]","[email protected]"] ] (only using the number part of the email) # use the first email as the original key and let the others point to it --- idx 0 ["D","[email protected]","[email protected]","[email protected]","[email protected]"] 0:[1,9,8]* 1:[0]* 9:[0]* 8:[0]* --- ["D","[email protected]","[email protected]"] 0:[1,9,8] 1:[0] 9:[0] 8:[0] 3:[4]* 4:[3]* --- ["D","[email protected]","[email protected]"] 0:[1,9,8] 1:[0] 9:[0] 8:[0] 3:[4] 4:[3,5]* 5:[4]* --- ["D","[email protected]","[email protected]"] 0:[1,9,8] 1:[0] 9:[0] 8:[0] 3:[4] 4:[3,5] 5:[4] 6:[8]* 8:[6]* --- ["D","[email protected]","[email protected]"], 0:[1,9,8] 1:[0] 9:[0] 8:[0] 3:[4,2]* 4:[3,5] 5:[4] 6:[8] 8:[6] 2:[3]* --- ["D","[email protected]","[email protected]"] 0:[1,9,8] 1:[0,2] * 9:[0] 8:[0] 3:[4,2] 4:[3,5] 5:[4] 6:[8] 8:[6] 2:[3,1] * --- after dfs [0,1,2,3,4,5,9,8] [6,8] """ class Solution: def accountsMerge(self, accounts): result = [] email_to_name = {} graph = collections.defaultdict(list) # Adjacency List for account in accounts: name = account[0] main_email = account[1] # add emails to graph for idx in range(1, len(account)): # point to each other graph[main_email].append(account[idx]) graph[account[idx]].append(main_email) # save name email_to_name[account[idx]] = name visited = set() for node in graph: emails_found = set() self.dfs(graph, node, visited, emails_found) if emails_found: sorted_emails = sorted(list(emails_found)) name = email_to_name[sorted_emails[0]] result.append([name]+sorted_emails) return result def dfs(self, graph, node, visited, emails_found): if node in visited: return visited.add(node) # add node to emails_found emails_found.add(node) for email in graph[node]: self.dfs(graph, email, visited, emails_found) -
Word Ladder **

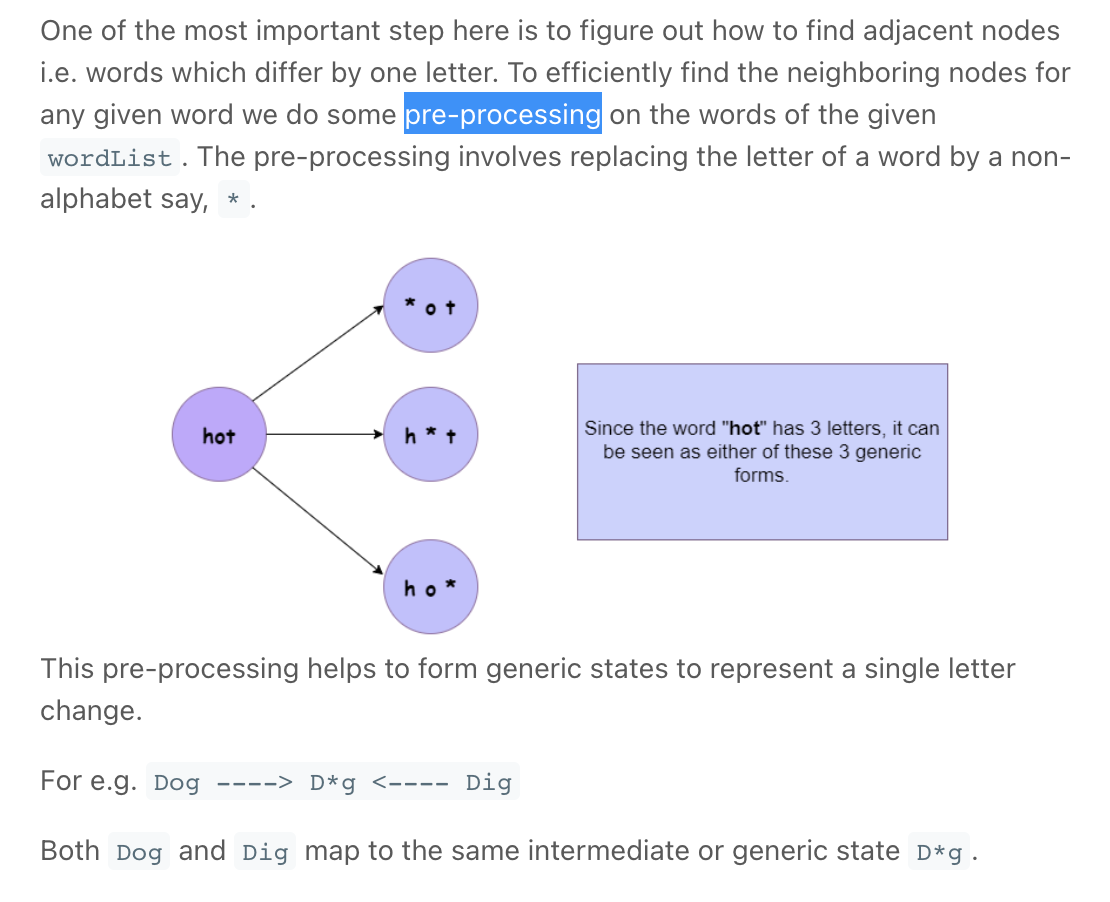

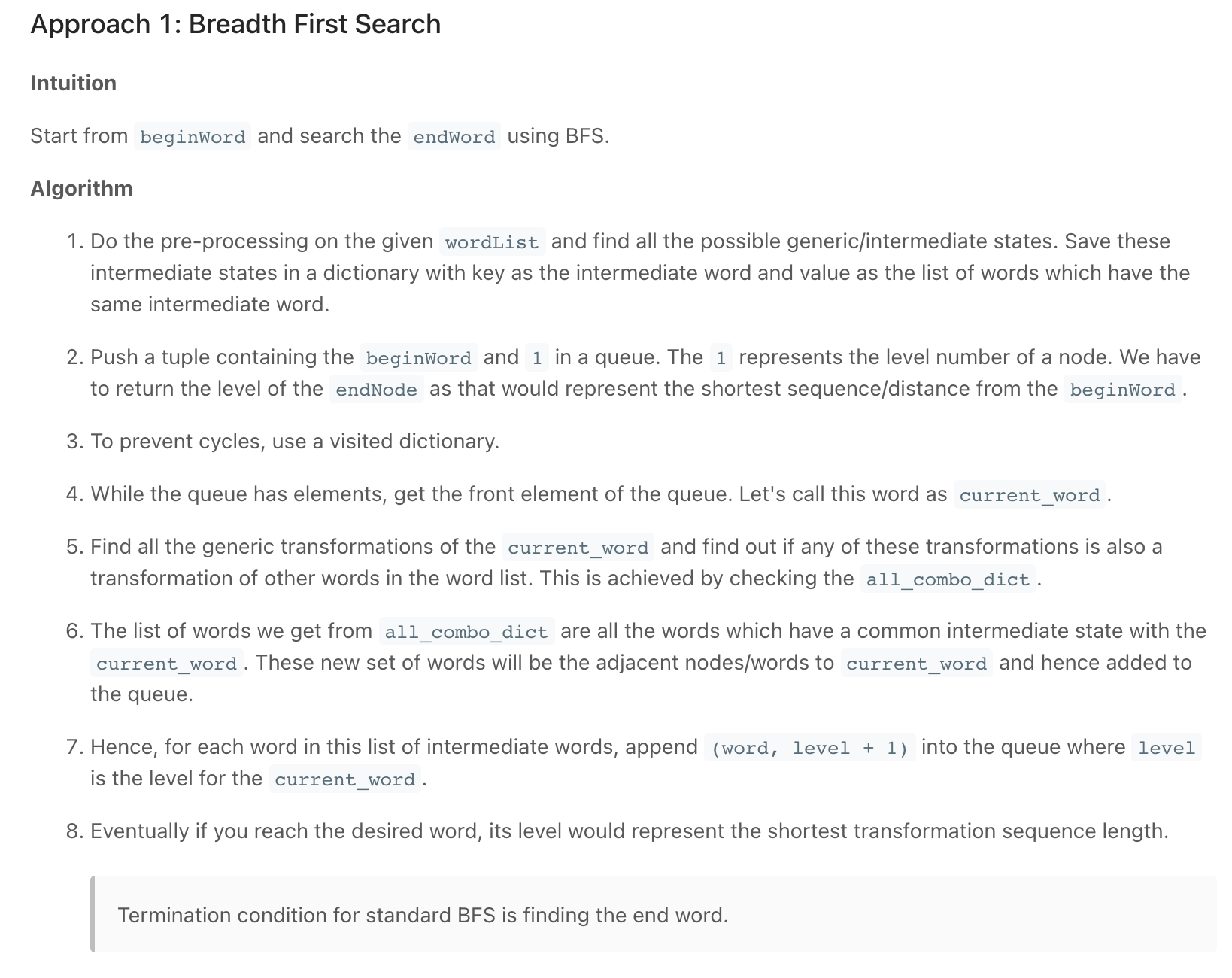
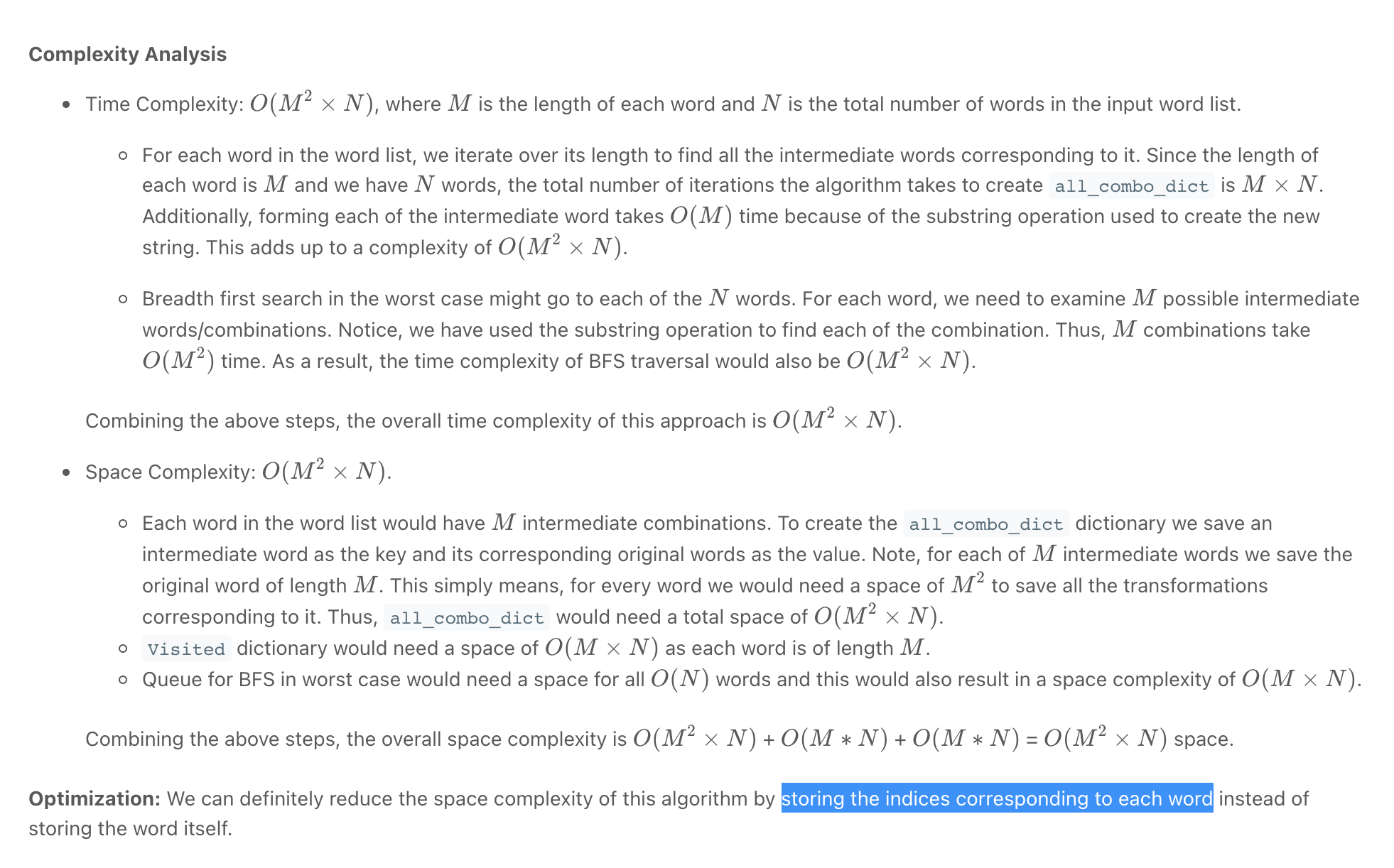

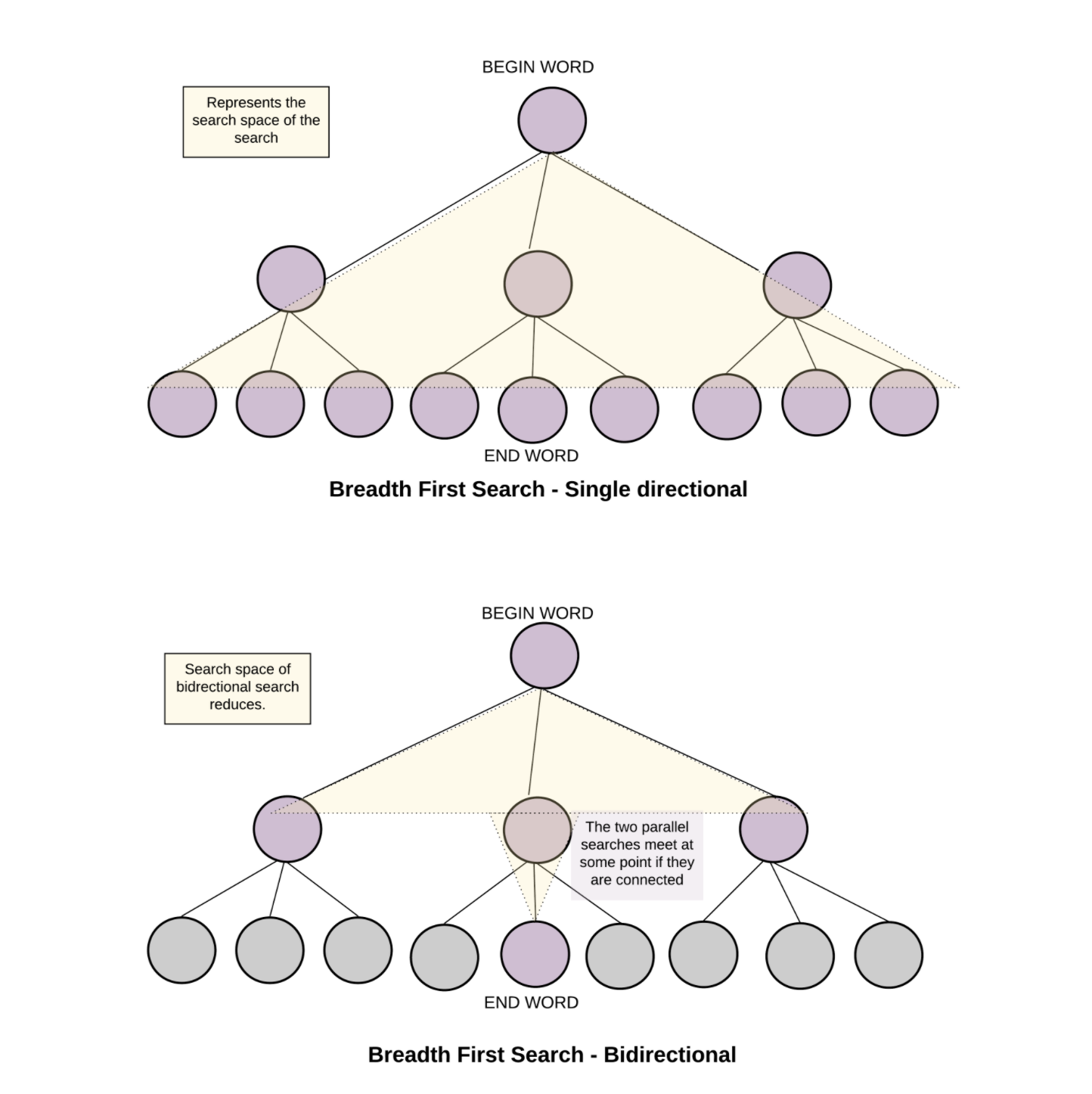

""" 127. Word Ladder A transformation sequence from word beginWord to word endWord using a dictionary wordList is a sequence of words beginWord -> s1 -> s2 -> ... -> sk such that: Every adjacent pair of words differs by a single letter. Every si for 1 <= i <= k is in wordList. Note that beginWord does not need to be in wordList. sk == endWord Given two words, beginWord and endWord, and a dictionary wordList, return the number of words in the shortest transformation sequence from beginWord to endWord, or 0 if no such sequence exists. Example 1: Input: beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log","cog"] Output: 5 Explanation: One shortest transformation sequence is "hit" -> "hot" -> "dot" -> "dog" -> cog", which is 5 words long. Example 2: Input: beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log"] Output: 0 Explanation: The endWord "cog" is not in wordList, therefore there is no valid transformation sequence. Constraints: 1 <= beginWord.length <= 10 endWord.length == beginWord.length 1 <= wordList.length <= 5000 wordList[i].length == beginWord.length beginWord, endWord, and wordList[i] consist of lowercase English letters. beginWord != endWord All the words in wordList are unique. https://leetcode.com/problems/word-ladder """ from collections import defaultdict, deque from typing import List """ https://www.notion.so/paulonteri/Trees-Graphs-edc3401e06c044f29a2d714d20ffe185#6f533b3f9c35463492e9378f632ef22b """ # N is the number of words, W is the length of the longest word, # Preprocess: process N words taking W time for each (N*W), forming each word takes W time. Total (N*W^2) time # BSF: might visit N words and at each word we need to examine need to examine M different combinations (creating them will take W^2 time). Total (N*W^2) time class Solution: def ladderLength(self, beginWord: str, endWord: str, wordList: List[str]): # preprocess words (record all words with a certain pattern/transformation) word_transfms = defaultdict(list) for word in wordList: for word_transfm in self.get_word_transf(word): word_transfms[word_transfm].append(word) # BFS (find shortest path) visited = set() queue = deque() queue.append((beginWord, 1)) while queue: word, dist = queue.popleft() # reached end if word == endWord: return dist # add neighbours to queue for word_transfm in self.get_word_transf(word): for next_word in word_transfms[word_transfm]: if next_word in visited: continue queue.append((next_word, dist+1)) visited.add(word) return 0 def get_word_transf(self, word): word_transformations = [] for idx in range(len(word)): word_transformations.append(word[:idx]+"*"+word[idx+1:]) return word_transformations -
Course Schedule/Tasks Scheduling
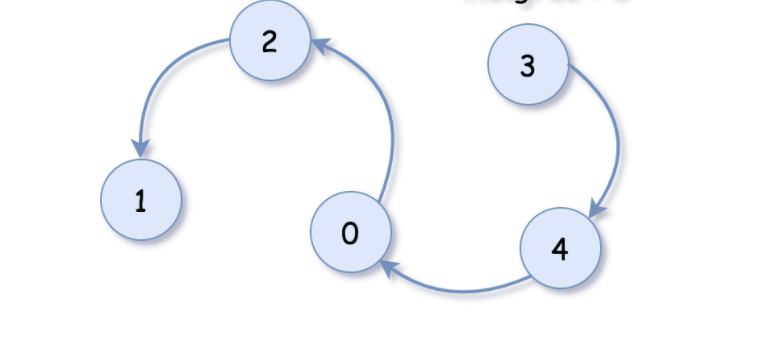
-
Minimum Passes Of Matrix
""" Minimum Passes Of Matrix: Write a function that takes in an integer matrix of potentially unequal height and width and returns the minimum number of passes required to convert all negative integers in the matrix to positive integers. A negative integer in the matrix can only be converted to a positive integer if one or more of its adjacent elements is positive. An adjacent element is an element that is to the left, to the right, above, or below the current element in the matrix. Converting a negative to a positive simply involves multiplying it by -1. Note that the 0 value is neither positive nor negative, meaning that a 0 can't convert an adjacent negative to a positive. A single pass through the matrix involves converting all the negative integers that can be converted at a particular point in time. For example, consider the following input matrix: [ [0, -2, -1], [-5, 2, 0], [-6, -2, 0], ] After a first pass, only 3 values can be converted to positives: [ [0, 2, -1], [5, 2, 0], [-6, 2, 0], ] After a second pass, the remaining negative values can all be converted to positives: [ [0, 2, 1], [5, 2, 0], [6, 2, 0], ] Note that the input matrix will always contain at least one element. If the negative integers in the input matrix can't all be converted to positives, regardless of how many passes are run, your function should return -1. Sample Input matrix = [ [0, -1, -3, 2, 0], [1, -2, -5, -1, -3], [3, 0, 0, -4, -1], ] Sample Output 3 https://www.algoexpert.io/questions/Minimum%20Passes%20Of%20Matrix """ """ - res = 0 - add all positive numbers to a queue - for each number in the queue: - remove it from the queue - convert all positive neighbours to positive and add them to the next queue - if a number was converted, increment res by one - repeat these steps until the queue is empty """ def minimumPassesOfMatrix(matrix): number = removeNegatives(matrix) for row in range(len(matrix)): for col in range(len(matrix[0])): # negative not removed if matrix[row][col] < 0: return -1 return number def removeNegatives(matrix): res = 0 queue = [] # create initial queue for row in range(len(matrix)): for col in range(len(matrix[0])): if matrix[row][col] > 0: queue.append((row, col)) # remove negatives while queue: has_negative = False for _ in range(len(queue)): row, col = queue.pop(0) # left if col-1 >= 0 and matrix[row][col-1] < 0: has_negative = True matrix[row][col-1] = matrix[row][col-1] * -1 queue.append((row, col-1)) # right if col+1 < len(matrix[0]) and matrix[row][col+1] < 0: has_negative = True matrix[row][col+1] = matrix[row][col+1] * -1 queue.append((row, col+1)) # above if row-1 >= 0 and matrix[row-1][col] < 0: has_negative = True matrix[row-1][col] = matrix[row-1][col] * -1 queue.append((row-1, col)) # below if row+1 < len(matrix) and matrix[row+1][col] < 0: has_negative = True matrix[row+1][col] = matrix[row+1][col] * -1 queue.append((row+1, col)) if has_negative: res += 1 return res -
Cycle In Graph
""" Cycle In Graph: You're given a list of edges representing an unweighted, directed graph with at least one node. Write a function that returns a boolean representing whether the given graph contains a cycle. For the purpose of this question, a cycle is defined as any number of vertices, including just one vertex, that are connected in a closed chain. A cycle can also be defined as a chain of at least one vertex in which the first vertex is the same as the last. The given list is what's called an adjacency list, and it represents a graph. The number of vertices in the graph is equal to the length of edges, where each index i in edges contains vertex i's outbound edges, in no particular order. Each individual edge is represented by a positive integer that denotes an index (a destination vertex) in the list that this vertex is connected to. Note that these edges are directed, meaning that you can only travel from a particular vertex to its destination, not the other way around (unless the destination vertex itself has an outbound edge to the original vertex). Also note that this graph may contain self-loops. A self-loop is an edge that has the same destination and origin; in other words, it's an edge that connects a vertex to itself. For the purpose of this question, a self-loop is considered a cycle. Sample Input edges = [ [1, 3], [2, 3, 4], [0], [], [2, 5], [], ] Sample Output true // There are multiple cycles in this graph: // 1) 0 -> 1 -> 2 -> 0 // 2) 0 -> 1 -> 4 -> 2 -> 0 // 3) 1 -> 2 -> 0 -> 1 // These are just 3 examples; there are more. https://www.algoexpert.io/questions/Cycle%20In%20Graph """ # ---------------------------------------------------------------------------------------------------------------------------------------------------------------- def cycleInGraph0(edges): # # start dfs at each vertex -> loop can start anywhere # handles case where vertex 0 = [] for i in range(len(edges)): # can be optimised by storing each vertex's result in a hash table if dfs0(edges, set(), i): return True return False # we use the visited set to keep track of the vertices currently in the recursive stack def dfs0(edges, visited, vertex): if vertex in visited: return True # backtracking visited.add(vertex) found_cycle = False for nxt in edges[vertex]: found_cycle = found_cycle or dfs0(edges, visited, nxt) # note visited.discard(vertex) return found_cycle # ---------------------------------------------------------------------------------------------------------------------------------------------------------------- # O(v + e) time | O(v) space - where v is the number of vertices and e is the number of edges in the graph # time -> basic DFS (we have to consider all the vertices & edges) def cycleInGraph(edges): # # start dfs at each vertex -> loop can start anywhere # handles case where vertex 0 = [] cache = {} for i in range(len(edges)): if dfs(edges, cache, set(), i): return True return False # we use the visited set to keep track of the vertices currently in the recursive stack def dfs(edges, cache, visited, vertex): if vertex in cache: return cache[vertex] if vertex in visited: # repeated (found cycle) return True # backtracking visited.add(vertex) found_cycle = False for nxt in edges[vertex]: found_cycle = found_cycle or dfs(edges, cache, visited, nxt) # note visited.discard(vertex) cache[vertex] = found_cycle return cache[vertex] """ edges = [ [1, 3], [2, 3, 4], [0], [], [2, 5], [], ] if starting at 0 visited = {} vertex = 0 visited = {0} vertex = 1 visited = {0,1} vertex = 2 visited = {0,1,2} vertex = 0 """ -
Remove Islands
""" Remove Islands: You're given a two-dimensional array (a matrix) of potentially unequal height and width containing only 0s and 1s. The matrix represents a two-toned image, where each 1 represents black and each 0 represents white. An island is defined as any number of 1s that are horizontally or vertically adjacent (but not diagonally adjacent) and that don't touch the border of the image. In other words, a group of horizontally or vertically adjacent 1s isn't an island if any of those 1s are in the first row, last row, first column, or last column of the input matrix. Note that an island can twist. In other words, it doesn't have to be a straight vertical line or a straight horizontal line; it can be L-shaped, for example. You can think of islands as patches of black that don't touch the border of the two-toned image. Write a function that returns a modified version of the input matrix, where all of the islands are removed. You remove an island by replacing it with 0s. Naturally, you're allowed to mutate the input matrix. https://www.algoexpert.io/questions/Remove%20Islands """ # O(wh) time | O(wh) space - where w and h # are the width and height of the input matrix def removeIslands(matrix): for row in range(1, len(matrix)-1): for col in range(1, len(matrix[0])-1): if matrix[row][col] == 1 and isIsland(matrix, row, col): removeOneIsland(matrix, row, col) return matrix def isIsland(matrix, row, col): # check if not island if matrix[row][col] != 1 or \ row <= 0 or col <= 0 or \ row >= len(matrix)-1 or col >= len(matrix[0])-1: return False matrix[row][col] = -1 # mark # check if still island up = True if row - 1 >= 0 and matrix[row-1][col] == 1: up = isIsland(matrix, row-1, col) down = True if row + 1 < len(matrix) and matrix[row+1][col] == 1: down = isIsland(matrix, row+1, col) left = True if col - 1 >= 0 and matrix[row][col-1] == 1: left = isIsland(matrix, row, col-1) right = True if col + 1 < len(matrix[0]) and matrix[row][col+1] == 1: right = isIsland(matrix, row, col+1) matrix[row][col] = 1 # unmark return left and right and down and up def removeOneIsland(matrix, row, col): if matrix[row][col] == 1: matrix[row][col] = 0 # remove # down if matrix[row+1][col] == 1: removeOneIsland(matrix, row+1, col) # left if matrix[row][col-1] == 1: removeOneIsland(matrix, row, col-1) # right if matrix[row][col+1] == 1: removeOneIsland(matrix, row, col+1) # Solution: # 1. iterate through every element in the matrix # 2. chsck if valid island # 3. if valid island, remove the island def checkIfIsland(matrix, row, col): is_at_end = row <= 0 or col <= 0 or \ row >= len(matrix)-1 or col >= len(matrix[0])-1 if is_at_end or matrix[row][col] != 1: return False matrix[row][col] = -1 # mark right = left = up = down = True # checks to ensure we don't run into a loop if matrix[row][col+1] == 1: # right right = checkIfIsland(matrix, row, col+1) if matrix[row][col-1] == 1: # left left = checkIfIsland(matrix, row, col-1) if matrix[row+1][col] == 1: # up up = checkIfIsland(matrix, row+1, col) if matrix[row-1][col] == 1: # down down = checkIfIsland(matrix, row-1, col) matrix[row][col] = 1 # unmark return left and right and up and down def removeAnIsland(matrix, row, col): if matrix[row][col] == 1: matrix[row][col] = 0 # remove # checks to ensure we don't run into a loop # down if matrix[row+1][col] == 1: removeAnIsland(matrix, row+1, col) # left if matrix[row][col-1] == 1: removeAnIsland(matrix, row, col-1) # right if matrix[row][col+1] == 1: removeAnIsland(matrix, row, col+1) def removeIslands2(matrix): for row in range(len(matrix)): for col in range(len(matrix[0])): if checkIfIsland(matrix, row, col): removeAnIsland(matrix, row, col) return matrix """ Sample Input matrix = [ [1, 0, 0, 0, 0, 0], [0, 1, 0, 1, 1, 1], [0, 0, 1, 0, 1, 0], [1, 1, 0, 0, 1, 0], [1, 0, 1, 1, 0, 0], [1, 0, 0, 0, 0, 1] ] Sample Output [ [1, 0, 0, 0, 0, 0], [0, 0, 0, 1, 1, 1], [0, 0, 0, 0, 1, 0], [1, 1, 0, 0, 1, 0], [1, 0, 0, 0, 0, 0], [1, 0, 0, 0, 0, 1] ] // The islands that were removed can be clearly seen here: // [ // [ , , , , , ], // [ , 1, , , , ], // [ , , 1, , , ], // [ , , , , , ], // [ , , 1, 1, , ], // [ , , , , , ] // ] matrix = [[1, 0, 0, 0, 0, 0], [0, 0, 0, 1, 1, 1], [0, 0, 0, 0, 1, 0], [1, 1, 0, 0, 1, 0], [1, 0, 0, 0, 0, 0], [1, 0, 0, 0, 0, 1] ] matrix_2 = [ [1, 0, 0, 0, 0, 0], [0, 1, 0, 1, 1, 1], [0, 0, 1, 0, 1, 0], [1, 1, 0, 0, 1, 0], [1, 0, 1, 1, 0, 0], [1, 0, 0, 0, 0, 1] ] """ mx = [ [1, 0, 0, 0, 0, 0], [0, 1, 0, 1, 1, 1], [0, 0, 1, 0, 1, 0], [1, 1, 0, 0, 1, 0], [1, 0, 1, 1, 0, 0], [1, 0, 0, 0, 0, 1] ] print(removeIslands(mx)) -
River Sizes
""" River Sizes: You're given a two-dimensional array (a matrix) of potentially unequal height and width containing only 0s and 1s. Each 0 represents land, and each 1 represents part of a river. A river consists of any number of 1s that are either horizontally or vertically adjacent (but not diagonally adjacent). The number of adjacent 1s forming a river determine its size. Note that a river can twist. In other words, it doesn't have to be a straight vertical line or a straight horizontal line; it can be L-shaped, for example. Write a function that returns an array of the sizes of all rivers represented in the input matrix. The sizes don't need to be in any particular order. Sample Input matrix = [ [1, 0, 0, 1, 0], [1, 0, 1, 0, 0], [0, 0, 1, 0, 1], [1, 0, 1, 0, 1], [1, 0, 1, 1, 0], ] Sample Output [1, 2, 2, 2, 5] // The numbers could be ordered differently. // The rivers can be clearly seen here: // [ // [1, , , 1, ], // [1, , 1, , ], // [ , , 1, , 1], // [1, , 1, , 1], // [1, , 1, 1, ], // ] https://www.algoexpert.io/questions/River%20Sizes """ """ Solution: 1. iterate through every element in the array 2. if we find a river (1) map out it's length while marking the river's elements as visited (-1) """ # O(wh) time | O(wh) space def riverSizes(matrix): river_sizes = [] for row in range(len(matrix)): for col in range(len(matrix[0])): if matrix[row][col] == 1: # if river river_sizes.append(findRiverSize(matrix, row, col)) return river_sizes def findRiverSize(matrix, row, col): if row < 0 or col < 0 or row >= len(matrix) or col >= len(matrix[0]) \ or matrix[row][col] != 1: # not river (base case) return 0 matrix[row][col] = -1 # mark point as visited left = findRiverSize(matrix, row, col-1) right = findRiverSize(matrix, row, col+1) down = findRiverSize(matrix, row+1, col) up = findRiverSize(matrix, row-1, col) return 1 + right + left + down + up # visit neighbours matrix = [ [1, 0, 0, 1, 0], [1, 0, 1, 0, 0], [0, 0, 1, 0, 1], [1, 0, 1, 0, 1], [1, 0, 1, 1, 0], ] x = [ [1, 0, 0, 1, 0, 1, 0, 0, 1, 1, 1, 0], [1, 0, 1, 0, 0, 1, 1, 1, 1, 0, 1, 0], [0, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1, 1], [1, 0, 1, 0, 1, 1, 0, 0, 0, 1, 0, 0], [1, 0, 1, 1, 0, 0, 0, 1, 1, 1, 0, 1] ] # [2, 1, 21, 5, 2, 1] print(riverSizes(matrix)) print(riverSizes([[1, 1, 1, 0, 1, 1, 0, 0, 0, 1, 0]])) print(riverSizes(x)) # print(findRiverSize(x, 0, 5)) -
Single Cycle Check
""" Single Cycle Check: You're given an array of integers where each integer represents a jump of its value in the array. For instance, the integer 2 represents a jump of two indices forward in the array; the integer -3 represents a jump of three indices backward in the array. If a jump spills past the array's bounds, it wraps over to the other side. For instance, a jump of -1 at index 0 brings us to the last index in the array. Similarly, a jump of 1 at the last index in the array brings us to index 0. Write a function that returns a boolean representing whether the jumps in the array form a single cycle. A single cycle occurs if, starting at any index in the array and following the jumps, every element in the array is visited exactly once before landing back on the starting index. Sample Input array = [2, 3, 1, -4, -4, 2] Sample Output true https://www.algoexpert.io/questions/Single%20Cycle%20Check """ # 0(n) time | 0(n) space def hasSingleCycle(array): visited = {} # visited indexes idx = 0 while True: # # jump logic (find where we are visiting) idx = getNextIdx(idx, array) # if we have been at this index before (which will eventually happen): if idx in visited: # if len(visited) is the same as len(array), # then we must have done one complete loop including every element # will handle cycles that do not cover all elements in the array return len(visited) == len(array) # # visit index visited[idx] = True """ ------------------------------------------------------------------------------------------------------------------------------------------------------------------------------ """ def hasSingleCycle00(array): indices = [0] * len(array) i = 0 for _ in range(len(array)*2): # mark current index as visted indices[i] = indices[i] + 1 # move to next index i += array[i] if i > len(array) - 1: # too large i = i % len(array) while i < 0: i += len(array) # look for invalid for num in indices: if num != 2: return False return True """ ------------------------------------------------------------------------------------------------------------------------------------------------------------------------------ after len(array)-1 visits, we should land at index 0 """ # 0(n) time | 0(1) space def hasSingleCycle2(array): # after len(array)-1 visits, we should land at index 0 num_elements_visited = 0 idx = 0 while num_elements_visited < len(array): if num_elements_visited > 0 and idx == 0: return False num_elements_visited += 1 idx = getNextIdx(idx, array) return idx == 0 def getNextIdx(idx, array): # # jump logic (find where we are visiting) idx = idx + array[idx] while idx >= len(array) or idx < 0: if idx >= len(array): idx -= len(array) if idx < 0: idx += len(array) return idx """ ------------------------------------------------------------------------------------------------------------------------------------------------------------------------------ """ def hasSingleCycle0(array): counter = 0 idx = 0 while counter < len(array): if array[idx] == float("-inf"): return False idx_val = array[idx] # mark as visited array[idx] = float("-inf") # jump idx += idx_val counter += 1 while idx < 0: idx += len(array) while idx > len(array) - 1: idx -= len(array) return idx == 0 """ [0, 1, 2, 3, 4, 5] [2, 1, 1, 1, 1, 1] [2, 3, 1, -4, -4, 2] """ -
Clone Graph
""" Clone Graph: Given a reference of a node in a connected undirected graph. Return a deep copy (clone) of the graph. Each node in the graph contains a val (int) and a list (List[Node]) of its neighbors. class Node { public int val; public List<Node> neighbors; } Test case format: For simplicity sake, each node's value is the same as the node's index (1-indexed). For example, the first node with val = 1, the second node with val = 2, and so on. The graph is represented in the test case using an adjacency list. Adjacency list is a collection of unordered lists used to represent a finite graph. Each list describes the set of neighbors of a node in the graph. The given node will always be the first node with val = 1. You must return the copy of the given node as a reference to the cloned graph. https://leetcode.com/problems/clone-graph/ """ from typing import List # Definition for a Node. class Node: def __init__(self, val=0, neighbors=None): self.val = val self.neighbors = neighbors if neighbors is not None else [] class Solution: def cloneGraph(self, node: 'Node'): if node is None: return None created_nodes = [] # node 1 will be at index 0, 2 at 1... return self.createNode(node, created_nodes) def createNode(self, node: Node, created_nodes): # ensure we have the index: node 1 will be at index 0, 2 at 1... while len(created_nodes) < node.val: created_nodes.append(None) # check if created: no need to create it again if created_nodes[node.val-1] is not None: return created_nodes[node.val-1] # # create new node new_node = Node(node.val) # add to created_nodes created_nodes[node.val-1] = new_node # create neighbors if node.neighbors: neighbors = [] for neighbour in node.neighbors: neighbors.append(self.createNode(neighbour, created_nodes)) new_node.neighbors = neighbors return new_node """ 1. create new node 2. add children to node - create child node node.neighnours = [createNode(child1), createNode(child2) """ -
Youngest Common Ancestor
""" Youngest Common Ancestor: You're given three inputs, all of which are instances of an AncestralTree class that have an ancestor property pointing to their youngest ancestor. The first input is the top ancestor in an ancestral tree (i.e., the only instance that has no ancestor--its ancestor property points to None / null), and the other two inputs are descendants in the ancestral tree. Write a function that returns the youngest common ancestor to the two descendants. Note that a descendant is considered its own ancestor. So in the simple ancestral tree below, the youngest common ancestor to nodes A and B is node A. https://www.algoexpert.io/questions/Youngest%20Common%20Ancestor """ # This is an input class. Do not edit. class AncestralTree: def __init__(self, name): self.name = name self.ancestor = None # 0(d) time | 0(d) space - where d is the depth (height) of the ancestral tree def getYoungestCommonAncestor1(topAncestor, descendantOne, descendantTwo): store_one = {} store_two = {} while descendantOne != topAncestor or descendantTwo != topAncestor: # # move up # one if descendantOne != topAncestor: if descendantOne.name in store_two: # if seen by other descendant return descendantOne else: store_one[descendantOne.name] = True descendantOne = descendantOne.ancestor # move up # two if descendantTwo != topAncestor: if descendantTwo.name in store_one: # if seen by other descendant return descendantTwo else: store_two[descendantTwo.name] = True descendantTwo = descendantTwo.ancestor # move up return topAncestor # will always be an ancestor # 0(d) time | 0(1) space def getYoungestCommonAncestor(topAncestor, descendantOne, descendantTwo): dist_top_one = 0 dist_top_two = 0 curr_one = descendantOne curr_two = descendantTwo # calculate height from top while curr_one != topAncestor or curr_two != topAncestor: if curr_one != topAncestor: dist_top_one += 1 curr_one = curr_one.ancestor if curr_two != topAncestor: dist_top_two += 1 curr_two = curr_two.ancestor # level nodes while dist_top_one != dist_top_two: # move the lower pointer upwards if dist_top_one > dist_top_two: dist_top_one -= 1 descendantOne = descendantOne.ancestor else: dist_top_two -= 1 descendantTwo = descendantTwo.ancestor # find common ancestor while descendantOne != topAncestor or descendantTwo != topAncestor: if descendantTwo == descendantOne: return descendantOne descendantOne = descendantOne.ancestor descendantTwo = descendantTwo.ancestor return topAncestor # will always be an ancestor """ Sample Input // The nodes are from the ancestral tree below. topAncestor = node A descendantOne = node E descendantTwo = node I A / \ B C / \ / \ D E F G / \ H I Sample Output node B Solution: 1. try to get the (pointers to the) nodes to be at the same level - for example pointer two should move up to D - this can be done by calculating the distance to the top ancestor, then moving the lower pointer upwards 2. iterate upwards and return when they are at the same node """ -
Shortest Distance from All Buildings *
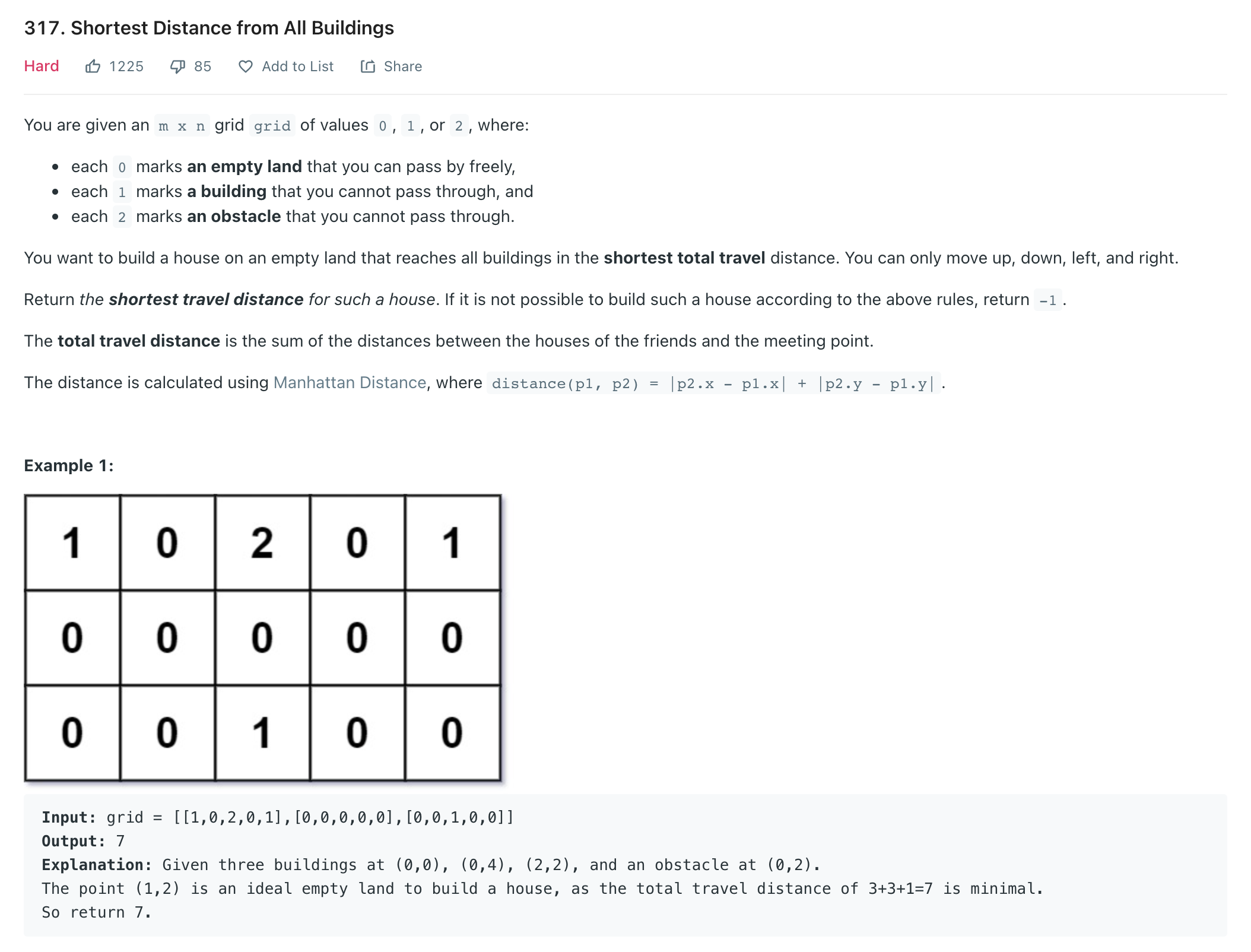
""" Shortest Distance from All Buildings You are given an m x n grid grid of values 0, 1, or 2, where: each 0 marks an empty land that you can pass by freely, each 1 marks a building that you cannot pass through, and each 2 marks an obstacle that you cannot pass through. You want to build a house on an empty land that reaches all buildings in the shortest total travel distance. You can only move up, down, left, and right. Return the shortest travel distance for such a house. If it is not possible to build such a house according to the above rules, return -1. The total travel distance is the sum of the distances between the houses of the friends and the meeting point. The distance is calculated using Manhattan Distance, where distance(p1, p2) = |p2.x - p1.x| + |p2.y - p1.y|. Example 1: Input: grid = [ [1,0,2,0,1], [0,0,0,0,0], [0,0,1,0,0] ] Output: 7 Explanation: Given three buildings at (0,0), (0,4), (2,2), and an obstacle at (0,2). The point (1,2) is an ideal empty land to build a house, as the total travel distance of 3+3+1=7 is minimal. So return 7. Example 2: Input: grid = [[1,0]] Output: 1 Example 3: Input: grid = [[1]] Output: -1 https://leetcode.com/problems/shortest-distance-from-all-buildings """ """ 1. BFS from free space to all houses 2. BFS from houses to free spaces """ # Let N and M be the number of rows and columns in grid respectively. # O(N^2 . M^2) time | O(N . M) time class Solution: def shortestDistance(self, grid): """ BFS from Houses to Empty Land """ houses_reached = [ [0 for _ in range(len(grid[0]))] for _ in range(len(grid))] # # count houses houses_count = 0 for row in range(len(grid)): for col in range(len(grid[0])): if grid[row][col] == 1: houses_count += 1 # # bfs on each house for row in range(len(grid)): for col in range(len(grid[0])): # check if house if grid[row][col] == 1: self.bfs(row, col, grid, houses_reached) # # find suitable free space largest = float('-inf') for row in range(len(grid)): for col in range(len(grid[0])): # check if valid free space if houses_reached[row][col] == houses_count and grid[row][col] < 0: largest = max(largest, grid[row][col]) if largest == float('-inf'): return -1 return largest * -1 def bfs(self, row, col, grid, houses_reached): visited = [ [False for _ in range(len(grid[0]))] for _ in range(len(grid))] queue = [] # initialise queue queue.append((row-1, col, -1)) queue.append((row+1, col, -1)) queue.append((row, col-1, -1)) queue.append((row, col+1, -1)) while queue: c_row, c_col, distance = queue.pop(0) if c_row < 0 or c_row >= len(grid): continue if c_col < 0 or c_col >= len(grid[0]): continue if visited[c_row][c_col]: continue if grid[c_row][c_col] > 0: continue visited[c_row][c_col] = True # # record distance grid[c_row][c_col] += distance houses_reached[c_row][c_col] += 1 # # move outward new_distance = distance - 1 queue.append((c_row-1, c_col, new_distance)) queue.append((c_row+1, c_col, new_distance)) queue.append((c_row, c_col-1, new_distance)) queue.append((c_row, c_col+1, new_distance)) -
Min Cost to Connect All Points
Prim's Algorithm - Minimum Spanning Tree - Min Cost to Connect all Points - Leetcode 1584 - Python
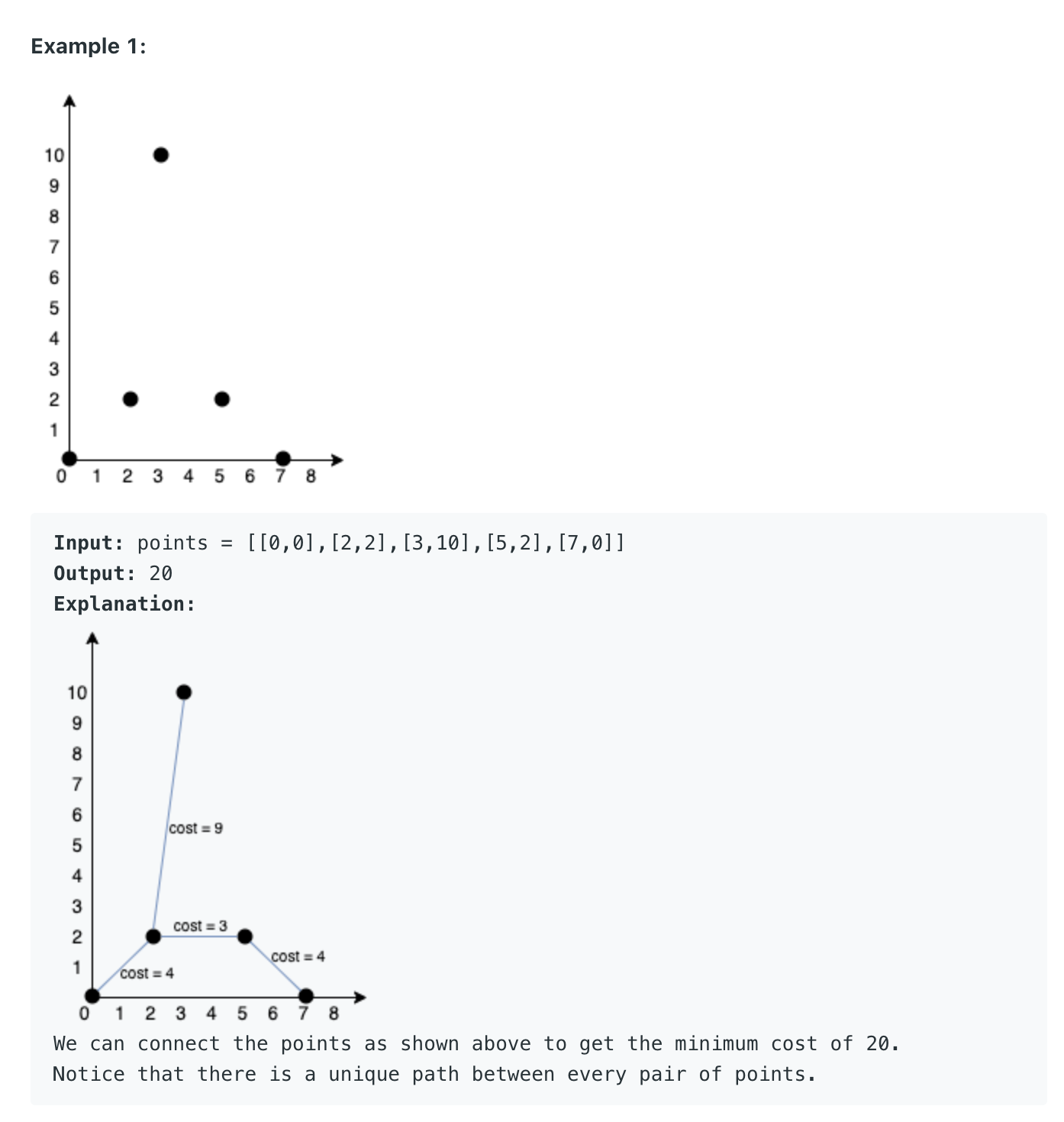
""" 1584. Min Cost to Connect All Points You are given an array points representing integer coordinates of some points on a 2D-plane, where points[i] = [xi, yi]. The cost of connecting two points [xi, yi] and [xj, yj] is the manhattan distance between them: |xi - xj| + |yi - yj|, where |val| denotes the absolute value of val. Return the minimum cost to make all points connected. All points are connected if there is exactly one simple path between any two points. Example 1: Input: points = [[0,0],[2,2],[3,10],[5,2],[7,0]] Output: 20 Explanation: We can connect the points as shown above to get the minimum cost of 20. Notice that there is a unique path between every pair of points. Example 2: Input: points = [[3,12],[-2,5],[-4,1]] Output: 18 Example 3: Input: points = [[0,0],[1,1],[1,0],[-1,1]] Output: 4 Example 4: Input: points = [[-1000000,-1000000],[1000000,1000000]] Output: 4000000 Example 5: Input: points = [[0,0]] Output: 0 https://leetcode.com/problems/min-cost-to-connect-all-points https://www.notion.so/paulonteri/Trees-Graphs-edc3401e06c044f29a2d714d20ffe185#2ac2c79816464704a3851de16d494dff """ import collections import heapq """ Prim's Minimum Spanning Tree Algorithm: https://www.notion.so/paulonteri/Trees-Graphs-edc3401e06c044f29a2d714d20ffe185#596bc798759a4edabe22a895aadeb12c https://youtu.be/f7JOBJIC-NA """ class Solution_: def minCostConnectPoints(self, points): total = 0 # # Create adjacency list # Will store nodes in the form => `parent: [[cost_to_1, node_1], [cost_to_2, node_2], ...]` graph = collections.defaultdict(list) for idx in range(len(points)): x1, y1 = points[idx] for idx2 in range(idx + 1, len(points)): x2, y2 = points[idx2] cost = abs(x1 - x2) + abs(y1 - y2) graph[str(x1)+str(y1)].append([cost, str(x2)+str(y2)]) graph[str(x2)+str(y2)].append([cost, str(x1)+str(y1)]) # # Prim's Minimum Spanning Tree Algorithm visited = set() priority_queue = [] first_node = str(points[0][0])+str(points[0][1]) heapq.heappush(priority_queue, (0, first_node)) # start from node 0 while len(visited) < len(graph): cost, node = heapq.heappop(priority_queue) # skip visited if node in visited: continue visited.add(node) # record cost total += cost # add neighbours for neighbour in graph[node]: if neighbour[1] not in visited: heapq.heappush(priority_queue, neighbour) return total class Solution: def minCostConnectPoints(self, points): total = 0 # # Create adjacency list # Will use the array indices as id's # Will store nodes in the form => `parent: [[cost_to_1, node_1], [cost_to_2, node_2], ...]` graph = collections.defaultdict(list) for idx in range(len(points)): x1, y1 = points[idx] for idx2 in range(idx + 1, len(points)): x2, y2 = points[idx2] cost = abs(x1 - x2) + abs(y1 - y2) graph[idx].append([cost, idx2]) graph[idx2].append([cost, idx]) # # Prim's Minimum Spanning Tree Algorithm visited = set() priority_queue = [] heapq.heappush(priority_queue, (0, 0)) # start from node 0 while len(visited) < len(graph): cost, node = heapq.heappop(priority_queue) # skip visited if node in visited: continue visited.add(node) # record cost total += cost # add neighbours for neighbour in graph[node]: if neighbour[1] not in visited: heapq.heappush(priority_queue, neighbour) return total -
Connecting Cities With Minimum Cost
""" 1584. Min Cost to Connect All Points You are given an array points representing integer coordinates of some points on a 2D-plane, where points[i] = [xi, yi]. The cost of connecting two points [xi, yi] and [xj, yj] is the manhattan distance between them: |xi - xj| + |yi - yj|, where |val| denotes the absolute value of val. Return the minimum cost to make all points connected. All points are connected if there is exactly one simple path between any two points. Example 1: Input: points = [[0,0],[2,2],[3,10],[5,2],[7,0]] Output: 20 Explanation: We can connect the points as shown above to get the minimum cost of 20. Notice that there is a unique path between every pair of points. Example 2: Input: points = [[3,12],[-2,5],[-4,1]] Output: 18 Example 3: Input: points = [[0,0],[1,1],[1,0],[-1,1]] Output: 4 Example 4: Input: points = [[-1000000,-1000000],[1000000,1000000]] Output: 4000000 Example 5: Input: points = [[0,0]] Output: 0 https://leetcode.com/problems/min-cost-to-connect-all-points https://www.notion.so/paulonteri/Trees-Graphs-edc3401e06c044f29a2d714d20ffe185#2ac2c79816464704a3851de16d494dff """ import collections import heapq """ Prim's Minimum Spanning Tree Algorithm: https://www.notion.so/paulonteri/Trees-Graphs-edc3401e06c044f29a2d714d20ffe185#596bc798759a4edabe22a895aadeb12c https://youtu.be/f7JOBJIC-NA """ class Solution_: def minCostConnectPoints(self, points): total = 0 # # Create adjacency list # Will store nodes in the form => `parent: [[cost_to_1, node_1], [cost_to_2, node_2], ...]` graph = collections.defaultdict(list) for idx in range(len(points)): x1, y1 = points[idx] for idx2 in range(idx + 1, len(points)): x2, y2 = points[idx2] cost = abs(x1 - x2) + abs(y1 - y2) graph[str(x1)+str(y1)].append([cost, str(x2)+str(y2)]) graph[str(x2)+str(y2)].append([cost, str(x1)+str(y1)]) # # Prim's Minimum Spanning Tree Algorithm visited = set() priority_queue = [] first_node = str(points[0][0])+str(points[0][1]) heapq.heappush(priority_queue, (0, first_node)) # start from node 0 while len(visited) < len(graph): cost, node = heapq.heappop(priority_queue) # skip visited if node in visited: continue visited.add(node) # record cost total += cost # add neighbours for neighbour in graph[node]: if neighbour[1] not in visited: heapq.heappush(priority_queue, neighbour) return total class Solution: def minCostConnectPoints(self, points): total = 0 # # Create adjacency list # Will use the array indices as id's # Will store nodes in the form => `parent: [[cost_to_1, node_1], [cost_to_2, node_2], ...]` graph = collections.defaultdict(list) for idx in range(len(points)): x1, y1 = points[idx] for idx2 in range(idx + 1, len(points)): x2, y2 = points[idx2] cost = abs(x1 - x2) + abs(y1 - y2) graph[idx].append([cost, idx2]) graph[idx2].append([cost, idx]) # # Prim's Minimum Spanning Tree Algorithm visited = set() priority_queue = [] heapq.heappush(priority_queue, (0, 0)) # start from node 0 while len(visited) < len(graph): cost, node = heapq.heappop(priority_queue) # skip visited if node in visited: continue visited.add(node) # record cost total += cost # add neighbours for neighbour in graph[node]: if neighbour[1] not in visited: heapq.heappush(priority_queue, neighbour) return total
Terminology & Definitions
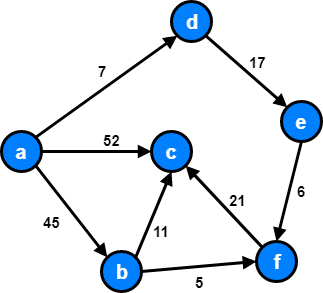
a directed, weighted, acyclic graph with 6 vertices and 8 edges
Vertex/Node
A vertex (also called a node) is a fundamental part of a graph. It can have a name (a key), it may also have additional information (the payload). Our graph has 6 vertices: V = {a, b, c, d, e, f}
Edge/Arc
An edge (also called an “arc”) is another fundamental part of a graph. An edge connects two vertices to show that there is a relationship between them. Our graph has 8 edges: E = {(a, b, 45), (a, c, 52), (a, d, 7), (b, c, 11), (b, f, 5), (d, e, 17), (e, f, 6), (f, c, 21)}
Weighted or Unweighted
If a graph is weighted, each edge has a “weight.” The weight could, for example, represent the distance between two locations, or the cost or time it takes to travel between the locations.
Directed or Undirected
In directed graphs, edges point from the node at one end to the node at the other end. In undirected graphs, the edges simply connect the nodes at each end.
Our example above is a directed graph.
Cyclic or Acyclic
A graph is cyclic if it has a cycle, an unbroken series of nodes with no repeating nodes or edges that connects back to itself. Graphs without cycles are acyclic. Our example above is an acyclic graph.

Connected vs Disconnected
If G is an undirected graph, vertices u and v are said to be connected if G contains a path from u to v; otherwise, u and v are said to be disconnected.
A graph is said to be connected if every pair of vertices in the graph is connected. A connected component is a maximal set of vertices C such that each pair of vertices in C is connected in G. E
Topological ordering
Topological Sort (for graphs) *
A directed acyclic graph (DAG) is a directed graph in which there are no cycles, i.e., paths that contain one or more edges and which begin and end at the same vertex.
Vertices in a directed acyclic graph that have no incoming edges are referred to as sources.
Vertices that have no outgoing edges are referred to as sinks.
Indegree → count of incoming edges of each vertex/node or how many parents it has (used to determine sources)
A topological ordering of the vertices in a DAG is an ordering of the vertices in which each edge is from a vertex earlier in the ordering to a vertex later in the ordering.
Representing Graphs in Code
There are a few ways to represent graphs in the code. We’ll look at the most common three, and the basic tradeoffs.
Let’s take this graph as an example:

Edge List
A list of all the edges in the graph: graph = [[4, 5], [2, 4], [2, 3], [1, 2], [0, 2], [0, 1]] Since node 0 has edges to nodes 1 and 2, [0, 1] and [0, 2] are in the edge list.
This is well suited to performant lookups of an edge, or listing all edges, but is slow with many other query types. For example, to find all vertices adjacent to a given vertex, every edge must be examined.
Adjacency List (Use of indexes & dicts) *
A list where the index represents the node and the value at that index is a list of the node’s neighbours: Since node 2 has edges to nodes 0, 1, 3 and 4, graph[2] has the adjacency list [0, 1, 3, 4].
We could also use a dictionary where the keys represent the node and the values are the lists of neighbours. This would be useful if the nodes were represented by strings, objects, or otherwise didn’t map cleanly to list indices.
graph = [
[1, 2],
[0, 2],
[0, 1, 3, 4],
[2],
[2, 5],
[4]
]
graph = {
0: [1, 2],
1: [0, 2],
2: [0, 1, 3, 4],
3: [2],
4: [2, 5],
5: [4]
}
This representation allows for constant-time lookup of adjacent vertices, which is useful in many query and pathfinding scenarios. It is slower for edge lookups, as the whole list of vertices adjacent to u must be examined for v, in order to find edge uv.
Adjacency lists are the typical choice for general purpose use, though edge lists or adjacency matrices have their own strengths, which may match a specific use case.
Pros:
- Saves on space (memory): the representation takes as many memory words as there are nodes and edge.
Cons:
- It can take up to O(n) time to determine if a pair of nodes (i,j) is an edge: one would have to search the linked list L[i], which takes time proportional to the length of L[i].
Adjacency Matrix *
A matrix of 0 and 1 indicates whether node x connects to node y (0 means no, 1 means yes).
Since node 4 has edges to nodes 2 and 5, graph[4][2] and graph[4][5] have value 1.
Pros:
- Simple to implement
- O(1) edge lookups. Easy and fast to tell if a pair (i,j) is an edge: simply check if A[i][j] is 1 or 0
Cons:
- No matter how few edges the graph has, the matrix takes O(n2) in memory
graph = [
[0, 1, 1, 0, 0, 0],
[1, 0, 1, 0, 0, 0],
[1, 1, 0, 1, 1, 0],
[0, 0, 1, 0, 0, 0],
[0, 0, 1, 0, 0, 1],
[0, 0, 0, 0, 1, 0]
]
Adjacency matrices perform strongly with edge lookups, with a constant-time lookup given a pair of vertex Id. They tend to be slow for other operations. For example, listing everything adjacent to a vertex requires checking every single vertex in the graph. They also typically require more space than other models, especially with sparse graphs (graphs with “few” edges)
Other
DFS & BFS time complexity: *
Bipartite graph/Look for even cycle using graph colouring
Possible Bipartition | Bipartite graph | Graph coloring | Leetcode #886
Examples
-
Is Graph Bipartite?
""" 785. Is Graph Bipartite? There is an undirected graph with n nodes, where each node is numbered between 0 and n - 1. You are given a 2D array graph, where graph[u] is an array of nodes that node u is adjacent to. More formally, for each v in graph[u], there is an undirected edge between node u and node v. The graph has the following properties: There are no self-edges (graph[u] does not contain u). There are no parallel edges (graph[u] does not contain duplicate values). If v is in graph[u], then u is in graph[v] (the graph is undirected). The graph may not be connected, meaning there may be two nodes u and v such that there is no path between them. A graph is bipartite if the nodes can be partitioned into two independent sets A and B such that every edge in the graph connects a node in set A and a node in set B. Return true if and only if it is bipartite. https://leetcode.com/problems/is-graph-bipartite https://www.notion.so/paulonteri/Trees-Graphs-edc3401e06c044f29a2d714d20ffe185#dc05cd22189b412f8a0a8c1d1a827bde """ class Solution: def isBipartite(self, graph): colours = [None] * len(graph) visited = [False] * len(graph) for node in range(len(graph)): if not self.dfs(graph, node, colours, visited): return False return True def dfs(self, graph, node, colours, visited): if visited[node]: return True if colours[node] is None: # https://www.notion.so/paulonteri/Trees-Graphs-edc3401e06c044f29a2d714d20ffe185#596387a8e4254e1690f5eca7996ab9a1 # if we do not know the colour then we can group it with the nodes in which we do not know the colours colours[node] = True visited[node] = True # Check colours & Dfs for child in graph[node]: if colours[child] is None: colours[child] = not colours[node] # check for correct colours if colours[child] == colours[node]: return False # Dfs if not self.dfs(graph, child, colours, visited): return False return True
https://encrypted-tbn0.gstatic.com/images?q=tbn:ANd9GcTxVsY_1LCKk5csP6iyLxE_PorhQYoAipU5a-zz2uoT9Q&s
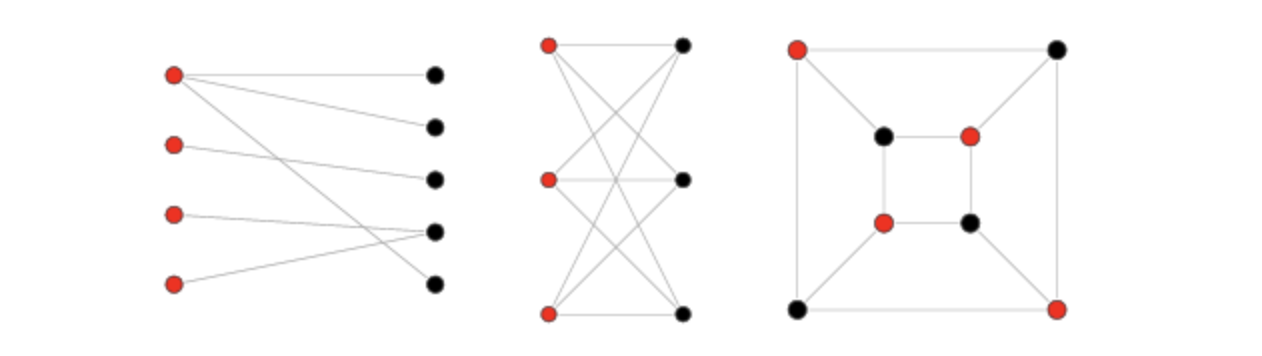
A Bipartite Graph is a graph whose vertices can be divided into two independent sets, U and V such that every edge (u, v) either connects a vertex from U to V or a vertex from V to U. In other words, for every edge (u, v), either u belongs to U and v to V, or u belongs to V and v to U. We can also say that there is no edge that connects vertices of same set.
Equivalently, a bipartite graph is a graph that does not contain any odd-length cycles.
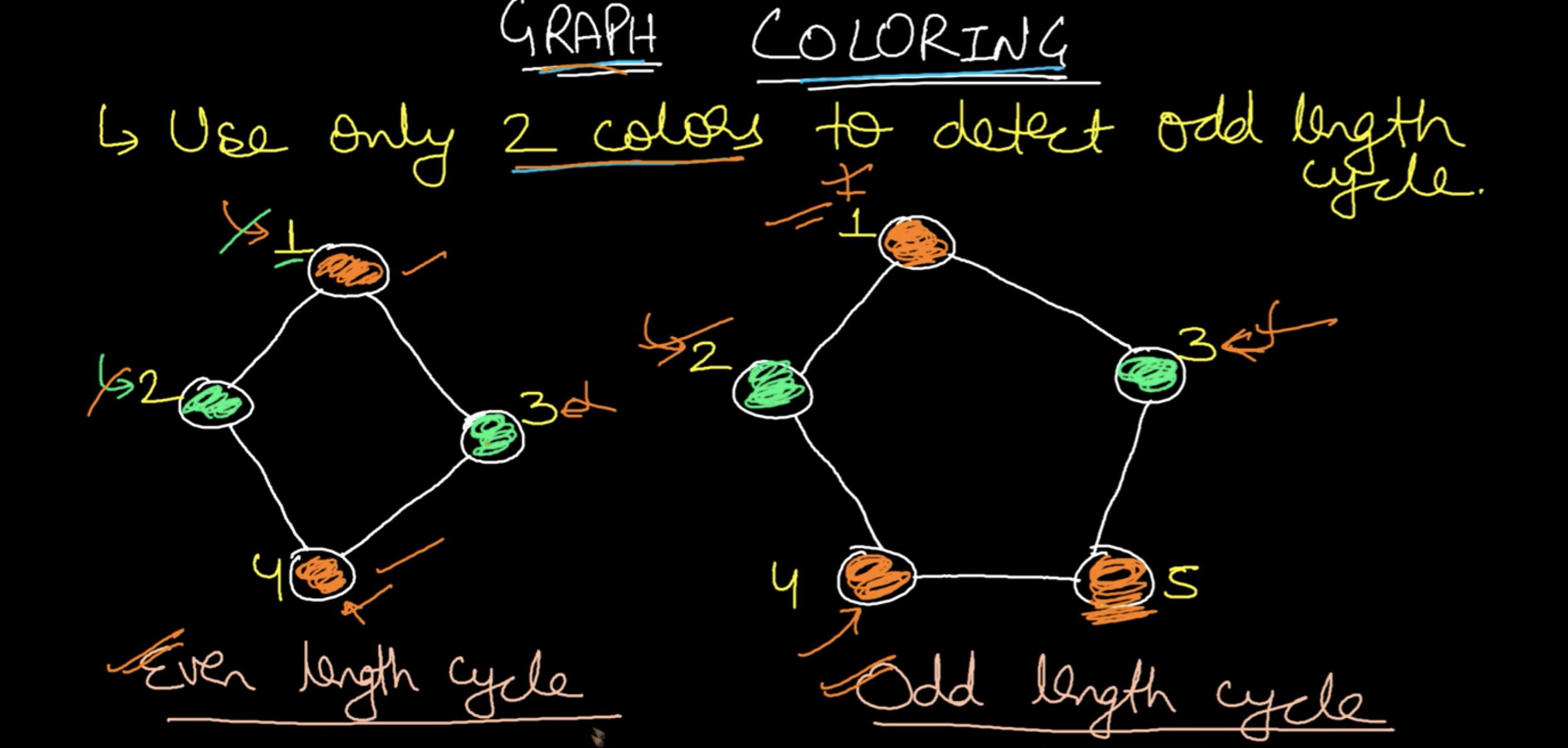
Graph colouring: - the graph on the left has an even cycle - the graph on the right failed to make an even cycle (at 4/5)
Binary Trees
Binary Tree Data Structure | Interview Cake
Binary Tree Bootcamp: Full, Complete, & Perfect Trees. Preorder, Inorder, & Postorder Traversal.
Binary Trees study guide - LeetCode Discuss
General
-
Implementation
class BinaryTree: def __init__(self, data): self.left = None self.right = None self.root = data def insert_left(self, value): if self.left is None: self.left = BinaryTree(value) else: new_node = BinaryTree(value) new_node.left = self.left self.left = new_node def insert_right(self, value): if self.right is None: self.right = BinaryTree(value) else: new_node = BinaryTree(value) new_node.left = self.left self.left = new_node def get_right_child(self): return self.right def get_left_child(self): return self.left def set_root_value(self, value): self.root = value def get_root_value(self): return self.root
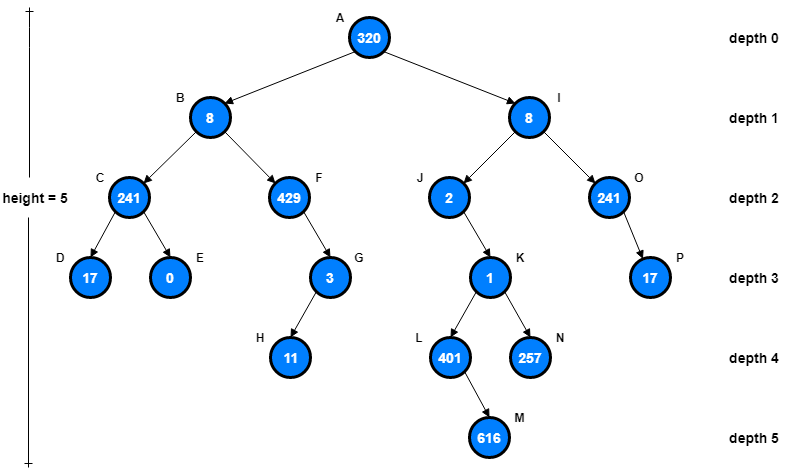
Binary Tree
Examples:
-
Symmetric Tree **
""" 101. Symmetric Tree Given the root of a binary tree, check whether it is a mirror of itself (i.e., symmetric around its center). https://leetcode.com/problems/symmetric-tree/ 1 / \ 2 2 / \ / \ 3 4 4 3 True """ # Definition for a binary tree node. class TreeNode: def __init__(self, val=0, left=None, right=None): self.val = val self.left = left self.right = right class Solution_: def isSymmetric(self, root): queue = [(root, 0, 0)] store = set() while queue: node, depth, horizontal = queue.pop(0) # # add children if node.left: queue.append((node.left, depth+1, horizontal-1)) if node.right: queue.append((node.right, depth+1, horizontal+1)) # # visit curr = (node.val, depth, horizontal) opposite_curr = (node.val, depth, horizontal*-1) # if opposite_curr in store: store.remove(opposite_curr) else: store.add(curr) return len(store) == 1 """ """ class Solution: def isSymmetric(self, root): queue = [root.left, root.right] while queue: one = queue.pop(0) two = queue.pop(0) if one == None or two == None: if one == None and two == None: continue else: return False if one.val != two.val: return False # # add children # the left child of one will match with the right child of two (diagram) queue.append(one.left) queue.append(two.right) # the right child of one will match with the left child of two (diagram) queue.append(one.right) queue.append(two.left) return True -
Binary Tree Zigzag Level Order Traversal
""" Binary Tree Zigzag Level Order Traversal: Given a binary tree, return the zigzag level order traversal of its nodes' values. (ie, from left to right, then right to left for the next level and alternate between). https://leetcode.com/problems/binary-tree-zigzag-level-order-traversal/ """ # Definition for a binary tree node. from collections import deque class TreeNode: def __init__(self, val=0, left=None, right=None): self.val = val self.left = left self.right = right class Solution: def zigzagLevelOrder(self, root: TreeNode): res = [] self.zigzagHelper(root, res, 1) return res def zigzagHelper(self, root, res, level): if not root: return if len(res) < level: # add array for level res.append([]) if level % 2 == 0: # right to left res[level-1].insert(0, root.val) else: # left to right res[level-1].append(root.val) self.zigzagHelper(root.left, res, level+1) self.zigzagHelper(root.right, res, level+1) """ Using a double ended queue makes the time complexity better (collections.dequeue) """ # Definition for a binary tree node. # class TreeNode: # def __init__(self, x): # self.val = x # self.left = None # self.right = None class Solution: def zigzagLevelOrder(self, root): """ :type root: TreeNode :rtype: List[List[int]] """ if root is None: return [] results = [] def dfs(node, level): if level >= len(results): results.append(deque([node.val])) else: if level % 2 == 0: results[level].append(node.val) else: results[level].appendleft(node.val) for next_node in [node.left, node.right]: if next_node is not None: dfs(next_node, level+1) # normal level order traversal with DFS dfs(root, 0) return results -
Binary Tree Paths
""" Binary Tree Paths Given the root of a binary tree, return all root-to-leaf paths in any order. https://leetcode.com/problems/binary-tree-paths """ # Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def binaryTreePaths(self, root): paths = [] if not root: return paths stack = [(root, [str(root.val)])] while stack: node, path = stack.pop() # leaf node if not node.left and not node.right: paths.append("->".join(path)) continue if node.left: stack.append((node.left, path+[str(node.left.val)])) if node.right: stack.append((node.right, path+[str(node.right.val)])) return paths -
Binary Tree Diameter *


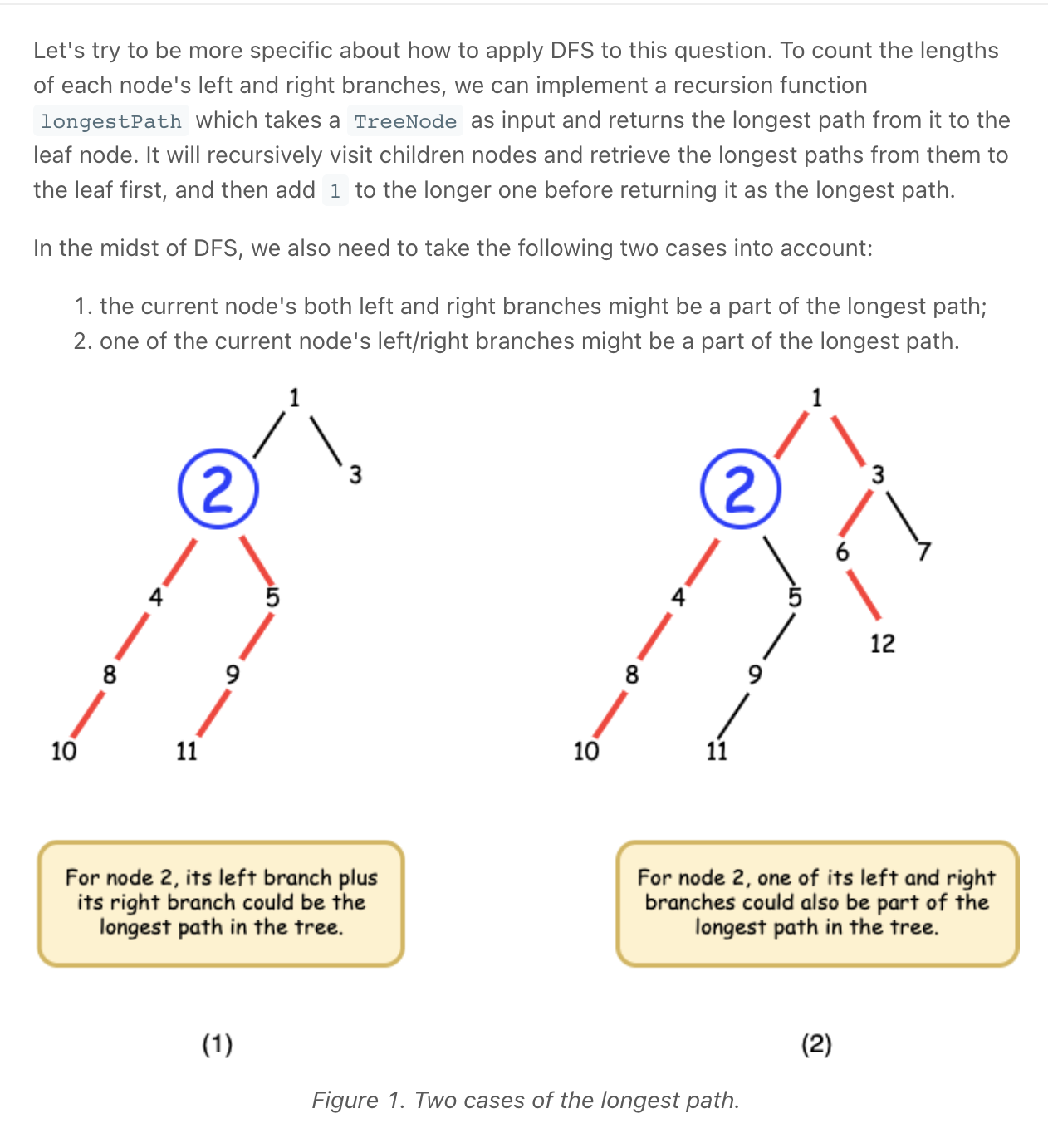


""" Binary Tree Diameter: Diameter of Binary Tree: Write a function that takes in a Binary Tree and returns its diameter. The diameter of a binary tree is defined as the length of its longest path, even if that path doesn't pass through the root of the tree. A path is a collection of connected nodes in a tree, where no node is connected to more than two other nodes. The length of a path is the number of edges between the path's first node and its last node. Each BinaryTree node has an integer value, a left child node, and a right child node. Children nodes can either be BinaryTree nodes themselves or None / null. https://www.algoexpert.io/questions/Binary%20Tree%20Diameter https://leetcode.com/problems/diameter-of-binary-tree/ """ """ Sample Input tree = 1 / \ 3 2 \ 7 4 / \ 8 5 / \ 9 6 Sample Output 6 // 9 -> 8 -> 7 -> 3 -> 4 -> 5 -> 6 // There are 6 edges between the // first node and the last node // of this tree's longest path. Sample Input tree = 1 Sample Output 0 """ """ The key observation to make is: the longest path has to be between two leaf nodes. We can prove this with contradiction. Imagine that we have found the longest path, and it is not between two leaf nodes. We can extend that path by 1, by adding the child node of one of the end nodes (as at least one must have a child, given that they aren't both leaves). This contradicts the fact that our path is the longest path. Therefore, the longest path must be between two leaf nodes. Moreover, we know that in a tree, nodes are only connected with their parent node and 2 children. Therefore we know that the longest path in the tree would consist of a node, its longest left branch, and its longest right branch. So, our algorithm to solve this problem will find the node where the sum of its longest left and right branches is maximized. This would hint at us to apply Depth-first search (DFS) to count each node's branch lengths, because it would allow us to dive deep into the leaves first, and then start counting the edges upwards. """ # Definition for a binary tree node. class TreeNode: def __init__(self, val=0, left=None, right=None): self.val = val self.left = left self.right = right class Solution: def diameterOfBinaryTree(self, root): if not root: return 0 diameter = 0 def diameter_helper(root): if not root: return 0 nonlocal diameter left = diameter_helper(root.left) right = diameter_helper(root.right) diameter = max(left + right, # Connect left & right branches diameter) # Create a branch that will be used to calculate longest_path by the root's parent node # we do not add the curr node's height/depth to any of the calculations/results for the longest_diameter, # it is only considered from its parent node # because if tree = 1 (node), longest_diameter = 0 return max(left, right) + 1 diameter_helper(root) return diameter """""" # This is an input class. Do not edit. class BinaryTree: def __init__(self, value, left=None, right=None): self.value = value self.left = left self.right = right # --------------------------------------------------------------------------------------------------------------------- def binaryTreeDiameter3(tree): max_diameter = [-1] depths(tree, max_diameter) return max_diameter[0] def depths(node, max_diameter): if node is None: return 0 # calculate diameter left = depths(node.left, max_diameter) right = depths(node.right, max_diameter) max_diameter[0] = max(max_diameter[0], left+right) return max(left, right) + 1 # add node to depth # --------------------------------------------------------------------------------------------------------------------- def binaryTreeDiameter(tree): return binaryTreeDiameterHelper(tree, 0).longest_diameter class Result: def __init__(self, longest_path, longest_diameter): self.longest_path = longest_path self.longest_diameter = longest_diameter def __str__(self): # for debugging return f"{self.longest_path} {self.longest_diameter}" def binaryTreeDiameterHelper(tree, depth): if tree is None: return Result(0, 0) left = binaryTreeDiameterHelper(tree.left, depth+1) right = binaryTreeDiameterHelper(tree.right, depth+1) curr_diameter = left.longest_path + right.longest_path prev_longest_diameter = max(left.longest_diameter, right.longest_diameter) curr_longest_diameter = max( curr_diameter, prev_longest_diameter, ) # we do not add the curr node's height/depth to any of the calculations/results for the longest_diameter, # it is only considered from its parent node # because if tree = 1 (node), longest_diameter = 0 nxt_longest_path = max(left.longest_path, right.longest_path) + 1 return Result(nxt_longest_path, curr_longest_diameter) -
Binary Tree Maximum Path Sum **
""" Max Path Sum In Binary Tree: Binary Tree Maximum Path Sum: A path in a binary tree is a sequence of nodes where each pair of adjacent nodes in the sequence has an edge connecting them. A node can only appear in the sequence at most once. Note that the path does not need to pass through the root. The path sum of a path is the sum of the node's values in the path. Given the root of a binary tree, return the maximum path sum of any path. Write a function that takes in a Binary Tree and returns its max path sum. A path is a collection of connected nodes in a tree, where no node is connected to more than two other nodes; a path sum is the sum of the values of the nodes in a particular path. Each BinaryTree node has an integer value, a left child node, and a right child node. Children nodes can either be BinaryTree nodes themselves or None / null. Sample Input tree = 1 / \ 2 3 / \ / \ 4 5 6 7 Sample Output 18 // 5 + 2 + 1 + 3 + 7 https://www.algoexpert.io/questions/Max%20Path%20Sum%20In%20Binary%20Tree https://leetcode.com/problems/binary-tree-maximum-path-sum """ # Definition for a binary tree node. class TreeNode: def __init__(self, val=0, left=None, right=None): self.val = val self.left = left self.right = right class Solution_: def maxPathSum(self, root): if not root: return 0 maximum = float('-inf') def max_path(root): nonlocal maximum if not root: return float('-inf') left = max_path(root.left) right = max_path(root.right) # longest continuous branch/straight line. curr_branch = max( root.val, root.val + left, root.val + right ) # longest branch/triangle we have seen so far maximum = max( maximum, curr_branch, root.val + left + right, # as triangle ) return curr_branch max_path(root) return maximum """""" class Solution: def maxPathSum(self, root): if not root: return 0 return self.max_path(root)[0] def max_path(self, root): if not root: return float("-inf"), float("-inf") left = self.max_path(root.left) right = self.max_path(root.right) max_as_path = max(root.val, root.val + left[1], root.val + right[1],) maximum = max(max_as_path, # Max as path root.val + left[1] + right[1], # Max as tree left[0], # Prev max right[0]) # Prev max return maximum, max_as_path """ """ class TreeInfo: def __init__(self, max_as_branch, max_as_branch_or_triangle): self.max_as_branch = max_as_branch # max continuous path as branch/tree self.max_as_branch_or_triangle = max_as_branch_or_triangle # O(n) time # O(log(n)) space - because it is a binary tree def maxPathSum(tree): res = maxPathSumHelper(tree) return res.max_as_branch_or_triangle def maxPathSumHelper(tree): if not tree: # handle negatives with float('-inf') # return TreeInfo(float('-inf'), float('-inf')) # <- also works. return TreeInfo(0, float('-inf')) left = maxPathSumHelper(tree.left) right = maxPathSumHelper(tree.right) # longest continuous branch/straight line. curr_max_as_branch = max( tree.value, tree.value + left.max_as_branch, tree.value + right.max_as_branch ) # longest branch/triangle we have seen so far note: curr_max_as_branch is automatically included curr_max_as_branch_or_triangle = max( curr_max_as_branch, tree.value + left.max_as_branch + right.max_as_branch, # curr_max_as_triangle left.max_as_branch_or_triangle, right.max_as_branch_or_triangle ) return TreeInfo(curr_max_as_branch, curr_max_as_branch_or_triangle) -
Smallest String Starting From Leaf - LeetCode
Smallest String Starting From Leaf - LeetCode
-
Path Sum II
Simple Python Solution: top-down DFS - LeetCode Discuss
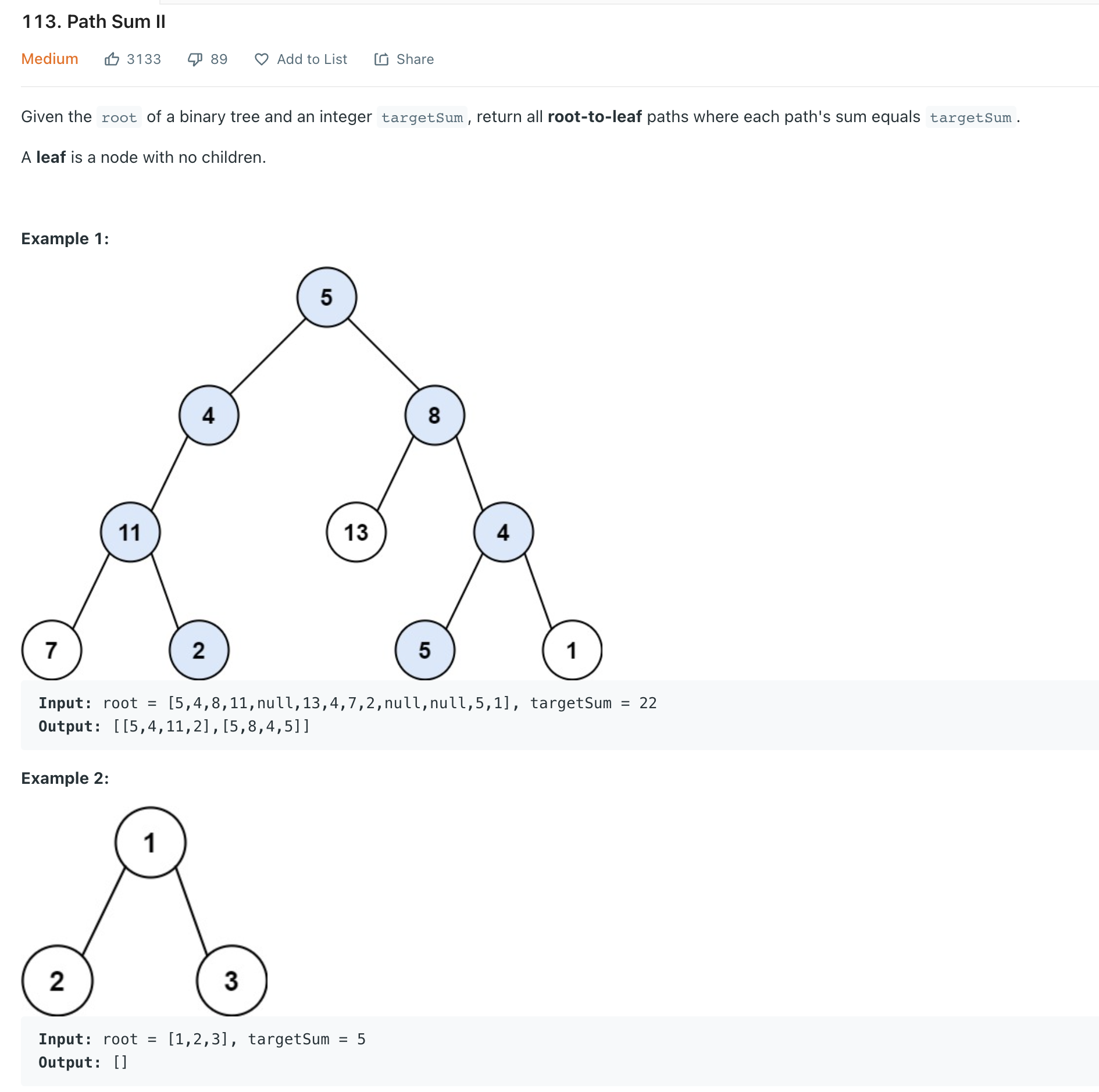
Path Sum II
""" Path Sum II Given a binary tree and a sum, find all root-to-leaf paths where each path's sum equals the given sum. Note: A leaf is a node with no children. https://leetcode.com/problems/path-sum-ii/ """ class Solution: def pathSum(self, root, targetSum): if not root: return [] targetSum -= root.val if targetSum == 0: if not root.left and not root.right: # leaf return [[root.val]] left = self.pathSum(root.left, targetSum) right = self.pathSum(root.right, targetSum) res = [] for arr in right: res.append([root.val]+arr) for arr in left: res.append([root.val]+arr) return res """ - iterate leaves checking if they add up to the path sum - if so, return an array of an array containing the leaf [[leaf,]] - and keep on adding the parent elements tto the array as you bubble up - if a parent has both of its children returning arrays, combine the inner arrays """ -
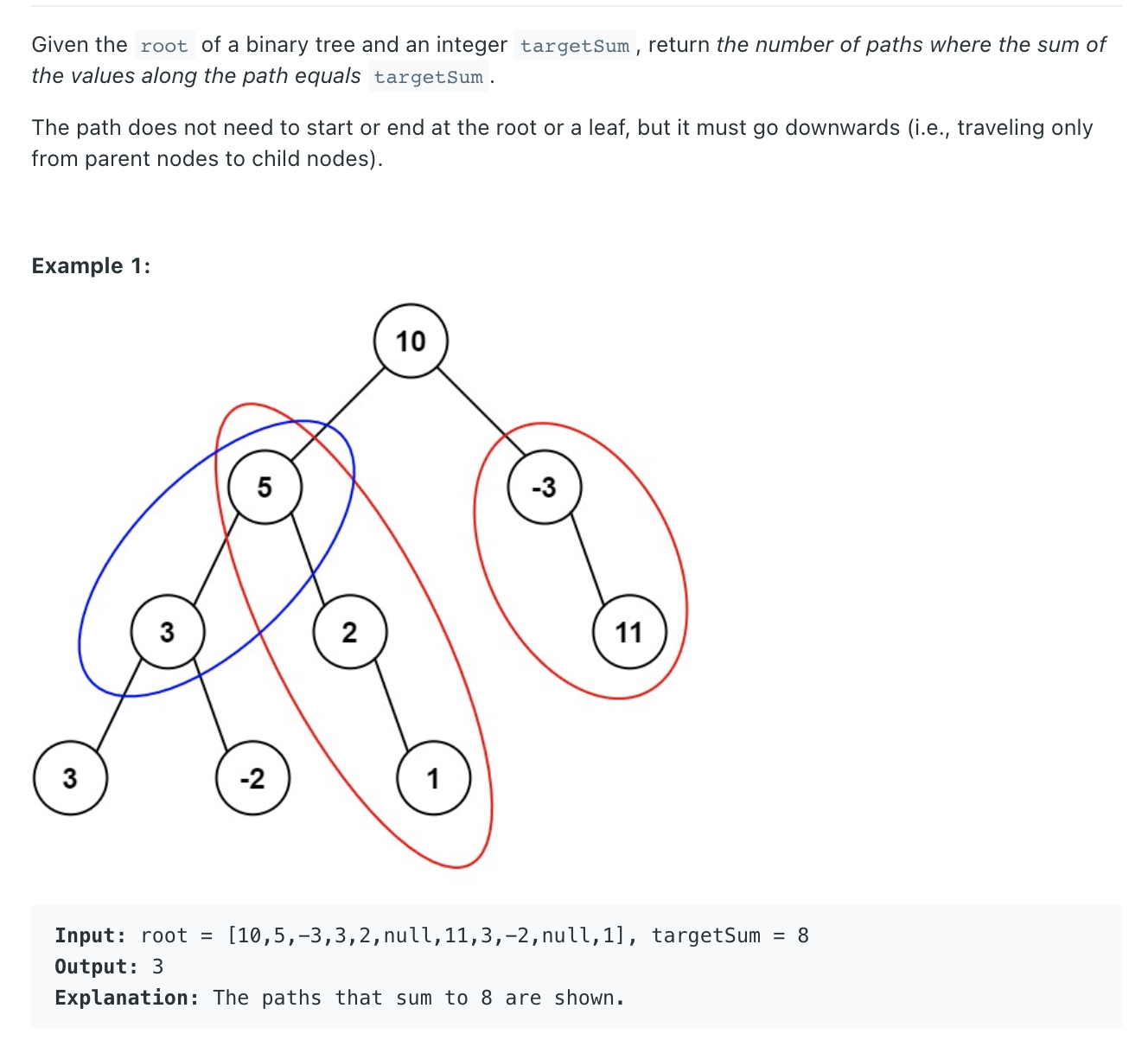
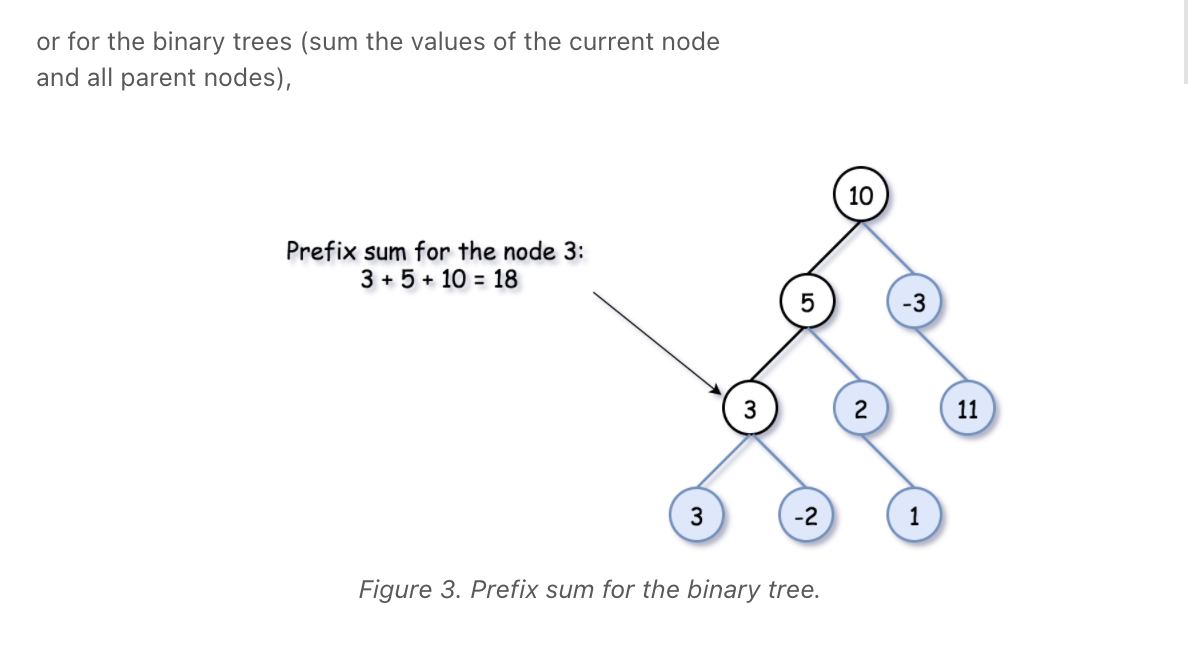
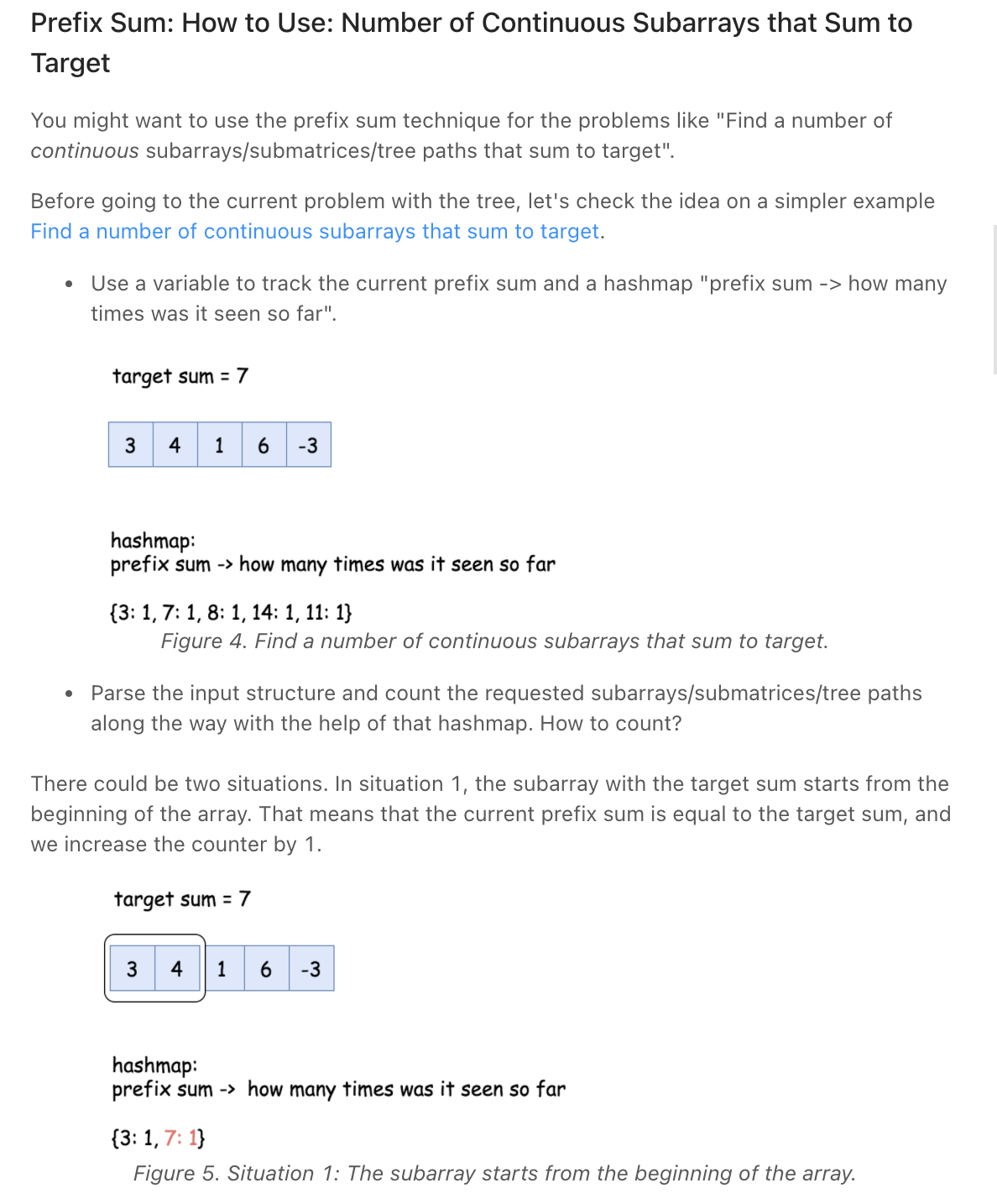
Path Sum III **


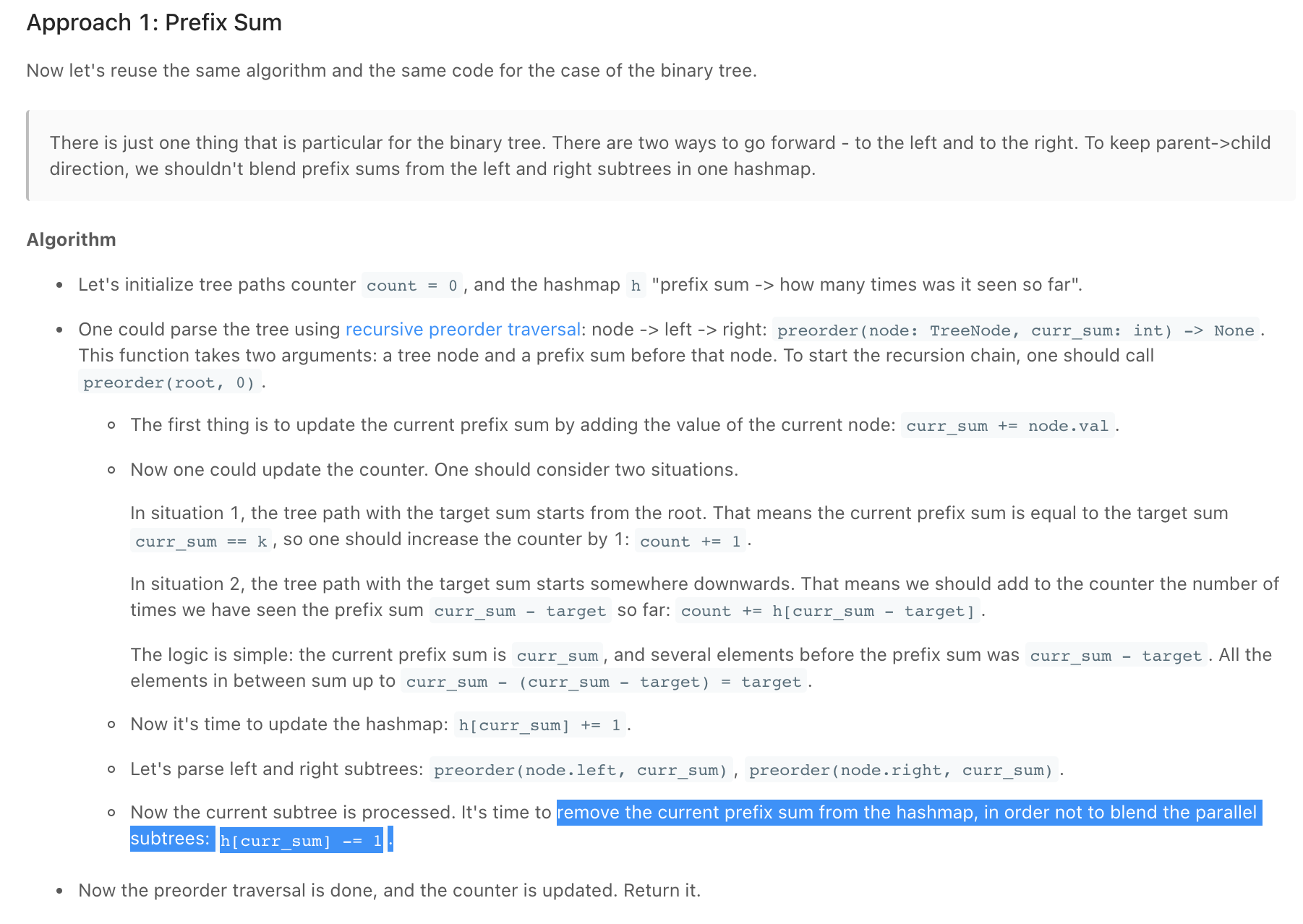
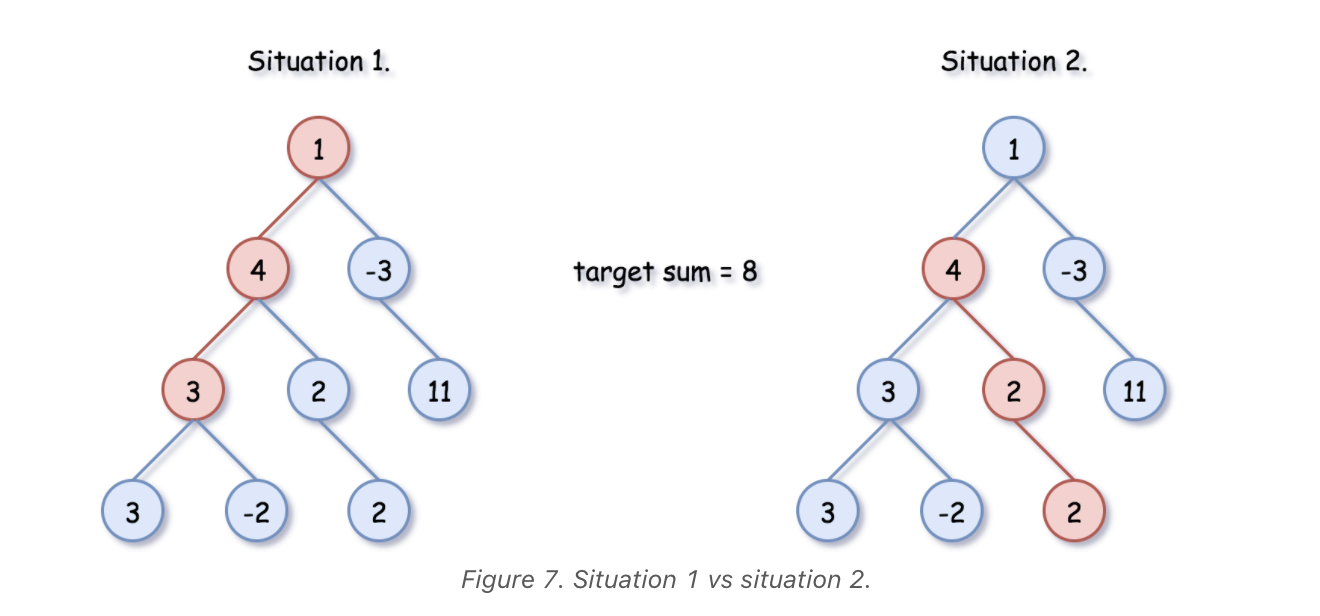
Screen Recording 2021-11-13 at 20.01.46.mov
""" 437. Path Sum III Given the root of a binary tree and an integer targetSum, return the number of paths where the sum of the values along the path equals targetSum. The path does not need to start or end at the root or a leaf, but it must go downwards (i.e., traveling only from parent nodes to child nodes). Example 1: Input: root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8 Output: 3 Explanation: The paths that sum to 8 are shown. Example 2: Input: root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22 Output: 3 Prerequisite: - https://leetcode.com/problems/subarray-sum-equals-k https://leetcode.com/problems/path-sum-iii """ from typing import Optional from collections import defaultdict # Definition for a binary tree node class TreeNode: def __init__(self, val=0, left=None, right=None): self.val = val self.left = left self.right = right """ The idea behind the approach below is as follows: - If the cumulative sum(represented by sum[i] in an array for sum up to i^th index) up to two indices is the same, the sum of the elements lying in between those indices is zero. - Extending the same thought further, if the cumulative sum up to two indices, say i and j is at a difference of k i.e. if sum[i] - sum[j] = k, the sum of elements lying between indices i and j is k. https://www.notion.so/paulonteri/Strings-Arrays-Linked-Lists-81ca9e0553a0494cb8bb74c5c85b89c8#2c097c6a479142b6bb1f584f122d3e9b """ class Solution: def pathSum(self, root: Optional[TreeNode], targetSum: int): sums = defaultdict(int) sums[0] = 1 return self.path_sum_helper(targetSum, sums, root, 0) def path_sum_helper(self, targetSum, sums, node, running_sum): if not node: return 0 total = 0 cur_sum = running_sum + node.val # check if the needed is in the sums dict needed = cur_sum - targetSum if needed in sums: total += sums[needed] # add the current sum to the sums dict sums[cur_sum] += 1 total += self.path_sum_helper(targetSum, sums, node.left, cur_sum) total += self.path_sum_helper(targetSum, sums, node.right, cur_sum) # remove the current sum to the sums dict sums[cur_sum] -= 1 if sums[cur_sum] == 0: sums.pop(cur_sum) return total -
Populating Next Right Pointers in Each Node *
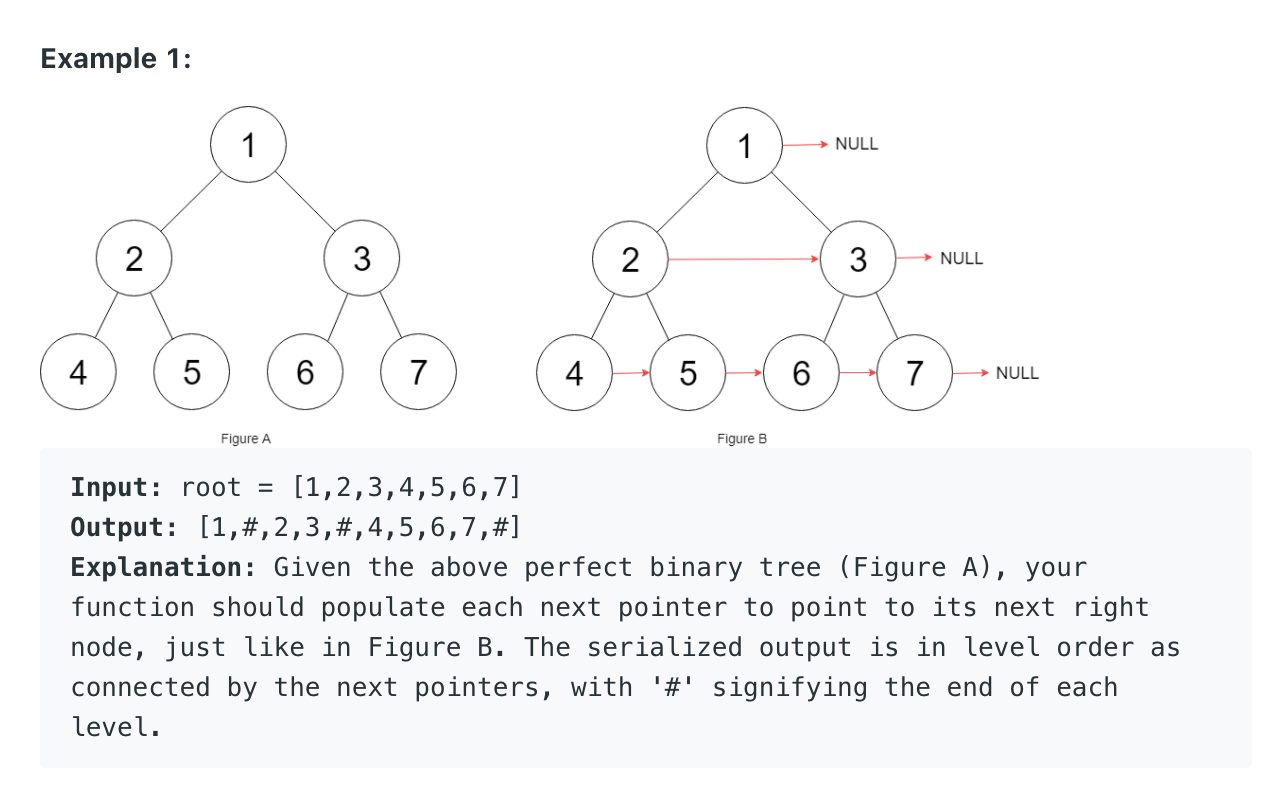
Remember that we are dealing with a perfect tree
""" 116. Populating Next Right Pointers in Each Node You are given a perfect binary tree where all leaves are on the same level, and every parent has two children. The binary tree has the following definition: struct Node { int val; Node *left; Node *right; Node *next; } Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to NULL. Initially, all next pointers are set to NULL. https://leetcode.com/problems/populating-next-right-pointers-in-each-node EPI 9.16 """ import collections # Definition for a Node. class Node: def __init__(self, val: int = 0, left: 'Node' = None, right: 'Node' = None, next: 'Node' = None): self.val = val self.left = left self.right = right self.next = next class Solution: def connect(self, root: 'Node'): if not root: return queue = [root] while queue: curr = queue.pop(0) if curr.left: curr.left.next = curr.right queue.append(curr.left) if curr.right: if curr.next: curr.right.next = curr.next.left queue.append(curr.right) return root """ """ class Solution_: def connect(self, root: 'Node'): if not root: return None prev_nodes = collections.defaultdict(lambda: None) queue = [(root, 0)] while queue: curr, depth = queue.pop(0) curr.next = prev_nodes[depth] prev_nodes[depth] = curr # next if curr.right: queue.append((curr.right, depth+1)) if curr.left: queue.append((curr.left, depth+1)) return root -
Flatten Binary Tree to Linked List **


Solution 1

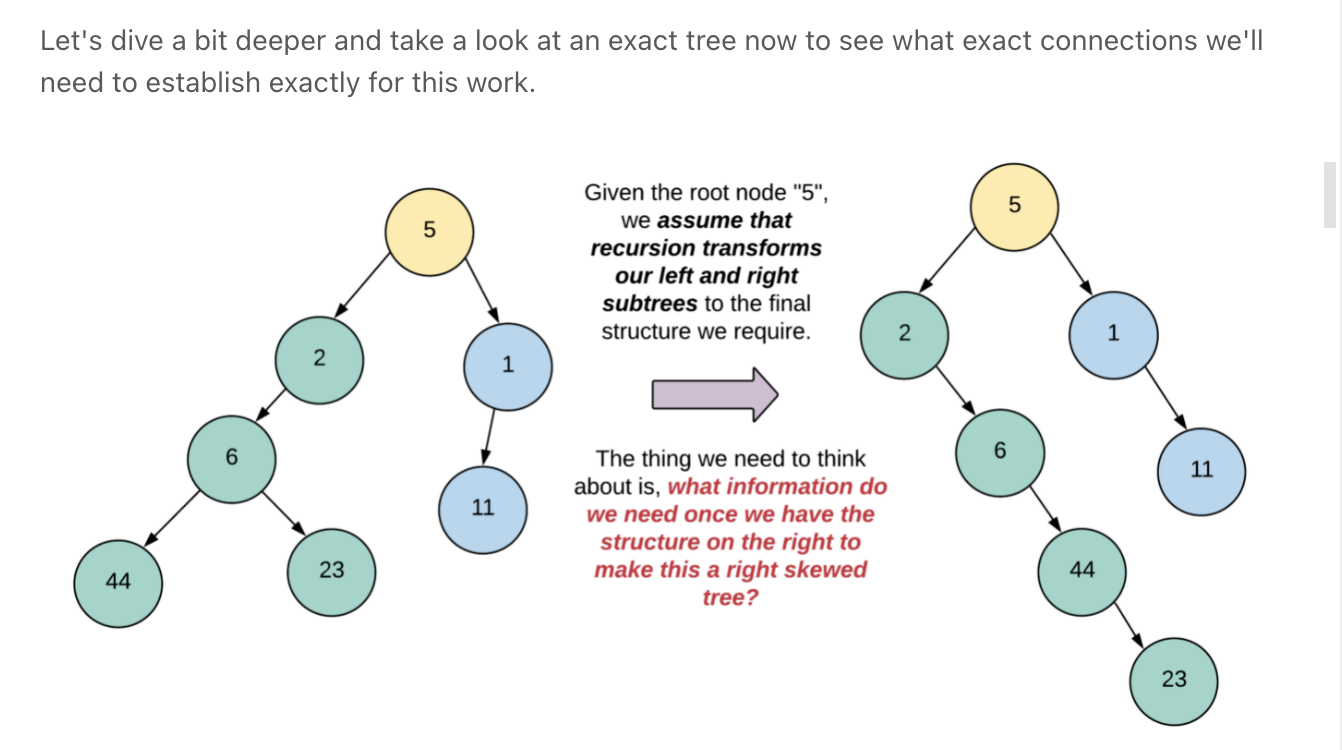
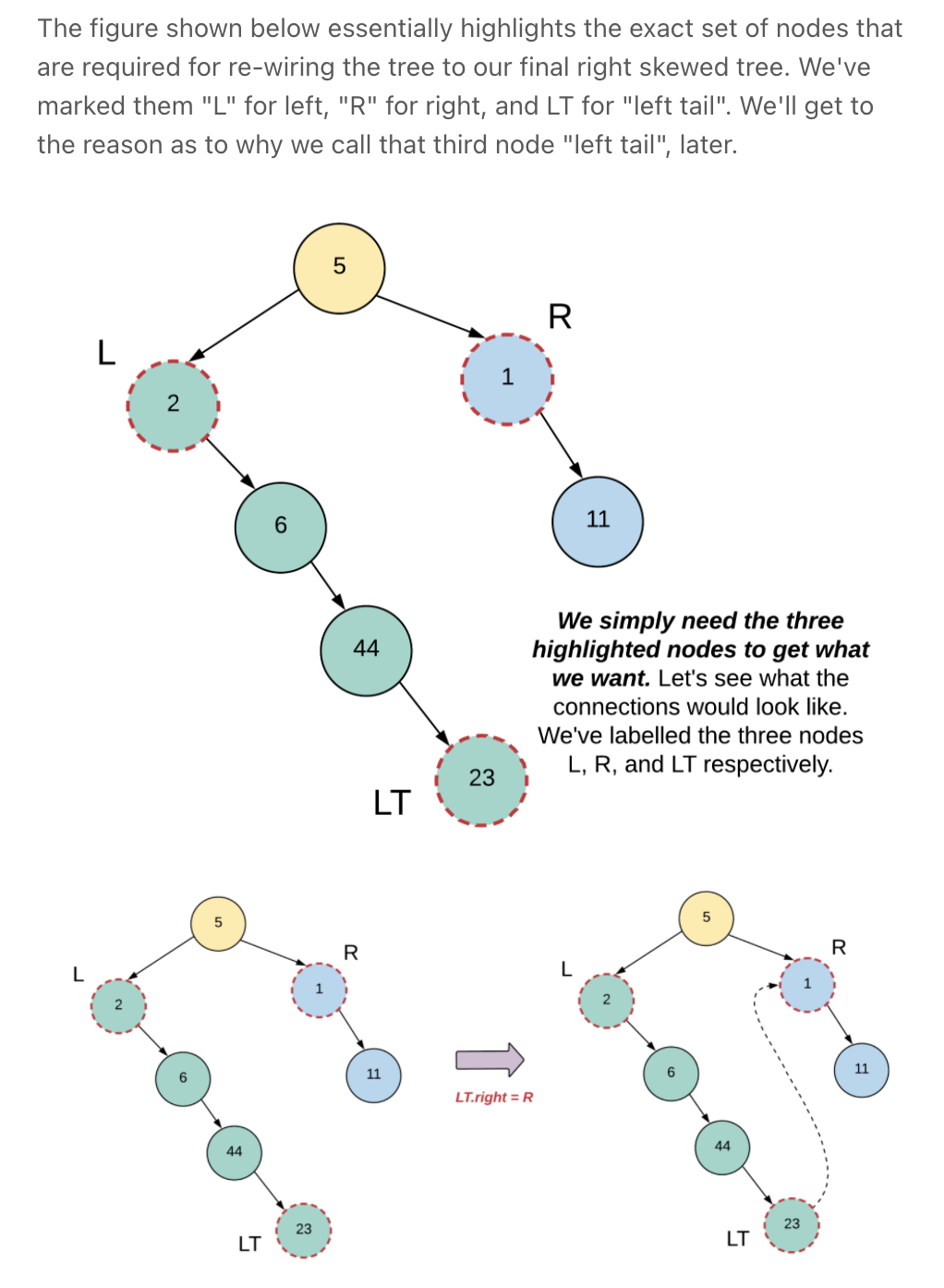
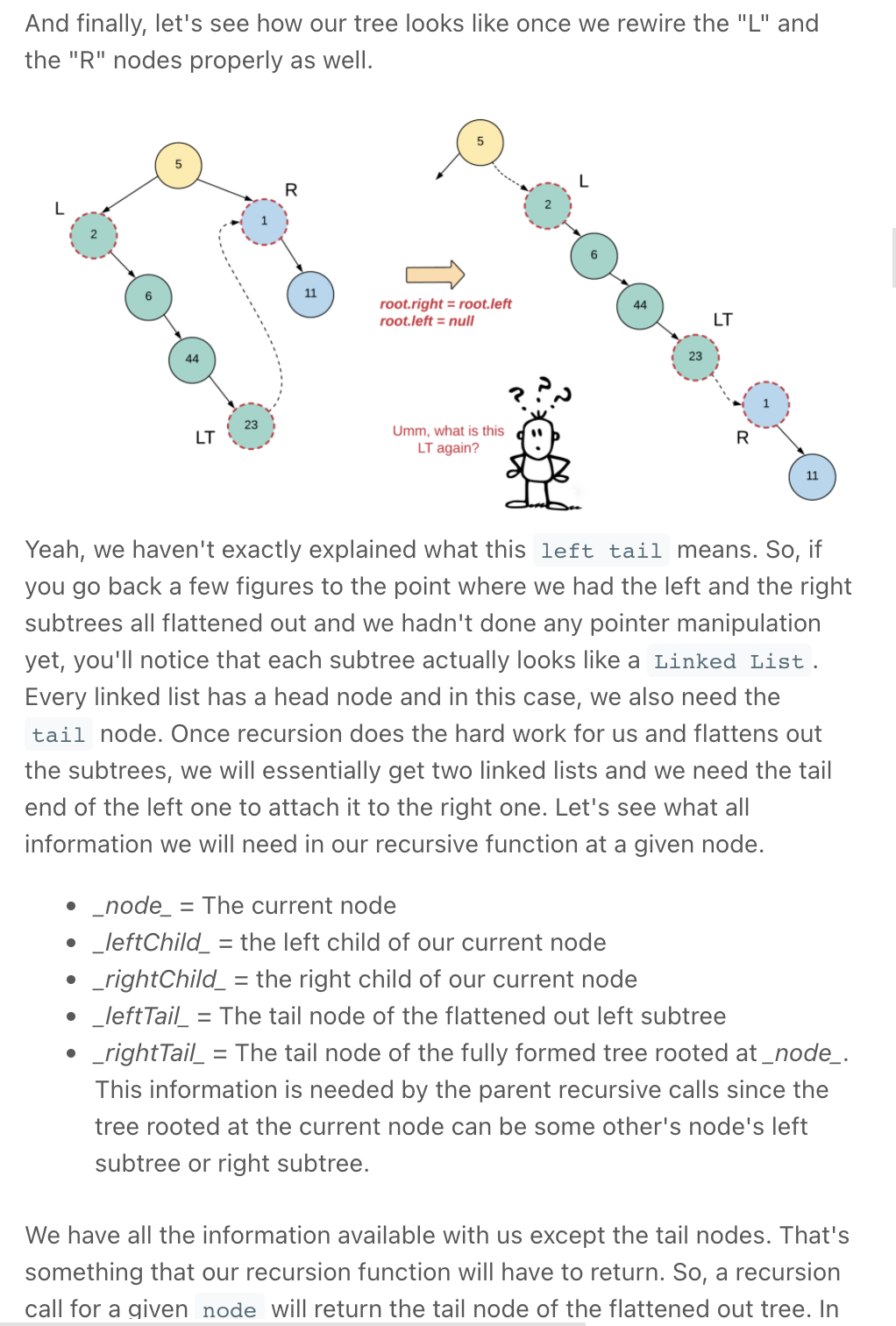


# Definition for a binary tree node. class TreeNode: def __init__(self, val=0, left=None, right=None): self.val = val self.left = left self.right = right class Solution_: def flatten(self, root): if not root: return None right = root.right if root.left: # place the left subtree between the root & root.right root.right = root.left left_ending = self.flatten(root.left) left_ending.right = right # remove left root.left = None furthest = self.flatten(root.right) return furthest or root """ our algorithm will return the tail node of the flattened out tree. For a given node, we will recursively flatten out the left and the right subtrees and store their corresponding tail nodes in left_ending and right_ending respectively. Next, we will make the following connections (only if there is a left child for the current node, else the left_ending would be null) (Place the left subtree between the root & root.right) left_ending.right = node.right node.right = node.left node.left = None Next we have to return the tail of the final, flattened out tree rooted at node. So, if the node has a right child, then we will return the right_ending, else, we'll return the left_ending """ class Solution: def flatten(self, root): if not root: return None left_ending = self.flatten(root.left) right_ending = self.flatten(root.right) # If there was a left subtree, we shuffle the connections # around so that there is nothing on the left side anymore. if left_ending: # Place the left subtree between the root & root.right left_ending.right = root.right root.right = root.left # Remove left root.left = None # We need to return the "rightmost" node after we are done wiring the new connections. # 2. For a node with only a left subtree, the rightmost node will be left_ending because it has been moved to the right subtree # 3. For a leaf node, we simply return the node return right_ending or left_ending or rootSolution 2

class Solution: def flatten(self, root): if not root: return None stack = [root] while stack: node = stack.pop() if node.right: stack.append(node.right) if node.left: stack.append(node.left) node.left = None if stack: node.right = stack[-1] # PeekApproach 3: O(1) Iterative Solution (Greedy & similar to Morris Traversal)
similar to Morris Traversal

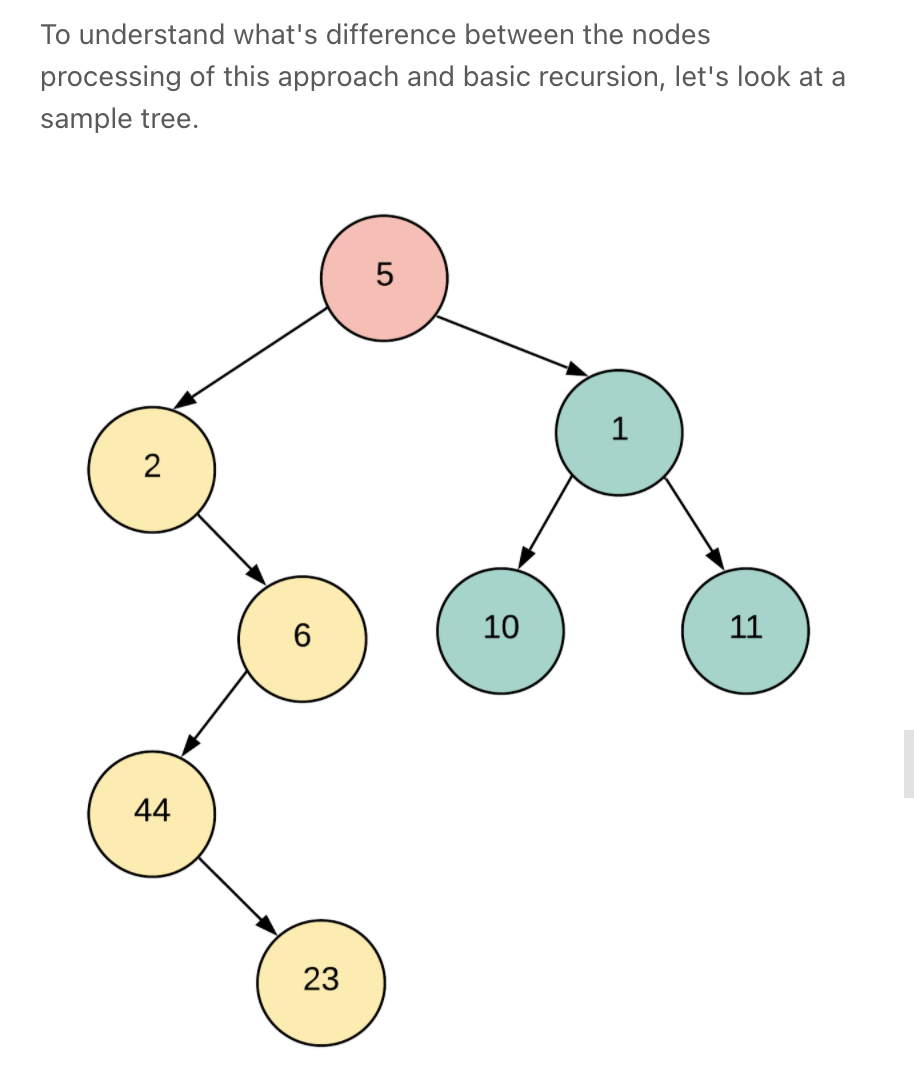
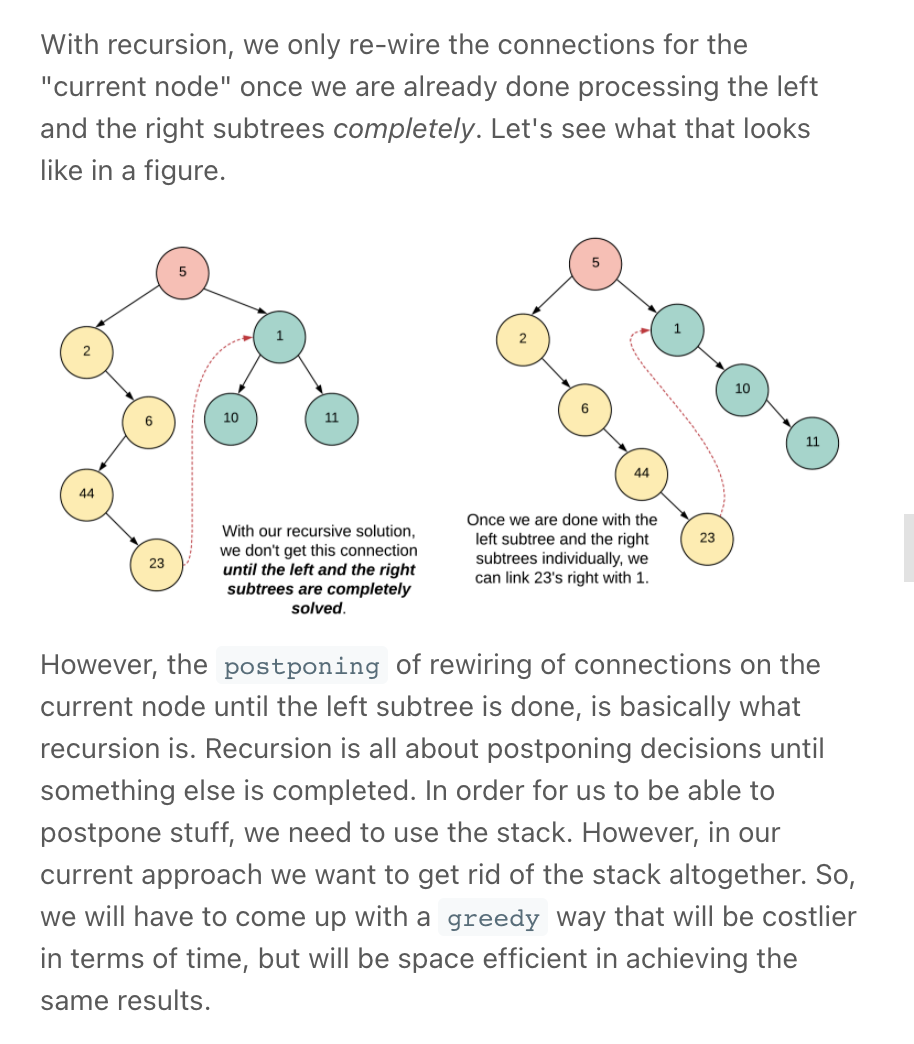

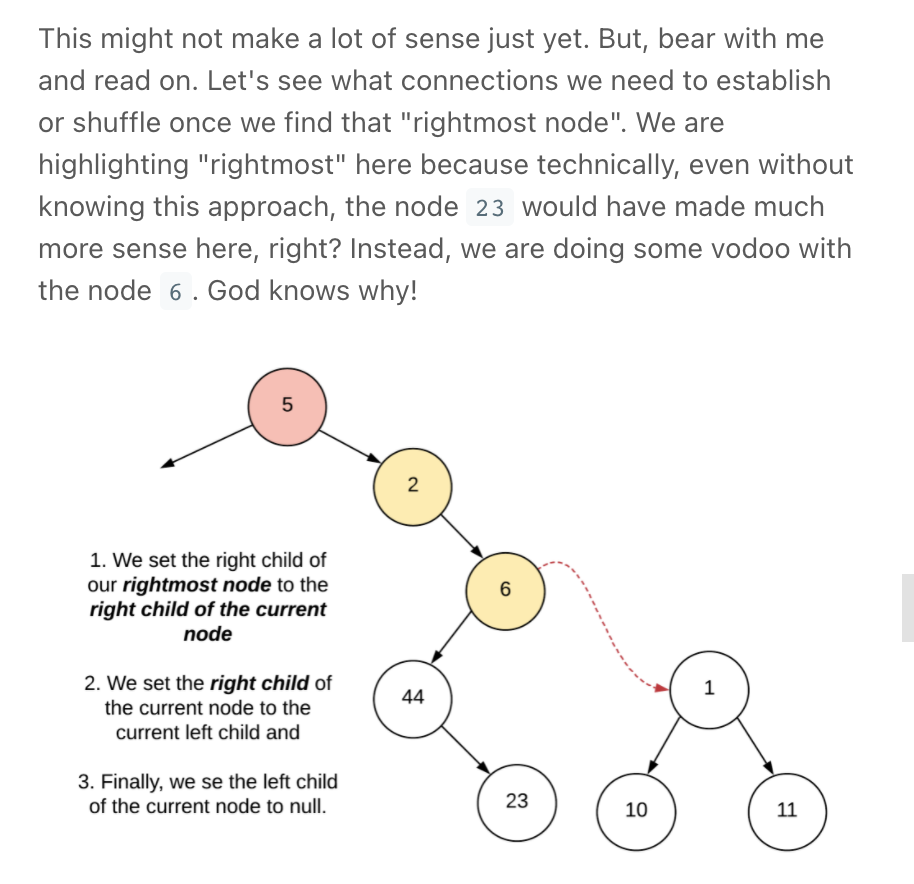


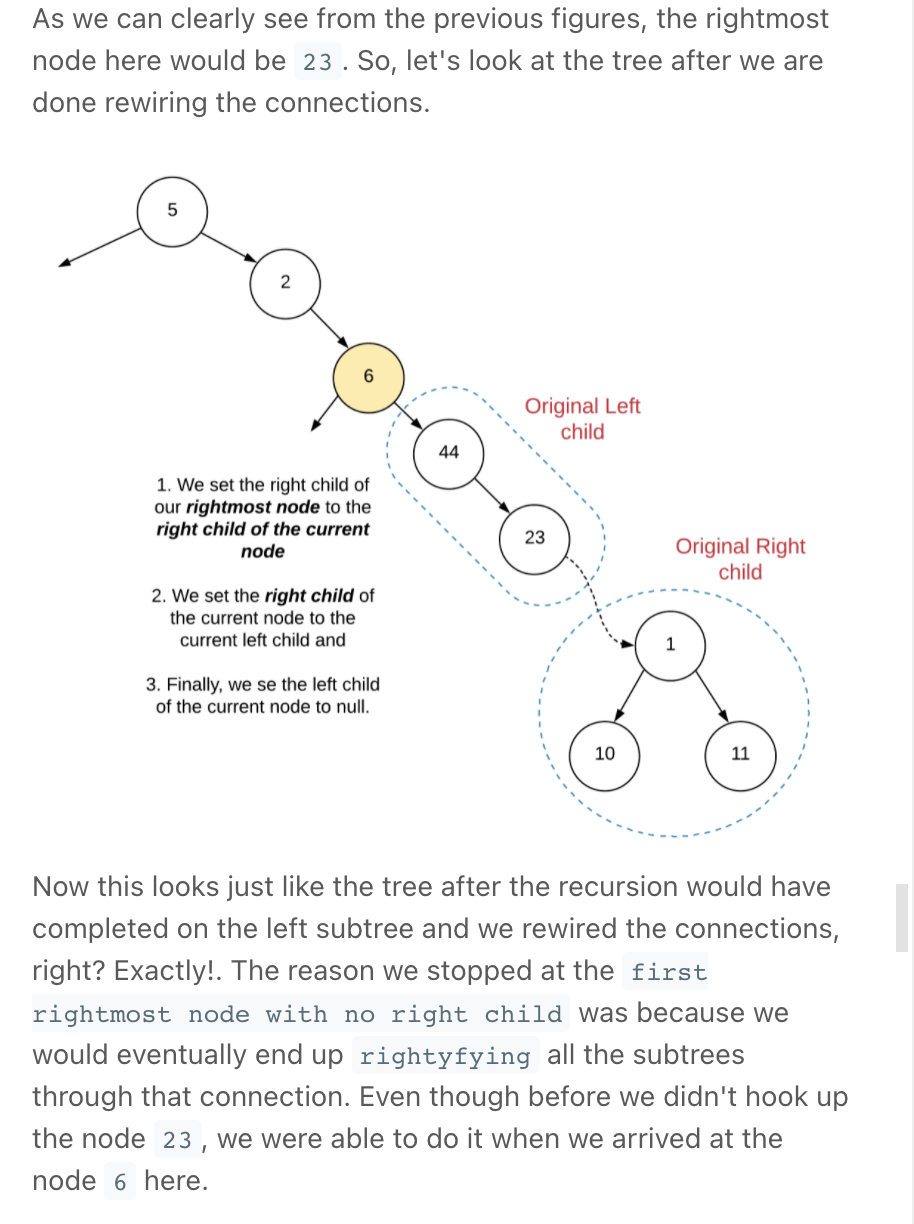

""" O(1) Iterative Solution (Greedy & similar to Morris Traversal) """ class Solution: def flatten(self, root): if not root: return None curr = root while curr: # If there was a left subtree, we shuffle the connections # around so that there is nothing on the left side anymore. if curr.left: l_right_most = self.find_right_most(curr.left) # place the left subtree between the root & root.right l_right_most.right = curr.right curr.right = curr.left # remove left curr.left = None curr = curr.right def find_right_most(self, root): curr = root while curr.right: curr = curr.right return curr -
Find Successor
""" Find Successor: Write a function that takes in a Binary Tree (where nodes have an additional pointer to their parent node) as well as a node contained in that tree and returns the given node's successor. A node's successor is the next node to be visited (immediately after the given node) when traversing its tree using the in-order tree-traversal technique. A node has no successor if it's the last node to be visited in the in-order traversal. If a node has no successor, your function should return None / null. Each BinaryTree node has an integer value, a parent node, a left child node, and a right child node. Children nodes can either be BinaryTree nodes themselves or None / null. Sample Input tree = 1 / \ 2 3 / \ 4 5 / 6 node = 5 Sample Output 1 // This tree's in-order traversal order is: // 6 -> 4 -> 2 -> 5 -> 1 -> 3 // 1 comes immediately after 5. https://www.algoexpert.io/questions/Find%20Successor """ # This is an input class. Do not edit. class BinaryTree: def __init__(self, value, left=None, right=None, parent=None): self.value = value self.left = left self.right = right self.parent = parent def findSuccessor(tree, node): if tree is None: return left = findSuccessor(tree.left, node) if tree == node: return findSuccessorHelper(tree, node) right = findSuccessor(tree.right, node) return left or right def findSuccessorHelper(tree, node): # if has a right child # will be left most node of right child if tree.right is not None: # find left most in right subtree left_most = tree.right while left_most.left is not None: left_most = left_most.left return left_most # no right child -> successor is ancestor: # find ancestor where child is left child else: # find where we first branched left while tree is not None: if tree.parent is not None and tree == tree.parent.left: return tree.parent tree = tree.parent return None """ If a node has a right subtree: - its successor is the futhest left node in the right subtree else: - its successor is the first point where we turned left - i.e if tree == tree.parent.left, return tree.parent Sample Input tree = 1 / \ 2 3 / \ 4 5 / / \ 6 7 8 node = 5 output = 8 node = 8 output = 1 node = 2 output = 7 node = 1 output = 3 """ -
Subtree of Another Tree *
-
Check subtree




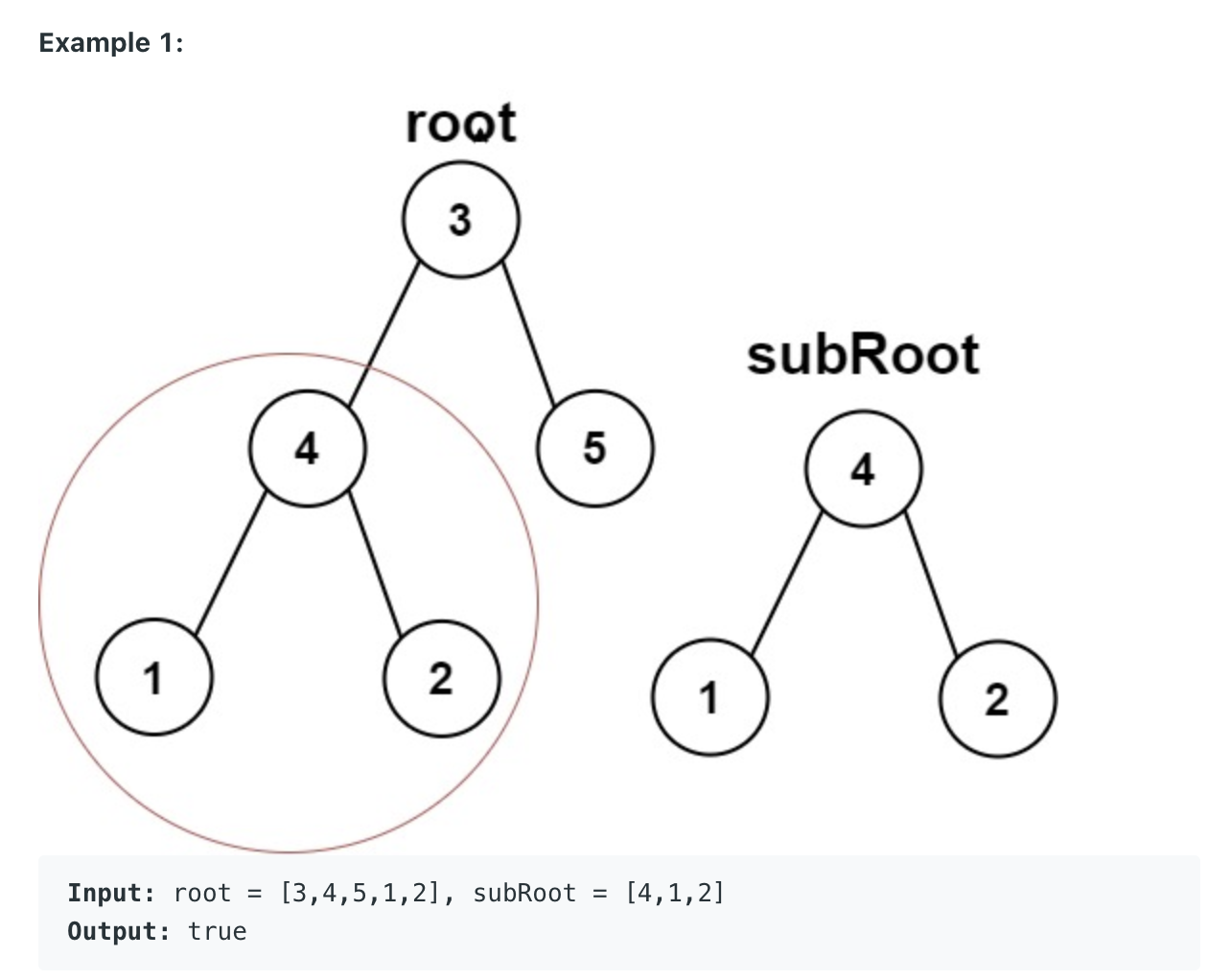
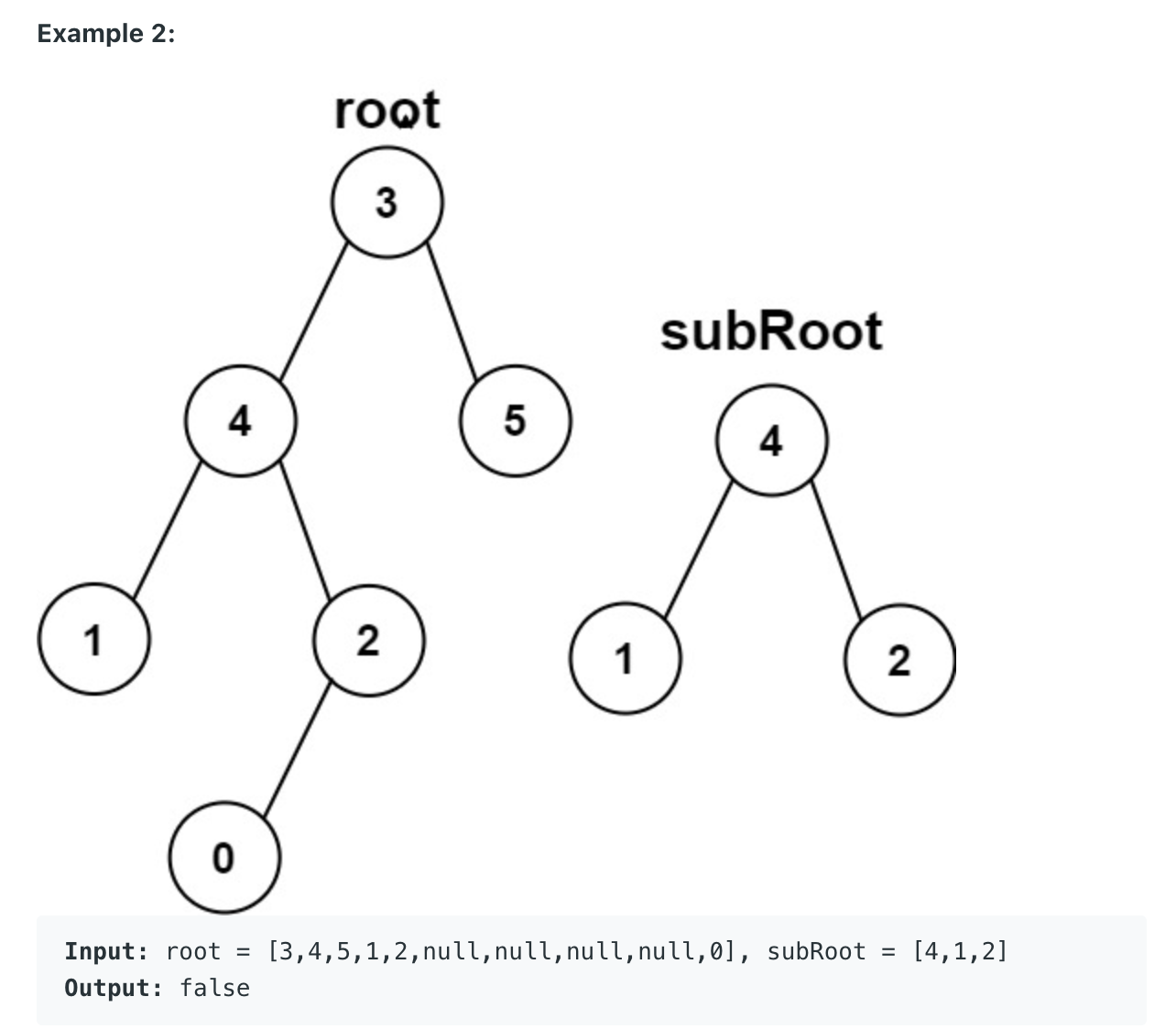
""" Subtree of Another Tree: Given two non-empty binary trees s and t, check whether tree t has exactly the same structure and node values with a subtree of s. A subtree of s is a tree consists of a node in s and all of this node's descendants. The tree s could also be considered as a subtree of itself. https://leetcode.com/problems/subtree-of-another-tree/ """ # Definition for a binary tree node. class TreeNode: def __init__(self, val=0, left=None, right=None): self.val = val self.left = left self.right = right class Solution: def isSubtree(self, s: TreeNode, t: TreeNode): return self.traverse(s, t) def traverse(self, s, t): if self.checkSubTreeFunction(s, t) == True: return True if s is None: return False return self.traverse(s.left, t) or self.traverse(s.right, t) def checkSubTreeFunction(self, s, t): if s == None and t == None: return True elif s == None or t == None or s.val != t.val: return False return self.checkSubTreeFunction(s.left, t.left) and self.checkSubTreeFunction(s.right, t.right) -
-
Construct Binary Tree from Preorder and Inorder Traversal
[1/3] CONSTRUCT BINARY TREE FROM PREORDER/INORDER TRAVERSAL - Code & Whiteboard
Construct Binary Tree from Inorder and Preorder Traversal - Leetcode 105 - Python
LeetCode 105. Construct Binary Tree from Preorder and Inorder Traversal (Algorithm Explained)
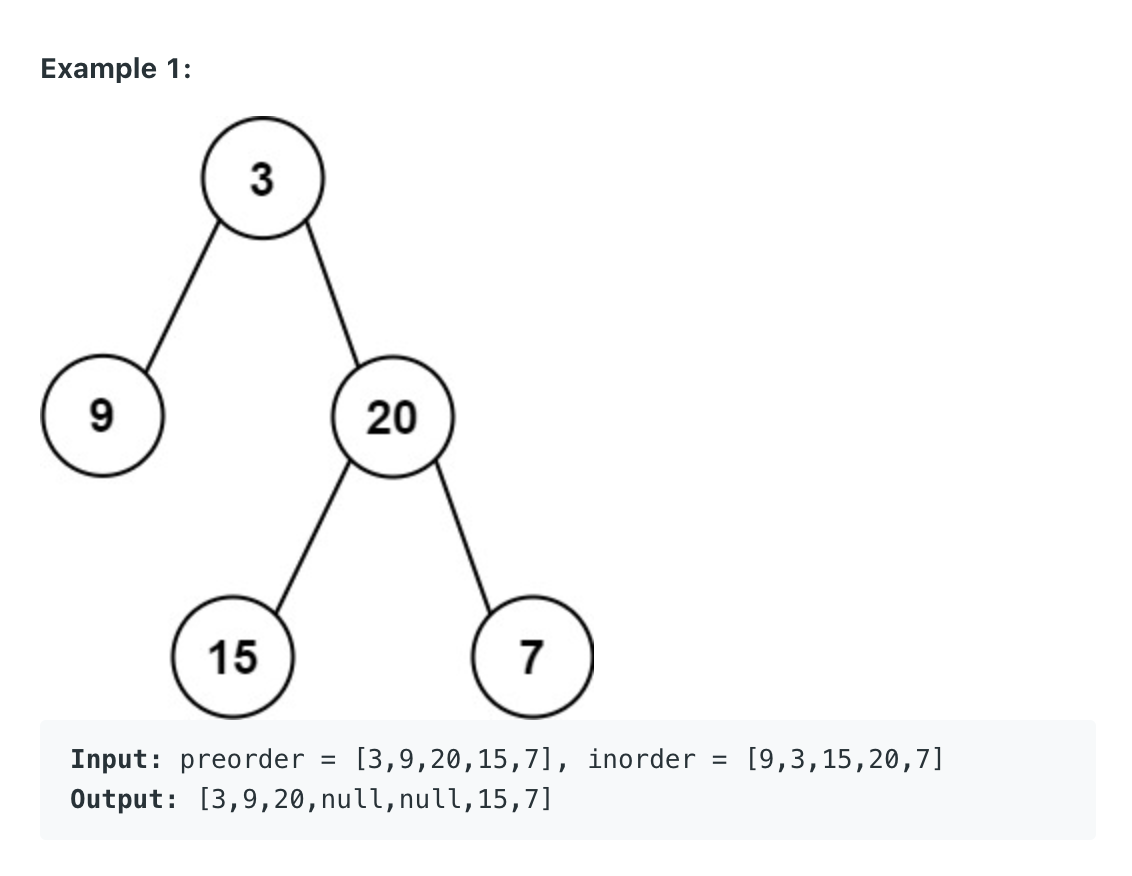
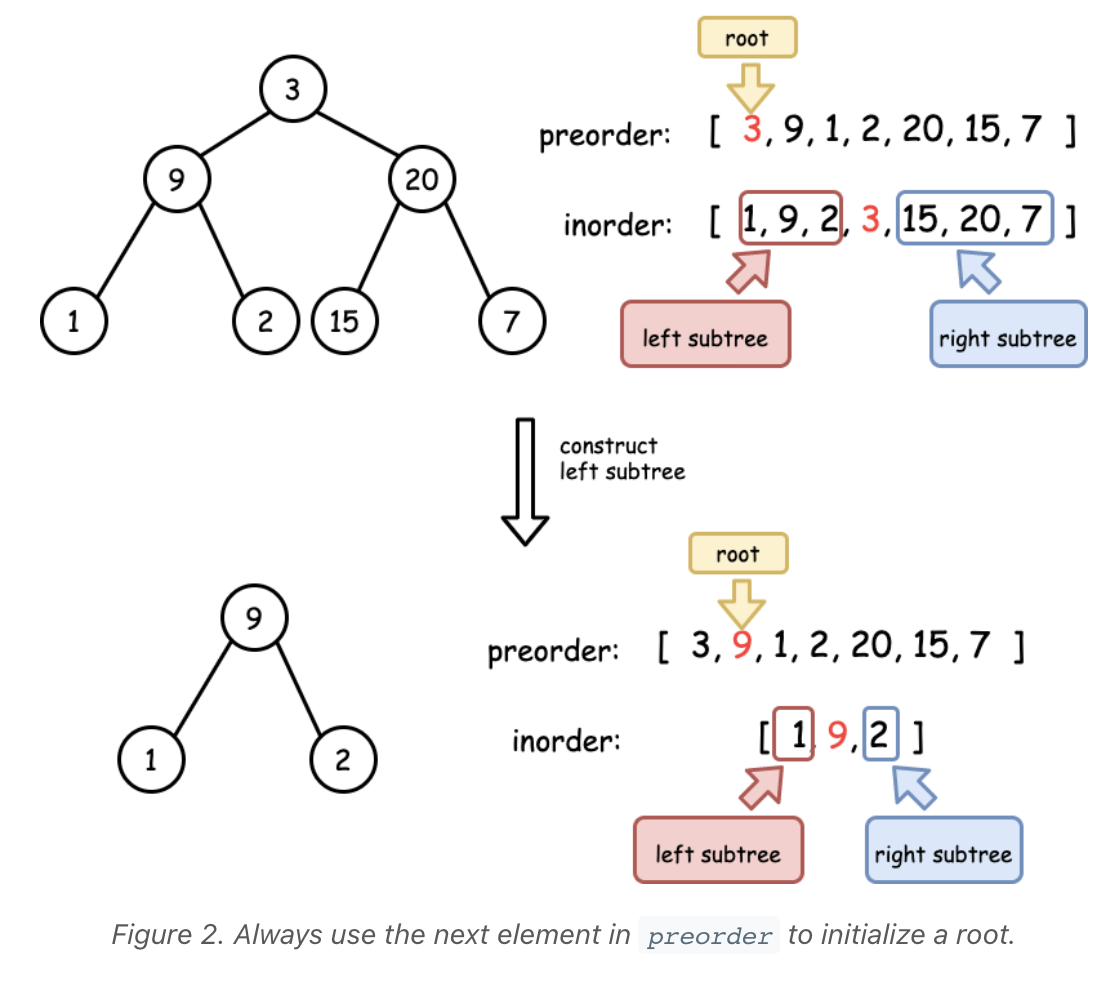
""" Construct Binary Tree from Preorder and Inorder Traversal: Given two integer arrays preorder and inorder where preorder is the preorder traversal of a binary tree and inorder is the inorder traversal of the same tree, construct and return the binary tree. Example 1: Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7] Output: [3,9,20,null,null,15,7] Example 2: Input: preorder = [-1], inorder = [-1] Output: [-1] https://leetcode.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal/ """ from typing import List class TreeNode: def __init__(self, val=0, left=None, right=None): self.val = val self.left = left self.right = right # --------------------------------------------------------------------------------------------------------------------- """ - The root will be the first element in the preorder sequence - Next, locate the index of the root node in the inorder sequence - this will help you know the number of nodes to its left & the number to its right - repeat this recursively """ class SolutionBF(object): def buildTree(self, preorder, inorder): return self.dfs(preorder, inorder) def dfs(self, preorder, inorder): if len(preorder) == 0: return None root = TreeNode(preorder[0]) mid = inorder.index(preorder[0]) root.left = self.dfs(preorder[1: mid+1], inorder[: mid]) root.right = self.dfs(preorder[mid+1:], inorder[mid+1:]) return root class SolutionBF0: def buildTree(self, preorder, inorder): if len(inorder) == 0: # the remaining preorder values do not belong in this subtree return None if len(preorder) == 1: return TreeNode(preorder[0]) ino_index = inorder.index(preorder.pop(0)) # remove from preorder node = TreeNode(inorder[ino_index]) node.left = self.buildTree(preorder, inorder[:ino_index]) node.right = self.buildTree(preorder, inorder[ino_index+1:]) return node class SolutionBF00: def buildTree(self, preorder, inorder): preorder_pos = 0 def buildTreeHelper(preorder, inorder): nonlocal preorder_pos # we do not have valid nodes to be placed if preorder_pos >= len(preorder): return # # create node # node inorder_idx = inorder.index(preorder[preorder_pos]) preorder_pos += 1 node = TreeNode(inorder[inorder_idx]) # children -> will pass only valid children below -> (inorder[:inorder_idx] & inorder[inorder_idx+1:] does that) node.left = buildTreeHelper(preorder, inorder[:inorder_idx]) node.right = buildTreeHelper(preorder, inorder[inorder_idx+1:]) return node return buildTreeHelper(preorder, inorder) # def buildTreeHelper2( preorder, inorder): # nonlocal preorder_pos # if preorder_pos >= len(preorder): # return # # # create node # # node # inorder_idx = inorder.index( preorder[preorder_pos] ) # preorder_pos += 1 # node = TreeNode(inorder[inorder_idx ]) # left = inorder[:inorder_idx] # right = inorder[inorder_idx+1:] # if left: # node.left = buildTreeHelper(preorder, left) # if right: # node.right = buildTreeHelper(preorder, right) # return node # return buildTreeHelper2(preorder, inorder) # --------------------------------------------------------------------------------------------------------------------- """ - The root will be the first element in the preorder sequence - Next, locate the index of the root node in the inorder sequence - this will help you know the number of nodes to its left & the number to its right - repeat this recursively - iterate through the preorder array and check if the current can be placed in the current tree(or recursive call) - We use the remaining inorder traversal to determine(restrict) whether the current preorder node is in the left or right """ class Solution: def buildTree(self, preorder, inorder): preorder_pos = 0 inorder_idxs = {val: idx for idx, val in enumerate(inorder)} def helper(inorder_left, inorder_right): nonlocal preorder_pos if preorder_pos == len(preorder): return if inorder_left > inorder_right: return val = preorder[preorder_pos] preorder_pos += 1 node = TreeNode(val) inorder_idx = inorder_idxs[val] # start with left ! node.left = helper(inorder_left, inorder_idx-1) node.right = helper(inorder_idx+1, inorder_right) return node return helper(0, len(inorder)-1) -
Construct Binary Tree from Inorder and Postorder Traversal
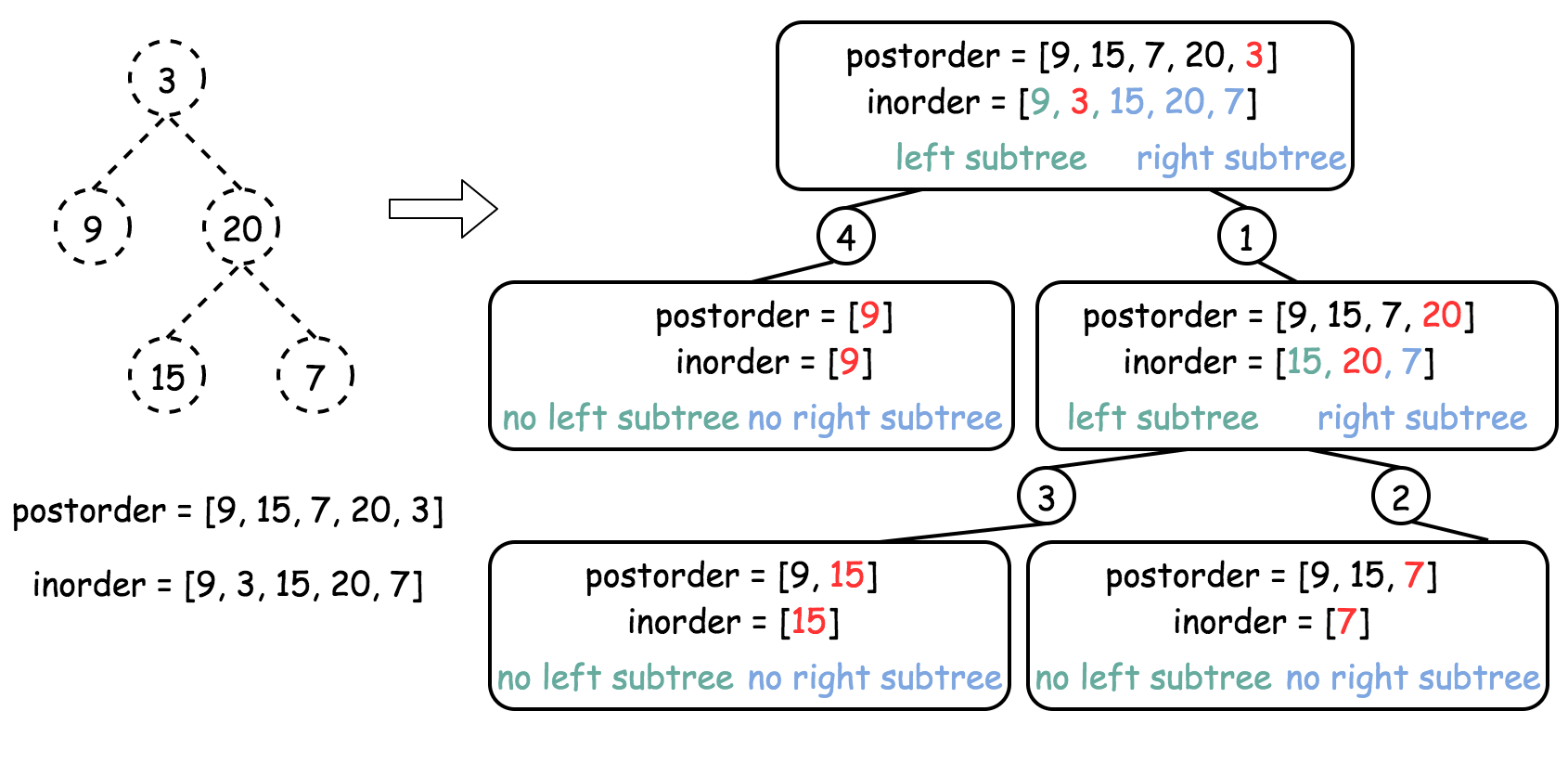
""" 106. Construct Binary Tree from Inorder and Postorder Traversal Given two integer arrays inorder and postorder where inorder is the inorder traversal of a binary tree and postorder is the postorder traversal of the same tree, construct and return the binary tree. Example 1: Input: inorder = [9,3,15,20,7], postorder = [9,15,7,20,3] Output: [3,9,20,null,null,15,7] Example 2: Input: inorder = [-1], postorder = [-1] Output: [-1] https://leetcode.com/problems/construct-binary-tree-from-inorder-and-postorder-traversal """ # Definition for a binary tree node. class TreeNode: def __init__(self, val=0, left=None, right=None): self.val = val self.left = left self.right = right class Solution: def buildTree(self, inorder, postorder): postorder_idx = len(postorder)-1 inorder_idxs = {val: idx for idx, val in enumerate(inorder)} def helper(inorder_left, inorder_right): nonlocal postorder_idx if postorder_idx < 0: return None if inorder_left > inorder_right: return None val = postorder[postorder_idx] postorder_idx -= 1 # create node node = TreeNode(val) inorder_idx = inorder_idxs[val] # start with right ! node.right = helper(inorder_idx+1, inorder_right) node.left = helper(inorder_left, inorder_idx-1) return node return helper(0, len(inorder)-1) -
Preorder/Postorder
-
Binary Tree Inorder Traversal - Iterative **
Screen Recording 2021-10-23 at 13.36.24.mov
""" Binary Tree Inorder Traversal: Given the root of a binary tree, return the inorder traversal of its nodes' values. https://leetcode.com/problems/binary-tree-inorder-traversal/ https://www.enjoyalgorithms.com/blog/iterative-binary-tree-traversals-using-stack https://www.educative.io/edpresso/how-to-perform-an-iterative-inorder-traversal-of-a-binary-tree https://www.techiedelight.com/inorder-tree-traversal-iterative-recursive After this: - https://leetcode.com/problems/binary-search-tree-iterator """ # Definition for a binary tree node. class TreeNode: def __init__(self, val=0, left=None, right=None): self.val = val self.left = left self.right = right """ - add all left nodes to stack - visit left most node - move to the right """ class Solution_: def inorderTraversal(self, root: TreeNode): if not root: return None result = [] stack = [] curr = root while stack or curr: # add all left # put the left most value(s) to the top of the stack while curr and curr.left: stack.append(curr) curr = curr.left # the top of the stack has the left most unvisited value # visit node if not curr: curr = stack.pop() result.append(curr.val) # - has no unvisited left # - itself is visited # so the next to be visited is right curr = curr.right return result """ class Solution: def inorderTraversal(self, root: TreeNode): output = [] stack = [] curr = root while curr is not None or len(stack) > 0: # add all left while curr is not None: stack.append(curr) curr = curr.left # visit node temp = stack.pop() output.append(temp.val) curr = temp.right return output """ # 10 # / \ # 4 17 # / \ \ # 2 5 19 # / / # 1 18 class Solution: def inorderTraversal(self, root: TreeNode): if not root: return None result = [] stack = [] curr = root while stack or curr: # put the left most value(s) to the top of the stack while curr: stack.append(curr) curr = curr.left # the top of the stack has the left most unvisited value # visit node curr = stack.pop() result.append(curr.val) # - has no unvisited left # - itself is visited # so the next to be visited is right # eg: after 4 is 5 in the example above curr = curr.right return result """ ------------------------------------------------------------------------------------------------------------ """ class Solution1: def inorderTraversal(self, root): output = [] self.inorderTraversalHelper(root, output) return output def inorderTraversalHelper(self, root, output): if not root: return self.inorderTraversalHelper(root.left, output) output.append(root.val) self.inorderTraversalHelper(root.right, output) -
Morris Inorder Tree Traversal - Inorder with O(1) space ***

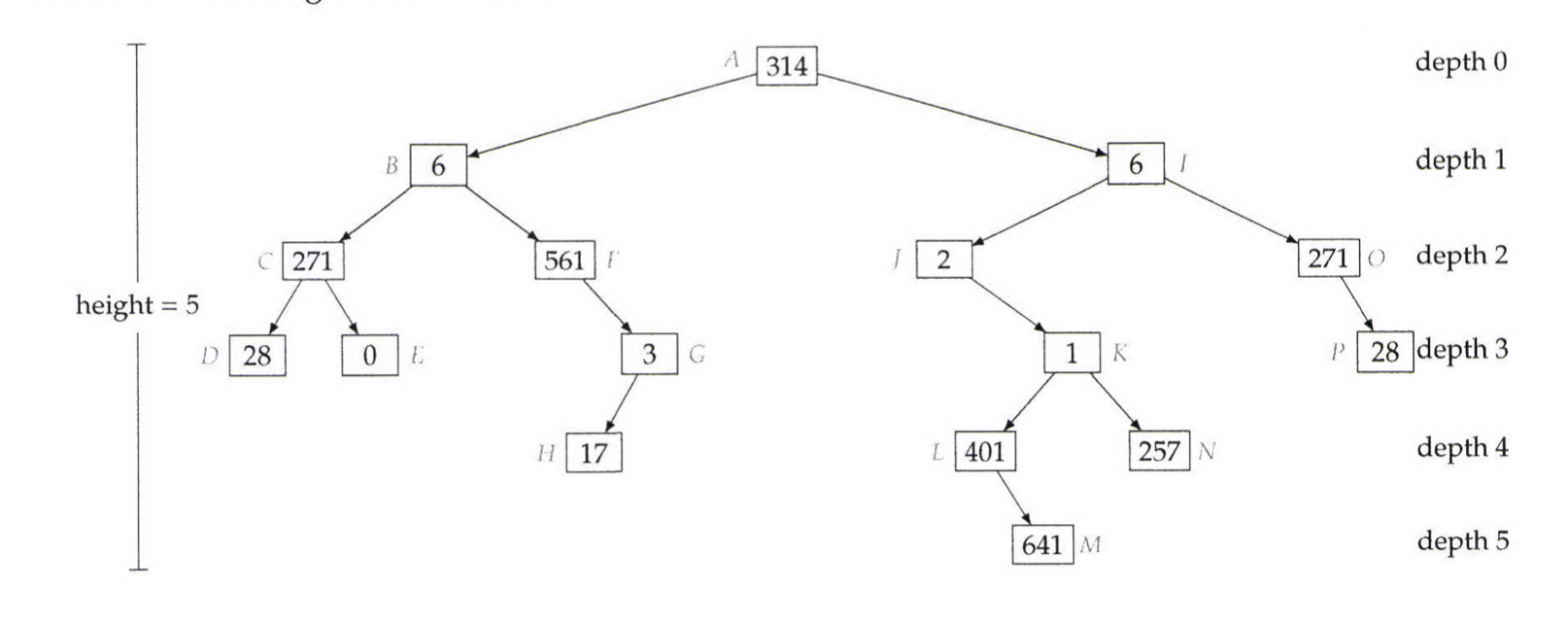

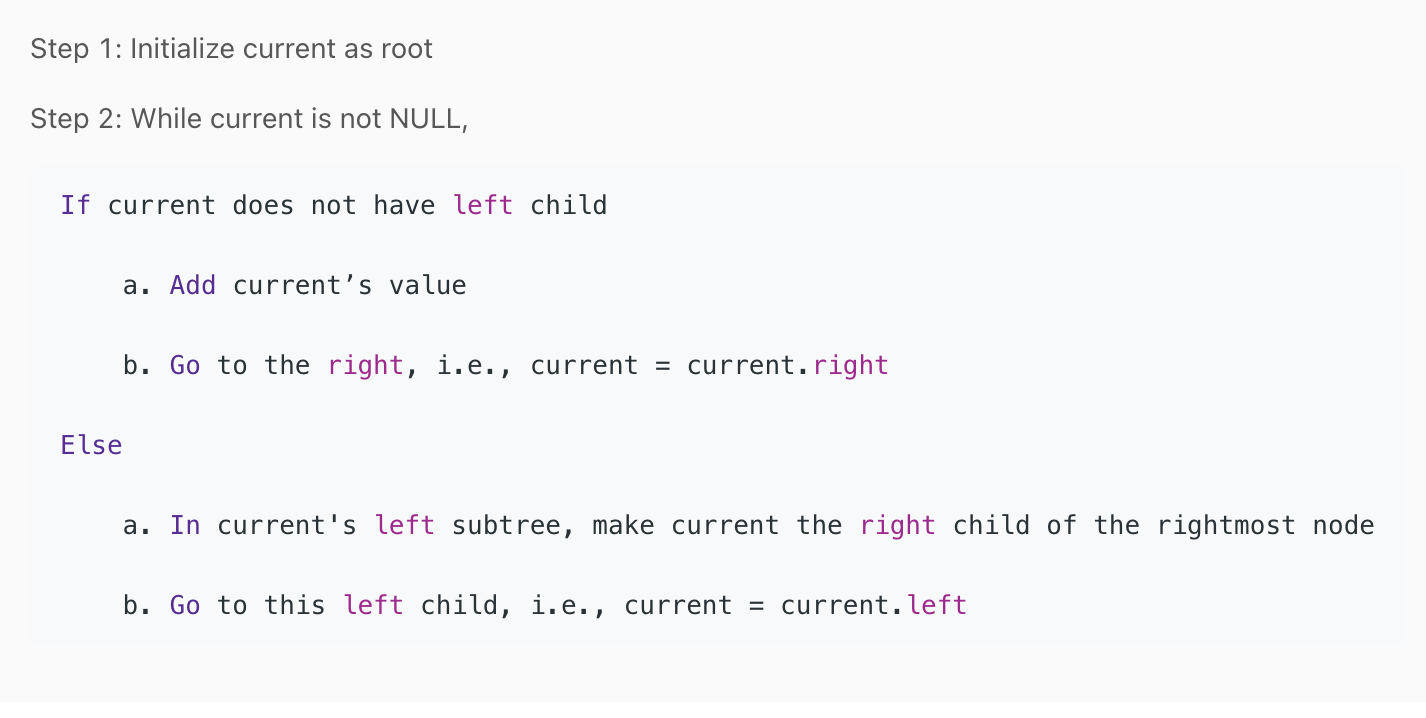
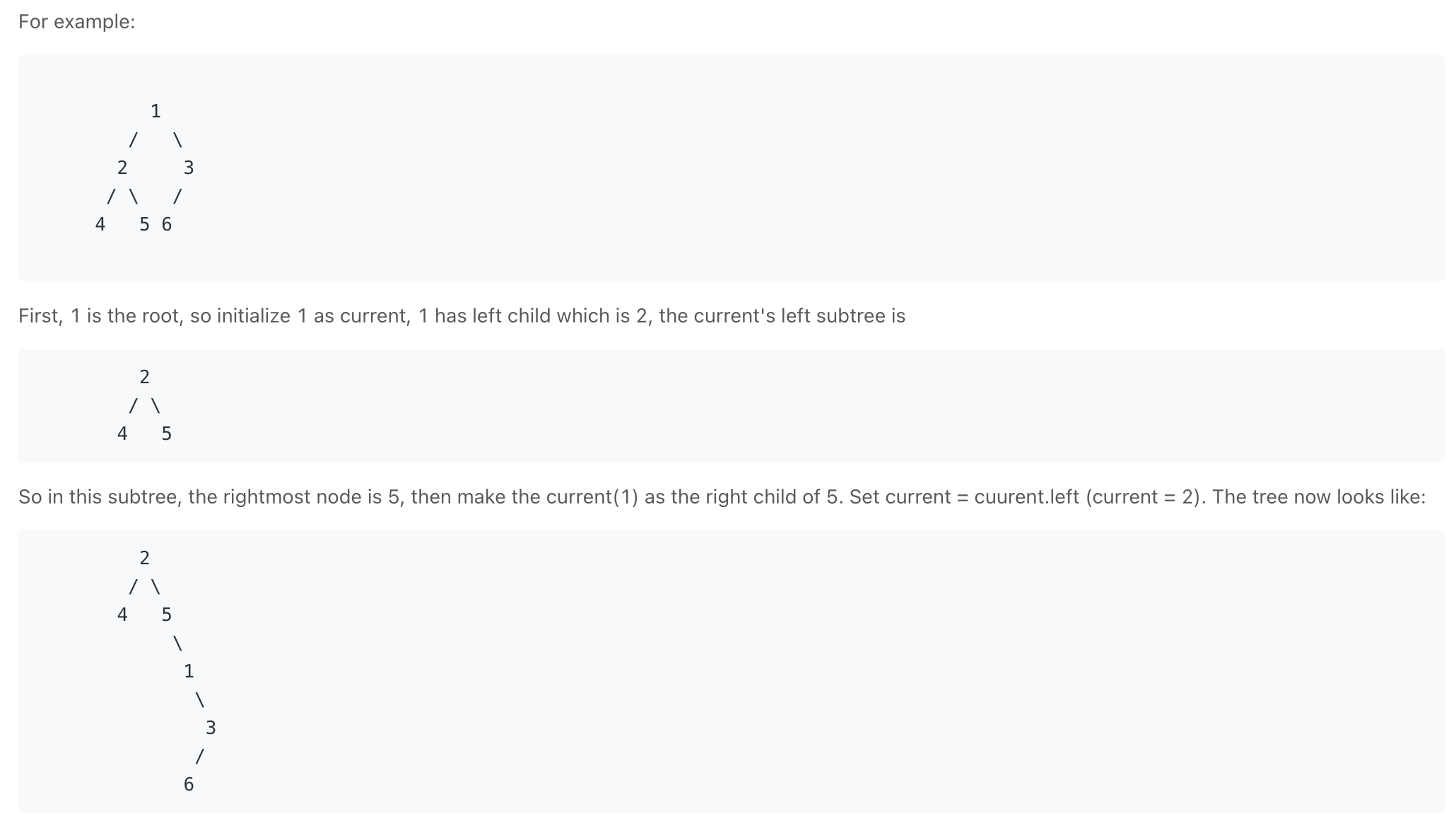
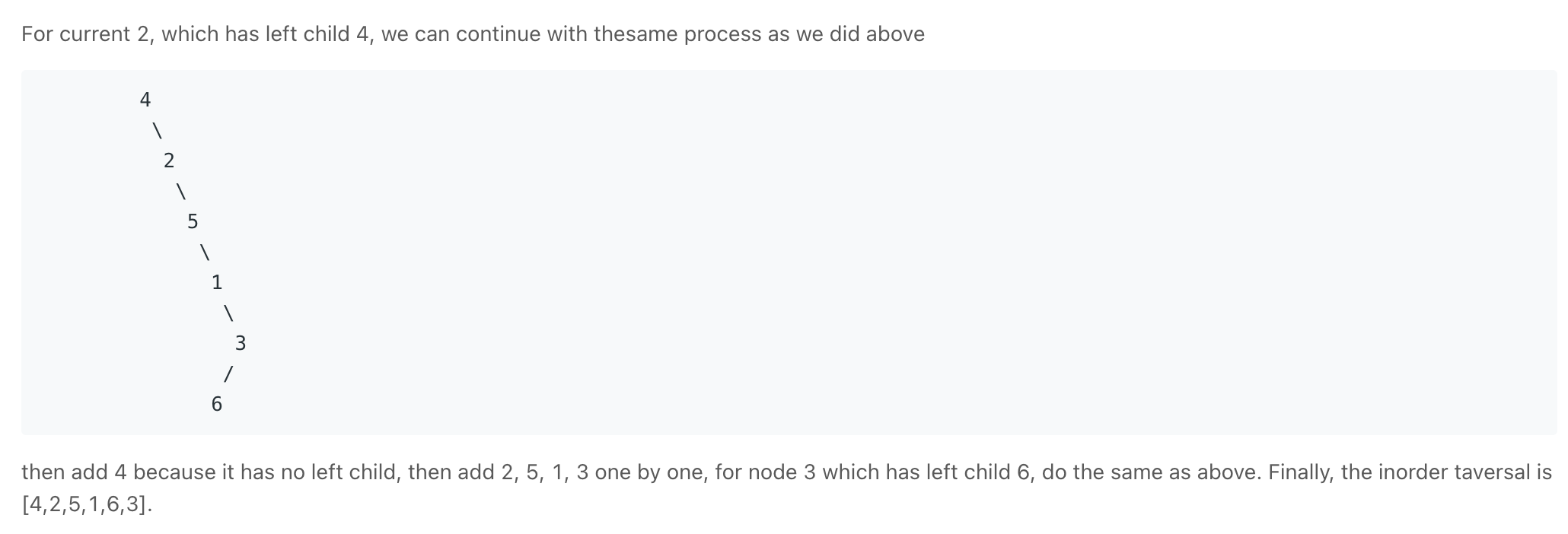
""" Morris Inorder Tree Traversal - Inorder with O(1) space https://leetcode.com/problems/binary-tree-inorder-traversal EPI 9.11 """ # Definition for a binary tree node. class TreeNode: def __init__(self, val=0, left=None, right=None): self.val = val self.left = left self.right = right class Solution: def inorderTraversal(self, root): res = [] curr = root while curr is not None: # has no left child - so is the next valid if not curr.left: res.append(curr.val) curr = curr.right # place the curr node as the right child of its predecessor # which is the rightmost node in the left subtree else: predecessor = self.get_inorder_predecessor(curr) # # move node down the tree left = curr.left curr.left = None # prevent loop predecessor.right = curr # # continue to left subtree curr = left return res def get_inorder_predecessor(self, node): curr = node.left while curr.right is not None: curr = curr.right return curr -
536. Construct Binary Tree from String
-
Serialize and Deserialize Binary Tree **
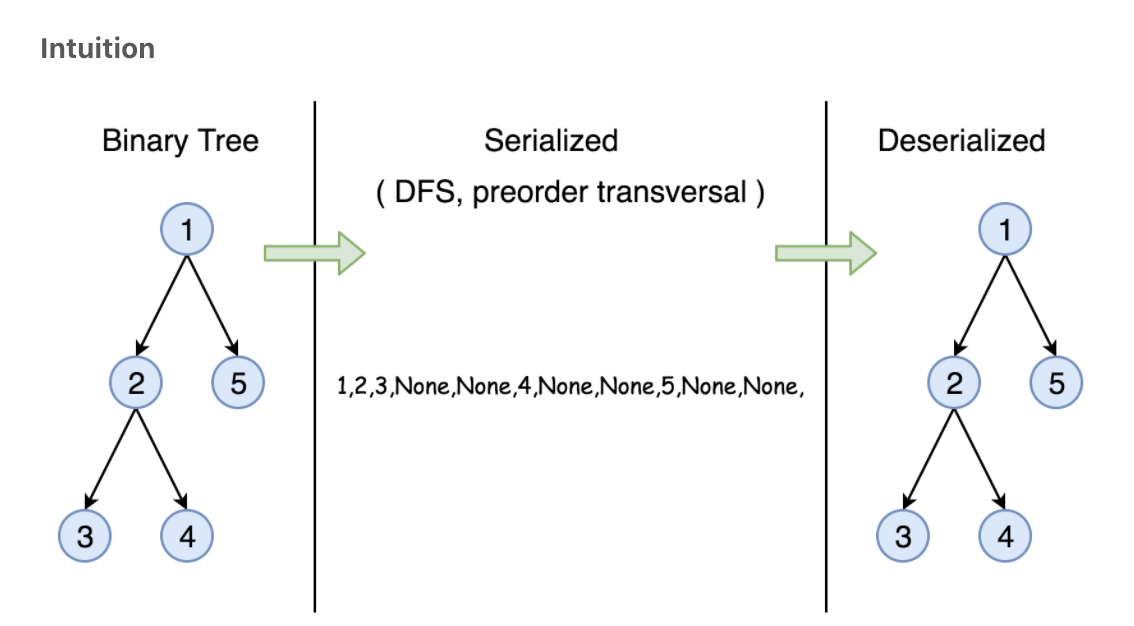
""" Serialize and Deserialize Binary Tree Serialization is the process of converting a data structure or object into a sequence of bits so that it can be stored in a file or memory buffer, or transmitted across a network connection link to be reconstructed later in the same or another computer environment. Design an algorithm to serialize and deserialize a binary tree. There is no restriction on how your serialization/deserialization algorithm should work. You just need to ensure that a binary tree can be serialized to a string and this string can be deserialized to the original tree structure. Clarification: The input/output format is the same as how LeetCode serializes a binary tree. You do not necessarily need to follow this format, so please be creative and come up with different approaches yourself. Example 1: Input: root = [1,2,3,null,null,4,5] Output: [1,2,3,null,null,4,5] Example 2: Input: root = [] Output: [] Example 3: Input: root = [1] Output: [1] Example 4: Input: root = [1,2] Output: [1,2] https://leetcode.com/problems/serialize-and-deserialize-binary-tree/ Prerequisites: - https://leetcode.com/problems/serialize-and-deserialize-bst - https://leetcode.com/problems/construct-binary-search-tree-from-preorder-traversal """ # Definition for a binary tree node. class TreeNode(object): def __init__(self, x): self.val = x self.left = None self.right = None class Codec: def serialize(self, root): preorder_result = [] # def preorder(node): # if not node: # preorder_result.append(str(None)) # return # preorder_result.append(str(node.val)) # preorder(node.left) # preorder(node.right) def preorder(node): if not node: preorder_result.append(str(None)) return preorder_result.append(str(node.val)) preorder(node.left) preorder(node.right) preorder(root) return " ".join(preorder_result) def deserialize(self, data): idx = 0 def reverse_preorder(arr): nonlocal idx if idx > len(arr): return None if arr[idx] == 'None': idx += 1 return None node = TreeNode(int(arr[idx])) idx += 1 node.left = reverse_preorder(arr) node.right = reverse_preorder(arr) return node return reverse_preorder(data.split(" ")) # Your Codec object will be instantiated and called as such: # ser = Codec() # deser = Codec() # ans = deser.deserialize(ser.serialize(root)) -
Construct Binary Tree from String
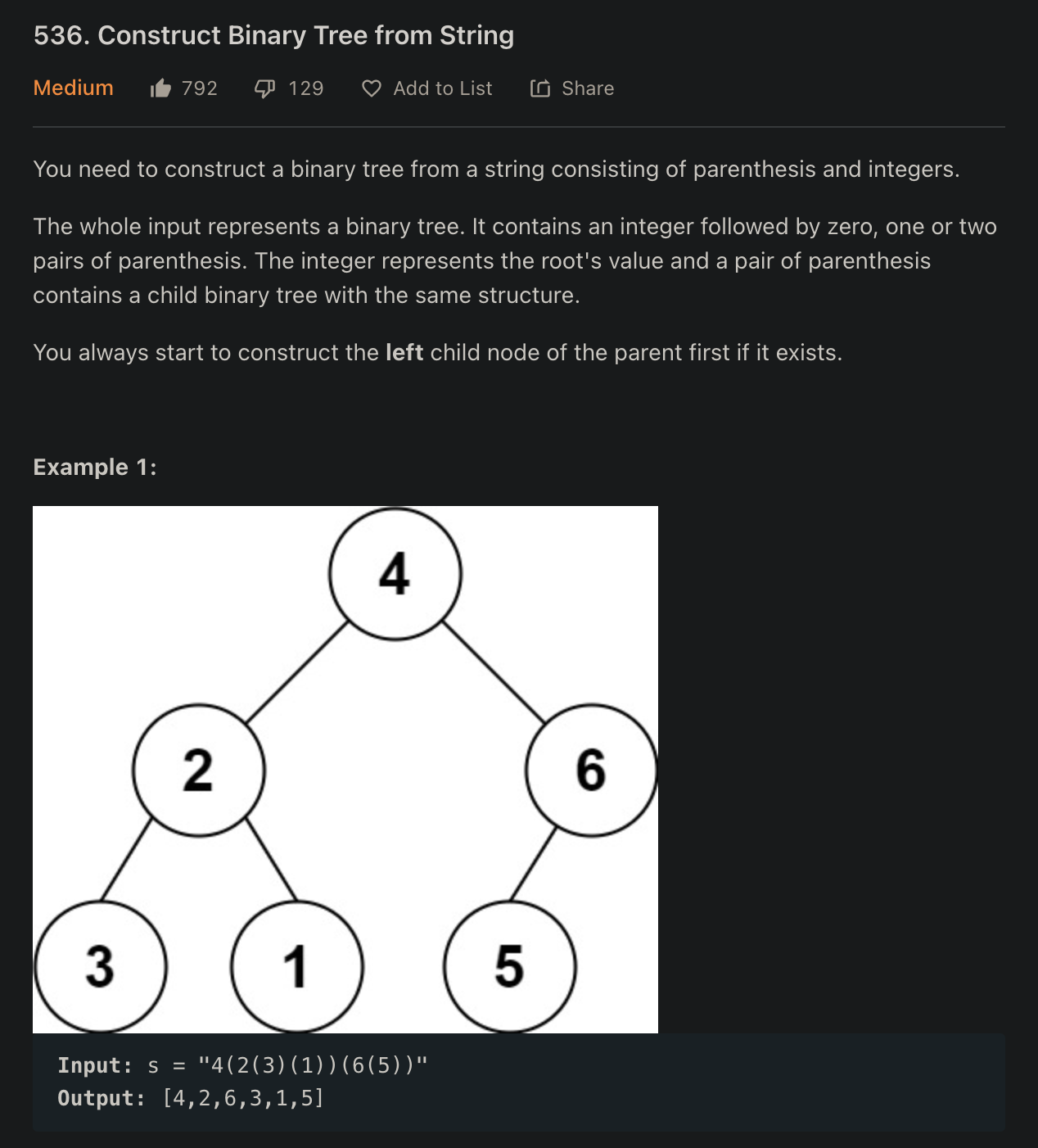

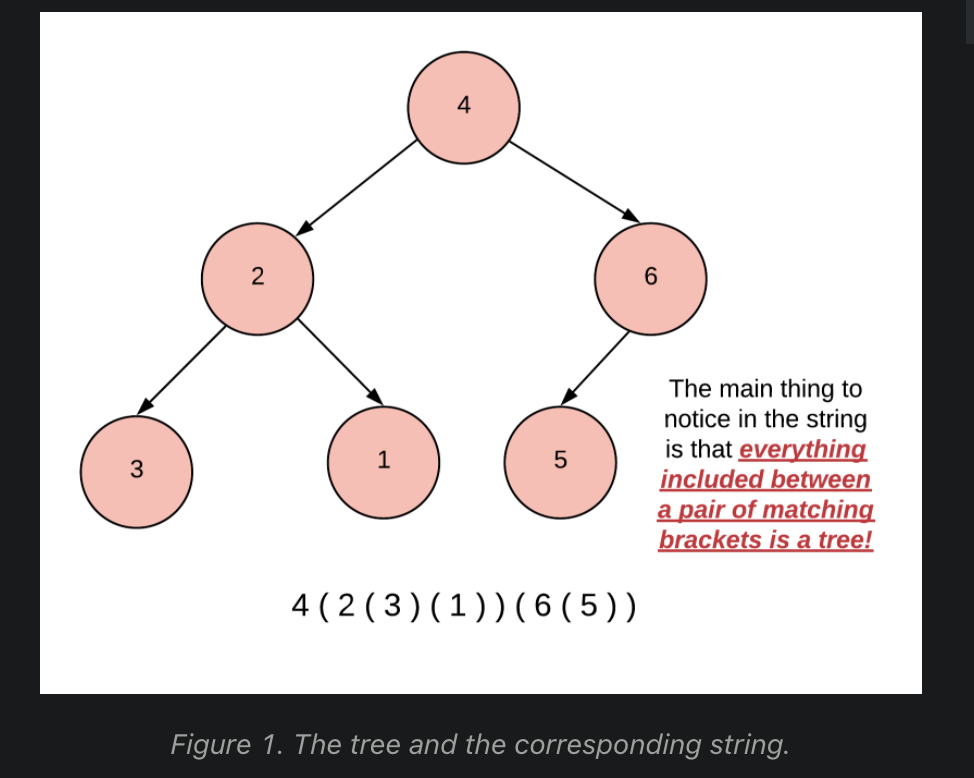
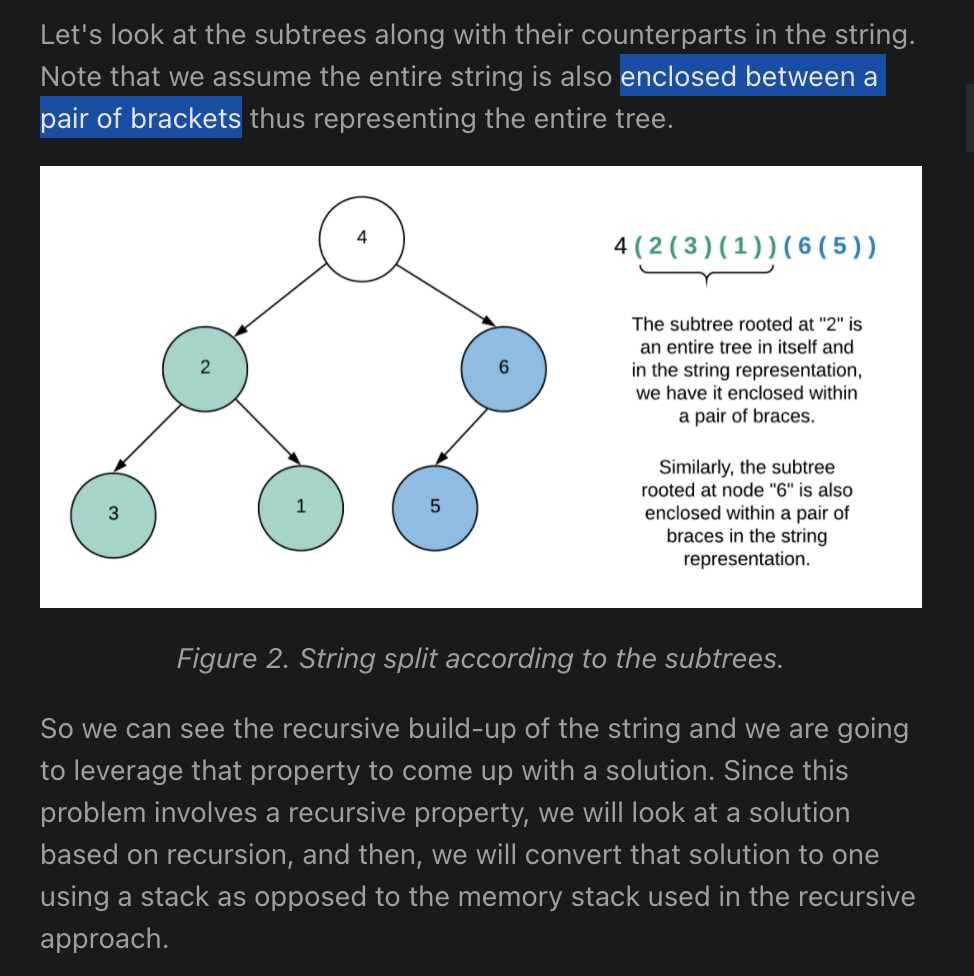
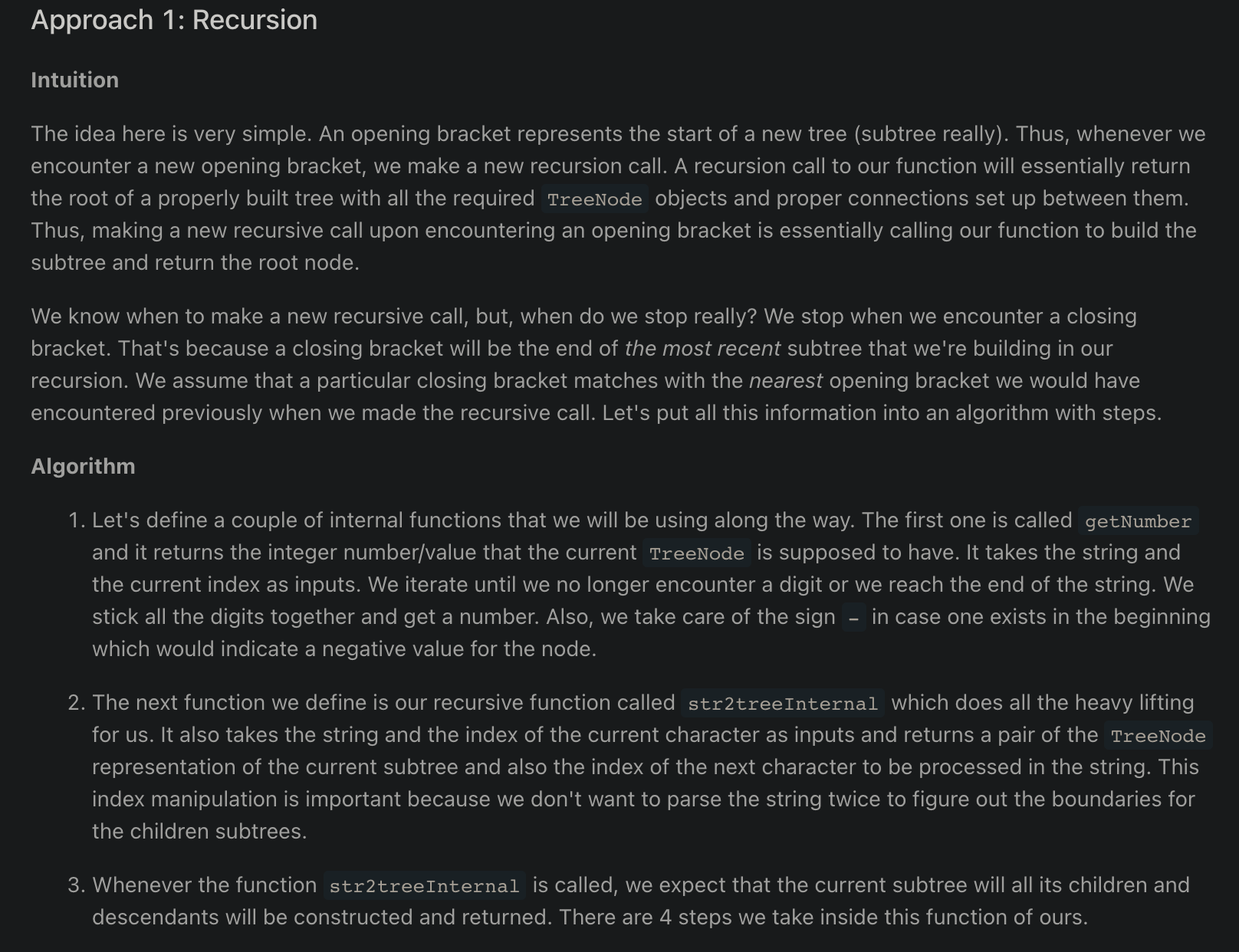
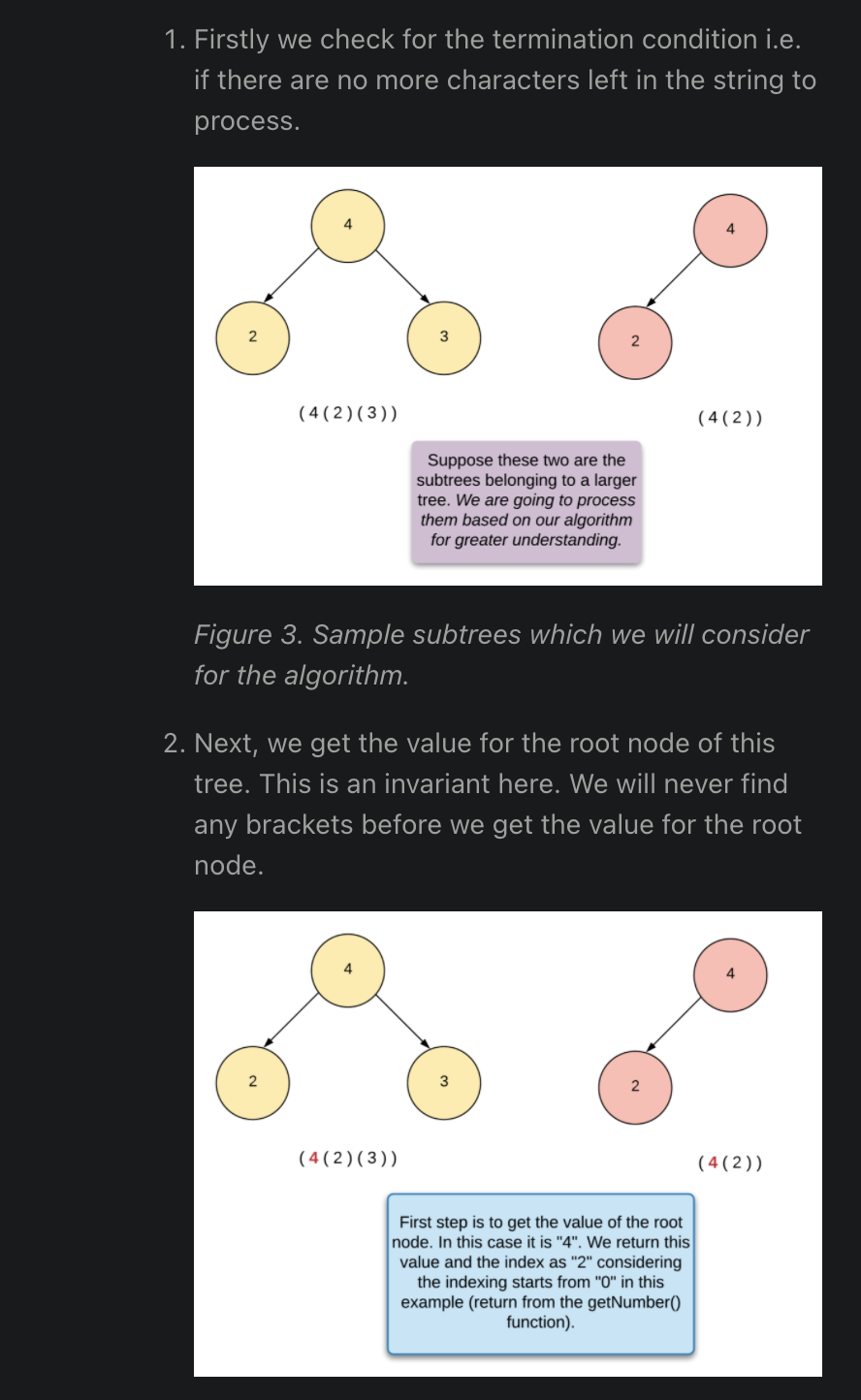
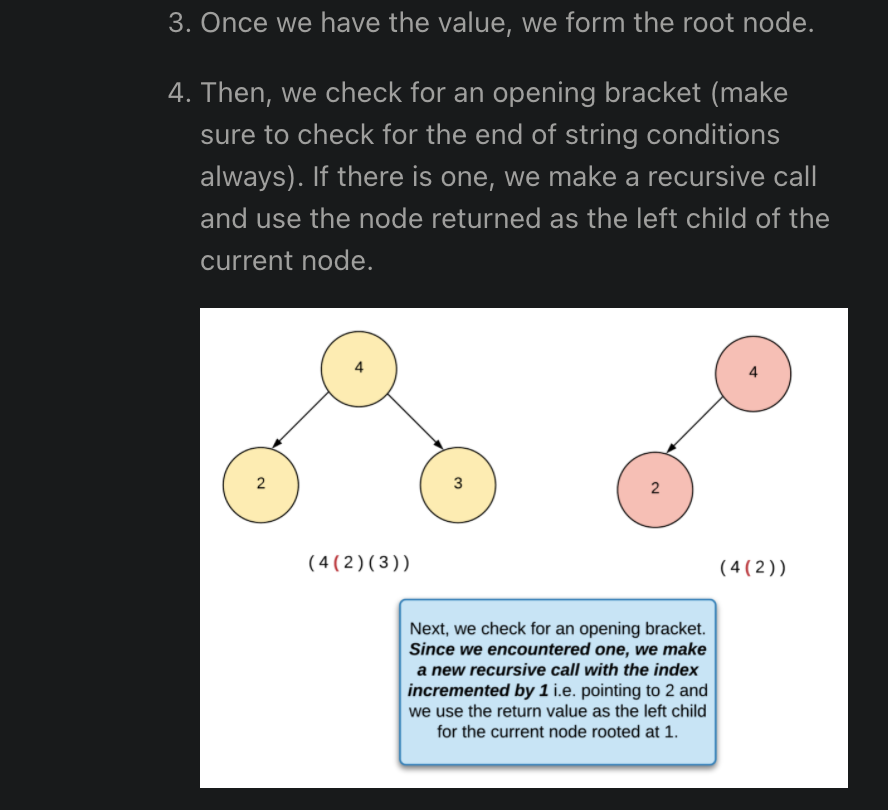
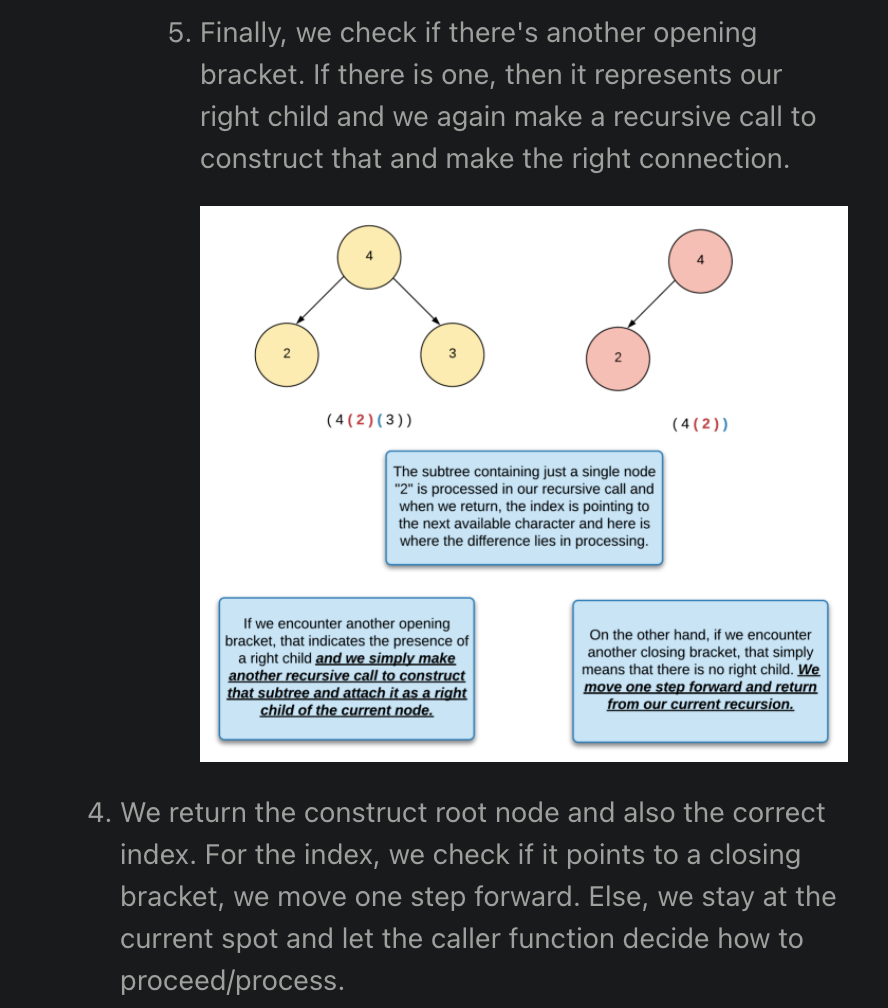

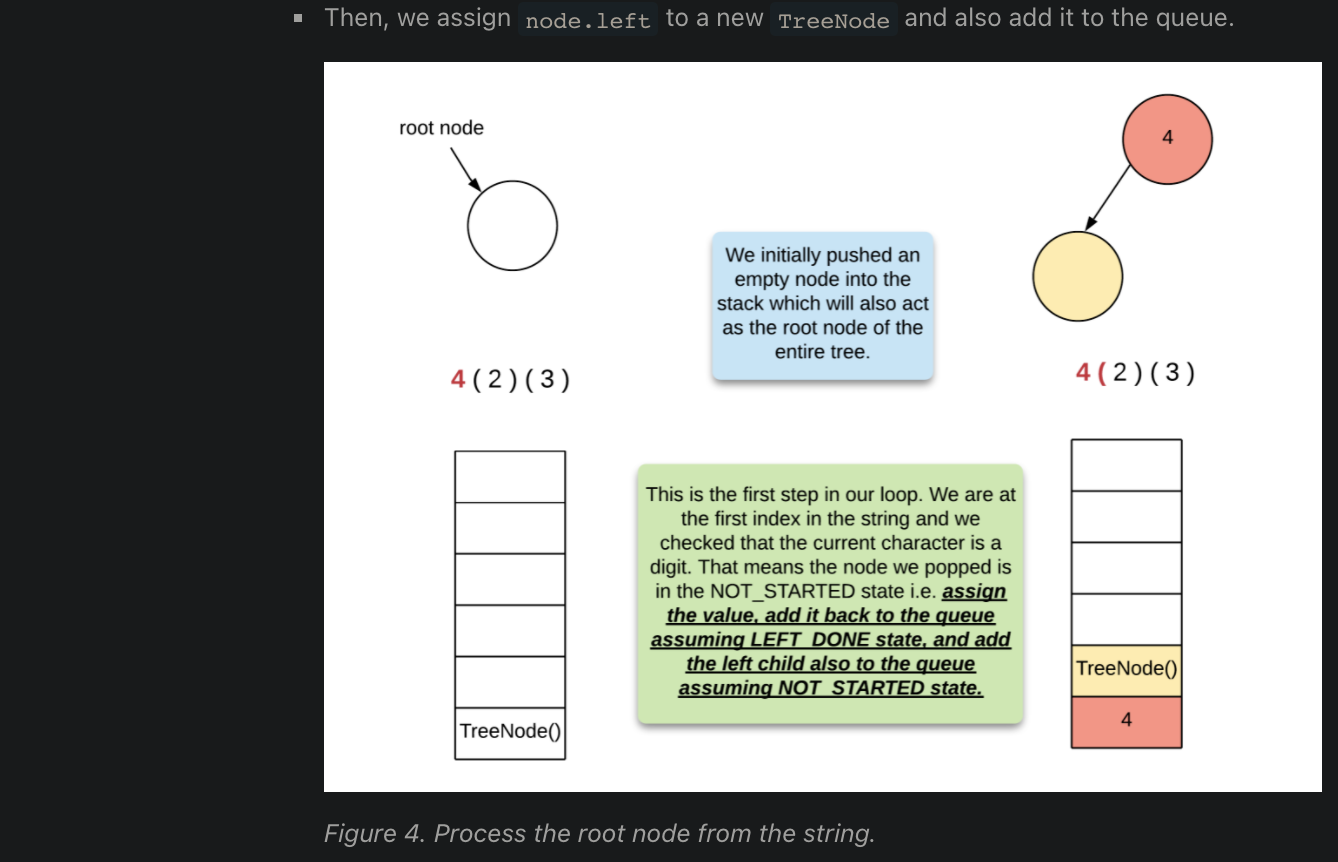


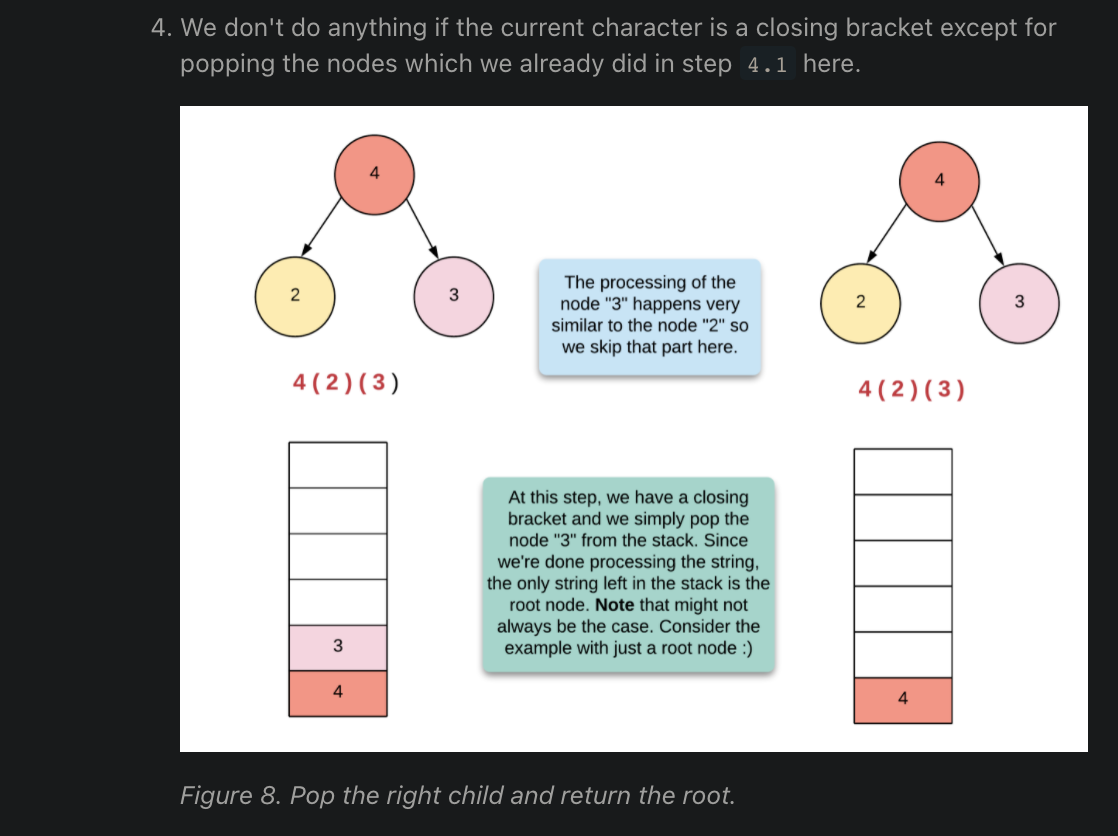
""" 536. Construct Binary Tree from String You need to construct a binary tree from a string consisting of parenthesis and integers. The whole input represents a binary tree. It contains an integer followed by zero, one or two pairs of parenthesis. The integer represents the root's value and a pair of parenthesis contains a child binary tree with the same structure. You always start to construct the left child node of the parent first if it exists. https://leetcode.com/problems/construct-binary-tree-from-string """ """ "4( 2( 3) ( 1) ) (6(5))" - tree startes at number - new opening bracket means new subtree - unclosable closing brackets means we return - record number as value then idx + 1 - left: if opening bracket, start new tree at idx + 1 - skip closing bracket move idx += 1 - right: if opening bracket, start new tree at idx + 1 - skip closing bracket move idx += 1 - else: return """ class TreeNode: def __init__(self, val=0, left=None, right=None): self.val = val self.left = left self.right = right class Solution: def str2tree(self, s: str): idx = 0 def build_tree(): nonlocal idx # base cases if idx >= len(s): return None start_idx = idx # get number while idx < len(s) and (s[idx].isnumeric() or s[idx] == '-'): idx += 1 node = TreeNode(s[start_idx:idx]) # subtrees if idx < len(s) and s[idx] == "(": idx += 1 node.left = build_tree() idx += 1 if idx < len(s) and s[idx] == "(": idx += 1 node.right = build_tree() idx += 1 return node return build_tree() -
Flatten Binary Tree to Linked List **


Solution 1






# Definition for a binary tree node. class TreeNode: def __init__(self, val=0, left=None, right=None): self.val = val self.left = left self.right = right class Solution_: def flatten(self, root): if not root: return None right = root.right if root.left: # place the left subtree between the root & root.right root.right = root.left left_ending = self.flatten(root.left) left_ending.right = right # remove left root.left = None furthest = self.flatten(root.right) return furthest or root """ our algorithm will return the tail node of the flattened out tree. For a given node, we will recursively flatten out the left and the right subtrees and store their corresponding tail nodes in left_ending and right_ending respectively. Next, we will make the following connections (only if there is a left child for the current node, else the left_ending would be null) (Place the left subtree between the root & root.right) left_ending.right = node.right node.right = node.left node.left = None Next we have to return the tail of the final, flattened out tree rooted at node. So, if the node has a right child, then we will return the right_ending, else, we'll return the left_ending """ class Solution: def flatten(self, root): if not root: return None left_ending = self.flatten(root.left) right_ending = self.flatten(root.right) # If there was a left subtree, we shuffle the connections # around so that there is nothing on the left side anymore. if left_ending: # Place the left subtree between the root & root.right left_ending.right = root.right root.right = root.left # Remove left root.left = None # We need to return the "rightmost" node after we are done wiring the new connections. # 2. For a node with only a left subtree, the rightmost node will be left_ending because it has been moved to the right subtree # 3. For a leaf node, we simply return the node return right_ending or left_ending or rootSolution 2

class Solution: def flatten(self, root): if not root: return None stack = [root] while stack: node = stack.pop() if node.right: stack.append(node.right) if node.left: stack.append(node.left) node.left = None if stack: node.right = stack[-1] # PeekApproach 3: O(1) Iterative Solution (Greedy & similar to Morris Traversal)
similar to Morris Traversal









""" O(1) Iterative Solution (Greedy & similar to Morris Traversal) """ class Solution: def flatten(self, root): if not root: return None curr = root while curr: # If there was a left subtree, we shuffle the connections # around so that there is nothing on the left side anymore. if curr.left: l_right_most = self.find_right_most(curr.left) # place the left subtree between the root & root.right l_right_most.right = curr.right curr.right = curr.left # remove left curr.left = None curr = curr.right def find_right_most(self, root): curr = root while curr.right: curr = curr.right return curr -
Lowest Common Ancestor of a Binary Tree
""" Lowest Common Ancestor of a Binary Tree: Given a binary tree, find the lowest common ancestor (LCA) of two given nodes in the tree. According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).” https://leetcode.com/problems/lowest-common-ancestor-of-a-binary-tree/ """ # Definition for a binary tree node. class TreeNode: def __init__(self, x): self.val = x self.left = None self.right = None class Solution: def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode'): return self.lowestCommonAncestorHelper(root, p, q) def lowestCommonAncestorHelper(self, curr: TreeNode, p: TreeNode, q: TreeNode): if curr is None: return None left = self.lowestCommonAncestorHelper(curr.left, p, q) right = self.lowestCommonAncestorHelper(curr.right, p, q) # found common ancestor if left == True and right == True: return curr elif (curr.val == p.val or curr.val == q.val) and (left == True or right == True): return curr # found p/q in current subtree elif curr.val == p.val or curr.val == q.val or left == True or right == True: return True # return the common ancestor return left or right -
Lowest Common Ancestor of a Binary Tree III
""" Lowest Common Ancestor of a Binary Tree III: Given two nodes of a binary tree p and q, return their lowest common ancestor (LCA). Each node will have a reference to its parent node. The definition for Node is below: class Node { public int val; public Node left; public Node right; public Node parent; } According to the definition of LCA on Wikipedia: "The lowest common ancestor of two nodes p and q in a tree T is the lowest node that has both p and q as descendants (where we allow a node to be a descendant of itself)." Example 1: Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1 Output: 3 Explanation: The LCA of nodes 5 and 1 is 3. Example 2: Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4 Output: 5 Explanation: The LCA of nodes 5 and 4 is 5 since a node can be a descendant of itself according to the LCA definition. Example 3: Input: root = [1,2], p = 1, q = 2 Output: 1 https://leetcode.com/problems/lowest-common-ancestor-of-a-binary-tree-iii/ """ # Definition for a Node. class Node: def __init__(self, val): self.val = val self.left = None self.right = None self.parent = None class Solution: def lowestCommonAncestor(self, p: 'Node', q: 'Node'): # # balance distance from root # calculate heights curr_p, curr_q = p, q height_p, height_q = 0, 0 while curr_p.parent is not None or curr_q.parent is not None: if curr_p.parent is not None: height_p += 1 curr_p = curr_p.parent if curr_q.parent is not None: height_q += 1 curr_q = curr_q.parent # two should be the lower one one, two = p, q if height_p > height_q: one, two = q, p # move two up for _ in range(abs(height_p-height_q)): two = two.parent # # find common ancestor while one != two: one = one.parent two = two.parent return one """ Other solutions: https://leetcode.com/problems/lowest-common-ancestor-of-a-binary-tree-iii/discuss/932499/Simple-Python-Solution-with-O(1)-space-complexity https://leetcode.com/problems/lowest-common-ancestor-of-a-binary-tree-iii/discuss/1142138/Python-Solution-with-Two-Pointers """ -
Vertical Order Traversal of a Binary Tree
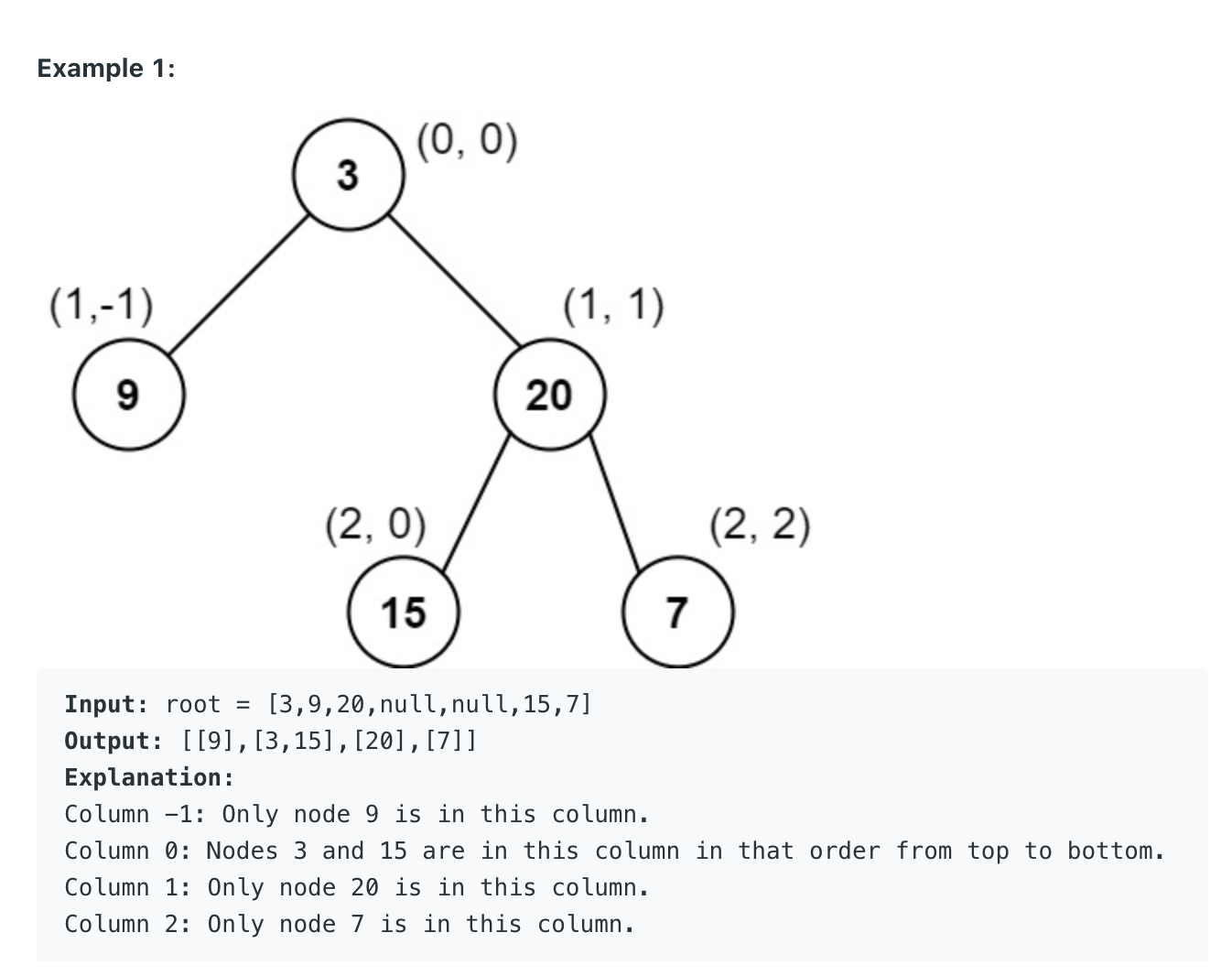
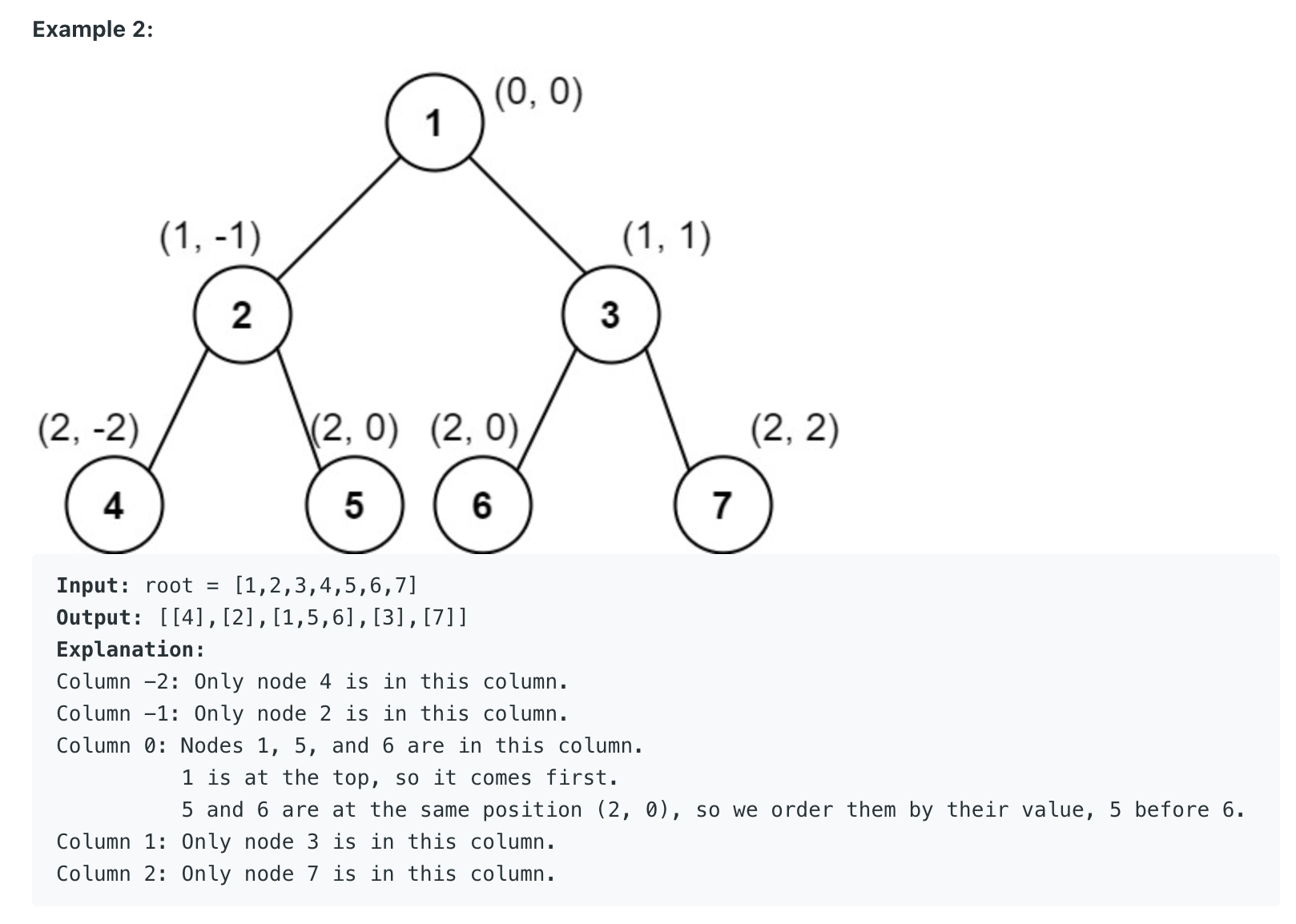
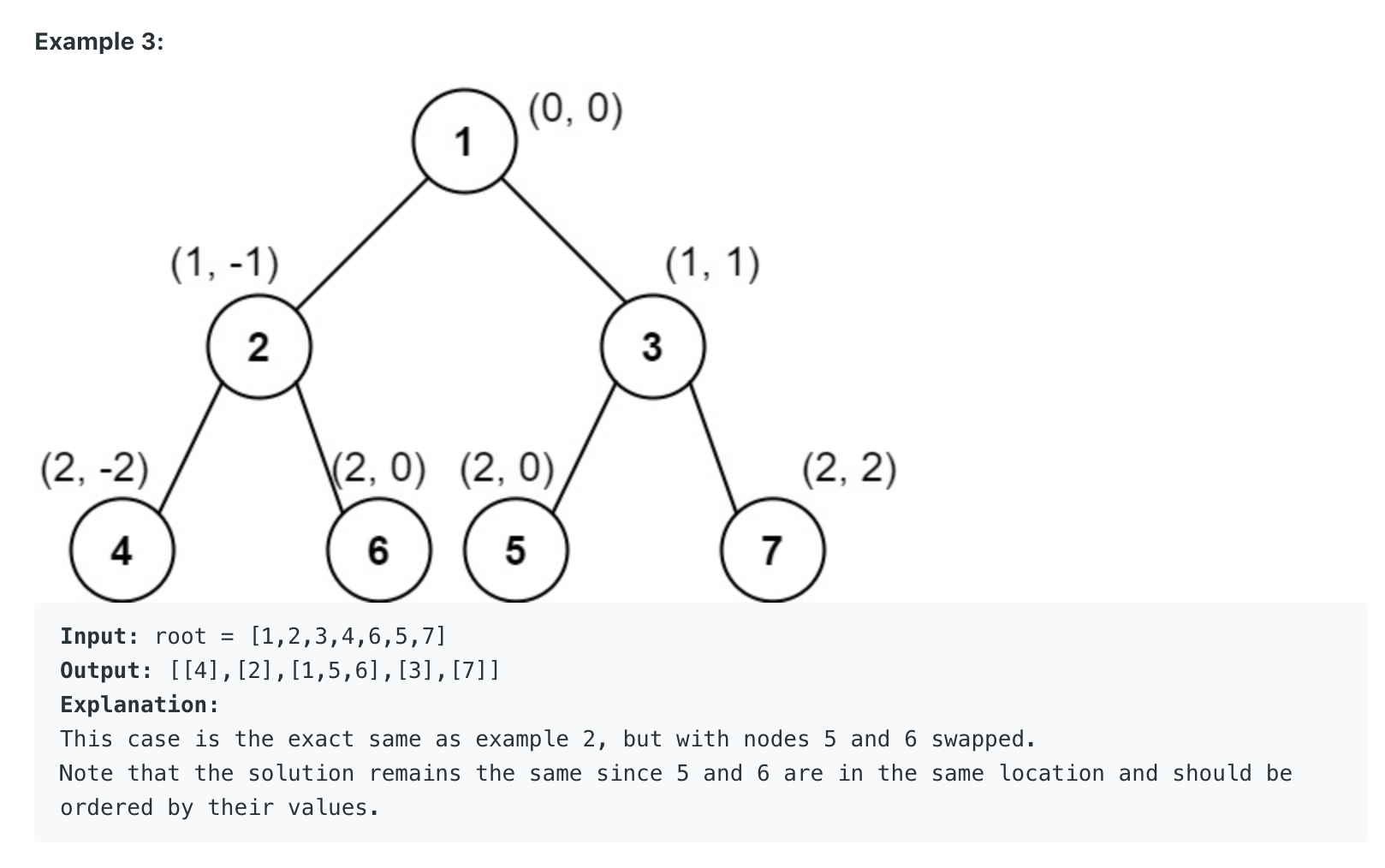
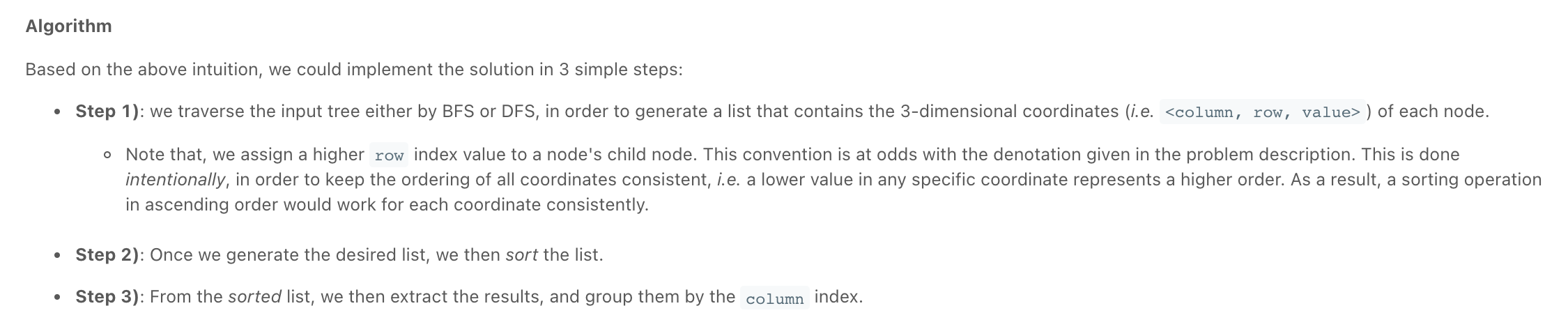

""" Vertical Order Traversal of a Binary Tree: Given the root of a binary tree, calculate the vertical order traversal of the binary tree. For each node at position (x, y), its left and right children will be at positions (x - 1, y - 1) and (x + 1, y - 1) respectively. The vertical order traversal of a binary tree is a list of non-empty reports for each unique x-coordinate from left to right. Each report is a list of all nodes at a given x-coordinate. The report should be primarily sorted by y-coordinate from highest y-coordinate to lowest. If any two nodes have the same y-coordinate in the report, the node with the smaller value should appear earlier. Return the vertical order traversal of the binary tree. https://leetcode.com/problems/vertical-order-traversal-of-a-binary-tree/ """ """ https://leetcode.com/problems/vertical-order-traversal-of-a-binary-tree/solution/999715 think the main time complexity is within sorting, in addition to the last solution, you can optimize and record both row and column min and max then there is no need for sorting for row and column, just need to sort the values with duplicate indices, which can greatly reduced time complexity, int minRow = 0; int maxRow = 0; int minCol = 0; int maxCol = 0; """ class TreeNode: def __init__(self, val=0, left=None, right=None): self.val = val self.left = left self.right = right class Solution: def verticalTraversal(self, root: TreeNode): if not root: return root node_positions = {} self.getNodesPositions(root, node_positions) # sort by x node_positions_vals = sorted(node_positions, key=lambda x: x) for idx, key in enumerate(node_positions_vals): node_positions_vals[idx] = node_positions[key] # sort by y for items_list in node_positions_vals: items_list.sort(key=lambda x: x[0]) for idx in range(len(items_list)): items_list[idx] = items_list[idx][1] # remove y return node_positions_vals # get each node's position # x will represent 'columns' and y 'rows' def getNodesPositions(self, node, node_positions, x=0, y=0): if node is None: return None if x not in node_positions: node_positions[x] = [] node_positions[x] = node_positions[x]+[[y, node.val]] self.getNodesPositions(node.left, node_positions, x-1, y+1) self.getNodesPositions(node.right, node_positions, x+1, y+1) """ Solution 2: BFS with queue - explained in EPI """ -
Binary Tree Vertical Order Traversal
# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right """ Better solution: - use BFS - instead of sorting keep track of the range of the column index (i.e. [min_column, max_column]) and iterate through it """ class Solution: def verticalOrder(self, root: TreeNode): if not root: return root node_positions = {} self.getNodesPositions(root, node_positions) # print(node_positions) # sort by x node_positions_vals = sorted(node_positions, key=lambda x: x) for idx, key in enumerate(node_positions_vals): node_positions_vals[idx] = node_positions[key] # print(node_positions_vals) # sort by y for items_list in node_positions_vals: # print(items_list) items_list.sort(key=lambda x: x[0]) # print(items_list) for idx in range(len(items_list)): items_list[idx] = items_list[idx][1] # remove y # print(node_positions_vals) return node_positions_vals # get each node's position # x will represent 'columns' and y 'rows' def getNodesPositions(self, node, node_positions, x=0, y=0): if node is None: return None if x not in node_positions: node_positions[x] = [] node_positions[x] = node_positions[x]+[[y, node.val]] self.getNodesPositions(node.left, node_positions, x-1, y+1) self.getNodesPositions(node.right, node_positions, x+1, y+1) -
Find Nodes Distance K *
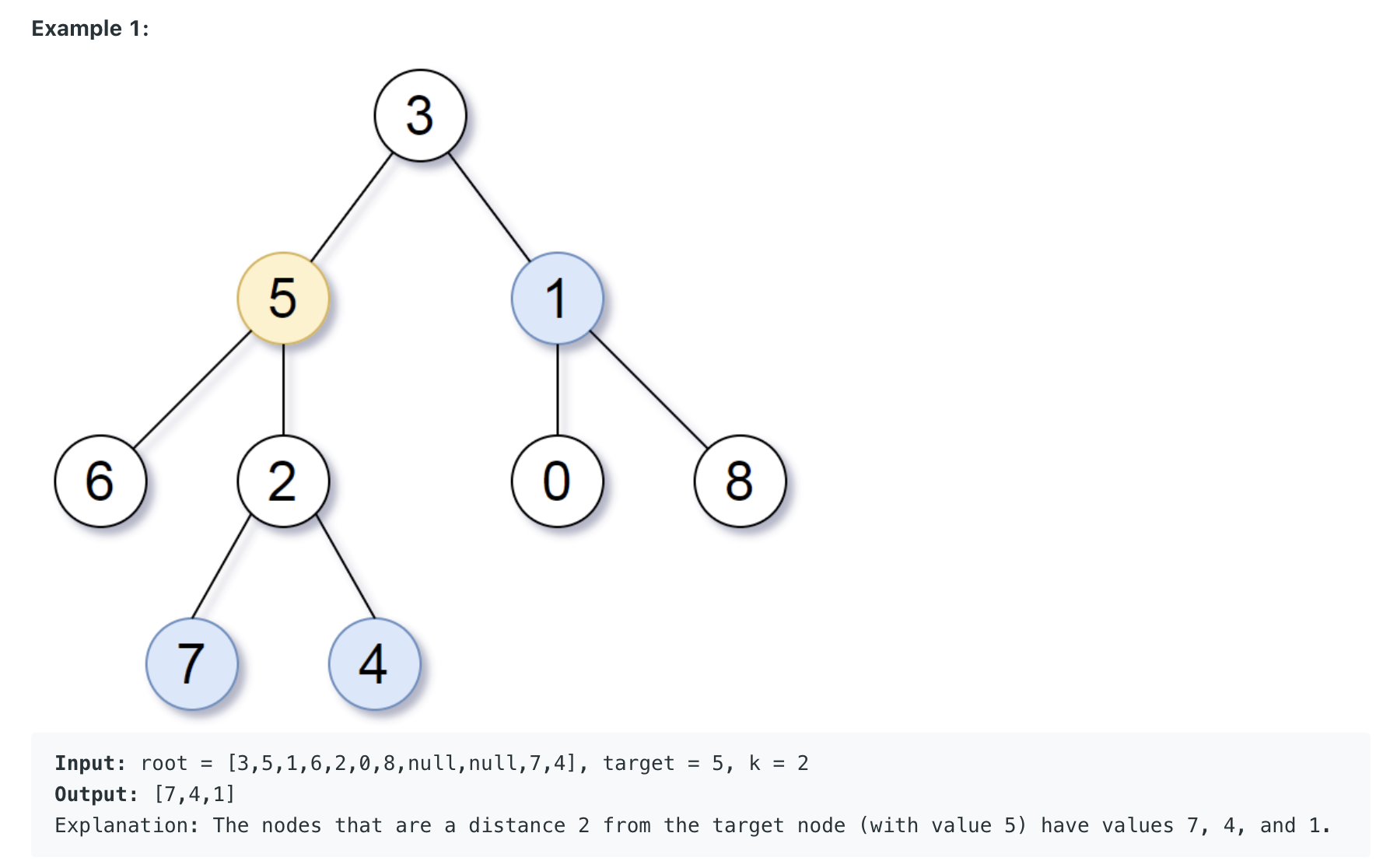
""" Find Nodes Distance K: You're given the root node of a Binary Tree, a target value of a node that's contained in the tree, and a positive integer k. Write a function that returns the values of all the nodes that are exactly distance k from the node with target value. The distance between two nodes is defined as the number of edges that must be traversed to go from one node to the other. For example, the distance between a node and its immediate left or right child is 1. The same holds in reverse: the distance between a node and its parent is 1. In a tree of three nodes where the root node has a left and right child, the left and right children are distance 2 from each other. Each BinaryTree node has an integer value, a left child node, and a right child node. Children nodes can either be BinaryTree nodes themselves or None / null. Note that all BinaryTree node values will be unique, and your function can return the output values in any order. Sample Input tree = 1 / \ 2 3 / \ \ 4 5 6 / \ 7 8 target = 3 k = 2 Sample Output [2, 7, 8] // These values could be ordered differently. https://www.algoexpert.io/questions/Find%20Nodes%20Distance%20K """ """ All Nodes Distance K in Binary Tree Given the root of a binary tree, the value of a target node target, and an integer k, return an array of the values of all nodes that have a distance k from the target node. You can return the answer in any order. Example 1: Input: root = [3,5,1,6,2,0,8,null,null,7,4], target = 5, k = 2 Output: [7,4,1] Explanation: The nodes that are a distance 2 from the target node (with value 5) have values 7, 4, and 1. https://leetcode.com/problems/all-nodes-distance-k-in-binary-tree/ """ # Definition for a binary tree node. class TreeNode: def __init__(self, x): self.val = x self.left = None self.right = None """ - a graph representation of this will make it easier - find/record parents - find target - dfs from target """ class Solution: def distanceK(self, root: TreeNode, target: TreeNode, k: int): res = [] parents = {} self.recordParents(root, parents, None) self.findNodesDistanceK(target, parents, k, res, target) return res def findNodesDistanceK(self, root, parents, k, res, prev): if root is None: return if k == 0: res.append(root.val) return if root.left != prev: # left self.findNodesDistanceK(root.left, parents, k-1, res, root) if root.right != prev: # right self.findNodesDistanceK(root.right, parents, k-1, res, root) if parents[root.val] != prev: # parent self.findNodesDistanceK(parents[root.val], parents, k-1, res, root) def recordParents(self, root, parents, parent): if root is None: return parents[root.val] = parent self.recordParents(root.left, parents, root) self.recordParents(root.right, parents, root) -
Random node




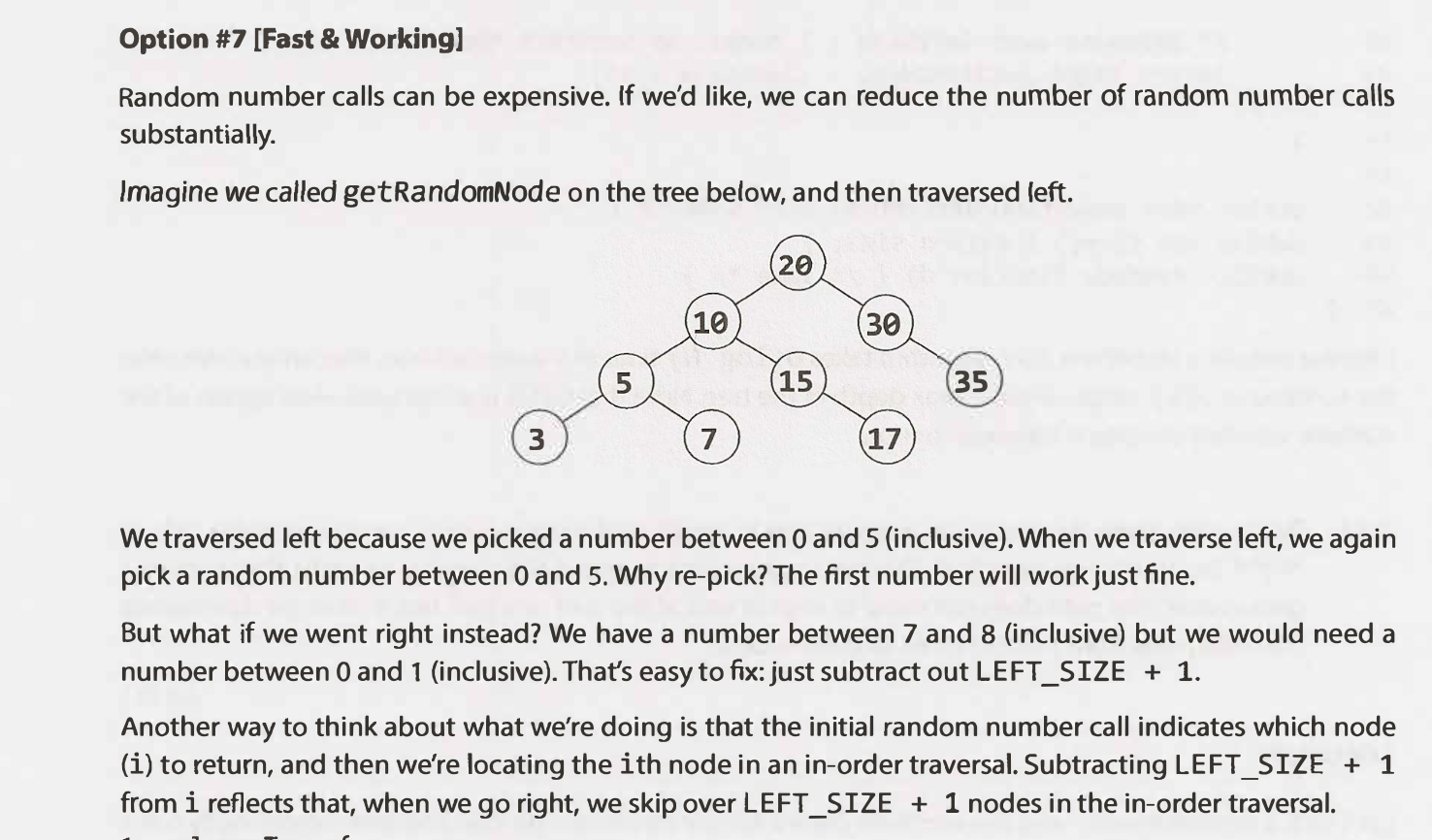

-
Boundary of Binary Tree

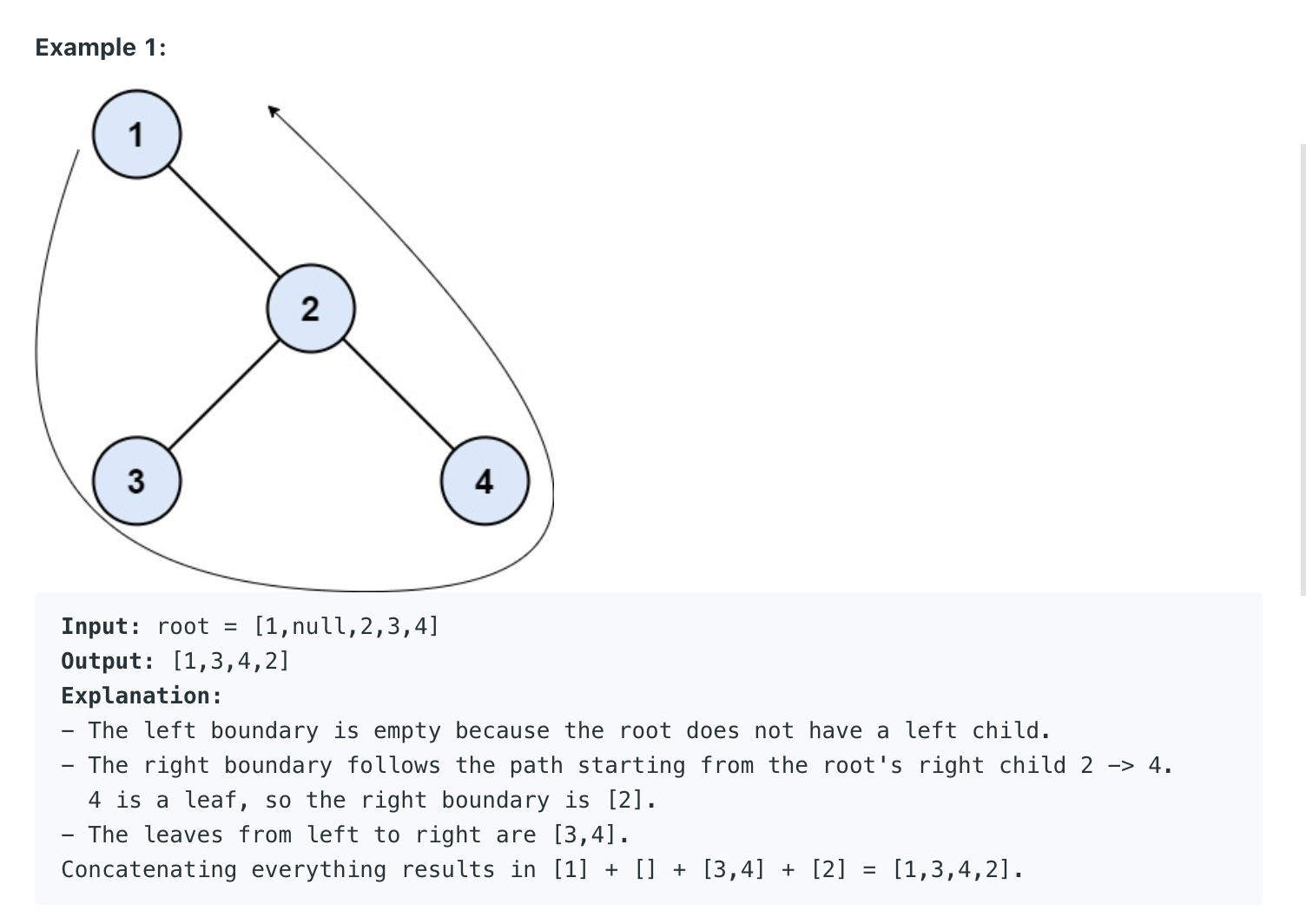
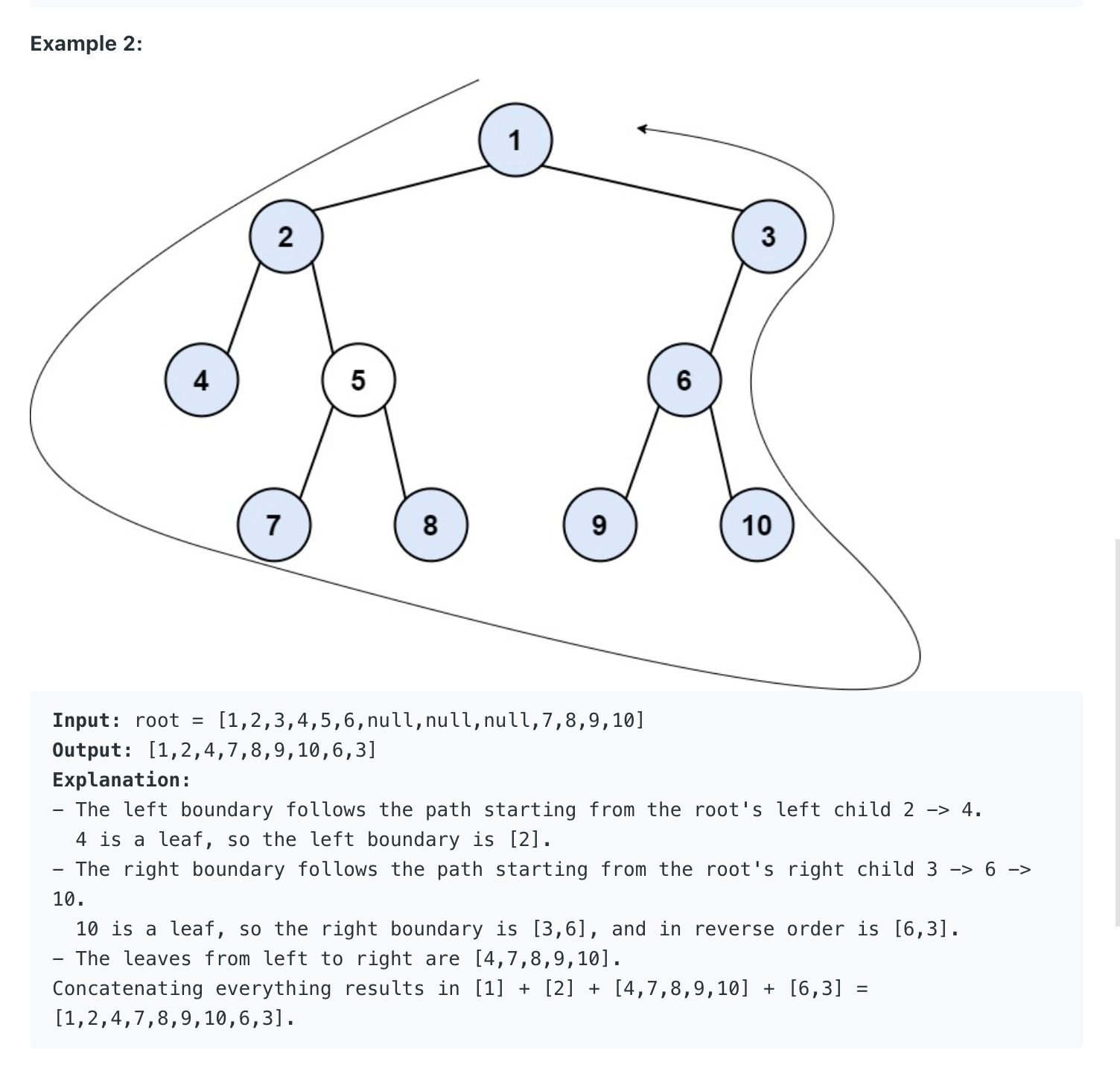

/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode(int x) { val = x; } * } */ public class Solution { public boolean isLeaf(TreeNode t) { return t.left == null && t.right == null; } public void addLeaves(List<Integer> res, TreeNode root) { if (isLeaf(root)) { res.add(root.val); } else { if (root.left != null) { addLeaves(res, root.left); } if (root.right != null) { addLeaves(res, root.right); } } } public List<Integer> boundaryOfBinaryTree(TreeNode root) { ArrayList<Integer> res = new ArrayList<>(); if (root == null) { return res; } if (!isLeaf(root)) { res.add(root.val); } TreeNode t = root.left; while (t != null) { if (!isLeaf(t)) { res.add(t.val); } if (t.left != null) { t = t.left; } else { t = t.right; } } addLeaves(res, root); Stack<Integer> s = new Stack<>(); t = root.right; while (t != null) { if (!isLeaf(t)) { s.push(t.val); } if (t.right != null) { t = t.right; } else { t = t.left; } } while (!s.empty()) { res.add(s.pop()); } return res; } }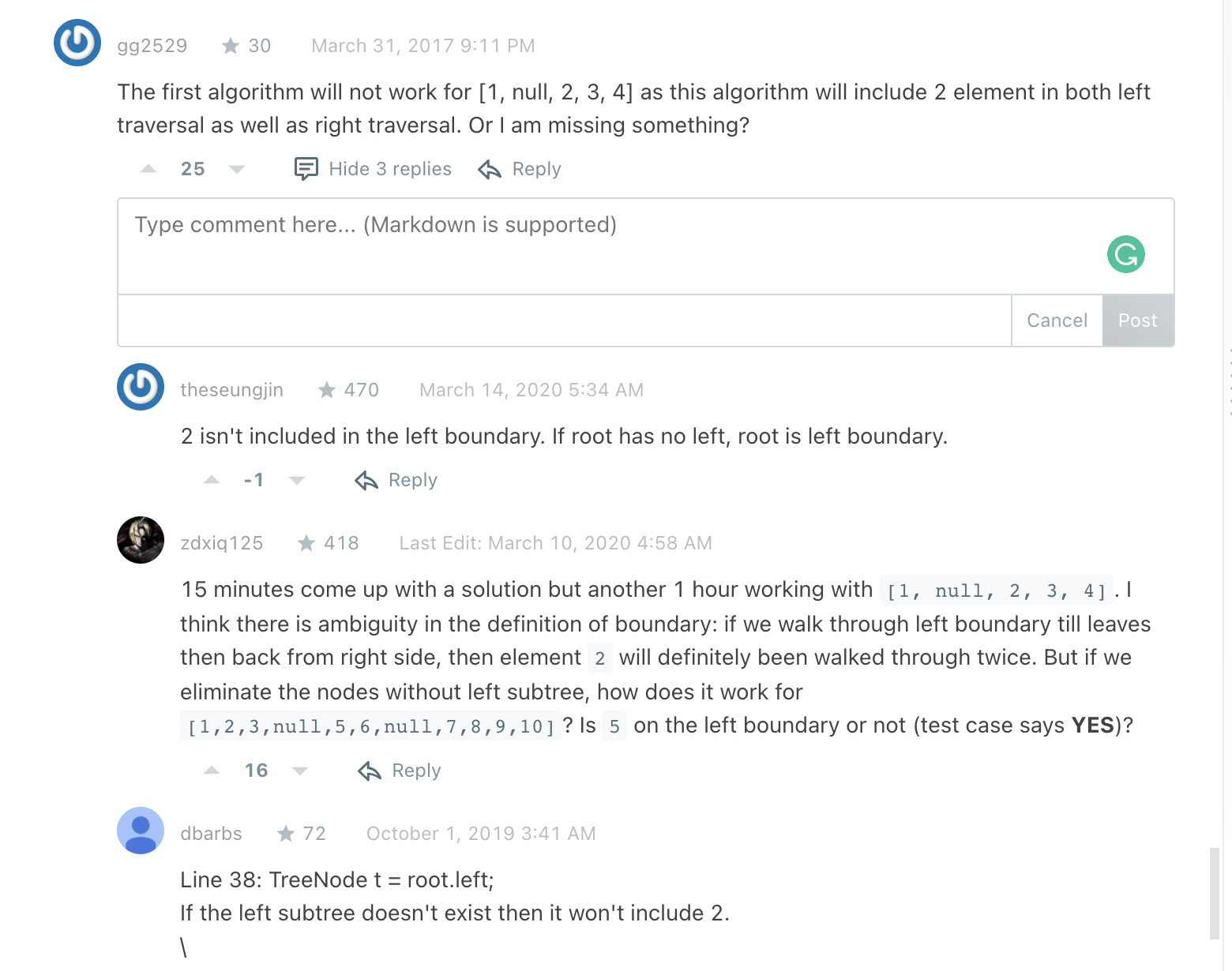
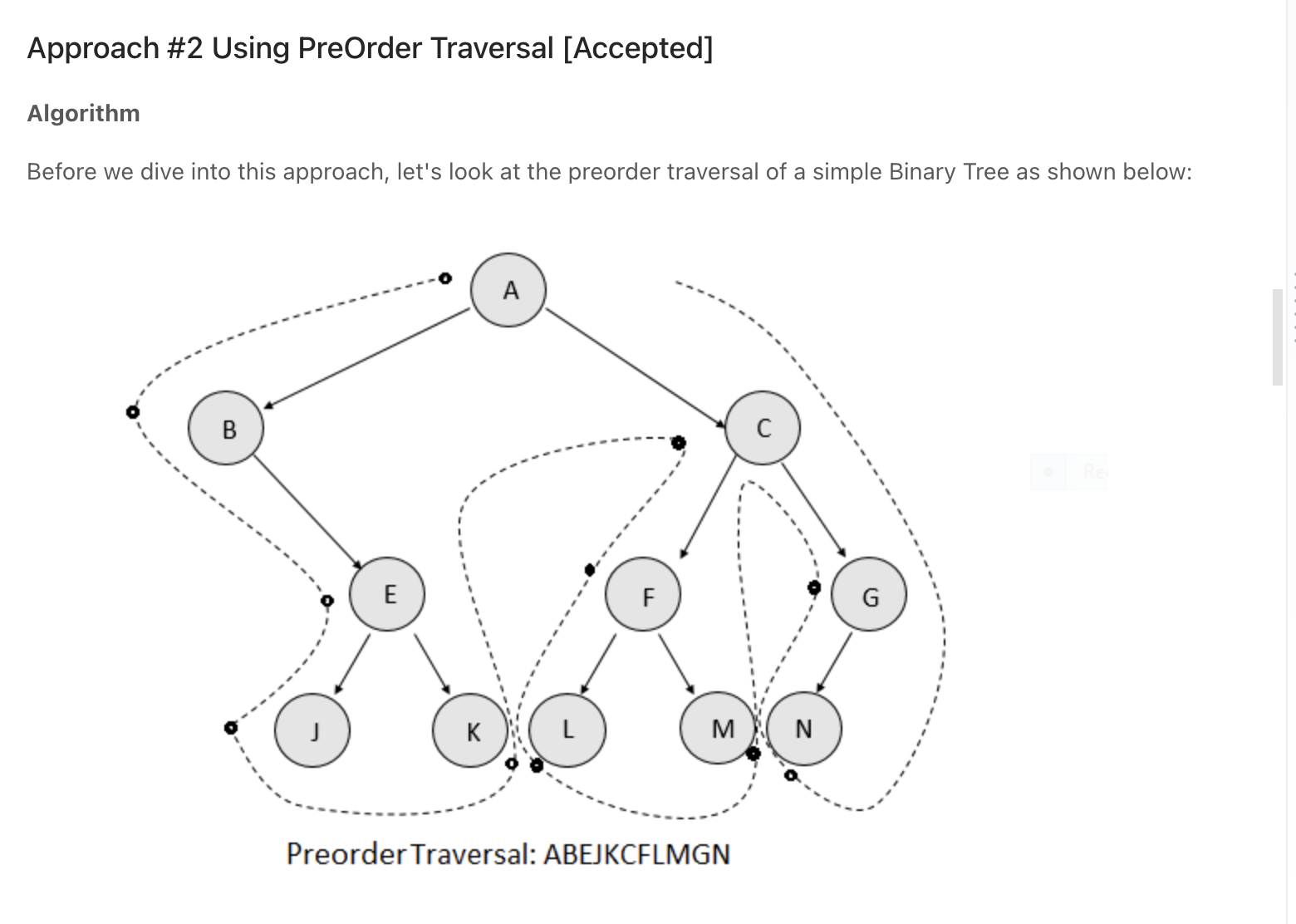
Definition of terms
The depth of a node n is the number of nodes on the search path from the root to n, not including n itself. The height of a binary tree is the maximum depth of any node in that tree. A level of a tree is all nodes at the same depth.
Balanced vs. Unbalanced
A balanced binary tree, also referred to as a height-balanced binary tree, is defined as a binary tree in which the height of the left and right subtree of any node differ by not more than 1. One way to think about it is that a "balanced" tree really means something more like "not terribly imbalanced:" It's balanced enough to ensure 0(logn) times for insert and find,but it's not necessarily as balanced as it could be.
While many trees are balanced, not all are. Ask your interviewer for clarification here. Note that balancing a tree does not mean the left and right subtrees are exactly the same size (like you see under "perfect binary trees").
Two common types of balanced trees are red-black trees and AVL trees.
Complete Binary Trees

A complete binary tree is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible (This terminology is not universal, e.g., some authors use complete binary tree where we write perfect binary tree.)
Full Binary Trees

A full binary tree is a binary tree in which every node other than the leaves has two children.
Perfect binary tree
A perfect binary tree is a full binary tree in which all leaves are at the same depth, and in which every parent has two children. (every level of the tree is completely full)
Binary trees have a few interesting properties when they're perfect:
-
The number of total nodes on each "level" doubles as we move down the tree.
-
The number of nodes on the last level is equal to the sum of the number of nodes on all other levels (plus 1). In other words, about half of our nodes are on the last level.
-
Populating Next Right Pointers in Each Node *

Remember that we are dealing with a perfect tree
""" 116. Populating Next Right Pointers in Each Node You are given a perfect binary tree where all leaves are on the same level, and every parent has two children. The binary tree has the following definition: struct Node { int val; Node *left; Node *right; Node *next; } Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to NULL. Initially, all next pointers are set to NULL. https://leetcode.com/problems/populating-next-right-pointers-in-each-node EPI 9.16 """ import collections # Definition for a Node. class Node: def __init__(self, val: int = 0, left: 'Node' = None, right: 'Node' = None, next: 'Node' = None): self.val = val self.left = left self.right = right self.next = next class Solution: def connect(self, root: 'Node'): if not root: return queue = [root] while queue: curr = queue.pop(0) if curr.left: curr.left.next = curr.right queue.append(curr.left) if curr.right: if curr.next: curr.right.next = curr.next.left queue.append(curr.right) return root """ """ class Solution_: def connect(self, root: 'Node'): if not root: return None prev_nodes = collections.defaultdict(lambda: None) queue = [(root, 0)] while queue: curr, depth = queue.pop(0) curr.next = prev_nodes[depth] prev_nodes[depth] = curr # next if curr.right: queue.append((curr.right, depth+1)) if curr.left: queue.append((curr.left, depth+1)) return root
Binary Tree Traversals (Inorder, Preorder and Postorder)
We can use DFS to do pre-order, in-order and post-order traversal. There is a common feature among these three traversal orders: we never trace back unless we reach the deepest node. That is also the largest difference between DFS and BFS, BFS never go deeper unless it has already visited all nodes at the current level. Typically, we implement DFS using recursion.
Pre-order Traversal (nlr)
In this traversal mode, one starts from the root, move to left child, then right child.
In-order Traversal (lnr)
Screen Recording 2021-10-23 at 13.31.41.mov
In this traversal mode, one starts visiting with the left child, followed by root and then the right child.
Check out how to do it iteratively.
Post-order Traversal (lrn)
In this traversal mode, one starts from the left child, move to the right child, and terminate at the root.
Examples
-
Binary Search Tree Iterator

""" Binary Search Tree Iterator: Implement the BSTIterator class that represents an iterator over the in-order traversal of a binary search tree (BST): BSTIterator(TreeNode root) Initializes an object of the BSTIterator class. The root of the BST is given as part of the constructor. The pointer should be initialized to a non-existent number smaller than any element in the BST. boolean hasNext() Returns true if there exists a number in the traversal to the right of the pointer, otherwise returns false. int next() Moves the pointer to the right, then returns the number at the pointer. Notice that by initializing the pointer to a non-existent smallest number, the first call to next() will return the smallest element in the BST. You may assume that next() calls will always be valid. That is, there will be at least a next number in the in-order traversal when next() is called. Example 1: 7 / \ 3 15 / \ 9 20 Input ["BSTIterator", "next", "next", "hasNext", "next", "hasNext", "next", "hasNext", "next", "hasNext"] [[[7, 3, 15, null, null, 9, 20]], [], [], [], [], [], [], [], [], []] Output [null, 3, 7, true, 9, true, 15, true, 20, false] Explanation BSTIterator bSTIterator = new BSTIterator([7, 3, 15, null, null, 9, 20]); bSTIterator.next(); // return 3 bSTIterator.next(); // return 7 bSTIterator.hasNext(); // return True bSTIterator.next(); // return 9 bSTIterator.hasNext(); // return True bSTIterator.next(); // return 15 bSTIterator.hasNext(); // return True bSTIterator.next(); // return 20 bSTIterator.hasNext(); // return False """ from typing import Optional """ ---- Solution 1: store the inorder traversal in an array and return them index by index --- Solution 2: controlled iteration check Binary Tree Inorder Traversal (Iterative) https://www.notion.so/paulonteri/Trees-Graphs-edc3401e06c044f29a2d714d20ffe185#8c489e8b02804929ab535f25f945a31b [3,7,9,15,20] """ # Definition for a binary tree node. class TreeNode: def __init__(self, val=0, left=None, right=None): self.val = val self.left = left self.right = right class BSTIterator: def __init__(self, root: Optional[TreeNode]): self.curr = root self.stack = [] def next(self): # put the left most value(s) to the top of the stack while self.curr: self.stack.append(self.curr) self.curr = self.curr.left # the left-most node is at the top of the stack node = self.stack.pop() # the next (only next unvisited valid node) will be at the right self.curr = node.right return node.val def hasNext(self): return self.curr or self.stack # Your BSTIterator object will be instantiated and called as such: # obj = BSTIterator(root) # param_1 = obj.next() # param_2 = obj.hasNext() -
Inorder Successor in BST
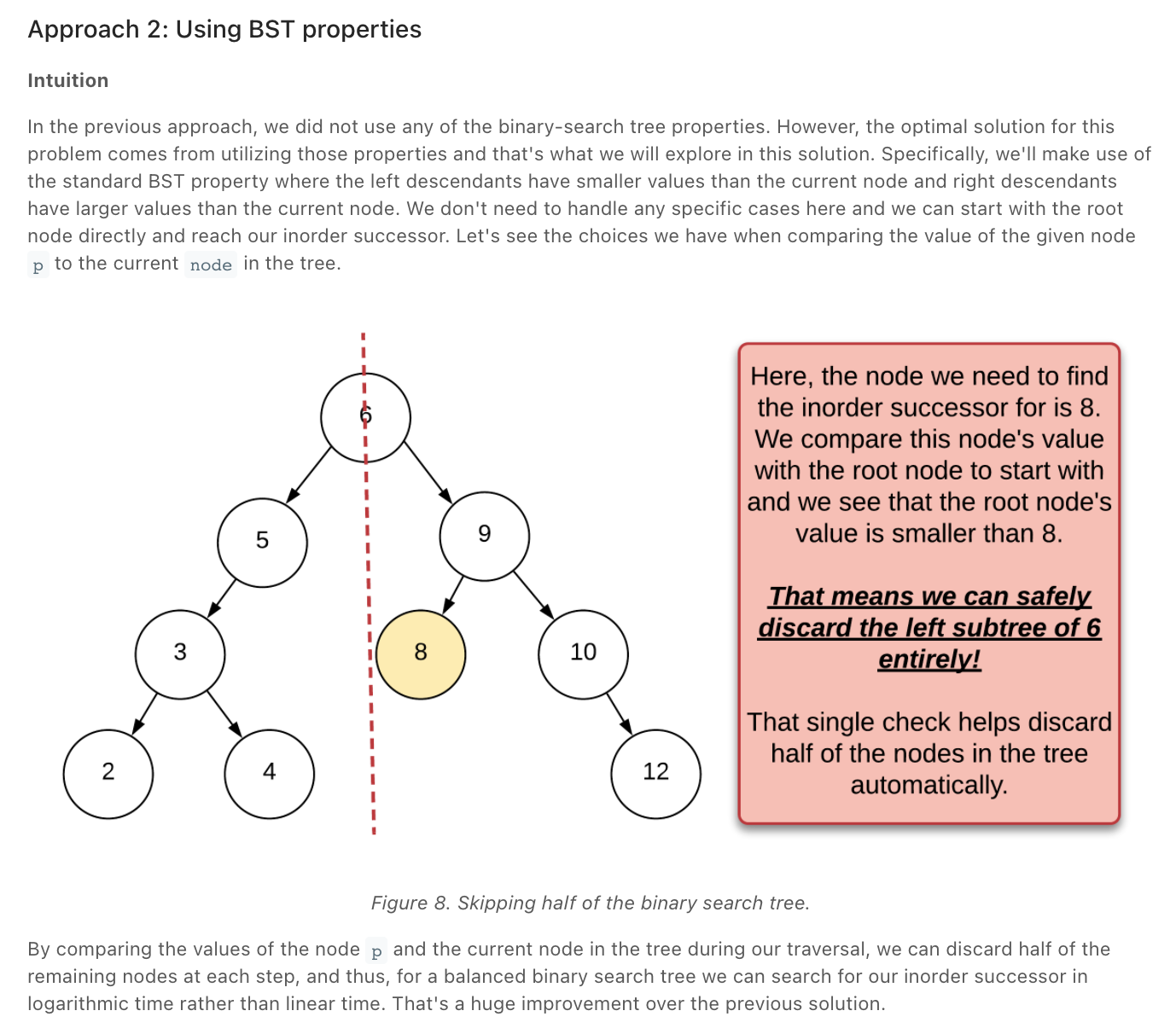

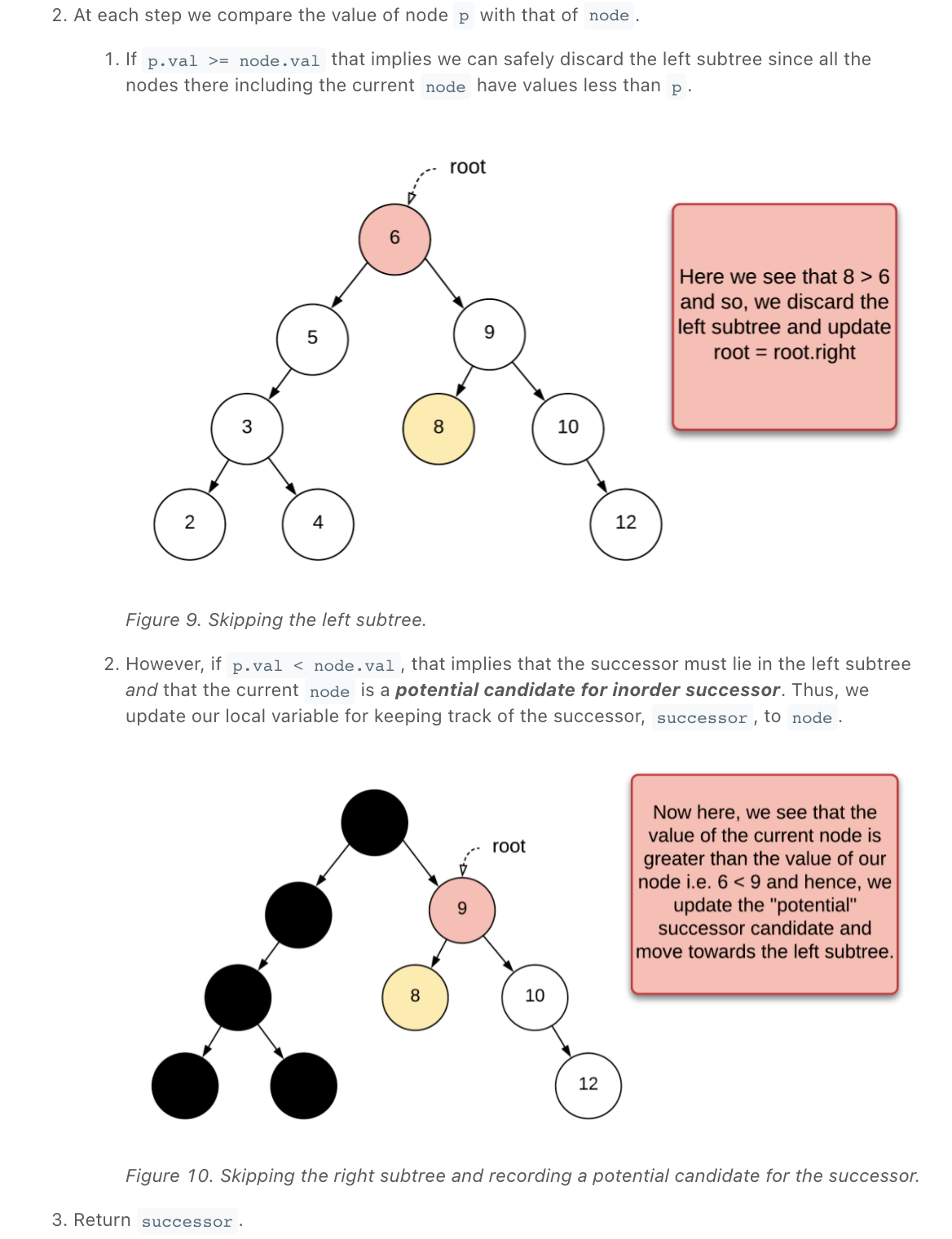
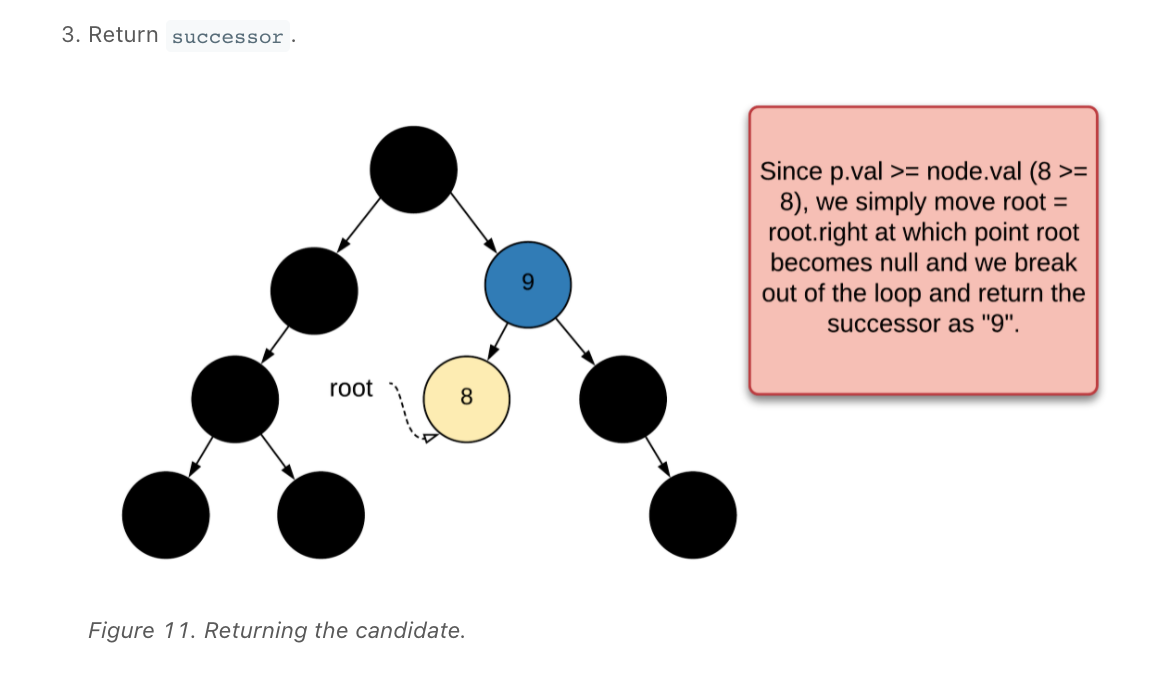
""" Inorder Successor in BST: FIND THE FIRST KEY GREATER THAN A GIVEN VALUE IN A BST: Given the root of a binary search tree and a node p in it, return the in-order successor of that node in the BST. If the given node has no in-order successor in the tree, return null. The successor of a node p is the node with the smallest key greater than p.val. https://leetcode.com/problems/inorder-successor-in-bst epi 14.2 """ # Definition for a binary tree node. class TreeNode: def __init__(self, x): self.val = x self.left = None self.right = None class Solution: def inorderSuccessor(self, root: 'TreeNode', p: 'TreeNode'): nxt = None curr = root while curr is not None: # successor will be the next larger value compared to the element if curr.val > p.val: nxt = curr # try to reduce the value curr = curr.left else: # try to increase the value curr = curr.right return nxt -
Inorder Successor in BST II
Example 1:
Input: tree = [2,1,3], node = 1 Output: 2 Explanation: 1's in-order successor node is 2. Note that both the node and the return value is of Node type.Example 2:
Input: tree = [5,3,6,2,4,null,null,1], node = 6 Output: null Explanation: There is no in-order successor of the current node, so the answer is null.Example 3:
Input: tree = [15,6,18,3,7,17,20,2,4,null,13,null,null,null,null,null,null,null,null,9], node = 15 Output: 17Example 4:
Input: tree = [15,6,18,3,7,17,20,2,4,null,13,null,null,null,null,null,null,null,null,9], node = 13 Output: 15Example 5:
Input: tree = [0], node = 0 Output: null
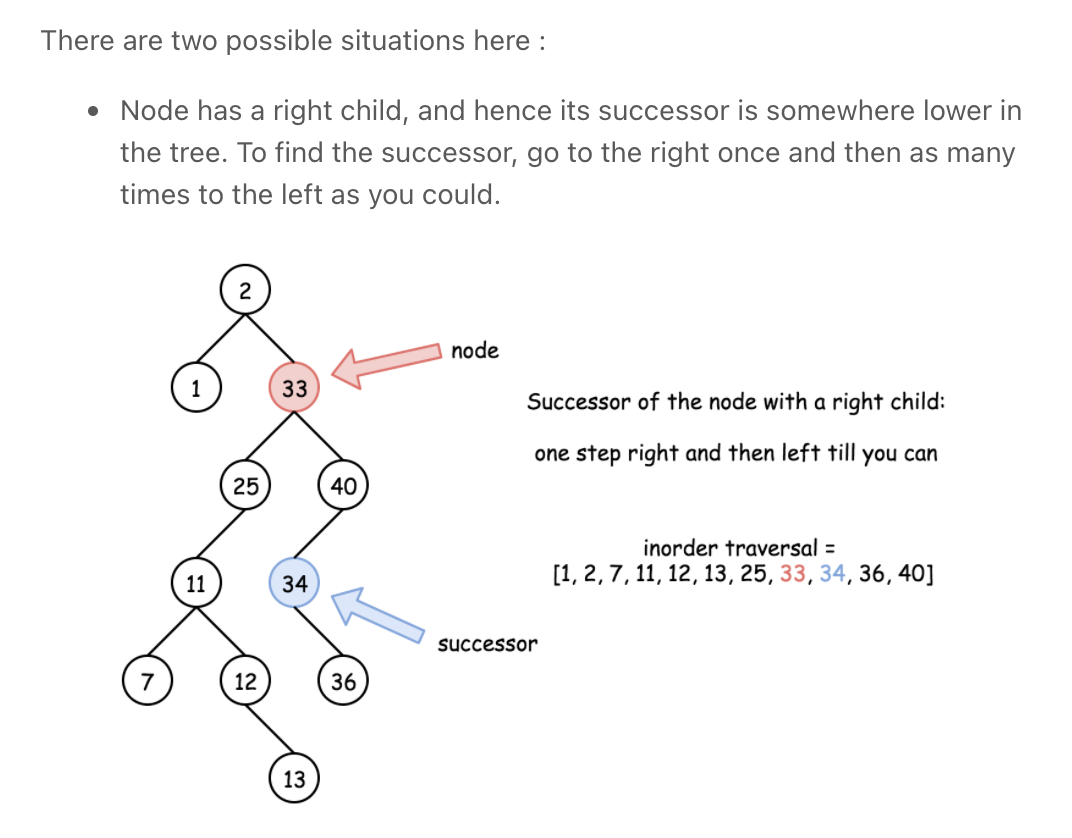
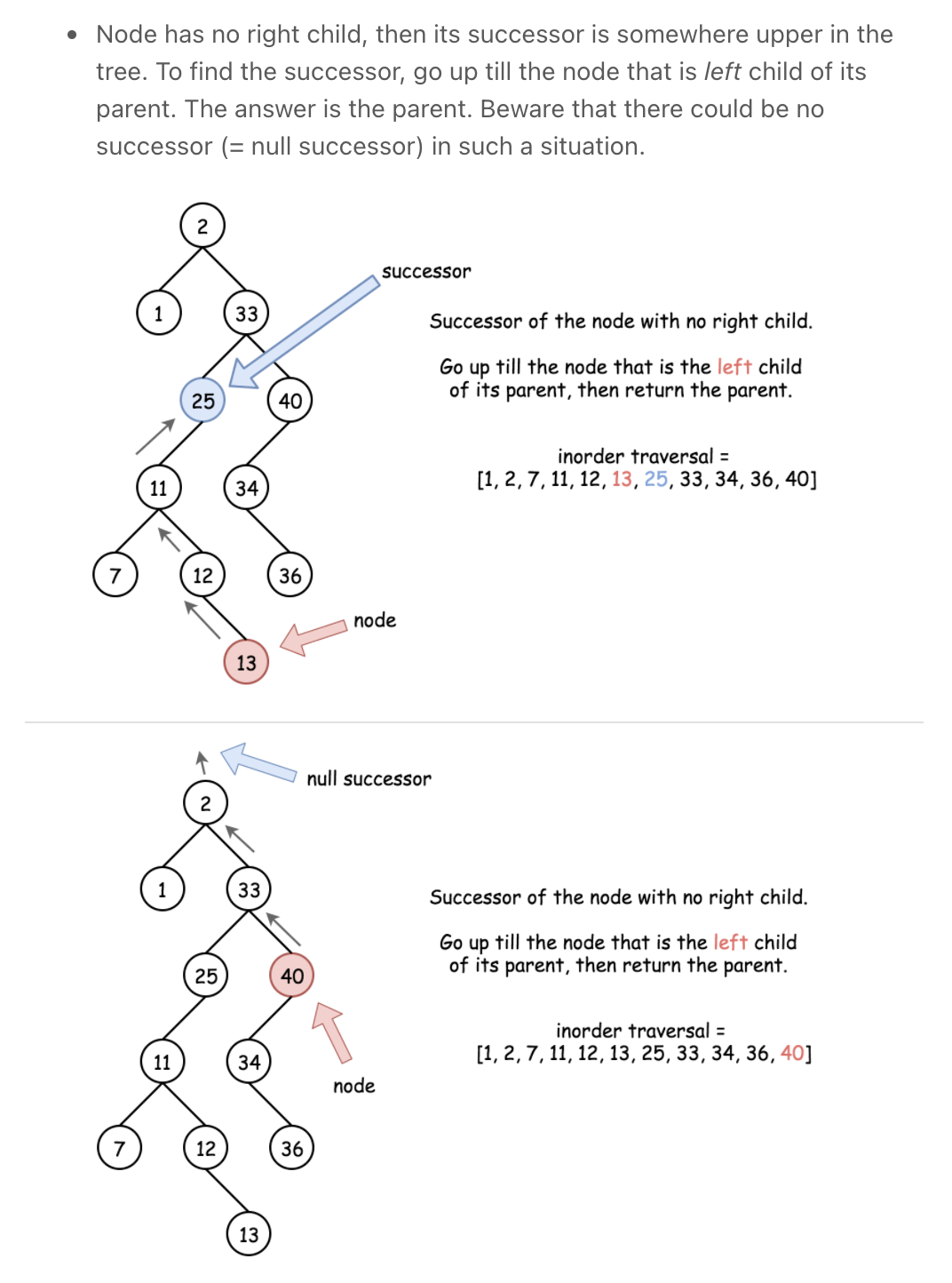

""" 510. Inorder Successor in BST II Given a node in a binary search tree, return the in-order successor of that node in the BST. If that node has no in-order successor, return null. The successor of a node is the node with the smallest key greater than node.val. You will have direct access to the node but not to the root of the tree. Each node will have a reference to its parent node. Below is the definition for Node: class Node { public int val; public Node left; public Node right; public Node parent; } """ """ Node has a right child, and hence its successor is somewhere lower in the tree. To find the successor, go to the right once and then as many times to the left as you could. Node has no right child, then its successor is somewhere upper in the tree. To find the successor, go up till the node that is left child of its parent. The answer is the parent. Beware that there could be no successor (= null successor) in such a situation. """ # Definition for a Node. class Node: def __init__(self, val): self.val = val self.left = None self.right = None self.parent = None class Solution: def inorderSuccessor(self, node): curr = node if curr.right: # get left most child in right subtree curr = curr.right while curr and curr.left: curr = curr.left return curr else: # find where the tree last branched left while curr: if curr.parent and curr.parent.left == curr: return curr.parent curr = curr.parent return None -
BST Traversal
""" BST Traversal: Write three functions that take in a Binary Search Tree (BST) and an empty array, traverse the BST, add its nodes' values to the input array, and return that array. The three functions should traverse the BST using the in-order, pre-order, and post-order tree-traversal techniques, respectively. Each BST node has an integer value, a left child node, and a right child node. A node is said to be a valid BST node if and only if it satisfies the BST property: its value is strictly greater than the values of every node to its left; its value is less than or equal to the values of every node to its right; and its children nodes are either valid BST nodes themselves or None / null. https://www.algoexpert.io/questions/BST%20Traversal """ # In -> lnr # Pre -> nlr # Post -> lrn def inOrderTraverse(node, array): if node is None: return # before we get to the append we inOrderTraverse() on the left, then we find anther left, we inOrderTraverse on the left again and again # till we are at the final left for a given tree/sub-tree # we finally append its value then call inOrderTraverse() on its right child and the process repeats istself again and again # we will keep on going till the furthest left before any other step like array.append(node.value) or inOrderTraverse(node.right, array) inOrderTraverse(node.left, array) array.append(node.value) inOrderTraverse(node.right, array) return array def preOrderTraverse(node, array): if node is None: return array.append(node.value) preOrderTraverse(node.left, array) preOrderTraverse(node.right, array) return array def postOrderTraverse(node, array): if node is None: return postOrderTraverse(node.left, array) postOrderTraverse(node.right, array) array.append(node.value) return array -
Find Kth Largest Value In BST
""" Find Kth Largest Value In BST: Write a function that takes in a Binary Search Tree (BST) and a positive integer k and returns the kth largest integer contained in the BST. You can assume that there will only be integer values in the BST and that k is less than or equal to the number of nodes in the tree. Also, for the purpose of this question, duplicate integers will be treated as distinct values. In other words, the second largest value in a BST containing values {5, 7, 7} will be 7—not 5. Each BST node has an integer value, a left child node, and a right child node. A node is said to be a valid BST node if and only if it satisfies the BST property: its value is strictly greater than the values of every node to its left; its value is less than or equal to the values of every node to its right; and its children nodes are either valid BST nodes themselves or None / null. Sample Input tree = 15 / \ 5 20 / \ / \ 2 5 17 22 / \ 1 3 k = 3 Sample Output 17 https://www.algoexpert.io/questions/Find%20Kth%20Largest%20Value%20In%20BST """ # This is an input class. Do not edit. class BST: def __init__(self, value, left=None, right=None): self.value = value self.left = left self.right = right class TreeInfo: def __init__(self, visits_remaining): self.visits_remaining = visits_remaining self.last_visited = None # O(h + k) time | O(h) space - where h is the height of the tree and k is the input parameter # we have to go to the largest element, at the furthest/deepest right (h) first before looking for k def findKthLargestValueInBst(tree, k): tree_info = TreeInfo(k) reverseInOrderTraverse(tree, tree_info) return tree_info.last_visited.value def reverseInOrderTraverse(tree, tree_info): if not tree: return reverseInOrderTraverse(tree.right, tree_info) # # visit node # tree_info was updated in the above function call if tree_info.visits_remaining > 0: tree_info.visits_remaining -= 1 tree_info.last_visited = tree else: return reverseInOrderTraverse(tree.left, tree_info) -
Reconstruct Binary Search Tree from Preorder Traversal with Less than, greater than patterns
""" Construct Binary Search Tree from Preorder Traversal: Return the root node of a binary search tree that matches the given preorder traversal. (Recall that a binary search tree is a binary tree where for every node, any descendant of node.left has a value < node.val, and any descendant of node.right has a value > node.val. Also recall that a preorder traversal displays the value of the node first, then traverses node.left, then traverses node.right.) It's guaranteed that for the given test cases there is always possible to find a binary search tree with the given requirements. https://leetcode.com/problems/construct-binary-search-tree-from-preorder-traversal/ """ """ Reconstruct BST: The pre-order traversal of a Binary Tree is a traversal technique that starts at the tree's root node and visits nodes in the following order: Current node Left subtree Right subtree Given a non-empty array of integers representing the pre-order traversal of a Binary Search Tree (BST), write a function that creates the relevant BST and returns its root node. The input array will contain the values of BST nodes in the order in which these nodes would be visited with a pre-order traversal. Each BST node has an integer value, a left child node, and a right child node. A node is said to be a valid BST node if and only if it satisfies the BST property: its value is strictly greater than the values of every node to its left; its value is less than or equal to the values of every node to its right; and its children nodes are either valid BST nodes themselves or None / null. Sample Input preOrderTraversalValues = [10, 4, 2, 1, 5, 17, 19, 18] Sample Output 10 / \ 4 17 / \ \ 2 5 19 / / 1 18 https://www.algoexpert.io/questions/Reconstruct%20BST """ from typing import List class TreeNode: def __init__(self, val=0, left=None, right=None): self.val = val self.left = left self.right = right """ use pointers to keep track of valid values for each subtree """ class SolutionBF: def bstFromPreorderHelper(self, preorder, start, end): if start > end: return None if start == end: return TreeNode(preorder[start]) node = TreeNode(preorder[start]) left_start = start + 1 left_end = left_start while left_end <= end and preorder[left_end] < preorder[start]: left_end += 1 left_end -= 1 # last valid value node.left = self.bstFromPreorderHelper(preorder, left_start, left_end) node.right = self.bstFromPreorderHelper(preorder, left_end+1, end) return node def bstFromPreorder(self, preorder): return self.bstFromPreorderHelper(preorder, 0, len(preorder)-1) # ---------------------------------------------------------------------------------------------------------------------- """ We will start by creating the root node while keeping track of the max and min values at any time: - if value is less than node & greater than min: pass ot to left - if value is greater than node & less than max: pass to right Then proceed to the left: passing the max to be the root's value & min to be -inf right: passing the min to be thr root's value & max to be inf """ """ Sample Input preOrderTraversalValues = [10, 4, 2, 1, 5, 17, 16, 19, 18] Sample Output 10 / \ 4 17 / \ / \ 2 5 16 19 / / 1 18 keep track of the largest and smallest node that can be placed left -> pass current node as largest right -> pass curr node as smallest if it does not satisfy the constraints we go back up the tree till where it will match else, insert it """ class Solution: def bstFromPreorder(self, preorder: List[int]): # if not preorder return self.bstFromPreorderHelper(preorder, [0], float('-inf'), float('inf')) def bstFromPreorderHelper(self, preorder, curr, minimum, maximum): if curr[0] >= len(preorder): # validate curr position on preoder array return None value = preorder[curr[0]] # get value from preoder array if value < minimum or value > maximum: # check whether it can be added return None node = TreeNode(value) # create Node # add left and right curr[0] = curr[0] + 1 # move pointer forward node.left = self.bstFromPreorderHelper(preorder, curr, minimum, value) node.right = self.bstFromPreorderHelper(preorder, curr, value, maximum) return node -
Same BSTs *
""" Same BSTs: An array of integers is said to represent the Binary Search Tree (BST) obtained by inserting each integer in the array, from left to right, into the BST. Write a function that takes in two arrays of integers and determines whether these arrays represent the same BST. Note that you're not allowed to construct any BSTs in your code. A BST is a Binary Tree that consists only of BST nodes. A node is said to be a valid BST node if and only if it satisfies the BST property: its value is strictly greater than the values of every node to its left; its value is less than or equal to the values of every node to its right; and its children nodes are either valid BST nodes themselves or None / null. Sample Input arrayOne = [10, 15, 8, 12, 94, 81, 5, 2, 11] arrayTwo = [10, 8, 5, 15, 2, 12, 11, 94, 81] Sample Output true // both arrays represent the BST below 10 / \ 8 15 / / \ 5 12 94 / / / 2 11 81 https://www.algoexpert.io/questions/Same%20BSTs """ # O(n^2) time | O(n^2) space - where n is the number of nodes in each array, respectively def sameBsts(arrayOne, arrayTwo): return sameBstsHelper(arrayOne, arrayTwo) def sameBstsHelper(arrayOne, arrayTwo): # must be same length if len(arrayOne) != len(arrayTwo): return False # we didn't find anything wrong if len(arrayOne) == 0: # any -> arrayOne/arrayTwo return True # must have same head if arrayOne[0] != arrayTwo[0]: return False # # split into right and left # elements larger or equal to than idx 0 right_one = [] right_two = [] # elements smaller than idx 0 left_one = [] left_two = [] for idx in range(1, len(arrayOne)): # any -> arrayOne/arrayTwo # one if arrayOne[idx] < arrayOne[0]: left_one.append(arrayOne[idx]) else: right_one.append(arrayOne[idx]) # two if arrayTwo[idx] < arrayTwo[0]: left_two.append(arrayTwo[idx]) else: right_two.append(arrayTwo[idx]) left = sameBstsHelper(left_one, left_two) right = sameBstsHelper(right_one, right_two) return left and right """ # ---------------------------------------------------------------------------------------------------------------------- # check roots - `build bst `(find all the roots at every point in the tree) and validate that they are same """ # O(n^2) time | O(d) space # where n is the number of nodes in each array, respectively, # and d is the depth of the BST that they represent def sameBsts(array_one, array_two): return buildTrees(array_one, array_two, 0, 0, float('-inf'), float('inf')) def buildTrees(array_one, array_two, idx_one, idx_two, minimum, maximum): # no extra elements to add (reached end) if idx_one == None or idx_two == None: return idx_one == idx_two # validate roots (roots should be same) if array_one[idx_one] != array_two[idx_two]: return False curr = array_one[idx_one] left_one = findNextValidSmaller(array_one, idx_one, minimum) left_two = findNextValidSmaller(array_two, idx_two, minimum) right_one = findNextValidLargerOrEqual(array_one, idx_one, maximum) right_two = findNextValidLargerOrEqual(array_two, idx_two, maximum) left = buildTrees( # the curr is the largest there will ever be array_one, array_two, left_one, left_two, minimum, curr) right = buildTrees( # curr is the smallest array_one, array_two, right_one, right_two, curr, maximum) return left and right def findNextValidSmaller(array, starting_idx, running_minimum): # used to find the next left root # Find the index of the first smaller value after the startingIdx. # Make sure that this value is greater than or equal to the minVal, # which is the value of the previous parent node in the BST. # If it isn't, then that value is located in the left subtree of the # previous parent node. for idx in range(starting_idx + 1, len(array)): if array[idx] < array[starting_idx] and array[idx] >= running_minimum: return idx return None def findNextValidLargerOrEqual(array, starting_idx, running_maximum): # used to find the next right root # Find the index of the first bigger/equal value after the startingIdx. # Make sure that this value is smaller than maxVal, which is the value # of the previous parent node in the BST. # If it isn't, then that value is located in the right subtree of the previous parent node. for idx in range(starting_idx + 1, len(array)): if array[idx] >= array[starting_idx] and array[idx] < running_maximum: return idx return None -
Serialize and Deserialize BST *
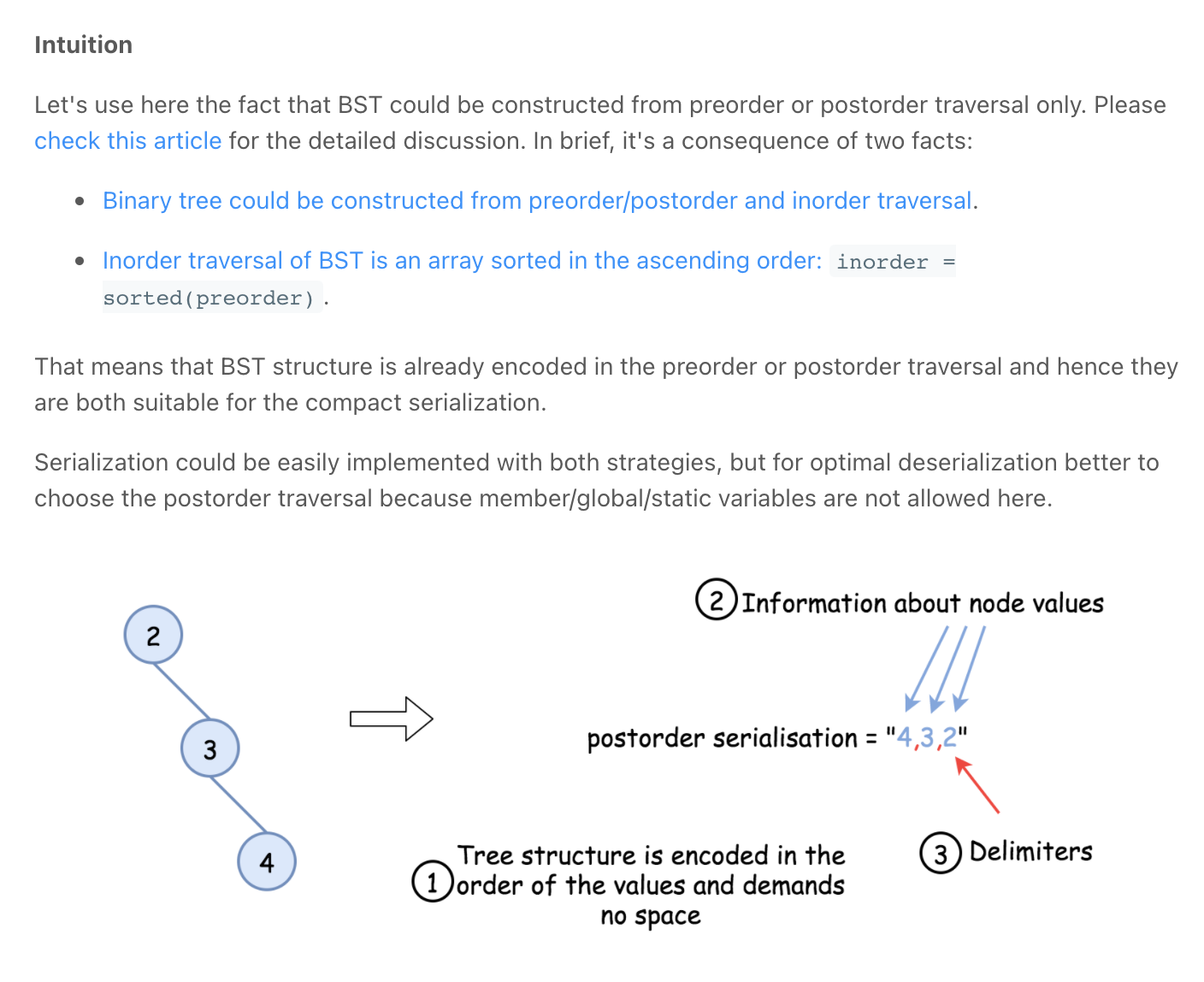
""" Serialize and Deserialize BST Serialization is converting a data structure or object into a sequence of bits so that it can be stored in a file or memory buffer, or transmitted across a network connection link to be reconstructed later in the same or another computer environment. Design an algorithm to serialize and deserialize a binary search tree. There is no restriction on how your serialization/deserialization algorithm should work. You need to ensure that a binary search tree can be serialized to a string, and this string can be deserialized to the original tree structure. The encoded string should be as compact as possible. Example 1: Input: root = [2,1,3] Output: [2,1,3] Example 2: Input: root = [] Output: [] After this: - https://leetcode.com/problems/serialize-and-deserialize-binary-tree https://leetcode.com/problems/serialize-and-deserialize-bst """ """ Alternative solutions: - using preorder traversal (here we use postorder) https://leetcode.com/problems/construct-binary-search-tree-from-preorder-traversal """ # Definition for a binary tree node. class TreeNode: def __init__(self, x): self.val = x self.left = None self.right = None class Codec: def serialize(self, root): """ Encodes a tree to a single postorder string. """ postorder_result = [] def postorder(node): if not node: return postorder(node.left) postorder(node.right) postorder_result.append(node.val) postorder(root) return ' '.join(map(str, postorder_result)) def deserialize(self, data): """ Decodes your encoded data to tree. """ def reverse_postorder(lower, upper): """ Reverse of postorder: postorder is `lrn`, here we do `nrl` """ if not data: return None if data[-1] < lower or data[-1] > upper: return None node = TreeNode(data.pop()) node.right = reverse_postorder(node.val, upper) node.left = reverse_postorder(lower, node.val) return node data = [int(x) for x in data.split(' ') if x] return reverse_postorder(float('-inf'), float('inf')) # Your Codec object will be instantiated and called as such: # Your Codec object will be instantiated and called as such: # ser = Codec() # deser = Codec() # tree = ser.serialize(root) # ans = deser.deserialize(tree) # return ans -
Subtree of Another Tree *
-
Check subtree






""" Subtree of Another Tree: Given two non-empty binary trees s and t, check whether tree t has exactly the same structure and node values with a subtree of s. A subtree of s is a tree consists of a node in s and all of this node's descendants. The tree s could also be considered as a subtree of itself. https://leetcode.com/problems/subtree-of-another-tree/ """ # Definition for a binary tree node. class TreeNode: def __init__(self, val=0, left=None, right=None): self.val = val self.left = left self.right = right class Solution: def isSubtree(self, s: TreeNode, t: TreeNode): return self.traverse(s, t) def traverse(self, s, t): if self.checkSubTreeFunction(s, t) == True: return True if s is None: return False return self.traverse(s.left, t) or self.traverse(s.right, t) def checkSubTreeFunction(self, s, t): if s == None and t == None: return True elif s == None or t == None or s.val != t.val: return False return self.checkSubTreeFunction(s.left, t.left) and self.checkSubTreeFunction(s.right, t.right) -
-
Construct Binary Tree from Preorder and Inorder Traversal
[1/3] CONSTRUCT BINARY TREE FROM PREORDER/INORDER TRAVERSAL - Code & Whiteboard
Construct Binary Tree from Inorder and Preorder Traversal - Leetcode 105 - Python
LeetCode 105. Construct Binary Tree from Preorder and Inorder Traversal (Algorithm Explained)


""" Construct Binary Tree from Preorder and Inorder Traversal: Given two integer arrays preorder and inorder where preorder is the preorder traversal of a binary tree and inorder is the inorder traversal of the same tree, construct and return the binary tree. Example 1: Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7] Output: [3,9,20,null,null,15,7] Example 2: Input: preorder = [-1], inorder = [-1] Output: [-1] https://leetcode.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal/ """ from typing import List class TreeNode: def __init__(self, val=0, left=None, right=None): self.val = val self.left = left self.right = right # --------------------------------------------------------------------------------------------------------------------- """ - The root will be the first element in the preorder sequence - Next, locate the index of the root node in the inorder sequence - this will help you know the number of nodes to its left & the number to its right - repeat this recursively """ class SolutionBF(object): def buildTree(self, preorder, inorder): return self.dfs(preorder, inorder) def dfs(self, preorder, inorder): if len(preorder) == 0: return None root = TreeNode(preorder[0]) mid = inorder.index(preorder[0]) root.left = self.dfs(preorder[1: mid+1], inorder[: mid]) root.right = self.dfs(preorder[mid+1:], inorder[mid+1:]) return root class SolutionBF0: def buildTree(self, preorder, inorder): if len(inorder) == 0: # the remaining preorder values do not belong in this subtree return None if len(preorder) == 1: return TreeNode(preorder[0]) ino_index = inorder.index(preorder.pop(0)) # remove from preorder node = TreeNode(inorder[ino_index]) node.left = self.buildTree(preorder, inorder[:ino_index]) node.right = self.buildTree(preorder, inorder[ino_index+1:]) return node class SolutionBF00: def buildTree(self, preorder, inorder): preorder_pos = 0 def buildTreeHelper(preorder, inorder): nonlocal preorder_pos # we do not have valid nodes to be placed if preorder_pos >= len(preorder): return # # create node # node inorder_idx = inorder.index(preorder[preorder_pos]) preorder_pos += 1 node = TreeNode(inorder[inorder_idx]) # children -> will pass only valid children below -> (inorder[:inorder_idx] & inorder[inorder_idx+1:] does that) node.left = buildTreeHelper(preorder, inorder[:inorder_idx]) node.right = buildTreeHelper(preorder, inorder[inorder_idx+1:]) return node return buildTreeHelper(preorder, inorder) # def buildTreeHelper2( preorder, inorder): # nonlocal preorder_pos # if preorder_pos >= len(preorder): # return # # # create node # # node # inorder_idx = inorder.index( preorder[preorder_pos] ) # preorder_pos += 1 # node = TreeNode(inorder[inorder_idx ]) # left = inorder[:inorder_idx] # right = inorder[inorder_idx+1:] # if left: # node.left = buildTreeHelper(preorder, left) # if right: # node.right = buildTreeHelper(preorder, right) # return node # return buildTreeHelper2(preorder, inorder) # --------------------------------------------------------------------------------------------------------------------- """ - The root will be the first element in the preorder sequence - Next, locate the index of the root node in the inorder sequence - this will help you know the number of nodes to its left & the number to its right - repeat this recursively - iterate through the preorder array and check if the current can be placed in the current tree(or recursive call) - We use the remaining inorder traversal to determine(restrict) whether the current preorder node is in the left or right """ class Solution: def buildTree(self, preorder, inorder): preorder_pos = 0 inorder_idxs = {val: idx for idx, val in enumerate(inorder)} def helper(inorder_left, inorder_right): nonlocal preorder_pos if preorder_pos == len(preorder): return if inorder_left > inorder_right: return val = preorder[preorder_pos] preorder_pos += 1 node = TreeNode(val) inorder_idx = inorder_idxs[val] # start with left ! node.left = helper(inorder_left, inorder_idx-1) node.right = helper(inorder_idx+1, inorder_right) return node return helper(0, len(inorder)-1) -
Construct Binary Tree from Inorder and Postorder Traversal

""" 106. Construct Binary Tree from Inorder and Postorder Traversal Given two integer arrays inorder and postorder where inorder is the inorder traversal of a binary tree and postorder is the postorder traversal of the same tree, construct and return the binary tree. Example 1: Input: inorder = [9,3,15,20,7], postorder = [9,15,7,20,3] Output: [3,9,20,null,null,15,7] Example 2: Input: inorder = [-1], postorder = [-1] Output: [-1] https://leetcode.com/problems/construct-binary-tree-from-inorder-and-postorder-traversal """ # Definition for a binary tree node. class TreeNode: def __init__(self, val=0, left=None, right=None): self.val = val self.left = left self.right = right class Solution: def buildTree(self, inorder, postorder): postorder_idx = len(postorder)-1 inorder_idxs = {val: idx for idx, val in enumerate(inorder)} def helper(inorder_left, inorder_right): nonlocal postorder_idx if postorder_idx < 0: return None if inorder_left > inorder_right: return None val = postorder[postorder_idx] postorder_idx -= 1 # create node node = TreeNode(val) inorder_idx = inorder_idxs[val] # start with right ! node.right = helper(inorder_idx+1, inorder_right) node.left = helper(inorder_left, inorder_idx-1) return node return helper(0, len(inorder)-1) -
Preorder/Postorder
-
Binary Tree Inorder Traversal - Iterative **

Screen Recording 2021-10-23 at 13.36.24.mov
""" Binary Tree Inorder Traversal: Given the root of a binary tree, return the inorder traversal of its nodes' values. https://leetcode.com/problems/binary-tree-inorder-traversal/ https://www.enjoyalgorithms.com/blog/iterative-binary-tree-traversals-using-stack https://www.educative.io/edpresso/how-to-perform-an-iterative-inorder-traversal-of-a-binary-tree https://www.techiedelight.com/inorder-tree-traversal-iterative-recursive After this: - https://leetcode.com/problems/binary-search-tree-iterator """ # Definition for a binary tree node. class TreeNode: def __init__(self, val=0, left=None, right=None): self.val = val self.left = left self.right = right """ - add all left nodes to stack - visit left most node - move to the right """ class Solution_: def inorderTraversal(self, root: TreeNode): if not root: return None result = [] stack = [] curr = root while stack or curr: # add all left # put the left most value(s) to the top of the stack while curr and curr.left: stack.append(curr) curr = curr.left # the top of the stack has the left most unvisited value # visit node if not curr: curr = stack.pop() result.append(curr.val) # - has no unvisited left # - itself is visited # so the next to be visited is right curr = curr.right return result """ class Solution: def inorderTraversal(self, root: TreeNode): output = [] stack = [] curr = root while curr is not None or len(stack) > 0: # add all left while curr is not None: stack.append(curr) curr = curr.left # visit node temp = stack.pop() output.append(temp.val) curr = temp.right return output """ # 10 # / \ # 4 17 # / \ \ # 2 5 19 # / / # 1 18 class Solution: def inorderTraversal(self, root: TreeNode): if not root: return None result = [] stack = [] curr = root while stack or curr: # put the left most value(s) to the top of the stack while curr: stack.append(curr) curr = curr.left # the top of the stack has the left most unvisited value # visit node curr = stack.pop() result.append(curr.val) # - has no unvisited left # - itself is visited # so the next to be visited is right # eg: after 4 is 5 in the example above curr = curr.right return result """ ------------------------------------------------------------------------------------------------------------ """ class Solution1: def inorderTraversal(self, root): output = [] self.inorderTraversalHelper(root, output) return output def inorderTraversalHelper(self, root, output): if not root: return self.inorderTraversalHelper(root.left, output) output.append(root.val) self.inorderTraversalHelper(root.right, output) -
Morris Inorder Tree Traversal - Inorder with O(1) space ***






""" Morris Inorder Tree Traversal - Inorder with O(1) space https://leetcode.com/problems/binary-tree-inorder-traversal EPI 9.11 """ # Definition for a binary tree node. class TreeNode: def __init__(self, val=0, left=None, right=None): self.val = val self.left = left self.right = right class Solution: def inorderTraversal(self, root): res = [] curr = root while curr is not None: # has no left child - so is the next valid if not curr.left: res.append(curr.val) curr = curr.right # place the curr node as the right child of its predecessor # which is the rightmost node in the left subtree else: predecessor = self.get_inorder_predecessor(curr) # # move node down the tree left = curr.left curr.left = None # prevent loop predecessor.right = curr # # continue to left subtree curr = left return res def get_inorder_predecessor(self, node): curr = node.left while curr.right is not None: curr = curr.right return curr -
536. Construct Binary Tree from String
-
Serialize and Deserialize Binary Tree **

""" Serialize and Deserialize Binary Tree Serialization is the process of converting a data structure or object into a sequence of bits so that it can be stored in a file or memory buffer, or transmitted across a network connection link to be reconstructed later in the same or another computer environment. Design an algorithm to serialize and deserialize a binary tree. There is no restriction on how your serialization/deserialization algorithm should work. You just need to ensure that a binary tree can be serialized to a string and this string can be deserialized to the original tree structure. Clarification: The input/output format is the same as how LeetCode serializes a binary tree. You do not necessarily need to follow this format, so please be creative and come up with different approaches yourself. Example 1: Input: root = [1,2,3,null,null,4,5] Output: [1,2,3,null,null,4,5] Example 2: Input: root = [] Output: [] Example 3: Input: root = [1] Output: [1] Example 4: Input: root = [1,2] Output: [1,2] https://leetcode.com/problems/serialize-and-deserialize-binary-tree/ Prerequisites: - https://leetcode.com/problems/serialize-and-deserialize-bst - https://leetcode.com/problems/construct-binary-search-tree-from-preorder-traversal """ # Definition for a binary tree node. class TreeNode(object): def __init__(self, x): self.val = x self.left = None self.right = None class Codec: def serialize(self, root): preorder_result = [] # def preorder(node): # if not node: # preorder_result.append(str(None)) # return # preorder_result.append(str(node.val)) # preorder(node.left) # preorder(node.right) def preorder(node): if not node: preorder_result.append(str(None)) return preorder_result.append(str(node.val)) preorder(node.left) preorder(node.right) preorder(root) return " ".join(preorder_result) def deserialize(self, data): idx = 0 def reverse_preorder(arr): nonlocal idx if idx > len(arr): return None if arr[idx] == 'None': idx += 1 return None node = TreeNode(int(arr[idx])) idx += 1 node.left = reverse_preorder(arr) node.right = reverse_preorder(arr) return node return reverse_preorder(data.split(" ")) # Your Codec object will be instantiated and called as such: # ser = Codec() # deser = Codec() # ans = deser.deserialize(ser.serialize(root)) -
Construct Binary Tree from String














""" 536. Construct Binary Tree from String You need to construct a binary tree from a string consisting of parenthesis and integers. The whole input represents a binary tree. It contains an integer followed by zero, one or two pairs of parenthesis. The integer represents the root's value and a pair of parenthesis contains a child binary tree with the same structure. You always start to construct the left child node of the parent first if it exists. https://leetcode.com/problems/construct-binary-tree-from-string """ """ "4( 2( 3) ( 1) ) (6(5))" - tree startes at number - new opening bracket means new subtree - unclosable closing brackets means we return - record number as value then idx + 1 - left: if opening bracket, start new tree at idx + 1 - skip closing bracket move idx += 1 - right: if opening bracket, start new tree at idx + 1 - skip closing bracket move idx += 1 - else: return """ class TreeNode: def __init__(self, val=0, left=None, right=None): self.val = val self.left = left self.right = right class Solution: def str2tree(self, s: str): idx = 0 def build_tree(): nonlocal idx # base cases if idx >= len(s): return None start_idx = idx # get number while idx < len(s) and (s[idx].isnumeric() or s[idx] == '-'): idx += 1 node = TreeNode(s[start_idx:idx]) # subtrees if idx < len(s) and s[idx] == "(": idx += 1 node.left = build_tree() idx += 1 if idx < len(s) and s[idx] == "(": idx += 1 node.right = build_tree() idx += 1 return node return build_tree() -
Flatten Binary Tree to Linked List **


Solution 1






# Definition for a binary tree node. class TreeNode: def __init__(self, val=0, left=None, right=None): self.val = val self.left = left self.right = right class Solution_: def flatten(self, root): if not root: return None right = root.right if root.left: # place the left subtree between the root & root.right root.right = root.left left_ending = self.flatten(root.left) left_ending.right = right # remove left root.left = None furthest = self.flatten(root.right) return furthest or root """ our algorithm will return the tail node of the flattened out tree. For a given node, we will recursively flatten out the left and the right subtrees and store their corresponding tail nodes in left_ending and right_ending respectively. Next, we will make the following connections (only if there is a left child for the current node, else the left_ending would be null) (Place the left subtree between the root & root.right) left_ending.right = node.right node.right = node.left node.left = None Next we have to return the tail of the final, flattened out tree rooted at node. So, if the node has a right child, then we will return the right_ending, else, we'll return the left_ending """ class Solution: def flatten(self, root): if not root: return None left_ending = self.flatten(root.left) right_ending = self.flatten(root.right) # If there was a left subtree, we shuffle the connections # around so that there is nothing on the left side anymore. if left_ending: # Place the left subtree between the root & root.right left_ending.right = root.right root.right = root.left # Remove left root.left = None # We need to return the "rightmost" node after we are done wiring the new connections. # 2. For a node with only a left subtree, the rightmost node will be left_ending because it has been moved to the right subtree # 3. For a leaf node, we simply return the node return right_ending or left_ending or rootSolution 2

class Solution: def flatten(self, root): if not root: return None stack = [root] while stack: node = stack.pop() if node.right: stack.append(node.right) if node.left: stack.append(node.left) node.left = None if stack: node.right = stack[-1] # PeekApproach 3: O(1) Iterative Solution (Greedy & similar to Morris Traversal)
similar to Morris Traversal









""" O(1) Iterative Solution (Greedy & similar to Morris Traversal) """ class Solution: def flatten(self, root): if not root: return None curr = root while curr: # If there was a left subtree, we shuffle the connections # around so that there is nothing on the left side anymore. if curr.left: l_right_most = self.find_right_most(curr.left) # place the left subtree between the root & root.right l_right_most.right = curr.right curr.right = curr.left # remove left curr.left = None curr = curr.right def find_right_most(self, root): curr = root while curr.right: curr = curr.right return curr
Binary Search Trees
General
Examples:
-
Implementation
# Binary Search Tree Implementation in Python # Blog post: https://emre.me/data-structures/binary-search-trees/ class Node: def __init__(self, key, val, left=None, right=None, parent=None): self.key = key self.payload = val self.leftChild = left self.rightChild = right self.parent = parent def has_left_child(self): return self.leftChild def has_right_child(self): return self.rightChild def is_left_child(self): return self.parent and self.parent.leftChild == self def is_right_child(self): return self.parent and self.parent.rightChild == self def is_root(self): return not self.parent def is_leaf(self): return not (self.rightChild or self.leftChild) def has_any_children(self): return self.rightChild or self.leftChild def has_both_children(self): return self.rightChild and self.leftChild def splice_out(self): if self.is_leaf(): if self.is_left_child(): self.parent.leftChild = None else: self.parent.rightChild = None elif self.has_any_children(): if self.has_left_child(): if self.is_left_child(): self.parent.leftChild = self.leftChild else: self.parent.rightChild = self.leftChild self.leftChild.parent = self.parent else: if self.is_left_child(): self.parent.leftChild = self.rightChild else: self.parent.rightChild = self.rightChild self.rightChild.parent = self.parent def find_successor(self): successor = None if self.has_right_child(): successor = self.rightChild.find_min() else: if self.parent: if self.is_left_child(): successor = self.parent else: self.parent.rightChild = None successor = self.parent.find_successor() self.parent.rightChild = self return successor def find_min(self): current = self while current.has_left_child(): current = current.leftChild return current def replace_node_data(self, key, value, lc, rc): self.key = key self.payload = value self.leftChild = lc self.rightChild = rc if self.has_left_child(): self.leftChild.parent = self if self.has_right_child(): self.rightChild.parent = self class BinarySearchTree: def __init__(self): self.root = None self.size = 0 def length(self): return self.size def __len__(self): return self.size def put(self, key, val): if self.root: self._put(key, val, self.root) else: self.root = Node(key, val) self.size = self.size + 1 def _put(self, key, val, current_node): if key < current_node.key: if current_node.has_left_child(): self._put(key, val, current_node.leftChild) else: current_node.leftChild = Node(key, val, parent=current_node) else: if current_node.has_right_child(): self._put(key, val, current_node.rightChild) else: current_node.rightChild = Node(key, val, parent=current_node) def __setitem__(self, k, v): self.put(k, v) def get(self, key): if self.root: res = self._get(key, self.root) if res: return res.payload else: return None else: return None def _get(self, key, current_node): if not current_node: return None elif current_node.key == key: return current_node elif key < current_node.key: return self._get(key, current_node.leftChild) else: return self._get(key, current_node.rightChild) def __getitem__(self, key): return self.get(key) def __contains__(self, key): if self._get(key, self.root): return True else: return False def delete(self, key): if self.size > 1: node_to_remove = self._get(key, self.root) if node_to_remove: self.remove(node_to_remove) self.size = self.size - 1 else: raise KeyError('Error, key not in tree') elif self.size == 1 and self.root.key == key: self.root = None self.size = self.size - 1 else: raise KeyError('Error, key not in tree') def __delitem__(self, key): self.delete(key) def remove(self, current_node): if current_node.is_leaf(): # leaf if current_node == current_node.parent.leftChild: current_node.parent.leftChild = None else: current_node.parent.rightChild = None elif current_node.has_both_children(): # interior successor = current_node.find_successor() successor.splice_out() current_node.key = successor.key current_node.payload = successor.payload else: # this node has one child if current_node.has_left_child(): if current_node.is_left_child(): current_node.leftChild.parent = current_node.parent current_node.parent.leftChild = current_node.leftChild elif current_node.is_right_child(): current_node.leftChild.parent = current_node.parent current_node.parent.rightChild = current_node.leftChild else: current_node.replace_node_data(current_node.leftChild.key, current_node.leftChild.payload, current_node.leftChild.leftChild, current_node.leftChild.rightChild) else: if current_node.is_left_child(): current_node.rightChild.parent = current_node.parent current_node.parent.leftChild = current_node.rightChild elif current_node.is_right_child(): current_node.rightChild.parent = current_node.parent current_node.parent.rightChild = current_node.rightChild else: current_node.replace_node_data(current_node.rightChild.key, current_node.rightChild.payload, current_node.rightChild.leftChild, current_node.rightChild.rightChild) -
Find Kth Largest Value In BST
""" Find Kth Largest Value In BST: Write a function that takes in a Binary Search Tree (BST) and a positive integer k and returns the kth largest integer contained in the BST. You can assume that there will only be integer values in the BST and that k is less than or equal to the number of nodes in the tree. Also, for the purpose of this question, duplicate integers will be treated as distinct values. In other words, the second largest value in a BST containing values {5, 7, 7} will be 7—not 5. Each BST node has an integer value, a left child node, and a right child node. A node is said to be a valid BST node if and only if it satisfies the BST property: its value is strictly greater than the values of every node to its left; its value is less than or equal to the values of every node to its right; and its children nodes are either valid BST nodes themselves or None / null. Sample Input tree = 15 / \ 5 20 / \ / \ 2 5 17 22 / \ 1 3 k = 3 Sample Output 17 https://www.algoexpert.io/questions/Find%20Kth%20Largest%20Value%20In%20BST """ # This is an input class. Do not edit. class BST: def __init__(self, value, left=None, right=None): self.value = value self.left = left self.right = right class TreeInfo: def __init__(self, visits_remaining): self.visits_remaining = visits_remaining self.last_visited = None # O(h + k) time | O(h) space - where h is the height of the tree and k is the input parameter # we have to go to the largest element, at the furthest/deepest right (h) first before looking for k def findKthLargestValueInBst(tree, k): tree_info = TreeInfo(k) reverseInOrderTraverse(tree, tree_info) return tree_info.last_visited.value def reverseInOrderTraverse(tree, tree_info): if not tree: return reverseInOrderTraverse(tree.right, tree_info) # # visit node # tree_info was updated in the above function call if tree_info.visits_remaining > 0: tree_info.visits_remaining -= 1 tree_info.last_visited = tree else: return reverseInOrderTraverse(tree.left, tree_info) -
Reconstruct Binary Search Tree from Preorder Traversal with Less than, greater than patterns
""" Construct Binary Search Tree from Preorder Traversal: Return the root node of a binary search tree that matches the given preorder traversal. (Recall that a binary search tree is a binary tree where for every node, any descendant of node.left has a value < node.val, and any descendant of node.right has a value > node.val. Also recall that a preorder traversal displays the value of the node first, then traverses node.left, then traverses node.right.) It's guaranteed that for the given test cases there is always possible to find a binary search tree with the given requirements. https://leetcode.com/problems/construct-binary-search-tree-from-preorder-traversal/ """ """ Reconstruct BST: The pre-order traversal of a Binary Tree is a traversal technique that starts at the tree's root node and visits nodes in the following order: Current node Left subtree Right subtree Given a non-empty array of integers representing the pre-order traversal of a Binary Search Tree (BST), write a function that creates the relevant BST and returns its root node. The input array will contain the values of BST nodes in the order in which these nodes would be visited with a pre-order traversal. Each BST node has an integer value, a left child node, and a right child node. A node is said to be a valid BST node if and only if it satisfies the BST property: its value is strictly greater than the values of every node to its left; its value is less than or equal to the values of every node to its right; and its children nodes are either valid BST nodes themselves or None / null. Sample Input preOrderTraversalValues = [10, 4, 2, 1, 5, 17, 19, 18] Sample Output 10 / \ 4 17 / \ \ 2 5 19 / / 1 18 https://www.algoexpert.io/questions/Reconstruct%20BST """ from typing import List class TreeNode: def __init__(self, val=0, left=None, right=None): self.val = val self.left = left self.right = right """ use pointers to keep track of valid values for each subtree """ class SolutionBF: def bstFromPreorderHelper(self, preorder, start, end): if start > end: return None if start == end: return TreeNode(preorder[start]) node = TreeNode(preorder[start]) left_start = start + 1 left_end = left_start while left_end <= end and preorder[left_end] < preorder[start]: left_end += 1 left_end -= 1 # last valid value node.left = self.bstFromPreorderHelper(preorder, left_start, left_end) node.right = self.bstFromPreorderHelper(preorder, left_end+1, end) return node def bstFromPreorder(self, preorder): return self.bstFromPreorderHelper(preorder, 0, len(preorder)-1) # ---------------------------------------------------------------------------------------------------------------------- """ We will start by creating the root node while keeping track of the max and min values at any time: - if value is less than node & greater than min: pass ot to left - if value is greater than node & less than max: pass to right Then proceed to the left: passing the max to be the root's value & min to be -inf right: passing the min to be thr root's value & max to be inf """ """ Sample Input preOrderTraversalValues = [10, 4, 2, 1, 5, 17, 16, 19, 18] Sample Output 10 / \ 4 17 / \ / \ 2 5 16 19 / / 1 18 keep track of the largest and smallest node that can be placed left -> pass current node as largest right -> pass curr node as smallest if it does not satisfy the constraints we go back up the tree till where it will match else, insert it """ class Solution: def bstFromPreorder(self, preorder: List[int]): # if not preorder return self.bstFromPreorderHelper(preorder, [0], float('-inf'), float('inf')) def bstFromPreorderHelper(self, preorder, curr, minimum, maximum): if curr[0] >= len(preorder): # validate curr position on preoder array return None value = preorder[curr[0]] # get value from preoder array if value < minimum or value > maximum: # check whether it can be added return None node = TreeNode(value) # create Node # add left and right curr[0] = curr[0] + 1 # move pointer forward node.left = self.bstFromPreorderHelper(preorder, curr, minimum, value) node.right = self.bstFromPreorderHelper(preorder, curr, value, maximum) return node -
Same BSTs *
""" Same BSTs: An array of integers is said to represent the Binary Search Tree (BST) obtained by inserting each integer in the array, from left to right, into the BST. Write a function that takes in two arrays of integers and determines whether these arrays represent the same BST. Note that you're not allowed to construct any BSTs in your code. A BST is a Binary Tree that consists only of BST nodes. A node is said to be a valid BST node if and only if it satisfies the BST property: its value is strictly greater than the values of every node to its left; its value is less than or equal to the values of every node to its right; and its children nodes are either valid BST nodes themselves or None / null. Sample Input arrayOne = [10, 15, 8, 12, 94, 81, 5, 2, 11] arrayTwo = [10, 8, 5, 15, 2, 12, 11, 94, 81] Sample Output true // both arrays represent the BST below 10 / \ 8 15 / / \ 5 12 94 / / / 2 11 81 https://www.algoexpert.io/questions/Same%20BSTs """ # O(n^2) time | O(n^2) space - where n is the number of nodes in each array, respectively def sameBsts(arrayOne, arrayTwo): return sameBstsHelper(arrayOne, arrayTwo) def sameBstsHelper(arrayOne, arrayTwo): # must be same length if len(arrayOne) != len(arrayTwo): return False # we didn't find anything wrong if len(arrayOne) == 0: # any -> arrayOne/arrayTwo return True # must have same head if arrayOne[0] != arrayTwo[0]: return False # # split into right and left # elements larger or equal to than idx 0 right_one = [] right_two = [] # elements smaller than idx 0 left_one = [] left_two = [] for idx in range(1, len(arrayOne)): # any -> arrayOne/arrayTwo # one if arrayOne[idx] < arrayOne[0]: left_one.append(arrayOne[idx]) else: right_one.append(arrayOne[idx]) # two if arrayTwo[idx] < arrayTwo[0]: left_two.append(arrayTwo[idx]) else: right_two.append(arrayTwo[idx]) left = sameBstsHelper(left_one, left_two) right = sameBstsHelper(right_one, right_two) return left and right """ # ---------------------------------------------------------------------------------------------------------------------- # check roots - `build bst `(find all the roots at every point in the tree) and validate that they are same """ # O(n^2) time | O(d) space # where n is the number of nodes in each array, respectively, # and d is the depth of the BST that they represent def sameBsts(array_one, array_two): return buildTrees(array_one, array_two, 0, 0, float('-inf'), float('inf')) def buildTrees(array_one, array_two, idx_one, idx_two, minimum, maximum): # no extra elements to add (reached end) if idx_one == None or idx_two == None: return idx_one == idx_two # validate roots (roots should be same) if array_one[idx_one] != array_two[idx_two]: return False curr = array_one[idx_one] left_one = findNextValidSmaller(array_one, idx_one, minimum) left_two = findNextValidSmaller(array_two, idx_two, minimum) right_one = findNextValidLargerOrEqual(array_one, idx_one, maximum) right_two = findNextValidLargerOrEqual(array_two, idx_two, maximum) left = buildTrees( # the curr is the largest there will ever be array_one, array_two, left_one, left_two, minimum, curr) right = buildTrees( # curr is the smallest array_one, array_two, right_one, right_two, curr, maximum) return left and right def findNextValidSmaller(array, starting_idx, running_minimum): # used to find the next left root # Find the index of the first smaller value after the startingIdx. # Make sure that this value is greater than or equal to the minVal, # which is the value of the previous parent node in the BST. # If it isn't, then that value is located in the left subtree of the # previous parent node. for idx in range(starting_idx + 1, len(array)): if array[idx] < array[starting_idx] and array[idx] >= running_minimum: return idx return None def findNextValidLargerOrEqual(array, starting_idx, running_maximum): # used to find the next right root # Find the index of the first bigger/equal value after the startingIdx. # Make sure that this value is smaller than maxVal, which is the value # of the previous parent node in the BST. # If it isn't, then that value is located in the right subtree of the previous parent node. for idx in range(starting_idx + 1, len(array)): if array[idx] >= array[starting_idx] and array[idx] < running_maximum: return idx return None -
Serialize and Deserialize BST *

""" Serialize and Deserialize BST Serialization is converting a data structure or object into a sequence of bits so that it can be stored in a file or memory buffer, or transmitted across a network connection link to be reconstructed later in the same or another computer environment. Design an algorithm to serialize and deserialize a binary search tree. There is no restriction on how your serialization/deserialization algorithm should work. You need to ensure that a binary search tree can be serialized to a string, and this string can be deserialized to the original tree structure. The encoded string should be as compact as possible. Example 1: Input: root = [2,1,3] Output: [2,1,3] Example 2: Input: root = [] Output: [] After this: - https://leetcode.com/problems/serialize-and-deserialize-binary-tree https://leetcode.com/problems/serialize-and-deserialize-bst """ """ Alternative solutions: - using preorder traversal (here we use postorder) https://leetcode.com/problems/construct-binary-search-tree-from-preorder-traversal """ # Definition for a binary tree node. class TreeNode: def __init__(self, x): self.val = x self.left = None self.right = None class Codec: def serialize(self, root): """ Encodes a tree to a single postorder string. """ postorder_result = [] def postorder(node): if not node: return postorder(node.left) postorder(node.right) postorder_result.append(node.val) postorder(root) return ' '.join(map(str, postorder_result)) def deserialize(self, data): """ Decodes your encoded data to tree. """ def reverse_postorder(lower, upper): """ Reverse of postorder: postorder is `lrn`, here we do `nrl` """ if not data: return None if data[-1] < lower or data[-1] > upper: return None node = TreeNode(data.pop()) node.right = reverse_postorder(node.val, upper) node.left = reverse_postorder(lower, node.val) return node data = [int(x) for x in data.split(' ') if x] return reverse_postorder(float('-inf'), float('inf')) # Your Codec object will be instantiated and called as such: # Your Codec object will be instantiated and called as such: # ser = Codec() # deser = Codec() # tree = ser.serialize(root) # ans = deser.deserialize(tree) # return ans -
Validate Binary Search Tree (with Less than, greater than patterns)
""" Validate Binary Search Tree Given a binary tree, determine if it is a valid binary search tree (BST). Assume a BST is defined as follows: The left subtree of a node contains only nodes with keys less than the node's key. The right subtree of a node contains only nodes with keys greater than the node's key. Both the left and right subtrees must also be binary search trees. Example 1: 2 / \ 1 3 Input: [2,1,3] Output: true Example 2: 5 / \ 1 4 / \ 3 6 Input: [5,1,4,null,null,3,6] Output: false Explanation: The root node's value is 5 but its right child's value is 4. https://leetcode.com/problems/validate-binary-search-tree/ """ # Definition for a binary tree node. # class TreeNode(object): # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right # O(n) time | O(d) space | where d is the depth of the tree (because of the callstack) def validateBst(node, maximum=float('inf'), minimum=float('-inf')): if node is None: return True # we didn't find an invalid node if node.value >= maximum or node.value < minimum: # validate with max & min return False # for every left child, it's maximum will be the value of it's parent and # for every right child, it's minimum will be the value of it's parent return validateBst(node.left, maximum=node.value, minimum=minimum) \ and validateBst(node.right, maximum=maximum, minimum=node.value) -
Min Height BST
""" Min Height BST: Write a function that takes in a non-empty sorted array of distinct integers, constructs a BST from the integers, and returns the root of the BST. The function should minimize the height of the BST. You've been provided with a BST class that you'll have to use to construct the BST. Each BST node has an integer value, a left child node, and a right child node. A node is said to be a valid BST node if and only if it satisfies the BST property: its value is strictly greater than the values of every node to its left; its value is less than or equal to the values of every node to its right; and its children nodes are either valid BST nodes themselves or None / null. A BST is valid if and only if all of its nodes are valid BST nodes. Note that the BST class already has an insert method which you can use if you want. Sample Input array = [1, 2, 5, 7, 10, 13, 14, 15, 22] Sample Output 10 / \ 2 14 / \ / \ 1 5 13 15 \ \ 7 22 // This is one example of a BST with min height // that you could create from the input array. // You could create other BSTs with min height // from the same array; for example: 10 / \ 5 15 / \ / \ 2 7 13 22 / \ 1 14 https://www.algoexpert.io/questions/Min%20Height%20BST """ # ---------------------------------------------------------------------------------------------------------------------- # O(nlog(n)) time | O(n) space - where n is the length of the array def minHeightBst00(array): return minHeightBstHelper00(array, None, 0, len(array)-1) def minHeightBstHelper00(array, node, left, right): if left > right: return None mid = (left+right) // 2 if node is None: node = BST(array[mid]) else: node.insert(array[mid]) minHeightBstHelper00(array, node, left, mid-1) # left minHeightBstHelper00(array, node, mid+1, right) # right return node # ---------------------------------------------------------------------------------------------------------------------- # O(n) time | O(n) space - where n is the length of the array def minHeightBst01(array): return minHeightBstHelper01(array, 0, len(array)-1) def minHeightBstHelper01(array, left, right): if left > right: return None mid = (left+right) // 2 node = BST(array[mid]) node.left = minHeightBstHelper01(array, left, mid-1) node.right = minHeightBstHelper01(array, mid+1, right) return node """ Sample Input array = [1, 2, 5, 7, 10, 13, 14, 15, 22] Sample Output 10 / \ 2 14 / \ / \ 1 5 13 15 \ \ 7 22 // This is one example of a BST with min height // that you could create from the input array. // You could create other BSTs with min height // from the same array; for example: 10 / \ 5 15 / \ / \ 2 7 13 22 / \ 1 14 [1, 2, 5, 7, 10, 13, 14, 15, 22]->10 [1, 2, 5, 7]->2 [13, 14, 15, 22]-> [1]->1 [5, 7]->5 [7][7]->7 """ -
Balance a Binary Search Tree
""" 1382. Balance a Binary Search Tree Given the root of a binary search tree, return a balanced binary search tree with the same node values. If there is more than one answer, return any of them. A binary search tree is balanced if the depth of the two subtrees of every node never differs by more than 1. https://leetcode.com/problems/balance-a-binary-search-tree similar to Min Height BST """ # Definition for a binary tree node. class TreeNode: def __init__(self, val=0, left=None, right=None): self.val = val self.left = left self.right = right """ 1. convert tree to sorted array using inorder traversal 2. build the tree from the sorted array - the root will be the middle of the array - the left of the middle will be passed to a recursive function to build the left children - the right of the middle will be passed to a recursive function to build the right children """ class Solution: def balanceBST(self, root: TreeNode): array = [] self.inOrderTraverse(root, array) return self.buildTree(array, 0, len(array)-1) def buildTree(self, array, start, end): if start > end: return None mid = (start+end) // 2 curr = array[mid] curr.left = self.buildTree(array, start, mid-1) curr.right = self.buildTree(array, mid+1, end) return curr def inOrderTraverse(self, root, array): stack = [] curr = root while curr or stack: # if has a left child, move left while curr and curr.left: stack.append(curr) curr = curr.left # curr is either the left most value or None # if none take the left-most from the top of stack if curr is None: curr = stack.pop() array.append(curr) # we are at the left most value so the only possible next place to go is right curr = curr.right -
Lowest Common Ancestor of a Binary Search Tree *
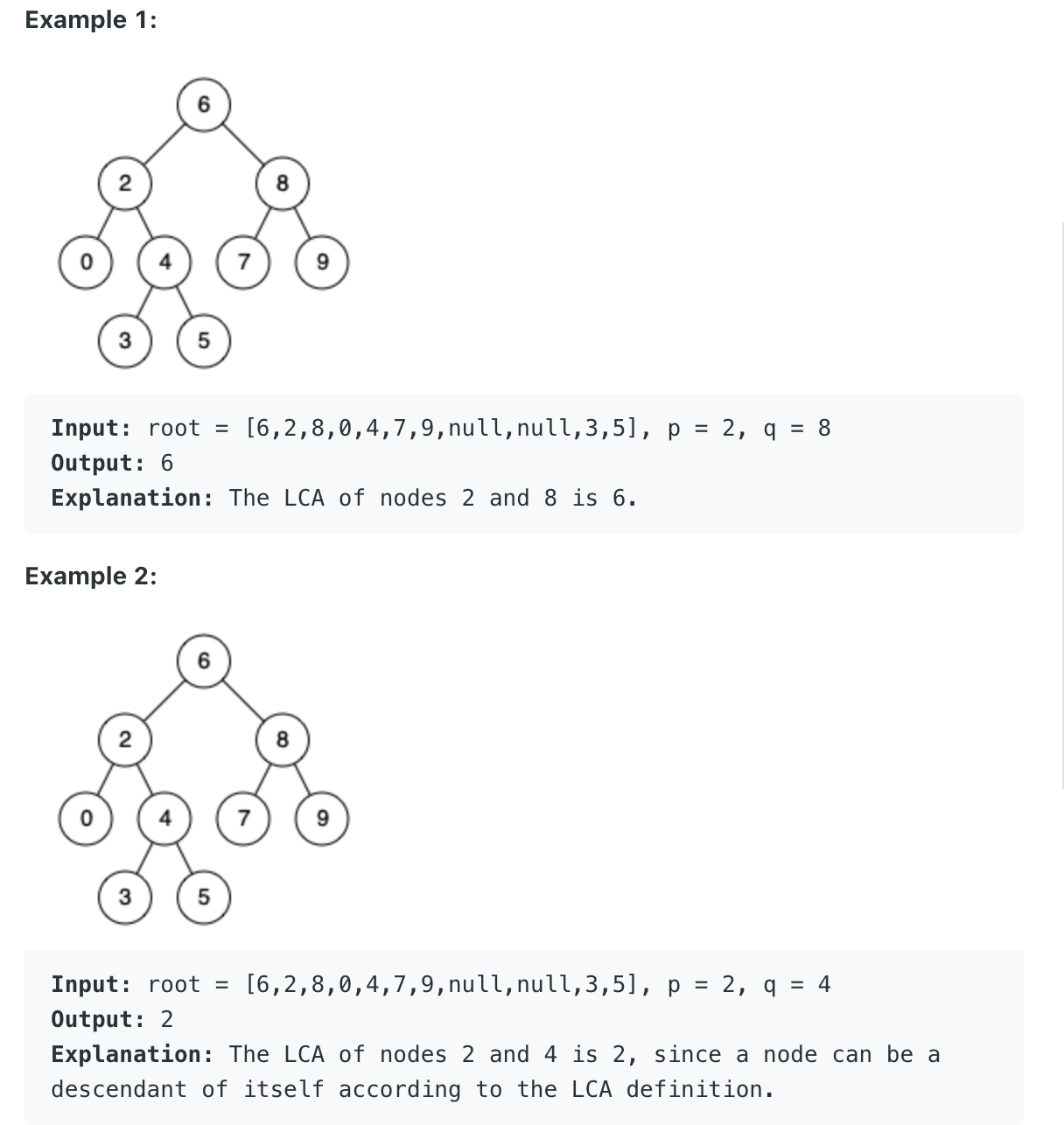
""" Lowest Common Ancestor of a Binary Search Tree: Given a binary search tree (BST), find the lowest common ancestor (LCA) of two given nodes in the BST. According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).” https://leetcode.com/problems/lowest-common-ancestor-of-a-binary-search-tree/ """ # Definition for a binary tree node. # class TreeNode: # def __init__(self, x): # self.val = x # self.left = None # self.right = None class Solution: def lowestCommonAncestor(self, root, p, q): curr = root while True: if curr.val < p.val and curr.val < q.val: curr = curr.right elif curr.val > p.val and curr.val > q.val: curr = curr.left else: break return curr """ First Approach: - take advantage of BST's properties: skip all valid ancestors """ -
Find Closest Value In BST
""" Find Closest Value In BST: Write a function that takes in a Binary Search Tree (BST) and a target integer value and returns the closest value to that target value contained in the BST. You can assume that there will only be one closest value. Each BST node has an integer value, a left child node, and a right child node. A node is said to be a valid BST node if and only if it satisfies the BST property: its value is strictly greater than the values of every node to its left; its value is less than or equal to the values of every node to its right; and its children nodes are either valid BST nodes themselves or None / null. https://www.algoexpert.io/questions/Find%20Closest%20Value%20In%20BST """ # This is the class of the input tree. Do not edit. class BST: def __init__(self, value): self.value = value self.left = None self.right = None # O(log(n)) time | O(1) space # worst: O(n) time | O(1) space -> tree with one branch def findClosestValueInBst(tree, target): curr = tree closest = float('inf') while curr is not None: # update closest if abs(curr.value-target) < abs(closest-target): closest = curr.value # move downwards if curr.left is None or (curr.right is not None and target >= curr.value): # target >= node.value: every value to the left will be further away from that target than the node.value curr = curr.right else: # target < node.value: every value to the right will be further away from that target than the node.value curr = curr.left return closest """ Sample Input tree = 10 / \ 5 15 / \ / \ 2 5 13 22 / \ 1 14 target = 12 t = 12 11 / \ 10 20 Sample Output 13 # Input: tree & target # Output: closest(int) # # First Approach: start at head # at every node: - update closest value - target >= node.value: every value to the left will be further away from that target than the node.value - move to the right - target < node.value: every value to the right will be further away from that target than the node.value - move to the left """ # Average: O(log(n)) time | O(1) space # Worst: O(n) time | O(1) space def findClosestValueInBst2(tree, target): closest = float('inf') curr = tree while curr is not None: # # update closest if abs(curr.value - target) < abs(closest - target): closest = curr.value # # move on to next node if curr.value == target: break # no need to go on elif curr.value < target: # 05:55 # because the curr node's value is less than the target, # all values to the left of curr will be futher away from the target (BST property -> are less then curr) curr = curr.right else: # curr node's value is greater than the target, all values to the right of curr, # will be further away from target as they are larger than curr curr = curr.left return closest -
Inorder Successor in BST




""" Inorder Successor in BST: FIND THE FIRST KEY GREATER THAN A GIVEN VALUE IN A BST: Given the root of a binary search tree and a node p in it, return the in-order successor of that node in the BST. If the given node has no in-order successor in the tree, return null. The successor of a node p is the node with the smallest key greater than p.val. https://leetcode.com/problems/inorder-successor-in-bst epi 14.2 """ # Definition for a binary tree node. class TreeNode: def __init__(self, x): self.val = x self.left = None self.right = None class Solution: def inorderSuccessor(self, root: 'TreeNode', p: 'TreeNode'): nxt = None curr = root while curr is not None: # successor will be the next larger value compared to the element if curr.val > p.val: nxt = curr # try to reduce the value curr = curr.left else: # try to increase the value curr = curr.right return nxt -
Inorder Successor in BST II
Example 1:
Input: tree = [2,1,3], node = 1 Output: 2 Explanation: 1's in-order successor node is 2. Note that both the node and the return value is of Node type.Example 2:
Input: tree = [5,3,6,2,4,null,null,1], node = 6 Output: null Explanation: There is no in-order successor of the current node, so the answer is null.Example 3:
Input: tree = [15,6,18,3,7,17,20,2,4,null,13,null,null,null,null,null,null,null,null,9], node = 15 Output: 17Example 4:
Input: tree = [15,6,18,3,7,17,20,2,4,null,13,null,null,null,null,null,null,null,null,9], node = 13 Output: 15Example 5:
Input: tree = [0], node = 0 Output: null



""" 510. Inorder Successor in BST II Given a node in a binary search tree, return the in-order successor of that node in the BST. If that node has no in-order successor, return null. The successor of a node is the node with the smallest key greater than node.val. You will have direct access to the node but not to the root of the tree. Each node will have a reference to its parent node. Below is the definition for Node: class Node { public int val; public Node left; public Node right; public Node parent; } """ """ Node has a right child, and hence its successor is somewhere lower in the tree. To find the successor, go to the right once and then as many times to the left as you could. Node has no right child, then its successor is somewhere upper in the tree. To find the successor, go up till the node that is left child of its parent. The answer is the parent. Beware that there could be no successor (= null successor) in such a situation. """ # Definition for a Node. class Node: def __init__(self, val): self.val = val self.left = None self.right = None self.parent = None class Solution: def inorderSuccessor(self, node): curr = node if curr.right: # get left most child in right subtree curr = curr.right while curr and curr.left: curr = curr.left return curr else: # find where the tree last branched left while curr: if curr.parent and curr.parent.left == curr: return curr.parent curr = curr.parent return None -
Binary Search Tree Iterator

""" Binary Search Tree Iterator: Implement the BSTIterator class that represents an iterator over the in-order traversal of a binary search tree (BST): BSTIterator(TreeNode root) Initializes an object of the BSTIterator class. The root of the BST is given as part of the constructor. The pointer should be initialized to a non-existent number smaller than any element in the BST. boolean hasNext() Returns true if there exists a number in the traversal to the right of the pointer, otherwise returns false. int next() Moves the pointer to the right, then returns the number at the pointer. Notice that by initializing the pointer to a non-existent smallest number, the first call to next() will return the smallest element in the BST. You may assume that next() calls will always be valid. That is, there will be at least a next number in the in-order traversal when next() is called. Example 1: 7 / \ 3 15 / \ 9 20 Input ["BSTIterator", "next", "next", "hasNext", "next", "hasNext", "next", "hasNext", "next", "hasNext"] [[[7, 3, 15, null, null, 9, 20]], [], [], [], [], [], [], [], [], []] Output [null, 3, 7, true, 9, true, 15, true, 20, false] Explanation BSTIterator bSTIterator = new BSTIterator([7, 3, 15, null, null, 9, 20]); bSTIterator.next(); // return 3 bSTIterator.next(); // return 7 bSTIterator.hasNext(); // return True bSTIterator.next(); // return 9 bSTIterator.hasNext(); // return True bSTIterator.next(); // return 15 bSTIterator.hasNext(); // return True bSTIterator.next(); // return 20 bSTIterator.hasNext(); // return False """ from typing import Optional """ ---- Solution 1: store the inorder traversal in an array and return them index by index --- Solution 2: controlled iteration check Binary Tree Inorder Traversal (Iterative) https://www.notion.so/paulonteri/Trees-Graphs-edc3401e06c044f29a2d714d20ffe185#8c489e8b02804929ab535f25f945a31b [3,7,9,15,20] """ # Definition for a binary tree node. class TreeNode: def __init__(self, val=0, left=None, right=None): self.val = val self.left = left self.right = right class BSTIterator: def __init__(self, root: Optional[TreeNode]): self.curr = root self.stack = [] def next(self): # put the left most value(s) to the top of the stack while self.curr: self.stack.append(self.curr) self.curr = self.curr.left # the left-most node is at the top of the stack node = self.stack.pop() # the next (only next unvisited valid node) will be at the right self.curr = node.right return node.val def hasNext(self): return self.curr or self.stack # Your BSTIterator object will be instantiated and called as such: # obj = BSTIterator(root) # param_1 = obj.next() # param_2 = obj.hasNext() -
Convert Binary Search Tree to Sorted Doubly Linked List
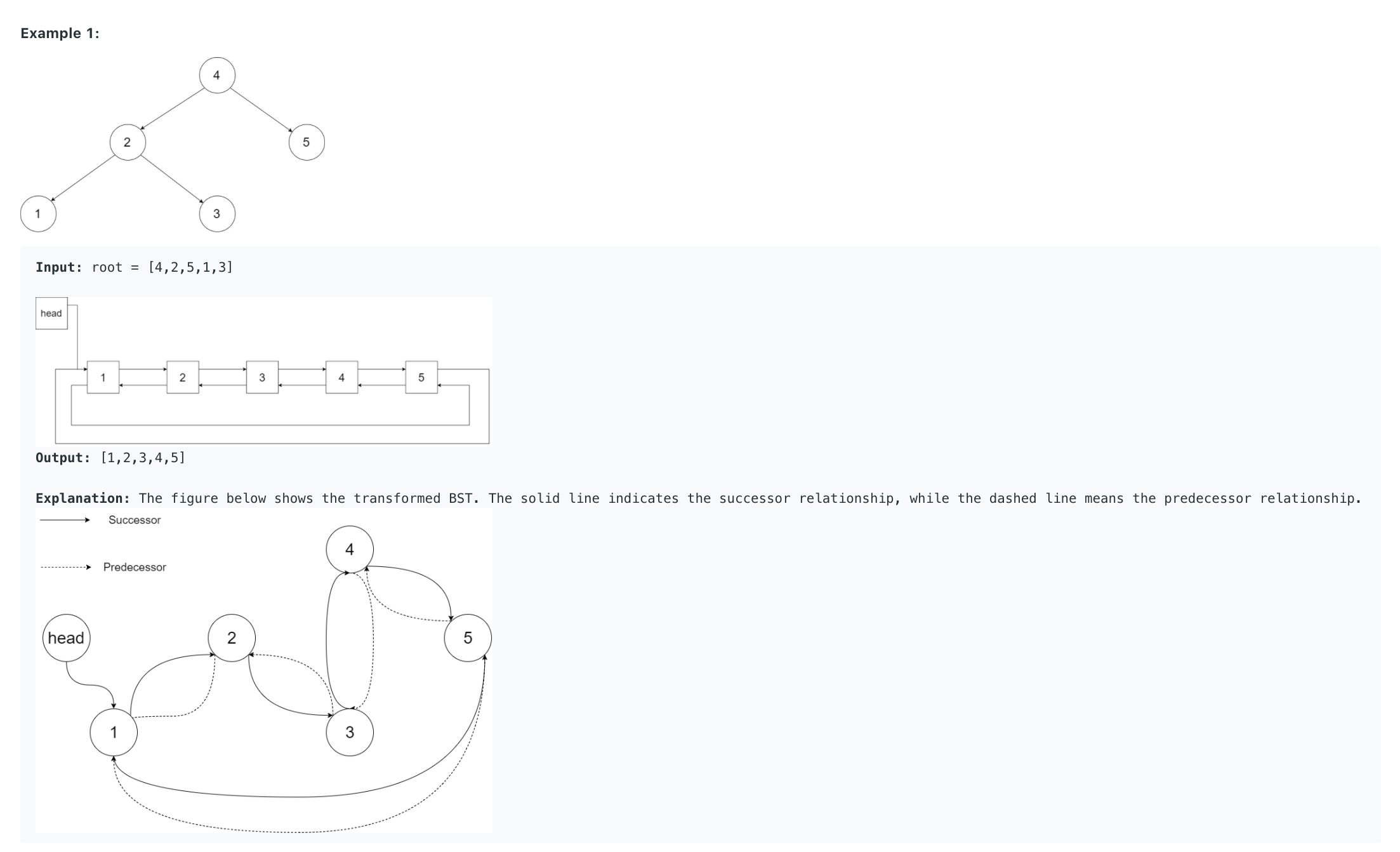
""" Convert Binary Search Tree to Sorted Doubly Linked List: Convert a Binary Search Tree to a sorted Circular Doubly-Linked List in place. You can think of the left and right pointers as synonymous to the predecessor and successor pointers in a doubly-linked list. For a circular doubly linked list, the predecessor of the first element is the last element, and the successor of the last element is the first element. We want to do the transformation in place. After the transformation, the left pointer of the tree node should point to its predecessor, and the right pointer should point to its successor. You should return the pointer to the smallest element of the linked list. 4 / \ 2 5 / \ 1 3 1 2 3 4 5 https://leetcode.com/problems/convert-binary-search-tree-to-sorted-doubly-linked-list """ """ 4 / \ 2 5 / \ 1 3 1 2 3 4 5 prev = None curr = 1 --- prev = 1 curr = 2 prev.right = curr curr.left = prev r --> <-- l r --> <-- l 1 2 3 --- prev = 2 curr = 3 2.right = 3 3.left = 2 O(tree depth), so O(n) worst case and O(log(n)) space """ # Definition for a Node. class Node: def __init__(self, val, left=None, right=None): self.val = val self.left = left self.right = right class TreeInfo: def __init__(self): self.smallest = None self.prev = None self.largest = None class Solution: def treeToDoublyList(self, root: 'Node'): tree_info = TreeInfo() self.in_order_traversal(root, tree_info) if tree_info.smallest and tree_info.largest: tree_info.smallest.left = tree_info.largest tree_info.largest.right = tree_info.smallest return tree_info.smallest def in_order_traversal(self, root, tree_info): if not root: return self.in_order_traversal(root.left, tree_info) # visit node if tree_info.smallest is None: # first node tree_info.smallest = root tree_info.prev = root tree_info.largest = root else: # pointers tree_info.prev.right = root root.left = tree_info.prev # update info tree_info.prev = root tree_info.largest = root self.in_order_traversal(root.right, tree_info) -
Delete Node in a BST
Delete Node in a BST - LeetCode
DELETE NODE IN A BST (Leetcode) - Code & Whiteboard
# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def findMinVal(self, root): curr = root while curr.left: curr = curr.left return curr def deleteNode(self, root: TreeNode, key: int) -> TreeNode: if not root: return None elif key < root.val: root.left = self.deleteNode(root.left, key) elif key > root.val: root.right = self.deleteNode(root.right, key) else: """ Removal Cases: - No Children - Right Child - Left Child - Both - replace with max of left or - replace with min of right """ if not root.right and not root.left: root = None elif not root.left: root = root.right elif not root.right: root = root.left else: temp = self.findMinVal(root.right) root.val = temp.val root.right = self.deleteNode(root.right, temp.val) return root
The Binary Search Tree (BST) is a Binary Tree with the following properties.
- Keys that are less than the parent are found in the left subtree
- Keys that are greater than or equal to the parent are found in the right subtree
- Both the left and right subtrees must also be binary search trees.
Binary Search Tree Operations
Key lookup, insertion, and deletion take time proportional to the height of the tree, which can in worst-case be O(n), if insertions and deletions are naively implemented. However, there are implementations of insert and delete which guarantee that the tree has height O(log n). These require storing and updating additional data at the tree nodes. Red-black trees are an example of height-balanced BSTs and are widely used in data structure libraries.
When we are talking about the average case, it is the time it takes for the operation on a balanced tree, and when we are talking about the worst case, it is the time it takes for the given operation on a non-balanced tree.
These are discussed in more depth below.

Implementation
Full Implementation
-
Implementation
# Binary Search Tree Implementation in Python # Blog post: https://emre.me/data-structures/binary-search-trees/ class Node: def __init__(self, key, val, left=None, right=None, parent=None): self.key = key self.payload = val self.leftChild = left self.rightChild = right self.parent = parent def has_left_child(self): return self.leftChild def has_right_child(self): return self.rightChild def is_left_child(self): return self.parent and self.parent.leftChild == self def is_right_child(self): return self.parent and self.parent.rightChild == self def is_root(self): return not self.parent def is_leaf(self): return not (self.rightChild or self.leftChild) def has_any_children(self): return self.rightChild or self.leftChild def has_both_children(self): return self.rightChild and self.leftChild def splice_out(self): if self.is_leaf(): if self.is_left_child(): self.parent.leftChild = None else: self.parent.rightChild = None elif self.has_any_children(): if self.has_left_child(): if self.is_left_child(): self.parent.leftChild = self.leftChild else: self.parent.rightChild = self.leftChild self.leftChild.parent = self.parent else: if self.is_left_child(): self.parent.leftChild = self.rightChild else: self.parent.rightChild = self.rightChild self.rightChild.parent = self.parent def find_successor(self): successor = None if self.has_right_child(): successor = self.rightChild.find_min() else: if self.parent: if self.is_left_child(): successor = self.parent else: self.parent.rightChild = None successor = self.parent.find_successor() self.parent.rightChild = self return successor def find_min(self): current = self while current.has_left_child(): current = current.leftChild return current def replace_node_data(self, key, value, lc, rc): self.key = key self.payload = value self.leftChild = lc self.rightChild = rc if self.has_left_child(): self.leftChild.parent = self if self.has_right_child(): self.rightChild.parent = self class BinarySearchTree: def __init__(self): self.root = None self.size = 0 def length(self): return self.size def __len__(self): return self.size def put(self, key, val): if self.root: self._put(key, val, self.root) else: self.root = Node(key, val) self.size = self.size + 1 def _put(self, key, val, current_node): if key < current_node.key: if current_node.has_left_child(): self._put(key, val, current_node.leftChild) else: current_node.leftChild = Node(key, val, parent=current_node) else: if current_node.has_right_child(): self._put(key, val, current_node.rightChild) else: current_node.rightChild = Node(key, val, parent=current_node) def __setitem__(self, k, v): self.put(k, v) def get(self, key): if self.root: res = self._get(key, self.root) if res: return res.payload else: return None else: return None def _get(self, key, current_node): if not current_node: return None elif current_node.key == key: return current_node elif key < current_node.key: return self._get(key, current_node.leftChild) else: return self._get(key, current_node.rightChild) def __getitem__(self, key): return self.get(key) def __contains__(self, key): if self._get(key, self.root): return True else: return False def delete(self, key): if self.size > 1: node_to_remove = self._get(key, self.root) if node_to_remove: self.remove(node_to_remove) self.size = self.size - 1 else: raise KeyError('Error, key not in tree') elif self.size == 1 and self.root.key == key: self.root = None self.size = self.size - 1 else: raise KeyError('Error, key not in tree') def __delitem__(self, key): self.delete(key) def remove(self, current_node): if current_node.is_leaf(): # leaf if current_node == current_node.parent.leftChild: current_node.parent.leftChild = None else: current_node.parent.rightChild = None elif current_node.has_both_children(): # interior successor = current_node.find_successor() successor.splice_out() current_node.key = successor.key current_node.payload = successor.payload else: # this node has one child if current_node.has_left_child(): if current_node.is_left_child(): current_node.leftChild.parent = current_node.parent current_node.parent.leftChild = current_node.leftChild elif current_node.is_right_child(): current_node.leftChild.parent = current_node.parent current_node.parent.rightChild = current_node.leftChild else: current_node.replace_node_data(current_node.leftChild.key, current_node.leftChild.payload, current_node.leftChild.leftChild, current_node.leftChild.rightChild) else: if current_node.is_left_child(): current_node.rightChild.parent = current_node.parent current_node.parent.leftChild = current_node.rightChild elif current_node.is_right_child(): current_node.rightChild.parent = current_node.parent current_node.parent.rightChild = current_node.rightChild else: current_node.replace_node_data(current_node.rightChild.key, current_node.rightChild.payload, current_node.rightChild.leftChild, current_node.rightChild.rightChild)
Insert Operation
We have a Node() and BinarySearchTree() classes, we are ready to insert elements to this BinarySearchTree() class.
We are going to implement a put(self, key, val) method. This method will check to see if the tree already has a root. If there is not a root then put() will create a new Node() and install it as the root of the tree. If a root node is already in place then put() calls the private, recursive, helper function _put() to search the tree according to the Binary Search Tree properties that we explained in the first paragraph of this article.
-
Code
def put(self, key, val): if self.root: self._put(key, val, self.root) else: self.root = Node(key, val) self.size = self.size + 1 def _put(self, key, val, current_node): if key < current_node.key: if current_node.has_left_child(): self._put(key, val, current_node.leftChild) else: current_node.leftChild = Node(key, val, parent=current_node) else: if current_node.has_right_child(): self._put(key, val, current_node.rightChild) else: current_node.rightChild = Node(key, val, parent=current_node) def __setitem__(self, k, v): self.put(k, v)
Lookup (Search) Operation
Once the tree is constructed, the next task is to implement the retrieval of a value for a given key. The get() method is even easier than the put() method because it simply searches the tree recursively until it gets to a non-matching leaf node or finds a matching key. When a matching key is found, the value stored in the payload of the node is returned.
-
Code
def get(self, key): if self.root: result = self._get(key, self.root) if result: return result.payload else: return None else: return None def _get(self, key, current_node): if not current_node: return None elif current_node.key == key: return current_node elif key < current_node.key: return self._get(key, current_node.leftChild) else: return self._get(key, current_node.rightChild) def __getitem__(self, key): return self.get(key) def __contains__(self, key): if self._get(key, self.root): return True else: return False
Delete Operation
delete() operation is the most challenging operation in the Binary Search Tree.
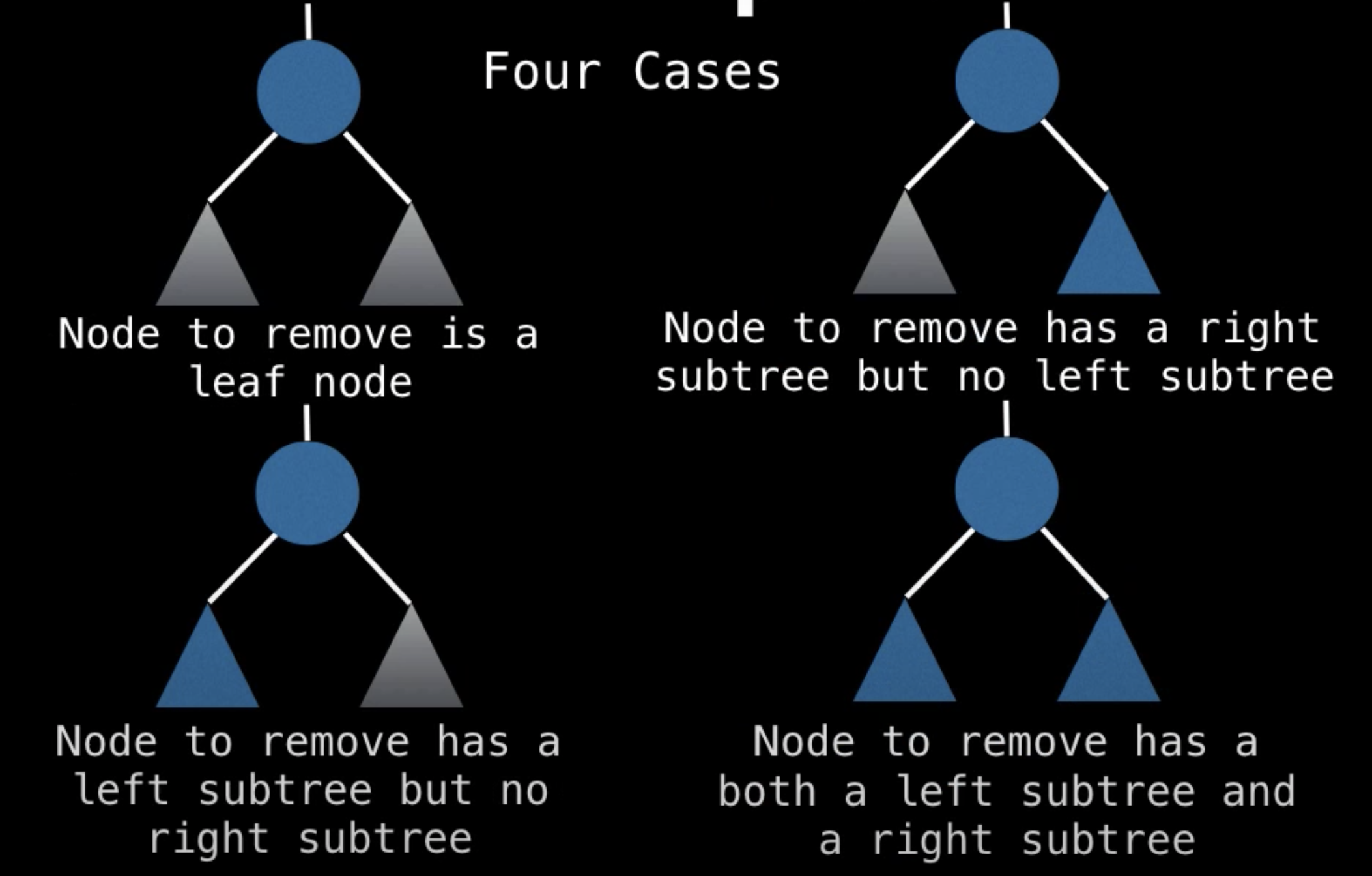
The first task is to find the node to delete by searching the tree. If the tree has more than one node we search using the _get() method to find the Node() that needs to be removed. If the tree only has a single node, that means we are removing the root of the tree, but we still must check to make sure the key of the root matches the key that is to be deleted. In either case if the key is not found the delete() method raises an error.
Once we have found the node containing the key we want to delete, there are three cases that we must consider:
- The node to be deleted has no children
- The node to be deleted has only one child
- The node to be deleted has two children
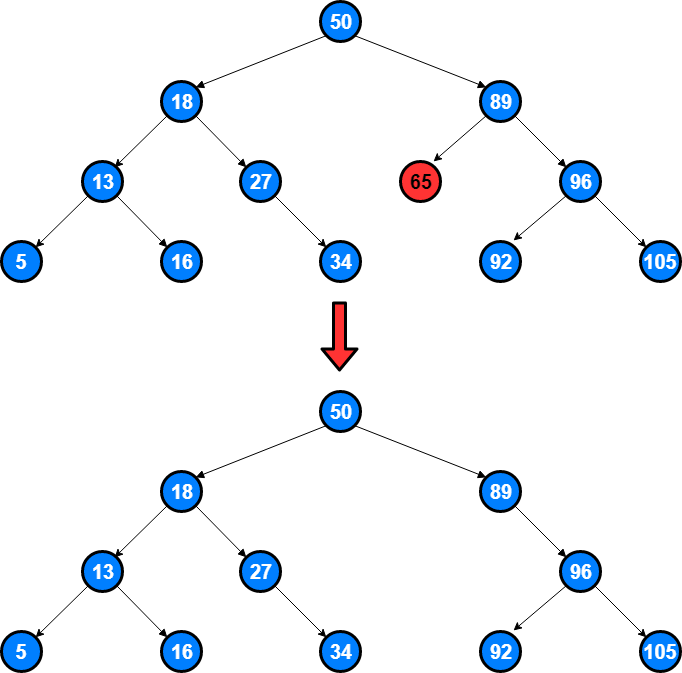
- The node to be deleted has no children
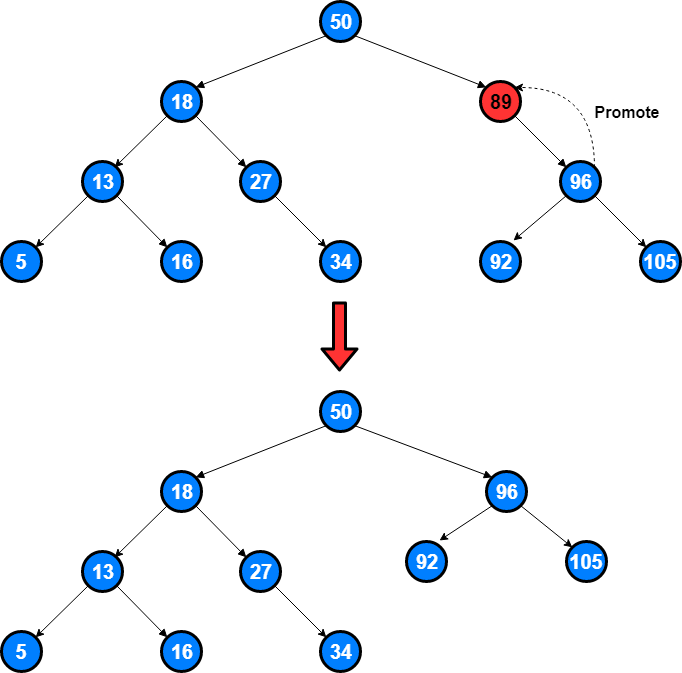
- The node to be deleted has only one child
- Handling the first case is pretty easy ↑
-
← If a node has only a single child, then we can simply promote the child to take the place of its parent.The decision proceeds as follows:
- If the current node is a left child then we only need to update the parent reference of the left child to point to the parent of the current node, and then update the left child reference of the parent to point to the current node’s left child.
- If the current node is a right child then we only need to update the parent reference of the left child to point to the parent of the current node, and then update the right child reference of the parent to point to the current node’s left child.
- If the current node has no parent, it must be the root. In this case we will just replace the
key,payload,leftChild, andrightChilddata by calling thereplace_node_data()method on theroot.
-
If a node has two children, we search the tree for a node that can be used to replace the one scheduled for deletion. What we need is a node that will preserve the binary search tree relationships for both of the existing left and right subtrees. The node that will do this is the node that has the next-largest key in the tree. We call this node the successor. There are three cases to consider when looking for a successor:
- If the node has a right child, then the successor is the smallest key in the right subtree
- If the node has no right child and is the left child of its parent, then the parent is the successor
- If the node is the right child of its parent, and itself has no right child, then the successor to this node is the successor of its parent, excluding this node.
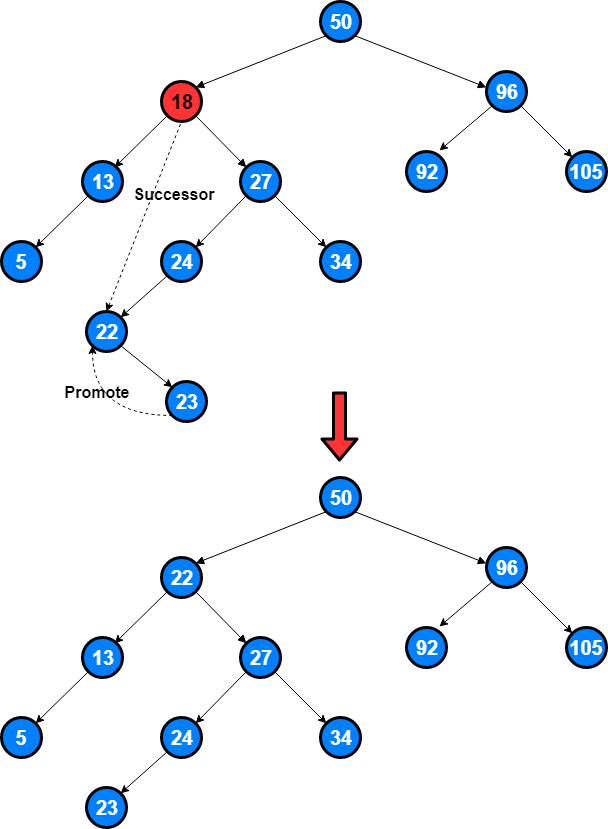
- The node to be deleted has two children
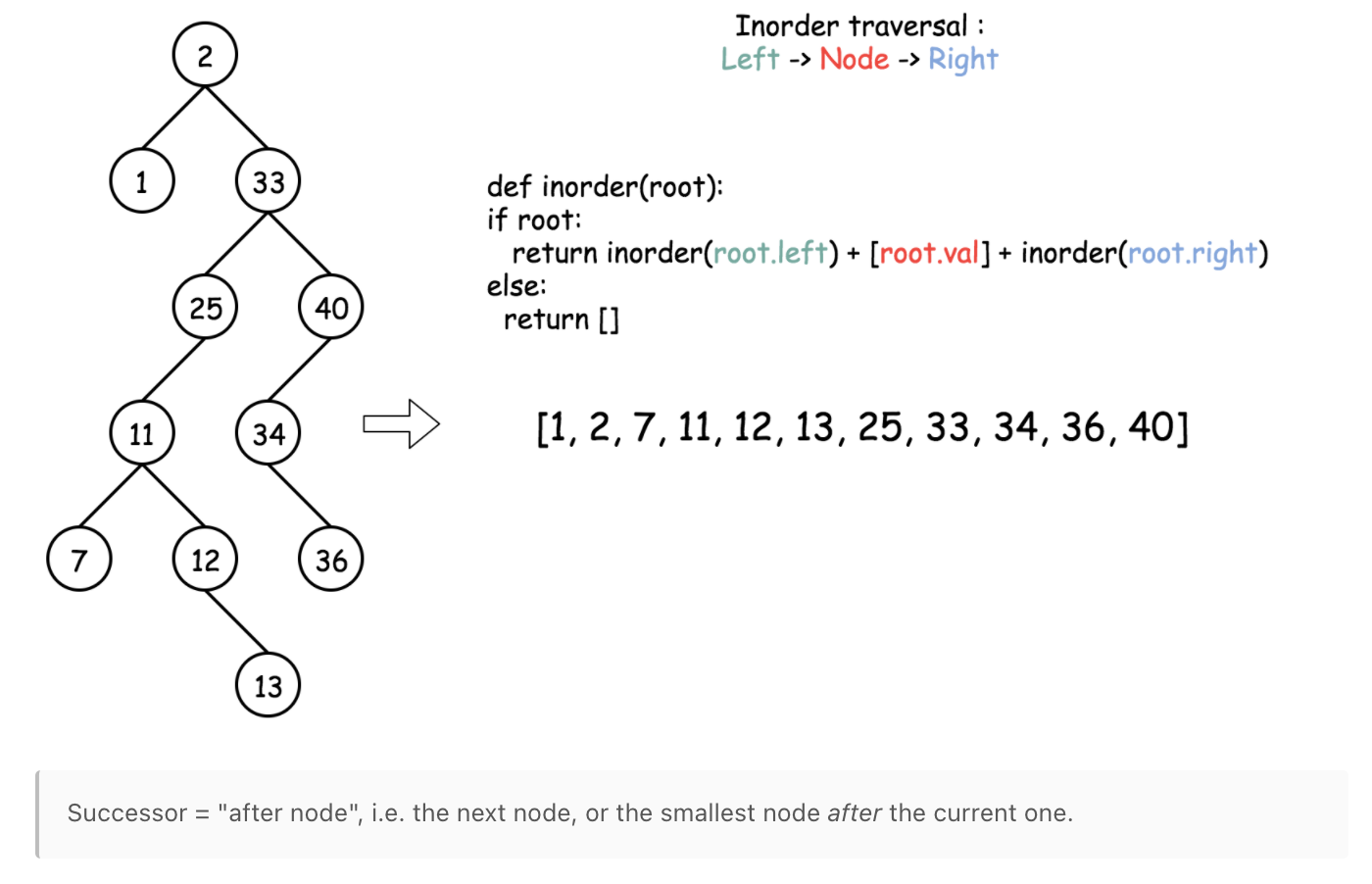
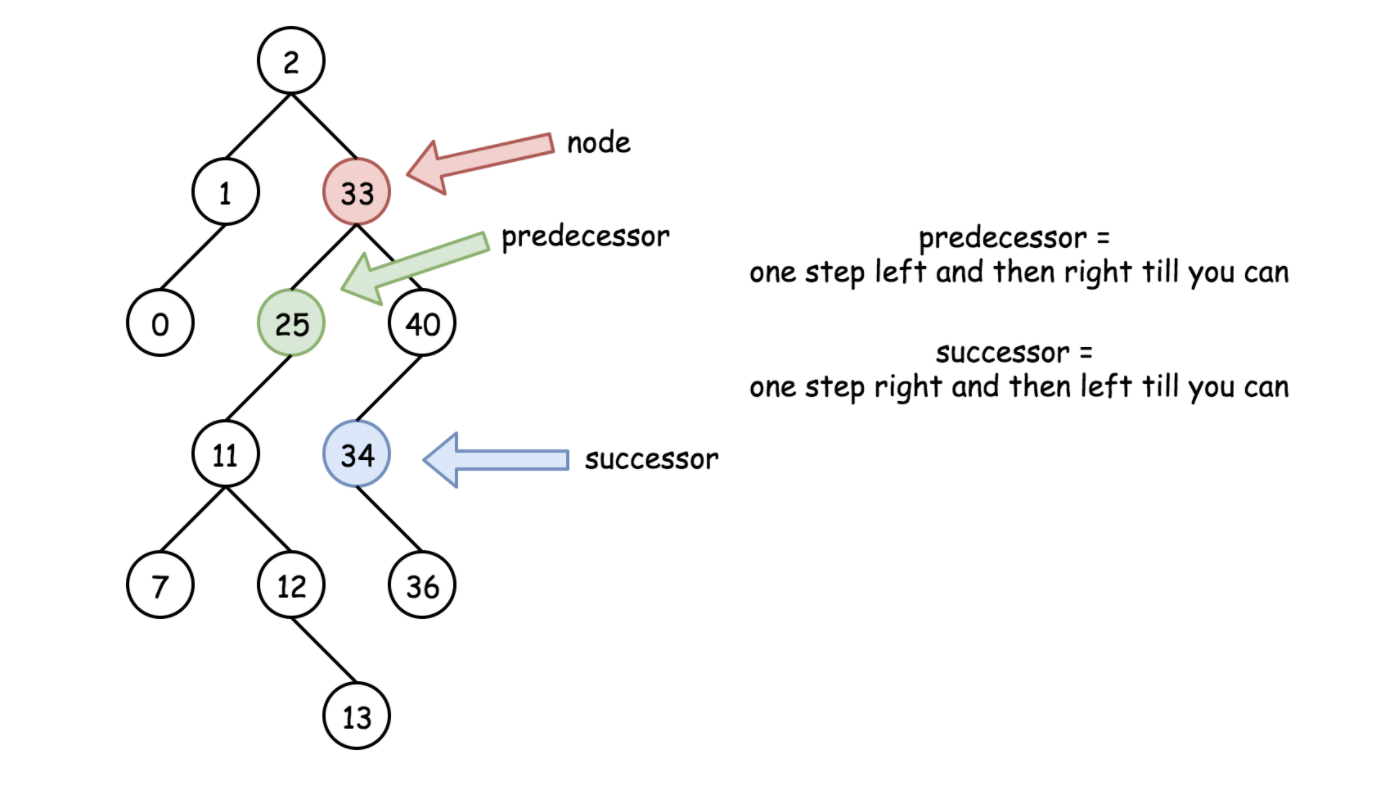
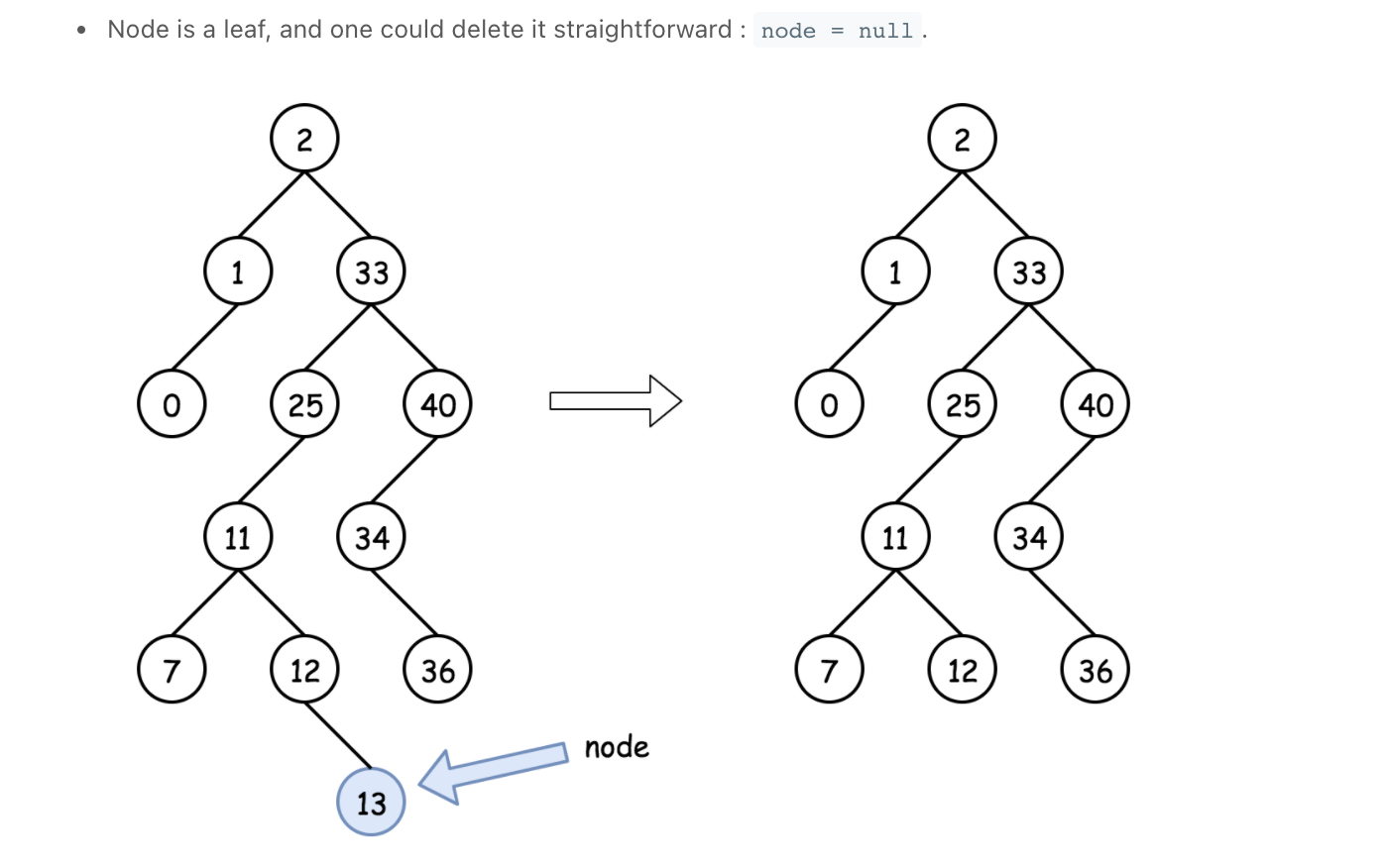
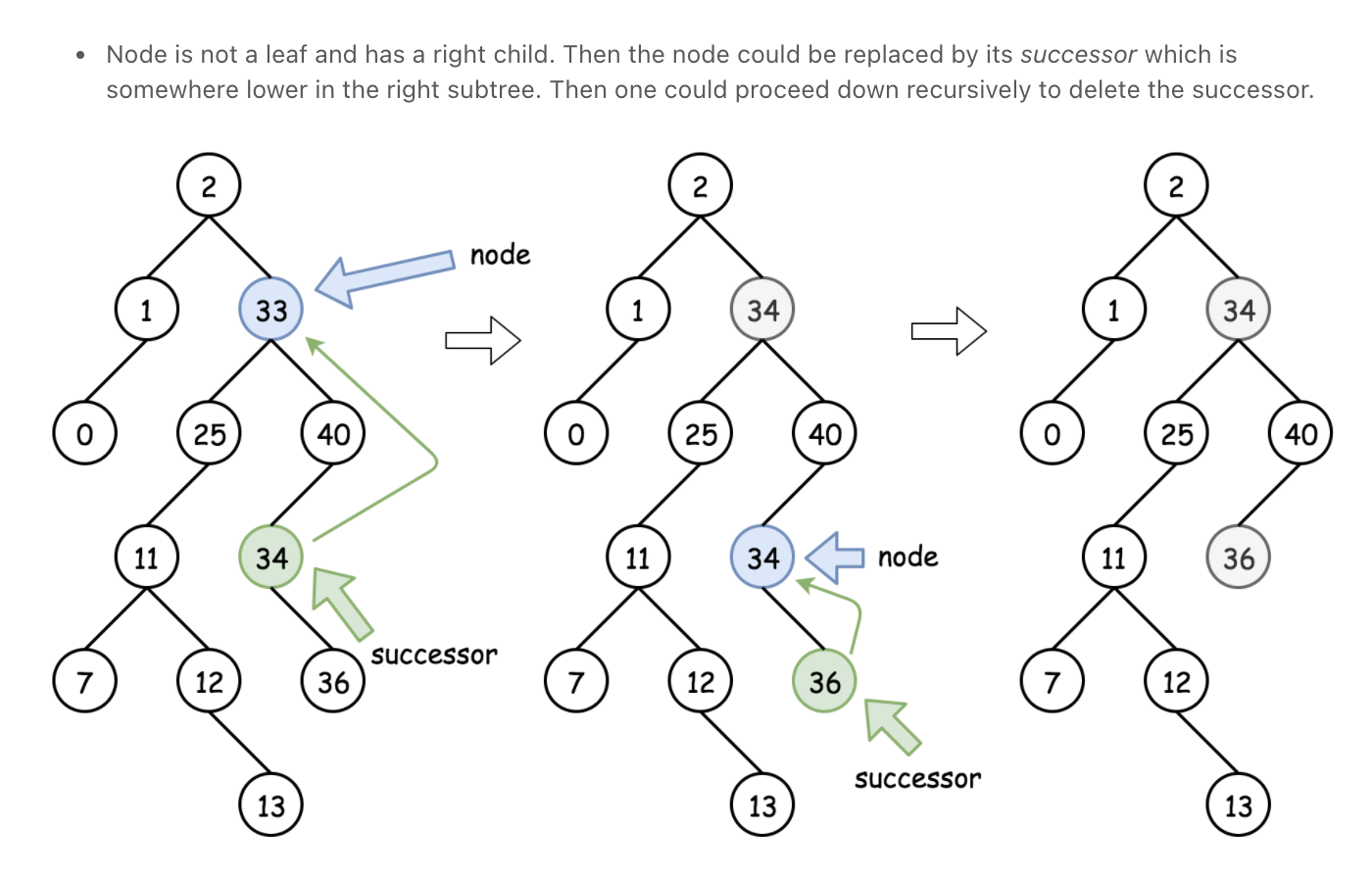
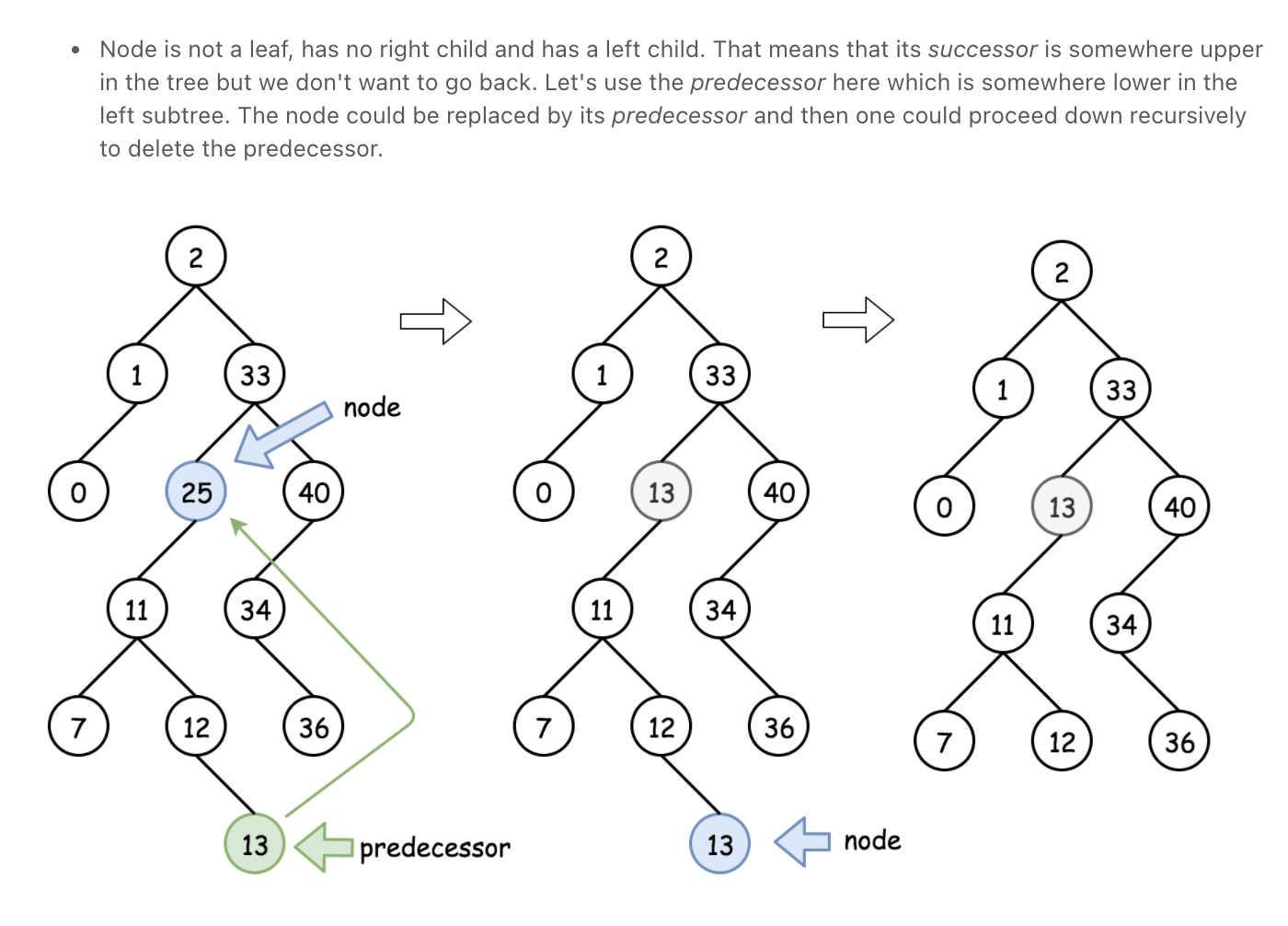
-
Delete Node in a BST
Delete Node in a BST - LeetCode
DELETE NODE IN A BST (Leetcode) - Code & Whiteboard
# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def findMinVal(self, root): curr = root while curr.left: curr = curr.left return curr def deleteNode(self, root: TreeNode, key: int) -> TreeNode: if not root: return None elif key < root.val: root.left = self.deleteNode(root.left, key) elif key > root.val: root.right = self.deleteNode(root.right, key) else: """ Removal Cases: - No Children - Right Child - Left Child - Both - replace with max of left or - replace with min of right """ if not root.right and not root.left: root = None elif not root.left: root = root.right elif not root.right: root = root.left else: temp = self.findMinVal(root.right) root.val = temp.val root.right = self.deleteNode(root.right, temp.val) return root
Prim's Minimum Spanning Tree Algorithm
Dijkstra's Algorithm vs Prim's Algorithm
Examples
-
Min Cost to Connect All Points
Prim's Algorithm - Minimum Spanning Tree - Min Cost to Connect all Points - Leetcode 1584 - Python

""" 1584. Min Cost to Connect All Points You are given an array points representing integer coordinates of some points on a 2D-plane, where points[i] = [xi, yi]. The cost of connecting two points [xi, yi] and [xj, yj] is the manhattan distance between them: |xi - xj| + |yi - yj|, where |val| denotes the absolute value of val. Return the minimum cost to make all points connected. All points are connected if there is exactly one simple path between any two points. Example 1: Input: points = [[0,0],[2,2],[3,10],[5,2],[7,0]] Output: 20 Explanation: We can connect the points as shown above to get the minimum cost of 20. Notice that there is a unique path between every pair of points. Example 2: Input: points = [[3,12],[-2,5],[-4,1]] Output: 18 Example 3: Input: points = [[0,0],[1,1],[1,0],[-1,1]] Output: 4 Example 4: Input: points = [[-1000000,-1000000],[1000000,1000000]] Output: 4000000 Example 5: Input: points = [[0,0]] Output: 0 https://leetcode.com/problems/min-cost-to-connect-all-points https://www.notion.so/paulonteri/Trees-Graphs-edc3401e06c044f29a2d714d20ffe185#2ac2c79816464704a3851de16d494dff """ import collections import heapq """ Prim's Minimum Spanning Tree Algorithm: https://www.notion.so/paulonteri/Trees-Graphs-edc3401e06c044f29a2d714d20ffe185#596bc798759a4edabe22a895aadeb12c https://youtu.be/f7JOBJIC-NA """ class Solution_: def minCostConnectPoints(self, points): total = 0 # # Create adjacency list # Will store nodes in the form => `parent: [[cost_to_1, node_1], [cost_to_2, node_2], ...]` graph = collections.defaultdict(list) for idx in range(len(points)): x1, y1 = points[idx] for idx2 in range(idx + 1, len(points)): x2, y2 = points[idx2] cost = abs(x1 - x2) + abs(y1 - y2) graph[str(x1)+str(y1)].append([cost, str(x2)+str(y2)]) graph[str(x2)+str(y2)].append([cost, str(x1)+str(y1)]) # # Prim's Minimum Spanning Tree Algorithm visited = set() priority_queue = [] first_node = str(points[0][0])+str(points[0][1]) heapq.heappush(priority_queue, (0, first_node)) # start from node 0 while len(visited) < len(graph): cost, node = heapq.heappop(priority_queue) # skip visited if node in visited: continue visited.add(node) # record cost total += cost # add neighbours for neighbour in graph[node]: if neighbour[1] not in visited: heapq.heappush(priority_queue, neighbour) return total class Solution: def minCostConnectPoints(self, points): total = 0 # # Create adjacency list # Will use the array indices as id's # Will store nodes in the form => `parent: [[cost_to_1, node_1], [cost_to_2, node_2], ...]` graph = collections.defaultdict(list) for idx in range(len(points)): x1, y1 = points[idx] for idx2 in range(idx + 1, len(points)): x2, y2 = points[idx2] cost = abs(x1 - x2) + abs(y1 - y2) graph[idx].append([cost, idx2]) graph[idx2].append([cost, idx]) # # Prim's Minimum Spanning Tree Algorithm visited = set() priority_queue = [] heapq.heappush(priority_queue, (0, 0)) # start from node 0 while len(visited) < len(graph): cost, node = heapq.heappop(priority_queue) # skip visited if node in visited: continue visited.add(node) # record cost total += cost # add neighbours for neighbour in graph[node]: if neighbour[1] not in visited: heapq.heappush(priority_queue, neighbour) return total -
Connecting Cities With Minimum Cost
""" 1584. Min Cost to Connect All Points You are given an array points representing integer coordinates of some points on a 2D-plane, where points[i] = [xi, yi]. The cost of connecting two points [xi, yi] and [xj, yj] is the manhattan distance between them: |xi - xj| + |yi - yj|, where |val| denotes the absolute value of val. Return the minimum cost to make all points connected. All points are connected if there is exactly one simple path between any two points. Example 1: Input: points = [[0,0],[2,2],[3,10],[5,2],[7,0]] Output: 20 Explanation: We can connect the points as shown above to get the minimum cost of 20. Notice that there is a unique path between every pair of points. Example 2: Input: points = [[3,12],[-2,5],[-4,1]] Output: 18 Example 3: Input: points = [[0,0],[1,1],[1,0],[-1,1]] Output: 4 Example 4: Input: points = [[-1000000,-1000000],[1000000,1000000]] Output: 4000000 Example 5: Input: points = [[0,0]] Output: 0 https://leetcode.com/problems/min-cost-to-connect-all-points https://www.notion.so/paulonteri/Trees-Graphs-edc3401e06c044f29a2d714d20ffe185#2ac2c79816464704a3851de16d494dff """ import collections import heapq """ Prim's Minimum Spanning Tree Algorithm: https://www.notion.so/paulonteri/Trees-Graphs-edc3401e06c044f29a2d714d20ffe185#596bc798759a4edabe22a895aadeb12c https://youtu.be/f7JOBJIC-NA """ class Solution_: def minCostConnectPoints(self, points): total = 0 # # Create adjacency list # Will store nodes in the form => `parent: [[cost_to_1, node_1], [cost_to_2, node_2], ...]` graph = collections.defaultdict(list) for idx in range(len(points)): x1, y1 = points[idx] for idx2 in range(idx + 1, len(points)): x2, y2 = points[idx2] cost = abs(x1 - x2) + abs(y1 - y2) graph[str(x1)+str(y1)].append([cost, str(x2)+str(y2)]) graph[str(x2)+str(y2)].append([cost, str(x1)+str(y1)]) # # Prim's Minimum Spanning Tree Algorithm visited = set() priority_queue = [] first_node = str(points[0][0])+str(points[0][1]) heapq.heappush(priority_queue, (0, first_node)) # start from node 0 while len(visited) < len(graph): cost, node = heapq.heappop(priority_queue) # skip visited if node in visited: continue visited.add(node) # record cost total += cost # add neighbours for neighbour in graph[node]: if neighbour[1] not in visited: heapq.heappush(priority_queue, neighbour) return total class Solution: def minCostConnectPoints(self, points): total = 0 # # Create adjacency list # Will use the array indices as id's # Will store nodes in the form => `parent: [[cost_to_1, node_1], [cost_to_2, node_2], ...]` graph = collections.defaultdict(list) for idx in range(len(points)): x1, y1 = points[idx] for idx2 in range(idx + 1, len(points)): x2, y2 = points[idx2] cost = abs(x1 - x2) + abs(y1 - y2) graph[idx].append([cost, idx2]) graph[idx2].append([cost, idx]) # # Prim's Minimum Spanning Tree Algorithm visited = set() priority_queue = [] heapq.heappush(priority_queue, (0, 0)) # start from node 0 while len(visited) < len(graph): cost, node = heapq.heappop(priority_queue) # skip visited if node in visited: continue visited.add(node) # record cost total += cost # add neighbours for neighbour in graph[node]: if neighbour[1] not in visited: heapq.heappush(priority_queue, neighbour) return total
Minimum Spanning Tree
A minimum spanning tree (or MST for short) is a tree that spans the whole graph connecting all nodes together while minimising the total edge cost. It's important to note that your spanning tree cannot contain any cycles, otherwise it's not a tree.
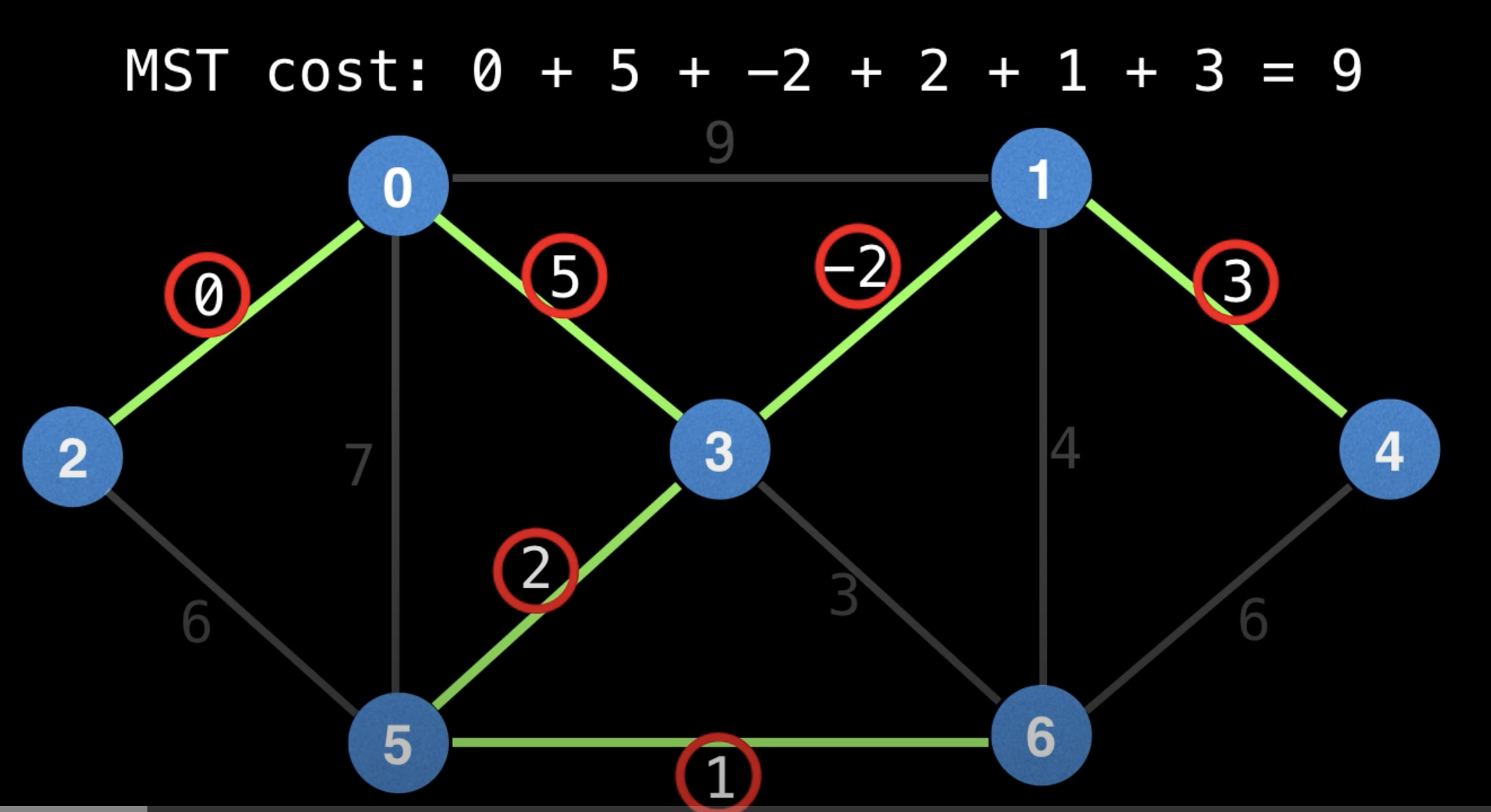
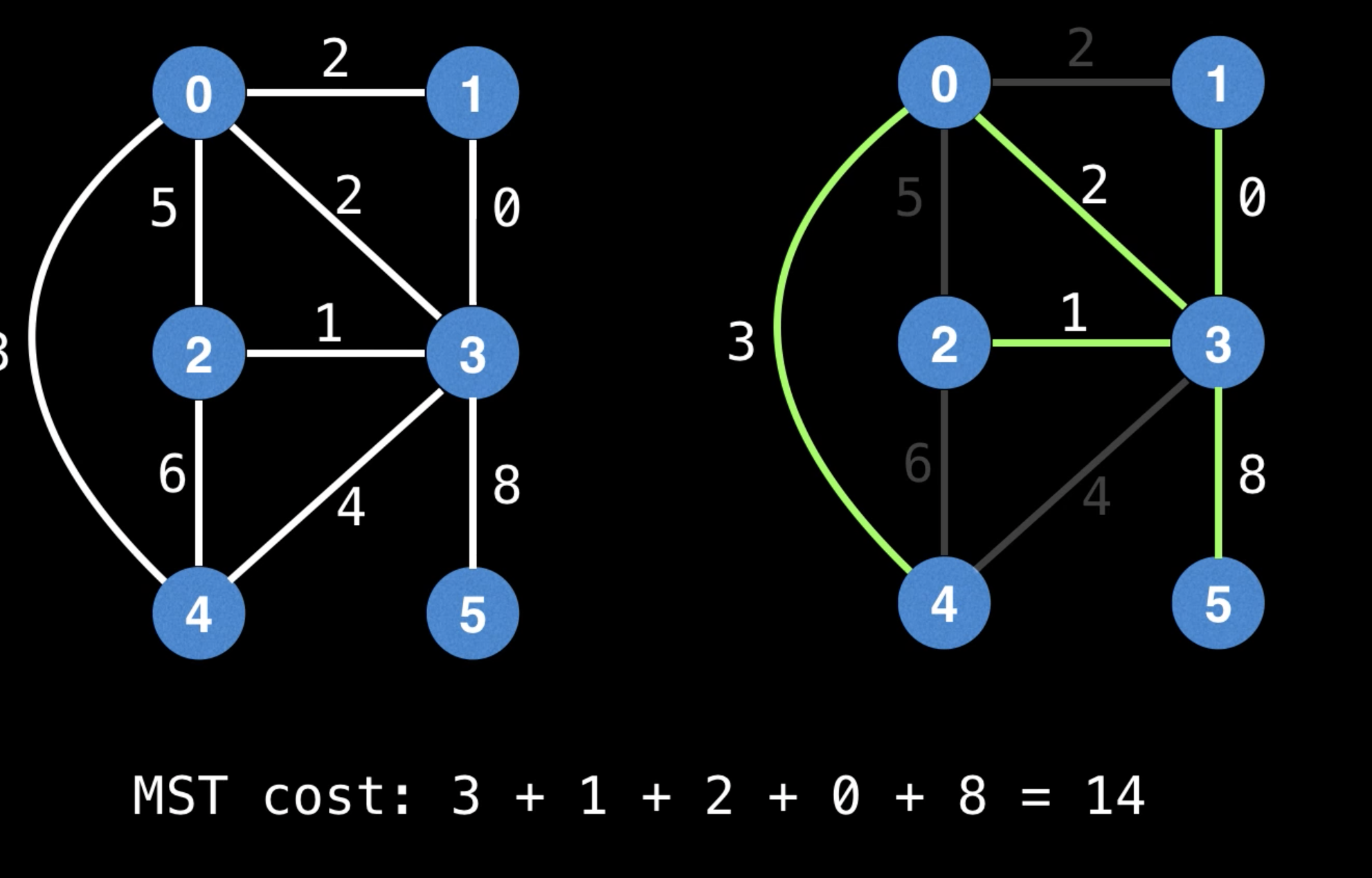
Given a connected and undirected graph, a spanning tree of that graph is a subgraph that is a tree and connects all the vertices together. A single graph can have many different spanning trees. A minimum spanning tree (MST) or minimum weight spanning tree for a weighted, connected, undirected graph is a spanning tree with a weight less than or equal to the weight of every other spanning tree. The weight of a spanning tree is the sum of weights given to each edge of the spanning tree.
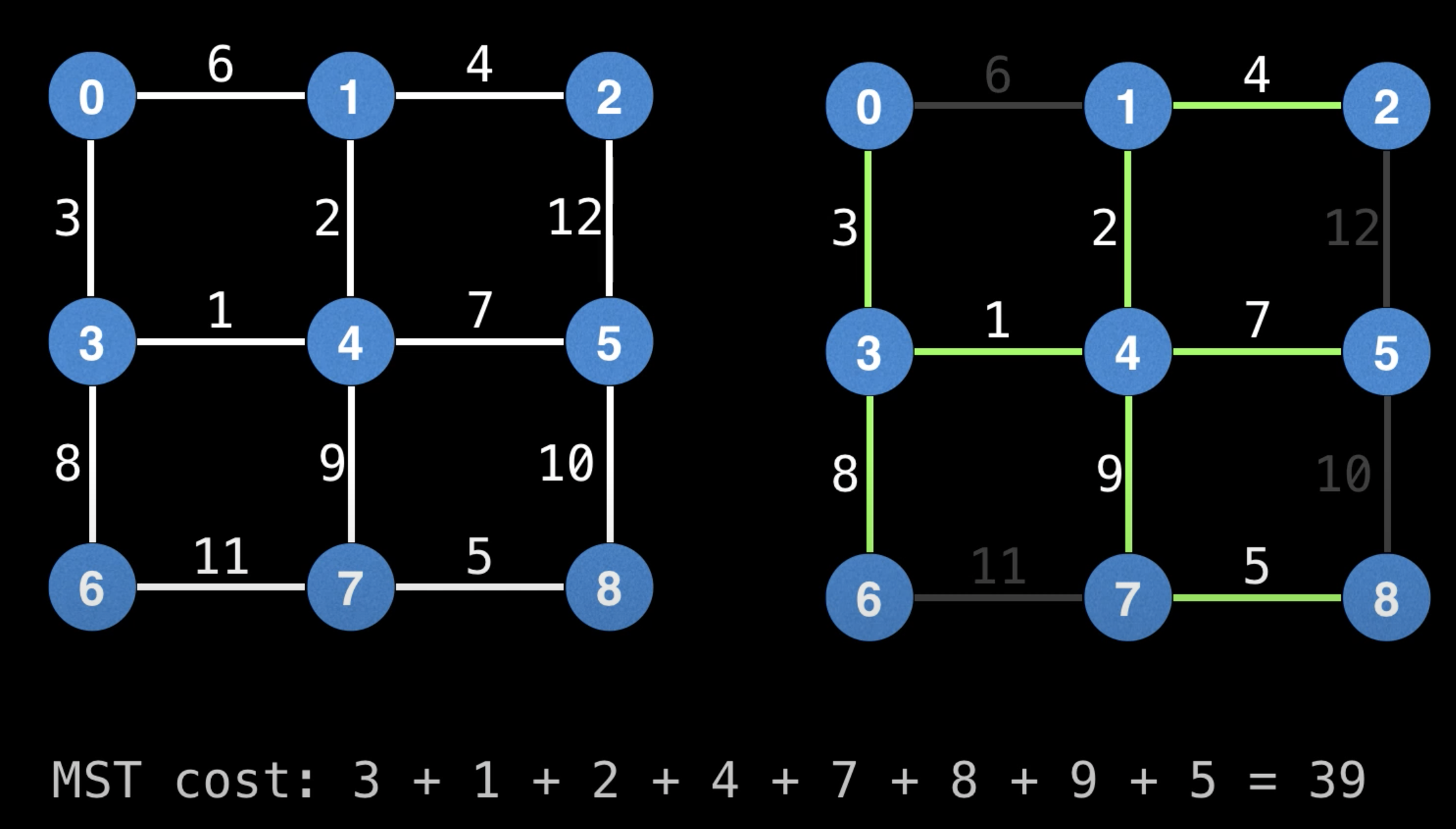
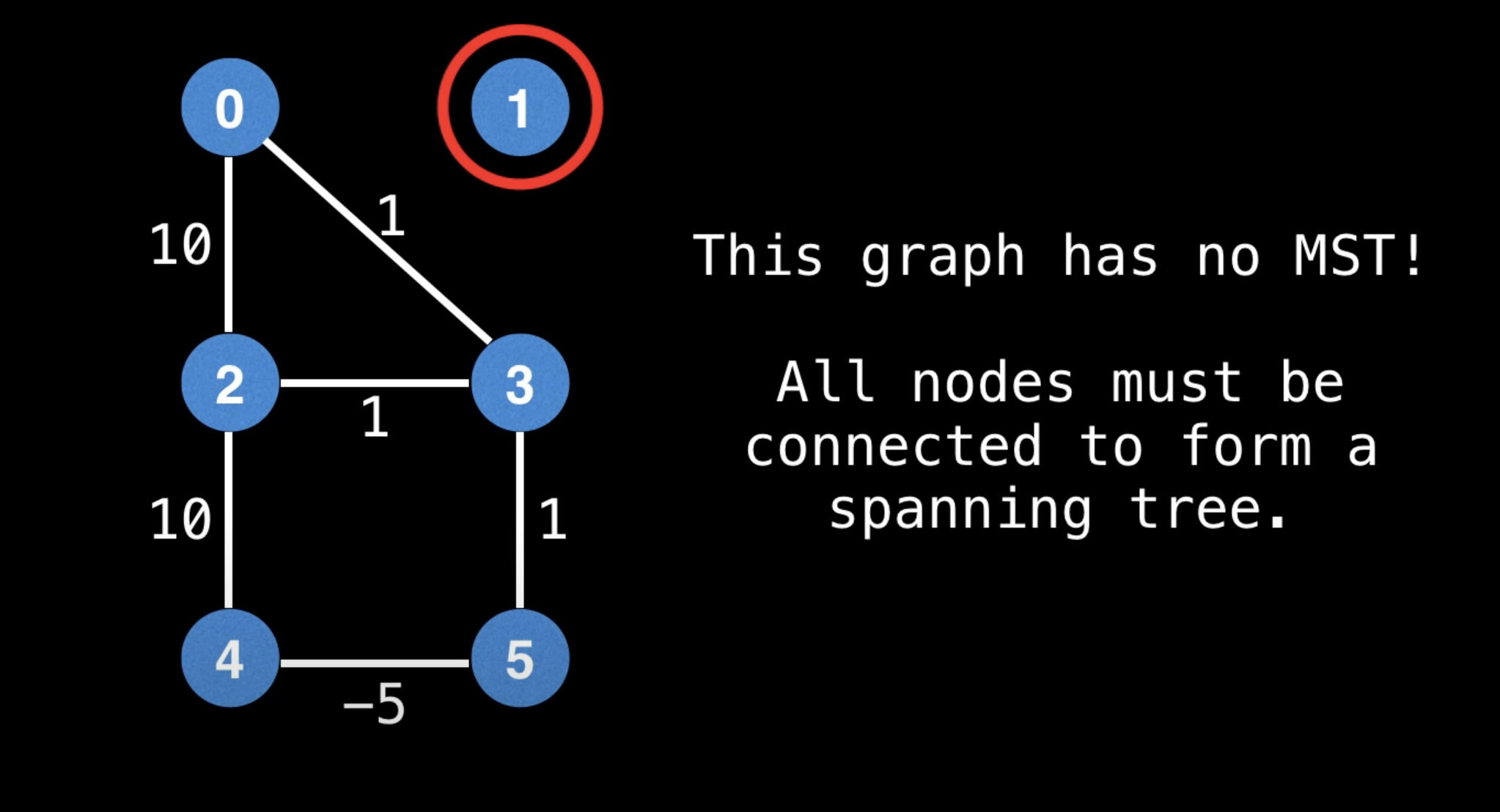
By nature, it's a greedy algorithm that always selects the next best edge to add to the MST and it works very well on dense graphs with lots of edges.
Prim's Minimum Spanning Tree Algorithm
Lazy Prim's Minimum Spanning Tree Algorithm
Maintain a Priority Queue that sorts edges based on minimum edge cost. This PQ is used to tell you which node to go to next and what edge was used to get there. Then the algorithm begins and we start on any starting node s and mark s as visited and iterate over all its edges and add them to the PQ. From this point on, while the PQ is not empty and an MST has not been formed, dequeue the next best edge from the PQ. If the dequeued edge is not outdated which it could be if we visit the node it points to via another path before getting to this edge then mark the current node as visited and add the selected edge to the PQ. If you selected a stale outdated edge simply poll again. Then repeat the process of iterating over the current node's edges and adding them to the PQ. While doing this care not to add edges that point to already visited nodes, this will reduce the number of outdated edges in the PQ.
Screen Recording 2021-10-19 at 06.15.29.mov
Eager Prim's Minimum Spanning Tree Algorithm
Eager Prim's Minimum Spanning Tree Algorithm | Graph Theory
The lazy implementation of Prim’s inserts E edges into the PQ. This results in each poll operation on the PQ to be O(log(E)). In the eager version, we maintain the idea that instead of adding edges to the PQ which could later become stale, that instead, we should track (node, edge) key-value pairs that can easily be updated and polled to determine the next best edge to add to the MST.
For this all to make sense there's a key realisation that needs to happen and that is: for any MST with directed edges, each node is paired with exactly one of its incoming edges (except for the start node). One way to see this is on an MST with possibly multiple edges leaving a node, but only ever one edge entering a node.
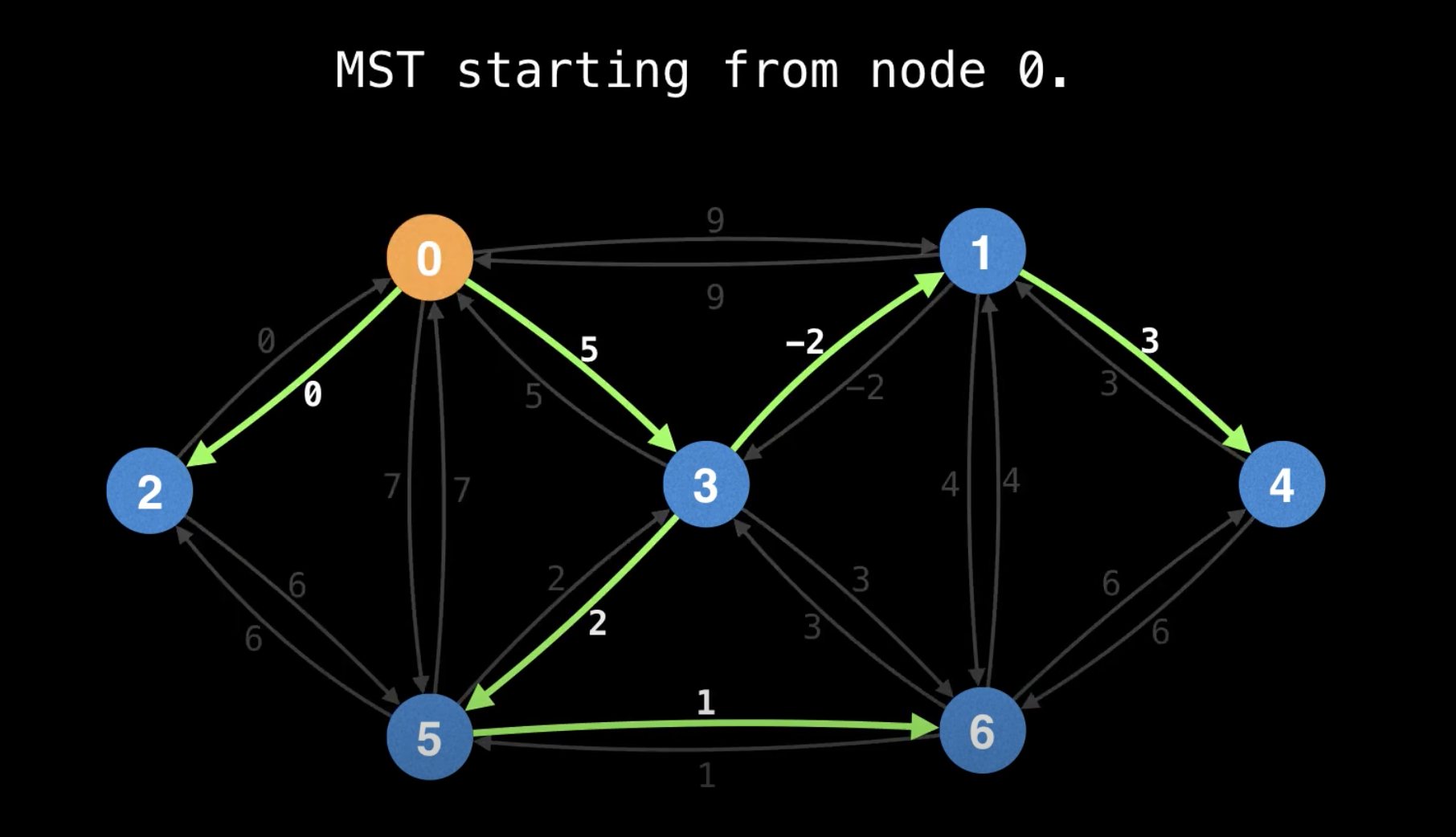
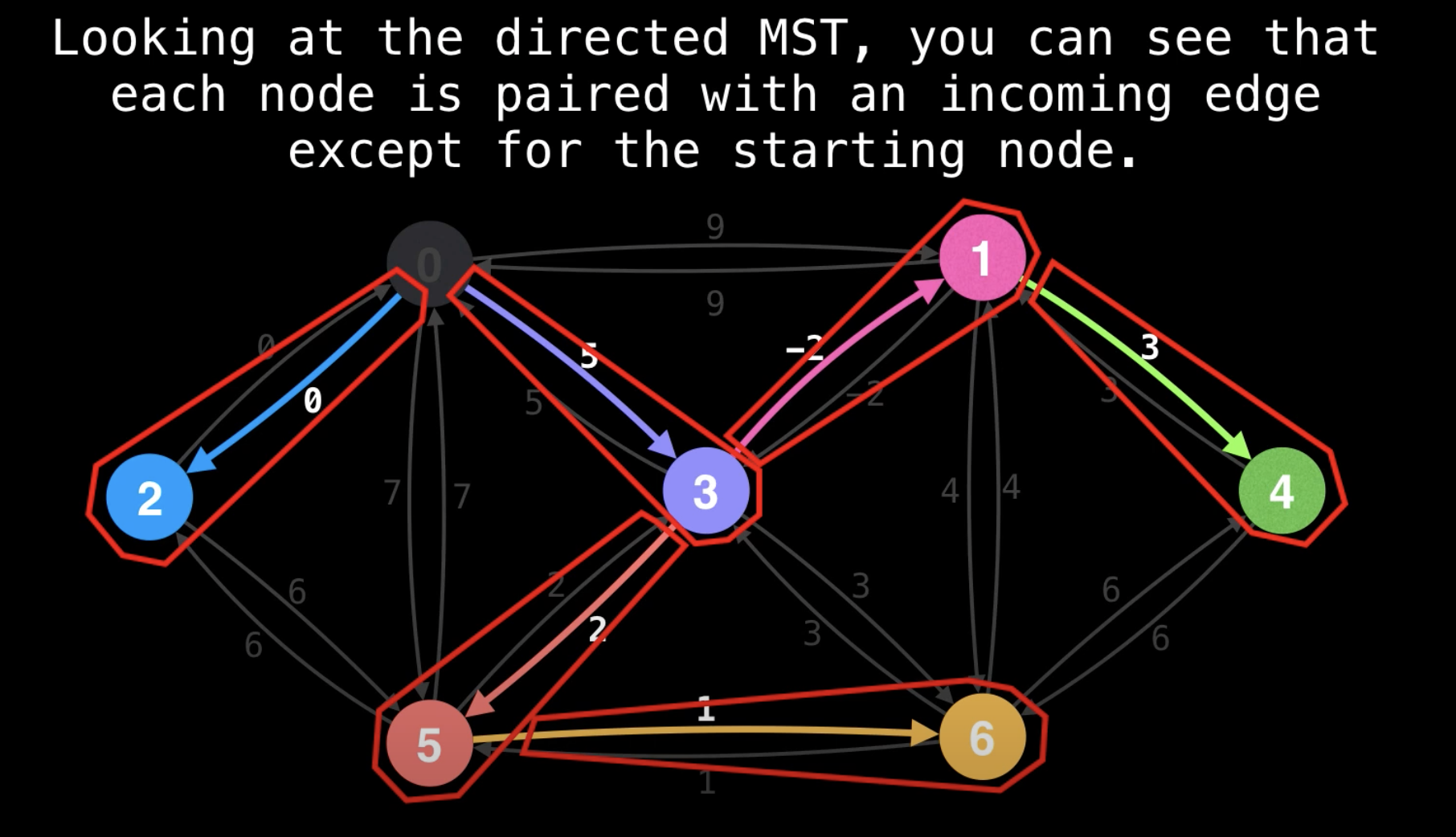
In the eager version, we are trying to determine which of a node's incoming edges we should select to include in the MST. The main difference coming from the lazy version is that instead of adding edges to the PQ as we iterate over the edges of node we’re going to relax (update) the destination node’s most promising incoming edge.

Think of an IPQ as the data structure you'd get if a hashtable and a priority queue had a baby together. It supports sorted key-value pair update and poll operations in logarithmic time.
Indexed Priority Queue | Data Structure
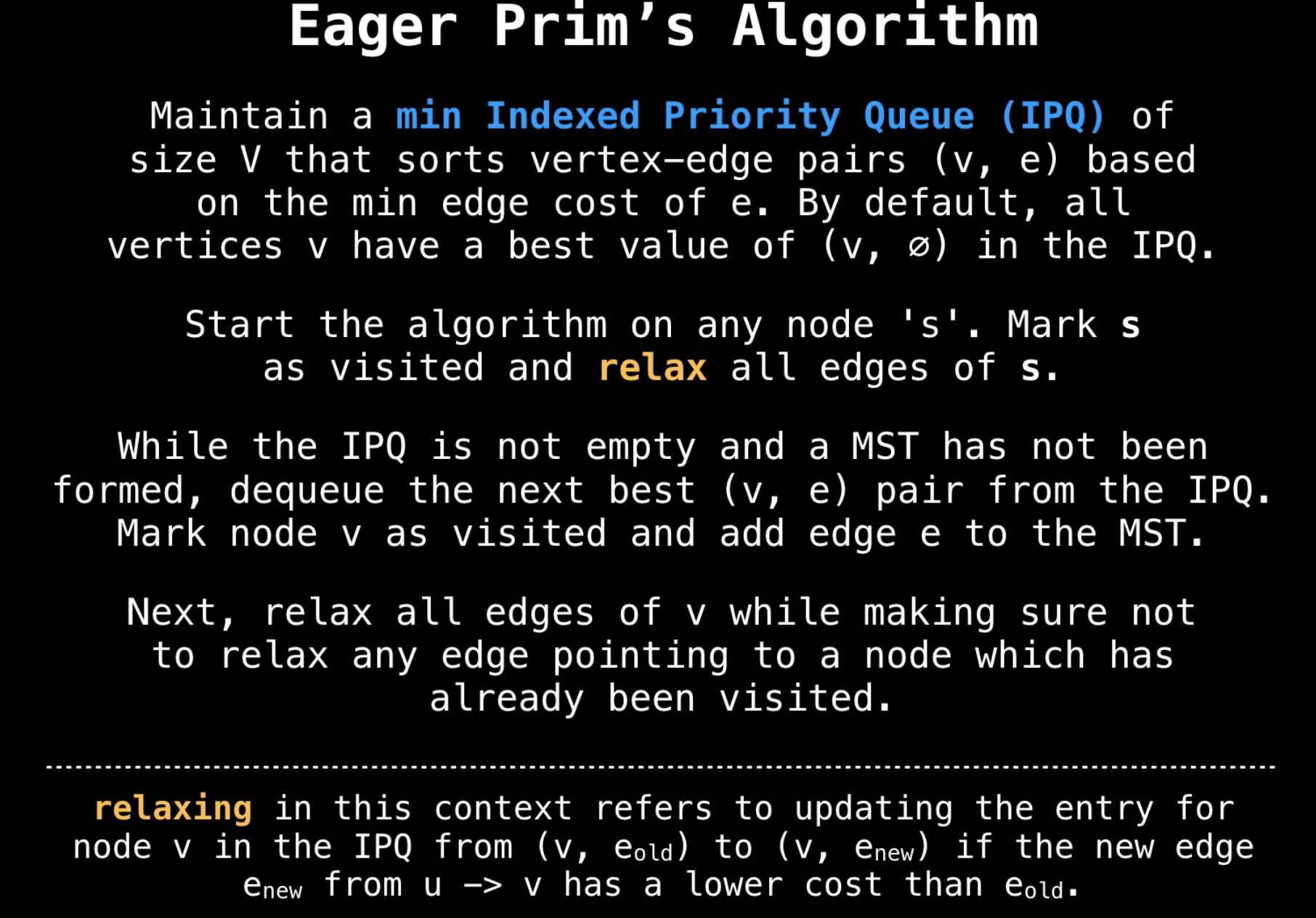
Screen Recording 2021-10-19 at 06.40.30.mov
Examples (do not add more here, add above)
-
Min Cost to Connect All Points
Prim's Algorithm - Minimum Spanning Tree - Min Cost to Connect all Points - Leetcode 1584 - Python

""" 1584. Min Cost to Connect All Points You are given an array points representing integer coordinates of some points on a 2D-plane, where points[i] = [xi, yi]. The cost of connecting two points [xi, yi] and [xj, yj] is the manhattan distance between them: |xi - xj| + |yi - yj|, where |val| denotes the absolute value of val. Return the minimum cost to make all points connected. All points are connected if there is exactly one simple path between any two points. Example 1: Input: points = [[0,0],[2,2],[3,10],[5,2],[7,0]] Output: 20 Explanation: We can connect the points as shown above to get the minimum cost of 20. Notice that there is a unique path between every pair of points. Example 2: Input: points = [[3,12],[-2,5],[-4,1]] Output: 18 Example 3: Input: points = [[0,0],[1,1],[1,0],[-1,1]] Output: 4 Example 4: Input: points = [[-1000000,-1000000],[1000000,1000000]] Output: 4000000 Example 5: Input: points = [[0,0]] Output: 0 https://leetcode.com/problems/min-cost-to-connect-all-points https://www.notion.so/paulonteri/Trees-Graphs-edc3401e06c044f29a2d714d20ffe185#2ac2c79816464704a3851de16d494dff """ import collections import heapq """ Prim's Minimum Spanning Tree Algorithm: https://www.notion.so/paulonteri/Trees-Graphs-edc3401e06c044f29a2d714d20ffe185#596bc798759a4edabe22a895aadeb12c https://youtu.be/f7JOBJIC-NA """ class Solution_: def minCostConnectPoints(self, points): total = 0 # # Create adjacency list # Will store nodes in the form => `parent: [[cost_to_1, node_1], [cost_to_2, node_2], ...]` graph = collections.defaultdict(list) for idx in range(len(points)): x1, y1 = points[idx] for idx2 in range(idx + 1, len(points)): x2, y2 = points[idx2] cost = abs(x1 - x2) + abs(y1 - y2) graph[str(x1)+str(y1)].append([cost, str(x2)+str(y2)]) graph[str(x2)+str(y2)].append([cost, str(x1)+str(y1)]) # # Prim's Minimum Spanning Tree Algorithm visited = set() priority_queue = [] first_node = str(points[0][0])+str(points[0][1]) heapq.heappush(priority_queue, (0, first_node)) # start from node 0 while len(visited) < len(graph): cost, node = heapq.heappop(priority_queue) # skip visited if node in visited: continue visited.add(node) # record cost total += cost # add neighbours for neighbour in graph[node]: if neighbour[1] not in visited: heapq.heappush(priority_queue, neighbour) return total class Solution: def minCostConnectPoints(self, points): total = 0 # # Create adjacency list # Will use the array indices as id's # Will store nodes in the form => `parent: [[cost_to_1, node_1], [cost_to_2, node_2], ...]` graph = collections.defaultdict(list) for idx in range(len(points)): x1, y1 = points[idx] for idx2 in range(idx + 1, len(points)): x2, y2 = points[idx2] cost = abs(x1 - x2) + abs(y1 - y2) graph[idx].append([cost, idx2]) graph[idx2].append([cost, idx]) # # Prim's Minimum Spanning Tree Algorithm visited = set() priority_queue = [] heapq.heappush(priority_queue, (0, 0)) # start from node 0 while len(visited) < len(graph): cost, node = heapq.heappop(priority_queue) # skip visited if node in visited: continue visited.add(node) # record cost total += cost # add neighbours for neighbour in graph[node]: if neighbour[1] not in visited: heapq.heappush(priority_queue, neighbour) return total -
Connecting Cities With Minimum Cost
""" 1584. Min Cost to Connect All Points You are given an array points representing integer coordinates of some points on a 2D-plane, where points[i] = [xi, yi]. The cost of connecting two points [xi, yi] and [xj, yj] is the manhattan distance between them: |xi - xj| + |yi - yj|, where |val| denotes the absolute value of val. Return the minimum cost to make all points connected. All points are connected if there is exactly one simple path between any two points. Example 1: Input: points = [[0,0],[2,2],[3,10],[5,2],[7,0]] Output: 20 Explanation: We can connect the points as shown above to get the minimum cost of 20. Notice that there is a unique path between every pair of points. Example 2: Input: points = [[3,12],[-2,5],[-4,1]] Output: 18 Example 3: Input: points = [[0,0],[1,1],[1,0],[-1,1]] Output: 4 Example 4: Input: points = [[-1000000,-1000000],[1000000,1000000]] Output: 4000000 Example 5: Input: points = [[0,0]] Output: 0 https://leetcode.com/problems/min-cost-to-connect-all-points https://www.notion.so/paulonteri/Trees-Graphs-edc3401e06c044f29a2d714d20ffe185#2ac2c79816464704a3851de16d494dff """ import collections import heapq """ Prim's Minimum Spanning Tree Algorithm: https://www.notion.so/paulonteri/Trees-Graphs-edc3401e06c044f29a2d714d20ffe185#596bc798759a4edabe22a895aadeb12c https://youtu.be/f7JOBJIC-NA """ class Solution_: def minCostConnectPoints(self, points): total = 0 # # Create adjacency list # Will store nodes in the form => `parent: [[cost_to_1, node_1], [cost_to_2, node_2], ...]` graph = collections.defaultdict(list) for idx in range(len(points)): x1, y1 = points[idx] for idx2 in range(idx + 1, len(points)): x2, y2 = points[idx2] cost = abs(x1 - x2) + abs(y1 - y2) graph[str(x1)+str(y1)].append([cost, str(x2)+str(y2)]) graph[str(x2)+str(y2)].append([cost, str(x1)+str(y1)]) # # Prim's Minimum Spanning Tree Algorithm visited = set() priority_queue = [] first_node = str(points[0][0])+str(points[0][1]) heapq.heappush(priority_queue, (0, first_node)) # start from node 0 while len(visited) < len(graph): cost, node = heapq.heappop(priority_queue) # skip visited if node in visited: continue visited.add(node) # record cost total += cost # add neighbours for neighbour in graph[node]: if neighbour[1] not in visited: heapq.heappush(priority_queue, neighbour) return total class Solution: def minCostConnectPoints(self, points): total = 0 # # Create adjacency list # Will use the array indices as id's # Will store nodes in the form => `parent: [[cost_to_1, node_1], [cost_to_2, node_2], ...]` graph = collections.defaultdict(list) for idx in range(len(points)): x1, y1 = points[idx] for idx2 in range(idx + 1, len(points)): x2, y2 = points[idx2] cost = abs(x1 - x2) + abs(y1 - y2) graph[idx].append([cost, idx2]) graph[idx2].append([cost, idx]) # # Prim's Minimum Spanning Tree Algorithm visited = set() priority_queue = [] heapq.heappush(priority_queue, (0, 0)) # start from node 0 while len(visited) < len(graph): cost, node = heapq.heappop(priority_queue) # skip visited if node in visited: continue visited.add(node) # record cost total += cost # add neighbours for neighbour in graph[node]: if neighbour[1] not in visited: heapq.heappush(priority_queue, neighbour) return total
Dijkstra's Algorithm
Dijkstra's Shortest Path Algorithm | Graph Theory
Dijkstra's Shortest Path Algorithm - A Detailed and Visual Introduction
Dijkstra's Algorithm vs Prim's Algorithm
Graphs in Python: Dijkstra's Algorithm
With Dijkstra's Algorithm, you can find the shortest path between nodes in a graph. Particularly, you can find the shortest path from a node (called the "source node") to all other nodes in the graph, producing a shortest-path tree.

Dr.Edsger Dijkstra at ETH Zurich in 1994
Dijkstra's Algorithm can only work with graphs that have positive weights. This is because, during the process, the weights of the edges have to be added to find the shortest path.
If there is a negative weight in the graph, then the algorithm will not work properly. Once a node has been marked as "visited", the current path to that node is marked as the shortest path to reach that node. And negative weights can alter this if the total weight can be decremented after this step has occurred.
Screen Recording 2021-10-22 at 20.17.10.mov



function dijkstra(G, S)
...
while Q IS NOT EMPTY
U <- Extract MIN from Q
for each unvisited neighbour V of U
tempDistance <- distance[U] + edge_weight(U, V)
if tempDistance < distance[V]
distance[V] <- tempDistance
previous[V] <- U
return distance[], previous[]
Time & Space complexity
O((v + e) * log(v)) time | O(v) space - where v is the number of vertices and e is the number of edges in the input graph
Examples:
-
Cheapest Flights Within K Stops

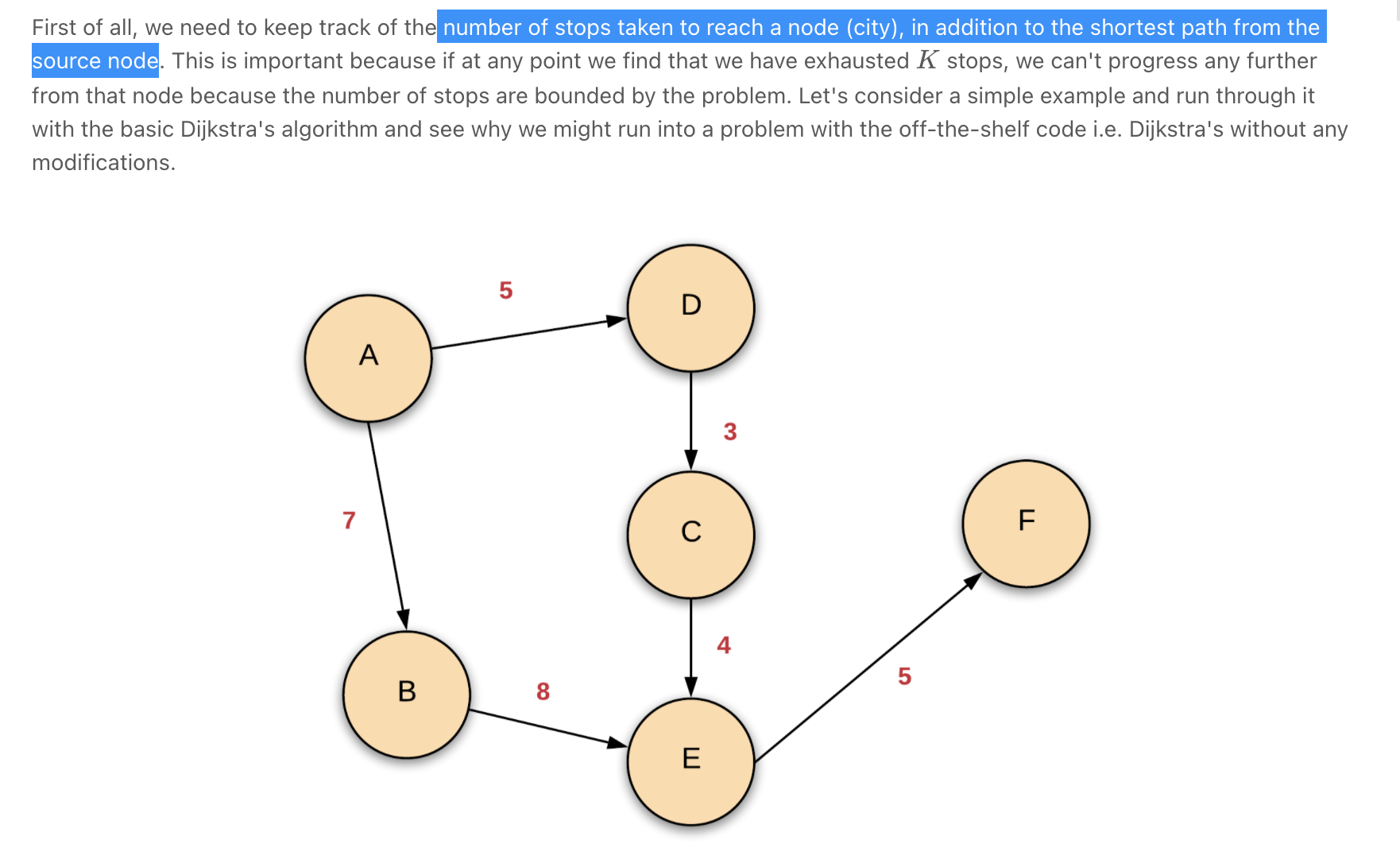
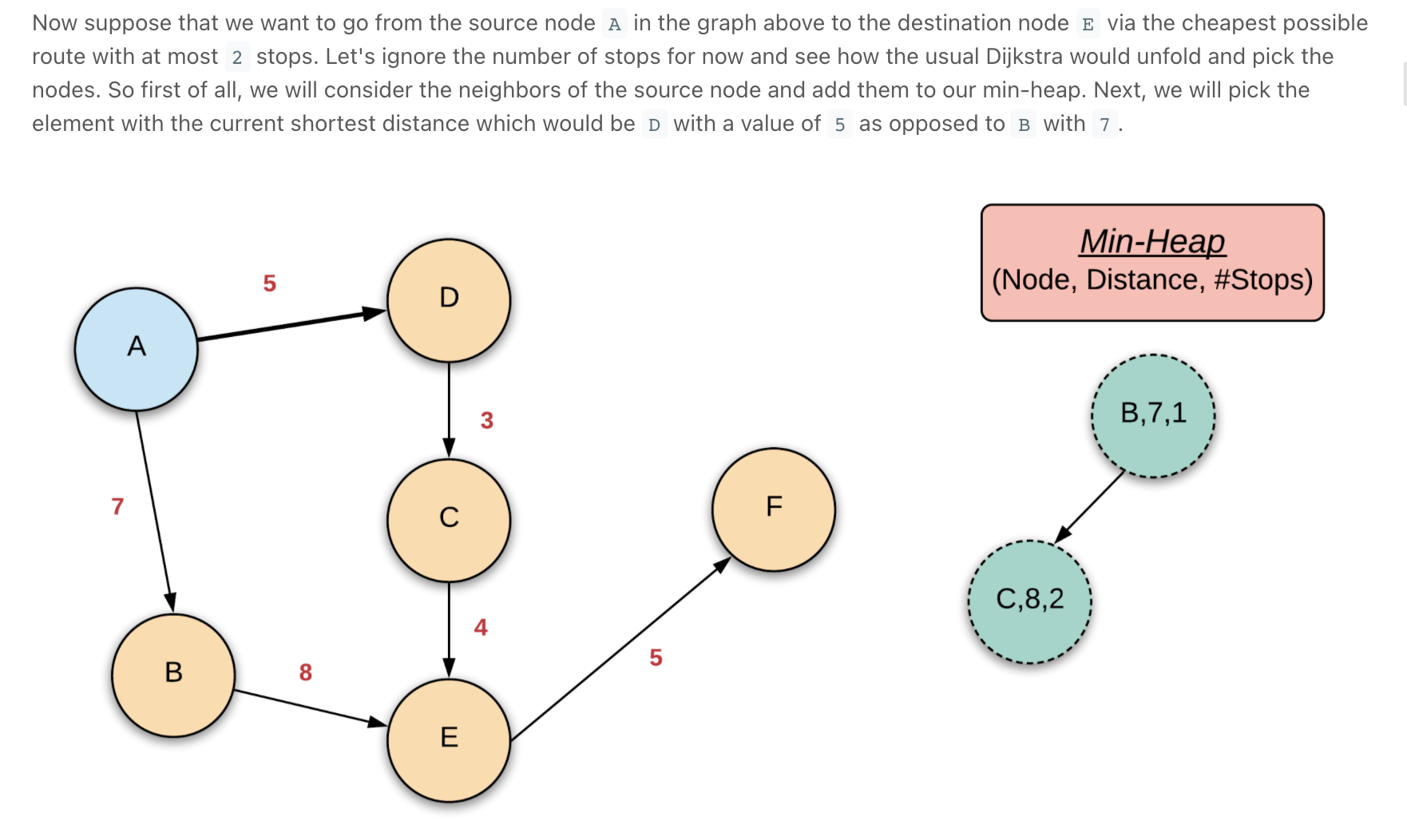
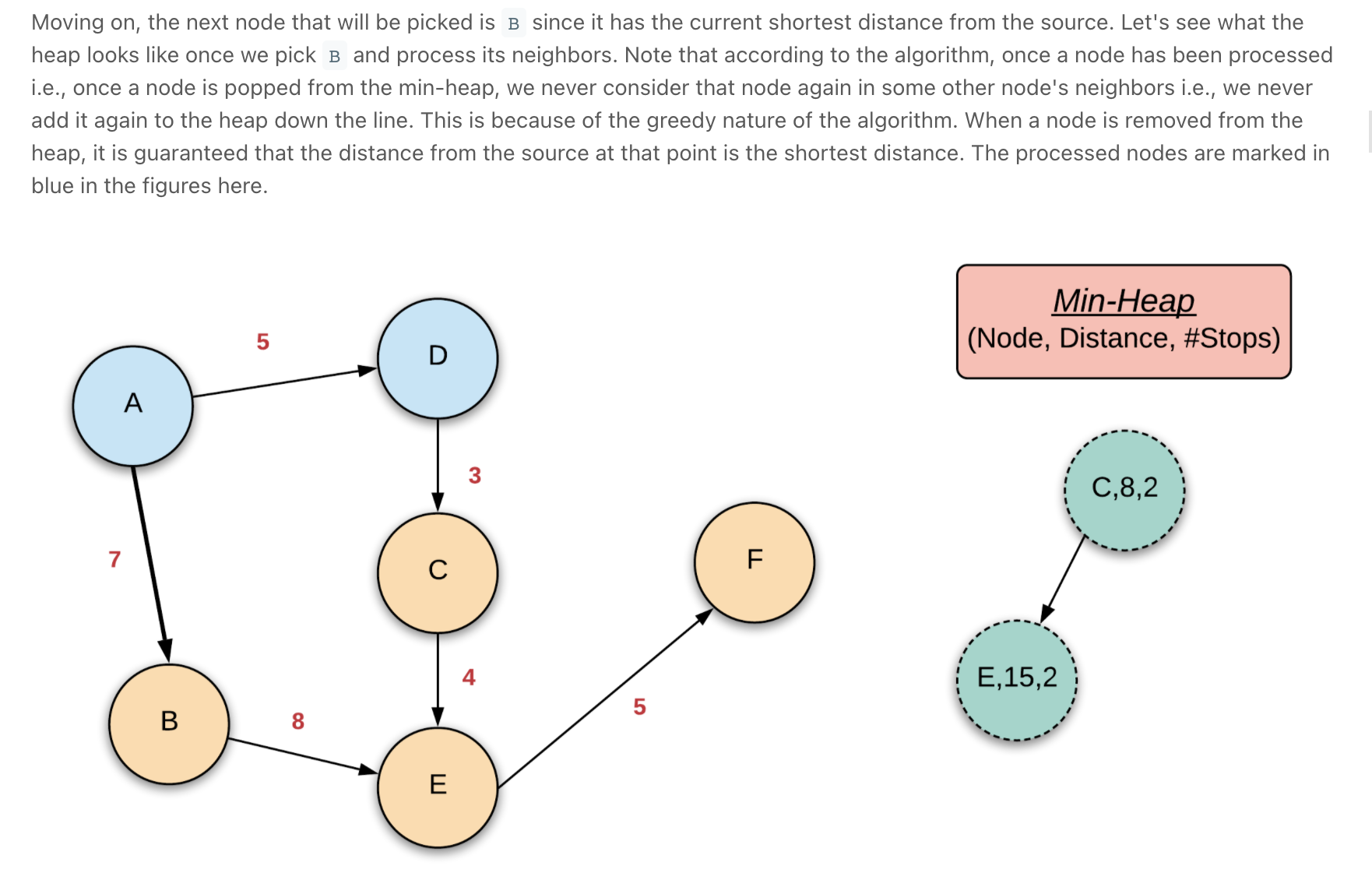
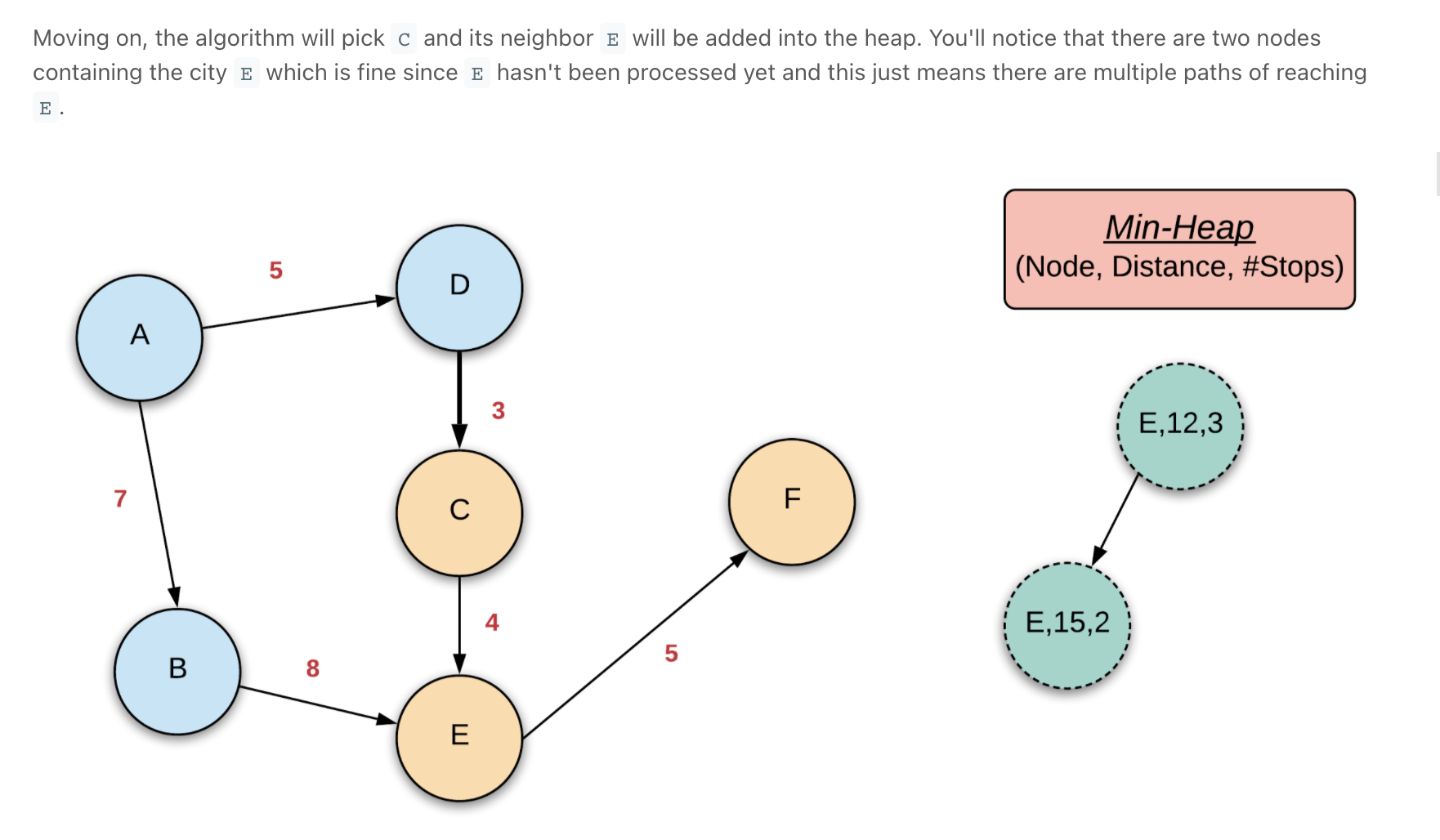


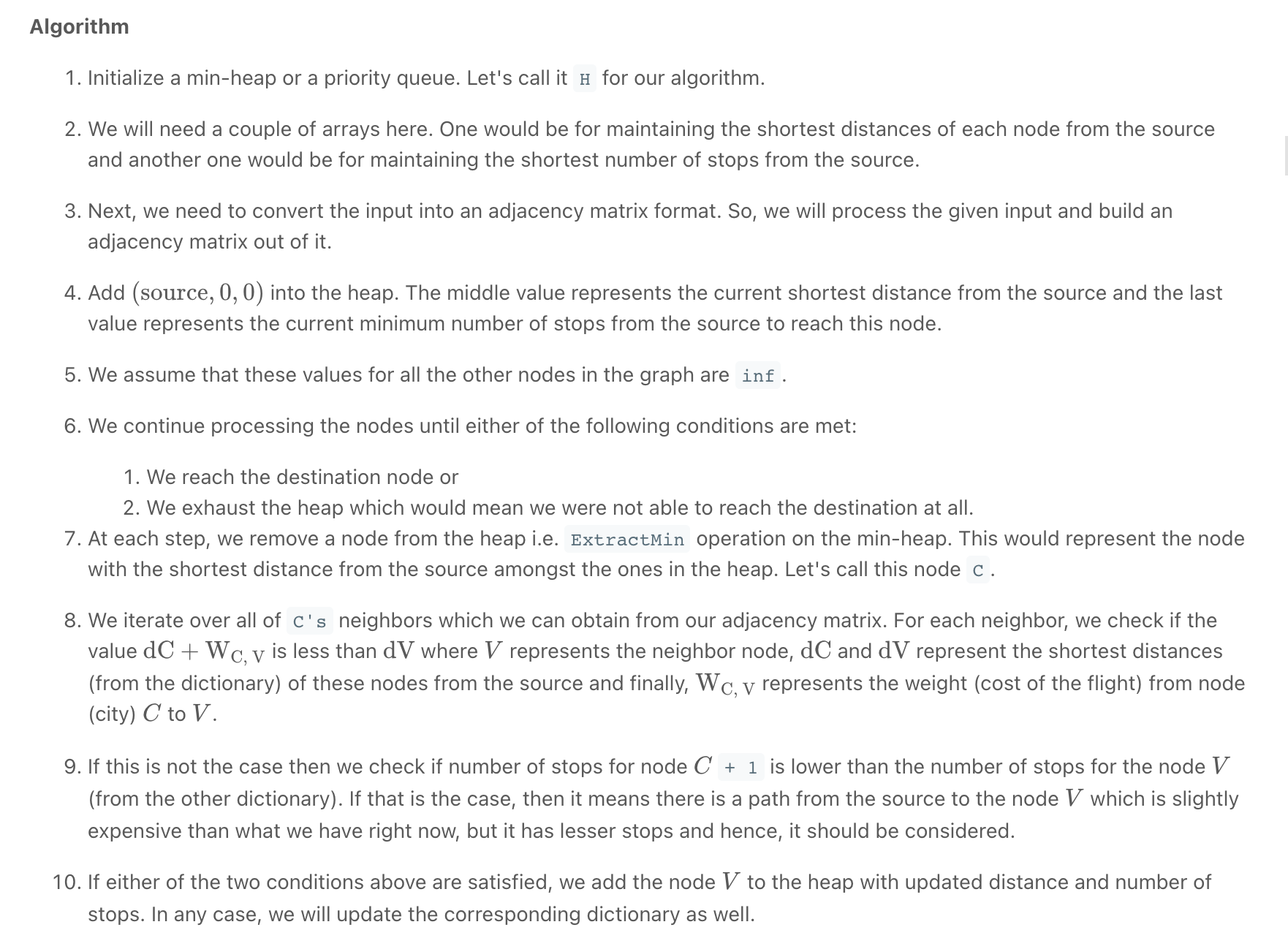
""" Cheapest Flights Within K Stops There are n cities connected by some number of flights. You are given an array flights where flights[i] = [fromi, toi, pricei] indicates that there is a flight from city fromi to city toi with cost pricei. You are also given three integers src, dst, and k, return the cheapest price from src to dst with at most k stops. If there is no such route, return -1. Example 1: Input: n = 3, flights = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 1 Output: 200 Explanation: The graph is shown. The cheapest price from city 0 to city 2 with at most 1 stop costs 200, as marked red in the picture. Example 2: Input: n = 3, flights = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 0 Output: 500 Explanation: The graph is shown. The cheapest price from city 0 to city 2 with at most 0 stop costs 500, as marked blue in the picture. https://leetcode.com/problems/cheapest-flights-within-k-stops """ import collections import heapq class Solution: def findCheapestPrice(self, n, flights, src, dst, k): # Build graph graph = collections.defaultdict(list) for from_node, to_node, price in flights: graph[from_node].append((price, to_node)) # Dijkstra's Algorithm heap = [(0, src, 0)] visited = set() city_stops = [float('inf')] * n # shortest distance/price to node while heap: price, city, stops = heapq.heappop(heap) if city == dst: return price if stops == k+1: continue # # Note: in Dijkstra's Algorithm, we never revisit nodes # Remember that our algorithm stops whenever we pass k stops/visits - we need to consider this & look for a path that will give us less stops # Therefore, if we ever encounter a node that has already been processed before # but the number of stops from the source is lesser than what was recorded before, # we will add it to the heap so that it gets considered again! # That's the only change we need to make to make Dijkstra's compliant with the limitation on the number of stops. # if city in visited: <- normal Dijkstra's Algorithm # if city in visited and stops > city_stops[city]: <- modified Dijkstra's Algorithm if city in visited and stops > city_stops[city]: continue visited.add(city) city_stops[city] = stops for neighbour_cost, neighbour in graph[city]: heapq.heappush( heap, (price+neighbour_cost, neighbour, stops+1,) ) return -1
Union find (disjoint set)
Disjoint Set Union (DSU)/Union-Find - A Complete Guide - LeetCode Discuss
Examples:
-
Making A Large Island
""" Making A Large Island You are given an n x n binary matrix grid. You are allowed to change at most one 0 to be 1. Return the size of the largest island in grid after applying this operation. An island is a 4-directionally connected group of 1s. Example 1: Input: grid = [[1,0],[0,1]] Output: 3 Explanation: Change one 0 to 1 and connect two 1s, then we get an island with area = 3. Example 2: Input: grid = [[1,1],[1,0]] Output: 4 Explanation: Change the 0 to 1 and make the island bigger, only one island with area = 4. Example 3: Input: grid = [[1,1],[1,1]] Output: 4 Explanation: Can't change any 0 to 1, only one island with area = 4. https://leetcode.com/problems/making-a-large-island """ from collections import defaultdict from typing import List # O(N^2) time | O(N^2) space # we traverse the graph twice in the worst case, for time, and only store row*col nodes, for space class Solution: def largestIsland(self, grid: List[List[int]]): """ * Based on union find: https://www.notion.so/paulonteri/Trees-Graphs-edc3401e06c044f29a2d714d20ffe185#02cd6da5a64447feab03037d22d40b38 - Group nodes into different islands - store the island sizes - record the island_id for each node - For each 0, try to merge its surrounding islands """ island_sizes, child_to_island_id = self.create_islands(grid) largest_island = 0 if island_sizes: largest_island = max(island_sizes.values()) for row in range(len(grid)): for col in range(len(grid[0])): if grid[row][col] != 0: continue """ Try to connect the surrounding islands if we have seen the island before, we don't need to do anything """ seen_island_ids = set() top_island, top = self.get_node_island_and_size(grid, row-1, col, island_sizes, child_to_island_id) seen_island_ids.add(top_island) bottom_island, bottom = self.get_node_island_and_size(grid, row+1, col, island_sizes, child_to_island_id) # is part of an island we saw above (in this case part of top_island) if bottom_island in seen_island_ids: bottom = 0 seen_island_ids.add(bottom_island) left_island, left = self.get_node_island_and_size(grid, row, col-1, island_sizes, child_to_island_id) if left_island in seen_island_ids: left = 0 seen_island_ids.add(left_island) right_island, right = self.get_node_island_and_size(grid, row, col+1, island_sizes, child_to_island_id) if right_island in seen_island_ids: right = 0 seen_island_ids.add(right_island) # merge all neighbouring islands + the current node (1) largest_island = max(largest_island, 1+top+bottom+left+right) return largest_island def get_node_island_and_size(self, grid, row, col, island_sizes, child_to_island_id): """ Returns the node's island_id and size """ if row < 0 or col < 0 or row >= len(grid) or col >= len(grid[0]): return None, 0 if grid[row][col] == 0: return None, 0 island_id = child_to_island_id[(row, col)] return island_id, island_sizes[island_id] def create_islands(self, grid: List[List[int]]): """ Creates islands - returns: - a dict of { `island_id` -> `island_size` } - a dict of {`child/node` -> `island_id` } """ island_sizes = defaultdict(int) child_to_island_id = {} def group_into_island(row, col, island_id): if row < 0 or col < 0 or row >= len(grid) or col >= len(grid[0]): return if (row, col) in child_to_island_id: return # skip if part of an island if grid[row][col] == 0: return island_sizes[island_id] += 1 child_to_island_id[(row, col)] = island_id group_into_island(row-1, col, island_id) group_into_island(row, col-1, island_id) group_into_island(row+1, col, island_id) group_into_island(row, col+1, island_id) curr_id = -1 for row in range(len(grid)): for col in range(len(grid[0])): group_into_island(row, col, curr_id) curr_id -= 1 return island_sizes, child_to_island_id

Screen Recording 2021-10-27 at 07.07.23.mov
The Disjoint set uses chaining to define a set. The chaining is defined as a parent-child relationship.
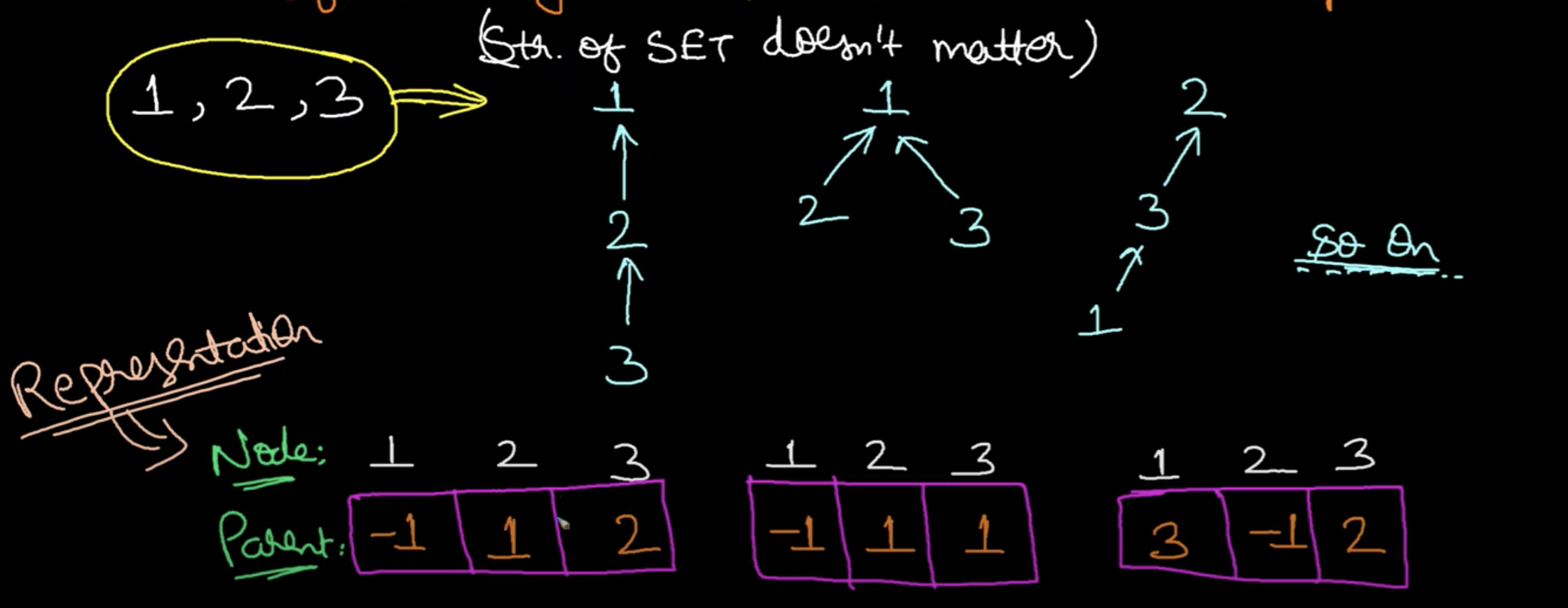
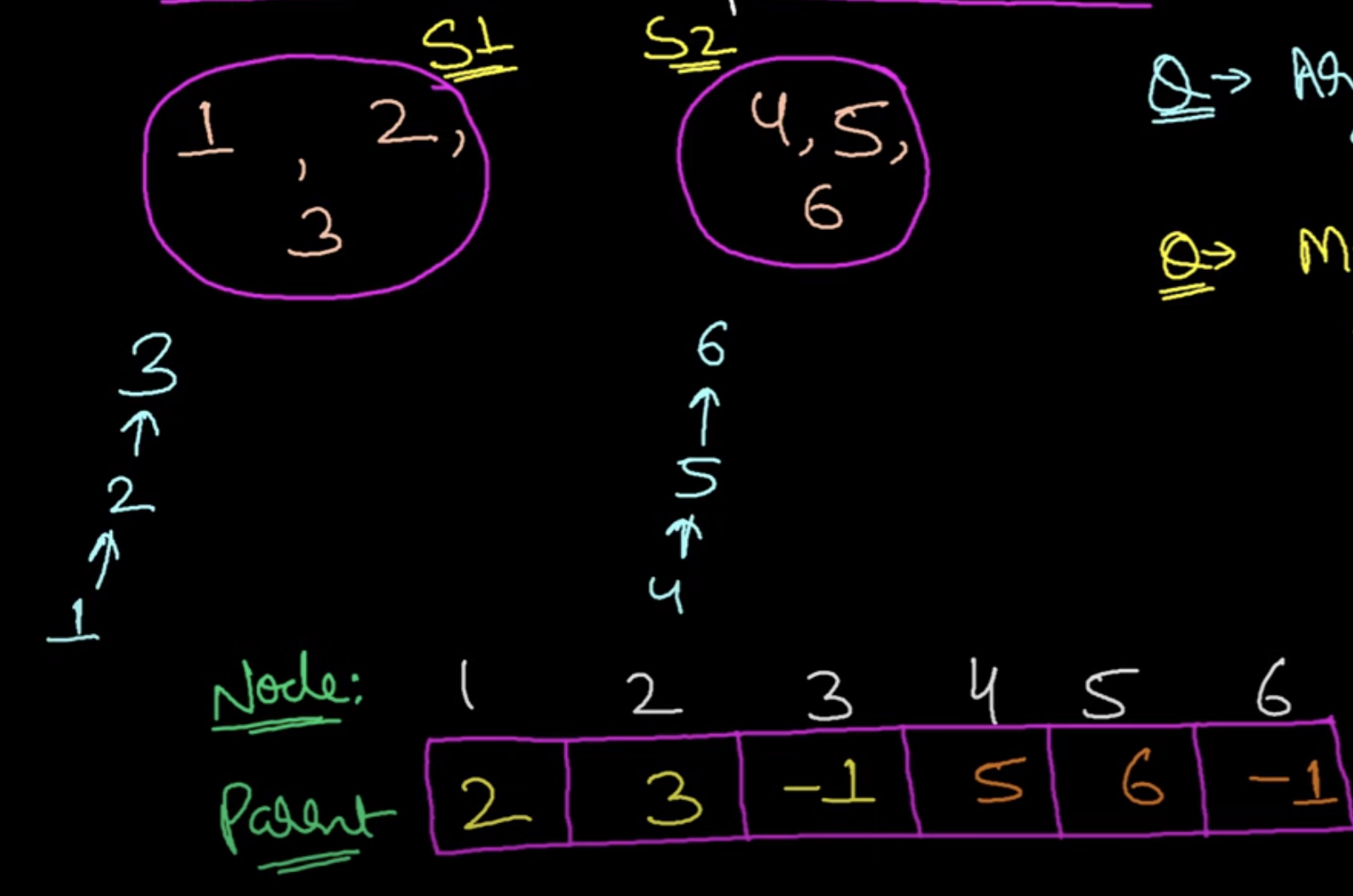
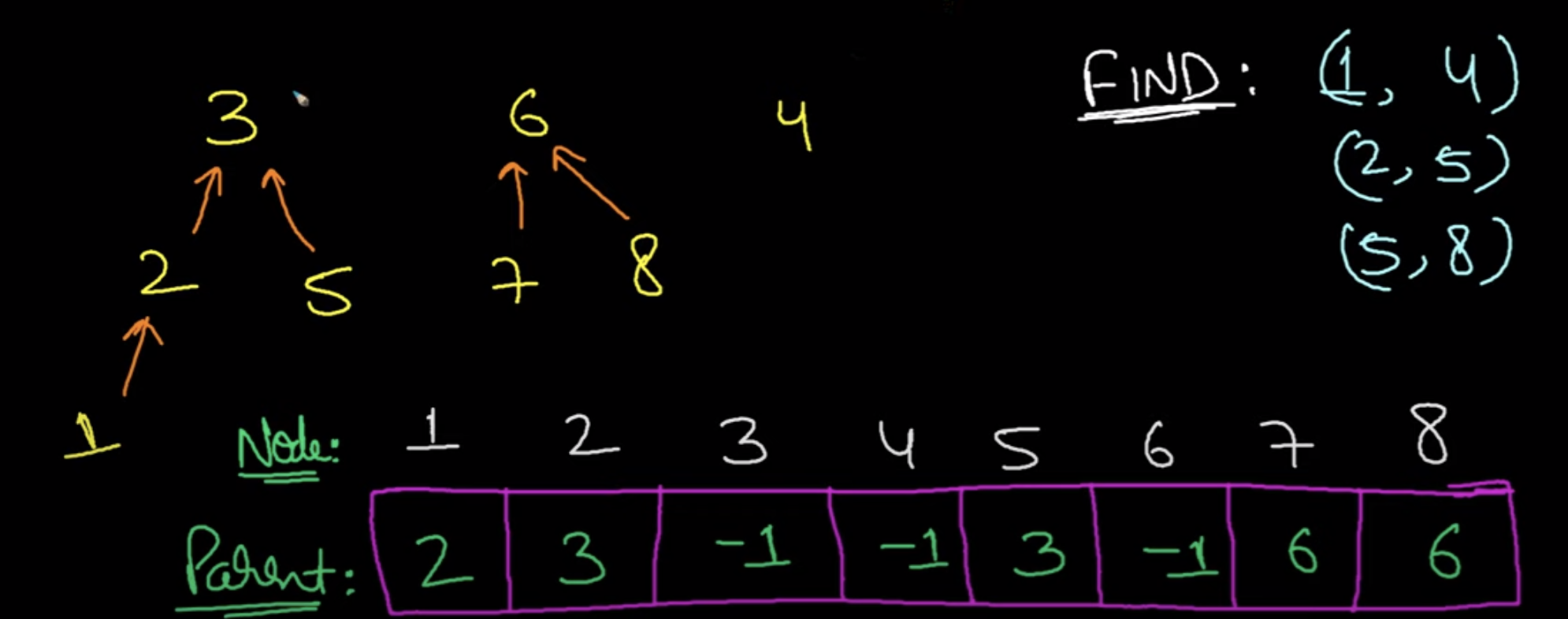
Every node points to its parent and absolute roots have no parent
Find:
- check if the two nodes share an absolute root and return True
Union:
- make the absolute root of one point to the absolutte root of another
Segment tree
Segment Trees Tutorials & Notes | Data Structures | HackerEarth
Understanding Range Queries and Updates: Segment Tree, Lazy Propagation and MO's Algorithm
Sum of given range | Segment tree construction and update | Simplest explanation
Introduction
A segment tree is a very flexible data structure, because it is used to solve numerous range query problems like finding minimum, maximum, sum, greatest common divisor, least common denominator in array in logarithmic time.
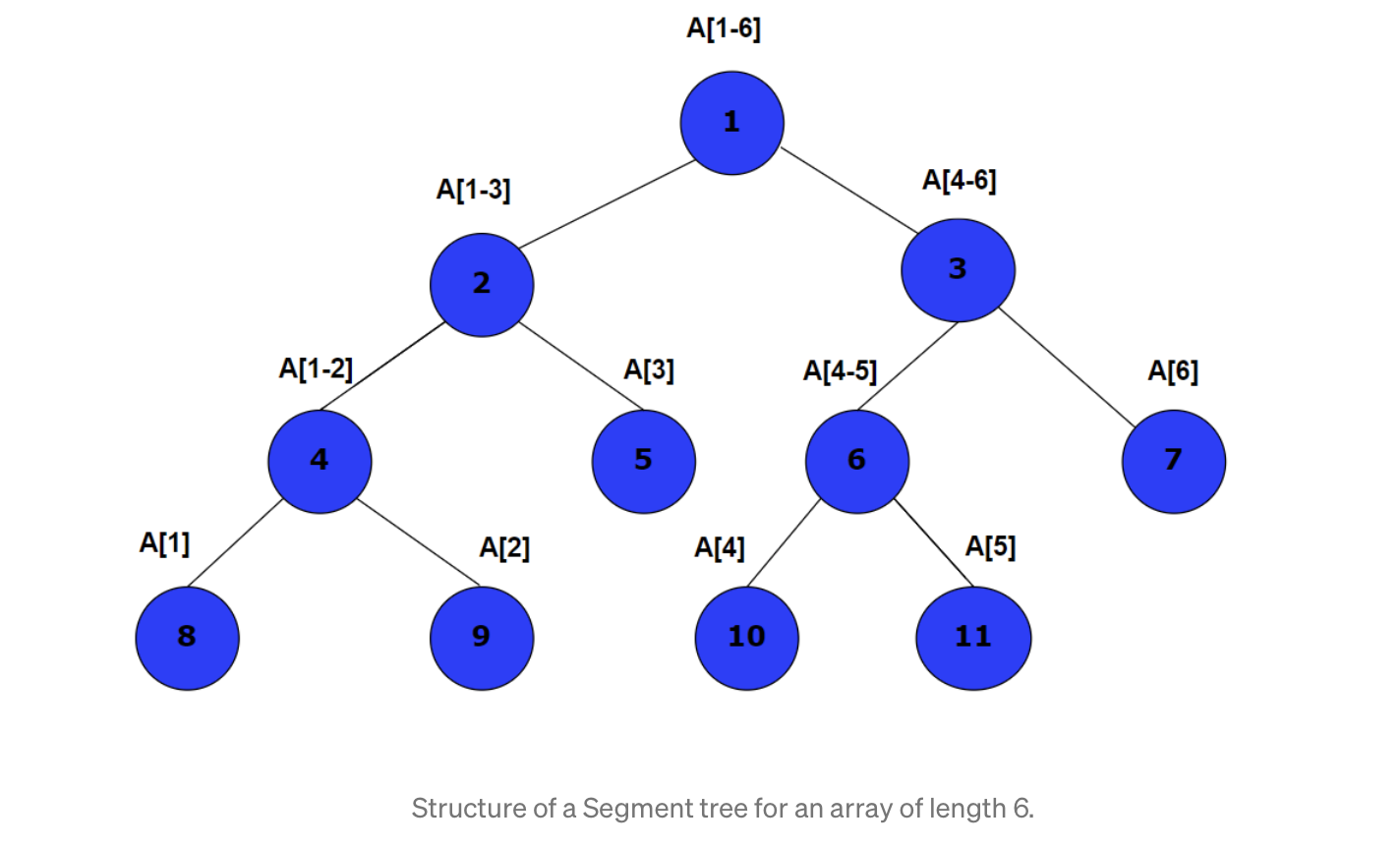
Let’s say we have an array A of size N. A segment of the array is a contiguous part of an array in form A[i:j] A segment tree is essentially a binary tree in whose nodes we store the information about the segments of a linear data structure such as an array. Do not worry about what kind of information as of now. We shall take a look at that later.
- The root node of the segment tree would contain the information about segment
A[0:N-1] - The left child of the root node would contain the information about segment
A[0:(N-1)/2]and similarly, - The right child of the root node would contain the information about segment
A[ 1+((N-1)/2) : (N-1) ]and so on.
In simpler terms the root node contains information about the whole array, its left child contains a similar kind of information about the left half of the array, and the right child of the root node will contain the information about the right half of the array and so on. Thus at each step (level of the tree), we divide the segment into two halves and the further children nodes contain the information about these two halves. This continues till we reach the leaf nodes which contain the element of the array A itself. The i-th leaf node contains A[i]. Thus we can say that there will be N leaf *nodes and the height of the tree will be log *N to the base 2.
Note: Once a segment tree is built for an array, its structure cannot be changed. We are allowed to update the values of the nodes but we cannot change the structure of the Segment Tree. That is to say, we cannot add more elements to the array and expect the segment tree to update. In that case, we will have to create a new segment tree altogether. However, we are allowed to update the values of the array and the segment tree shall be updated accordingly.
Segment Trees allow for the following two operations:
- Update: This operation allows us to update the values of array A and reflect the corresponding changes in the segment tree.
- Query: This operation allows us to perform a range query on the array. For example, let's say we have an array of size 15 and we wish to find the maximum element in the segment of an array with start index as 3 and end index 9. This is an example of a range query.
Thus we can say that a segment tree comes in handy when we have a lot of range-based queries to be performed on an array along with value updates on the same array. The process of creation of a segment tree takes some time but once it's done, the operation of range queries becomes very fast.
What kind of information does a segment tree hold?
Now that we have a basic understanding of the structure of the segment tree let us have a look at what kind of information does a segment tree hold. Consider an array A = [1, 4, 5, 8, 0, 13]
Now a segment tree is always associated with a piece of certain information that is directly linked with the kind of range queries we wish to perform. A couple of them are as follows:
- Find the sum/product of elements of an array in the range
A[i:j] - Find the maximum/minimum element in the range
A[i:j] - Find the count of even/odd/prime etc, numbers in the range
A[i:j]
There can be many others depending upon the usage. Let us have a look at how we can make use of a segment tree to find the sum of elements in a given range.
Construction
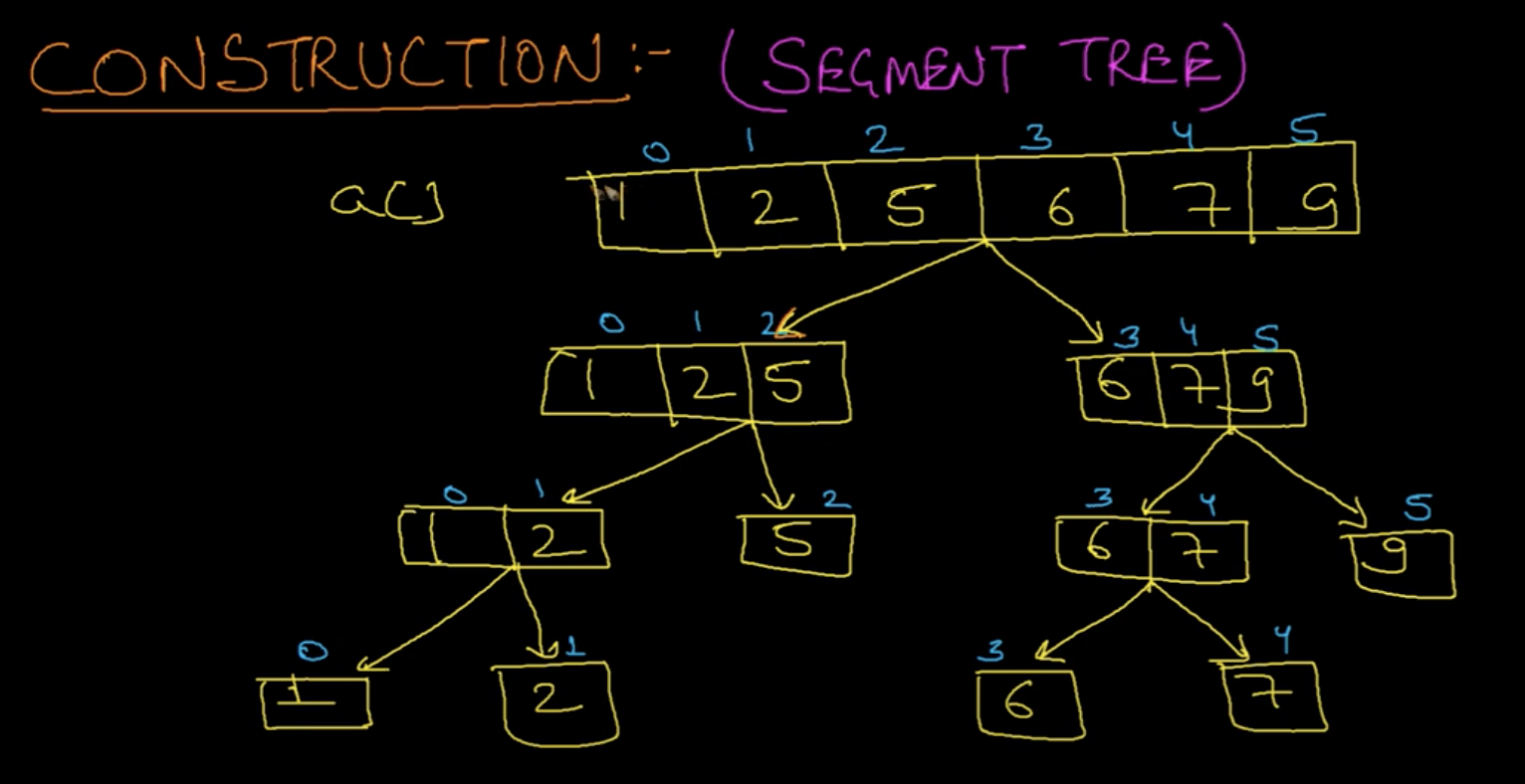
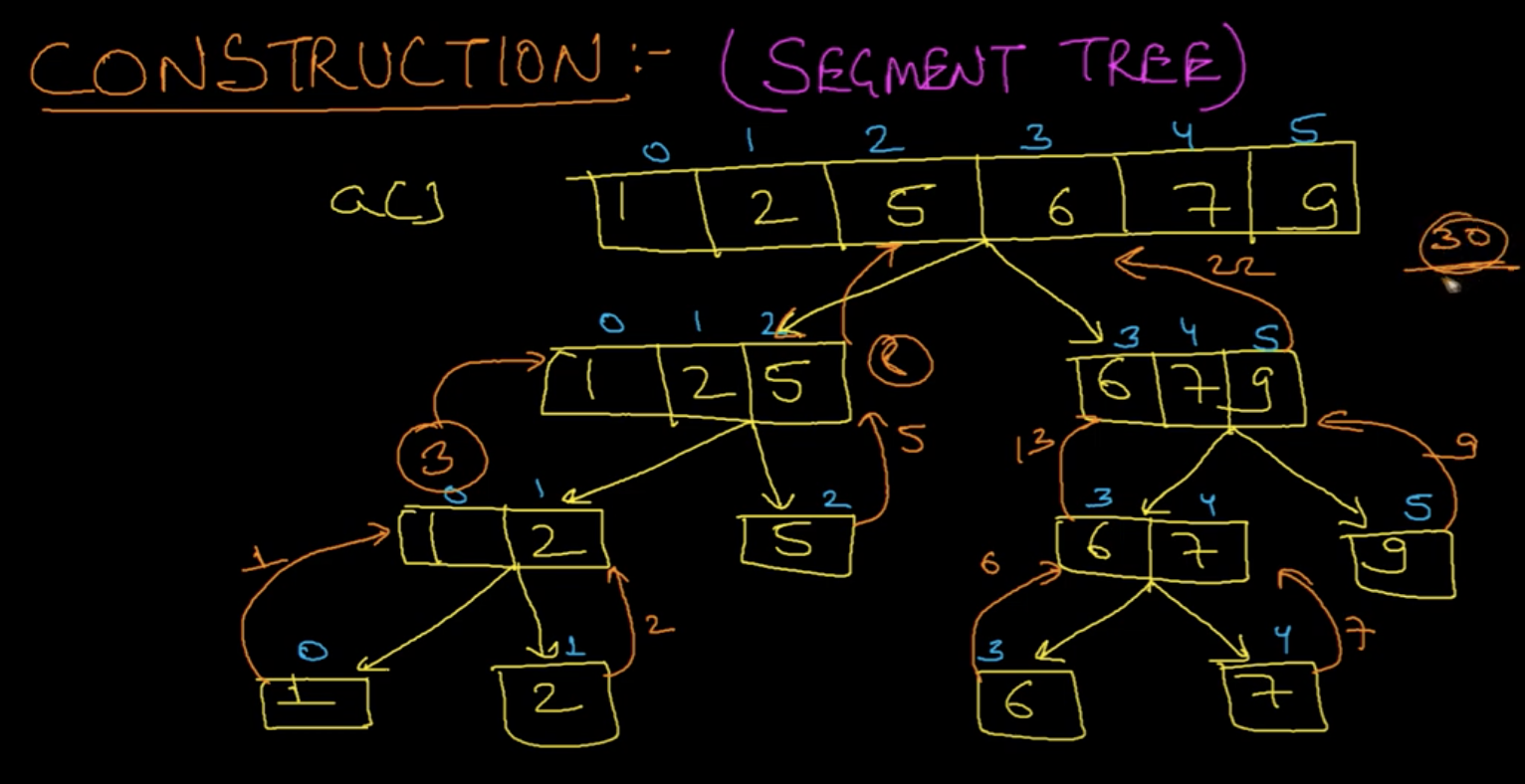
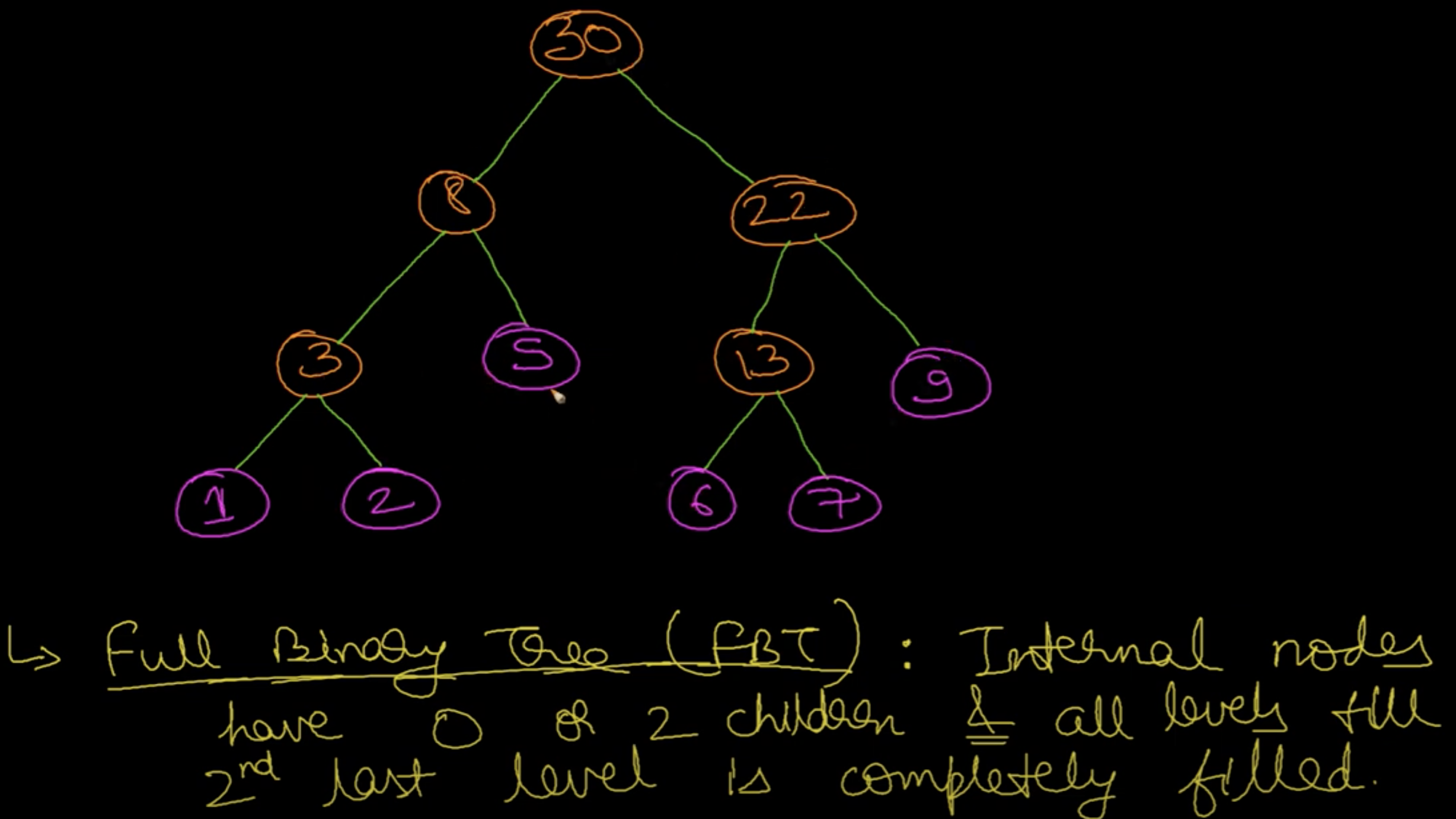

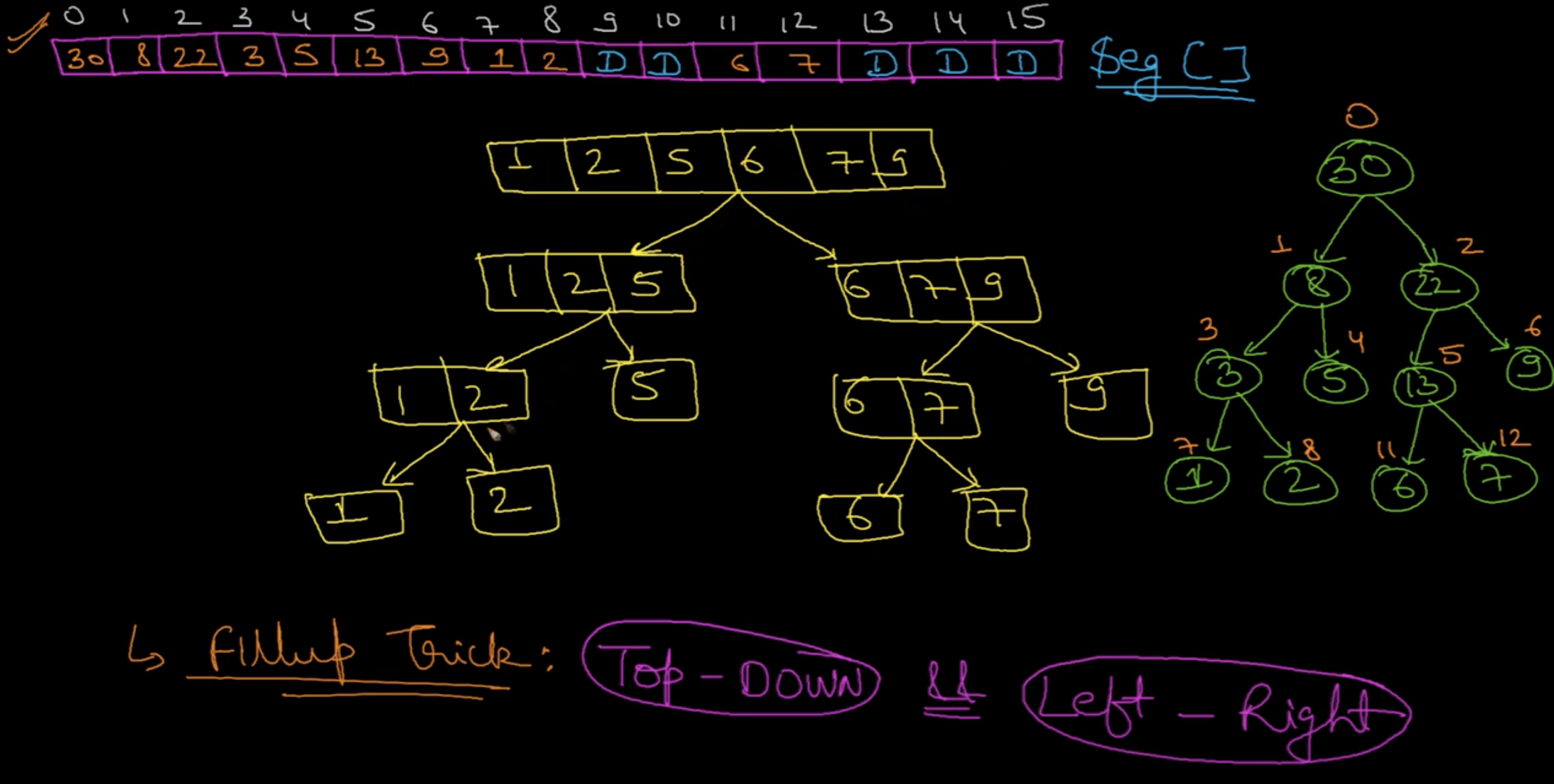
Screen Recording 2021-11-12 at 12.03.56.mov
Let’s say we have an array A = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] ****and we wish to find the sum of elements in a given range. Then each node would store the sum of its children nodes, except the leaf nodes which store the array elements. Then the segment tree for the same would look something like this:
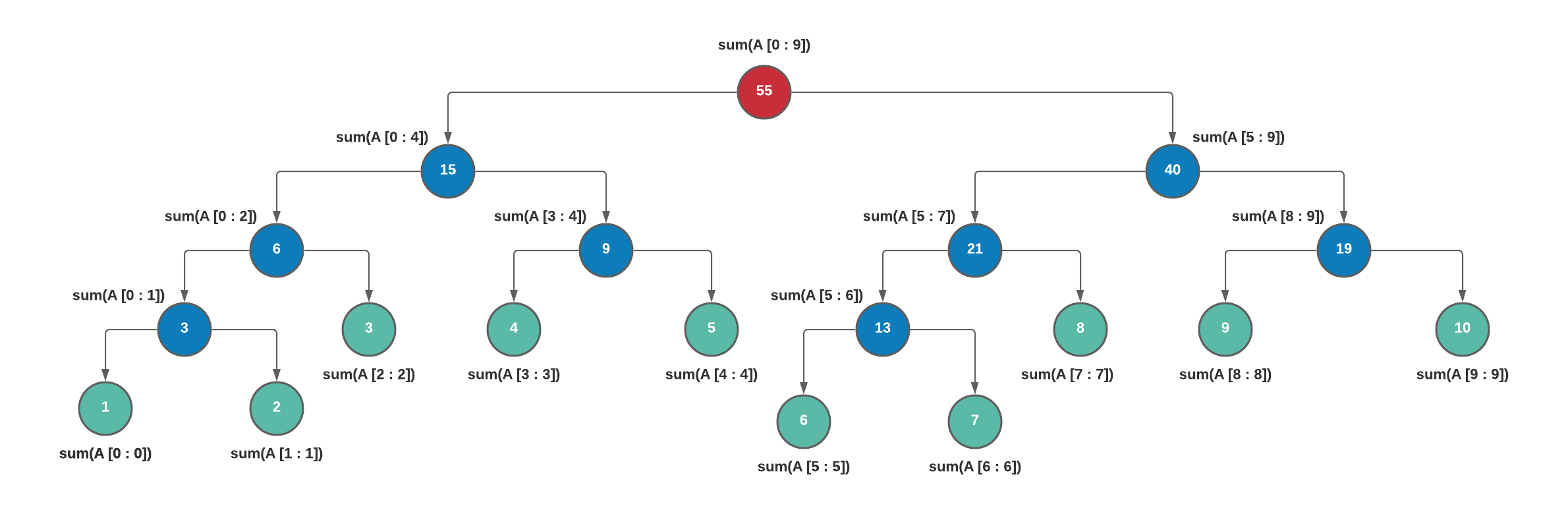
The red node being the root node, the blue nodes being the internal nodes and the green nodes being the leaf nodes. Each node contains information about a particular segment of the array. In this example,
- Root node contains the sum of all the elements of the array
- The left child of the root node contains the information about the sum of the left half of the array i.e. [1, 2, 3, 4, 5]. Its left child in turn contains the sum of the segment [1, 2, 3] and the right child contains the sum of the segment [4, 5] and so on.
- The right child of the root node contains the information about the sum of the left half of the array i.e. [6, 7, 8, 9, 10]. Its left child in turn contains the sum of the segment [6, 7, 8] and the right child contains the sum of the segment [9, 10] and so on.
If we wanted to compute, let's say, the maximum element then we would be storing the maximum element in each segment in the corresponding nodes. Thus before building the Segment Tree one must figure out the intent behind building the tree and the type of values to be stored in the tree’s nodes.
Thus we can also notice that a segment tree is always going to be a full binary tree i.e. each node either has 2 or 0 children.
The total number of leaf nodes is at least N. Total number of internal nodes = N-1. So, the total number of nodes = 2N-1. But generally, to build a segment tree over an array of size N, we use a tree of 4N nodes**. (Why?)
Array representation of above segment tree will be
Tree[] = {1,2,3,4,5,6,7,8,9,dummy,dummy,10,11,dummy,dummy};
Since we use the array representation of the segment tree, so a bit of space is wasted as you can see in the above example. This wasted space can be removed but in that case, its implementation would be more complex. Considering these waste spaces, for the smooth working of data structure, a tree of size 4*N is used, which is still of linear space complexity.
4*N size is enough for an array of size N. Why?
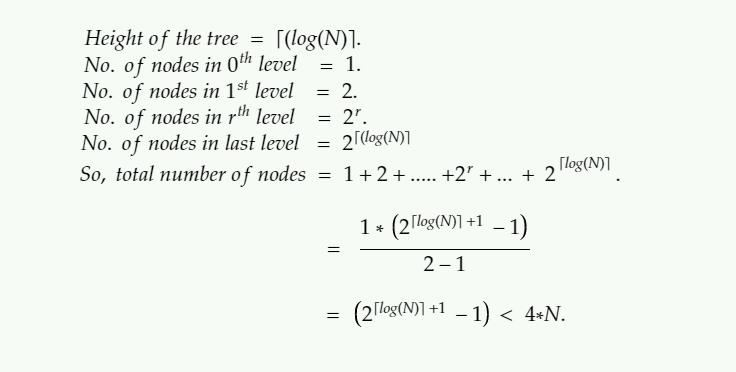
void build(int node, int start, int end)
{
if(start == end)
{
// Leaf node will have a single element
tree[node] = A[start];
}
else
{
int mid = (start + end) / 2;
// Recurse on the left child
build(2*node, start, mid);
// Recurse on the right child
build(2*node+1, mid+1, end);
// Internal node will have the sum of both of its children
tree[node] = tree[2*node] + tree[2*node+1];
}
}
void Build_Tree(int node, int st, int end)
{
if(st == end)
{
/*Leaf node will store the single array element*/
tree[node] = A[st];
return ;
}
int mid = (st+end)/2;
/*Call recursion for left child*/
Build_Tree(node*2, st, mid);
/*Call recursion for right child*/
Build_Tree(node*2+1, mid+1, end);
/*Update the current node as minimum of both children*/
tree[node] = min(tree[2*node], tree[2*node+1]);
return;
}
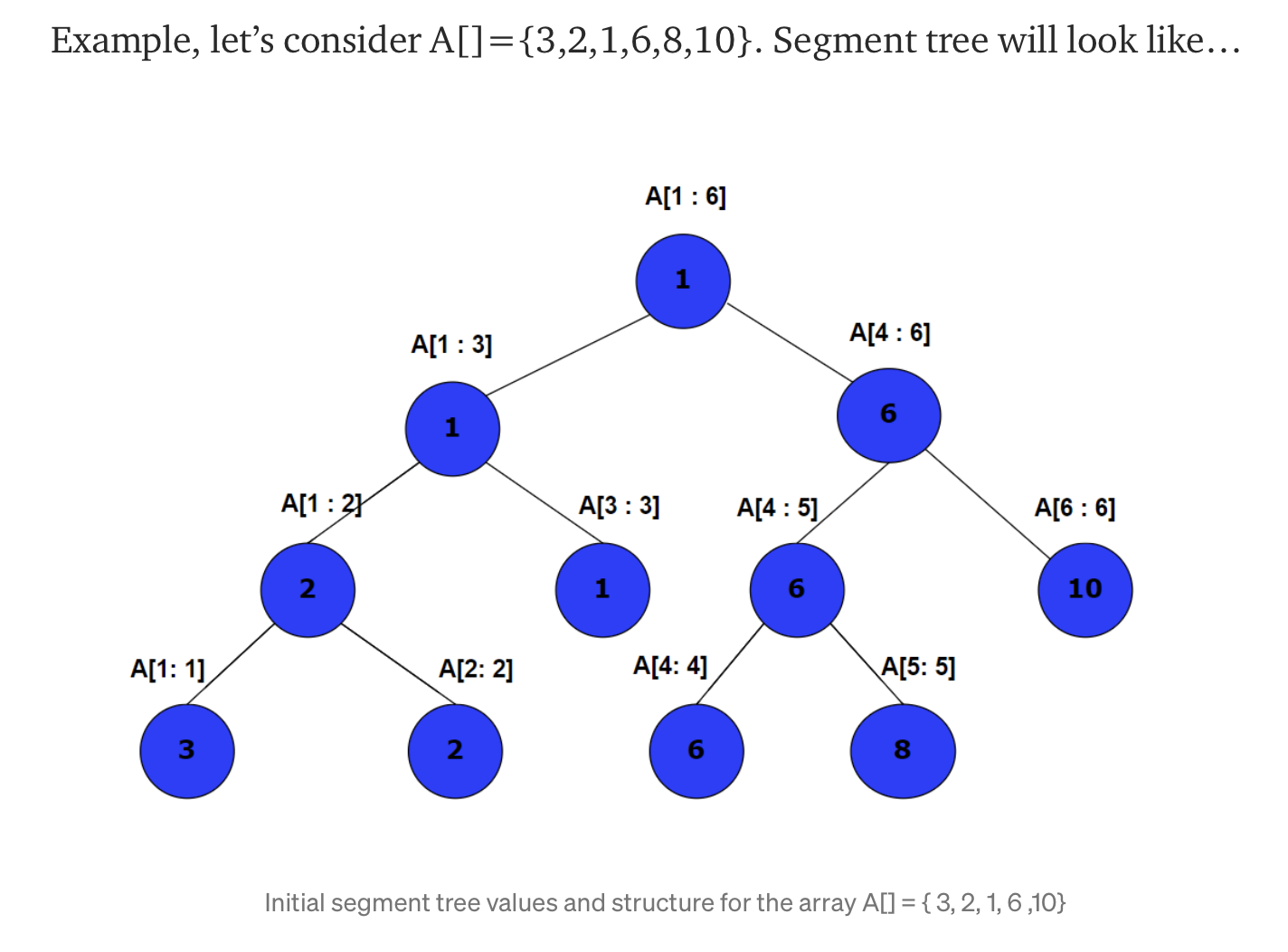
In the above function, node represents the current node of the tree being processed and variables st and end represent the range (segment) of that current node. Recall that segment tree is a binary tree, left child, given by 2node, contains the range A[st : mid] and right child, which is given by 2node+1, contains the range A [mid+1: end] where mid=(st+end)/2.
Since the build function is being called once for each node (total maximum 4N node), so the time complexity of the build() is O(N)*.
Update the Tree
Screen Recording 2021-11-12 at 12.05.24.mov
Now, we want to modify the array element as A[a] = b and hence we have to modify the segment tree. Looking at the tree, one can clearly observe that index to be updated lies only in one segment of each level so we need to update only log(N) nodes. Starting from the root node we will recursively call the update function for the node which contains required index till we reach the leaf node representing that index. Then we will update that node, and in backtracking all the ancestors till root will be updated as minimum of its children.
Code for the same is:
void update(int node, int start, int end, int idx, int val)
{
if(start == end)
{
// Leaf node
A[idx] += val;
tree[node] += val;
}
else
{
int mid = (start + end) / 2;
if(start <= idx and idx <= mid)
{
// If idx is in the left child, recurse on the left child
update(2*node, start, mid, idx, val);
}
else
{
// if idx is in the right child, recurse on the right child
update(2*node+1, mid+1, end, idx, val);
}
// Internal node will have the sum of both of its children
tree[node] = tree[2*node] + tree[2*node+1];
}
}
void update(int node, int st, int end, int idx, int value)
{
if(st == end)
{
/*Update leaf node*/
tree[node] = value;
A[idx] = value;
return ;
}
int mid = (st+end)/2;
/*if index lies in the left child call update() for left child*/
if(idx<=mid)
update(2*node, st, mid, idx, value);
/*else index would lie in the right child, call update() for the right child*/
else
update(2*node+1, mid+1, end, idx, value);
/*after updating the children,update the current node as smallest of its children */
tree[node] = min(tree[2*node], tree[2*node+1]);
return ;
}
TIme complexity of update function is O(log(N)).
P.S. Often we don’t need to write one special build() function for building the segment tree. It can be done using the update function as well. For that we need to initialize the tree nodes with such a value that will never affect our answer.
Range query
Screen Recording 2021-11-12 at 12.05.58.mov
We are given two integers l and r, we need to find the smallest element in this range (l and r inclusive).
To accomplish the task, we will traverse the segment tree and use the pre-computed values of the intervals. Let’s consider that currently, we are at a vertex that covers the interval A[st, st+1, st+2, . . ., end]. Then there are three possibilities:
- Range represented by the node lies completely inside the given query range: In this case, we will just return the value stored at that node in the segment tree.
- The range represented by the node lies completely outside the given query range: In this case, the query function should return such a value that will not affect our answer. For example, if we want to find the minimum element, our function should return infinity (INT_MAX).
- Range represented by the node lies partially inside and partially outside the given query range: As in this case, our answer depends on both the children so we will make two recursive calls one for each child. Let’s say partial answer from left child is ans1 and that from right child is ans2, so our answer would be min(ans1, ans2).
int query(int node, int start, int end, int l, int r)
{
if(r < start or end < l)
{
// range represented by a node is completely outside the given range
return 0;
}
if(l <= start and end <= r)
{
// range represented by a node is completely inside the given range
return tree[node];
}
// range represented by a node is partially inside and partially outside the given range
int mid = (start + end) / 2;
int p1 = query(2*node, start, mid, l, r);
int p2 = query(2*node+1, mid+1, end, l, r);
return (p1 + p2);
}
int range_min_query(int node, int st, int end, int l, int r)
{
/*if range of the current node lies inside the query range*/
if(l <= st && end <= r )
{
return tree[node];
}
/*If current range is completely outside the query range*/
if(st>r || end<l)
return INT_MAX;
/*If query range intersects both the children*/
int mid = (st+end)/2;
int ans1 = range_min_query(2*node, st, mid, l, r);
int ans2 = range_min_query(2*node+1, mid+1, end, l, r);
return min(ans1, ans2);
}
Time Complexity: Since at any level at most 4 nodes will be visited and the total number of levels in the tree is log(N). The upper bound of all the visited nodes would be 4log(N). Hence, the time complexity of each query would be O(log(N).*
Range Sum Query - Mutable
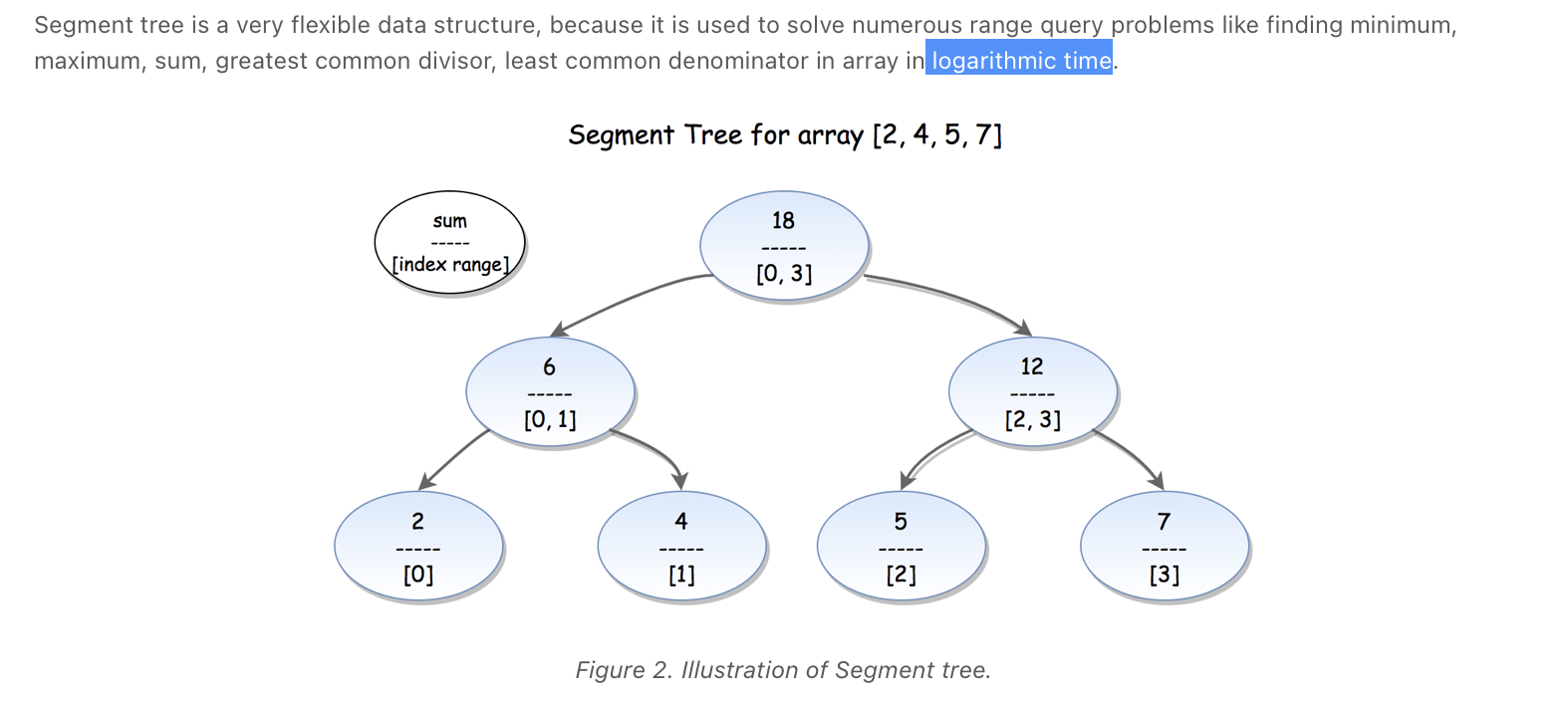

Tries
Topological sort
Topological Sort (for graphs) *
Morris Traversal
Find the original version of this page (with additional content) on Notion here.
Created: December 13, 2021 16:05:48