Topological Sort (for graphs) *
Introduction
Introduction to Topological Sort - LeetCode Discuss
Topological Sort Algorithm | Graph Theory
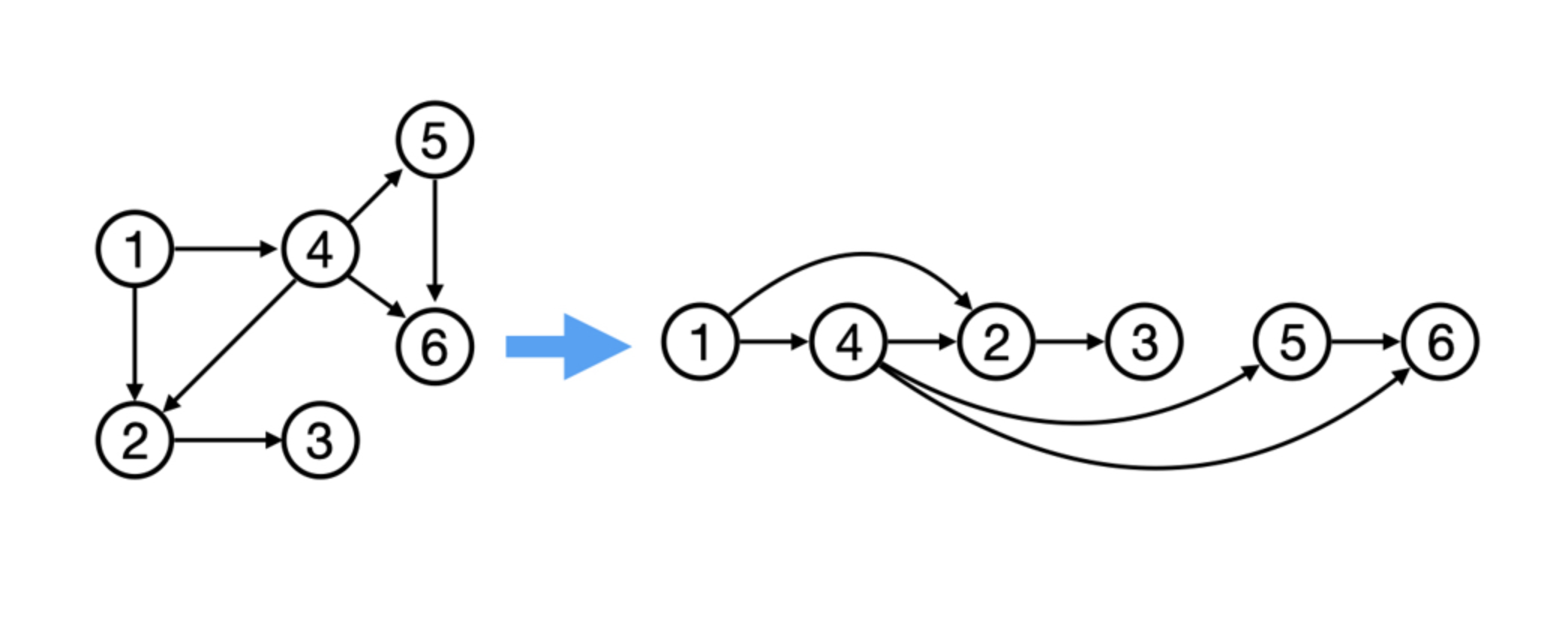

Topological Sort is used to find a linear ordering of elements that have dependencies on each other. For example, if event ‘B’ is dependent on event ‘A’, ‘A’ comes before ‘B’ in topological ordering.
This pattern defines an easy way to understand the technique for performing topological sorting of a set of elements and then solves a few problems using it.
A topological ordering is an ordering of nodes where for each edge from node A to node B, node A appears before node B in the ordering. If it helps, this is a fancy way of saying that we can align all the nodes in line and have all the edges pointing to the right. An important note to make about topological orderings is that they are not unique. As you can imagine there are multiple valid ways to enrol in courses and still graduate.
Sadly not every type of graph can have a topological ordering. For example, any graph which contains a directed cycle cannot have a valid ordering. Think of why this might be true, there cannot be an order if there is a cyclic dependency since there is nowhere to start. Every node in the cycle depends on another. So any graph with a directed cycle is forbidden. The only graphs that have valid topological orderings are Directed Acyclic Graphs, that is graphs with directed edges and no cycles.
The basic idea behind the topological sort is to provide a partial ordering among the vertices of the graph such that if there is an edge from U to V then U≤V i.e., U comes before V in the ordering. Here are a few fundamental concepts related to topological sort:
- Source: Any node that has no incoming edge and has only outgoing edges is called a source.
- Sink: Any node that has only incoming edges and no outgoing edge is called a sink.
- Indegree: count of incoming edges of each vertex/node or how many parents it has (used to determine sources)
- So, we can say that a topological ordering starts with one of the sources and ends at one of the sinks.
- A topological ordering is possible only when the graph has no directed cycles, i.e. if the graph is a Directed Acyclic Graph (DAG). If the graph has a cycle, some vertices will have cyclic dependencies which makes it impossible to find a linear ordering among vertices.
Topological sort
Problem
"""
Topological Sort:
Topological Sort of a directed graph (a graph with unidirectional edges) is a linear ordering of its vertices
such that for every directed edge (U, V) from vertex U to vertex V, U comes before V in the ordering.
Given a directed graph, find the topological ordering of its vertices.
Example 1:
Input: Vertices=4, Edges=[3, 2], [3, 0], [2, 0], [2, 1]
Output: Following are the two valid topological sorts for the given graph:
1) 3, 2, 0, 1
2) 3, 2, 1, 0
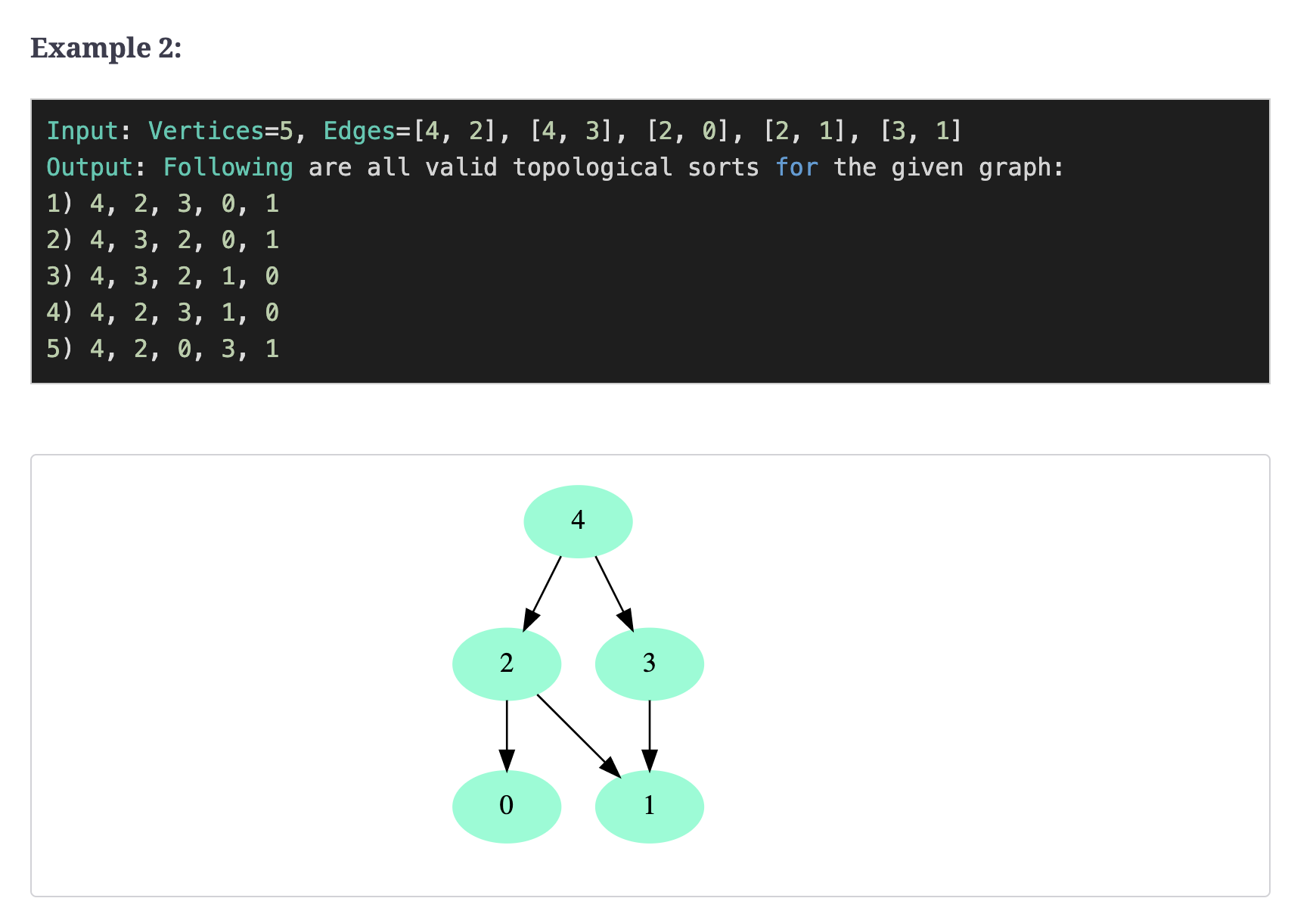
Example 2:
Input: Vertices=5, Edges=[4, 2], [4, 3], [2, 0], [2, 1], [3, 1]
Output: Following are all valid topological sorts for the given graph:
1) 4, 2, 3, 0, 1
2) 4, 3, 2, 0, 1
3) 4, 3, 2, 1, 0
4) 4, 2, 3, 1, 0
5) 4, 2, 0, 3, 1
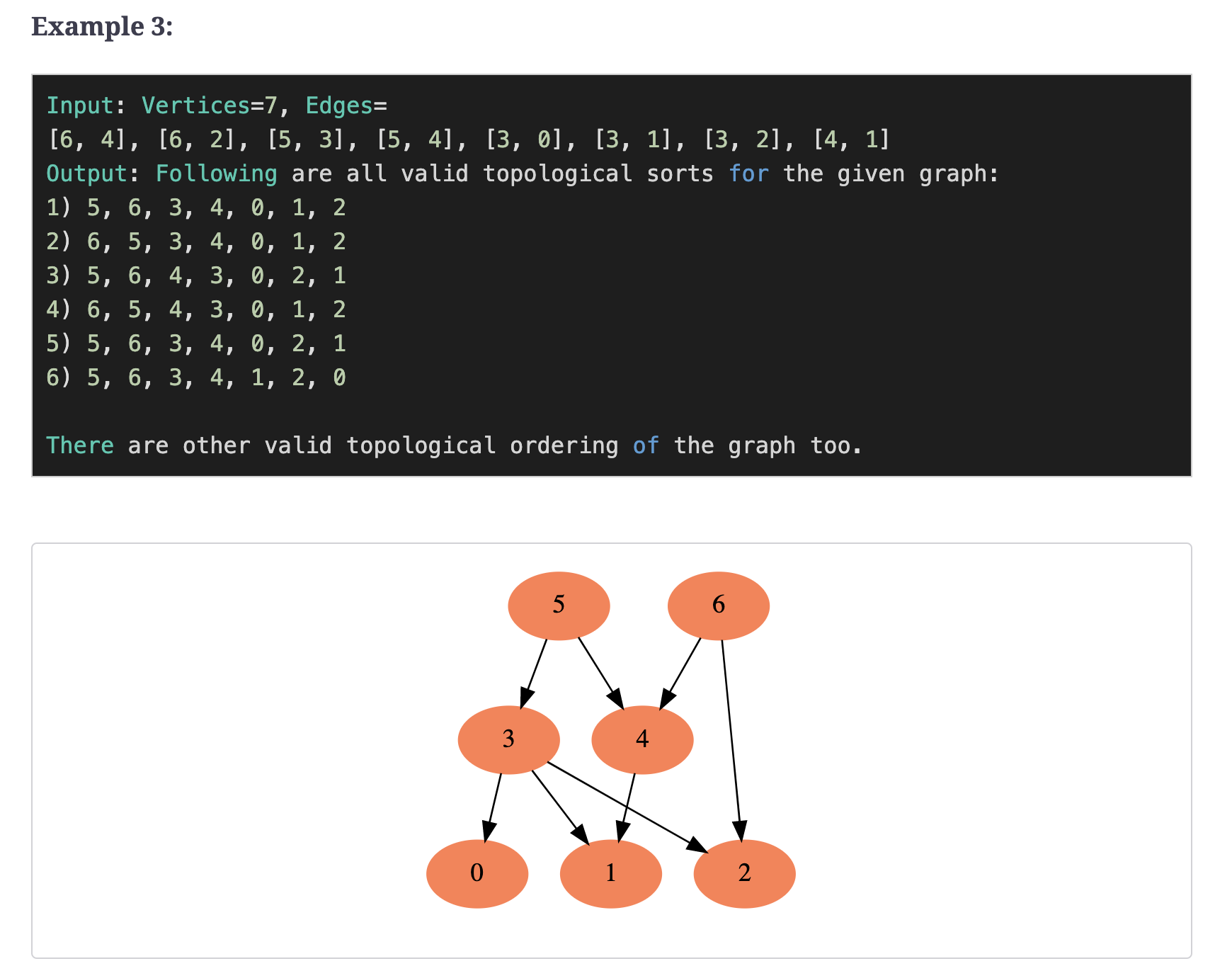
Example 3:
Input: Vertices=7, Edges=[6, 4], [6, 2], [5, 3], [5, 4], [3, 0], [3, 1], [3, 2], [4, 1]
Output: Following are all valid topological sorts for the given graph:
1) 5, 6, 3, 4, 0, 1, 2
2) 6, 5, 3, 4, 0, 1, 2
3) 5, 6, 4, 3, 0, 2, 1
4) 6, 5, 4, 3, 0, 1, 2
5) 5, 6, 3, 4, 0, 2, 1
6) 5, 6, 3, 4, 1, 2, 0
There are other valid topological ordering of the graph too.
https://www.educative.io/courses/grokking-the-coding-interview/m25rBmwLV00
"""
Solution
Solution one using sources → most optimal and can be used in many cases
Introduction to Topological Sort - LeetCode Discuss
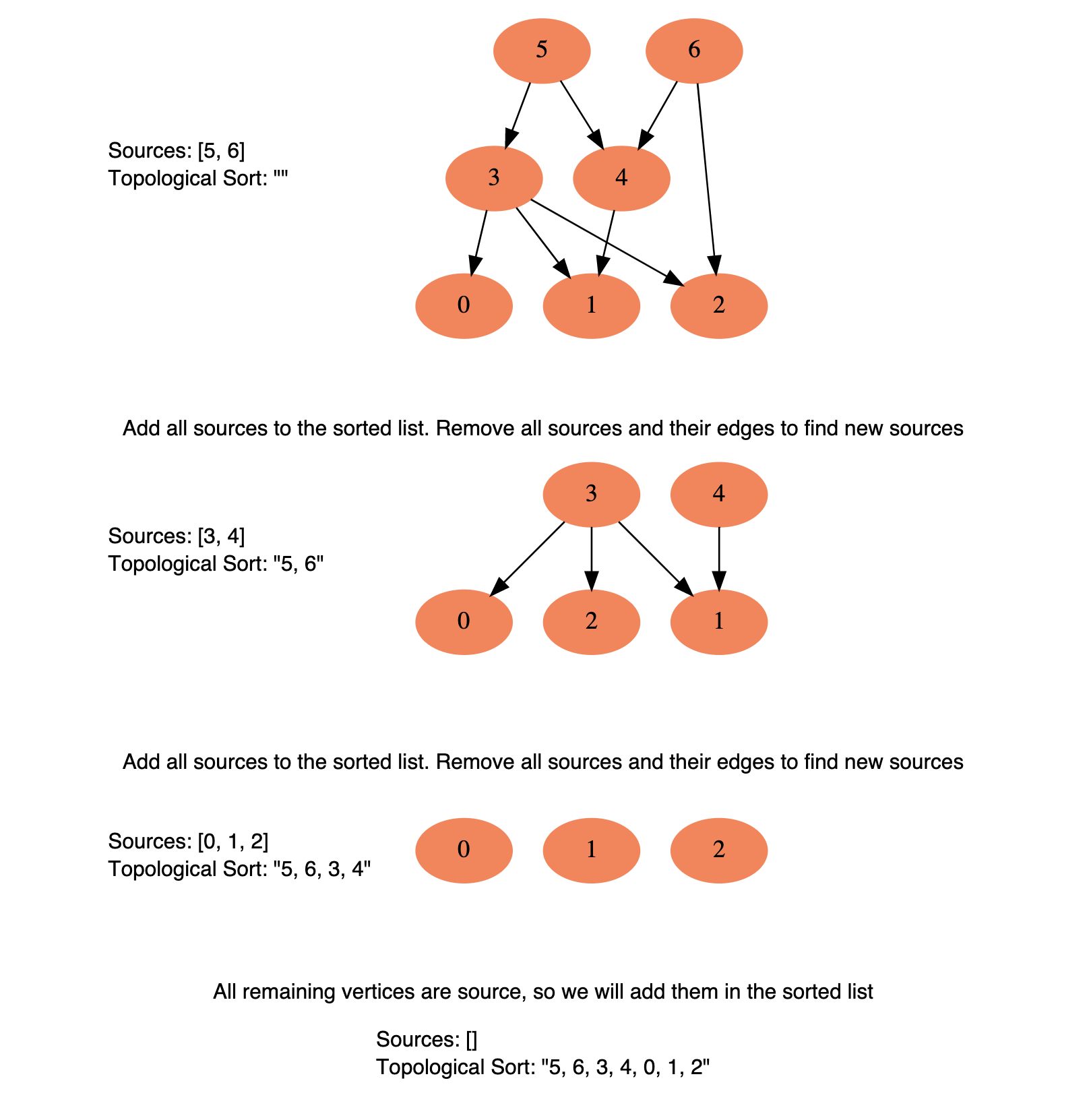
To find the topological sort of a graph we can traverse the graph in a Breadth-First Search (BFS) way. We will start with all the sources, and in a stepwise fashion, save all sources to a sorted list. We will then remove all sources and their edges from the graph. After the removal of the edges, we will have new sources, so we will repeat the above process until all vertices are visited.
This is how we can implement this algorithm:
- Initialization
- We will store the graph in Adjacency Lists, which means each parent vertex will have a list containing all of its children. We will do this using a HashMap where the ‘key’ will be the parent vertex number and the value will be a List containing children vertices.
- To find the sources, we will keep a HashMap to count the in-degrees i.e., count of incoming edges of each vertex. Any vertex with ‘0’ in-degree will be a source.
- Build the graph and find in-degrees of all vertices
- We will build the graph from the input and populate the in-degrees HashMap.
- Find all sources
- All vertices with ‘0’ in-degrees will be our sources and we will store them in a Queue.
- Sort
- For each source, do the following things:
- Add it to the sorted list.
- Get all of its children from the graph.
- Decrement the in-degree of each child by 1.
- If a child’s in-degree becomes ‘0’, add it to the sources Queue.
- Repeat step 1, until the source Queue is empty.
- For each source, do the following things:
"""
Solution:
To find the **topological sort of a graph we can traverse the graph in a Breadth-First Search (BFS) way**.
We will start with all the sources, and in a stepwise fashion, save all sources to a sorted list.
We will then remove all sources and their edges from the graph. After the removal of the edges, we will have new sources, so we will repeat the above process until all vertices are visited.
This is how we can implement this algorithm:
1. Initialization
- We will store the graph in Adjacency Lists, which means each parent vertex will have a list containing all of its children.
We will do this using a HashMap where the ‘key’ will be the parent vertex number and the value will be a List containing children vertices.
- To find the sources, we will keep a HashMap to count the in-degrees
i.e., count of incoming edges of each vertex. Any vertex with ‘0’ in-degree will be a source.
2. Build the graph and find in-degrees of all vertices
- We will build the graph from the input and populate the in-degrees HashMap.
3. Find all sources
- All vertices with ‘0’ in-degrees will be our sources and we will store them in a Queue.
4. Sort
- For each source, do the following things:
- Add it to the sorted list.
- Get all of its children from the graph.
- Decrement the in-degree of each child by 1.
- If a child’s in-degree becomes ‘0’, add it to the sources Queue.
- Repeat the step above, until the source Queue is empty.
"""
import collections
def topological_sort(vertices, edge_list):
sorted_order = []
# # convert edge list to an adjacency list & record the edge depths
# graph
adjacency_list = collections.defaultdict(list)
# count of incoming edges of each vertex/node or how many parents it has (used to determine sources)
in_degree = collections.defaultdict(int)
for edge in edge_list:
parent, child = edge[0], edge[1]
adjacency_list[parent].append(child)
in_degree[child] += 1 # increment child's in_degree
# # find all sources (have no parents)
queue = []
for key in adjacency_list:
if in_degree[key] == 0:
queue.append(key)
# # add into sorted_order each source
while len(queue) > 0:
vertex = queue.pop(0)
sorted_order.append(vertex)
# decrement the in-degree of each child by 1 & if a child’s in-degree becomes ‘0’, add it to the sources Queue.
for child in adjacency_list[vertex]:
in_degree[child] -= 1
if in_degree[child] == 0:
queue.append(child)
return sorted_order
Solution two using sinks (reverse of solution one) → crashes if a cycle is there
-
not recommended as one can be used for many other problems
Topological Sort Algorithm | Graph Theory
Algorithms/topsort.txt at 80a2593fca238d47636b44bb08c2323d8b4e5a9d · williamfiset/Algorithms
An easy way to find a topological ordering with trees is to iteratively pick off the leaf nodes. It's like you're cherry-picking from the bottom, it doesn't matter the order you do it. This procedure continues until no more nodes are left...
- First find an unvisited node, it doesn't matter which.
- From this node do a Depth First Search exploring only reachable unvisited nodes.
- On recursive callbacks add the current node to the topological ordering in reverse order.
import collections def dfs(graph, visited, vertex, sorted_order): if visited[vertex]: return for child in graph[vertex]: dfs(graph, visited, child, sorted_order) visited[vertex] = True sorted_order.append(vertex) def topological_sort(vertices, edge_list): sorted_order = [] # # convert edge list to an adjacency list adjacency_list = collections.defaultdict(list) for edge in edge_list: adjacency_list[edge[0]].append(edge[1]) visited = collections.defaultdict(bool) for edge in edge_list: dfs(adjacency_list, visited, edge[0], sorted_order) sorted_order.reverse() return sorted_order
Course Schedule II
"""
Course Schedule II:
There are a total of numCourses courses you have to take, labeled from 0 to numCourses - 1.
You are given an array prerequisites where prerequisites[i] = [ai, bi] indicates that you must take course bi first if you want to take course ai.
For example, the pair [0, 1], indicates that to take course 0 you have to first take course 1.
Return the ordering of courses you should take to finish all courses.
If there are many valid answers, return any of them.
If it is impossible to finish all courses, return an empty array.
Example 1:
Input: numCourses = 2, prerequisites = [[1,0]]
Output: [0,1]
Explanation: There are a total of 2 courses to take. To take course 1 you should have finished course 0. So the correct course order is [0,1].
Example 2:
Input: numCourses = 4, prerequisites = [[1,0],[2,0],[3,1],[3,2]]
Output: [0,2,1,3]
Explanation: There are a total of 4 courses to take. To take course 3 you should have finished both courses 1 and 2. Both courses 1 and 2 should be taken after you finished course 0.
So one correct course order is [0,1,2,3]. Another correct ordering is [0,2,1,3].
Example 3:
Input: numCourses = 1, prerequisites = []
Output: [0]
https://leetcode.com/problems/course-schedule-ii/
"""
"""
# indegree = count of incoming edges of each vertex/node or how many parents it has (used to determine sources)
# source: Any node that has no incoming edge and has only outgoing edges is called a source (indegree==0)
- top_sort = []
- get the topological sort of the courses
- initialization:
- create an adjacency list from the edge list given
- while doing so, create an indegree record for each vertex/node
- add all the sources into a queue
- while queue:
- get the element at the top of the queue (curr)
- add it to the output
- reduce the indegree for all of its children by one
- if any child has an indegree of one after that, add it to the queue
- if the length of the sorted list == numCourses, it is possible to complete the courses, it is an asyclic graph
"""
import collections
class Solution:
def findOrder(self, numCourses, prerequisites):
top_sort = []
# # create an adjacency list from the edge list given
# while doing so, create an indegree record for each vertex/node
adjacency_list = collections.defaultdict(list)
indegrees = collections.defaultdict(int)
for arr in prerequisites:
child, parent = arr[0], arr[1]
adjacency_list[parent].append(child)
indegrees[child] += 1
# # add all the sources into a queue
queue = []
for vertex in range(numCourses):
if indegrees[vertex] == 0:
queue.append(vertex)
# # build top_sort list
while queue:
vertex = queue.pop(0)
top_sort.append(vertex)
for child in adjacency_list[vertex]:
indegrees[child] -= 1
if indegrees[child] == 0:
queue.append(child)
# if the length of the sorted list == numCourses, it is possible to complete the courses
if len(top_sort) == numCourses:
return top_sort
return []
Course Schedule/Tasks Scheduling
Problem
"""
Course Schedule/Tasks Scheduling:
Course Schedule II is a prerequisite to this.
There are a total of numCourses courses you have to take, labeled from 0 to numCourses - 1.
You are given an array prerequisites where prerequisites[i] = [ai, bi] indicates that you must take course bi first if you want to take course ai.
For example, the pair [0, 1], indicates that to take course 0 you have to first take course 1.
Return true if you can finish all courses. Otherwise, return false.
Example 1:
Input: numCourses = 2, prerequisites = [[1,0]]
Output: true
Explanation: There are a total of 2 courses to take.
To take course 1 you should have finished course 0. So it is possible.
Example 2:
Input: numCourses = 2, prerequisites = [[1,0],[0,1]]
Output: false
Explanation: There are a total of 2 courses to take.
To take course 1 you should have finished course 0, and to take course 0 you should also have finished course 1. So it is impossible.
Example 3:
Input: numCourses = 3, prerequisites=[0, 1], [1, 2]
Output: true
Explanation: To execute task '1', task '0' needs to finish first. Similarly, task '1' needs
to finish before '2' can be scheduled. One possible scheduling of tasks is: [0, 1, 2]
Example 4:
Input: numCourses = 3, prerequisites=[0, 1], [1, 2], [2, 0]
Output: false
Explanation: The tasks have a cyclic dependency, therefore they cannot be scheduled.
Example 5:
Input: numCourses = 6, prerequisites=[2, 5], [0, 5], [0, 4], [1, 4], [3, 2], [1, 3]
Output: true
Explanation: A possible scheduling of tasks is: [0 1 4 3 2 5]
https://leetcode.com/problems/course-schedule/
"""
Solution
Topological sort
"""
SOLUTION:
https://leetcode.com/discuss/general-discussion/1078072/introduction-to-topological-sort
# indegree = count of incoming edges of each vertex/node or how many parents it has (used to determine sources)
# source: Any node that has no incoming edge and has only outgoing edges is called a source (indegree==0)
- top_sort = []
- get the topological sort of the courses
- initialization:
- create an adjacency list from the edge list given
- while doing so, create an indegree record for each vertex/node
- add all the sources into a queue
- while queue:
- get the element at the top of the queue (curr)
- add it to the output
- reduce the indegree for all of its children by one
- if any child has an indegree of one after that, add it to the queue
- return len(top_sort) == len(adjacency_list)
- if len(top_sort) == len(adjacency_list), it means the graph is acyclic
"""
import collections
class Solution:
def topSort(self, edge_list):
top_sort = []
# # create an adjacency list from the edge list given
# while doing so, create an indegree record for each vertex/node
adjacency_list = collections.defaultdict(list)
indegrees = collections.defaultdict(int)
for arr in edge_list:
child, parent = arr[0], arr[1]
adjacency_list[parent].append(child)
indegrees[child] += 1
# # add all the sources into a queue
queue = []
for vertex in adjacency_list:
if indegrees[vertex] == 0:
queue.append(vertex)
# # build top_sort list
while queue:
vertex = queue.pop(0)
top_sort.append(vertex)
for child in adjacency_list[vertex]:
indegrees[child] -= 1
if indegrees[child] == 0:
queue.append(child)
# if len(top_sort) == len(adjacency_list), it means the graph is acyclic
return len(top_sort) == len(adjacency_list)
def canFinish(self, numCourses, prerequisites):
return self.topSort(prerequisites)
DFS
class SolutionDFS:
def dfs(self, adjacency_list, visited_cache, vertex, curr_visiting):
if vertex in visited_cache:
return True
if vertex in curr_visiting:
return False
curr_visiting.add(vertex)
for child in adjacency_list[vertex]:
if not self.dfs(adjacency_list, visited_cache, child, curr_visiting):
return False
curr_visiting.remove(vertex)
visited_cache.add(vertex)
return True
def canFinish(self, numCourses, prerequisites):
# # create an adjacency list from the edge list given
adjacency_list = collections.defaultdict(list)
for arr in prerequisites:
child, parent = arr[0], arr[1]
adjacency_list[parent].append(child)
visited_cache = set()
for vertex in list(adjacency_list.keys()):
if not self.dfs(adjacency_list, visited_cache, vertex, set()):
return False
return True
Alien Dictionary
Problem
Solution
"""
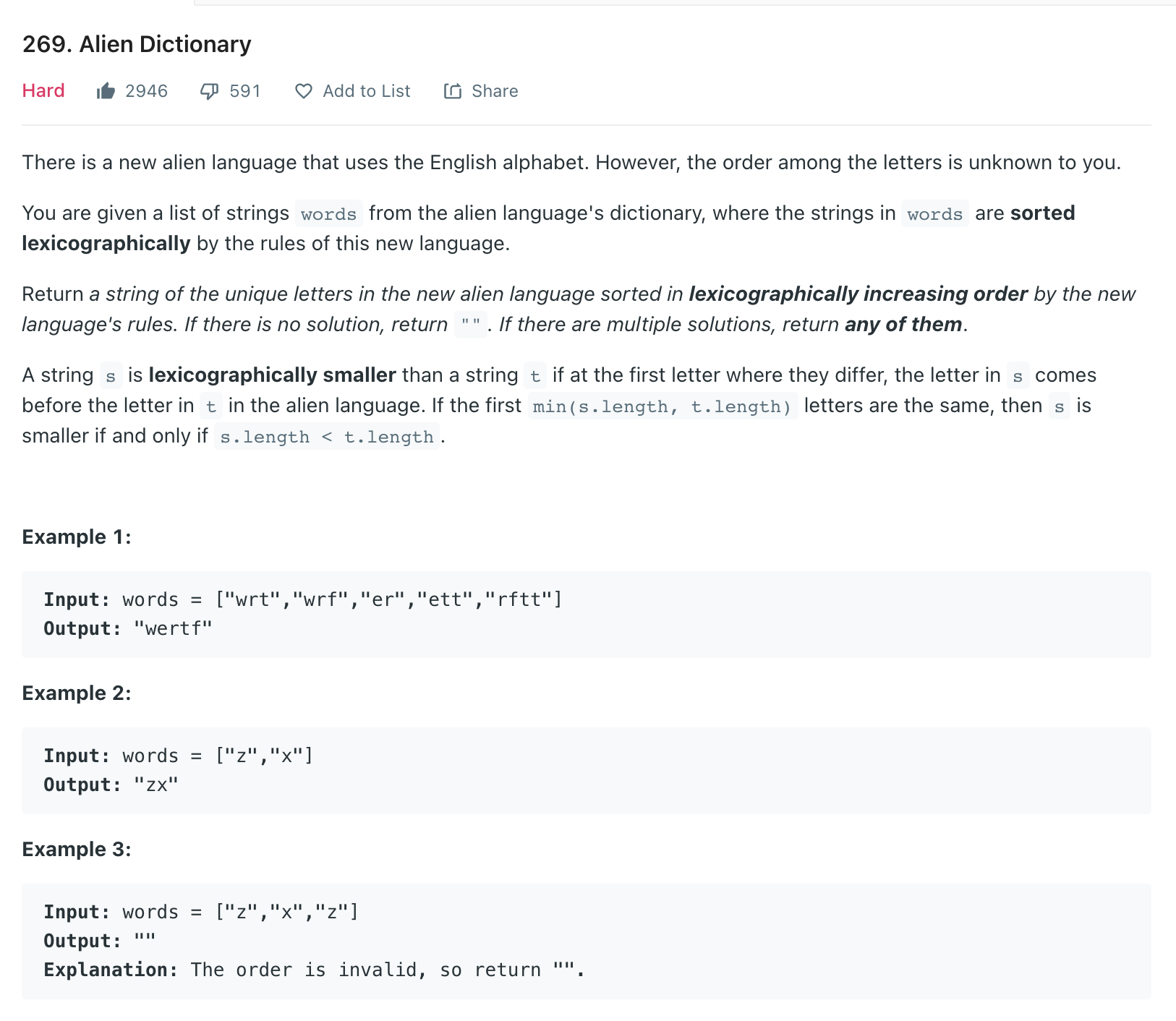
269. Alien Dictionary:
There is a new alien language that uses the English alphabet.
However, the order among the letters is unknown to you.
You are given a list of strings words from the alien language's dictionary, where the strings in words are sorted lexicographically by the rules of this new language.
Return a string of the unique letters in the new alien language sorted in lexicographically increasing order by the new language's rules.
If there is no solution, return "". If there are multiple solutions, return any of them.
A string s is lexicographically smaller than a string t if at the first letter where they differ,
the letter in s comes before the letter in t in the alien language.
If the first min(s.length, t.length) letters are the same, then s is smaller if and only if s.length < t.length.
Test cases:
["wrt", "wrf", "er", "ett", "rftt"]
["z", "x"]
["z", "x", "z"]
["ab", "adc"]
["z", "z"]
["abc", "ab"]
["z", "x", "a", "zb", "zx"]
["w", "wnlb"]
["wnlb"]
["aba"]
Results:
"wertf"
"zx"
""
"abcd"
"z"
""
""
"wnlb"
"wnlb"
"ab"
['f', 't', 'r', 'e', 'w']
['x', 'z']
['x', 'z']
['a', 'd', 'b', 'c']
['z']
['a', 'x', 'z', 'b']
['w', 'n', 'l', 'b']
['w', 'n', 'l', 'b']
['a', 'b']
https://leetcode.com/problems/alien-dictionary/
"""
import collections
"""
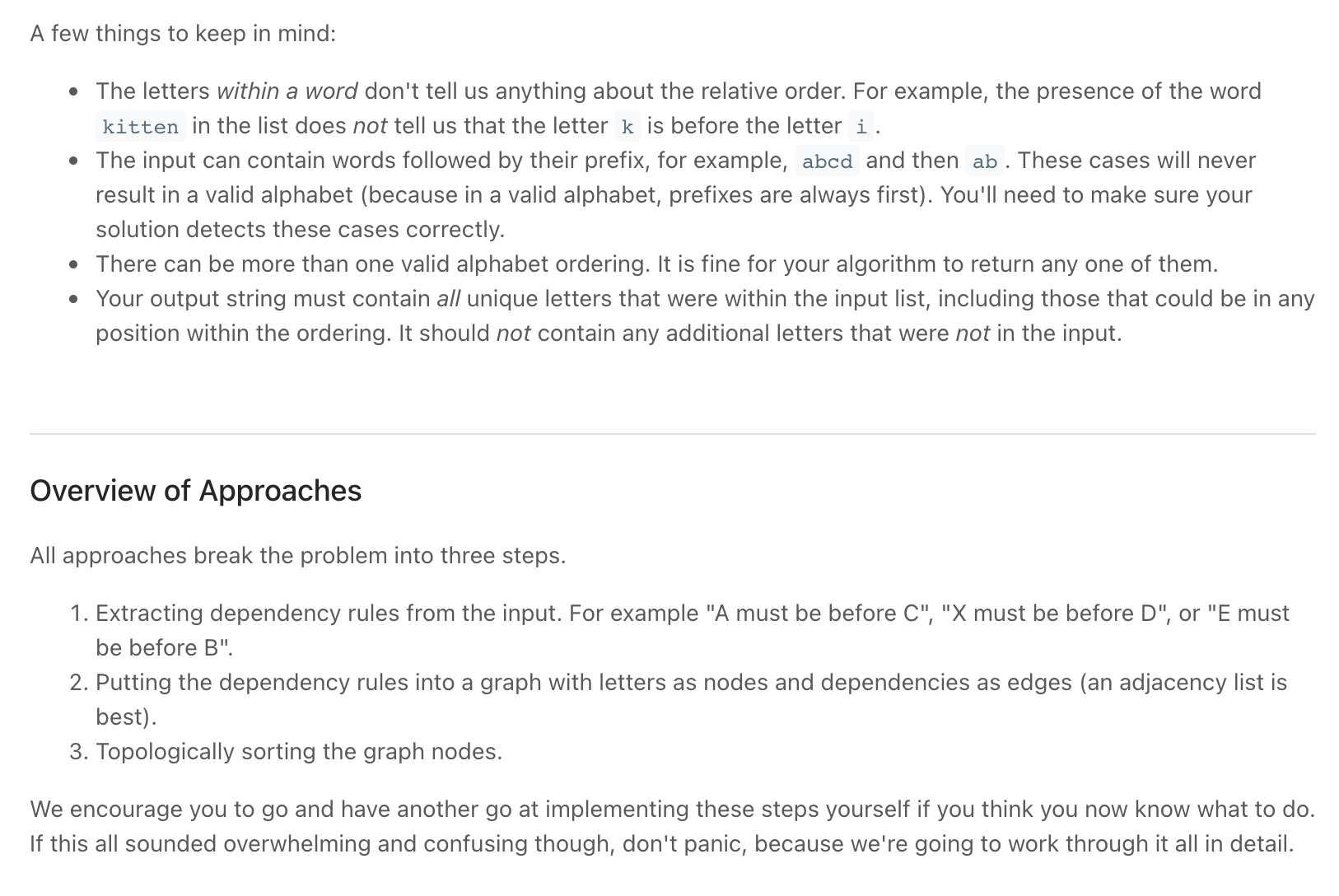
A few things to keep in mind:
- The letters within a word don't tell us anything about the relative order.
For example, the presence of the word kitten in the list does not tell us that the letter k is before the letter i.
- The input can contain words followed by their prefix, for example, abcd and then ab.
These cases will never result in a valid alphabet (because in a valid alphabet, prefixes are always first).
You'll need to make sure your solution detects these cases correctly.
- There can be more than one valid alphabet ordering. It is fine for your algorithm to return any one of them.
- Your output string must contain all unique letters that were within the input list, including those that could be in any position within the ordering.
It should not contain any additional letters that were not in the input.
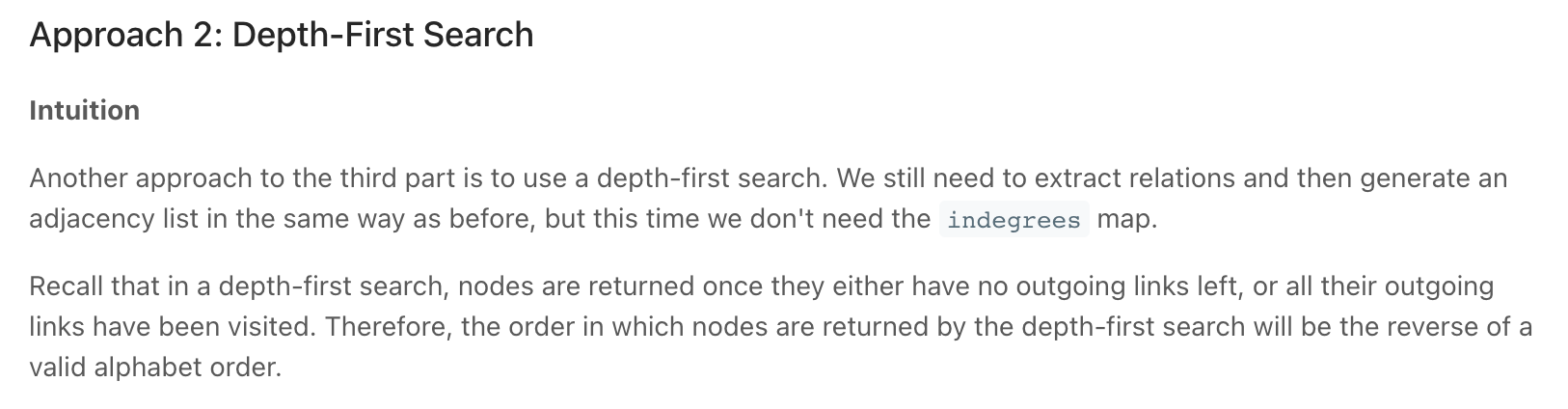
All approaches break the problem into three steps:
- Extracting dependency rules from the input.
For example "A must be before C", "X must be before D", or "E must be before B".
- Putting the dependency rules into a graph with letters as nodes and dependencies as edges (an adjacency list is best).
- Topologically sorting the graph nodes
"""
class Solution:
def alienOrder(self, words):
graph = collections.defaultdict(set) # Adjacency list
# build graph
for idx in range(len(words)):
self.add_word_letters(graph, words[idx])
# if not at end
if idx < len(words)-1:
self.add_word_letters(graph, words[idx+1])
if not self.compare_two_words(graph, words[idx], words[idx+1]):
return ""
return "".join(self.top_sort(graph))
def top_sort(self, graph):
"""
Topological sort
Remember that:
If the number of nodes in the the top sort result is
less than the number of nodes in the graph, we have a cycle.
Which means that we cannot have a valid ordering. Return []
"""
res = []
queue = []
indegrees = collections.defaultdict(int)
# calculate indegrees
for node in graph:
for child in graph[node]:
indegrees[child] += 1
# get sources
for node in graph:
if indegrees[node] == 0:
queue.append(node)
# sort
while queue:
node = queue.pop(0)
res.append(node) # Add to result
for child in graph[node]:
indegrees[child] -= 1
if indegrees[child] == 0: # Has become a source
queue.append(child)
# check if has_cycle
if len(res) != len(graph):
return []
return res
def compare_two_words(self, graph, one, two):
"""
Where two words are adjacent, we need to look for the first difference between them.
That difference tells us the relative order between two letters.
Handle edge cases like:
ab, a => error(a should be before ab)
"""
idx = 0
while idx < len(one) and idx < len(two) and one[idx] == two[idx]:
idx += 1
if idx < len(one) and idx < len(two):
graph[one[idx]].add(two[idx])
elif idx < len(one):
return False # Invalid
return True
def add_word_letters(self, graph, word):
for idx in range(len(word)):
graph[word[idx]] # Add letter to graph.
"""
DFS / reveese of Topological sort
"""
class SolutionDFS:
def alienOrder(self, words):
graph = collections.defaultdict(set) # Adjacency list
# build graph
for idx in range(len(words)):
self.add_word_letters(graph, words[idx])
# if not at end
if idx < len(words)-1:
self.add_word_letters(graph, words[idx+1])
if not self.compare_two_words(graph, words[idx], words[idx+1]):
return ""
if self.has_cycle(graph):
return ""
return "".join(reversed(self.dfs(graph)))
def compare_two_words(self, graph, one, two):
"""
Where two words are adjacent, we need to look for the first difference between them.
That difference tells us the relative order between two letters.
Handle edge cases like:
ab, a => error(a should be before ab)
"""
idx = 0
while idx < len(one) and idx < len(two) and one[idx] == two[idx]:
idx += 1
if idx < len(one) and idx < len(two):
graph[one[idx]].add(two[idx])
elif idx < len(one):
return False # Invalid
return True
def add_word_letters(self, graph, word):
for idx in range(len(word)):
graph[word[idx]] # Add letter to graph.
def dfs(self, graph):
"""
DFS => reveese of Topological sort
Remember that:
If the number of nodes in the the top sort result is
less than the number of nodes in the graph, we have a cycle.
Which means that we cannot have a valid ordering. Return []
"""
res = []
visited = set()
for node in graph:
self.dfs_helper(graph, visited, node, res)
# check if has_cycle
if len(res) != len(graph):
return []
return res
def dfs_helper(self, graph, visited, curr, res):
if curr in visited:
return
visited.add(curr)
for node in graph[curr]:
self.dfs_helper(graph, visited, node, res)
res.append(curr)
def has_cycle(self, graph):
checked = {}
for node in graph:
if self._has_cycle_helper(graph, checked, set(), node):
return True
return False
def _has_cycle_helper(self, graph, checked, visiting, node):
if node in visiting:
return True
if node in checked:
return checked[node]
visiting.add(node)
result = False
for child in graph[node]:
result = result or self._has_cycle_helper(
graph, checked, visiting, child)
# remember to add this!
# because it is a directed graph
# we might reach the node several times but it doesn't mean it is is a cycle
# eg: https://www.notion.so/paulonteri/Searching-733ff84c808c4c9cb5c40787b2df7b98#c7458268f05e4e2db359f9990366a411
visiting.discard(node)
checked[node] = result
return checked[node]
Find the original version of this page (with additional content) on Notion here.
Created: December 13, 2021 16:05:48