0/1 Knapsack (Dynamic Programming)
0/1 Knapsack problem
Dynamic Programming - Knapsack Problem
Coding Patterns: 0/1 Knapsack (DP)
Introduction
Given the weights and profits of ‘N’ items, we are asked to put these items in a knapsack that has a capacity ‘C’. The goal is to get the maximum profit from the items in the knapsack. Each item can only be selected once, as we don’t have multiple quantities of any item.
Let’s take Merry’s example, who wants to carry some fruits in the knapsack to get maximum profit. Here are the weights and profits of the fruits: Items: { Apple, Orange, Banana, Melon } Weights: { 2, 3, 1, 4 } Profits: { 4, 5, 3, 7 } Knapsack capacity: 5 Let’s try to put different combinations of fruits in the knapsack, such that their total weight is not more than 5: Apple + Orange (total weight 5) => 9 profit Apple + Banana (total weight 3) => 7 profit Orange + Banana (total weight 4) => 8 profit Banana + Melon (total weight 5) => 10 profit This shows that Banana + Melon is the best combination, as it gives us the maximum profit and the total weight does not exceed the capacity.
Problem Statement
Given two integer arrays to represent weights and profits of ‘N’ items, we need to find a subset of these items which will give us maximum profit such that their cumulative weight is not more than a given number ‘C’. Write a function that returns the maximum profit. Each item can only be selected once, which means either we put an item in the knapsack or skip it.
"""
0/1 Knapsack:
Given two integer arrays to represent weights and profits of ‘N’ items,
we need to find a subset of these items which will give us maximum profit
such that their cumulative weight is not more than a given number ‘C’.
Write a function that returns the maximum profit.
Each item can only be selected once, which means either we put an item in the knapsack or skip it.
https://www.educative.io/courses/grokking-dynamic-programming-patterns-for-coding-interviews/RM1BDv71V60
"""
Brute force (complete search)
Basic bruteforce
def solve_knapsack_helper(profits, weights, capacity, total_profits):
if len(profits) == 0 or capacity < 0:
return -1
highest = -1
for idx, weight in enumerate(weights):
rem_profits = profits[:idx] + profits[idx+1:]
rem_weights = weights[:idx] + weights[idx+1:]
highest = max(
highest,
solve_knapsack_helper(rem_profits, rem_weights, capacity-weight, total_profits+profits[idx])
)
return max(total_profits, highest)
def solve_knapsack(profits, weights, capacity):
return solve_knapsack_helper(profits, weights, capacity, 0)
![All green boxes have a total weight that is less than or equal to the capacity (7), and all the red ones have a weight that is more than 7. The best solution we have is with items [B, D] having a total profit of 22 and a total weight of 7.](0%201%20Knapsack%20%28Dynamic%20Programming%29%20b70111b897a547b6afdc2fc5cec2fbb6/Screenshot_2021-07-25_at_10.22.23.png)
All green boxes have a total weight that is less than or equal to the capacity (7), and all the red ones have a weight that is more than 7. The best solution we have is with items [B, D] having a total profit of 22 and a total weight of 7.
Improved Bruteforce
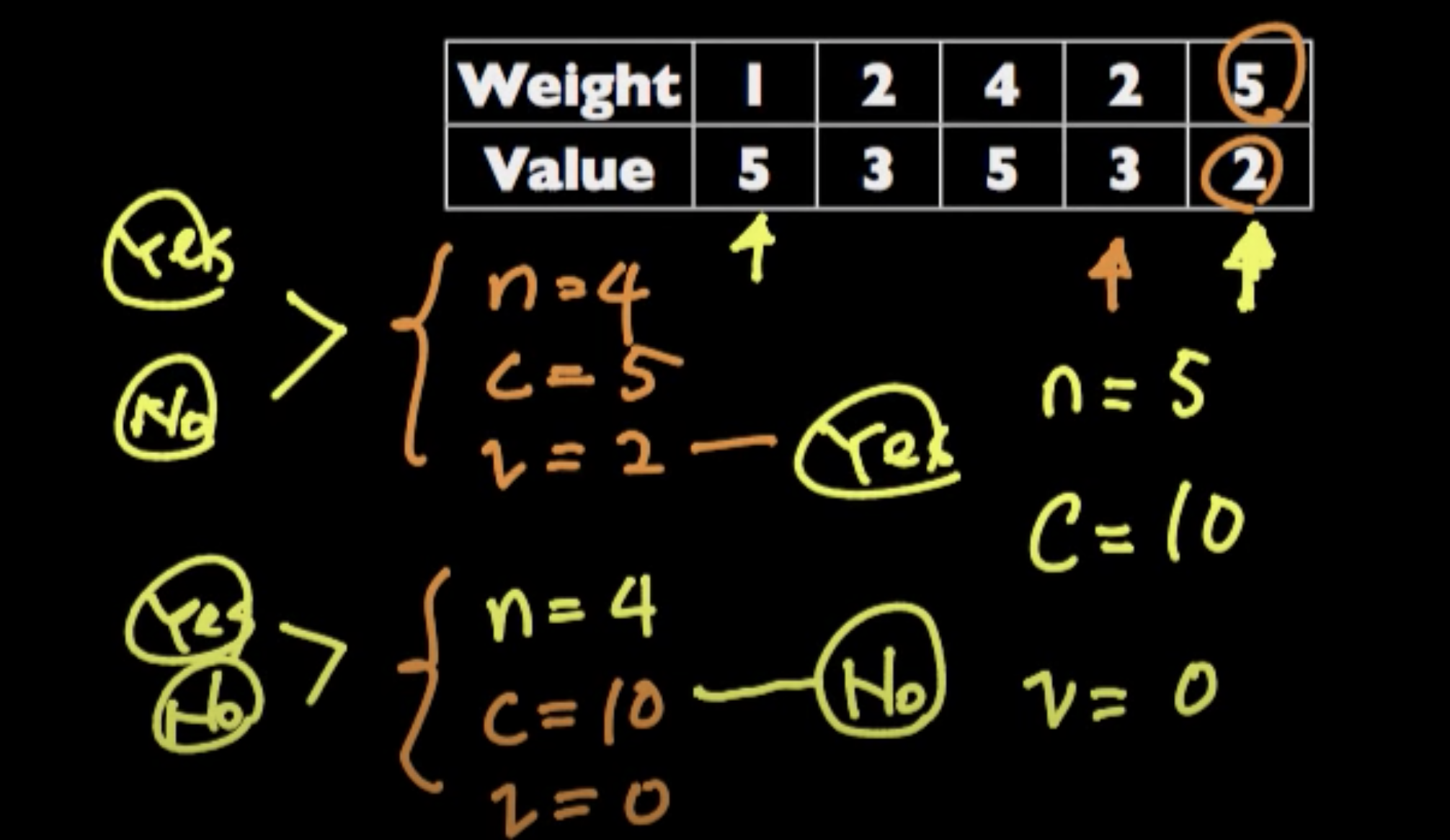
(in reverse) When given problems (involving choice) with two arrays, where their indices represent an entity, you can recurse by iterating through each index deciding to include it or not
"""
Brute force:
A basic brute-force solution could be to try all combinations of the given items,
allowing us to choose the one with maximum profit and a weight that doesn’t exceed ‘C.’
The algorithm’s time complexity is exponential O(2^n)
The space complexity is O(n). This space will be used to store the recursion stack.
Since our recursive algorithm works in a depth-first fashion,
which means, we can’t have more than ‘n’ recursive calls on the call stack at any time.
"""
# "iterate" through all the elements & at each element,
# see which will give max - choosing or excluding the element
# has some backtracking
def knapsack_recursive(profits, weights, capacity, idx, curr_profit):
if capacity < 0: # we made an invalid choice & went beyond the capacity
return -1
if idx == len(weights): # no more to choose
return curr_profit
# can only be selected once
if_chosen = knapsack_recursive(profits, weights, capacity - weights[idx], idx + 1, curr_profit + profits[idx])
if_excluded = knapsack_recursive(profits, weights, capacity, idx + 1, curr_profit)
return max(curr_profit, if_chosen, if_excluded)
# return max(if_chosen, if_excluded) # -> this also works
def solve_knapsack(profits, weights, capacity):
return knapsack_recursive(profits, weights, capacity, 0, 0)
# ----------------------------
# avoids backtracking
def knapsack_recursive_2(profits, weights, capacity, idx):
if capacity <= 0 or idx >= len(profits):
return 0
if_chosen = 0
if weights[idx] <= capacity: # avoid backtracking
if_chosen = profits[idx] + knapsack_recursive_2(profits, weights, capacity - weights[idx], idx + 1)
if_excluded = knapsack_recursive_2(profits, weights, capacity, idx + 1)
return max(if_chosen, if_excluded)
def solve_knapsack_2(profits, weights, capacity):
return knapsack_recursive_2(profits, weights, capacity, 0)
We have overlapping sub-problems
Let’s visually draw the recursive calls to see if there are any overlapping sub-problems. As we can see, in each recursive call, profits and weights arrays remain constant, and only capacity and currentIndex change. For simplicity, let’s denote capacity with ‘c’ and idx/currentIndex with ‘i’:
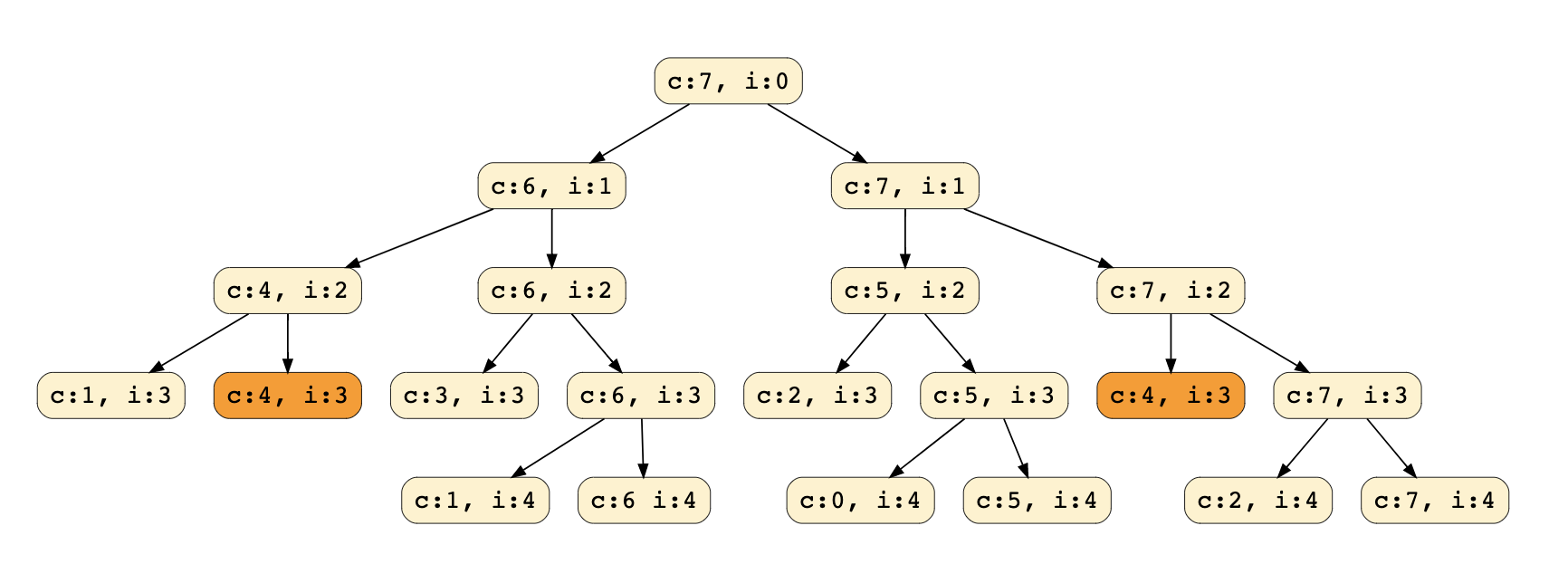
Denoted capacity with c and idx/currentIndex with i
We can clearly see that ‘c:4, i:3’ has been called twice; hence we have an overlapping sub-problems pattern. As we discussed above, overlapping sub-problems can be solved through Memoization. Let's look at how we can do that next.
Top-down Dynamic Programming with Memoization
We can use memoization to overcome the overlapping sub-problems. To reiterate, memoization is when we store the results of all the previously solved sub-problems and return the results from memory if we encounter a problem that has already been solved.
Since we have two changing values (capacity and idx) in our recursive function knapsack_recursive(), we can use a two-dimensional array to store the results of all the solved sub-problems. As mentioned above, we need to store results for every sub-array (i.e., for every possible index ‘i’) and for every possible capacity ‘c’.
"""
Top-down Dynamic Programming with Memoization:
We can use memoization to overcome the overlapping sub-problems from the brute force solution.
Since we have two changing values (`capacity` and `idx`) in our recursive function `knapsack_recursive()`,
we can use a two-dimensional array to store the results of all the solved sub-problems.
As mentioned above, we need to store results for every sub-array (i.e., for every possible index ‘i’) and for every possible capacity ‘c’.
"""
# -----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
def knapsack_recursive(profits, weights, cache, capacity, idx, curr_profit):
if capacity < 0:
return -1
if idx == len(weights):
return curr_profit
# if we have already solved a similar problem, return the result from memory/cache
if cache[idx][capacity]:
return cache[idx][capacity]
if_chosen = knapsack_recursive(profits, weights, cache, capacity - weights[idx], idx + 1, curr_profit + profits[idx])
if_excluded = knapsack_recursive(profits, weights, cache, capacity, idx + 1, curr_profit)
# store result in cache
cache[idx][capacity] = max(if_chosen, if_excluded)
return cache[idx][capacity]
def solve_knapsack(profits, weights, capacity):
cache = [[False] * (capacity+1)] * len(weights) # use a two-dimensional array to store the results of all the solved sub-problems
return knapsack_recursive(profits, weights, cache, capacity, 0, 0)
Time & space complexity
Since our memoization array cache[profits.length/weights.length][capacity+1] stores the results for all subproblems, we can conclude that we will not have more than N*C subproblems (where ‘N’ is the number of items and ‘C’ is the knapsack capacity).
This means that our time complexity will be O(N*C).
The above algorithm will use O(N*C) space for the memoization array. Other than that, we will use O(N) space for the recursion call-stack. So the total space complexity will be O(N∗C + N), which is asymptotically equivalent to O(N*C)
Bottom-up Dynamic Programming
0/1 Knapsack Problem Dynamic Programming
0/1 Knapsack problem | Dynamic Programming
Let’s try to populate our dp[][] array from the above solution, working in a bottom-up fashion. Essentially, we want to find the maximum profit for every sub-array and for every possible capacity. This means, dp[i][c] will represent the maximum knapsack profit for capacity c calculated from the first i items.
How to work this out
Formulae discussed below

So, for each item at index i \((0 <= i < items.length)\) and capacity c \((0 <= c <= capacity)\), we have two options:
- Exclude the item at index
i. In this case, we will take whatever profit we get from the sub-array excluding this item =>dp[i-1][c](the top of curr i in the chart) - Include the item at index
iif its weight is not more than the capacity. In this case, we include its profit plus whatever profit we get from the remaining capacity and from remaining items =>profits[i] + dp[i-1][c-weights[i]]
Finally, our optimal solution will be maximum of the above two values:
dp[i][c] = max( dp[i-1][c], # **exclude item:** take prev/top profit
profits[i] + dp[i-1][c-weights[i]] # **include item:** include its profit plus whatever profit we get from the remaining capacity
)
# dp[i][c] = max(exclude curr, include curr + fill the remaining capacity)
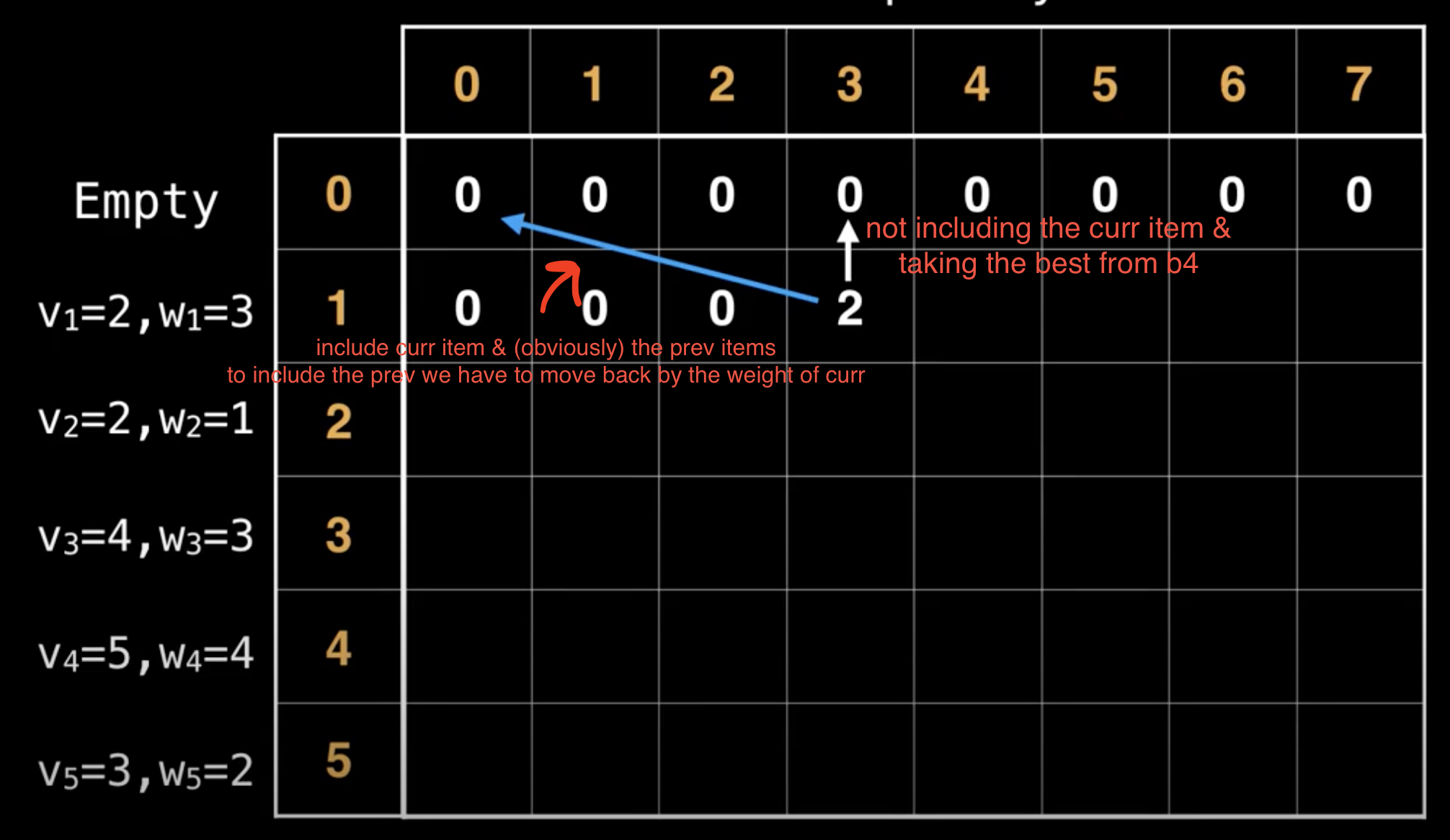
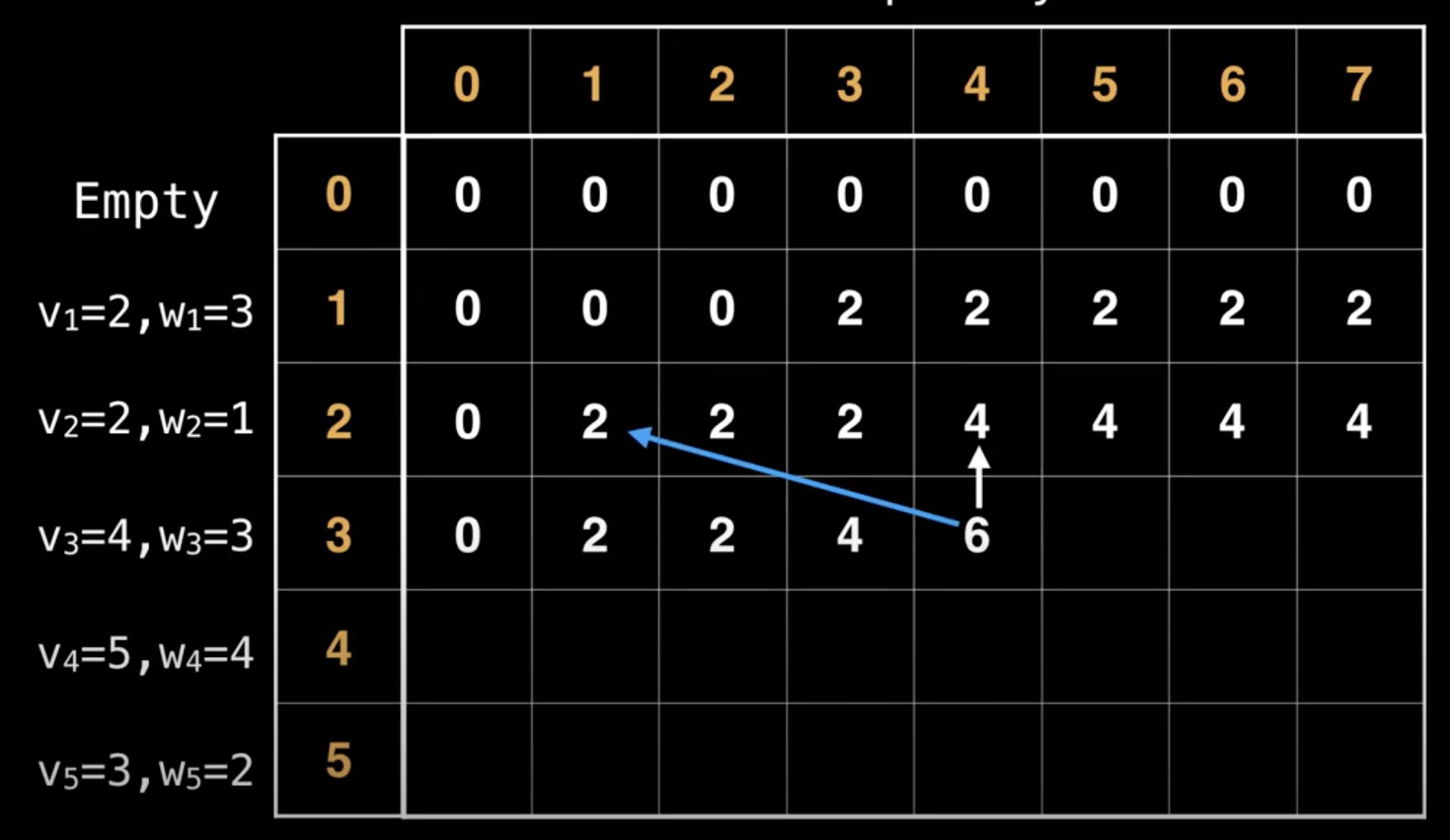
Decide whether not to include curr item (v=4,w=3) and have a value/profit of 4 (the prev best val) or include it and have a value/profit of 6 → 2+4, include its profit plus whatever profit we get from the remaining capacity (move w steps back in the top row(2) + curr val(4))
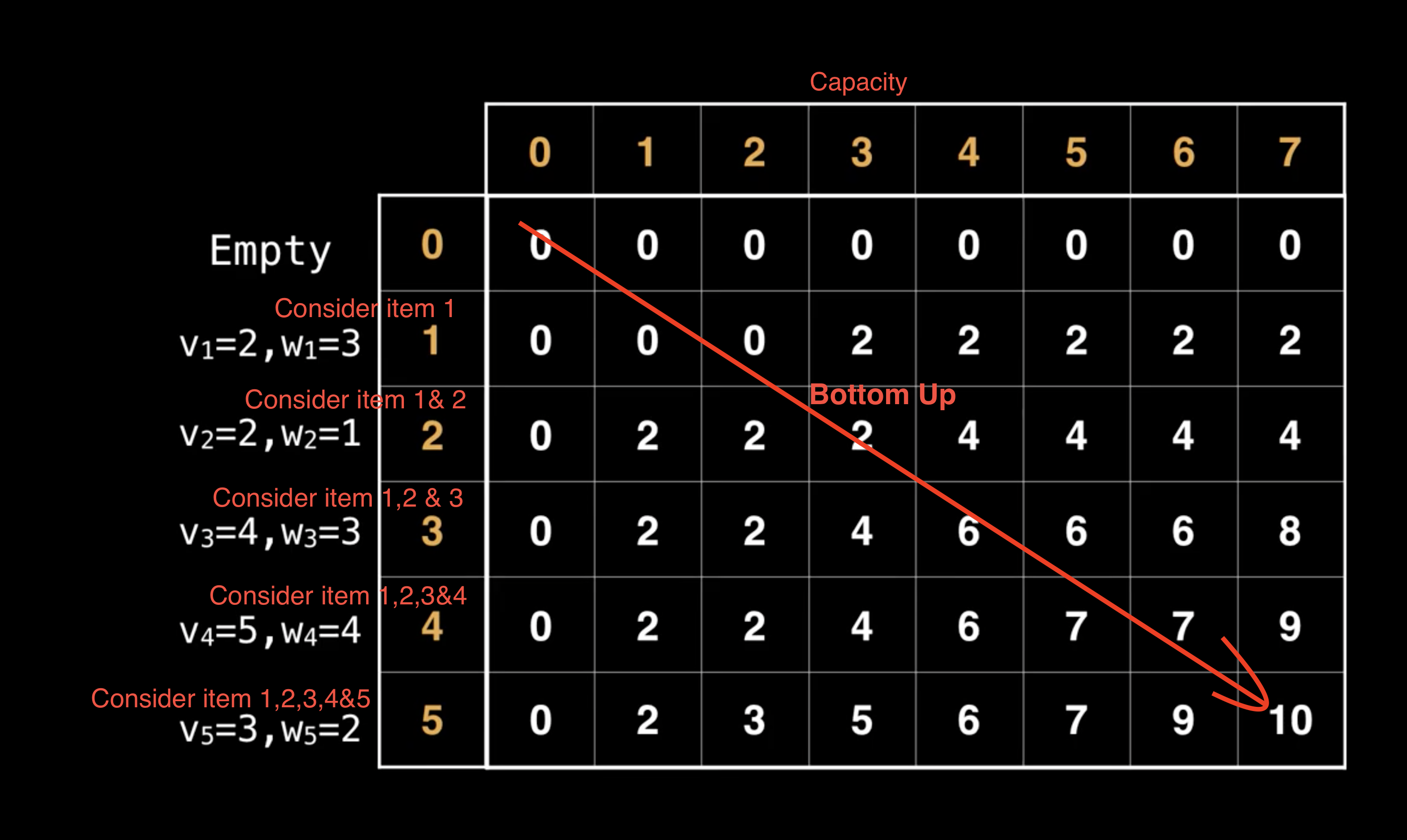
Start at 0 to the max
Code
def solve_knapsack(profits, weights, capacity):
table = [[0 for _ in range(capacity+1)] for _ in range(len(profits))]
for item in range(len(profits)):
for cap in range(capacity + 1):
excluded = 0
included = 0
prev_items = item - 1
# # exclude item -> take prev largest
if prev_items >= 0:
excluded = table[prev_items][cap]
# # include item
if weights[item] <= cap:
included = profits[item]
# fill remaining capacity -> add prev items that can fit in the remaining capacity
rem_cap = cap - weights[item]
if rem_cap >= 0 and prev_items >= 0:
included += table[prev_items][rem_cap]
# # record max
table[item][cap] = max(included, excluded)
return table[-1][-1]
How to find the selected items?
0/1 Knapsack problem | Dynamic Programming
Equal Subset Sum Partition
Introduction
"""
Given a set of positive numbers, find if we can partition it into two subsets such that the sum of elements in both the subsets is equal.
Example 1
Input: {1, 2, 3, 4}
Output: True
Explanation: The given set can be partitioned into two subsets with equal sum: {1, 4} & {2, 3}
Example 2
Input: {1, 1, 3, 4, 7}
Output: True
Explanation: The given set can be partitioned into two subsets with equal sum: {1, 3, 4} & {1, 7}
Example 3
Input: {2, 3, 4, 6}
Output: False
Explanation: The given set cannot be partitioned into two subsets with equal sum.
https://www.educative.io/courses/grokking-dynamic-programming-patterns-for-coding-interviews/3jEPRo5PDvx
"""
Given a set of positive numbers, find if we can partition it into two subsets such that the sum of elements in both the subsets is equal.
Example 1
Input: {1, 2, 3, 4}
Output: True
# Explanation: The given set can be partitioned into two subsets with equal sum: {1, 4} & {2, 3}
Example 2
Input: {1, 1, 3, 4, 7}
Output: True
# Explanation: The given set can be partitioned into two subsets with equal sum: {1, 3, 4} & {1, 7}
Example 3
Input: {2, 3, 4, 6}
Output: False
# Explanation: The given set cannot be partitioned into two subsets with equal sum.
Solution
"""
We know that if we can partition it into equal subsets that each set’s sum will have to be sum/2.
If the sum is an odd number we cannot possibly have two equal sets.
This changes the problem into finding if a subset of the input array has a sum of sum/2.
We know that if we find a subset that equals sum/2,
the rest of the numbers must equal sum/2 so we’re good since they will both be equal to sum/2.
We can solve this using dynamic programming similar to the knapsack problem.
We basically need to find two groups of numbers that will each be equal to sum(input_array) / 2
Finding one such group (with its sum = sum(input_array)/2) will imply that there will be another with a similar sum
We can use the 0/1 knapsack pattern
"""
Brute force
Code
# ----------------------------------------------------------------------------------------------------------------------------------------------------------------
"""
Brute Force 1:
While using recursion, `iterate` through the input array,
choosing whether to include each number in one of two arrays: "one" & "two" stop once the sum of elements in each of the arrays are equal to sum(input_array) / 2
"""
def can_partition_helper_bf1(num, total, res, idx, one, two):
# base cases
if sum(one) == total/2 and sum(two) == total/2:
res.append([one, two])
return
if sum(one) > total/2 or sum(two) > total/2:
return
if idx >= len(num):
return
can_partition_helper_bf1(num, total, res, idx+1, one+[num[idx]], two) # one
can_partition_helper_bf1(num, total, res, idx+1, one, two+[num[idx]]) # two
def can_partition_bf1(num):
res = []
total = sum(num)
can_partition_helper_bf1(num, total, res, 0, [], [])
return len(res) > 0
# ----------------------------------------------------------------------------------------------------------------------------------------------------------------
"""
Brute Force 2:
While using recursion, `iterate` through the input array,
choosing whether to include each number in one of two sums: "one" & "two" stop once each of the sums are equal to sum(input_array) / 2
Basically Brute Force 1 without remembering the numbers
"""
def can_partition_helper_bf2(num, total, idx, one, two):
# base cases
if one == total/2 and two == total/2:
return True
if one > total/2 or two > total/2:
return False
if idx >= len(num):
return False
in_one = can_partition_helper_bf2(num, total, idx+1, one+num[idx], two)
in_two = can_partition_helper_bf2(num, total, idx+1, one, two+num[idx])
return in_one or in_two
def can_partition_bf2(num):
total = sum(num)
return can_partition_helper_bf2(num, total, 0, 0, 0)
# ----------------------------------------------------------------------------------------------------------------------------------------------------------------
"""
Brute Force 3:
We basically need to find one group of numbers that will be equal to sum(input_array) / 2
Finding one such group (with its sum = sum(input_array)/2) will imply that there will be another with a similar sum
While using recursion, `iterate` through the input array,
choosing whether to include each number in the sum stop once the sum is equal to sum(input_array) / 2
Basically Brute Force 2 but dealing with one sum
"""
def can_partition_helper_bf3_0(num, total, idx, one):
# base cases
if one == total/2:
return True
if one > total/2:
return False
if idx >= len(num):
return False
included = can_partition_helper_bf3_0(num, total, idx+1, one+num[idx])
excluded = can_partition_helper_bf3_0(num, total, idx+1, one)
return included or excluded
# O(2^n) time | O(n) space
def can_partition_bf3_0(num):
total = sum(num)
return can_partition_helper_bf3_0(num, total, 0, 0)
# -----------------------------------
def can_partition_helper_bf3(num, total, idx):
# base cases
if total == 0:
return True
if total < 0:
return False
if idx >= len(num):
return False
included = can_partition_helper_bf3(num, total-num[idx], idx+1)
excluded = can_partition_helper_bf3(num, total, idx+1)
return included or excluded
# O(2^n) time | O(n) space
def can_partition_bf3(num):
total = sum(num)
return can_partition_helper_bf3(num, total/2, 0)
Time complexity
The time complexity for Brute Force 3 is exponential O(2^n), where ‘n’ represents the total number. The space complexity is O(n), this memory will be used to store the recursion stack.
Top-down Dynamic Programming with Memoization
We can use memoization to overcome the overlapping sub-problems. Since we need to store the results for every subset and for every possible sum, therefore we will be using a two-dimensional array to store the results of the solved sub-problems. The first dimension of the array will represent different subsets and the second dimension will represent different ‘sums’ that we can calculate from each subset. These two dimensions of the array can also be inferred from the two changing values (total and idx) in our recursive function
Code
"""
Top-down Dynamic Programming with Memoization:
We can use memoization to overcome the overlapping sub-problems.
Since we need to store the results for every subset and for every possible sum,
therefore we will be using a two-dimensional array to store the results of the solved sub-problems.
The first dimension of the array will represent different subsets and the second dimension will represent different ‘sums’ that we can calculate from each subset.
These two dimensions of the array can also be inferred from the two changing values (total and idx) in our recursive function.
"""
def can_partition_helper_memo(num, cache, total, idx):
if total == 0:
return True
if total < 0 or idx >= len(num):
return False
if cache[idx][total] == True or cache[idx][total] == False:
return cache[idx][total]
included = can_partition_helper_memo(num, cache, total-num[idx], idx+1)
excluded = can_partition_helper_memo(num, cache, total, idx+1)
cache[idx][total] = included or excluded
return cache[idx][total]
def can_partition_memo(num):
half_total = int(sum(num)/2) # convert to int for use in range
if half_total != sum(num)/2: # ensure it wasn't a decimal number
# if its a an odd number, we can't have two subsets with equal sum
return False
cache = [[-1 for _ in range(half_total+1)] for _ in range(len(num))]
return can_partition_helper_memo(num, cache, half_total, 0)
Time complexity
The above algorithm has a time and space complexity of O(N*S), where ‘N’ represents total numbers and ‘S’ is the total sum of all the numbers.
Bottom-up Dynamic Programming
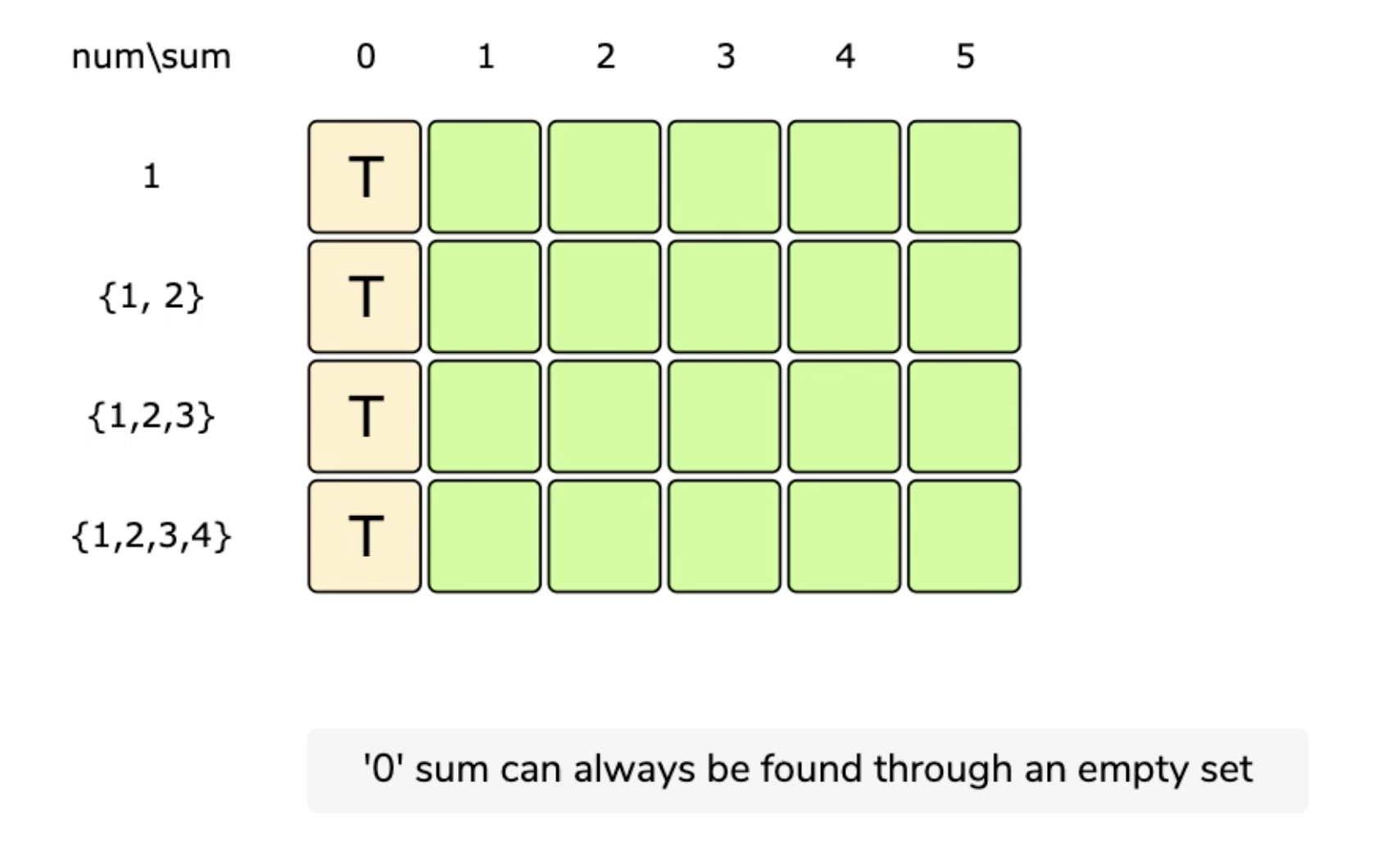
dp[n][total] means whether the specific sum 'total' can be gotten from the first 'n' numbers.
If we can find such numbers from 0-'n' whose sum is total, dp[n][total] is true, otherwise, it is false.
dp[0][0] is true since with 0 elements a subset-sum of 0 is possible (both empty sets).
dp[n][total] is true if dp[n-1][total] is true (meaning that we skipped this element, and took the sum of the previous result) or dp[n-1][total- element’s value(num[n])] assuming this isn’t out of range (meaning that we added this value to our subset-sum so we look at the sum — the current element’s value).
This means dp[n][total] will be ‘true’ if we can make sum ‘total’ from the first ‘n’ numbers.
For each n and sum, we have two options:
-
Exclude the n. In this case, we will see if we can get the total from the subset excluding this n:
dp[n-1][total] -
Include the n if its value is not more than ‘total’. In this case, we will see if we can find a subset to get the remaining sum:
dp[n-1][total-num[n]]
Code
"""
dp[n][total] means whether the specific sum 'total' can be gotten from the first 'n' numbers.
If we can find such numbers from 0-'n' whose sum is total, dp[n][total] is true, otherwise it is false.
dp[0][0] is true since with 0 elements a subset-sum of 0 is possible (both empty sets).
dp[n][total] is true if dp[n-1][total] is true (meaning that we skipped this element, and took the sum of the previous result)
or dp[n-1][total- element’s value(num[n])] assuming this isn’t out of range (meaning that we added this value to our subset-sum so we look at the sum — the current element’s value).
This means, dp[n][total] will be ‘true’ if we can make sum ‘total’ from the first ‘n’ numbers.
For each n and sum, we have two options:
1. Exclude the n. In this case, we will see if we can get total from the subset excluding this n: dp[n-1][total]
2. Include the n if its value is not more than ‘total’.
In this case, we will see if we can find a subset to get the remaining sum: dp[n-1][total-num[n]]
"""
def can_partition_bu(num):
half_total = int(sum(num)/2) # convert to int for use in range
if half_total != sum(num)/2: # ensure it wasn't a decimal number
# if its a an odd number, we can't have two subsets with equal sum
return False
dp = [[False for _ in range(half_total+1)] for _ in range(len(num))] # type: ignore
for n in range(len(num)):
for total in range(half_total+1):
if total == 0: # '0' sum can always be found through an empty set
dp[n][total] = True
continue
included = False
excluded = False
# # exclude
if n-1 >= 0:
excluded = dp[n-1][total]
# # include
if n <= total:
rem_total = total - num[n]
included = rem_total == 0 # fills the whole total
if n-1 >= 0:
# prev n can fill the remaining total
included = included or dp[n-1][rem_total]
dp[n][total] = included or excluded
return dp[-1][-1]
Time complexity
The above algorithm has a time and space complexity of O(N*S), where ‘N’ represents total numbers and ‘S’ is the total sum of all the numbers.
Honourable mentions
Find the original version of this page (with additional content) on Notion here.
Created: December 13, 2021 16:05:48