Data Structures and Algorithms

Binary search: BS can be used in so many different situations!
Leap year, GCD, LCM, isPrime, prime finding, prime factorization
Bit manipulation
Reservoir sampling
2 pointer strategy and sliding window
cumulative sum, prefix sum (1d, 2d, 3d)
Sorting: selection sort, quick sort, quick select, insertion sort (with binary search optimization), merge sort, heap sort, radix sort, counting sort, bucket sort
String strategies: rabin-karp, KMP, Boyer-Moore
Graph: Dijkstra, Bellman-Ford, Union find, Kruskal, Prim, Floyd-Warshall, Tarjan, DFS, BFS, Ford Fulkerson & Edmond (Min cut max flow), Hamiltonion path (with bitmasking), Eulerian cycle, Topological sorting
DFS: backtracking
Monotonically increasing stack, queue, etc.
DP: Top-down using recursion and memoization, Bottom up using iteration and tabulation
Classic DP patterns: LCS, LIS, LIS (strictly increasing), Equal sum partition
BIT: binary indexed tree/sedgwick tree
Interval trees
Tree: inorder, preorder, postorder traversal: iterative and recursive, morris traversal to do those 3 in O(1) space
Binary search trees (BSTs), heaps, splay trees, red-black trees, skip list, avl tree

Tools:

Grokking the coding interview
AgoExpert ?

Tips:

https://www.topcoder.com/thrive/articles/Greedy is Good

https://www.topcoder.com/thrive/articles/An Introduction to Recursion Part Two

Data structures in 5 min:

https://www.youtube.com/playlist?list=PLlipSLnrfrUlclWAcvmyxcn6R7tzwALhM

How to approach problems

Data Structures and Algorithms 16913c6fbd244de481b6b1705cbfa6be ↵

Complexity Analysis & Big O

O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(2^n) < O(n!)

# if the value of n is large, (which it usually is, when we are considering Big O ie worst case), logn can be greater than 1

The following are examples of common complexities and their Big O notations, ordered from fastest to slowest:

Constant: O(1)
Logarithmic: O(log(n))
Linear: O(n)
Log-linear: O(nlog(n))
Quadratic: O(n^2)
Cubic: O(n^3)
Exponential: O(2^n)
Factorial: O(n!)

Note that in the context of coding interviews, Big O notation is usually understood to describe the worst-case complexity of an algorithm, even though the worst-case complexity might differ from the average-case complexity.

Screenshot 2021-09-21 at 16.57.00.png

Important rules to know with Big O

1. Different steps get added

# O(a+b)
def do_something():
    do_step_one() # O(a)
    do_step_two() # O(b)

2. Drop constants

# O(2n) => O(n)

3. Different inputs ⇒ Different variables

# O(a.b)
def random(array_a, array_b):
    ...

4. Drop non-dominant terms

# O(n^2)
def do_something(array):
    do_step_one(array) # O(n)
    do_step_two(array) # O(n^2)

5. Multi-Part Algorithms: Add vs. Multiply

If your algorithm is in the form "do this, then, when you're all done, do that" then you add the runtimes.

If your algorithm is in the form "do this for each time you do that" then you multiply the runtimes.

6. Recursive Runtimes

Try to remember this pattern. When you have a recursive function that makes multiple calls, the runtime will often (but not always) look like O( branches ^ depth ), where branches is the number of times each recursive call branches.

Complexity%20Analysis%20&%20Big%20O%20ded85f7996b548c7953055302969348c/Screenshot_2021-06-25_at_08.21.52.png

Memory

Accessing a memory slot is a very basic operation that takes constant time. For example, Accessing a value in an array at a given index → array[34]

Constant time/space complexity:

No matter how you change the input size, the time it takes to get your output is the same. With constant space complexity, the amount of memory you use doesn’t change as the input size grows. Examples:

Basic Math Operators (+, -, *, /, %)
Array Index Lookups (arr[5])
Hash Map Get/Set Operations (map.get(“key”), map.set(“key”, “value”))
Property Lookups (array.length, list.head, node.value…)
Class Instantiations (let c = new Circle(radius = 5, colour = “blue”))

There are also a number of operations that typically fall in this category if implemented most efficiently. Usually, they boil down to doing one or more of the previously mentioned operations, like instantiating an object or looking up some property.

Some examples include:

Linked List append(), prepend(), head(), tail()
Stack push(), pop(), peek()
Queue enqueue(), dequeue()
Binary Tree Node getleftChild(), getrightChild()
Graph Node getAdjacentNodes(node), connectNodes(node1, node2)

A lot of engineers get tripped up by O(1) space, but all this means the amount of memory you use doesn’t scale with the input size.

A Wrinkle (finite character set)

Example:

Suppose you wanted to write a function that counted all the frequencies of characters in a string. A really simple (and efficient) way to do it would be to loop through all of the string’s characters and then tally them up in a hash map:

The runtime of this function depends on the length of the string. 1 more character, means 1 more step, so the runtime is O(N).

But what about space complexity? We’re using a few variables, but the obvious one that seems to scale up with the size of the string is the counts hashmap. The more characters you have, the more it seems like you’ll have to keep track of, so it might seem like it’s also O(N).

But the reality is that it’s actually O(1) 🤯 because you are only dealing with a finite character set. Sometimes see this big-O notation written as O(C). It’s used to express the fact that constant time/space isn’t just limited to one step or one unit of memory usage. There can be some amount of scaling up in runtime or memory usage, as long as it’s to some fixed, finite upper limit.

Examples

Logarithm

A mathematical concept that's widely used in Computer Science and that's defined by the following equation:

In the context of coding interviews, the logarithm is used to describe the complexity analysis of algorithms, and its usage always implies a logarithm of base 2. In other words, the logarithm used in the context of coding interviews is defined by the following equation:

In plain English, if an algorithm has a logarithmic time complexity O(log(n), where n is the size of the input), then whenever the algorithm's input doubles in size (i.e., whenever n doubles), the number of operations needed to complete the algorithm only increases by one unit. Conversely, an algorithm with a linear time complexity would see its number of operations double if its input size doubled.

As an example, a linear-time-complexity algorithm with an input of size 1,000 might take roughly 1,000 operations to complete, whereas a logarithmic-time-complexity algorithm with the same input would take roughly 10 operations to complete, since 210 ~= 1,000.

2n (2^n) - whenever the algorithm's input increases in size, the number of operations needed to complete the algorithm doubles**.

If n is the size of the input), then whenever the algorithm's input increases in size (i.e., n+1), the number of operations needed to complete the algorithm doubles.

Screenshot 2021-10-11 at 16.44.02.png

Factorial - N * (N-1) * (N-2) * (N-3) * ... * 2 * 1 == N!

Factorial - Wikipedia

Untitled

The factorial function (symbol: !) says to multiply all whole numbers from our chosen number down to 1.

Examples:

4! = 4 × 3 × 2 × 1 = 24

7! = 7 × 6 × 5 × 4 × 3 × 2 × 1 = 5040

1! = 1

Not factorial 😂 - (N-1) + (N-2) + (N-3) + ... + 2 + 1 ~= N^2

Screenshot 2021-09-26 at 10.41.34.png

Two loops but on different arrays O(a.b) instead of O(n^2)

Screenshot 2021-09-26 at 10.43.45.png

An algorithm that took in an array of strings, sorted each string and then sorted the full array

Screenshot 2021-09-26 at 10.52.35.png

O(squareroot n) time.

Screenshot 2021-09-26 at 10.56.20.png

Common

Graph DFS & BFS

Depth First Search or DFS for a Graph - GeeksforGeeks

The time complexity of DFS & BFS if the entire tree is traversed is O(V) where V is the number of nodes. In the case of a graph, the time complexity is where V is the number of vertexes and E is the number of edges.

Pseudocode of BFS:

put starting node in the queue
while queue is not empty
- get first node from the queue, name it v
- (process v)
- for each edge e going from v to other nodes
  - put the other end of edge e at the end of the queue

As you can see, the worst case (which is what O means), is basically for all vertices if the graph, do a O(1) operation with them - getting it from the queue, then for all outbound edges of v do another O(1) operation, adding their other end to the queue. Thus summing the first O(1) operation for all vertices gives O(V) and summing the O(outbound edge count) over all the vertices gives O(E), which gives O(V) + O(E) = O(V+E). Without the processing of course, or assuming it is O(1) like adding the vertex to a list.

Find the original version of this page (with additional content) on Notion here.

Greedy Algorithms

Greedy Approach: A Deep Dive - Algorithms for Coding Interviews in Python

Greedy Algorithms | Interview Cake

Greedy Algorithm - InterviewBit

Basics of Greedy Algorithms Tutorials & Notes | Algorithms | HackerEarth

Introduction

A greedy algorithm, as the name suggests, always makes the choice that seems to be the best at that moment. This means that it makes a locally-optimal choice in the hope that this choice will lead to a globally-optimal solution. They never look backwards at what they’ve done to see if they could optimise globally. This is the main difference between Greedy and Dynamic Programming.

Greedy is an algorithmic paradigm in which the solution is built piece by piece. The next piece that offers the most obvious and immediate benefit is chosen. The greedy approach will always make the choice that will maximize the profit and minimize the cost at any given point. It means that a locally-optimal choice is made in the hope that it will lead to a globally-optimal solution.

A greedy algorithm builds up a solution by choosing the option that looks the best at every step.

Sometimes greedy algorithm fails to find the optimal solution because it does not consider all available data and make choices which seems best at that moment. A famous example for this limitation is searching the largest path in a tree.

The greedy algorithm fails to solve this problem because it makes decisions purely based on what the best answer at the time is:

at each step it did choose the largest number and solve the problem as

7 -> 12 -> 6 -> 9. Total is: 34.

This is not the optimal solution. Correct solution to this problem is, 7 -> 3 -> 1 -> 99. Total is: 110.

A greedy algorithm works if a problem exhibits the following two properties:

Greedy Choice Property*: A globally optimal solution can be reached at by creating a locally optimal solution. In other words, an optimal solution can be obtained by creating "greedy" choices.
Optimal substructure: Optimal solutions contain optimal subsolutions. In other words, answers to subproblems of an optimal solution are optimal.

Examples

Connect Ropes

Minimum Cost to Connect Sticks

""" 
1167. Minimum Cost to Connect Sticks

You have some number of sticks with positive integer lengths. These lengths are given as an array sticks, where sticks[i] is the length of the ith stick.
You can connect any two sticks of lengths x and y into one stick by paying a cost of x + y. 
You must connect all the sticks until there is only one stick remaining.
Return the minimum cost of connecting all the given sticks into one stick in this way.

Example 1:
    Input: sticks = [2,4,3]
    Output: 14
    Explanation: You start with sticks = [2,4,3].
        1. Combine sticks 2 and 3 for a cost of 2 + 3 = 5. Now you have sticks = [5,4].
        2. Combine sticks 5 and 4 for a cost of 5 + 4 = 9. Now you have sticks = [9].
        There is only one stick left, so you are done. The total cost is 5 + 9 = 14.
Example 2:
    Input: sticks = [1,8,3,5]
    Output: 30
    Explanation: You start with sticks = [1,8,3,5].
        1. Combine sticks 1 and 3 for a cost of 1 + 3 = 4. Now you have sticks = [4,8,5].
        2. Combine sticks 4 and 5 for a cost of 4 + 5 = 9. Now you have sticks = [9,8].
        3. Combine sticks 9 and 8 for a cost of 9 + 8 = 17. Now you have sticks = [17].
        There is only one stick left, so you are done. The total cost is 4 + 9 + 17 = 30.
Example 3:
    Input: sticks = [5]
    Output: 0
    Explanation: There is only one stick, so you don't need to do anything. The total cost is 0.

https://leetcode.com/problems/minimum-cost-to-connect-sticks
"""
from typing import List
from heapq import heapify, heappop, heappush

# O(n log n) time
class Solution:
    def connectSticks(self, sticks: List[int]):
        total = 0

        heapify(sticks)
        while len(sticks) > 1:
            stick = heappop(sticks) + heappop(sticks)
            total += stick
            heappush(sticks, stick)

        return total

Minimum Waiting Time

"""
Minimum Waiting Time:

You're given a non-empty array of positive integers representing the amounts of time that specific queries take to execute. 
Only one query can be executed at a time, but the queries can be executed in any order.
A query's waiting time is defined as the amount of time that it must wait before its execution starts.
In other words, if a query is executed second, then its waiting time is the duration of the first query; 
    if a query is executed third, then its waiting time is the sum of the durations of the first two queries.
Write a function that returns the minimum amount of total waiting time for all of the queries. 
For example, if you're given the queries of durations [1, 4, 5], 
    then the total waiting time if the queries were executed in the order of [5, 1, 4] would be (0) + (5) + (5 + 1) = 11. 
The first query of duration 5 would be executed immediately, so its waiting time would be 0, 
    the second query of duration 1 would have to wait 5 seconds (the duration of the first query) to be executed, 
    and the last query would have to wait the duration of the first two queries before being executed.

Note: you're allowed to mutate the input array.
https://www.algoexpert.io/questions/Minimum%20Waiting%20Time
"""

""" 
ensure the longest waiting times are at the end
"""

def minimumWaitingTime(queries):
    queries.sort()
    total = 0

    prev_time = 0
    for time in queries:
        total += prev_time
        prev_time += time

    return total

def minimumWaitingTime2(queries):
    queries.sort()
    total = 0
    for idx, num in enumerate(queries):
        last_idx = len(queries)-1
        # add waiting time for the elements to the right of the current element
        total += num * (last_idx - idx)

    return total

Class Photos

"""
Class Photos:

It's photo day at the local school, and you're the photographer assigned to take
class photos. The class that you'll be photographing has an even number of is students, and all these students are wearing red or blue shirts. 
In fact, exactlyhalf of the class is wearing red shirts, and the other half is wearing blue shirts.
You're responsible for arranging the students in two rows before taking the photo. 
Each row should contain the same number of the students and shouldadhere to the following guidelines:

All students wearing red shirts must be in the same row. 
All students wearing blue shirts must be in the same row.
Each student in the back row must be strictly taller than the student directly in front of them in the front row.

You're given two input arrays: one containing the heights of all the students with red shirts and another one containing the heights of all the students with blue shirts.
These arrays will always have the same length, and each height will be a positive integer. 
Write a function that returns whether or not a class photo that follows the stated guidelines can be taken.
Note: you can assume that each class has at least 2 students.

https://www.algoexpert.io/questions/Class%20Photos
"""

"""
Each student in the back row must be strictly taller than the student directly in front of them in the front row.
"""

def classPhotos(redShirtHeights, blueShirtHeights):
    redShirtHeights.sort()
    blueShirtHeights.sort()

    isRedTaller = redShirtHeights[0] > blueShirtHeights[0]
    for idx in range(len(redShirtHeights)):
        if isRedTaller:
            if redShirtHeights[idx] <= blueShirtHeights[idx]:
                return False
        else:
            if redShirtHeights[idx] >= blueShirtHeights[idx]:
                return False

    return True

Two City Scheduling

""" 
1029. Two City Scheduling

A company is planning to interview 2n people. Given the array costs where costs[i] = [aCosti, bCosti], 
the cost of flying the ith person to city a is aCosti, and the cost of flying the ith person to city b is bCosti.
Return the minimum cost to fly every person to a city such that exactly n people arrive in each city.

Example 1:
    Input: costs = [[10,20],[30,200],[400,50],[30,20]]
    Output: 110
    Explanation: 
    The first person goes to city A for a cost of 10.
    The second person goes to city A for a cost of 30.
    The third person goes to city B for a cost of 50.
    The fourth person goes to city B for a cost of 20.

    The total minimum cost is 10 + 30 + 50 + 20 = 110 to have half the people interviewing in each city.
Example 2:
    Input: costs = [[259,770],[448,54],[926,667],[184,139],[840,118],[577,469]]
    Output: 1859
Example 3:
    Input: costs = [[515,563],[451,713],[537,709],[343,819],[855,779],[457,60],[650,359],[631,42]]
    Output: 3086


Constraints:
    2 * n == costs.length
    2 <= costs.length <= 100
    costs.length is even.
    1 <= aCosti, bCosti <= 1000

https://leetcode.com/problems/two-city-scheduling
"""

from typing import List
""""""

class Solution:
    def twoCitySchedCost(self, costs: List[List[int]]):
        total_cost = 0

        # sort be how much we save by going to city A
        costs.sort(key=lambda x: x[1]-x[0], reverse=True)

        for idx, cost_arr in enumerate(costs):
            if idx < len(costs)/2:
                # consider A:
                # the 1st half are best suited to traveling to A, saves us the most money
                total_cost += cost_arr[0]
            else:
                # consoder B
                total_cost += cost_arr[1]

        return total_cost

Task Assignment

"""
Task Assignment:

You're given an integer k representing a number of workers and an array of positive integers representing durations of tasks that must be completed by the workers.
Specifically, each worker must complete two unique tasks and can only work on one task at a time.
The number of tasks will always be equal to 2k such that each worker always has exactly two tasks to complete.
All tasks are independent of one another and can be completed in any order. Workers will complete their assigned tasks in parallel, and the time taken to complete all tasks will be equal to the time taken to complete the longest pair of tasks.

Write a function that returns the optimal assignment of tasks to each worker such that the tasks are completed as fast as possible.
Your function should return a list of pairs, where each pair stores the indices of the tasks that should be completed by one worker. 
The pairs should be in the following format: [task1, task2], where the order of task1 and task2 doesn't matter.
Your function can return the pairs in any order. If multiple optimal assignments exist, any correct answer will be accepted.
Note: you'll always be given at least one worker (i.e., k will always be greater than 0).

https://www.algoexpert.io/questions/Task%20Assignment
"""

def taskAssignment(k, tasks):
    output = []

    # add indices to tasks
    for idx in range(len(tasks)):
        tasks[idx] = [tasks[idx], idx]
    # sort by task duration
    tasks.sort(key=lambda x: x[0])

    # add first half to output
    for idx in range(k):
        output.append([tasks[idx][1]])

    # add second half: from largest task to smallest
    pos = 0
    for idx in reversed(range(k, len(tasks))):
        output[pos] = output[pos] + [tasks[idx][1]]
        pos += 1

    return output

def taskAssignment1(k, tasks):
    output = []

    # add indices to tasks
    for idx in range(len(tasks)):
        tasks[idx] = [tasks[idx], idx]
    # sort by task duration
    tasks.sort(key=lambda x: x[0])

    tasks_length = len(tasks)
    # add largest and smallest task
    for idx in range(k):
        first_task = tasks[idx][1]
        second_task = tasks[(tasks_length - 1) - idx][1]
        output.append([first_task, second_task])

    return output

Valid Starting City

"""
Valid Starting City:

Imagine you have a set of cities that are laid out in a circle, connected by a circular road that runs clockwise. 
Each city has a gas station that provides gallons of fuel, and each city is some distance away from the next city.
You have a car that can drive some number of miles per gallon of fuel, and your goal is to pick a starting city such that you can fill up your car with that city's fuel,
 drive to the next city, refill up your car with that city's fuel, drive to the next city,
  and so on and so forth until you return back to the starting city with 0 or more gallons of fuel left.
This city is called a valid starting city, and it's guaranteed that there will always be exactly one valid starting city.
For the actual problem, you'll be given an array of distances such that city i is distances[i] away from city i + 1.
Since the cities are connected via a circular road, the last city is connected to the first city.
In other words, the last distance in the distances array is equal to the distance from the last city to the first city.
You'll also be given an array of fuel available at each city, where fuel[i] is equal to the fuel available at city i.
The total amount of fuel available (from all cities combined) is exactly enough to travel to all cities.
Your fuel tank always starts out empty, and you're given a positive integer value for the number of miles that your car can travel per gallon of fuel (miles per gallon, or MPG).
You can assume that you will always be given at least two cities.
Write a function that returns the index of the valid starting city.

Sample Input
    distances = [5, 25, 15, 10, 15]
    fuel = [1, 2, 1, 0, 3]
    mpg = 10
Sample Output
    4

https://www.algoexpert.io/questions/Valid%20Starting%20City
"""

def validStartingCity0(distances, fuel, mpg):
    start = 0
    end = 0
    miles_remaining = 0
    visited = 1

    while visited < len(distances):

        miles_if_move = miles_remaining - distances[end] + (fuel[end]*mpg)

        # is a valid move
        if miles_if_move >= 0:
            miles_remaining = miles_if_move
            visited += 1
            end = movePointerForward(distances,  end)

        # not a valid move -> move start forward
        else:
            if end == start:
                end += 1  # move to where start will be
                miles_remaining = 0
                visited = 1
            else:
                miles_remaining = miles_remaining + \
                    distances[start] - (fuel[start]*mpg)
                visited -= 1
            start += 1

    return start

def movePointerForward(array, pointer):
    if pointer + 1 < len(array):
        return pointer + 1
    return 0

"""
[0,1,2,3]
start = 0

# if we reach a point where we will have < 0 fuel when we move forward,
# we pause and start += 1 and remove the effects of the starting point:
# remove fuel added and add fuel spent
"""

""" 
------------------------------------------------------------------------------------------------------------------------------------

start at city 0 and calculate the lowest amount of fuel you will ever have:
    - this will be the valid starting city (it is the furthest by mpg)
    - whatever city we start from, we will always reach there with a negative amount of fuel

10 mile  = 1 gal (mpg)
5 miles =  ? gal -> 5/10

"""

class StartingCity:
    def __init__(self, index, fuel_remaining):
        self.index = index
        self.fuel_remaining = fuel_remaining

def validStartingCity(distances, fuel, mpg):
    starting_city = StartingCity(-1, float('inf'))

    current_fuel = 0
    for i in range(len(fuel)):
        # # the city with the lowest amount of fuel you will ever have is the valid starting city
        if current_fuel < starting_city.fuel_remaining:
            starting_city.index = i
            starting_city.fuel_remaining = current_fuel

        # # add fuel
        current_fuel += fuel[i]

        # # travel to next city
        fuel_consumed = distances[i]/mpg
        # 1 - 1.2 = -0.19999999999999996
        # 0.1 + 0.2 = 0.30000000000000004
        current_fuel = round(current_fuel - fuel_consumed, 10)

    return starting_city.index

Two City Scheduling *

Two City Scheduling - LeetCode

class Solution:
    def twoCitySchedCost(self, costs: List[List[int]]):
        total_cost = 0

        # sort be how much we save by going to city A
        costs.sort(key=lambda x: x[1]-x[0], reverse=True)

        for idx, cost_arr in enumerate(costs):
            if idx < len(costs)/2:
                # consider A: 
                # the 1st half are best suited to traveling to A, saves us the most money
                total_cost += cost_arr[0]
            else:
                # consoder B
                total_cost += cost_arr[1]

        return total_cost

Partition Labels

Screenshot 2021-10-18 at 15.39.21.png

""" 
763. Partition Labels

You are given a string s. 
We want to partition the string into as many parts as possible so that each letter appears in at most one part.
Return a list of integers representing the size of these parts.

Example 1:
    Input: s = "ababcbacadefegdehijhklij"
    Output: [9,7,8]
    Explanation:
        The partition is "ababcbaca", "defegde", "hijhklij".
        This is a partition so that each letter appears in at most one part.
        A partition like "ababcbacadefegde", "hijhklij" is incorrect, because it splits s into less parts.
Example 2:
    Input: s = "eccbbbbdec"
    Output: [10]

https://leetcode.com/problems/partition-labels/
Prerequisite: https://leetcode.com/problems/merge-intervals    
"""

""" 
Solution:

find intervals - merge intervals

Let's try to repeatedly choose the smallest left-justified partition. 
Consider the first label, say it's 'a'. 
The first partition must include it, and also the last occurrence of 'a'. 
However, between those two occurrences of 'a', there could be other labels that make the minimum size of this partition bigger. 
    For example, in "abccaddbeffe", the minimum first partition is "abccaddb". 
This gives us the idea for the algorithm: For each letter encountered, process the last occurrence of that letter, extending the current partition [anchor, j] appropriately.
"""

# O(n) time | O(1) space
class Solution:
    def partitionLabels(self, s: str):
        """ 
        Divide string into intervals/partitions and merge overlapping intervals.
        """
        result = []

        # mark the last index of each character
        last_pos = {}
        for idx, char in enumerate(s):
            last_pos[char] = idx

        # divide the characters into partitions
        partition_start = 0
        partition_end = 0
        for idx, char in enumerate(s):

            # if outside the current partition, save the prev partition length & start a new one
            if idx > partition_end:
                result.append(partition_end-partition_start+1)
                # start new partition
                partition_end = idx
                partition_start = idx

            # update the end of the partition
            partition_end = max(last_pos[char], partition_end)

            # once we find a pertition that ends at the last character, save it
            if partition_end == len(s)-1:
                # save the last partition
                result.append(partition_end-partition_start+1)
                return result

        return result

Jump Game

[Java] A general greedy solution to process similar problems - LeetCode Discuss

""" 
Jump Game

You are given an integer array nums. 
You are initially positioned at the array's first index, and each element in the array represents your maximum jump length at that position.
Return true if you can reach the last index, or false otherwise.

Example 1:
    Input: nums = [2,3,1,1,4]
    Output: true
    Explanation: Jump 1 step from index 0 to 1, then 3 steps to the last index.
Example 2:
    Input: nums = [3,2,1,0,4]
    Output: false
    Explanation: You will always arrive at index 3 no matter what. Its maximum jump length is 0, which makes it impossible to reach the last index.

https://leetcode.com/problems/jump-game
"""

""" 
Top down:
try every single jump pattern that takes us from the first position to the last. 
We start from the first position and jump to every index that is reachable. 
We repeat the process until last index is reached. When stuck, backtrack.

One quick optimization we can do for the code above is to check the nextPosition from right to left. (jump furthest)
The theoretical worst case performance is the same, but in practice, for silly examples, the code might run faster. 
Intuitively, this means we always try to make the biggest jump such that we reach the end as soon as possible

Top-down Dynamic Programming can be thought of as optimized backtracking. 
It relies on the observation that once we determine that a certain index is good / bad, this result will never change. 
This means that we can store the result and not need to recompute it every time.
Therefore, for each position in the array, we remember whether the index is good or bad. 

O(n^2) time | O(2n) == O(n) space
"""

class SolutionMEMO:
    def canJump(self, nums):

        return self.jump_helper(nums, [None]*len(nums), 0)

    def jump_helper(self, nums, cache, idx):
        if idx >= len(nums)-1:
            return True
        if cache[idx] is not None:
            return cache[idx]

        for i in reversed(range(idx+1, idx+nums[idx]+1)):
            if self.jump_helper(nums, cache, i):
                cache[idx] = True
                return cache[idx]

        cache[idx] = False
        return cache[idx]

""" 
Bottom up:
Top-down to bottom-up conversion is done by eliminating recursion. 
In practice, this achieves better performance as we no longer have the method stack overhead and might even benefit from some caching. 
More importantly, this step opens up possibilities for future optimization. 
The recursion is usually eliminated by trying to reverse the order of the steps from the top-down approach.

The observation to make here is that we only ever jump to the right. 
This means that if we start from the right of the array, every time we will query a position to our right, that position has already be determined as being GOOD or BAD. 
This means we don't need to recurse anymore, as we will always hit the memo/cache table.

O(n^2) time | O(n) space

-------------------------------------------------------------------------------------------------------------------------

Greedy

Once we have our code in the bottom-up state, we can make one final, important observation. 
From a given position, when we try to see if we can jump to a GOOD position, we only ever use one - the first one. 
    In other words, the left-most one. 
If we keep track of this left-most GOOD position as a separate variable, we can avoid searching for it in the array. 
    Not only that, but we can stop using the array altogether.

O(n) time | O(1) space
"""

class SolutionBU:
    def canJump(self, nums):
        dp = [None]*len(nums)
        dp[-1] = True

        for idx in reversed(range(len(nums)-1)):

            for idx_2 in range(idx+1, idx+nums[idx]+1):
                if dp[idx_2] == True:
                    dp[idx] = True
                    break

        return dp[0]

class Solution:
    def canJump(self, nums):

        last_valid = len(nums)-1
        for idx in reversed(range(len(nums)-1)):

            if idx+nums[idx] >= last_valid:
                last_valid = idx

        return last_valid == 0

Jump Game II

Jump Game II - Greedy - Leetcode 45 - Python

[Java] A general greedy solution to process similar problems - LeetCode Discuss

Screenshot 2021-10-20 at 09.37.49.png

Screenshot 2021-10-20 at 09.38.14.png

Screenshot 2021-10-20 at 09.38.47.png

Screenshot 2021-10-20 at 09.39.13.png

""" 
45. Jump Game II

Given an array of non-negative integers nums, you are initially positioned at the first index of the array.
Each element in the array represents your maximum jump length at that position.
Your goal is to reach the last index in the minimum number of jumps.
You can assume that you can always reach the last index.

Example 1:
    Input: nums = [2,3,1,1,4]
    Output: 2
    Explanation: The minimum number of jumps to reach the last index is 2. Jump 1 step from index 0 to 1, then 3 steps to the last index.
Example 2:
    Input: nums = [2,3,0,1,4]
    Output: 2

https://leetcode.com/problems/jump-game-ii

Prerequisites:
- https://leetcode.com/problems/jump-game
"""

""" 
DP Memoization
"""

class SolutionMEMO:
    def jump(self, nums):
        cache = [None]*len(nums)
        cache[-1] = 0

        self.jump_helper(nums, 0, cache)

        return cache[0]

    def jump_helper(self, nums, idx, cache):
        if idx >= len(nums):
            return 0
        if cache[idx] is not None:
            return cache[idx]

        result = float('inf')
        for i in range(idx+1, idx+nums[idx]+1):
            result = min(result, self.jump_helper(nums, i, cache))

        result += 1  # add current jump

        cache[idx] = result
        return cache[idx]

""" 
DP Bottom up
"""

class Solution:
    def jump(self, nums):
        cache = [None]*len(nums)
        cache[-1] = 0

        for idx in reversed(range(len(nums)-1)):
            if nums[idx] != 0:
                cache[idx] = min(cache[idx+1:idx+nums[idx]+1]) + 1
            else:
                cache[idx] = float('inf')

        return cache[0]

""" 
Greedy
https://www.notion.so/paulonteri/Greedy-Algorithms-b9b0a6dd66c94e7db2cbbd9f2d6b50af#255fab0c8c0242df8f7e53d9ec2a83b8
https://leetcode.com/problems/minimum-number-of-taps-to-open-to-water-a-garden/discuss/506853/Java-A-general-greedy-solution-to-process-similar-problems
"""

class Solution_:
    def jump(self, nums):
        result = 0

        current_jump_end = 0
        farthest_possible = 0  # furthest jump we made/could have made
        for i in range(len(nums) - 1):

            # we continuously find the how far we can reach in the current jump
            # record the futhest point accessible in our current jump
            farthest_possible = max(farthest_possible, i + nums[i])

            # if we have come to the end of the current jump, we need to make another jump
            if i == current_jump_end:
                result += 1
                # move to the furthest possible point
                current_jump_end = farthest_possible

        return result

class Solution:
    def jump(self, nums):
        result = 0

        i = 0
        farthest_possible = 0  # furthest jump we made/could have made
        while i < len(nums) - 1:
            # # create new jump & move to the furthest possible point
            farthest_possible = max(farthest_possible, i + nums[i])
            # new jump - jump furthest
            result += 1
            current_jump_end = farthest_possible
            # next
            i += 1

            # # move to end of current jump
            while i < len(nums) - 1 and i < current_jump_end:
                # we continuously find the how far we can reach in the current jump
                # record the futhest point accessible in our current jump
                farthest_possible = max(farthest_possible, i + nums[i])
                i += 1

        return result

Video Stitching

""" 
Video Stitching

You are given a series of video clips from a sporting event that lasted time seconds. 
These video clips can be overlapping with each other and have varying lengths.
Each video clip is described by an array clips where clips[i] = [starti, endi] indicates that the ith clip started at starti and ended at endi.
We can cut these clips into segments freely.
For example, a clip [0, 7] can be cut into segments [0, 1] + [1, 3] + [3, 7].
Return the minimum number of clips needed so that we can cut the clips into segments that cover the entire sporting event [0, time]. 
If the task is impossible, return -1.

Example 1:
    Input: clips = [[0,2],[4,6],[8,10],[1,9],[1,5],[5,9]], time = 10
    Output: 3
    Explanation: 
        We take the clips [0,2], [8,10], [1,9]; a total of 3 clips.
        Then, we can reconstruct the sporting event as follows:
        We cut [1,9] into segments [1,2] + [2,8] + [8,9].
        Now we have segments [0,2] + [2,8] + [8,10] which cover the sporting event [0, 10].
Example 2:
    Input: clips = [[0,1],[1,2]], time = 5
    Output: -1
    Explanation: We can't cover [0,5] with only [0,1] and [1,2].
Example 3:
    Input: clips = [[0,1],[6,8],[0,2],[5,6],[0,4],[0,3],[6,7],[1,3],[4,7],[1,4],[2,5],[2,6],[3,4],[4,5],[5,7],[6,9]], time = 9
    Output: 3
    Explanation: We can take clips [0,4], [4,7], and [6,9].
Example 4:
    Input: clips = [[0,4],[2,8]], time = 5
    Output: 2
    Explanation: Notice you can have extra video after the event ends.

https://leetcode.com/problems/video-stitching
"""

class SolutionDP:
    def videoStitching(self, clips, time):
        clips.sort()

        dp = [float('inf')] * (time+1)
        dp[0] = 0

        for left, right in clips:
            # ignore ranges that will be greater than the time
            if left > time:
                continue

            # reach every point possible
            for idx in range(left, min(right, time)+1):
                # steps to reach idx = min((prevoiusly recorded), (steps to reach left + the one step to idx))
                dp[idx] = min(dp[idx], dp[left]+1)

        if dp[-1] == float('inf'):
            return -1
        return dp[-1]

class Solution:
    def videoStitching(self, clips, T):
        result = 0

        # # Save the right-most possible valid jump for each left most index
        max_jumps = [-1]*(T+1)
        for left, right in clips:
            if left > T:
                continue
            if right-left <= 0:
                continue
            max_jumps[left] = max(max_jumps[left], min(right, T))

        # Jump Game II: it is then a jump game
        idx = 0
        current_jump_end = 0
        furthest_jump = 0  # furthest jump we made/could have made
        while idx < T:

            # # create a new jump
            furthest_jump = max(max_jumps[idx], furthest_jump)
            # check if we can make a valid jump
            if max_jumps[idx] == -1 and furthest_jump <= idx:
                # if we cannot make a jump and we need to make a jump to increase the furthest_jump
                return -1
            # make jump - move end to the furthest possible point
            result += 1
            current_jump_end = furthest_jump

            idx += 1

            # # reach end of jump
            while idx <= T and idx < current_jump_end:
                # we continuously find the how far we can reach in the current jump
                # record the futhest point accessible in our current jump
                furthest_jump = max(max_jumps[idx], furthest_jump)
                idx += 1

        return result

Minimum Number of Taps to Open to Water a Garden

""" 
Minimum Number of Taps to Open to Water a Garden

There is a one-dimensional garden on the x-axis. The garden starts at the point 0 and ends at the point n. (i.e The length of the garden is n).
There are n + 1 taps located at points [0, 1, ..., n] in the garden.
Given an integer n and an integer array ranges of length n + 1 where ranges[i] (0-indexed) means the i-th tap can water the area [i - ranges[i], i + ranges[i]] if it was open.
Return the minimum number of taps that should be open to water the whole garden, If the garden cannot be watered return -1.

Example 1:
    Input: n = 5, ranges = [3,4,1,1,0,0]
    Output: 1
    Explanation: The tap at point 0 can cover the interval [-3,3]
        The tap at point 1 can cover the interval [-3,5]
        The tap at point 2 can cover the interval [1,3]
        The tap at point 3 can cover the interval [2,4]
        The tap at point 4 can cover the interval [4,4]
        The tap at point 5 can cover the interval [5,5]
        Opening Only the second tap will water the whole garden [0,5]
Example 2:
    Input: n = 3, ranges = [0,0,0,0]
    Output: -1
    Explanation: Even if you activate all the four taps you cannot water the whole garden.
Example 3:
    Input: n = 7, ranges = [1,2,1,0,2,1,0,1]
    Output: 3
Example 4:
    Input: n = 8, ranges = [4,0,0,0,0,0,0,0,4]
    Output: 2
Example 5:
    Input: n = 8, ranges = [4,0,0,0,4,0,0,0,4]
    Output: 1

https://leetcode.com/problems/minimum-number-of-taps-to-open-to-water-a-garden
"""

""" 

Prerequisites:
- https://leetcode.com/problems/jump-game
- https://leetcode.com/problems/jump-game-ii
- https://leetcode.com/problems/video-stitching

https://www.notion.so/paulonteri/Greedy-Algorithms-b9b0a6dd66c94e7db2cbbd9f2d6b50af#d7578cbb76c7423d9c819179fc749be5
https://leetcode.com/problems/minimum-number-of-taps-to-open-to-water-a-garden/discuss/506853/Java-A-general-greedy-solution-to-process-similar-problems
"""

class Solution_:
    def minTaps(self, n, ranges):
        taps = 0

        # # Save the right-most possible jump for each left most index
        jumps = [-1]*(n)
        for idx, num in enumerate(ranges):
            if num == 0:
                continue
            left_most = max(0, idx-num)
            right_most = min(n, idx+num)

            jumps[left_most] = max(jumps[left_most], right_most)

        # # Jump Game II
        current_jump_end = 0
        furthest_can_reach = -1  # furthest jump we made/could have made
        for idx, right_most in enumerate(jumps):

            # we continuously find the how far we can reach in the current jump
            # record the futhest point accessible in our current jump
            furthest_can_reach = max(right_most, furthest_can_reach)

            # if we have come to the end of the current jump, we need to make another jump
            # the new  jump should start immediately after the old jump
            if idx == current_jump_end:
                # if we cannot make a jump and we need to make a jump to increase the furthest_can_reach
                if right_most == -1 and furthest_can_reach <= idx:
                    return -1
                # move end to the furthest possible point
                current_jump_end = furthest_can_reach
                taps += 1

        if furthest_can_reach == n:
            return taps
        return -1

class Solution:
    def minTaps(self, n, ranges):
        taps = 0

        # # Save the right-most possible jump for each left most index
        jumps = [-1]*(n)
        for idx, num in enumerate(ranges):
            if num == 0:
                continue
            left_most = max(0, idx-num)
            right_most = min(n, idx+num)

            jumps[left_most] = max(jumps[left_most], right_most)

        # # Jump Game II
        idx = 0
        furthest_can_reach = -1  # furthest jump we made/could have made
        while idx < n:

            # # create a new jump
            furthest_can_reach = max(jumps[idx], furthest_can_reach)
            # check if we can make a valid jump
            if jumps[idx] == -1 and furthest_can_reach <= idx:
                # if we cannot make a jump and we need to make a jump to increase the furthest_can_reach
                return -1
            # make jump - move end to the furthest possible point
            taps += 1
            current_jump_end = furthest_can_reach

            idx += 1

            # # reach end of jump
            while idx < n and idx < current_jump_end:
                # we continuously find the how far we can reach in the current jump
                # record the futhest point accessible in our current jump
                furthest_can_reach = max(jumps[idx], furthest_can_reach)
                idx += 1

        if furthest_can_reach == n:
            return taps
        return -1

Honourable mentions

0/1 Knapsack

Find the original version of this page (with additional content) on Notion here.

Hashtables & Hashsets

Hash Tables

A data structure that provides fast insertion, deletion, and lookup of key/value pairs.

Under the hood, a hash table uses a dynamic array of linked lists to efficiently store key/value pairs. When inserting a key/value pair, a hash function first maps the key, which is typically a string (or any data that can be hashed, depending on the implementation of the hash table), to an integer value and, by extension, to an index in the underlying dynamic array. Then, the value associated with the key is added to the linked list stored at that index in the dynamic array, and a reference to the key is also stored with the value

Iteration

Iteration over a key-value collection yields the keys. To iterate over the key-value pairs, iterate over .items(); to iterate over values use .values(); the .keys() method returns an iterator to the keys.

Check for keys

days_set = {"Mon", "Tue", "Wed"}
print("Mon" in days_set) # True
print("Sun" in days_set) # False

days_dict = {"Mon": 1, "Tue": 2, "Wed": 3}
print("Mon" in days_dict) # True
print("Sun" in days_dict) # False

Deleting items

this_dict = {
  "brand": "Ford",
  "model": "Mustang",
  "year": 1964
}

this_dict.pop("model")

foo = {42,41}
foo.remove(42)
# foo.remove(42) -> **throws error**
foo.discard(41)
foo.discard(41) # -> **no error .discard()**

Examples

Invalid Transactions **

Record all transactions done at a particular time. Recording the person and the location.Example:

{time: {person: {location}, person2: {location1, location2}}, time: {person: {location}}}

['alice,20,800,mtv', 'bob,50,1200,mtv', 'bob,20,100,beijing']

{
20: {'alice': {'mtv'}, 'bob': {'beijing'}},
50: {'bob': {'mtv'}}
}

For each transaction, check if the amount is invalid - and add it to the invalid transactions if so.
For each transaction, go through invalid times (+-60), check if a transaction by the same person happened in a different city - and add it to the invalid transactions if so.

from collections import defaultdict

""" 
https://www.notion.so/paulonteri/Hashtables-Hashsets-220d9f0e409044c58ec6c2b0e7fe0ab5#cf22995975274881a28b544b0fce4716
"""

class Solution(object):
    def invalidTransactions(self, transactions):
        """ 
        - Record all transactions done at a particular time. Recording the person and the location. Example:
            `['alice,20,800,mtv','bob,50,1200,mtv','bob,20,100,beijing']` :\n
            ` 
            {   
            20: {'alice': {'mtv'}, 'bob': {'beijing'}}, 
            50: {'bob': {'mtv'}}
            } 
            ` \n
            `{time: {person: {location}, person2: {location1, location2}}, time: {person: {location}}}`
        - For each transaction, check if the amount is invalid - and add it to the invalid transactions if so.
        - For each transaction, go through invalid times (+-60), check if a transaction by the same person happened
            in a different city - and add it to the invalid transactions if so.
        """
        invalid = []

        # Record all transactions done at a particular time
        #   including the person and the location.
        transaction_time = defaultdict(dict)
        for transaction in transactions:
            name, str_time, amount, city = transaction.split(",")
            time = int(str_time)

            if name not in transaction_time[time]:
                transaction_time[time][name] = {city, }
            else:
                transaction_time[time][name].add(city)

        for transaction in transactions:
            name, str_time, amount, city = transaction.split(",")
            time = int(str_time)

            # # check amount
            if int(amount) > 1000:
                invalid.append(transaction)
                continue

            # # check if person did transaction within 60 minutes in a different city
            for inv_time in range(time-60, time+61):
                if inv_time not in transaction_time:
                    continue
                if name not in transaction_time[inv_time]:
                    continue

                trans_by_name_at_time = transaction_time[inv_time][name]

                # check if transactions were done in a different city
                if city not in trans_by_name_at_time or len(trans_by_name_at_time) > 1:
                    invalid.append(transaction)
                    break

        return invalid

Longest Substring with K Distinct Characters

Dot Product of Two Sparse Vectors

""" 
Dot Product of Two Sparse Vectors:

Given two sparse vectors, compute their dot product.
Implement class SparseVector:
SparseVector(nums) Initializes the object with the vector nums
dotProduct(vec) Compute the dot product between the instance of SparseVector and vec
A sparse vector is a vector that has mostly zero values, you should store the sparse vector efficiently and compute the dot product between two SparseVector.

Follow up: What if only one of the vectors is sparse?

Example 1:
    Input: nums1 = [1,0,0,2,3], nums2 = [0,3,0,4,0]
    Output: 8
    Explanation: v1 = SparseVector(nums1) , v2 = SparseVector(nums2)
    v1.dotProduct(v2) = 1*0 + 0*3 + 0*0 + 2*4 + 3*0 = 8
Example 2:
    Input: nums1 = [0,1,0,0,0], nums2 = [0,0,0,0,2]
    Output: 0
    Explanation: v1 = SparseVector(nums1) , v2 = SparseVector(nums2)
    v1.dotProduct(v2) = 0*0 + 1*0 + 0*0 + 0*0 + 0*2 = 0
Example 3:
    Input: nums1 = [0,1,0,0,2,0,0], nums2 = [1,0,0,0,3,0,4]
    Output: 6

https://leetcode.com/problems/dot-product-of-two-sparse-vectors
"""

class SparseVector:
    def __init__(self, nums):
        self.non_zero = {}
        for idx, num in enumerate(nums):
            if num != 0:
                self.non_zero[idx] = num

    # Return the dotProduct of two sparse vectors
    def dotProduct(self, vec: 'SparseVector'):
        total = 0
        for idx in self.non_zero:
            if idx in vec.non_zero:
                total += self.non_zero[idx] * vec.non_zero[idx]

        return total

# Your SparseVector object will be instantiated and called as such:
# v1 = SparseVector(nums1)
# v2 = SparseVector(nums2)
# ans = v1.dotProduct(v2)

Random Pick Index *

""" 
398. Random Pick Index

Given an integer array nums with possible duplicates, randomly output the index of a given target number. You can assume that the given target number must exist in the array.
Implement the Solution class:
    Solution(int[] nums) Initializes the object with the array nums.
    int pick(int target) Picks a random index i from nums where nums[i] == target. 
        If there are multiple valid i's, then each index should have an equal probability of returning.


Example 1:
    Input
        ["Solution", "pick", "pick", "pick"]
        [[[1, 2, 3, 3, 3]], [3], [1], [3]]
    Output
        [null, 4, 0, 2]
    Explanation
        Solution solution = new Solution([1, 2, 3, 3, 3]);
        solution.pick(3); // It should return either index 2, 3, or 4 randomly. Each index should have equal probability of returning.
        solution.pick(1); // It should return 0. Since in the array only nums[0] is equal to 1.
        solution.pick(3); // It should return either index 2, 3, or 4 randomly. Each index should have equal probability of returning.

https://leetcode.com/problems/random-pick-index
"""

from typing import List
import collections
import random

class Solution:

    def __init__(self, nums):
        self.store = collections.defaultdict(list)
        for idx, num in enumerate(nums):
            self.store[num].append(idx)

    def pick(self, target: int):
        indices = self.store[target]
        return indices[random.randint(0, len(indices)-1)]

# Your Solution object will be instantiated and called as such:
# obj = Solution(nums)
# param_1 = obj.pick(target)

# Other solution https://leetcode.com/problems/random-pick-index/discuss/88153/Python-reservoir-sampling-solution.

class Solution:

    def __init__(self, nums: List[int]):
        self.nums = nums

    def pick(self, target: int):
        """ 
        Reservoir sampling
        - at every valid index, try to see whether the current index can be picked
        """
        count = 0
        idx = 0
        for i in range(len(self.nums)):
            if self.nums[i] == target:
                count += 1
                if random.randint(0, count - 1) == 0:
                    idx = i
        return idx

How to store an class in a hashtable

# it can also work without the __hash__ function lol
class Node:
    def __init__(self, x):
        self.val = int(x)

x = Node(1)
y = Node(2)
z = Node(2)

store = {x: 1}
store[y] = 2
store[z] = 2

print(store.keys())
# dict_keys([<__main__.Node object at 0x7fe0482a5f50>, <__main__.Node object at 0x7fe0482a5fd0>, <__main__.Node object at 0x7fe0482a8050>])

Sorting by keys/value

store = {'Zebra':2, 'Apple':3, 'Honey Badger':1 }

print(sorted(store)) # ['Apple', 'Honey Badger', 'Zebra']
print(sorted(store, reverse=True)) # ['Zebra', 'Honey Badger', 'Apple']
print(sorted(store, key=lambda x: store[x])) # ['Honey Badger', 'Zebra', 'Apple']

hashtable vs hashset vs hashmap python

HashTable == HashMap == Dictionary

Hashset == Set

You can compare hashtables

>>> x = {'a': 1, 'e': 1, 'b': 1}
>>> y = {'e': 1, 'a': 1, 'b': 1}
>>> x == y
True

Examples:

Hash table libraries

There are multiple hash table-based data structures commonly used in set, dict, collections.defaultdict, collections.OrderedDict and collections.Counter.

The difference between set and the other three is that is set simply stores keys, whereas the others store key-value pairs. All have the property that they do not allow for duplicate keys.

`collections.defaultdict`

In a dict, accessing value associated with a key that is not present leads to a KeyError exception. However, a collections.defaultdict returns the default value of the type that was specified when the collection was instantiated.

from collections import defaultdict

list_dict = defaultdict(list)
print(list_dict['key']) # []
list_dict['key'].append(1) # adding constant 1 to the list
print(list_dict['key']) # [1] -> list containing the constant [1]

int_dict = defaultdict(int)
print(int_dict['key2']) # 0
int_dict['key2'] += 1 
print(int_dict['key2']) # 1

ice_cream = defaultdict(lambda: 'Vanilla')
ice_cream['Sarah'] = 'Chunky Monkey'
ice_cream['Abdul'] = 'Butter Pecan'
print(ice_cream['Sarah']) # Chunky Monkey
print(ice_cream['Joe']) # Vanilla
print(ice_cream.values()) # dict_values(['Chunky Monkey', 'Butter Pecan', 'Vanilla'])

# Works like normal dict
for key in list_dict:
    print(key, list_dict[key])

when it comes to build hash's hash's hash kind of jobs, defaultdict is really handy.

The behavior of defaultdict can be easily mimicked using dict.setdefault instead of d[key] in every call.

In other words, the code:

from collections import defaultdict

d = defaultdict(list)

print(d['key'])                        # empty list []
d['key'].append(1)                     # adding constant 1 to the list
print(d['key'])                        # list containing the constant [1]

is equivalent to:

d = dict()

print(d.setdefault('key', list()))     # empty list []
d.setdefault('key', list()).append(1)  # adding constant 1 to the list
print(d.setdefault('key', list()))     # list containing the constant [1]

Invalid Transactions **

Record all transactions done at a particular time. Recording the person and the location.Example:

{time: {person: {location}, person2: {location1, location2}}, time: {person: {location}}}

['alice,20,800,mtv', 'bob,50,1200,mtv', 'bob,20,100,beijing']

{
20: {'alice': {'mtv'}, 'bob': {'beijing'}},
50: {'bob': {'mtv'}}
}

For each transaction, check if the amount is invalid - and add it to the invalid transactions if so.
For each transaction, go through invalid times (+-60), check if a transaction by the same person happened in a different city - and add it to the invalid transactions if so.

from collections import defaultdict

""" 
https://www.notion.so/paulonteri/Hashtables-Hashsets-220d9f0e409044c58ec6c2b0e7fe0ab5#cf22995975274881a28b544b0fce4716
"""

class Solution(object):
    def invalidTransactions(self, transactions):
        """ 
        - Record all transactions done at a particular time. Recording the person and the location. Example:
            `['alice,20,800,mtv','bob,50,1200,mtv','bob,20,100,beijing']` :\n
            ` 
            {   
            20: {'alice': {'mtv'}, 'bob': {'beijing'}}, 
            50: {'bob': {'mtv'}}
            } 
            ` \n
            `{time: {person: {location}, person2: {location1, location2}}, time: {person: {location}}}`
        - For each transaction, check if the amount is invalid - and add it to the invalid transactions if so.
        - For each transaction, go through invalid times (+-60), check if a transaction by the same person happened
            in a different city - and add it to the invalid transactions if so.
        """
        invalid = []

        # Record all transactions done at a particular time
        #   including the person and the location.
        transaction_time = defaultdict(dict)
        for transaction in transactions:
            name, str_time, amount, city = transaction.split(",")
            time = int(str_time)

            if name not in transaction_time[time]:
                transaction_time[time][name] = {city, }
            else:
                transaction_time[time][name].add(city)

        for transaction in transactions:
            name, str_time, amount, city = transaction.split(",")
            time = int(str_time)

            # # check amount
            if int(amount) > 1000:
                invalid.append(transaction)
                continue

            # # check if person did transaction within 60 minutes in a different city
            for inv_time in range(time-60, time+61):
                if inv_time not in transaction_time:
                    continue
                if name not in transaction_time[inv_time]:
                    continue

                trans_by_name_at_time = transaction_time[inv_time][name]

                # check if transactions were done in a different city
                if city not in trans_by_name_at_time or len(trans_by_name_at_time) > 1:
                    invalid.append(transaction)
                    break

        return invalid

`collections.OrderedDict`

An OrderedDict is a dictionary subclass that remembers the order that keys were first inserted. The only difference between dict() and collections.OrderedDict() is that:

OrderedDict preserves the order in which the keys are inserted. A regular dict doesn’t track the insertion order, and iterating it gives the values in an arbitrary order. By contrast, the order the items are inserted is remembered by OrderedDict.

from collections import OrderedDict

od = OrderedDict()
od['a'] = 1
od['b'] = 2
od['c'] = 3
od['d'] = 4

print(od.keys()) # odict_keys(['a', 'b', 'c', 'd'])
od.popitem(last=True)
print(od.keys()) # odict_keys(['a', 'b', 'c'])

`sortedcontainers.SortedDict`

`set`

A set is an unordered collection of items. Every set element is unique (no duplicates) and must be immutable (cannot be changed).

However, a set itself is mutable. We can add or remove items from it.

Sets can also be used to perform mathematical set operations like union, intersection, symmetric difference, etc.

A set is a collection that is both unordered and unindexed.

Simple operations

The remove() method raises an error when the specified element doesn’t exist in the given set, however, the discard() method doesn’t raise any error if the specified element is not present in the set and the set remains unchanged.

Examples

foo = set()

foo.add(42)
foo.remove(42)
# foo.remove(42) -> **throws error**
foo.add(41)
foo.discard(41)
foo.discard(41) # -> **no error**
foo.add(43)
foo.add(43)
foo.add(44)
print(foo)  # {43, 44}

bar = {1, 2, 2, 2, 3, 3} 
print(bar) # {1, 2, 3}

# empty set
print(set())
# from string
print(set('Python'))  # {'n', 'P', 'o', 't', 'h', 'y'}
# from list
print(set(['a', 'e', 'i', 'o', 'u']))  # {'a', 'o', 'e', 'i', 'u'}
# from set
print(set({'a', 'e', 'i', 'o', 'u'}))  # {'u', 'i', 'a', 'o', 'e'}
# from dictionary
# {'u', 'i', 'a', 'o', 'e'}
print(set({'a': 1, 'e': 2, 'i': 3, 'o': 4, 'u': 5}))
# from frozen set
frozen_set = frozenset(('a', 'e', 'i', 'o', 'u'))  # {'u', 'i', 'a', 'o', 'e'}
print(set(frozen_set))

Advanced operations

Union of Sets

The union operation on two sets produces a new set containing all the distinct elements from both the sets. In the below example the element “Wed” is present in both the sets.

DaysA = set(["Mon","Tue","Wed"])
DaysB = set(["Wed","Thu","Fri","Sat","Sun"])
AllDays = DaysA|DaysB
print(AllDays) # set(['Wed', 'Fri', 'Tue', 'Mon', 'Thu', 'Sat'])

Intersection of Sets

The intersection operation on two sets produces a new set containing only the common elements from both the sets. In the below example the element “Wed” is present in both the sets.

DaysA = set(["Mon","Tue","Wed"])
DaysB = set(["Wed","Thu","Fri","Sat","Sun"])
AllDays = DaysA & DaysB
print(AllDays) # set(['Wed'])

Difference of Sets

The difference operation on two sets produces a new set containing only the elements from the first set and none from the second set. In the below example the element “Wed” is present in both the sets so it will not be found in the result set.

DaysA = set(["Mon","Tue","Wed"])
DaysB = set(["Wed","Thu","Fri","Sat","Sun"])
AllDays = DaysA - DaysB
print(AllDays) # set(['Mon', 'Tue'])

Compare Sets

We can check if a given set is a subset or superset of another set. The result is True or False depending on the elements present in the sets.

DaysA = set(["Mon","Tue","Wed"])
DaysB = set(["Mon","Tue","Wed","Thu","Fri","Sat","Sun"])
print(DaysA <= DaysB) # True
print(DaysB >= DaysA) # True

`collections.Counter`

A collections.Counter is used for counting the number of occurrences of keys, with a number of setlike operations. Missing keys will return a count of 0.

import collections

list1 = ['x', 'y', 'z', 'x', 'x', 'x', 'y', 'z']
x = collections.Counter(list1)
print(x)  # Counter({'x': 4, 'y': 2, 'z': 2})
x['a'] -= 1
print(x['a']) # -1

foo = collections.Counter(a=3, b=1)
bar = collections.Counter(a=1, b=2)

# add two counters together
print(foo+bar)  # Counter({'a': 4, 'b': 3})
# subract -> ignores negative
print(foo - bar)  # Counter({'a': 2})
# intersection:  min(foo[x], bar[x]),
print(foo & bar)  # Counter({'a': 1, 'b': 1})
# union: max(foo[x], bar[x]),
print(foo | bar)  # ({'a': 3, 'b': 2})

"""
>>> c
Counter({'5': 2, '3': 2, '.': 1, 'e': 1, '9': 1})

>>> c['E']
0

>>> 'E' in c
False

"""

Find the original version of this page (with additional content) on Notion here.

Heaps & Priority Queues

Heaps

Coding Patterns: Two Heaps

Heaps And Maps - InterviewBit

Implement A Binary Heap - An Efficient Implementation of The Priority Queue ADT (Abstract Data Type)

Heap Visualization

A heap is a specialized binary tree. Specifically, it is a complete binary tree. The keys must satisfy the heap property — the key at each node is at least as great as the keys stored at its children. (Min and Max heaps are complete binary trees with some unique properties)

A max-heap can be implemented as an array; the children of the node at index i are at indices 2i + 1 and 2i + 2. The array representation for the max-heap in Figure [561, 314, 401, 28, 156, 359, 271, 11, 3].

A max-heap supports O(log n) insertions, O(1) time lookup for the max element, and O(log n) deletion of the max element. The extract-max operation is defined to delete and return the maximum element. Searching for arbitrary keys has O(n) time complexity.

A heap is sometimes referred to as a priority queue because it behaves like a queue, with one difference: each element has a “priority” associated with it, and deletion removes the element with the highest priority.

The min-heap is a completely symmetric version of the data structure and supports O(1) timelookups for the minimum element.

Screenshot 2021-10-02 at 18.52.22.png

A heap, as an implementation of a priority queue, is a good tool for solving problems that involve extremes, like the most or least of a given metric.

There are other words that indicate a heap might be useful:

Largest
Smallest
Biggest
Smallest
Best
Worst
Top
Bottom
Maximum
Minimum
Optimal

Whenever a problem statement indicates that you’re looking for some extreme element, it’s worthwhile to think about whether a priority queue would be useful.

Representation as an array

Root node, i = 0 is the first item of the array
A left child node, left(i) = 2i + 1
A right child node, right(i) = 2i + 2
A parent node, parent(i) = (i-1) / 2

Screenshot 2021-10-03 at 08.03.11.png

Time complexity

Screenshot 2021-08-17 at 05.30.39.png

Get Max or Min Element
- The Time Complexity of this operation is O(1).
Remove Max or Min Element
- The time complexity of this operation is O(Log n) because we need to maintain the max/mix at their root node, which takes Log n operations.
Insert an Element
- Time Complexity of this operation is O(Log n) because we insert the value at the end of the tree and traverse up to remove violated property of min/max heap.

        Heap                  Sorted array
        Average  Worst case   Average   Worst case

Space   O(n)     O(n)         O(n)      O(n)

Search  O(n)     O(n)         O(log n)  O(log n)

Insert* O(1)     **O(log n)**     O(n)      O(n)

Delete* O(log n) **O(log n)**     O(n)      O(n)

Examples:

🌳 Prim's Minimum Spanning Tree Algorithm *

n smallest value → min heap, n largest value → max heap
Kth Largest Number in a Stream
Continuous Median

Meeting Rooms II/Laptop Rentals

"""
Meeting Rooms II

Given an array of meeting time intervals consisting of start and end times:
[[s1,e1],[s2,e2],...] (si < ei), find the minimum number of conference rooms required.

Input:
    [[0,30],[5,10],[15,20]]
    [[0,30]]
    [[0,30],[5,10],[1,20],[7,30],[50,10],[15,20],[0,30],[5,10],[15,20]]
Output:
    2
    1
    6

https://leetcode.com/problems/meeting-rooms-ii/
"""
from typing import List
import heapq
"""
Laptop Rentals:

You're given a list of time intervals during which students at a school need a laptop.
These time intervals are represented by pairs of integers [start, end], where 0 <= start < end.
However, start and end don't represent real times; therefore, they may be greater than 24.
No two students can use a laptop at the same time, but immediately after a student is done using a laptop,
    another student can use that same laptop. For example, if one student rents a laptop during the time interval [0, 2],
    another student can rent the same laptop during any time interval starting with 2.
Write a function that returns the minimum number of laptops that the school needs to rent
 such that all students will always have access to a laptop when they need one.

Sample Input
    times =
    [
    [0, 2],
    [1, 4],
    [4, 6],
    [0, 4],
    [7, 8],
    [9, 11],
    [3, 10],
    ]
Sample Output
    3

https://www.algoexpert.io/questions/Laptop%20Rentals
"""

# this can be optimized futher plus variables have been overused:
# this is to help in undertanding the solution
# time O(n log(n)) | space O(n)
class Solution:
    def minMeetingRooms(self, intervals: List[List[int]]):

        if not intervals:
            return 0

        # sort meetings by starting time
        intervals.sort(key=lambda x: x[0])

        # # Logic:
        # if the next meeting is earlier than the earliest ending time, then no room will be free for it.
        # Otherwise, update the ending time (for the room)

        # # (ending_times heap) used to store the ending times of all meeting rooms
        # if a second meeting is held in a room, we replace the 1st's ending time,
        # we delete the 1st meeting ending time and add the 2nd's

        # create ending times heap
        # the heap will help us in keep the earliest ending time per room 'on top, [0]'
        ending_times = [intervals[0][1]]

        i = 1
        while i < len(intervals):
            # in any case, we will add the meeting's ending time to the ending_times,
            # however, if the earliest ending time is less than it's starting, it means those two can share a room
            # so we remove the earlier one's ending time

            # # check if (curr starting time) overlaps earliest ending time
            curr_meeting = intervals[i]
            # cannot share room
            if curr_meeting[0] < ending_times[0]:
                # similar to adding another meeting room
                heapq.heappush(ending_times, curr_meeting[1])
            # can share room
            # meeting starts later than the earliest ending
            # free room -> not overlap
            else:
                # remove the first room's ending time from the count
                # similar to updating meeting room's earliest ending
                heapq.heappop(ending_times)
                heapq.heappush(ending_times, curr_meeting[1])

            i += 1

        # we always added rooms to the heap and:
        # whenever we found conflicts in times we didn't remove from the heap but,
        # we removed when we were reusing the same room
        # the meeting ending times that were not replaced
        return len(ending_times)

"""
-----------------------------------------------------------------------------------------------------------------------------------------------
[[0, 2], [0, 4], [1, 4], [3, 10], [4, 6], [7, 8], [9, 11]]

[9,7,10]

[[0, 10], [0, 20], [1, 9], [2, 8], [3, 7], [4, 6], [5, 6], [10, 15], [11, 12]]

[15, 20, 12, 8, 7, 6, 6]
"""

# time O(n^2) time | space O(n)
def laptopRentalsBF(times):
    times.sort()

    # will record when the currently borrowed laptop will be free (end time)
    needed = []
    for time in times:

        added = False
        # check if we can find a laptop that we will use once it is free
        for idx in range(len(needed)):
            if needed[idx] <= time[0]:
                # use laptop when it gets free
                needed[idx] = time[1]
                added = True
                break

        if not added:
            # no free laptop -> we need another one
            needed.append(time[1])

    return len(needed)

"""
-----------------------------------------------------------------------------------------------------------------------------------------------
use a min-heap to get the earliest time a laptop will be free
sort the input array to ensure the ones with the earliest times come first
"""

def laptopRentals(times):
    times.sort()

    # will record when the currently borrowed laptop will be free (end time)
    needed = []
    for time in times:

        # # check if we can find a laptop that we will use once it is free
        if needed and needed[0] <= time[0]:
            # replace the earliest free laptop
            heapq.heappop(needed)
            heapq.heappush(needed, time[1])
        else:
            # no free laptop -> we need another one
            heapq.heappush(needed, time[1])

    return len(needed)

Path With Maximum Minimum Value *

Screenshot 2021-10-18 at 21.25.17.png

Screenshot 2021-10-18 at 21.25.29.png

Screenshot 2021-10-18 at 21.25.47.png

Screenshot 2021-10-18 at 21.26.00.png

Uses: reversed Prim's Minimum Spanning Tree Algorithm

""" 
Path With Maximum Minimum Value:

Given an m x n integer matrix grid, 
    return the maximum score of a path starting at (0, 0) and ending at (m - 1, n - 1) moving in the 4 cardinal directions.
The score of a path is the minimum value in that path.
For example, the score of the path 8 → 4 → 5 → 9 is 4.

Example 1:
    Input: grid = [[5,4,5],[1,2,6],[7,4,6]]
    Output: 4
    Explanation: The path with the maximum score is highlighted in yellow. 
Example 2:
    Input: grid = [[2,2,1,2,2,2],[1,2,2,2,1,2]]
    Output: 2
Example 3:
    Input: grid = [[3,4,6,3,4],[0,2,1,1,7],[8,8,3,2,7],[3,2,4,9,8],[4,1,2,0,0],[4,6,5,4,3]]
    Output: 3

https://leetcode.com/problems/path-with-maximum-minimum-value/
https://leetcode.com/problems/path-with-maximum-minimum-value/discuss/457525/JAVA-A-Summery-of-All-Current-Solutions
https://www.notion.so/paulonteri/Heaps-Priority-Queues-bb4a8de1dbe54089854d8d03c833126c#a8a0e9b8526c4b42a37090b4df52ed3a
"""

import heapq

""" 
To prune our search tree, we take a detailed look at our problem. 
Since we have no need to find the shortest path, we could only focus on how to find a path avoiding small values. 
To do so, we could sort adjacents of our current visited vertices to find the maximum, 
    and always choose the maximum as our next step. 
To implement, we could use a heap to help us maintaining all adjacents and the top of the heap is the next candidate.

Time: O(Vlog(V) + E). Because the maximum number of element in the queue cannot be larger than V so pushing and popping from queue is O(log(V)). 
    Also we only push each vertex to the queue once, so at maximum we do it V times. Thats Vlog(V). The E bit comes from the for loop inside the while loop.
Space: O(V) where V is the maximum depth of our search tree.

Uses: reversed Prim's Minimum Spanning Tree Algorithm
https://www.notion.so/paulonteri/Trees-Graphs-edc3401e06c044f29a2d714d20ffe185#596bc798759a4edabe22a895aadeb12c
"""

class Solution(object):
    def maximumMinimumPath(self, A):
        """
        ensure we always visit the larger neighbours 
        the max_heap will ensure that the smallest neighbours are not visited

        Even if we took a wrong path, we can always take the right path again 
            because the max_heap will return us to the next valid large spot/neighbour
        """
        DIRS = [[0, 1], [1, 0], [0, -1], [-1, 0]]

        maxscore = A[0][0]
        max_heap = []
        # negate element to simulate max heap
        heapq.heappush(max_heap, (-A[0][0], 0, 0))

        while len(max_heap) != 0:
            val, row, col = heapq.heappop(max_heap)

            # update max
            maxscore = min(maxscore, -val)

            # reached last node
            if row == len(A) - 1 and col == len(A[0]) - 1:
                break

            for d in DIRS:
                new_row, new_col = d[0] + row, d[1] + col

                is_valid_row = new_row >= 0 and new_row < len(A)
                is_valid_col = new_col >= 0 and new_col < len(A[0])
                if is_valid_row and is_valid_col and A[new_row][new_col] >= 0:
                    heapq.heappush(
                        max_heap, (-A[new_row][new_col], new_row, new_col)
                    )
                    # mark as visited
                    A[new_row][new_col] = -1

        return maxscore

Task Scheduler *

"""
621. Task Scheduler

Given a characters array tasks, representing the tasks a CPU needs to do, where each letter represents a different task.
Tasks could be done in any order. Each task is done in one unit of time. 
For each unit of time, the CPU could complete either one task or just be idle.
However, there is a non-negative integer n that represents the cooldown period between two same tasks (the same letter in the array), 
    that is that there must be at least n units of time between any two same tasks.
Return the least number of units of times that the CPU will take to finish all the given tasks.

Example 1:
    Input: tasks = ["A","A","A","B","B","B"], n = 2
    Output: 8
    Explanation: 
        A -> B -> idle -> A -> B -> idle -> A -> B
        There is at least 2 units of time between any two same tasks.
Example 2:
    Input: tasks = ["A","A","A","B","B","B"], n = 0
    Output: 6
        Explanation: On this case any permutation of size 6 would work since n = 0.
        ["A","A","A","B","B","B"]
        ["A","B","A","B","A","B"]
        ["B","B","B","A","A","A"]
        ...
        And so on.
Example 3:
    Input: tasks = ["A","A","A","A","A","A","B","C","D","E","F","G"], n = 2
    Output: 16
    Explanation: 
        One possible solution is
        A -> B -> C -> A -> D -> E -> A -> F -> G -> A -> idle -> idle -> A -> idle -> idle -> A

Constraints:
    1 <= task.length <= 104
    tasks[i] is upper-case English letter.
    The integer n is in the range [0, 100].

https://leetcode.com/problems/task-scheduler
"""

from typing import List
from collections import Counter
from heapq import heapify, heappop, heappush

""" 
tasks = ["A","A","A","B","B","B"], n = 2

A B A B ,n=2 -> A,B,ID,A,B 
A A B A ,n=2 -> A,B,ID,A,ID,A 
A A B B ,n=2 -> A,B,ID,A,B 

["A","A","A","A","A","A","B","C","D","E","F","G"], n = 2
Counter({'A': 6, 'B': 1, 'C': 1, 'D': 1, 'E': 1, 'F': 1, 'G': 1})
[A, , ,A, , ,A, , ,A, , ,A, , ,A]
[A,B, ,A, , ,A, , ,A, , ,A, , ,A]
[A,B,C,A, , ,A, , ,A, , ,A, , ,A]
[A,B,C,A,D, ,A, , ,A, , ,A, , ,A]
[A,B,C,A,D,E,A,F,G,A, , ,A, , ,A] ... quickly fill
[A,B,C, A,D,E, A,F,G, A,idle,idle, A,idle,idle, A] => length 16

"""

class Solution:
    def leastInterval(self, tasks: List[str], n: int):
        """ 
        Steps:
        - `time_taken` = 0
        - Have a `max_heap` that contains the counts of each task
        - Have a while loop:
            - takes at most n+1 tasks from the `max_heap`
            - processes them (reduce count by one)
            - records how many tasks it has processed ( add them to `time_taken`)
                - if not at the end of the task queue / max_heap is not empty:
                    - the minimum time taken is n+1 `{tasks processed + waiting time(if any)} == n+1`
                - else: time taken is the number of tasks done

        Video tutorials:
        - https://youtu.be/Z2Plc8o1ld4
        - https://youtu.be/ySTQCRya6B0

        """
        if n == 0:
            return len(tasks)

        time_taken = 0

        # create max_heap (negate values added to simulate max_heap)
        max_heap = [-count for count in Counter(tasks).values()]
        heapify(max_heap)
        while max_heap:
            curr_processing = []

            # # get tasks to be processed
            for _ in range(n+1):
                if not max_heap:
                    continue
                curr_processing.append(-heappop(max_heap))

            # # process tasks and return to heap if not yet done with task
            for task_count in curr_processing:
                if task_count-1 > 0:
                    heappush(max_heap, -(task_count-1))

            # # record how many tasks we processed
            if not max_heap:
                # if we reached the end, (no more tasks)
                # we might have processed less than n+1 items as there is no waiting time after each
                time_taken += len(curr_processing)
            else:
                # if not at the end,
                # always, (tasks processed + waiting time(if any)) == n+1
                time_taken += n+1

        return time_taken

Reorganize String **

""" 
Reorganize String

Given a string s, rearrange the characters of s so that any two adjacent characters are not the same.
Return any possible rearrangement of s or return "" if not possible.

Example 1
    Input: s = "aab"
    Output: "aba"
Example 2:
    Input: s = "aaab"
    Output: ""
3:
    "aaaabbbbbccd"
    "babababcabcd"

Constraints:
    1 <= s.length <= 500
    s consists of lowercase English letters.

https://leetcode.com/problems/reorganize-string
"""

from collections import Counter
from heapq import heapify, heappush, heappop

class Solution:
    def reorganizeString(self, s: str):
        """ 
        The goal is to first exhaust the most-frequent chars. 
            We build a frequency dict of the letters in the string. We push all the letters into a max heap together with their frequencies
        We pop two letters at a time from the heap, add them to our result string, decrement their frequencies and push them back into heap. 
            Why do we have to pop two items/letters at a time you're wondering? 
            Because if we only pop one at a time, we will keep popping and pushing the same letter over and over again if that letter has a freq greater than 1. 
            Hence by popping two at time, adding them to result, decrementing their freq and finally pushing them back into heap, we guarantee that we are always alternating between letters.
        https://leetcode.com/problems/reorganize-string/discuss/492827/Python-Simple-heap-solution-with-detailed-explanation
        """
        res = []

        character_count = [(-count, char)
                           for char, count in Counter(s).items()]
        heapify(character_count)
        while len(res) < len(s):
            # # add most frequent
            # 1
            count_1, char_1 = heappop(character_count)
            count_1 *= -1
            res.append(char_1)
            # 2
            count_2 = 0
            if character_count:
                count_2, char_2 = heappop(character_count)
                count_2 *= -1
                res.append(char_2)

            # # return into heap
            if count_1 > 1:
                count_1 -= 1
                heappush(character_count, (-count_1, char_1))
            if count_2 > 1:
                count_2 -= 1
                heappush(character_count, (-count_2, char_2))

        for idx in range(1, len(s)):
            if res[idx-1] == res[idx]:
                return ""

        return "".join(res)

Heap sort

Priority Queue

Priority Queue Playlist

`heapq`

`heapq.heapify(a)`

import heapq
a = [3, 5, 1, 2, 6, 8, 7]

heapq.heapify(a)

a
# [1, 2, 3, 5, 6, 8, 7]

heapify() modifies the list in place but doesn’t sort it. A heap doesn’t have to be sorted to satisfy the heap property. However, since every sorted list does satisfy the heap property, running heapify() on a sorted list won’t change the order of elements in the list.

The first element, a[0], will always be the smallest element.

`heapq.heappop(a)`

To pop the smallest element while preserving the heap property, the Python heapq module defines heappop().

import heapq
a = [1, 2, 3, 5, 6, 8, 7]

heapq.heappop(a)
# 1

a
# [2, 5, 3, 7, 6, 8]

`heapq.heappush(a, 4)`

The Python heapq module also includes heappush() for pushing an element to the heap while preserving the heap property.

import heapq
a = [2, 5, 3, 7, 6, 8]

heapq.heappush(a, 4)
a
# [2, 5, 3, 7, 6, 8, 4]

heapq.heappop(a)
# 2
heapq.heappop(a)
# 3
heapq.heappop(a)
# 4

With miltidementional arrays

import heapq

arr = [[2, 1], [1, 1], [1, 2]]

heapq.heappop(arr)
# [1, 1]
heapq.heappop(arr)
# [1, 2]
heapq.heappop(arr)
# [2, 1]

🌳 Prim's Minimum Spanning Tree Algorithm *

Find the original version of this page (with additional content) on Notion here.

Math Tricks

Introduction

📌 TIPS | HACKS WHICH YOU CAN'T IGNORE AS A CODER ✨🎩 - LeetCode Discuss

Whenever you get an integer conversion problem, think of modulo % and floor division //

6.2 epi

Tips & Tricks

How to multiply matrices

Multiplying Matrices

https://youtu.be/vzt9c7iWPxs

row * col

Examples

Integer to Roman

$Screenshot 2021-11-23 at 18.31.32.png$

$Screenshot 2021-11-23 at 18.32.46.png$

$Screenshot 2021-11-23 at 18.33.33.png$

$Screenshot 2021-11-23 at 18.34.37.png$

class Solution {
    private static final int[] values = {1000, 900, 500, 400, 100, 90, 50, 40, 10, 9, 5, 4, 1};    
    private static final String[] symbols = {"M","CM","D","CD","C","XC","L","XL","X","IX","V","IV","I"};

    public String intToRoman(int num) {
        StringBuilder sb = new StringBuilder();
        // Loop through each symbol, stopping if num becomes 0.
        for (int i = 0; i < values.length && num > 0; i++) {
            // Repeat while the current symbol still fits into num.
            while (values[i] <= num) {
                num -= values[i];
                sb.append(symbols[i]);
            }
        }
        return sb.toString();
    }
}

class Solution:
    def intToRoman(self, num: int) -> str:
        digits = [(1000, "M"), (900, "CM"), (500, "D"), (400, "CD"), (100, "C"), 
                  (90, "XC"), (50, "L"), (40, "XL"), (10, "X"), (9, "IX"), 
                  (5, "V"), (4, "IV"), (1, "I")]

        roman_digits = []
        # Loop through each symbol.
        for value, symbol in digits:
            # We don't want to continue looping if we're done.
            if num == 0: break
            count, num = divmod(num, value)
            # Append "count" copies of "symbol" to roman_digits.
            roman_digits.append(symbol * count)
        return "".join(roman_digits)

Screen Recording 2021-11-23 at 18.34.59.mov

Reverse Integer

"""
Reverse Integer:

Given a 32-bit signed integer, reverse digits of an integer.
Assume we are dealing with an environment that could only store integers within the 32-bit signed integer range: [−231,  231 − 1].
For the purpose of this problem, assume that your function returns 0 when the reversed integer overflows.

https://leetcode.com/problems/reverse-integer/
"""

class Solution:
    def reverse(self, x):
        res = 0

        num = abs(x)
        while num > 0:
            last_digit = num % 10 # get last digit
            res = (10 * res) + last_digit

            num //= 10  # remove last digit

        # confirm 32-bit signed integer
        if res < -2**31 or res > 2**31-1:
            return 0

        #
        if x < 0:
            return -res
        return res

class SolutionB:
    def reverse(self, x: int):

        # check if negative
        negative = False
        if x < 0:
            negative = True

        num = list(str(x))
        rev_num = []

        # skip the minus sign(for negative values)
        length = len(num)
        maximum = length
        if negative:
            maximum = length - 1

        # reverse each character
        i = 0
        while i < maximum:
            rev_num.append(num.pop())
            i += 1

        # create new integer
        res = int("".join(rev_num))
        if negative:
            res = -res

        # confirm 32-bit signed integer
        if res < -2**31 or res > 2**31-1:
            return 0
        return res

Valid Number

""" 
Valid Number

A valid number can be split up into these components (in order):
    A decimal number or an integer.
    (Optional) An 'e' or 'E', followed by an integer.
A decimal number can be split up into these components (in order):
    (Optional) A sign character (either '+' or '-').
    One of the following formats:
        One or more digits, followed by a dot '.'.
        One or more digits, followed by a dot '.', followed by one or more digits.
        A dot '.', followed by one or more digits.
An integer can be split up into these components (in order):
    (Optional) A sign character (either '+' or '-').
    One or more digits.

For example, 
    all the following are valid numbers: 
        ["2", "0089", "-0.1", "+3.14", "4.", "-.9", "2e10", "-90E3", "3e+7", "+6e-1", "53.5e93", "-123.456e789"], 
    while the following are not valid numbers: 
        ["abc", "1a", "1e", "e3", "99e2.5", "--6", "-+3", "95a54e53"].
Given a string s, return true if s is a valid number.

Example 1:
    Input: s = "0"
    Output: true
Example 2:
    Input: s = "e"
    Output: false
Example 3:
    Input: s = "."
    Output: false
Example 4:
    Input: s = ".1"
    Output: true

https://leetcode.com/problems/valid-number
"""

from collections import Counter

# O(N) time | O(N) space
class Solution:
    def isNumber(self, s: str):
        """ 
        - verify all characters are 0-9,e,E,+,-,.
        - if has e/E's: 
            - run the verifyNumberWithEs(s)
        - else:
            - run the verifyNumberWithoutEs(s)
        """
        if not s:
            return False
        # verify all characters are 0-9,e,E,+,-,.
        for char in s:
            if not (char.isnumeric() or char in "eE+-."):
                return False
        # if has e/E's
        if 'e' in s or 'E' in s:
            return self.verifyNumberWithEs(s)
        else:
            return self.verifyNumberWithoutEs(s)

    def verifyNumberWithEs(self, s):
        """ 
        - verify e/E's 
            - only one

        - split s by the E's
            - followed by integer (not float)
            - order: [number, e, number]
                - run the verifyNumberWithoutEs() on the numbers
        """

        # only one E
        char_count = Counter(s)
        if char_count['e'] + char_count['E'] != 1:
            return False

        # split s
        e_split = []
        if 'e' in char_count:
            e_split = s.split("e")
        else:
            e_split = s.split("E")
        if len(e_split) != 2:
            return False

        # followed by integer (not float)
        if "." in e_split[1]:
            return False

        # run the verifyNumberWithoutEs() on the numbers
        return self.verifyNumberWithoutEs(e_split[0]) and self.verifyNumberWithoutEs(e_split[1])

    def verifyNumberWithoutEs(self, s):
        """ 
        Checks if a number is valid without considering e/E's
        - has numeric characters
        - check if has zero or one of -,+ at the beginning and remove it
        - check if has zero or one of .
            - verify . has digits on either side
        """
        char_count = Counter(s)

        # has numeric characters
        if not self.has_numeric_chars(s):
            return False

        # check if has zero or one of -,+ at the beginning and remove it
        sign_count = char_count['+'] + char_count['-']
        if not (sign_count == 1 or sign_count == 0):
            return False
        s_wo_signs = s
        if sign_count:
            s_wo_signs = s[1:]
            if not self.has_numeric_chars(s_wo_signs):
                return False
            if '+' in s_wo_signs or '-' in s_wo_signs:
                return False

        # check if has zero or one of .
        if not (char_count['.'] == 1 or char_count['.'] == 0):
            return False
        # verify . has digits on either side
        dot_split = s_wo_signs.split('.')
        if not self.has_numeric_chars(dot_split[0]) and not self.has_numeric_chars(dot_split[1]):
            return False

        return True

    def has_numeric_chars(self, s):
        for char in s:
            if char.isnumeric():
                return True
        return False

""" 
Constant space

"""

# O(N) time | O(1) space
class Solution_:
    def isNumber(self, s: str):
        """ 
        Digits
            - must exist
        Signs
            - one on either side of exponent
            - at beginning of string or just after exponent
            - must have digits after it
        Exponents
            - must have digits b4 & after it
            - can only be one
        Dots
            - cannot be after exponent
                - can be only on left side of exponent
                - max of one
            - digit on either side
        Anything else
            - invalid input
        """

        seen_digit = False
        seen_exponent = False
        seen_dot = False
        for idx, char in enumerate(s):
            # 0-9
            if char.isnumeric():
                seen_digit = True

            # "+-" one on either side of exponent
            # can be at beginning of string or just after exponent & must have digits after it
            elif char in "+-":
                if not (idx == 0 or s[idx-1] in "eE") or idx == len(s)-1:
                    return False

            # "eE" - must have digits b4 & after it & can only be one
            elif char in "eE":
                if not seen_digit or seen_exponent or idx == len(s)-1:
                    return False
                seen_exponent = True

            # "." max of one & can be only on left side of exponent & digit on either side
            elif char == ".":
                # max of one & can be only on left side of exponent
                if seen_dot or seen_exponent:
                    return False
                # digit on either side
                has_left_digit = False
                has_right_digit = False
                if idx > 0 and s[idx-1].isnumeric():
                    has_left_digit = True
                if idx < len(s)-1 and s[idx+1].isnumeric():
                    has_right_digit = True

                if not (has_left_digit or has_right_digit):
                    return False
                seen_dot = True

            # invalid character
            else:
                return False

        # digits must exist
        return seen_digit

""" 
test cases:
    "2"
    "0089"
    "-0.1"
    "+3.14"
    "4."
    "-.9"
    "2e10"
    "-90E3"
    "3e+7"
    "+6e-1"
    "53.5e93"
    "-123.456e789"
    "abc"
    "1a"
    "1e"
    "e3"
    "99e2.5"
    "--6"
    "-+3"
    "95a54e53"
"""

Maximum Swap

""" 
670. Maximum Swap:

You are given an integer num. You can swap two digits at most once to get the maximum valued number.
Return the maximum valued number you can get.

Example 1:
    Input: num = 2736
    Output: 7236
    Explanation: Swap the number 2 and the number 7.
Example 2:
    Input: num = 9973
    Output: 9973
    Explanation: No swap.

Needs many examples to understand
Drawing a chart of heaps and valleys can make it a bit easier to understand

4123 => 4321  
4312 => 4321 
4321 => 4321 
98368 => 98863
1993 => 9913

https://leetcode.com/problems/maximum-swap

similar to https://leetcode.com/problems/next-permutation/
"""

# use two pointers
class Solution_:
    def maximumSwap(self, num: int):
        """ 
        Ensure the largest value is as left as possible
        """
        num_arr = list(str(num))

        for i in range(len(num_arr)):
            # find largest that is as right as possible: eg 1993 => 9913
            largest = i
            for idx in range(i+1, len(num_arr)):
                if int(num_arr[idx]) >= int(num_arr[largest]):
                    largest = idx

            # if we found a larger value, swap & return
            if int(num_arr[largest]) > int(num_arr[i]):
                num_arr[largest], num_arr[i] = num_arr[i], num_arr[largest]
                return int("".join(num_arr))

        return num

""" 

"""

class Solution:
    def maximumSwap(self, num: int):
        """ 
        Ensure the largest values are as left as possible
        """
        num_arr = list(str(num))
        largest_idx_arr = list(range(len(num_arr)))

        # fill in the largest values to the right for each index in the array
        largest = len(num_arr)-1
        for idx in reversed(range(len(num_arr))):
            if int(num_arr[idx]) > int(num_arr[largest]):
                largest = idx
            largest_idx_arr[idx] = largest

        # swap left most
        for idx in range(len(num_arr)):
            largest_idx = largest_idx_arr[idx]
            # ignore same size numbers
            if num_arr[idx] == num_arr[largest_idx]:
                continue

            # swap and return
            num_arr[largest_idx], num_arr[idx] = num_arr[idx], num_arr[largest_idx]
            return int("".join(num_arr))

        return num

https://leetcode.com/problems/next-greater-element-iii/

$Screenshot 2021-11-29 at 05.27.01.png$

$Screenshot 2021-11-29 at 05.25.32.png$

$Screenshot 2021-11-29 at 05.25.57.png$

Screen Recording 2021-11-29 at 05.26.15.mov

Next Permutation **

$Screenshot 2021-10-15 at 06.47.46.png$

$Screenshot 2021-10-15 at 06.48.20.png$

$Screenshot 2021-10-15 at 06.48.42.png$

""" 
Next Permutation:

Implement next permutation, which rearranges numbers into the lexicographically next greater permutation of numbers.
If such an arrangement is not possible, 
    it must rearrange it as the lowest possible order (i.e., sorted in ascending order).
The replacement must be in place and use only constant extra memory.

Example 1:
    Input: nums = [1,2,3]
    Output: [1,3,2]
Example 2:
    Input: nums = [3,2,1]
    Output: [1,2,3]
Example 3:
    Input: nums = [1,1,5]
    Output: [1,5,1]
Example 4:
    Input: nums = [1]
    Output: [1]

Needs many examples to understand
Drawing a chart of heaps and valleys can make it a bit easier to understand

[1,3,2] => [2,1,3]

[1,2,3,4] => [1,2,4,3]
[4,1,2,3] => [4,1,3,2]
[3,4,2,1] => [4,1,2,3] - swapped 3 & 4 then sorted the numbers to the right of 4
[2,3,4,1] => [2,4,1,3] - swapped 3 & 4 then sorted the numbers to the right of 4

[15,2,--4--,6,--5--,2] => [15,2,--5--,2,4,6] - swapped 4 & 5 then sorted the numbers to the right of 5

https://leetcode.com/problems/next-permutation/
https://www.notion.so/paulonteri/Math-Tricks-8c99fd21a1d343f7bee1eaf0467ea362#4bda6bec59634b1ebf5bc34fb2edc542

similar to https://leetcode.com/problems/maximum-swap
"""

class Solution:
    def nextPermutation(self, nums):
        """
        1. look for peak that has its larger & smaller number furthest to the right
            - Note: peak => num[right] > num[left]
            - find **first smaller number** (furthest to the right)
            - then **find the number furthest to the right that is larger than it**
            - swap the smaller and larger
        2. if no peak was found srt the whole array and return
        3. sort the array to the right of where the larger number was placed 

        """
        small_num_idx = None

        # find first smaller number (furthest to the right)
        i = len(nums)-1
        largest = nums[-1]
        while not small_num_idx and i >= 0:
            if nums[i] < largest:
                small_num_idx = i
            largest = max(largest, nums[i])
            i -= 1

        # array is sorted in descending order
        if small_num_idx is None:
            nums.sort()
            return

        # find number (furthest to the right) larger than small_num
        for idx in reversed(range(small_num_idx+1, len(nums))):
            if nums[idx] > nums[small_num_idx]:
                # swap larger and smaller number
                nums[small_num_idx], nums[idx] = nums[idx], nums[small_num_idx]
                # sort area after where the larger swapped number was placed
                self.sort(nums, small_num_idx+1)

                return

    def sort(self, nums, sort_start):
        # nums[sort_start:] = list(sorted(nums[sort_start:]))
        for idx in range(sort_start, len(nums)):
            smallest = idx
            for i in range(idx, len(nums)):
                if nums[i] < nums[smallest]:
                    smallest = i
            nums[smallest], nums[idx] = nums[idx], nums[smallest]

String to Integer & Integer to String

"""
Integer to String
"""

def single_digit_to_char(digit):
    return chr(ord('0')+digit)

def int_to_string(x: int):
    if x == 0:
        return "0"

    is_neg = False
    if x < 0:
        is_neg, x = True, -x

    result = []
    while x > 0:
        digit = x % 10
        result.append(single_digit_to_char(digit))
        x = x // 10

    if is_neg:
        result.append('-')
    return "".join(reversed(result))

"""
String to Integer
"""

def single_char_to_int(character):
    # num_mapping = {
    #     "1": 1,
    #     "2": 2,
    #     "3": 3,
    #     "4": 4,
    #     "5": 5,
    #     "6": 6,
    #     "7": 7,
    #     "8": 8,
    #     "9": 9,
    #     "0": 0,
    # }
    # return num_mapping[character]
    return ord(character) - ord('0')

def string_to_int(s: str):
    is_neg = False
    num = 0
    multiplier = 1

    start_idx = 0
    if s and s[0] == "-":
        is_neg, start_idx = True, 1
    if s and s[0] == "+":
        start_idx = 1
    for idx in reversed(range(start_idx, len(s))):
        num += single_char_to_int(s[idx])*multiplier
        multiplier *= 10

    if is_neg:
        return -num
    return num

print(string_to_int("22"), type(string_to_int("22")))

String to Integer (atoi)

"""
String to Integer (atoi):

Implement atoi which converts a string to an integer.
The function first discards as many whitespace characters as necessary until the first non-whitespace character is found. 
Then, starting from this character takes an optional initial plus or minus sign followed by as many numerical digits as possible, and interprets them as a numerical value.
The string can contain additional characters after those that form the integral number, which are ignored and have no effect on the behavior of this function.
If the first sequence of non-whitespace characters in str is not a valid integral number,
 or if no such sequence exists because either str is empty or it contains only whitespace characters, no conversion is performed.
If no valid conversion could be performed, a zero value is returned.

Only the space character ' ' is considered a whitespace character.
Assume we are dealing with an environment that could only store integers within the 32-bit signed integer range: [−231,  231 − 1]. If the numerical value is out of the range of representable values, 231 − 1 or −231 is returned.
https://leetcode.com/problems/string-to-integer-atoi/
"""

class Solution:
    def myAtoi(self, string: str):

        idx = 0

        # skip whitespace
        while idx < len(string) and string[idx] == ' ':
            idx += 1

        # deal with number
        if idx < len(string) and (string[idx] == '-' or string[idx] == '+' or string[idx].isnumeric()):
            # find number
            start = idx
            if string[idx] == '-' or string[idx] == '+':  # handle stuff like "+-12"
                idx += 1
            while idx < len(string) and string[idx].isnumeric():
                idx += 1

            # convert into number
            if string[start] == '-':
                if idx-start == 1:
                    return 0
                return -self.convertToIntNeg(string[start+1:idx])
            elif string[start] == '+':
                if idx-start == 1:
                    return 0
                return self.convertToIntPos(string[start+1:idx])
            return self.convertToIntPos(string[start:idx])

        return 0

    def convertToIntPos(self, string):
        integer = int(string)
        if integer >= 2**31:
            return 2**31 - 1
        return integer

    def convertToIntNeg(self, string):
        integer = int(string)
        if integer >= 2**31:
            return 2**31
        return integer

"""
# Input: valid string
# Output: integer
# Assumptions:
    - some strings might start without white space
    - only ' ' is considered whitespace
    - some strings will not contain numerical digits after the whitespace
    - ignore everythong after the whitespace thet is not a -, + , or a numerical value
    - return 0 if no valis sol is found

# Examples:
'  -502apple' -> -502
'  -502 apple' -> -502
'  -502 200' -> -502
'+502 200' -> 502
'  t-502apple' -> 0

# # First Approach: 
- iterate through the string
# skip all the whitespace (while loop 1)
# check whether next character is -, +  or number: (while loop 2)
    - if not, return 0
    - if it is: continue iterating while storing all it's characters in an array ### O(1) time
# convert the stored characters into a number and return the number ### O(n) time
    - convert the array into an string (skipping -, +) then return it or negate and return it
# return 0
## time O(n) | O(n) space - where n is len(string) 

# # Second Approach:
- iterate through the string
# skip all the whitespace (while loop 1)
# check whether next character is -, +  or number: (while loop 2)
    - if not, return 0
    - if it is: continue iterating (keep track of the satrting and ending indices) ### O(1) time
# convert the found number string (we can get it using slicing) into a number and return the number ### O(n) time
    - return it or negate and return it
# return 0
## time O(n) | O(n) space - where n is len(string) 

def myAtoi(self, s: str):
    idx = 0

    # skip whitespace
    while idx < len(string) and string[idx] == ' ':
        idx += 1

    # deal with number
    if idx < len(string) and (string[idx] == '-' or string[idx] == '+' or string[idx].isnumeric())
        # find number
        start = idx
        while idx < len(string) and (string[idx] == '-' or string[idx] == '+' or string[idx].isnumeric())
            idx += 1

        # convert into number
        if string[start] == '-':
            return -int(string[start+1:idx])
        elif string[start] == '-':
            return int(string[start+1:idx])
        return int(string[start:idx])

    return 0

"""

Multiply Strings *

$Screenshot 2021-10-15 at 15.13.21.png$

$Screenshot 2021-10-15 at 15.53.19.png$

$Screenshot 2021-10-15 at 15.56.42.png$

""" 
Multiply Strings:

Given two non-negative integers num1 and num2 represented as strings, 
return the product of num1 and num2, also represented as a string.

Note: You must not use any built-in BigInteger library or convert the inputs to integer directly.

Example 1:
    Input: num1 = "2", num2 = "3"
    Output: "6"
Example 2:
    Input: num1 = "123", num2 = "456"
    Output: "56088"

https://leetcode.com/problems/multiply-strings
"""

class Solution:
    def multiply(self, num1: str, num2: str):
        if num1 == "0" or num2 == "0":
            return "0"
        res = [0] * (len(num1) + len(num2))

        for i_one in reversed(range(len(num1))):
            for i_two in reversed(range(len(num2))):
                # +1 is used to handle (0,0) i_one=0 i_two=0 carries
                # placing their carry will be easier if we move every element one step back/ to the right
                pos = i_one + i_two + 1

                carry = res[pos]
                multiplication = (int(num1[i_one]) * int(num2[i_two])) + carry

                # save
                res[pos] = multiplication % 10
                # place carry
                res[pos-1] += multiplication // 10

        # remove leading zeros
        idx = 0
        while res[idx] == 0:
            idx += 1
        res = res[idx:]

        # return answer
        return "".join([str(num) for num in res])

Pascal's Triangle

""" 
Pascal's Triangle

Given an integer numRows, return the first numRows of Pascal's triangle.

Example 1:
    Input: numRows = 5
    Output: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]
Example 2:
    Input: numRows = 1
    Output: [[1]]

https://leetcode.com/problems/pascals-triangle
"""

class Solution:
    def generate(self, numRows: int):
        triangle = []
        if numRows < 1:
            return triangle

        # add the first row
        triangle.append([1])

        for i in range(1, numRows):  # start with 2nd row
            row = []

            # we handle the first and last indices separately
            row.append(1)  # first index

            # items to calculate/add will always be equal to the index (i) - 1
            # for example in the 4th row (i=3) we calculate 2 values
            for x in range(1, i):
                # we know that each character is the sum of those above it: above left and above right
                row.append(triangle[i-1][x-1] + triangle[i-1][x])

            row.append(1)  # last index for row

            triangle.append(row)

        return triangle

Roman to Integer

""" 
Roman to Integer

Roman numerals are represented by seven different symbols: I, V, X, L, C, D and M.
        Symbol       Value
        I             1
        V             5
        X             10
        L             50
        C             100
        D             500
        M             1000
For example, 2 is written as II in Roman numeral, just two one's added together. 
12 is written as XII, which is simply X + II. The number 27 is written as XXVII, which is XX + V + II.

Roman numerals are usually written largest to smallest from left to right. 
However, the numeral for four is not IIII. Instead, the number four is written as IV. 
Because the one is before the five we subtract it making four. The same principle applies to the number nine, which is written as IX. 
There are six instances where subtraction is used:
    I can be placed before V (5) and X (10) to make 4 and 9. 
    X can be placed before L (50) and C (100) to make 40 and 90. 
    C can be placed before D (500) and M (1000) to make 400 and 900.
Given a roman numeral, convert it to an integer.

Example 1:
    Input: s = "III"
    Output: 3
Example 2:
    Input: s = "IV"
    Output: 4
Example 3:
    Input: s = "IX"
    Output: 9
Example 4:
    Input: s = "LVIII"
    Output: 58
    Explanation: L = 50, V= 5, III = 3.
Example 5:
    Input: s = "MCMXCIV"
    Output: 1994
    Explanation: M = 1000, CM = 900, XC = 90 and IV = 4.

https://leetcode.com/problems/roman-to-integer
"""

class Solution_:
    def romanToInt(self, s: str):

        key_map = {
            "I": 1,
            "V": 5,
            "X": 10,
            "L": 50,
            "C": 100,
            "D": 500,
            "M": 1000
        }

        num = 0

        idx = 0
        while idx < len(s):
            if s[idx] == "I":
                if idx+1 < len(s) and s[idx+1] == "V":
                    num += 4
                    idx += 2
                elif idx+1 < len(s) and s[idx+1] == "X":
                    num += 9
                    idx += 2
                else:
                    num += key_map[s[idx]]
                    idx += 1

            elif s[idx] == "X":
                if idx+1 < len(s) and s[idx+1] == "L":
                    num += 40
                    idx += 2
                elif idx+1 < len(s) and s[idx+1] == "C":
                    num += 90
                    idx += 2
                else:
                    num += key_map[s[idx]]
                    idx += 1

            elif s[idx] == "C":
                if idx+1 < len(s) and s[idx+1] == "D":
                    num += 400
                    idx += 2
                elif idx+1 < len(s) and s[idx+1] == "M":
                    num += 900
                    idx += 2
                else:
                    num += key_map[s[idx]]
                    idx += 1

            else:
                num += key_map[s[idx]]
                idx += 1
        return num

""" 

"""

class Solution:
    def romanToInt(self, s: str):
        key_map = {
            "I": 1,
            "V": 5,
            "X": 10,
            "L": 50,
            "C": 100,
            "D": 500,
            "M": 1000
        }

        num = 0
        idx = 0
        while idx < len(s):

            if idx+1 < len(s) and key_map[s[idx]] < key_map[s[idx+1]]:
                num += key_map[s[idx+1]] - key_map[s[idx]]
                idx += 2
            else:
                num += key_map[s[idx]]
                idx += 1

        return num

Basic Calculator II **

$Screenshot 2021-11-29 at 10.18.58.png$

"""
Basic Calculator II:

Given a string s which represents an expression, evaluate this expression and return its value. 
The integer division should truncate toward zero.
You may assume that the given expression is always valid. All intermediate results will be in the range of [-231, 231 - 1].
Note: You are not allowed to use any built-in function which evaluates strings as mathematical expressions, such as eval().

Example 1:
    Input: s = "3+2*2"
    Output: 7
Example 2:
    Input: s = " 3/2 "
    Output: 1
Example 3:
    Input: s = " 3+5 / 2 "
    Output: 5

https://leetcode.com/problems/basic-calculator-ii/
"""

import math
"""
-------------------------- PROBLEM ----------------------------------
string s which represents an expression, evaluate this expression and return its value
not allowed to use any built-in function which evaluates strings as mathematical expressions
integer division should truncate toward zero.
s represents a valid expression
s consists of integers and operators ('+', '-', '*', '/')

-------------------------- EXAMPLES ----------------------------------
D/MA/S

"1+2"   => 3
"3+2*2" => 3+4 = 7
"5/2+3" => 2+3 = 5
"3+5/2" => 3+2 = 5
"3+5/2+5/2" => 3+2+2 = 7

"38765456789+43434345/23434+53434/2" 

-------------------------- BRUTE FORCE ----------------------------------
O(n^2) time | O(1) time 
-  evaluate each of DMAS and add it back to the string
    - do division, add it back to the string
    - multiplication...

-------------------------- OPTIMAL ----------------------------------

-------------------------- ONE
O(n) time | O(1) time 

- separate the s into an array that contain intergers and the signs

-  evaluate each of D/M A/S and add it to an array
    - do division on array, add the results to after_div array
    - do multiplication on after_div, add the results to after_mult array
    - do addition on after_mult...

-------------------------- TWO:

stack = [0]
current_number = ""
prev_operand = "+"

# deal with * and /:
- iterate through the array:
    - try to build up a number while the characters are numeric
    - if you get to a sign:
        - if the prev_operand is * or / :
            - get the currentNumber and the prevNumber and apply the prev_operand on them then add the result to the stack
        - if the prev_operand is -:
            - add neg the number to the stack
        - if the prev_operand is +:
            - add the number to the stack

        - record the new prev_operand
        - reset current_number = ""
- add all the number in the stack

"""

""" 
------------------------------------------------------------------------------------------
"""

class Solution1:
    def calculate(self, s: str):

        # separate the s into an array that contain integers and the signs
        arr = []
        i = 0
        while i < len(s):
            if s[i].isnumeric():
                end = i
                while end+1 < len(s) and s[end+1].isnumeric():
                    end += 1
                arr.append(int(s[i:end+1]))
                i = end + 1
            elif s[i] == " ":
                i += 1
            else:
                arr.append(s[i])
                i += 1

        # division or multiplication
        after_dm = []
        i = 0
        while i < len(arr):
            # check for division
            if arr[i] == "/":
                after_dm[-1] = after_dm[-1] // arr[i+1]
                i += 2
            # check for multiplication
            elif arr[i] == "*":
                after_dm[-1] = after_dm[-1] * arr[i+1]
                i += 2
            else:
                after_dm.append(arr[i])
                i += 1

        # addition or subtraction
        after_sa = []
        i = 0
        while i < len(after_dm):
            # check for subtraction
            if after_dm[i] == "-":
                after_sa[-1] = after_sa[-1] - after_dm[i+1]
                i += 2
            # check for addition
            elif after_dm[i] == "+":
                after_sa[-1] = after_sa[-1] + after_dm[i+1]
                i += 2
            else:
                after_sa.append(after_dm[i])
                i += 1

        return "".join([str(item) for item in after_sa])

""" 

"""

class Solution3:
    def calculate(self, s: str):

        # separate the s into an array that contain integers and the signs
        arr = []
        i = 0
        while i < len(s):
            if s[i].isnumeric():
                end = i
                while end+1 < len(s) and s[end+1].isnumeric():
                    end += 1
                arr.append(s[i:end+1])
                i = end + 1
            elif s[i] == " ":
                i += 1
            else:
                arr.append(s[i])
                i += 1

        stack = []
        # evaluate addition or subtraction
        for idx in range(len(arr)):
            if not arr[idx].isnumeric():
                continue

            current_number = arr[idx]
            # ignore first number
            if idx == 0:
                stack.append(int(current_number))
                continue

            prev_operand = arr[idx-1]

            if prev_operand == "-":
                stack.append(-int(current_number))

            elif prev_operand == "+":
                stack.append(int(current_number))

            elif prev_operand == "*":
                prev_num = stack.pop()
                stack.append(prev_num * int(current_number))

            elif prev_operand == "/":
                prev_num = stack.pop()
                stack.append(math.trunc(prev_num / int(current_number)))

            if idx < len(arr):
                prev_operand = arr[idx]

        number = 0
        while stack:
            number += stack.pop()

        return number

""" 
------------------------------------------------------------------------------------------
"""

class Solution2:
    def calculate(self, s: str):

        # separate the s into an array that contain integers and the signs
        arr = []
        i = 0
        while i < len(s):
            if s[i].isnumeric():
                end = i
                while end+1 < len(s) and s[end+1].isnumeric():
                    end += 1
                arr.append(s[i:end+1])
                i = end + 1
            elif s[i] == " ":
                i += 1
            else:
                arr.append(s[i])
                i += 1

        stack = []
        current_number = ""
        prev_operand = "+"

        # evaluate addition or subtraction
        for idx in range(len(arr)+1):
            if idx < len(arr) and arr[idx].isnumeric():
                current_number = arr[idx]
                continue

            if prev_operand == "-":
                stack.append(-int(current_number))

            elif prev_operand == "+":
                stack.append(int(current_number))

            elif prev_operand == "*":
                prev_num = stack.pop()
                stack.append(prev_num * int(current_number))

            elif prev_operand == "/":
                prev_num = stack.pop()
                stack.append(math.trunc(prev_num / int(current_number)))

            if idx < len(arr):
                prev_operand = arr[idx]

        number = 0
        while stack:
            number += stack.pop()

        return number

'K' Closest Points to the Origin

Angle Between Hands of a Clock

$Screenshot 2021-10-15 at 19.24.58.png$

$Screenshot 2021-10-15 at 19.25.13.png$

$Screenshot 2021-10-15 at 19.25.48.png$

$Screenshot 2021-10-15 at 19.26.02.png$

""" 
Angle Between Hands of a Clock

Given two numbers, hour and minutes. 
Return the smaller angle (in degrees) formed between the hour and the minute hand.

Example 1:
    Input: hour = 12, minutes = 30
    Output: 165
Example 2:
    Input: hour = 3, minutes = 30
    Output: 75
Example 3:
    Input: hour = 3, minutes = 15
    Output: 7.5
Example 4:
    Input: hour = 4, minutes = 50
    Output: 155
Example 5:
    Input: hour = 12, minutes = 0
    Output: 0

https://leetcode.com/problems/angle-between-hands-of-a-clock
"""

class Solution:
    def angleClock(self, hour: int, minutes: int):
        """ 
        - calculate hour degree
            (hour/12 * 360) + (minute/60 * 30)
        - calculate minute degree
            - minute/60 * 360
        """
        hours = hour
        if hour == 12:
            hours = 0

        hours_degree = (360 * hours/12) + (30 * minutes/60)
        minutes_degree = 360 * minutes/60

        diff = abs(hours_degree-minutes_degree)
        return min(diff, abs(360-diff))

Count Primes *

$Screenshot 2021-11-04 at 07.59.39.png$

$Screenshot 2021-11-04 at 07.56.56.png$

$Screenshot 2021-11-04 at 07.57.29.png$

$Screenshot 2021-11-04 at 07.57.46.png$

$Screenshot 2021-11-04 at 07.58.49.png$

$Screenshot 2021-11-04 at 07.59.20.png$

"""
Count Primes:

Given an integer n, return the number of prime numbers that are strictly less than n.

Example 1:
    Input: n = 10
    Output: 4
    Explanation: There are 4 prime numbers less than 10, they are 2, 3, 5, 7.
Example 2:
    Input: n = 0
    Output: 0
Example 3:
    Input: n = 1
    Output: 0

https://leetcode.com/problems/count-primes
"""

""" 
The basic brute-force solution for this problem is to iterate from 0 to n and for each number, we do a prime-check. 
To check if a number is prime or not, we simply check if its divisors include anything other than 1 and the number itself. 
If so, then it is not a prime number. This method will not scale for the given limits on n. 
The iteration itself has O(n) time complexity and for each iteration, we have the prime check which takes O(sqrt)O( n). 
This will exceed the problem's time limit. Therefore, we need a more efficient solution.

Instead of checking if each number is prime or not, what if we mark the multiples of a prime number as non-prime?
"""

import math
class Solution_:  # times out on leetcode
    def isPrime(self, n):

        for num in range(2, math.floor(math.sqrt(n))):
            if n % num == 0:
                return False

        return True

    def countPrimes(self, n: int):
        if n <= 2:
            return 0

        numbers = [-1] * n
        numbers[0] = False
        numbers[1] = False

        for idx in range(2, n):
            if numbers[idx] == False:
                continue

            numbers[idx] = self.isPrime(idx)

            if numbers[idx]:  # only consider primes to ensure not calculating duplicates

                multiplier = idx
                while multiplier * idx < n:
                    numbers[multiplier * idx] = False
                    multiplier += 1

        return numbers.count(True)

""" 
"""

class Solution:
    def countPrimes(self, n: int):
        if n <= 2:
            return 0

        numbers = [True] * n
        numbers[0] = False
        numbers[1] = False

        for idx in range(2, n):

            if numbers[idx]:  # only consider primes to ensure not calculating duplicates

                for multiple in range(idx+idx, n, idx):  # start,stop+1,step
                    numbers[multiple] = False

        return numbers.count(True)

Robot Bounded In Circle

""" 
Robot Bounded In Circle:

On an infinite plane, a robot initially stands at (0, 0) and faces north. 
The robot can receive one of three instructions:
    "G": go straight 1 unit;
    "L": turn 90 degrees to the left;
    "R": turn 90 degrees to the right.
The robot performs the instructions given in order, and repeats them forever.
Return true if and only if there exists a circle in the plane such that the robot never leaves the circle.

Example 1:
    Input: instructions = "GGLLGG"
    Output: true
    Explanation: The robot moves from (0,0) to (0,2), turns 180 degrees, and then returns to (0,0).
    When repeating these instructions, the robot remains in the circle of radius 2 centered at the origin.
Example 2:
    Input: instructions = "GG"
    Output: false
    Explanation: The robot moves north indefinitely.
Example 3:
    Input: instructions = "GL"
    Output: true
    Explanation: The robot moves from (0, 0) -> (0, 1) -> (-1, 1) -> (-1, 0) -> (0, 0) -> ...

https://leetcode.com/problems/robot-bounded-in-circle
https://leetcode.com/problems/robot-bounded-in-circle/discuss/290856/JavaC%2B%2BPython-Let-Chopper-Help-Explain
"""
from enum import Enum
""" 
MOVING: 
- moving north is adding 1 to y
- moving left is adding 1 to x
- moving south is subreacting 1 from y
- moving left is subreacting 1 from x

DIRECTIONS:
    north
west    east
    south

SOLUTION:
- if we have a loop,
    because the turnings are of 90 degrees,
    we should return to 0,0 after running the instructions 4 times

if we are done with the instruction once and have changed direction by ((dir) cumulative direction which might be south, east, west)
it means that if this (dir) is applied at most 4 times (for east & west (horizontal)) or even 2 times (for north (vertical)) we will be back to the origin
"""

class Direction(Enum):
    NORTH = "north"
    SOUTH = "south"
    EAST = "east"
    WEST = "west"

class Solution:
    def isRobotBounded(self, instructions: str):
        position = [0, 0]
        direction = Direction.NORTH

        for _ in range(4):
            # run instructions
            for char in instructions:
                if char == "G":
                    self.move(position, direction)
                else:
                    direction = self.change_direction(direction, char)

            # check if back to start
            if position[0] == 0 and position[1] == 0:
                return True

        return False

    def move(self, position, direction):
        if direction == Direction.NORTH:
            position[1] = position[1]+1
        elif direction == Direction.SOUTH:
            position[1] = position[1]-1
        elif direction == Direction.EAST:
            position[0] = position[0]+1
        elif direction == Direction.WEST:
            position[0] = position[0]-1

    def change_direction(self, direction, change):
        if change == "L":
            if direction == Direction.NORTH:
                return Direction.WEST
            elif direction == Direction.SOUTH:
                return Direction.EAST
            elif direction == Direction.EAST:
                return Direction.NORTH
            elif direction == Direction.WEST:
                return Direction.SOUTH
        if change == "R":
            if direction == Direction.NORTH:
                return Direction.EAST
            elif direction == Direction.SOUTH:
                return Direction.WEST
            elif direction == Direction.EAST:
                return Direction.SOUTH
            elif direction == Direction.WEST:
                return Direction.NORTH

""" 
---------------------------------------------
"""

class Solution1:
    def isRobotBounded(self, instructions: str):
        position = [0, 0]
        direction = Direction.NORTH

        for char in instructions:
            if char == "G":
                self.move(position, direction)
            else:
                direction = self.change_direction(direction, char)

        # check if back to start
        if position[0] == 0 and position[1] == 0:
            return True
        # check if changed direction
        return direction != Direction.NORTH

    def move(self, position, direction):
        if direction == Direction.NORTH:
            position[1] = position[1]+1
        elif direction == Direction.SOUTH:
            position[1] = position[1]-1
        elif direction == Direction.EAST:
            position[0] = position[0]+1
        elif direction == Direction.WEST:
            position[0] = position[0]-1

    def change_direction(self, direction, change):
        if change == "L":
            if direction == Direction.NORTH:
                return Direction.WEST
            elif direction == Direction.SOUTH:
                return Direction.EAST
            elif direction == Direction.EAST:
                return Direction.NORTH
            elif direction == Direction.WEST:
                return Direction.SOUTH
        if change == "R":
            if direction == Direction.NORTH:
                return Direction.EAST
            elif direction == Direction.SOUTH:
                return Direction.WEST
            elif direction == Direction.EAST:
                return Direction.SOUTH
            elif direction == Direction.WEST:
                return Direction.NORTH

""" 
---------------------------------------------
"""

# same as above but using math tricks
class Solution2:
    def isRobotBounded(self, instructions: str):
        direction = (0, 1)
        start = [0, 0]

        for x in instructions:
            if x == 'G':
                start[0] += direction[0]
                start[1] += direction[1]
            elif x == 'L':
                direction = (-direction[1], direction[0])
            elif x == 'R':
                direction = (direction[1], -direction[0])

        # check if back to start or if changed direction
        return start == [0, 0] or direction != (0, 1)

https://leetcode.com/problems/integer-to-english-words/

$Screenshot 2021-10-15 at 20.59.35.png$

Screen Recording 2021-10-15 at 21.00.14.mov

""" 
This problem is about the decomposition of the problem -- how do you break it down. Not about efficiency.

max => 2,147,483,647 ("Two Billion - One Hundred Forty Seven Million - Four Hundred Eighty Three Thousand - Six Hundred Forty Seven")

the `len_three` function and how it's used is what you should understand
"""

class Solution:

    def len_one(self, num):
        store = {1: 'One', 2: 'Two', 3: 'Three', 4: 'Four',
                 5: 'Five', 6: 'Six', 7: 'Seven', 8: 'Eight', 9: 'Nine'}
        return store[num]

    def len_two(self, num):
        tens_less_20 = {10: 'Ten', 11: 'Eleven', 12: 'Twelve', 13: 'Thirteen', 14: 'Fourteen',
                        15: 'Fifteen', 16: 'Sixteen', 17: 'Seventeen', 18: 'Eighteen', 19: 'Nineteen'}
        tens_greater_20 = {2: 'Twenty', 3: 'Thirty', 4: 'Forty',
                           5: 'Fifty', 6: 'Sixty', 7: 'Seventy', 8: 'Eighty', 9: 'Ninety'}

        if num < 10:
            return self.len_one(num)
        elif num < 20:
            return tens_less_20[num]
        # tens > 20
        elif num >= 20:
            tens = num // 10
            ones = num % 10
            if ones:
                return tens_greater_20[tens] + ' ' + self.len_one(ones)
            else:
                return tens_greater_20[tens]
        return ''

    def len_three(self, num):
        hundred = num // 100
        rest = num % 100

        if hundred and rest:
            return self.len_one(hundred) + ' Hundred ' + self.len_two(rest)
        elif hundred and not rest:
            return self.len_one(hundred) + ' Hundred'
        elif not hundred and rest:
            return self.len_two(rest)
        return ''  # not needed

    def numberToWords(self, num):
        # special case
        if not num:
            return 'Zero'

        billion = num // 1000000000
        million = (num - billion * 1000000000) // 1000000
        thousand = (num - billion * 1000000000 - million * 1000000) // 1000
        rest = num - billion * 1000000000 - million * 1000000 - thousand * 1000

        result = ''
        if billion:
            result = self.len_three(billion) + ' Billion'
        if million:
            result += ' ' if result else ''
            result += self.len_three(million) + ' Million'
        if thousand:
            result += ' ' if result else ''
            result += self.len_three(thousand) + ' Thousand'
        if rest:
            result += ' ' if result else ''
            result += self.len_three(rest)
        return result

Add Binary

Screen Recording 2021-10-15 at 21.29.59.mov

""" 
Add Binary

Given two binary strings a and b, return their sum as a binary string.

Example 1:
    Input: a = "11", b = "1"
    Output: "100"
Example 2:
    Input: a = "1010", b = "1011"
    Output: "10101"

https://leetcode.com/problems/add-binary
"""

class Solution:
    def addBinary(self, a: str, b: str):
        n = max(len(a), len(b))
        res = [0]*(n+1)

        one_idx = len(a)-1
        two_idx = len(b)-1
        for idx in reversed(range(n+1)):
            carry = res[idx]
            one = 0
            two = 0
            if one_idx >= 0:
                one = int(a[one_idx])
                one_idx -= 1
            if two_idx >= 0:
                two = int(b[two_idx])
                two_idx -= 1

            addition = one + two + carry

            res[idx] = addition % 2  # save result
            # save carry
            if addition // 2:  # prevent saving carry in idx 0
                res[idx-1] = addition // 2

        # remove preceeding zeros
        start_idx = 0
        while res[start_idx] == 0 and start_idx < len(res)-1:
            start_idx += 1
        res = res[start_idx:]

        return "".join([str(item) for item in res])

https://leetcode.com/problems/sparse-matrix-multiplication/
https://leetcode.com/problems/evaluate-division/

EVALUATE DIVISION (Leetcode) - Code & Whiteboard

Google | Phone | Currency Conversion - LeetCode Discuss

Find the original version of this page (with additional content) on Notion here.

One of those

If you get one of these in an interview, just know they don't want to hire you lol

They're not that hard but if you haven't seen them before it's unlikely you'll come up with the most optimal solution & explain its time and space complexity within the typical 15 min time constraint.

Extra

Find the original version of this page (with additional content) on Notion here.

Python basics

20+ helpful Python syntax patterns for coding interviews

Integers

Integers in python3 are unbounded

Examples

Happy Number

Power

x = -2

print(x**2) # 4
print(x*x) # 4

Square root *

import math

math.sqrt(49)
# 7

Modulus(%) vs Floor(//)

Modulus: The modulus-function computes the remainder of a division, which is the "leftover" of an integral division.

Floor: The floor-function provides the lower-bound of an integral division. The upper-bound is computed by the ceil function. (Basically speaking, the floor-function cuts off all decimals).

# modulus
print(324 % 10) # 4

# floor
print(324 // 10) # 32

math.ceil() & math.floor()

import math

math.ceil(2.17) # 3
math.floor(2.17) # 2

Infinity (can be used for math.max)

float("inf")
float("-inf")

.isalpha() .isnumeric() & .isalnum()

chr() & ord()

Other

Lambda functions

>>> (lambda x, y: x + y)(2, 3)
5
>>> double = lambda x: x * 2
>>> double(4)

Example usage

# Program to double each item in a list using map()

my_list = [1, 5, 4, 6, 8, 11, 3, 12]

new_list = list(map(lambda x: x * 2 , my_list))

print(new_list) # [2, 10, 8, 12, 16, 22, 6, 24]

Sort

Random

random.random()

Return the next random floating point number in the range [0.0, 1.0]

import random

>>> random.random()
0.6280590213451548
>>> random.random()
0.1623939995862359
>>> random.random()
0.6704949828925247
>>> random.random()
0.6838627536588555

random.randrange(start,stop,step)

Return a randomly selected element from range(start, stop, step). This is equivalent to choice(range(start, stop, step)), but doesn’t actually build a range object.

import random

>>> random.randrange(20)
7
>>> random.randrange(10,20,2)
16
>>> random.randrange(start=10,stop=20,step=2)
18
>>> random.randrange(start=10,stop=20,step=2)
14
>>> random.randrange(start=10,stop=20,step=2)
12
>>> random.randrange(start=10,stop=20,step=2)
14
>>> random.randrange(start=10,stop=20,step=2)
16
>>> random.randrange(start=10,stop=20,step=2)
18
>>> random.randrange(start=10,stop=20,step=2)
18
>>> random.randrange(start=10,stop=20,step=2)
18
>>> random.randrange(start=10,stop=20,step=2)
16
>>> random.randrange(start=10,stop=20,step=2)
16
>>> random.randrange(start=10,stop=20,step=2)

random.randint(a,b)

Return a random integer N such that a <= N <= b. Alias for randrange(a, b+1)

import random

>>> random.randint(10,20)
19
>>> random.randint(10,20)
16
>>> random.randint(10,20)
15
>>> random.randint(10,20)
20
>>> random.randint(10,20)
11
>>> random.randint(10,20)
17
>>> random.randint(10,20)
20
>>> random.randint(10,20)

random.choice(seq)

Return a random element from the non-empty sequence seq

import random

>>> random.choice(['win', 'lose', 'draw'])
'lose'
>>> random.choice(['win', 'lose', 'draw'])
'win'
>>> random.choice(['win', 'lose', 'draw'])
'win'
>>> random.choice(['win', 'lose', 'draw'])
'win'
>>> random.choice(['win', 'lose', 'draw'])
'lose'
>>> random.choice(['win', 'lose', 'draw'])
'lose'
>>> random.choice(['win', 'lose', 'draw'])
'draw'

heapq

Heaps & Priority Queues

collections

`collections.deque()` *

`collections.defaultdict`

`collections.OrderedDict`

`sortedcontainers.SortedDict`

Find the original version of this page (with additional content) on Notion here.

Quick Tips

Concepts that are easy for me to forget

Solving problems

Think of data structures

Example:

Strings

Storing alphanumeric characters

You can store all alphanumeric characters in an array of length 26 → constant space & sometimes time

Sorting an array of strings (M * N log N)

Let n be the number of elements in the str array. Let m be the average/maximum # of characters for the strings in the str arrayThen, calling Arrays.sort(str) on this array would have the performance characteristic of O(m * n log n).

Hashtables

`collections.OrderedDict`

collections.OrderedDict() can be used as a stack with the help of .popitem() and a queue with .popitem(last=False)

Binary trees

Definition of terms

A balanced binary tree is a binary tree in which the height of the left and right subtree of any node differ by not more than 1.

A complete binary tree is a binary tree in which every level, except possibly the last is completely filled, and all nodes are as far left as possible

A full binary tree is a binary tree in which every node other than the leaves has two children.

A perfect binary tree is a full binary tree in which all leaves are at the same depth, and in which every parent has two children. (every level of the tree is completely full)

Binary Search Tree

The key lookup, insertion, and deletion take time proportional to the height of the tree, which can in the worst-case be O(n) if insertions and deletions are naively implemented. Eg if the tree looks like a linked list.

When we are talking about the average case, it is the time it takes for the operation on a balanced tree, and when we are talking about the worst case, it is the time it takes for the given operation on a non-balanced tree.

Graphs

Vertex/Node & Edge/Arc

Topological ordering

Vertices in a directed acyclic graph that have no incoming edges are referred to as sources. Vertices that have no outgoing edges are referred to as sinks**.

Indegree → count of incoming edges of each vertex/node or how many parents it has (used to determine sources)

Representing Graphs in Code

Edge List: well suited to performant lookups of an edge, or listing all edges

Adjacency List: this representation allows for constant-time lookup of adjacent vertices, which is useful in many query and pathfinding scenarios.

Adjacency Matrix: O(1) edge lookups. Easy and fast to tell if a pair (i,j) is an edge: simply check if A[i][j] is 1 or 0

DFS & BFS

The Time complexity of BFS is O(V+E) when Adjacency List is used and O(V^2) when Adjacency Matrix is used, where V stands for vertices and E stands for edges.

stack for DFS, imagine a vertical flow queue for BFS, horizontal flow

Remember to unvisit nodes when doing DFS on a graph

Dijkstra's Algorithm Time & Space complexity

O((v + e) * log(v)) time | O(v) space - where v is the number of vertices and e is the number of edges in the input graph

Searching

Quick select

""" Time complexity
Best: O(n) time | O(1) space - where n is the length of the input array 
Average: O(n) time | O(1) space
Worst: O(n^2) time | O(1) space
"""

Sorting

Remember these exist:

Topological sort
Cyclic sort

Bubble sort

# Best: O(n) time | O(1) space -> if already sorted
# Average: O(n^2) time | O(1) space
# Worst: O(n^2) time | O(1) space

Insertion sort

Take an element from the second and insert it to the first.
Sort the first using something similar to Bubble sort.

# Best: O(n) time | O(1) space -> if already sorted
# Average: O(n^2) time | O(1) space
# Worst: O(n^2) time | O(1) space

Selection sort

Divide the input array into two subarrays in place. The first subarray should be sorted at all times and should start with a length of 0, while the second subarray should be unsorted. Select the smallest (or largest) element in the unsorted subarray and insert it into the sorted subarray with a swap.

# Best: O(n^2) time | O(1) space
# Average: O(n^2) time | O(1) space
# Worst: O(n^2) time | O(1) space

Merge Sort

two halves → merge. The time complexity of merge sort is n log(n)

Quicksort

We first select an element that we will call the pivot from the array.
Move all elements that are smaller than the pivot to the left of the pivot; move all elements that are larger than the pivot to the right of the pivot. This is called the partition operation.
Recursively apply the above 2 steps separately to each of the sub-arrays of elements with smaller and bigger values than the last pivot.

# Average: O(nlog(n)) time | O(log(n)) space
# Worst: O(n^2) time | O(log(n)) space

Heap Sort

Heap sort is the improved version of the Selection sort, which takes advantage of a heap data structure rather than a linear-time search to find the max value item. Using the heap, finding the next largest element takes O(log(n)) time, instead of O(n) for a linear scan as in simple selection sort. This allows heap sort to run in O(n log(n)) time, and this is also the worst-case complexity.

Bit manipulation

Shifting

Left shift: **0010 << 1 → 0100 A single left shift multiplies a binary number by 2**

Arithmetic Right shift: **1011 >> 1 → 1101**

Logical Right Shifts: (not in python) divides a number by 2, throwing out any remainders.

Find the original version of this page (with additional content) on Notion here.

Recursion, DP & Backtracking

Dynamic Programming, Recursion, & Backtracking

Recursion,%20DP%20&%20Backtracking%20525dddcdd0874ed98372518724fc8753/1_lOvVlLI91bXBK3sF3ryqNw.gif

Recursion

Thinking Recursively in Python - Real Python

5 Simple Steps for Solving Any Recursive Problem

Explore - LeetCode

Master Recursion

Recursion is an approach to solving problems using a function that calls itself as a subroutine.

Recursion,%20DP%20&%20Backtracking%20525dddcdd0874ed98372518724fc8753/fixing_problems.webp

When do you use recursion? making one choice, then one after that, on and on. Or in hierarchies, networks and graphs.

Screenshot 2021-10-12 at 06.38.06.png

Recursive strategy:

Order your data (not necessarily via code - just conceptually)

Helps in identifying the base case

Decompose the original problem into simpler instances of the same problem. This is the recursive case:
```
# Factorial
n! = n x (n−1) x (n−2) x (n−3) ⋅⋅⋅⋅ x 3 x 2 x 1
n! = n x (n−1)!

# Fibonacci
Fn = Fn-1 + Fn-2
```
Whatever data we are operating on, whether it is numbers, strings, lists, binary trees or people, it is necessary to explicitly find an appropriate ordering that gives us a direction to move in to make the problem smaller. This ordering depends entirely on the problem, but a good start is to think of the obvious orderings: numbers come with their own ordering, strings and lists can be ordered by their length, binary trees can be ordered by depth.

Once we’ve ordered our data, we can think of it as something that we can reduce. In fact, we can write out our ordering as a sequence:
- 0, 1, 2, …, n for integers (i.e. for integer data d, degree(d) = d) Moving from right to left we move through the general (‘big’) cases, to the base (‘little’) cases
- [], [■], [■, ■], …, [■, … , ■] for lists(notice len = 0, len = 1, …, len = n i.e. for list data d, degree(d) = len(d))
Solve the Little Cases & identify Base cases

elf delivering presents for santa

Identifying the base cases, which are to be solved directly

The case for which the solution can be stated non-recursively.

As the large problem is broken down into successively less complex ones, those subproblems must eventually become so simple that they can be solved without further subdivision.
```
n! = n x (n−1)! 
n! = n x (n−1) x (n−2)!
n! = n x (n−1) x (n−2) x (n−3)!
⋅
⋅
n! = n x (n−1) x (n−2) x (n−3) ⋅⋅⋅⋅ x 3!
n! = n x (n−1) x (n−2) x (n−3) ⋅⋅⋅⋅ x 3 x 2!
n! = n x (n−1) x (n−2) x (n−3) ⋅⋅⋅⋅ x 3 x 2 x 1!
```
we have the correct ordering, we need to look at the smallest elements in our ordering, and decide how we are going to handle them.

Once we have solved our base cases, and we know our ordering, then solving the general case is as simple as reducing the problem in such a way that the degree of the data we’re operating on moves towards the base cases.

find a general case
Solve the Big Cases - General (recursive) case

Ensuring progress, that is the recursion converges to the solution.

case for which the solution to a problem is expressed in terms of a smaller version of itself.

Here, we handle the data rightwards in our ordering, that is, data of high degree. Usually, we consider data of arbitrary degree and aim to find a way to solve the problem by reducing it to an expression containing the same problem of lesser degree, e.g. in our Fibonacci example we started with arbitrary n and reduced fib(n) to fib(n-1) + fib(n-2) which is an expression containing two instances of the problem we started with, of lesser degree (n-1 and n-2, respectively).

Draw a recursion stack (tree) if you suspect it involves recursion - not necessarily at the last point in the strategy

Example:

"""
Permutations: Leetcode 46

Given an array nums of distinct integers, return all the possible permutations. You can return the answer in any order.

Example 1:
    Input: nums = [1,2,3]
    Output: [[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
"""

class Solution:
    def helper(self, permutations, curr_perm, elements):
        if len(elements) < 1:
            permutations.append(curr_perm)
            return
        for idx, num in enumerate(elements):
            self.helper(permutations, curr_perm+[num], elements[:idx]+elements[idx+1:])


    def permute(self, nums: List[int]):
        permutations = []
        self.helper(permutations, [], nums)
        return permutations

"""
[
[1,2,3],
[1,3,2],
[2,1,3],
[2,3,1],
[3,1,2],
[3,2,1]
]

                     []
          /               |    \
        [1]              [2]
        / \              / \     
    [1,2]  [1,3]     [2,1] [2,3]
      |        |       |      |
[1,2,3]     [1,3,2]  [2,1,3]  [2,3,1]

                                                  ([], [], [1,2,3])

        ([], [1], [2,3])                           ([], [2], [1,3])              ([], [3], [1,2])

([], [1, 2], [3]) ([], [1, 3], [3])

perm(1,2)
              [][1,2]
      [1][2]     [2][1]
    [1,2][]       [2,1][]     

perm(1,2,3)
                            [][1,2,3]
                /             |                \
          [1][2,3]          [2][1,3]           [3][2,1]
          /  \              /      \              /   \
    [1,2][3] [1,3][2]    [2,1][3] [2,3][1]   [3,2][1] [3,1][2]
    |             |          |         |          |         |
  [1,2,3]      [1,3,2]    [2,1,3]   [2,3,1]    [3,2,1]    [3,1,2]

"""

Recursion,%20DP%20&%20Backtracking%20525dddcdd0874ed98372518724fc8753/Screenshot_2021-07-10_at_09.30.29.png

"""
order data:

find smaller/base cases:

solve little cases then big cases:

recursion stack:

"""

Examples

Tower of Hanoi

Towers of Hanoi: A Complete Recursive Visualization

5.10. Tower of Hanoi - Problem Solving with Algorithms and Data Structures

Screenshot 2021-10-12 at 07.16.38.png

""" 
Tower of Hanoi

https://youtu.be/rf6uf3jNjbo
https://runestone.academy/runestone/books/published/pythonds/Recursion/TowerofHanoi.html
https://leetcode.com/discuss/general-discussion/1517167/Tower-of-Hanoi-Algorithm-%2B-Python-code
https://www.notion.so/paulonteri/Recursion-DP-Backtracking-525dddcdd0874ed98372518724fc8753#0fa86da6418247199688a4f435447d86
"""

""" 
Here is a high-level outline of how to move a tower from the starting pole, to the goal pole, using an intermediate pole:
    1. Move a tower of height-1 to an intermediate pole
    2. Move the last/remaining disk to the final pole.
    3. Move the disks height-1 to the first rod and repeat the above steps.
        Move the tower of height-1 from the intermediate pole to the final pole using the original pole.

As long as we always obey the rule that the larger disks remain on the bottom of the stack, 
    we can use the three steps above recursively, 
    treating any larger disks as though they were not even there.

The only thing missing from the outline above is the identification of a base case. 
The simplest Tower of Hanoi problem is a tower of one disk. 
In this case, we need move only a single disk to its final destination. 
A tower of one disk will be our base case. 
"""

def tower_of_hanoi(n, from_rod="A", to_rod="C", aux_rod="B"):
    if n == 1:
        # The simplest Tower of Hanoi problem is a tower of one disk.
        # In this case, we need move only a single disk to its final destination.
        print("Move disk 1 from rod", from_rod, "to rod", to_rod)
        return

    # Move a tower of height-1 to an intermediate pole
    tower_of_hanoi(n-1, from_rod, aux_rod, to_rod)

    # Move the last/remaining disk to the final pole
    print("Move disk", n, "from rod", from_rod, "to rod", to_rod)

    # Move the disks height-1 to the first rod and repeat the above steps
    # Move the tower of height-1 from the intermediate pole to the final pole using the original pole.
    tower_of_hanoi(n-1, aux_rod, to_rod, from_rod)

tower_of_hanoi(1)
print("____________")
tower_of_hanoi(2)
print("____________")
tower_of_hanoi(3)
print("____________")
tower_of_hanoi(4)
print("____________")
tower_of_hanoi(5)

https://runestone.academy/runestone/books/published/pythonds/Recursion/TowerofHanoi.html

Recursive multiply

""" 
Recursive multiply
"""

def recursive_multiply(x, y):
    # reduce number of recursive calls - ensure y is smaller
    if y > x:
        return recursive_multiply(y, x)

    return recursive_multiply_helper(x, y)

def recursive_multiply_helper(x, y):
    if y == 0:
        return 0
    if y == 1:
        return x

    return x + recursive_multiply_helper(x, y-1)

print(recursive_multiply(5, 4))
print(recursive_multiply(7, 3))
print(recursive_multiply(2, 2))

Subsets With Duplicates
Permutation

Letter Combinations of a Phone Number

"""
Letter Combinations of a Phone Number:

Given a string containing digits from 2-9 inclusive, return all possible letter combinations that the number could represent.
Return the answer in any order.
A mapping of digit to letters (just like on the telephone buttons) is given below. Note that 1 does not map to any letters.

https://leetcode.com/problems/letter-combinations-of-a-phone-number/
"""
"""
Phone Number Mnemonics:
If you open the keypad of your mobile phone, it'll likely look like this:

   ----- ----- -----
  |     |     |     |
  |  1  |  2  |  3  |
  |     | abc | def |
   ----- ----- -----
  |     |     |     |
  |  4  |  5  |  6  |
  | ghi | jkl | mno |
   ----- ----- -----
  |     |     |     |
  |  7  |  8  |  9  |
  | pqrs| tuv | wxyz|
   ----- ----- -----
        |     |
        |  0  |
        |     |
         -----

Almost every digit is associated with some letters in the alphabet; this allows certain phone numbers to spell out actual words.
For example, the phone number 8464747328 can be written as timisgreat; similarly, the phone number 2686463 can be written as antoine or as ant6463.
It's important to note that a phone number doesn't represent a single sequence of letters, but rather multiple combinations of letters.
For instance, the digit 2 can represent three different letters (a, b, and c).
A mnemonic is defined as a pattern of letters, ideas, or associations that assist in remembering something
Companies oftentimes use a mnemonic for their phone number to make it easier to remember.
Given a stringified phone number of any non-zero length, write a function that returns all mnemonics for this phone number, in any order.
For this problem, a valid mnemonic may only contain letters and the digits 0 and 1.
In other words, if a digit is able to be represented by a letter, then it must be. Digits 0 and 1 are the only two digits that don't have letter representations on the keypad.
Note that you should rely on the keypad illustrated above for digit-letter associations.

Sample Input
    phoneNumber = "1905"
Sample Output
    [
    "1w0j",
    "1w0k",
    "1w0l",
    "1x0j",
    "1x0k",
    "1x0l",
    "1y0j",
    "1y0k",
    "1y0l",
    "1z0j",
    "1z0k",
    "1z0l",
    ]
    // The mnemonics could be ordered differently.
https://www.algoexpert.io/questions/Phone%20Number%20Mnemonics
"""

class Solution0:
    def letterCombinations(self, digits: str):

        if not digits:
            return []

        key_map = {
            2: ['a', 'b', 'c'],
            3: ['d', 'e', 'f'],
            4: ['g', 'h', 'i'],
            5: ['j', 'k', 'l'],
            6: ['m', 'n', 'o'],
            7: ['p', 'q', 'r', 's'],
            8: ['t', 'u', 'v'],
            9: ['w', 'x', 'y', 'z']
        }

        res = ['']

        for num in digits:
            new_res = []

            for idx in range(len(res)):
                for letter in key_map[int(num)]:
                    new_res.append(res[idx] + letter)

            res = new_res

        return res

# ----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

key_map = {
    0: ["0"],
    1: ["1"],
    2: ['a', 'b', 'c'],
    3: ['d', 'e', 'f'],
    4: ['g', 'h', 'i'],
    5: ['j', 'k', 'l'],
    6: ['m', 'n', 'o'],
    7: ['p', 'q', 'r', 's'],
    8: ['t', 'u', 'v'],
    9: ['w', 'x', 'y', 'z']
}

# # # # #

def phoneNumberMnemonics00(phoneNumber):
    all_combinations = []
    phoneNumberMnemonicsHelper00(phoneNumber, 0, all_combinations, [])
    return all_combinations

def phoneNumberMnemonicsHelper00(phoneNumber, idx, all_combinations, curr_combination):

    if idx >= len(phoneNumber):
        all_combinations.append("".join(curr_combination))
        return

    letters = key_map[int(phoneNumber[idx])]
    for letter in letters:
        phoneNumberMnemonicsHelper00(
            phoneNumber, idx + 1, all_combinations, curr_combination + [letter])

# ----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

# O(4^n * n) time | O(4^n * n) space - where n is the length of the phone number
def phoneNumberMnemonics(phoneNumber):
    all_combinations = []
    curr_combination_template = list(range(len(phoneNumber)))
    phoneNumberMnemonicsHelper(
        phoneNumber, 0, all_combinations, curr_combination_template)
    return all_combinations

def phoneNumberMnemonicsHelper(phoneNumber, idx, all_combinations, curr_combination):

    if idx >= len(phoneNumber):
        all_combinations.append("".join(curr_combination))
        return

    letters = key_map[int(phoneNumber[idx])]
    for letter in letters:
        # place current letter in curr_combination and go forward to other idxs
        # we will backtrack and place the other letters too
        curr_combination[idx] = letter
        phoneNumberMnemonicsHelper(
            phoneNumber, idx + 1, all_combinations, curr_combination)

Interleaving String/Interweaving Strings

""" 
Interleaving String/Interweaving Strings:

Given strings s1, s2, and s3, find whether s3 is formed by an interleaving of s1 and s2.
An interleaving of two strings s and t is a configuration where they are divided into non-empty substrings such that:
    s = s1 + s2 + ... + sn
    t = t1 + t2 + ... + tm
    |n - m| <= 1
The interleaving is s1 + t1 + s2 + t2 + s3 + t3 + ... or t1 + s1 + t2 + s2 + t3 + s3 + ...
Note: a + b is the concatenation of strings a and b.

Example 1:
    Input: s1 = "aabcc", s2 = "dbbca", s3 = "aadbbcbcac"
    Output: true
Example 2:
    Input: s1 = "aabcc", s2 = "dbbca", s3 = "aadbbbaccc"
    Output: false
Example 3:
    Input: s1 = "", s2 = "", s3 = ""
    Output: true

https://www.algoexpert.io/questions/Interweaving%20Strings
https://leetcode.com/problems/interleaving-string/
https://leetcode.com/problems/interleaving-string/discuss/326347/C-dynamic-programming-practice-in-August-2018-with-interesting-combinatorics-warmup
"""

""" 
------------------------------------------------------------------------------------------------------------------------------------------------------
"""

def interweavingStringsBF_(one, two, three):
    if len(three) != len(one) + len(two):
        return False
    return interweavingStringsHelperBF_(one, two, three, 0, 0, 0)

def interweavingStringsHelperBF_(one, two, three, one_idx, two_idx, three_idx):
    if three_idx == len(three):
        return True

    one_res = False
    two_res = False
    if one_idx < len(one) and one[one_idx] == three[three_idx]:
        one_res = interweavingStringsHelperBF_(
            one, two, three, one_idx+1, two_idx, three_idx+1)

    if two_idx < len(two) and two[two_idx] == three[three_idx]:
        two_res = interweavingStringsHelperBF_(
            one, two, three, one_idx, two_idx+1, three_idx+1)

    return one_res or two_res

""" 
BF that can be cached
"""

def interweavingStringsBF(one, two, three):
    if len(three) != len(one) + len(two):
        return False
    return interweavingStringsHelperBF(one, two, three, 0, 0)

def interweavingStringsHelperBF(one, two, three, one_idx, two_idx, ):
    three_idx = one_idx + two_idx
    if three_idx == len(three):
        return True

    one_res = False
    two_res = False
    if one_idx < len(one) and one[one_idx] == three[three_idx]:
        one_res = interweavingStringsHelperBF(
            one, two, three, one_idx+1, two_idx)

    if two_idx < len(two) and two[two_idx] == three[three_idx]:
        two_res = interweavingStringsHelperBF(
            one, two, three, one_idx, two_idx+1)

    return one_res or two_res

""" 
------------------------------------------------------------------------------------------------------------------------------------------------------
"""

def interweavingStringsMEMO(one, two, three):
    if len(three) != len(one) + len(two):
        return False
    cache = [[None for _ in range(len(two)+1)] for _ in range(len(one)+1)]
    return interweavingStringsHelperMEMO(one, two, three, cache, 0, 0)

def interweavingStringsHelperMEMO(one, two, three, cache, one_idx, two_idx, ):
    three_idx = one_idx + two_idx
    if three_idx == len(three):
        return True
    if cache[one_idx][two_idx] is not None:
        return cache[one_idx][two_idx]

    one_res = False
    two_res = False
    if one_idx < len(one) and one[one_idx] == three[three_idx]:
        one_res = interweavingStringsHelperMEMO(one, two, three, cache, one_idx+1, two_idx)

    if two_idx < len(two) and two[two_idx] == three[three_idx]:
        two_res = interweavingStringsHelperMEMO(one, two, three, cache, one_idx, two_idx+1)

    cache[one_idx][two_idx] = one_res or two_res
    return cache[one_idx][two_idx]

""" 
------------------------------------------------------------------------------------------------------------------------------------------------------

Bottom up:

- for each char(in one or two) check if it matches what is in three:
    - if it does: if we had built the prev string up to that point == True (
            one idx behind the curr idx in three (up or left depending on if the row or column matches) )
        - then True

# can be optimised to 1D array
"""

def interweavingStrings(one, two, three):
    if len(three) != len(one) + len(two):
        return False

    dp = [[False for _ in range(len(two)+1)] for _ in range(len(one)+1)]

    # # fill in the defaults that will be used to generate the next
    dp[0][0] = True
    for i in range(1, len(one)+1):  # left column
        actual_idx = i-1
        if one[actual_idx] == three[actual_idx] and dp[i-1][0] == True:
            dp[i][0] = True
    for i in range(1, len(two)+1):  # top row
        actual_idx = i-1
        if two[actual_idx] == three[actual_idx] and dp[0][i-1] == True:
            dp[0][i] = True

    # # fill in the rest
    for one_idx in range(1, len(one)+1):
        for two_idx in range(1, len(two)+1):
            actual_one_idx = one_idx-1
            actual_two_idx = two_idx-1
            actual_three_idx = one_idx + two_idx - 1

            # # check if the string matches then check if we had built it successfully up to that point
            # check one
            if one[actual_one_idx] == three[actual_three_idx] and dp[one_idx-1][two_idx] == True:
                dp[one_idx][two_idx] = True
            # check two
            if two[actual_two_idx] == three[actual_three_idx] and dp[one_idx][two_idx-1] == True:
                dp[one_idx][two_idx] = True

    return dp[-1][-1]

Magic Index

Screenshot 2021-10-11 at 18.07.55.png

"""
Magic Index: 

A magic index in an array A[ 0••• n -1] is defined to be an index such that A[ i] = i. 
Given a sorted array of distinct integers, write a method to find a magic index, if one exists, in array A.

FOLLOW UP:
What if the values are not distinct?
"""

""" 
What if the values are not distinct? - cannot use two pointers
"""

def magicIndex(array):
    return magicIndexHelper(array, 0, len(array)-1)

def magicIndexHelper(array, left, right):

    if left > right:
        return -1

    mid = (left+right) // 2
    if array[mid] == mid:
        return mid

    left_side = magicIndexHelper(array, left, min(mid-1, array[mid]))
    right_side = magicIndexHelper(array,  max(mid+1, array[mid]), right)

    if left_side >= 0:
        return left_side
    elif right_side >= 0:
        return right_side

    return -1

def FillArray():
    array = [0] * 10
    array[0] = -14
    array[1] = -12
    array[2] = 0
    array[3] = 1
    array[4] = 2
    array[5] = 5
    array[6] = 9
    array[7] = 10
    array[8] = 23
    array[9] = 25
    return array

array = FillArray()
print(magicIndex(array))
print(magicIndex([1, 3, 2, 4, 5]))
print(magicIndex([0, 6, 6, 6, 6]))
print(magicIndex([1, 4, 4, 4, 4]))

Sort Stack *

""" 
Sort Stack

Write a function that takes in an array of integers representing a stack,
 recursively sorts the stack in place (i.e., doesn't create a brand new array), and returns it.
The array must be treated as a stack, with the end of the array as the top of the stack.
Therefore, you're only allowed to:
    Pop elements from the top of the stack by removing elements from the end of the array using the built-in .pop() method in your programming language of choice.
    Push elements to the top of the stack by appending elements to the end of the array using the built-in .append() method in your programming language of choice.
    Peek at the element on top of the stack by accessing the last element in the array.
You're not allowed to perform any other operations on the input array, 
 including accessing elements (except for the last element),
 moving elements, etc.. 
You're also not allowed to use any other data structures, and your solution must be recursive.

Sample Input
    stack = [-5, 2, -2, 4, 3, 1]
    Sample Output
    [-5, -2, 1, 2, 3, 4]

https://www.algoexpert.io/questions/Sort%20Stack
"""

# # this will work by looping through all the elements of the stack
# # a bottom-up recursion approach where we start by sorting a stack of len 0, len 1, then 2, then 3
# remove every element till we have an empty stack
#   then insert them one by one at their correct position

# O(n^2) time | O(n) space - where n is the length of the stack
def sortStack(stack):
    # base case
    if len(stack) == 0:
        return stack

    # remove element at the top (element top),
    # sort the rest of the stack,
    # insert top back to the stack but at its correct position
    #   this will be work easily because the rest of the stack is sorted
    top = stack.pop()

    sortStack(stack)
    insertElementInCorrectPosition(stack, top)

    return stack

# assumes stack is sorted or empty
def insertElementInCorrectPosition(stack, num):
    # base cases
    # correct positions to insert num
    if len(stack) == 0 or stack[-1] <= num:
        stack.append(num)

    # remove the element at the top and try to insert num at a lower position
    #   insert num at a lower position than top
    #   return top once that is done
    else:
        top = stack.pop()
        insertElementInCorrectPosition(stack, num)
        stack.append(top)

Regular Expression Matching

""" 
Regular Expression Matching

Given an input string s and a pattern p, implement regular expression matching with support for '.' and '*' where:
    '.' Matches any single character.
    '*' Matches zero or more of the preceding element.
    The matching should cover the entire input string (not partial).



Example 1:
    Input: s = "aa", p = "a"
    Output: false
    Explanation: "a" does not match the entire string "aa".
Example 2:
    Input: s = "aa", p = "a*"
    Output: true
    Explanation: '*' means zero or more of the preceding element, 'a'. Therefore, by repeating 'a' once, it becomes "aa".
Example 3:
    Input: s = "ab", p = ".*"
    Output: true
    Explanation: ".*" means "zero or more (*) of any character (.)".
Example 4:
    Input: s = "aab", p = "c*a*b"
    Output: true
    Explanation: c can be repeated 0 times, a can be repeated 1 time. Therefore, it matches "aab".
Example 5:
    Input: s = "mississippi", p = "mis*is*p*."
    Output: false

https://leetcode.com/problems/regular-expression-matching/
"""

"""
Basic Regex Parser:

Implement a regular expression function isMatch that supports the '.' and '*' symbols. 
The function receives two strings - text and pattern - and should return true if the text matches the pattern as a regular expression. 
For simplicity, assume that the actual symbols '.' and '*' do not appear in the text string and are used as special symbols only in the pattern string.
In case you aren’t familiar with regular expressions, the function determines if the text and pattern are the equal, 
    where the '.' is treated as a single a character wildcard (see third example), 
    and '*' is matched for a zero or more sequence of the previous letter (see fourth and fifth examples). 
For more information on regular expression matching, see the Regular Expression Wikipedia page.

Explain your algorithm, and analyze its time and space complexities.

Examples:

input:  text = "aa", pattern = "a"
output: false

input:  text = "aa", pattern = "aa"
output: true

input:  text = "abc", pattern = "a.c"
output: true

input:  text = "abbb", pattern = "ab*"
output: true

input:  text = "acd", pattern = "ab*c."
output: true

https://www.pramp.com/challenge/KvZ3aL35Ezc5K9Eq9Llp
"""

class Solution:
    def isMatch(self, text, pattern):
        if len(text) == 0 and len(pattern) == 0:
            return True
        if len(pattern) == 0:
            return False

        return self.is_match_helper(text, pattern, 0, 0)

    def is_match_helper(self, text, pattern, text_idx, pattern_idx):
        # base cases
        if text_idx == len(text):
            if pattern_idx == len(pattern):
                return True
            if pattern_idx+1 < len(pattern) and pattern[pattern_idx+1] == '*':
                return self.is_match_helper(text, pattern, text_idx, pattern_idx+2)
            return False
        if pattern_idx == len(pattern):
            return False

        # '*'
        if pattern_idx < len(pattern)-1 and pattern[pattern_idx+1] == '*':
            prev_char = pattern[pattern_idx]

            # many of prev_char
            after_pattern = text_idx
            if prev_char == ".":
                after_pattern = len(text)
            else:
                while after_pattern < len(text) and text[after_pattern] == prev_char:
                    after_pattern += 1

            # try all possibilities
            for idx in range(text_idx, after_pattern+1):
                if self.is_match_helper(text, pattern, idx, pattern_idx+2):
                    return True
            return False

        # '.'
        elif pattern[pattern_idx] == '.':
            return self.is_match_helper(text, pattern, text_idx+1, pattern_idx+1)

        # other characters
        else:
            if pattern[pattern_idx] != text[text_idx]:
                return False

            return self.is_match_helper(text, pattern, text_idx+1, pattern_idx+1)

"""
"""

class Solution_:
    def isMatch(self, text, pattern):
        if len(text) == 0 and len(pattern) == 0:
            return True
        if len(pattern) == 0:
            return False

        cache = [[None for _ in range(len(pattern))] for _ in range(len(text))]
        return self.is_match_helper(text, pattern, cache, 0, 0)

    def is_match_helper(self, text, pattern, cache, text_idx, pattern_idx):
        # base cases
        if text_idx == len(text):
            if pattern_idx == len(pattern):
                return True
            if pattern_idx+1 < len(pattern) and pattern[pattern_idx+1] == '*':
                return self.is_match_helper(text, pattern, cache, text_idx, pattern_idx+2)
            return False
        if pattern_idx == len(pattern):
            return False
        if cache[text_idx][pattern_idx] is not None:
            return cache[text_idx][pattern_idx]

        # '*'
        if pattern_idx < len(pattern)-1 and pattern[pattern_idx+1] == '*':
            prev_char = pattern[pattern_idx]

            # many of prev_char
            after_pattern = text_idx
            if prev_char == ".":
                after_pattern = len(text)
            else:
                while after_pattern < len(text) and text[after_pattern] == prev_char:
                    after_pattern += 1

            # try all possibilities
            for idx in range(text_idx, after_pattern+1):
                if self.is_match_helper(text, pattern, cache, idx, pattern_idx+2):
                    cache[text_idx][pattern_idx] = True
                    return cache[text_idx][pattern_idx]

            cache[text_idx][pattern_idx] = False
            return cache[text_idx][pattern_idx]

        # '.'
        elif pattern[pattern_idx] == '.':
            cache[text_idx][pattern_idx] = self.is_match_helper(
                text, pattern, cache, text_idx+1, pattern_idx+1)
            return cache[text_idx][pattern_idx]

        # other characters
        else:
            if pattern[pattern_idx] != text[text_idx]:
                cache[text_idx][pattern_idx] = False
            else:
                cache[text_idx][pattern_idx] = self.is_match_helper(
                    text, pattern, cache, text_idx+1, pattern_idx+1)
            return cache[text_idx][pattern_idx]

Strobogrammatic Number II *

""" 
Strobogrammatic Number II

Given an integer n, return all the strobogrammatic numbers that are of length n. 
You may return the answer in any order.
A strobogrammatic number is a number that looks the same when rotated 180 degrees (looked at upside down).

Example 1:
    Input: n = 2
    Output: ["11","69","88","96"]
Example 2:
    Input: n = 1
    Output: ["0","1","8"]

https://leetcode.com/problems/strobogrammatic-number-ii
"""

""" 
We realised that we have 2 base cases (simplest subproblems):
    - n=1  --> ['0', '1', '8']
    - n=2  --> ['00', '11', '88', '69', '96']
The rest can be built around that:
    - n=3  
        -->               ["101","808","609","906","111","818","619","916","181","888","689","986"] 
        all w invalid --> ["000","101","808","609","906","010","111","818","619","916","080","181","888","689","986"]
    - n=4  
        -->               ["1001","8008","6009","9006","1111","8118","6119","9116","1881","8888","6889","9886","1691","8698","6699","9696","1961","8968","6969","9966"]
        all w invalid --> ["0000","1001","8008","6009","9006","0110","1111","8118","6119","9116","0880","1881","8888","6889","9886","0690","1691","8698","6699","9696","0960","1961","8968","6969","9966"]

Have a recursive function that builds from the base cases upwards:
Example:
    ```
    def helper(n):
        if n == 1:
            return ['0', '1', '8']
        if n == 2:
            return ['00', '11', '88', '69', '96']
        result = []

        for base in helper(n-2):
            result.append('0' + base + '0')
            result.append('1' + base + '1')
            result.append('6' + base + '9')
            result.append('8' + base + '8')
            result.append('9' + base + '6')

        return result
    ```
then return the valid results
"""

class Solution_:
    def findStrobogrammatic(self, n: int):
        result = []

        for num in self.findStrobogrammatic_helper(n):
            # remove leading zeros
            if str(int(num)) == num:
                result.append(num)

        return result

    def findStrobogrammatic_helper(self, n):
        # Base cases
        if n == 1:
            return ['0', '1', '8']
        if n == 2:
            return ['00', '11', '88', '69', '96']
        result = []

        # this is the only way they can be expanded
        for base in self.findStrobogrammatic_helper(n-2):
            result.append('0' + base + '0')
            result.append('1' + base + '1')
            result.append('6' + base + '9')
            result.append('8' + base + '8')
            result.append('9' + base + '6')

        return result

# Time complexity O(n). We iterate n//2 times in for _ in range(n//2). Within this, we iterate for num in output at most 5 times, since output has at most 5 numbers.
# Space complexity O(n).
class Solution:
    def findStrobogrammatic(self, n: int):
        result = []

        # handle even or odd
        combinations = [''] if n % 2 == 0 else ['0', '1', '8']
        for _ in range(n//2):
            temp = []
            for num in combinations:
                temp.append('0' + num + '0')
                temp.append('1' + num + '1')
                temp.append('8' + num + '8')
                temp.append('6' + num + '9')
                temp.append('9' + num + '6')
            combinations = temp

        for num in combinations:
            # remove leading zeros
            if str(int(num)) == num:
                result.append(num)

        return result

How do you determine if there is a recursive solution to a problem?

Base case question Is there a base case? Is there a way out of the function that does not require a recursive call and in which the function works correctly?
Smaller caller question Does each recursive call result in a smaller version of the original problem which leads inescapably to the base case.
General case question Assuming each recursive call works correctly, does this lead to the correct solution to the whole problem? The answer to this question can be shown through induction:
1. Show that the solution works for the base case, i.e. SumOfSquares(n, n).
2. Assume that the solution works for the case of SumOfSquares(n, n+1).
3. Now to finish the proof show that the solution works for SumOfSquares(n, n+2):
  1. The return value from the first recursive call to the function would be n + SumOfSquares(n+1, n+2).
  2. This is just the results of a call to the base case SumOfSquares(n, n) which we have already shown to work, and a call to what is syntactically equivalent to SumOfSquares(n, n+1) which we have assumed works.
  3. Thus, by induction, we have shown that the function works for all values of m and n where m < n. - number of choices to make

Ways of dividing a problem into subproblems:

Recursive solutions, by definition, are built off of solutions to subproblems. Many times, this will mean simply to compute f(n) by adding something, removing something, or otherwise changing the solution for f(n-1). In other cases, you might solve the problem for the first half of the data set, then the second half, and then merge those results.

There are many ways you might divide a problem into subproblems. Three of the most common approaches to developing an algorithm are bottom-up, top-down, and half-and-half.

Top-down and bottom-up refer to two general approaches to dynamic programming. A top-down solution starts with the final result and recursively breaks it down into subproblems. The bottom-up method does the opposite. It takes an iterative approach to solve the subproblems first and then works up to the desired solution.

1. Top-Down Approach

The top-down approach can be more complex since it's less concrete. But sometimes, it's the best way to think about the problem. In these problems, we think about how we can divide the problem for case N into subproblems. Be careful of overlap between the cases.

Top-down with Memoization:

In this approach, we try to solve the bigger problem by recursively finding the solution to smaller sub-problems. Whenever we solve a sub-problem, we cache its result so that we don’t end up solving it repeatedly if it’s called multiple times. Instead, we can just return the saved result. This technique of storing the results of already solved subproblems is called Memoization.

2. Bottom-Up Approach

The bottom-up approach is often the most intuitive. We start with knowing how to solve the problem for a simple case, like a list with only one element. Then we figure out how to solve the problem for two elements, then for three elements, and so on. The key here is to think about how you can build the solution for one case off of the previous case (or multiple previous cases).

Bottom-up with Tabulation:

Tabulation is the opposite of the top-down approach and avoids recursion. In this approach, we solve the problem “bottom-up” (i.e. by solving all the related sub-problems first). This is typically done by filling up an n-dimensional table. Based on the results in the table, the solution to the top/original problem is then computed.

Tabulation is the opposite of Memoization, as in Memoization we solve the problem and maintain a map of already solved sub-problems. In other words, in memoization, we do it top-down in the sense that we solve the top problem first (which typically recurses down to solve the sub-problems).

Examples:

Sort stack

""" 
Sort Stack: (Under stacks)

Write a function that takes in an array of integers representing a stack,
 recursively sorts the stack in place (i.e., doesn't create a brand new array), and returns it.
The array must be treated as a stack, with the end of the array as the top of the stack.
Therefore, you're only allowed to:
    Pop elements from the top of the stack by removing elements from the end of the array using the built-in .pop() method in your programming language of choice.
    Push elements to the top of the stack by appending elements to the end of the array using the built-in .append() method in your programming language of choice.
    Peek at the element on top of the stack by accessing the last element in the array.
You're not allowed to perform any other operations on the input array, 
 including accessing elements (except for the last element),
 moving elements, etc.. 
You're also not allowed to use any other data structures, and your solution must be recursive.

Sample Input
    stack = [-5, 2, -2, 4, 3, 1]
    Sample Output
    [-5, -2, 1, 2, 3, 4]

https://www.algoexpert.io/questions/Sort%20Stack
"""

# O(n^2) time | O(n) space - where n is the length of the stack
# # this will work by looping through all the elements of the stack
# # a bottom-up recursion approach where we start by sorting a stack of len 0, len 1, then 2, then 3
# remove every element till we have an empty stack
#   then insert them one by one at their correct position
def sortStack(stack):
    # base case
    if len(stack) == 0:
        return stack

    # remove element at the top (element top),
    # sort the rest of the stack,
    # insert top back to the stack but at its correct position
    #   this will be work easily because the rest of the stack is sorted
    top = stack.pop()
    sortStack(stack)
    insertElementInCorrectPosition(stack, top)
    return stack

# requires a sorted stack
def insertElementInCorrectPosition(stack, num):
    # base cases
    # correct positions to insert num
    if len(stack) == 0 or stack[-1] <= num:
        stack.append(num)

    # remove the element at the top and try to insert num at a lower position
    #   return top once that is done
    else:
        top = stack.pop()
        insertElementInCorrectPosition(stack, num)
        stack.append(top)

3. Half-and-Half Approach

In addition to top-down and bottom-up approaches, it's often effective to divide the data set in half. For example, a binary search works with a "half-and-half" approach. When we look for an element in a sorted array, we first figure out which half of the array contains the value. Then we recurse and search for it in that half. Merge sort is also a "half-and-half" approach. We sort each half of the array and then merge together the sorted halves.

Maintaining State

When dealing with recursive functions, keep in mind that each recursive call has its own execution context, so to maintain state during recursion you have to either:

Thread (pass down) the state through each recursive call so that the current state is part of the current call’s execution context
Keep the state in the global scope
- eg: use nonlocal

Guides:

Recursion is especially suitable when the input is expressed in recursive rules such as a computer grammar.
Recursion is a good choice for search, enumeration, and divide-and-conquer.
Use recursion as an alternative to deeply nested iteration loops. For example, recursion is much better when you have an undefined number of levels, such as the IP address problem generalized to k substrings.
If you are asked to remove recursion from a program, consider mimicking call stack with the stack data structure.
Recursion can be easily removed from a tail-recursive program by using a while-loop no stack is needed. (Optimizing compilers do this.)
If a recursive function may end up being called with the same arguments more than once, cache the results-this is the idea behind Dynamic Programming

A divide-and-conquer algorithm works by repeatedly decomposing a problem into two or more smaller independent subproblems of the same kind until it gets to instances that are simple enough to be solved directly.

More explanation

A useful mantra to adopt when solving problems recursively is ‘fake it ’til you make it’, that is, pretend you’ve already solved the problem for a simpler case, and then try to reduce the larger problem to use the solution for this simpler case. If a problem is suited to recursion, there should actually only be a small number of simple cases which you need to explicitly solve, i.e. this method of reducing to a simpler problem can be used to solve every other case.

Recursion,%20DP%20&%20Backtracking%20525dddcdd0874ed98372518724fc8753/1_cxQUnD3J3jMDIQTpsB7PNQ.gif

Suppose we are given some actual data of some data type, call it dₒ. The idea with recursion is to pretend that we have already solved the problem or computed the desired function f for all forms of this data type that are simpler than dₒ according to some degree of difficulty that we need to define. Then, if we can find a way of expressing f(dₒ) in terms of one or more f(d)s, where all of these d s are less difficult (have a smaller degree) than dₒ, then we have found a way to reduce and solve for f(dₒ). We repeat this process, and hopefully, at some point, the remaining f(d)s will get so simple that we can easily implement a fixed, closed solution to them. Then, our solution to the original problem will reveal itself as our solutions to progressively simpler problems aggregate and cascade back up to the top.

Honourable mentions

Use indexes to eliminate elements in an array instead of creating a new array all the time in recursion

Creating new array:

def getPermutationsHelper(res, curr_perm, array):
    if len(array) == 0:
        if len(curr_perm) > 0:
            res.append(curr_perm)
        return

    for i in range(len(array)):
        # add the number(array[i]), add it to the permutation and remove it from the array
        new_array = array[:i] + array[i+1:]  # remove number form array
        new_perm = curr_perm + [array[i]]  # add number to the permutation

        getPermutationsHelper(res, new_perm, new_array)

def getPermutations(array):
    res = []
    getPermutationsHelper(res, [], array)
    return res

Using indexes:

def swap(array, a, b):
    array[a], array[b] = array[b], array[a]

def getPermutationsHelper(res, curr_perm, array, pos):
    if pos >= len(array):
        if len(curr_perm) > 0:
            res.append(curr_perm)
        return

    for i in range(pos, len(array)):
        # add the number(array[i]) to the permutation
        # place the element of interest at the first position (pos)
        #  Example: for getPermutationsHelper(res, [], [1,2,3], 0), while in this for loop
        #       when at value 1 (i=0), we want 1 to be at pos(0), so that we can iterate through [2,3,4] next without adding 1 again
        #       when at 2, we want 2 to be at pos(0), so that we can iterate through [1,3,4] next ([2,1,3,4])
        #       when at 3, we want it to be at pos(0), so that we can iterate through [2,1,4] next ([3,2,1,4])
        #   so we have to manually place it there (via swapping with the element at pos), then we return it just before the loop ends
        # and move pos forward

        new_perm = curr_perm + [array[i]]  # add number to the permutation

        # place the element of interest at the first position (pos)
        swap(array, pos, i)
        getPermutationsHelper(res, new_perm, array, pos+1)
        # return the element of interest to its original position
        swap(array, i, pos)

def getPermutations(array):
    res = []
    getPermutationsHelper(res, [], array, 0)
    return res

Even better

def swap(array, a, b):
    array[a], array[b] = array[b], array[a]

def getPermutationsHelper(res, array, pos):
    if pos == len(array) - 1:
        res.append(array[:])
        return

    for i in range(pos, len(array)):
        # place the element of interest at the first position (pos)
        #  Example: for getPermutationsHelper(res, [], [1,2,3], 0), while in this for loop
        #       when at value 1 (i=0), we want 1 to be at pos(0), so that we can iterate through [2,3,4] next without adding 1 again
        #       when at 2, we want 2 to be at pos(0), so that we can iterate through [1,3,4] next ([2,1,3,4])
        #       when at 3, we want it to be at pos(0), so that we can iterate through [2,1,4] next ([3,2,1,4])
        #   so we have to manually place it there (via swapping with the element at pos), then we return it just before the loop ends
        # and move pos forward
        # place the element of interest at the first position (pos)
        swap(array, pos, i)
        getPermutationsHelper(res, array, pos+1)
        # return the element of interest to its original position
        swap(array, i, pos)

def getPermutations(array):
    res = []
    getPermutationsHelper(res, array, 0)
    return res

Combination Sum III

Screenshot 2021-10-17 at 06.42.45.png

Screenshot 2021-10-17 at 06.43.04.png

Screenshot 2021-10-17 at 06.43.19.png

Screenshot 2021-10-17 at 06.43.36.png

Screenshot 2021-10-17 at 06.43.50.png

Screenshot 2021-11-03 at 10.00.20.png

"""
216. Combination Sum III

Find all valid combinations of k numbers that sum up to n such that the following conditions are true:
    Only numbers 1 through 9 are used.
    Each number is used at most once.
Return a list of all possible valid combinations. The list must not contain the same combination twice, and the combinations may be returned in any order.

Example 1:
    Input: k = 3, n = 7
    Output: [[1,2,4]]
    Explanation:
        1 + 2 + 4 = 7
        There are no other valid combinations.
Example 2:
    Input: k = 3, n = 9
    Output: [[1,2,6],[1,3,5],[2,3,4]]
    Explanation:
        1 + 2 + 6 = 9
        1 + 3 + 5 = 9
        2 + 3 + 4 = 9
        There are no other valid combinations.
Example 3:
    Input: k = 4, n = 1
    Output: []
    Explanation: There are no valid combinations.
        Using 4 different numbers in the range [1,9], 
        the smallest sum we can get is 1+2+3+4 = 10 and since 10 > 1, there are no valid combination.
Example 4:
    Input: k = 3, n = 2
    Output: []
    Explanation: There are no valid combinations.
Example 5:
    Input: k = 9, n = 45
    Output: [[1,2,3,4,5,6,7,8,9]]
    Explanation:
        1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45
        There are no other valid combinations.

https://leetcode.com/problems/combination-sum-iii/

Do after:
- https://leetcode.com/problems/combination-sum
"""

# O(9! * K) time
class Solution(object):
    def combinationSum3(self, k, n):
        res = []
        self.helper(n, res, 1, 0, [0]*k, 0)
        return res

    def helper(self, n, res, start_num, curr_idx, curr, total):
        if total == n and curr_idx == len(curr):
            res.append(curr[:])
            return
        if total >= n or start_num > 9 or curr_idx >= len(curr):
            return

        for number in range(start_num, 10):
            curr[curr_idx] = number
            self.helper(n, res, number+1, curr_idx+1, curr, total+number)
            curr[curr_idx] = 0

Combination Sum

Combination Sum - Backtracking - Leetcode 39 - Python

Screenshot 2021-11-03 at 09.54.39.png

Screenshot 2021-11-03 at 09.58.27.png

""" 
Combination Sum

Given an array of distinct integers candidates and a target integer target, 
    return a list of all unique combinations of candidates where the chosen numbers sum to target. 
You may return the combinations in any order.
The same number may be chosen from candidates an unlimited number of times. 
Two combinations are unique if the frequency of at least one of the chosen numbers is different.
It is guaranteed that the number of unique combinations that sum up to target is less than 150 combinations for the given input.


Example 1:
    Input: candidates = [2,3,6,7], target = 7
    Output: [[2,2,3],[7]]
    Explanation:
        2 and 3 are candidates, and 2 + 2 + 3 = 7. Note that 2 can be used multiple times.
        7 is a candidate, and 7 = 7.
        These are the only two combinations.
Example 2:
    Input: candidates = [2,3,5], target = 8
    Output: [[2,2,2,2],[2,3,3],[3,5]]
Example 3:
    Input: candidates = [2], target = 1
    Output: []
Example 4:
    Input: candidates = [1], target = 1
    Output: [[1]]
Example 5:
    Input: candidates = [1], target = 2
    Output: [[1,1]]

https://leetcode.com/problems/combination-sum

Prerequisite:
- https://leetcode.com/problems/combination-sum-iii
"""

"""

candidates = [2,3,6,7], target = 7
                                                    7[]
                                              5[2]         4[3]
                                           3[2,2] 2[2,3]

                   []rem_target
           /          /     \     \
    [2]5            [3]4  [6]1  [7]0
 /       /    
[2,2]3   [2,3]2  
|        |
[2,2,3]0 [2,3,2]0

"""

class Solution(object):
    def combinationSum(self, candidates, target):
        return self.helper(candidates, 0, target)

    def helper(self, candidates, idx, target):
        # base cases
        if target == 0:
            return [[]]
        if target < 0 or idx >= len(candidates):
            return []
        result = []

        # add number
        # remember to give the current number another chance, rather than moving on (idx instead of idx+1)
        for arr in self.helper(candidates, idx, target-candidates[idx]):
            result.append(arr + [candidates[idx]])

        # skip number
        result += self.helper(candidates, idx+1, target)

        return result

""" 
Let N be the number of candidates, T be the target value, and M be the minimal value among the candidates.

Time Complexity: O(N ^ T/M)
Space Complexity: O(T/M)

    The execution of the backtracking is unfolded as a DFS traversal in a n-ary tree. The total number of steps during the backtracking would be the number of nodes in the tree.
    At each node, it takes a constant time to process, except the leaf nodes which could take a linear time to make a copy of combination. So we can say that the time complexity is linear to the number of nodes of the execution tree.
    Here we provide a loose upper bound on the number of nodes:
        First of all, the fan-out of each node would be bounded to N, i.e. the total number of candidates.
        The maximal depth of the tree, would be T/M, where we keep on adding the smallest element to the combination.
        As we know, the maximal number of nodes in N-ary tree of T/M, height would be : O(N ^ (T/M + 1))
    Note that, the actual number of nodes in the execution tree would be much smaller than the upper bound, since the fan-out of the nodes are decreasing level by level.
"""

class Solution_:
    def combinationSum(self, candidates, target):

        results = []

        def backtrack(remain, comb, start):
            if remain == 0:
                results.append(list(comb))
                return
            elif remain < 0:
                return

            for i in range(start, len(candidates)):
                # add the number into the combination
                comb.append(candidates[i])

                # give the current number another chance, rather than moving on (i instead of i+1)
                backtrack(remain - candidates[i], comb, i)

                # backtrack, remove the number from the combination
                comb.pop()

        backtrack(target, [], 0)

        return results

Dynamic programming

Dynamic Programming - 7 Steps to Solve any DP Interview Problem

Patterns

Grokking Dynamic Programming Patterns for Coding Interviews - Learn Interactively

Dynamic Programming

Fibonacci Numbers - Coderust: Hacking the Coding Interview

Demystifying Dynamic Programming

5 Simple Steps for Solving Dynamic Programming Problems

Calculating Fibonacci Numbers - Algorithms for Coding Interviews in Python

Memoization and Dynamic Programming | Interview Cake

Bottom-Up Algorithms and Dynamic Programming | Interview Cake

Introduction to Dynamic Programming 1 Tutorials & Notes | Algorithms | HackerEarth

leetcode/dynamic-programming-en.md at master · azl397985856/leetcode

Dynamic Programming - 7 Steps to Solve any DP Interview Problem

Dynamic Programming

Dynamic programming is simple #3 (multi-root recursion) - LeetCode Discuss

Patterns

Dynamic programming is basically, recursion plus using common sense. The intuition behind dynamic programming is that we trade space for time, i.e. to say that instead of calculating all the states taking a lot of time but no space, we take up space to store the results of all the sub-problems to save time later.

One can also think of dynamic programming as a table-filling algorithm: you know the calculations you have to do, so you pick the best order to do them in and ignore the ones you don't have to fill in.

DP is an optimisation technique → can reduce exponential to polynomial time

Common problems:

Combinatory: Answer question... how many?
Optimisation: maximises or minimises some function Examples: what is the minimum/maximum?

Dynamic programming is mostly just a matter of taking a recursive algorithm and finding the overlapping subproblems (that is, the repeated calls). You then cache those results for future recursive calls. Alternatively, you can study the pattern of the recursive calls and implement something iterative. You still "cache" previous work

Dynamic programming amounts to breaking down an optimization problem into simpler sub-problems and storing the solution to each sub-problem so that each sub-problem is only solved once. One of the simplest examples of dynamic programming is computing the nth Fibonacci number. A good way to approach such a problem is often to implement it as a normal recursive solution, and then add the caching part.

Every Dynamic Programming problem has a schema to be followed:

Show that the problem can be broken down into optimal sub-problems.
Recursively define the value of the solution by expressing it in terms of optimal solutions for smaller sub-problems.
Compute the value of the optimal solution in a bottom-up fashion.
Construct an optimal solution from the computed information.

The majority of the Dynamic Programming problems can be categorized into two types:

Optimization problems The optimization problems expect you to select a feasible solution so that the value of the required function is minimized or maximized.
Combinatorial problems expect you to figure out the number of ways to do something, or the probability of some event happening.

Examples

0/1 Knapsack

0/1 Knapsack (Dynamic Programming)
Levenshtein Distance

Coin Change 2 (Total Unique Ways To Make Change)

Problem

""" 
Coin Change 2/Total Unique Ways To Make Change:

You are given an integer array coins representing coins of different denominations and an integer amount representing a total amount of money.
Return the number of combinations that make up that amount. If that amount of money cannot be made up by any combination of the coins, return 0.
You may assume that you have an infinite number of each kind of coin.
The answer is guaranteed to fit into a signed 32-bit integer.

Example 1:
    Input: amount = 5, coins = [1,2,5]
    Output: 4
    Explanation: there are four ways to make up the amount:
    5=5
    5=2+2+1
    5=2+1+1+1
    5=1+1+1+1+1
Example 2:
    Input: amount = 3, coins = [2]
    Output: 0
    Explanation: the amount of 3 cannot be made up just with coins of 2.
Example 3:
    Input: amount = 10, coins = [10]
    Output: 1

https://leetcode.com/problems/coin-change-2/
https://www.algoexpert.io/questions/Number%20Of%20Ways%20To%20Make%20Change
"""

Memoization

Coin Change 2 - Dynamic Programming Unbounded Knapsack - Leetcode 518 - Python

Screenshot 2021-08-28 at 08.22.55.png

Duplicate recursive trees (we should avoid this)

"""
- have a recursive function:
    - for each number in the array, choose to include it:
        - subtract the number from the amount and pass it down the recursive function
        - once you reach 0 return one of less than 0 return 0
    - add up all the results

    - cache the total for each amount

    - ensure no duplicates by dividing the recursion trees by starting index
        - for examples for coins = [1,2,5]
            - index 0 tree: [1,2,5]
            - index 1 tree: [2,5]
            - index 2 tree: [5]
"""

class SolutionSLOW: # times out on leetcode
    def changeHelper(self, amount, coins, cache, idx):
        if amount == 0:
            return 1
        if amount < 0:
            return 0
        if (idx, amount) in cache:
            return cache[(idx, amount)]

        total = 0
        for i in range(idx, len(coins)):
            total += self.changeHelper(amount-coins[i], coins, cache, i)

        cache[(idx, amount)] = total
        return cache[(idx, amount)]

    def change(self, amount, coins):
        return self.changeHelper(amount, coins, {}, 0)

class SolutionSLOW2: # times out on leetcode
    def changeHelper(self, amount, coins, cache, idx):
        if amount == 0:
            return 1
        if amount < 0 or idx == len(coins):
            return 0
        if cache[idx][amount] != False:
            return cache[idx][amount]

        total = 0
        # use it then next time we can decide to leave it out or use it again
        total += self.changeHelper(amount-coins[idx], coins, cache, idx)
        # not use coin and skip to the next
        total += self.changeHelper(amount, coins, cache, idx+1)

        cache[idx][amount] = total
        return cache[idx][amount]

    def change(self, amount, coins):
        cache = [[False for _ in range(amount+1)] for _ in range(len(coins))]
        return self.changeHelper(amount, coins, cache, 0)

class Solution:
    def changeHelper(self, amount, coins, cache, idx):
        if amount == 0:
            return 1
        if amount < 0 or idx == len(coins):
            return 0
        if (idx, amount) in cache:
            return cache[(idx, amount)]

        total = 0
        total += self.changeHelper(amount-coins[idx], coins, cache, idx) # use it then next time we can decide to leave it out or use it again
        total += self.changeHelper(amount, coins, cache, idx+1) # not use coin and skip to the next

        cache[(idx, amount)] = total
        return cache[(idx, amount)]

    def change(self, amount, coins):
        return self.changeHelper(amount, coins, {}, 0)

Tabulation

coin change 2 | coin change 2 leetcode

Total Unique Ways To Make Change - Dynamic Programming ("Coin Change 2" on LeetCode)

Leetcode - Coin Change 2 (Python)

Coin Change 2 | LeetCode 518 | C++, Java, Python

Similar to knapsack

Screenshot 2021-08-29 at 09.14.50.png

"""

# if amount is zero you can always make that change with zero/no coins
# if there are no coins there is no way to make change for amounts greater than zero

number of ways = (
    using the coin     => reduce the amount by the coin's value (move left by the coin's value)
+   not using the coin => remove the coin (move up by one)
)

        0  1  2  3  4  5
[]      1  0  0  0  0  0
[1]     1  1  1  1  1  1
[1,2]   1
[1,2,5] 1

"""

class Solution:

    def change(self, amount, coins):
        dp = [[-1 for _ in range(amount+1)] for _ in range(len(coins)+1)]

        # Fill in defaults
        # if amount is zero you can always make that change with zero/no coins
        for i in range(len(coins)+1):
            dp[i][0] = 1
        # if there are no coins there is no way to make change for amounts greater than zero
        for i in range(1, amount+1):
            dp[0][i] = 0

        for coin in range(1, len(coins)+1):
            for amount in range(1, amount+1):
                actual_coin = coins[coin-1]
                total = 0

                # not use coin => remove the coin (move up by one)
                total += dp[coin-1][amount]
                # use coin => reduce the amount by the coin's value (move left by the coin's value)
                if actual_coin <= amount:
                    total += dp[coin][amount-actual_coin]

                # print(coin,actual_coin,amount,total) 
                dp[coin][amount] = total

        return dp[-1][-1]

# only keep needed fields in memory
class Solution:

    def change(self, amount, coins):
        dp = [0 for _ in range(amount+1)]
        # if amount is zero you can always make that change with zero/no coins
        dp[0] = 1

        for coin in coins:
            for amount in range(1, amount+1):
                total = dp[amount] # (ways_for_prev_coin) coin not added

                if coin <= amount:
                    total += dp[amount-coin] # coin added

                dp[amount] = total

        return dp[-1]

Coin Change

"""
Coin Change:

You are given an integer array coins representing coins of different denominations and 
 an integer amount representing a total amount of money.
Return the fewest number of coins that you need to make up that amount. 
If that amount of money cannot be made up by any combination of the coins, return -1.
You may assume that you have an infinite number of each kind of coin.

Example 1:

    Input: coins = [1,2,5], amount = 11
    Output: 3
    Explanation: 11 = 5 + 5 + 1
Example 2:

    Input: coins = [2], amount = 3
    Output: -1
Example 3:

    Input: coins = [1], amount = 0
    Output: 0
Example 4:

    Input: coins = [1], amount = 1
    Output: 1
Example 5:

    Input: coins = [1], amount = 2
    Output: 2

https://leetcode.com/problems/coin-change/

"""
""" 
Min Number Of Coins For Change:

Given an array of positive integers representing coin denominations and a single non-negative integer n representing a target amount of money, 
write a function that returns the smallest number of coins needed to make change for (to sum up to) that target amount using the given coin denominations.
Note that you have access to an unlimited amount of coins. 
    In other words, if the denominations are [1, 5, 10], you have access to an unlimited amount of 1s, 5s, and 10s.
If it's impossible to make change for the target amount, return -1.

https://www.algoexpert.io/questions/Min%20Number%20Of%20Coins%20For%20Change
"""

class SolutionMEM:
    def coinChange(self, coins, amount):

        cache = [[False for _ in range(amount+1)] for _ in range(len(coins))]
        res = self.coinChangeHelper(coins, 0, amount, cache)
        if res == float('inf'):
            return -1
        return res

    def coinChangeHelper(self, coins, idx, amount, cache):
        if amount == 0:
            return 0
        if amount < 0:
            return float('inf')
        if idx == len(coins):
            return float('inf')

        if cache[idx][amount]:
            return cache[idx][amount]

        # use it then next time we can decide to leave it out or use it again
        used = 1 + self.coinChangeHelper(coins, idx, amount-coins[idx], cache)

        # not use coin and skip to the next
        not_used = self.coinChangeHelper(coins, idx+1, amount, cache)

        cache[idx][amount] = min(used, not_used)

        return cache[idx][amount]

"""
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

i = infinity
         0 1 2 3 4 5 6 7 8 9 10 11
[]       0 i i i i i i i i i i  i
[1]      0 1 2 3 4 5 6 7 8 9 10 11
[1,2]    0 1 1 2 2 3 3 4 4 5 5  6
[1,2,5]  0 1 1 2 2 1 2 2 3 4 2  3

"""

class SolutionDP:
    def coinChange(self, coins, amount):
        if amount == 0:
            return 0
        if len(coins) == 0:
            return -1

        dp = [
            [float('inf') for _ in range(amount+1)] for _ in range(len(coins)+1)]
        for i in range(len(coins)+1):
            dp[i][0] = 0

        for coin in range(1, len(coins)+1):
            for amount in range(1, amount+1):
                coin_val = coins[coin-1]

                not_use = dp[coin-1][amount]
                use = float('inf')
                if coin_val <= amount:
                    use = 1 + dp[coin][amount-coin_val]

                dp[coin][amount] = min(use, not_use)

        if dp[-1][-1] == float('inf'):
            return -1
        return dp[-1][-1]

class SolutionDPImproved:
    def coinChange(self, coins, amount):
        if amount == 0:
            return 0
        if len(coins) == 0:
            return -1

        dp = [float('inf') for _ in range(amount+1)]
        dp[0] = 0

        for amount in range(1, amount+1):
            for coin in coins:
                if coin > amount:
                    continue
                use = 1 + dp[amount-coin]
                dp[amount] = min(use, dp[amount])

        if dp[-1] == float('inf'):
            return -1
        return dp[-1]

Equal Subset Sum Partition

""" 
Equal Subset Sum Partition:

Given a set of positive numbers, find if we can partition it into two subsets such that the sum of elements in both the subsets is equal.

Example 1
    Input: {1, 2, 3, 4}
    Output: True
    Explanation: The given set can be partitioned into two subsets with equal sum: {1, 4} & {2, 3}
Example 2
    Input: {1, 1, 3, 4, 7}
    Output: True
    Explanation: The given set can be partitioned into two subsets with equal sum: {1, 3, 4} & {1, 7}
Example 3
    Input: {2, 3, 4, 6}
    Output: False
    Explanation: The given set cannot be partitioned into two subsets with equal sum.

https://leetcode.com/problems/partition-equal-subset-sum
https://www.educative.io/courses/grokking-dynamic-programming-patterns-for-coding-interviews/3jEPRo5PDvx
https://afteracademy.com/blog/partition-equal-subset-sum
"""

""" 
We know that if we can partition it into equal subsets that each set’s sum will have to be sum/2. 
If the sum is an odd number we cannot possibly have two equal sets.
This changes the problem into finding if a subset of the input array has a sum of sum/2.
We know that if we find a subset that equals sum/2, 
    the rest of the numbers must equal sum/2 so we’re good since they will both be equal to sum/2. 
We can solve this using dynamic programming similar to the knapsack problem.

We basically need to find two groups of numbers that will each be equal to sum(input_array) / 2
Finding one such group (with its sum = sum(input_array)/2) will imply that there will be another with a similar sum
"""

# ----------------------------------------------------------------------------------------------------------------------------------------------------------------
""" 
Brute Force 1:
While using recursion, `iterate` through the input array,
choosing whether to include each number in one of two arrays: "one" & "two"
stop once the sum of elements in each of the arrays are equal to sum(input_array) / 2
"""

def can_partition_helper_bf1(num, total, res, idx, one, two):
    # base cases
    if sum(one) == total/2 and sum(two) == total/2:
        res.append([one, two])
        return

    if sum(one) > total/2 or sum(two) > total/2:
        return

    if idx >= len(num):
        return

    can_partition_helper_bf1(num, total, res, idx+1,
                             one+[num[idx]], two)  # one
    can_partition_helper_bf1(num, total, res, idx+1,
                             one, two+[num[idx]])  # two

def can_partition_bf1(num):
    res = []
    total = sum(num)
    can_partition_helper_bf1(num, total, res, 0, [], [])
    return len(res) > 0

# ----------------------------------------------------------------------------------------------------------------------------------------------------------------
""" 
Brute Force 2:
While using recursion, `iterate` through the input array,
choosing whether to include each number in one of two sums: "one" & "two"
stop once each of the sums are equal to sum(input_array) / 2

Basically Brute Force 1 without remembering the numbers
"""

def can_partition_helper_bf2(num, total,  idx, one, two):
    # base cases
    if one == total/2 and two == total/2:
        return True

    if one > total/2 or two > total/2:
        return False
    if idx >= len(num):
        return False

    in_one = can_partition_helper_bf2(num, total,  idx+1, one+num[idx], two)
    in_two = can_partition_helper_bf2(num, total,  idx+1, one, two+num[idx])

    return in_one or in_two

def can_partition_bf2(num):
    total = sum(num)
    return can_partition_helper_bf2(num, total,  0, 0, 0)

# ----------------------------------------------------------------------------------------------------------------------------------------------------------------
""" 
Brute Force 3:

We basically need to find one group of numbers that will be equal to sum(input_array) / 2
Finding one such group (with its sum = sum(input_array)/2) will imply that there will be another with a similar sum

While using recursion, `iterate` through the input array,
choosing whether to include each number in the sum
stop once the sum is equal to sum(input_array) / 2

Basically Brute Force 2 but dealing with one sum
"""

def can_partition_helper_bf3_0(num, total,  idx, one):
    # base cases
    if one == total/2:
        return True

    if one > total/2:
        return False
    if idx >= len(num):
        return False

    included = can_partition_helper_bf3_0(num, total,  idx+1, one+num[idx])
    excluded = can_partition_helper_bf3_0(num, total,  idx+1, one)

    return included or excluded

# O(2^n) time | O(n) space
def can_partition_bf3_0(num):
    total = sum(num)
    return can_partition_helper_bf3_0(num, total,  0, 0)

# -----------------------------------

def can_partition_helper_bf3(num, total, idx):
    # base cases
    if total == 0:
        return True

    if total < 0:
        return False
    if idx >= len(num):
        return False

    included = can_partition_helper_bf3(num, total-num[idx], idx+1)
    excluded = can_partition_helper_bf3(num, total, idx+1)

    return included or excluded

# O(2^n) time | O(n) space
def can_partition_bf3(num):
    total = sum(num)
    return can_partition_helper_bf3(num, total/2,  0)

# ----------------------------------------------------------------------------------------------------------------------------------------------------------------

"""
Top-down Dynamic Programming with Memoization:

We can use memoization to overcome the overlapping sub-problems. 
Since we need to store the results for every subset and for every possible sum,
 therefore we will be using a two-dimensional array to store the results of the solved sub-problems.
The first dimension of the array will represent different subsets and the second dimension will represent different ‘sums’ that we can calculate from each subset.
These two dimensions of the array can also be inferred from the two changing values (total and idx) in our recursive function.

The above algorithm has time and space complexity of O(N*S), where ‘N’ represents total numbers and ‘S’ is the total sum of all the numbers.
"""

def can_partition_helper_memo(num, cache, total, idx):
    if total == 0:
        return True
    if total < 0 or idx >= len(num):
        return False

    if cache[idx][total] == True or cache[idx][total] == False:
        return cache[idx][total]

    included = can_partition_helper_memo(num, cache, total-num[idx], idx+1)
    excluded = can_partition_helper_memo(num, cache, total, idx+1)

    cache[idx][total] = included or excluded
    return cache[idx][total]

# O(n*(s/2)) time & space -> where n represents total numbers & s is the total sum of all the numbers.
def can_partition_memo(num):
    half_total = int(sum(num)/2)  # convert to int for use in range
    if half_total != sum(num)/2:  # ensure it wasn't a decimal number
        # if sum(num)/2 is an odd number, we can't have two subsets with equal sum
        return False

    cache = [[-1 for _ in range(half_total+1)]
             for _ in range(len(num))]  # type: ignore

    return can_partition_helper_memo(num, cache, half_total,  0)

# ----------------------------------------------------------------------------------------------------------------------------------------------------------------

"""
Bottom-up Dynamic Programming:

dp[n][total] means whether the specific sum 'total' can be gotten from the first 'n' numbers. 
If we can find such numbers from 0-'n' whose sum is total, dp[n][total] is true, otherwise it is false.

dp[0][0] is true since with 0 elements a subset-sum of 0 is possible (both empty sets).

dp[n][total] is true if dp[n-1][total] is true (meaning that we skipped this element, and took the sum of the previous result) 
 or dp[n-1][total- element’s value(num[n])] assuming this isn’t out of range (meaning that we added this value to our subset-sum so we look at the sum — the current element’s value).
This means, dp[n][total] will be ‘true’ if we can make sum ‘total’ from the first ‘n’ numbers.

For each n and sum, we have two options:
1. Exclude the n. In this case, we will see if we can get total from the subset excluding this n: dp[n-1][total]
2. Include the n if its value is not more than ‘total’. In this case, we will see if we can find a subset to get the remaining sum: dp[n-1][total-num[n]]

"""

def can_partition_bu(num):
    half_total = int(sum(num)/2)  # convert to int for use in range
    if half_total != sum(num)/2:  # ensure it wasn't a decimal number
        # if its a an odd number, we can't have two subsets with equal sum
        return False

    dp = [[False for _ in range(half_total+1)]
          for _ in range(len(num))]  # type: ignore

    for n in range(len(num)):
        for total in range(half_total+1):
            if total == 0:  # '0' sum can always be found through an empty set
                dp[n][total] = True
                continue

            included = False
            excluded = False

            # # exclude
            if n-1 >= 0:
                excluded = dp[n-1][total]

            # # include
            if n <= total:
                rem_total = total - num[n]
                included = rem_total == 0  # fills the whole total
                if n-1 >= 0:
                    # prev n can fill the remaining total
                    included = included or dp[n-1][rem_total]

            dp[n][total] = included or excluded

    return dp[-1][-1]

Maximum Subarray

Longest Common Subsequence **

DP pattern

""" 
Longest Common Subsequence

Given two strings text1 and text2, return the length of their longest common subsequence. 
If there is no common subsequence, return 0.
A subsequence of a string is a new string generated from the original string with some characters (can be none)
    deleted without changing the relative order of the remaining characters.
For example, "ace" is a subsequence of "abcde".
A common subsequence of two strings is a subsequence that is common to both strings.

Example 1:
    Input: text1 = "abcde", text2 = "ace" 
    Output: 3  
    Explanation: The longest common subsequence is "ace" and its length is 3.
Example 2:
    Input: text1 = "abc", text2 = "abc"
    Output: 3
    Explanation: The longest common subsequence is "abc" and its length is 3.
Example 3:
    Input: text1 = "abc", text2 = "def"
    Output: 0
    Explanation: There is no such common subsequence, so the result is 0.

Constraints:
    1 <= text1.length, text2.length <= 1000
    text1 and text2 consist of only lowercase English characters.

https://leetcode.com/problems/longest-common-subsequence
"""

class Solution:
    def longestCommonSubsequence(self, text1: str, text2: str):
        cache = [[None for _ in text2] for _ in text1]
        return self.lcs_helper(cache, text1, text2, 0, 0)

    def lcs_helper(self, cache, text1, text2, idx_1, idx_2):
        """ 
        - base cases:
            - out of bounds
            - in cache
        - Check if characters match or not:
            - if match: move both idxs forwards and and add 1 to the result of that and return
            - else: try moving both idxs forward in separate function calls and return the longer one
        """
        if idx_1 >= len(text1) or idx_2 >= len(text2):
            return 0
        if cache[idx_1][idx_2]:
            return cache[idx_1][idx_2]

        if text1[idx_1] == text2[idx_2]:
            cache[idx_1][idx_2] = 1 + self.lcs_helper(cache, text1, text2, idx_1+1, idx_2+1)
        else:
            cache[idx_1][idx_2] = max(
                self.lcs_helper(cache, text1, text2, idx_1+1, idx_2),
                self.lcs_helper(cache, text1, text2, idx_1, idx_2+1)
            )

        return cache[idx_1][idx_2]

class Solution_:
    def longestCommonSubsequence(self, text1: str, text2: str):
        dp = [[0 for _ in range(len(text2)+1)] for _ in range(len(text1)+1)]

        for idx_1 in reversed(range(len(text1))):
            for idx_2 in reversed(range(len(text2))):

                # if match
                if text1[idx_1] == text2[idx_2]:
                    dp[idx_1][idx_2] = 1 + dp[idx_1+1][idx_2+1]
                # add previous count
                else:
                    dp[idx_1][idx_2] = max(dp[idx_1+1][idx_2], dp[idx_1][idx_2+1])

        return dp[0][0]

Longest Increasing Subsequence *

Longest Increasing Subsequence - Dynamic Programming - Leetcode 300

Tabulation_2

""" 
Longest Increasing Subsequence

Given an integer array nums, return the length of the longest strictly increasing subsequence.
A subsequence is a sequence that can be derived from an array by deleting some or 
 no elements without changing the order of the remaining elements. 
For example, [3,6,2,7] is a subsequence of the array [0,3,1,6,2,2,7].

Example 1:
    Input: nums = [10,9,2,5,3,7,101,18]
    Output: 4
    Explanation: The longest increasing subsequence is [2,3,7,101], therefore the length is 4.
Example 2:
    Input: nums = [0,1,0,3,2,3]
    Output: 4
Example 3:
    Input: nums = [7,7,7,7,7,7,7]
    Output: 1

https://leetcode.com/problems/longest-increasing-subsequence/
"""

"""

[9] => 1

[8,9] => 2

[7,8,0,9] => 2

"""

class Solution:
    def lengthOfLIS(self, nums):
        result = 0

        cache = [None]*len(nums)
        # subsequence can start at any element
        for idx in range(len(nums)):
            result = max(self.helper(nums, idx, cache), result)

        return result

    def helper(self, nums, idx, cache):
        if cache[idx] is not None:
            return cache[idx]

        result = 1  # smallest subsequence for each number
        # next larger may be any larger element to the right
        for i in range(idx+1, len(nums)):
            if nums[i] > nums[idx]:
                result = max(1+self.helper(nums, i, cache), result)

        cache[idx] = result
        return cache[idx]

    # def lengthOfLIS(self, nums):
    #     cache = [None]*len(nums)
    #     for idx in range(len(nums)):
    #         self.helper(nums, idx, cache)
    #     return max(cache)

class Solution_Tabulation_2:
    """ 
    1. Initialize an array dp with length nums.length and all elements equal to 1. 
        - dp[i] represents the length of the longest increasing subsequence that ends with the element at index i.

    2. Iterate from i = 1 to i = nums.length - 1. 
        - At each iteration, use a second for loop to iterate from j = 0 to j = i - 1 (all the elements before i). 
        - For each element before i, check if that element is smaller than nums[i]. 
        - If so, set dp[i] = max(dp[i], dp[j] + 1).

    3. Return the max value from dp.
    """

    def lengthOfLIS(self, nums):
        dp = [0] * len(nums)

        for right in range(len(nums)):
            largest_prev_subs = 0

            for left in range(right):
                if nums[right] > nums[left]:
                    #
                    largest_prev_subs = max(
                        dp[left],  largest_prev_subs)

            dp[right] = largest_prev_subs + 1

        return max(dp)

    def lengthOfLIS_2(self, nums):
        dp = [1] * len(nums)

        for curr_idx in range(1, len(nums)):
            for prev_idx in range(curr_idx):

                if nums[curr_idx] > nums[prev_idx]:

                    dp[curr_idx] = max(
                        dp[curr_idx],
                        dp[prev_idx] + 1
                    )

        return max(dp)

""" 
[10,9,2,5,3,7,101,18]

[ 2,2,4,3,3,2, 1, 1]
"""

class Solution_Tabulation_1:
    def lengthOfLIS(self, nums):
        dp = [1]*len(nums)

        for idx in reversed(range(len(dp))):
            largest = 0

            for i in range(idx+1, len(dp)):
                if nums[i] > nums[idx]:
                    largest = max(dp[i], largest)

            dp[idx] = 1 + largest

        return max(dp)

""" 
[10, 9, 2, 5, 3, 7, 101, 18]
[ 0, 1, 2, 3, 4, 5,   6,  7]

0
[ 1, 1, 1, 1, 1, 1,   1,  1]
1
[ 1, 1, 1, 1, 1, 1,   1,  1]
2
[ 1, 1, 1, 1, 1, 1,   1,  1]
3 values smaller than 5 => 2
[ 1, 1, 1, 2, 1, 1,   1,  1]
4 values smaller than 3 => 2
[ 1, 1, 1, 2, 2, 1,   1,  1]
5 values smaller than 7 => 2,5,3
[ 1, 1, 1, 2, 2, 3,   1,  1]
6 values smaller than 101 => 2,5,3,7
[ 1, 1, 1, 2, 2, 3,   4,  1]
7 values smaller than 18 => 2,5,3,7
[ 1, 1, 1, 2, 2, 3,   4,  4]

1. Initialize an array dp with length nums.length and all elements equal to 1. 
    dp[i] represents the length of the longest increasing subsequence that ends with the element at index i.

2. Iterate from i = 1 to i = nums.length - 1. 
    At each iteration, use a second for loop to iterate from j = 0 to j = i - 1 (all the elements before i). 
    For each element before i, check if that element is smaller than nums[i]. 
    If so, set dp[i] = max(dp[i], dp[j] + 1).

3. Return the max value from dp.

"""

https://leetcode.com/problems/longest-string-chain/

Longest Arithmetic Subsequence **

""" 
1027. Longest Arithmetic Subsequence

Given an array nums of integers, return the length of the longest arithmetic subsequence in nums.
Recall that a subsequence of an array nums is a list nums[i1], nums[i2], ..., nums[ik] with 0 <= i1 < i2 < ... < ik <= nums.length - 1, and that a sequence seq is arithmetic if seq[i+1] - seq[i] are all the same value (for 0 <= i < seq.length - 1).

Example 1:
    Input: nums = [3,6,9,12]
    Output: 4
    Explanation: 
        The whole array is an arithmetic sequence with steps of length = 3.
Example 2:
    Input: nums = [9,4,7,2,10]
    Output: 3
    Explanation: 
        The longest arithmetic subsequence is [4,7,10].
Example 3:
    Input: nums = [20,1,15,3,10,5,8]
    Output: 4
    Explanation: 
        The longest arithmetic subsequence is [20,15,10,5].

Constraints:
    2 <= nums.length <= 1000
    0 <= nums[i] <= 500

https://leetcode.com/problems/longest-arithmetic-subsequence
"""

from collections import defaultdict
from typing import List

class Solution:
    def longestArithSeqLength(self, nums: List[int]):
        """ 
        - have a `sequence_cache` hashmap for each element in the array
            with the keys and values: `{sequence_difference: count/length}`
        - iterate in reverse order
        - for each `element_1`:
            - iterate through all the elements to its right, and for each `element_2`:
                - get the `sequence difference`: (`element_1-element_2`)
                - check if staring a sequence with that sequence difference will be greater than what we have seen b4 for the same sequence difference
                - update the longest var to reflect the longest we have seen so far
        """
        longest = 0
        seq_cache = [defaultdict(lambda: 1) for num in nums]

        for idx_1 in reversed(range(len(nums))):
            for idx_2 in range(idx_1+1, len(nums)):
                seq_diff = nums[idx_2] - nums[idx_1]

                # current_seq_len = max(current_seq_len, seq_starting_at_idx_2_len+1)
                seq_cache[idx_1][seq_diff] = max(seq_cache[idx_1][seq_diff], seq_cache[idx_2][seq_diff]+1)

                longest = max(longest, seq_cache[idx_1][seq_diff])

        return longest

Russian Doll Envelopes **

Screenshot 2021-11-03 at 08.57.34.png

""" 
Russian Doll Envelopes:

You are given a 2D array of integers envelopes where envelopes[i] = [wi, hi] represents the width and the height of an envelope.
One envelope can fit into another if and only if both the width 
    and height of one envelope are greater than the other envelope's width and height.
Return the maximum number of envelopes you can Russian doll (i.e., put one inside the other).
Note: You cannot rotate an envelope.



Example 1:
    Input: envelopes = [[5,4],[6,4],[6,7],[2,3]]
    Output: 3
    Explanation: The maximum number of envelopes you can Russian doll is 3 ([2,3] => [5,4] => [6,7]).
Example 2:
    Input: envelopes = [[1,1],[1,1],[1,1]]
    Output: 1

https://leetcode.com/problems/russian-doll-envelopes/
Based on: Longest Increasing Subsequence https://leetcode.com/problems/longest-increasing-subsequence
"""

class SolutionSLOW:  # time limit exceeded
    def maxEnvelopes(self, envelopes):
        items = list({tuple(item) for item in envelopes})
        items.sort(key=lambda x: x[0]+x[1])
        return self.longest_increasing_subsequence(items)

    def longest_increasing_subsequence(self, envelopes):
        dp = [1]*len(envelopes)

        for idx in reversed(range(len(dp))):
            largest = 0

            for i in range(idx+1, len(dp)):
                curr = envelopes[idx]
                nxt = envelopes[i]

                if curr[0] < nxt[0] and curr[1] < nxt[1]:
                    largest = max(dp[i], largest)

            dp[idx] = 1 + largest

        return max(dp)

""" 
"""

class Solution:
    def maxEnvelopes(self, arr):
        arr.sort(key=lambda x: (x[0], -x[1]))

        # extract the second dimension and run the LIS
        # already sorted by width
        return self.length_of_longest_increasing_subsequence([i[1] for i in arr])

    def length_of_longest_increasing_subsequence(self, nums):
        dp = [0] * len(nums)

        for right in range(len(nums)):
            largest_prev_subs = 0

            for left in range(right):
                if nums[right] > nums[left]:
                    #
                    largest_prev_subs = max(dp[left],  largest_prev_subs)

            dp[right] = largest_prev_subs + 1

        return max(dp)

Maximum Height by Stacking Cuboids *

Screenshot 2021-11-03 at 09.01.50.png

""" 
Maximum Height by Stacking Cuboids
(Not worth your time lol)

Given n cuboids where the dimensions of the ith cuboid is cuboids[i] = [widthi, lengthi, heighti] (0-indexed). 
Choose a subset of cuboids and place them on each other.

You can place cuboid i on cuboid j if widthi <= widthj and lengthi <= lengthj and heighti <= heightj. 
You can rearrange any cuboid's dimensions by rotating it to put it on another cuboid.

Return the maximum height of the stacked cuboids.

https://leetcode.com/problems/maximum-height-by-stacking-cuboids/

Based on:
    Longest Increasing Subsequence: https://leetcode.com/problems/longest-increasing-subsequence
    Russian Doll Envelopes: https://leetcode.com/problems/russian-doll-envelopes/
"""

""" 
https://leetcode.com/problems/maximum-height-by-stacking-cuboids/discuss/970364/Python-Top-Down-DP
https://leetcode.com/problems/maximum-height-by-stacking-cuboids/discuss/970293/JavaC%2B%2BPython-DP-Prove-with-Explanation
https://leetcode.com/problems/maximum-height-by-stacking-cuboids/discuss/971046/Formal-Proof-for-Greedy-Sorting-Dimensions
"""

class Solution:
    def maxHeight(self, cuboids):
        for cuboid in cuboids:
            cuboid.sort()
        return self.longest_increasing_subsequence(cuboids)

    def longest_increasing_subsequence(self, cuboids):
        result = 0
        cuboids.sort()

        cache = [None]*len(cuboids)
        # subsequence can start at any element
        for idx in range(len(cuboids)):
            result = max(self.lis_helper(cuboids, idx, cache), result)

        return result

    def lis_helper(self, cuboids, idx, cache):
        if cache[idx] is not None:
            return cache[idx]
        result = cuboids[idx][2]

        for i in reversed(range(idx+1, len(cuboids))):
            curr = cuboids[idx]
            nxt = cuboids[i]

            if curr[0] <= nxt[0] and curr[1] <= nxt[1] and curr[2] <= nxt[2]:
                result = max(
                    curr[2]+self.lis_helper(cuboids, i, cache),
                    result
                )

        cache[idx] = result
        return cache[idx]

Longest Palindromic Subsequence **

""" 
516. Longest Palindromic Subsequence

Given a string s, find the longest palindromic subsequence's length in s.
A subsequence is a sequence that can be derived from another sequence by deleting some or no elements without changing the order of the remaining elements.

Example 1:
    Input: s = "bbbab"
    Output: 4
    Explanation: One possible longest palindromic subsequence is "bbbb".
Example 2:
    Input: s = "cbbd"
    Output: 2
    Explanation: One possible longest palindromic subsequence is "bb".

https://leetcode.com/problems/longest-palindromic-subsequence
"""

class Solution:
    def longestPalindromeSubseq(self, s: str):
        cache = [[None for _ in s] for _ in s]
        return self.lps_helper(s, cache, 0, len(s)-1)

    def lps_helper(self, s, cache, start, end):
        """ 
        - if the characters at the ends match, 
            we dive deeper and add 2 to the result of going deeper
        - if not: skip the start and the end and return the one with the highest result
        """
        if start > end:
            return 0
        if start == end:
            return 1
        if cache[start][end]:
            return cache[start][end]

        if s[start] == s[end]:
            # dive deeper
            cache[start][end] = 2 + self.lps_helper(s, cache, start+1, end-1)
        else:
            # skip one character
            cache[start][end] = max(self.lps_helper(s, cache, start+1, end), self.lps_helper(s, cache, start, end-1))
        return cache[start][end]

https://leetcode.com/problems/valid-palindrome-iii/submissions/

Climbing Stairs / Triple Step

"""
Climbing Stairs / Triple Step:

You are climbing a staircase. It takes n steps to reach the top.
Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?

https://leetcode.com/problems/climbing-stairs/
"""

class Solution:
    def climbStairs(self, n):
        return self.helper(n)

    # in case we reach remaining=0, then we have found way (a correct set of steps)
    def helper(self, remaining, store={0: 1}):  # store={0:1} is a base case
        if remaining < 0:
            return 0

        if remaining in store:
            return store[remaining]

        total = self.helper(remaining-1, store) + \
            self.helper(remaining-2, store)

        store[remaining] = total

        return store[remaining]

"""
Staircase Traversal:
You're given two positive integers representing the height of a staircase and the maximum number of steps that you can advance up the staircase at a time.
Write a function that returns the number of ways in which you can climb the staircase.

For example, if you were given a staircase of height = 3 and maxSteps = 2 you could climb the staircase in 3 ways.
You could take 1 step, 1 step, then 1 step, you could also take 1 step, then 2 steps, and you could take 2 steps, then 1 step.

Note that maxSteps <= height will always be true.

Sample Input:
    height = 4
    maxSteps = 2
Sample Output:
    5
    // You can climb the staircase in the following ways: 
    // 1, 1, 1, 1
    // 1, 1, 2
    // 1, 2, 1
    // 2, 1, 1
    // 2, 2

https://www.algoexpert.io/questions/Staircase%20Traversal
"""

# 0(k^n) time, 0(n) space - where k is the max steps, n - number of steps
def staircaseTraversal00(height, maxSteps):
    return staircaseTraversalHelper00(height, maxSteps)

def staircaseTraversalHelper00(height_remaining, max_steps):

    if height_remaining == 0:
        # if are exactly at the last step, we have found a way
        return 1
    elif height_remaining < 0:
        # if we pass the last step, we made a mistake
        return 0

    ways = 0
    for step in range(1, max_steps+1):
        ways += staircaseTraversalHelper00(height_remaining - step, max_steps)

    return ways

# memoization:
# 0(k*n) time, 0(n) space - where k is the max steps, n - number of steps
# for each call, we'll have to sum k elements together
# for each of our n recursive calls, we have to do k work
def staircaseTraversal(height, maxSteps):
    return staircaseTraversalHelper(height, maxSteps, {0: 1})

def staircaseTraversalHelper(height_remaining, max_steps, store):

    if height_remaining < 0:
        # if we pass the last step, we made a mistake
        return 0

    # memoize
    if height_remaining in store:
        return store[height_remaining]

    ways = 0
    for step in range(1, max_steps+1):
        ways += staircaseTraversalHelper(height_remaining - step,
                                         max_steps, store)

    store[height_remaining] = ways  # memoize

    return store[height_remaining]

"""
ordering:

legend=> [step][remaining]

h=3 max_steps=2
            [][3]
    [1][2]          [2][1]
[1][1]  [2][0]      [1][0]
[1][0]

h=4 max_steps=3
            [][4]
    [1][3]              [2][2]              [3][1]
[1][2] [2][1] [3][0]    [1][1] [2][0]       [1][0]

h=0 max_steps=2 ways=1
h=1 max_steps=2 ways=1
h=2 max_steps=2 ways=2
h=3 max_steps=2 ways=3
h=4 max_steps=2 ways=5

we realise that:
ways(n) = ways(n-1) + (n-2) .... + (n-max-steps)

The number of ways to climb a staircase of height k with a max number of steps s is: 
numWays[k - 1] + numWays[k - 2] + ... + numWays[k - s]. 
This is because if you can advance between 1 and s steps, 
    then from each step k - 1, k - 2, ..., k - s, 
    you can directly advance to the top of a staircase of height k. 
By adding the number of ways to reach all steps that you can directly advance to the top step from, 
    you determine how many ways there are to reach the top step.
"""

# <---------------------------------------------------------------------------------------------------------->
# DP Solution
# we will run the loop n times each with k work
# O(k^n) time | O(n) space - where n is the height of the staircase and k is the number of allowed steps
def staircaseTraversal04(height, maxSteps):

    # the indices represent the heights & the values the no. of ways
    max_ways = [0] * (height + 1)
    # base cases
    max_ways[0] = 1
    max_ways[1] = 1

    # try all steps: start from maxSteps, maxSteps-1, ..., 2 & 1
    # ways(n) = ways(n-1) + (n-2) .... + (n-max-steps)
    for idx in range(2, height+1):
        ways = 0

        start_idx = max(idx-maxSteps, 0)  # prevent negatives
        for i in range(start_idx, idx):
            ways += max_ways[i]

        max_ways[idx] = ways

    return max_ways[-1]

# <---------------------------------------------------------------------------------------------------------->
# DP Solution improved
# we will run the loop n times each with k work
# O(n) time | O(n) space - where n is the height of the staircase and k is the number of allowed steps
def staircaseTraversal05(height, maxSteps):

    # the indices represent the heights & the values the no. of ways
    max_ways = [0] * (height + 1)
    # base cases
    max_ways[0] = 1
    max_ways[1] = 1

    # # try all steps: start from maxSteps, maxSteps-1, ..., 2 & 1
    # # ways(n) = ways(n-1) + (n-2) .... + (n-max-steps)

    # start with a window size of one
    window = max_ways[0]
    window_size = 1  # this cab be removed -> (idx == prev window_size)
    for idx in range(1, height+1):
        max_ways[idx] = window

        # manipulate window size
        window += max_ways[idx]
        if window_size == maxSteps:
            window -= max_ways[idx-maxSteps]
        else:
            window_size += 1

    return max_ways[-1]

Decode ways

Screenshot 2021-10-23 at 15.16.57.png

Screenshot 2021-10-23 at 15.17.30.png

Screenshot 2021-10-23 at 15.19.01.png

Screenshot 2021-10-23 at 15.19.17.png

Screenshot 2021-10-23 at 16.08.33.png

Screenshot 2021-10-23 at 16.09.00.png

Screenshot 2021-10-23 at 15.19.40.png

Screenshot 2021-10-23 at 15.20.09.png

Screenshot 2021-10-23 at 15.24.03.png

Screenshot 2021-10-23 at 15.25.20.png

Screenshot 2021-10-23 at 15.25.52.png

Screenshot 2021-10-23 at 15.26.06.png

""" 
Decode Ways

A message containing letters from A-Z can be encoded into numbers using the following mapping:
    'A' -> "1"
    'B' -> "2"
    ...
    'Z' -> "26"
To decode an encoded message, all the digits must be grouped then mapped back into letters using the reverse of the mapping above (there may be multiple ways). For example, "11106" can be mapped into:
    "AAJF" with the grouping (1 1 10 6)
    "KJF" with the grouping (11 10 6)
    Note that the grouping (1 11 06) is invalid because "06" cannot be mapped into 'F' since "6" is different from "06".
Given a string s containing only digits, return the number of ways to decode it.
The answer is guaranteed to fit in a 32-bit integer.

Example 1:
    Input: s = "12"
    Output: 2
    Explanation: "12" could be decoded as "AB" (1 2) or "L" (12).
Example 2:
    Input: s = "226"
    Output: 3
    Explanation: "226" could be decoded as "BZ" (2 26), "VF" (22 6), or "BBF" (2 2 6).
Example 3:
    Input: s = "0"
    Output: 0
    Explanation: There is no character that is mapped to a number starting with 0.
        The only valid mappings with 0 are 'J' -> "10" and 'T' -> "20", neither of which start with 0.
        Hence, there are no valid ways to decode this since all digits need to be mapped.
Example 4:
    Input: s = "06"
    Output: 0
    Explanation: "06" cannot be mapped to "F" because of the leading zero ("6" is different from "06").


Constraints:
    1 <= s.length <= 100
    s contains only digits and may contain leading zero(s).

https://leetcode.com/problems/decode-ways
"""

""" 
https://www.notion.so/paulonteri/Recursion-DP-Backtracking-525dddcdd0874ed98372518724fc8753#fb64620280c74255982bb1d93455881b
"""

class Solution:
    def numDecodings(self, s: str):
        return self.helper(s, 0, [None]*len(s))

    def helper(self, s, idx, cache):
        if idx == len(s):
            return 1
        if cache[idx] is not None:
            return cache[idx]

        ways = 0

        if s[idx] != "0":
            # length one
            ways += self.helper(s, idx+1, cache)

            # length two
            if idx < len(s)-1:
                num = int(s[idx:idx+2])

                if num >= 1 and num <= 26:
                    ways += self.helper(s, idx+2, cache)

        cache[idx] = ways
        return cache[idx]

""" 
Bottom up DP
"""

class SolutionBU:
    def numDecodings(self, s: str):
        """ 
        What if s was of length 1? 2? 3? 4? ... n?
        """
        if not s or s[0] == "0":
            return 0

        # # create array to store the subproblem results ---------------------------------
        dp = [0]*len(s)
        dp[0] = 1
        # index 1: should handle 10, 11, 33, 30
        if len(s) >= 2:
            # Check if successful single digit decode is possible.
            if s[1] != '0':
                dp[1] = 1
            # Check if successful two digit decode is possible.
            two_digit = int(s[:2])
            if two_digit >= 10 and two_digit <= 26:
                dp[1] += 1

        # # fill in subproblem results ----------------------------------------------------------
        for i in range(2, len(dp)):
            # Check if successful single digit decode is possible.
            if s[i] != '0':
                dp[i] = dp[i - 1]

            # Check if successful two digit decode is possible.
            two_digit = int(s[i-1: i+1])
            if two_digit >= 10 and two_digit <= 26:
                # result: dp[i] = dp[i - 1] + dp[i - 2]
                dp[i] += dp[i - 2]

        return dp[-1]

class SolutionBU2:
    def numDecodings(self, s: str):
        # Array to store the subproblem results
        dp = [0 for _ in range(len(s) + 1)]

        dp[0] = 1
        # Ways to decode a string of size 1 is 1. Unless the string is '0'.
        # '0' doesn't have a single digit decode.
        dp[1] = 0 if s[0] == '0' else 1

        for i in range(2, len(dp)):

            # Check if successful single digit decode is possible.
            if s[i - 1] != '0':
                dp[i] = dp[i - 1]

            # Check if successful two digit decode is possible.
            two_digit = int(s[i - 2: i])
            if two_digit >= 10 and two_digit <= 26:
                dp[i] += dp[i - 2]

        return dp[len(s)]

""" 
Iterative, Constant Space
"""

class SolutionITER:
    def numDecodings(self, s: str):
        if s[0] == "0":
            return 0

        two_back = 1
        one_back = 1
        for i in range(1, len(s)):
            current = 0
            if s[i] != "0":
                current = one_back
            two_digit = int(s[i - 1: i + 1])
            if two_digit >= 10 and two_digit <= 26:
                current += two_back
            two_back = one_back
            one_back = current

        return one_back

Interleaving String/Interweaving Strings

""" 
Interleaving String/Interweaving Strings:

Given strings s1, s2, and s3, find whether s3 is formed by an interleaving of s1 and s2.
An interleaving of two strings s and t is a configuration where they are divided into non-empty substrings such that:
    s = s1 + s2 + ... + sn
    t = t1 + t2 + ... + tm
    |n - m| <= 1
The interleaving is s1 + t1 + s2 + t2 + s3 + t3 + ... or t1 + s1 + t2 + s2 + t3 + s3 + ...
Note: a + b is the concatenation of strings a and b.

Example 1:
    Input: s1 = "aabcc", s2 = "dbbca", s3 = "aadbbcbcac"
    Output: true
Example 2:
    Input: s1 = "aabcc", s2 = "dbbca", s3 = "aadbbbaccc"
    Output: false
Example 3:
    Input: s1 = "", s2 = "", s3 = ""
    Output: true

https://www.algoexpert.io/questions/Interweaving%20Strings
https://leetcode.com/problems/interleaving-string/
https://leetcode.com/problems/interleaving-string/discuss/326347/C-dynamic-programming-practice-in-August-2018-with-interesting-combinatorics-warmup
"""

""" 
------------------------------------------------------------------------------------------------------------------------------------------------------
"""

def interweavingStringsBF_(one, two, three):
    if len(three) != len(one) + len(two):
        return False
    return interweavingStringsHelperBF_(one, two, three, 0, 0, 0)

def interweavingStringsHelperBF_(one, two, three, one_idx, two_idx, three_idx):
    if three_idx == len(three):
        return True

    one_res = False
    two_res = False
    if one_idx < len(one) and one[one_idx] == three[three_idx]:
        one_res = interweavingStringsHelperBF_(
            one, two, three, one_idx+1, two_idx, three_idx+1)

    if two_idx < len(two) and two[two_idx] == three[three_idx]:
        two_res = interweavingStringsHelperBF_(
            one, two, three, one_idx, two_idx+1, three_idx+1)

    return one_res or two_res

""" 
BF that can be cached
"""

def interweavingStringsBF(one, two, three):
    if len(three) != len(one) + len(two):
        return False
    return interweavingStringsHelperBF(one, two, three, 0, 0)

def interweavingStringsHelperBF(one, two, three, one_idx, two_idx, ):
    three_idx = one_idx + two_idx
    if three_idx == len(three):
        return True

    one_res = False
    two_res = False
    if one_idx < len(one) and one[one_idx] == three[three_idx]:
        one_res = interweavingStringsHelperBF(
            one, two, three, one_idx+1, two_idx)

    if two_idx < len(two) and two[two_idx] == three[three_idx]:
        two_res = interweavingStringsHelperBF(
            one, two, three, one_idx, two_idx+1)

    return one_res or two_res

""" 
------------------------------------------------------------------------------------------------------------------------------------------------------
"""

def interweavingStringsMEMO(one, two, three):
    if len(three) != len(one) + len(two):
        return False
    cache = [[None for _ in range(len(two)+1)] for _ in range(len(one)+1)]
    return interweavingStringsHelperMEMO(one, two, three, cache, 0, 0)

def interweavingStringsHelperMEMO(one, two, three, cache, one_idx, two_idx, ):
    three_idx = one_idx + two_idx
    if three_idx == len(three):
        return True
    if cache[one_idx][two_idx] is not None:
        return cache[one_idx][two_idx]

    one_res = False
    two_res = False
    if one_idx < len(one) and one[one_idx] == three[three_idx]:
        one_res = interweavingStringsHelperMEMO(one, two, three, cache, one_idx+1, two_idx)

    if two_idx < len(two) and two[two_idx] == three[three_idx]:
        two_res = interweavingStringsHelperMEMO(one, two, three, cache, one_idx, two_idx+1)

    cache[one_idx][two_idx] = one_res or two_res
    return cache[one_idx][two_idx]

""" 
------------------------------------------------------------------------------------------------------------------------------------------------------

Bottom up:

- for each char(in one or two) check if it matches what is in three:
    - if it does: if we had built the prev string up to that point == True (
            one idx behind the curr idx in three (up or left depending on if the row or column matches) )
        - then True

# can be optimised to 1D array
"""

def interweavingStrings(one, two, three):
    if len(three) != len(one) + len(two):
        return False

    dp = [[False for _ in range(len(two)+1)] for _ in range(len(one)+1)]

    # # fill in the defaults that will be used to generate the next
    dp[0][0] = True
    for i in range(1, len(one)+1):  # left column
        actual_idx = i-1
        if one[actual_idx] == three[actual_idx] and dp[i-1][0] == True:
            dp[i][0] = True
    for i in range(1, len(two)+1):  # top row
        actual_idx = i-1
        if two[actual_idx] == three[actual_idx] and dp[0][i-1] == True:
            dp[0][i] = True

    # # fill in the rest
    for one_idx in range(1, len(one)+1):
        for two_idx in range(1, len(two)+1):
            actual_one_idx = one_idx-1
            actual_two_idx = two_idx-1
            actual_three_idx = one_idx + two_idx - 1

            # # check if the string matches then check if we had built it successfully up to that point
            # check one
            if one[actual_one_idx] == three[actual_three_idx] and dp[one_idx-1][two_idx] == True:
                dp[one_idx][two_idx] = True
            # check two
            if two[actual_two_idx] == three[actual_three_idx] and dp[one_idx][two_idx-1] == True:
                dp[one_idx][two_idx] = True

    return dp[-1][-1]

Unique Paths **

Unique Paths - Dynamic Programming - Leetcode 62

Screenshot 2021-11-02 at 15.50.50.png

Screenshot 2021-10-14 at 12.52.46.png

Screenshot 2021-10-14 at 12.53.16.png

starting from end to beginning

Screenshot 2021-10-14 at 12.59.31.png

Screenshot 2021-10-14 at 13.00.15.png

Screenshot 2021-10-14 at 12.50.42.png

Screen Recording 2021-10-14 at 12.51.31.mov

""" 
Unique Paths:

A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).
The robot can only move either down or right at any point in time. 
The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).
How many possible unique paths are there?

Example 1:
    Input: m = 3, n = 7
    Output: 28
Example 2:
    Input: m = 3, n = 2
    Output: 3
    Explanation:
    From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:
    1. Right -> Down -> Down
    2. Down -> Down -> Right
    3. Down -> Right -> Down
Example 3:
    Input: m = 7, n = 3
    Output: 28
Example 4:
    Input: m = 3, n = 3
    Output: 6
Example:
        99*1 => 1
Example
    99*2 => 99

Number Of Ways To Traverse Graph:
You're given two positive integers representing the width and height of a grid-shaped, rectangular graph.
Write a function that returns the number of ways to reach the bottom right corner of the graph when starting at the top left corner.
Each move you take must either go down or right. In other words, you can never move up or left in the graph.
For example, given the graph illustrated below, with width = 2 and height = 3, 
    there are three ways to reach the bottom right corner when starting at the top left corner:
        _ _
        |_|_|
        |_|_|
        |_|_|
        Down, Down, Right
        Right, Down, Down
        Down, Right, Down
Note: you may assume that width * height >= 2.
In other words, the graph will never be a 1x1 grid.
    Sample Input
    width = 4
    height = 3
    Sample Output
    10

https://leetcode.com/problems/unique-paths
https://www.algoexpert.io/questions/Number%20Of%20Ways%20To%20Traverse%20Graph
https://www.notion.so/paulonteri/Recursion-DP-Backtracking-525dddcdd0874ed98372518724fc8753#f980e95403a24443a371a10430a198ad

Unique Paths II can help in understanding this
"""

"""
Since robot can move either down or right, 
    there is only one path to reach the cells in the first row: right->right->...->right.
    The same is valid for the first column, though the path here is down->down-> ...->down.
"""

""" 
[
  1  2  3  4
1[1, 1, 1, 1],
2[1, 2, 3, 4],
3[1, 3, 6, 10],
4[1, 4, 10, 20]
]

"""

# starting from end to beginning
# note that the start is 1,1.   0,0 is out of bounds
class SolutionMEMO:
    def uniquePaths(self, m, n):
        cache = [[False for _ in range(n+1)] for _ in range(m+1)]
        return self.uniquePathsHelper(m, n, cache)

    def uniquePathsHelper(self, m, n, cache):
        if m == 1 and n == 1:
            return 1
        if m < 1 or n < 1:
            return 0
        if cache[m][n]:
            return cache[m][n]

        total = 0
        total += self.uniquePathsHelper(m, n-1, cache)
        total += self.uniquePathsHelper(m-1, n, cache)

        cache[m][n] = total
        return cache[m][n]

""" 
-------------------------------------------------------------------------------------------------------------------------------------

what if the graph was:
[
  1
1[1],
]

[
  1  2
1[1, 1],
2[1, 2],
]

[
  1  2  3
1[1, 1, 1],
2[1, 2, 3],
3[1, 3, 6]
]

[
  1  2  3  4
1[1, 1, 1, 1],
2[1, 2, 3, 4],
3[1, 3, 6, 10],
4[1, 4, 10, 20]
]

"""

class Solution:
    def uniquePaths(self, m, n):
        if m == 1 and n == 1:
            return 1
        cache = [[0 for _ in range(n+1)] for _ in range(m+1)]

        # fill in defaults
        for i in range(1, n+1):
            cache[1][i] = 1
        for i in range(1, m+1):
            cache[i][1] = 1

        for h in range(2, m+1):
            for w in range(2, n+1):
                #                      top  +  left
                cache[h][w] = cache[h-1][w] + cache[h][w-1]

        # print(cache)
        return cache[-1][-1]

Unique Paths II

"""
Unique Paths II / Robot in Grid:

A robot is located at the top-left corner of a m x n grid.
The robot can only move either down or right at any point in time. 
The robot is trying to reach the bottom-right corner of the grid.
Now consider if some obstacles are added to the grids. How many unique paths would there be?
An obstacle and space is marked as 1 and 0 respectively in the grid.

https://leetcode.com/problems/unique-paths-ii/
"""

class Solution:
    def uniquePathsWithObstacles(self, obstacleGrid):
        if obstacleGrid[len(obstacleGrid)-1][len(obstacleGrid[0])-1] == 1:
            return 0

        return self.helper(obstacleGrid)

    def helper(self, obstacleGrid,  row=0, col=0):
        # out of bounds
        if row >= len(obstacleGrid) or col >= len(obstacleGrid[0]):
            return 0
        # reached end
        elif row == len(obstacleGrid)-1 and col == len(obstacleGrid[0])-1:
            return 1
        # is occupied with obstacle
        elif obstacleGrid[row][col] == 1:
            return 0
        # get cached result
        elif obstacleGrid[row][col] < 0:
            return -obstacleGrid[row][col]

        # move right
        right = self.helper(obstacleGrid,  row, col+1)
        # move down
        down = self.helper(obstacleGrid,  row+1, col)

        obstacleGrid[row][col] = -(right + down)  # cache results

        return right + down

Honourable mentions

0/1 Knapsack (Dynamic Programming)

Characteristics of Dynamic Programming:

Before moving on to understand different methods of solving a DP problem, let’s first take a look at what are the characteristics of a problem that tells us that we can apply DP to solve it.

1. Optimal Substructure Property

02 - What is DP? (Dynamic Programming for Beginners)

Optimal substructure requires that you can solve a problem based on the solutions of subproblems. Any problem has optimal substructure property if its overall optimal solution can be constructed from the optimal solutions of its subproblems. For Fibonacci numbers, as we know,Fib(n) = Fib(n-1) + Fib(n-2). This clearly shows that a problem of size ‘n’ has been reduced to subproblems of size ‘n-1’ and ‘n-2’. Therefore, Fibonacci numbers have optimal substructure property.

A useful way to think about optimal substructure is whether a problem can be easily solved recursively. Recursive solutions inherently solve a problem by breaking it down into smaller subproblems. If you can solve a problem recursively, it most likely has an optimal substructure.

2. Overlapping Subproblems

02 - What is DP? (Dynamic Programming for Beginners)

Sub-problems are smaller versions of the original problem. In fact, sub-problems often look like a reworded version of the original problem. If formulated correctly, sub-problems build on each other in order to obtain the solution to the original problem. Any problem has overlapping sub-problems if finding its solution involves solving the same subproblem multiple times.

Recursion,%20DP%20&%20Backtracking%20525dddcdd0874ed98372518724fc8753/Screenshot_2021-07-24_at_18.39.16.png

Take the example of the Fibonacci numbers; to find the fib(4), we need to break it down into the following sub-problems: fib(4)fib(3)fib(2)fib(2)fib(1)fib(1)fib(0)fib(0)fib(1)

We can clearly see the overlapping subproblem pattern here, as fib(2) has been evaluated twice and fib(1) has been evaluated three times.

Later we'll learn that: Whenever we solve a sub-problem, we cache its result so that we don’t end up solving it repeatedly if it’s called multiple times. Instead, we can just return the saved result. This technique of storing the results of already solved subproblems is called Memoization.

Dynamic Programming Methods

Memoization is the technique of writing a function that remembers the results of previous computations. Memoization ensures that a function doesn't run for the same inputs more than once by keeping a record of the results for the given inputs (usually in a dictionary).

Bottom-Up Algorithms: Going bottom-up is a way to avoid recursion, saving the memory cost that recursion incurs when it builds up the call stack. Put simply, a bottom-up algorithm "starts from the beginning," while a recursive algorithm often "starts from the end and works backwards."

1. Top-down with Memoization

In this approach, we try to solve the bigger problem by recursively finding the solution to smaller sub-problems. Whenever we solve a sub-problem, we cache its result so that we don’t end up solving it repeatedly if it’s called multiple times. Instead, we can just return the saved result. This technique of storing the results of already solved subproblems is called Memoization.

Fibonacci - This problem is normally solved with Divide and Conquer algorithm. There are 3 main parts in this technique:

Divide: divide the problem into smaller sub-problems of same type
Conquer: solve the sub-problems recursively
Combine: combine all the sub-problems to create a solution to the original problem

Example

Recursion,%20DP%20&%20Backtracking%20525dddcdd0874ed98372518724fc8753/Untitled.png

def calculateFibonacci(n):
  memoize = [-1 for x in range(n+1)]
  return calculateFibonacciRecur(memoize, n)

def calculateFibonacciRecur(memoize, n):
  if n < 2:
    return n
  if memoize[n] >= 0:   # if we have already solved this subproblem, simply return the result from the cache
    return memoize[n]

  memoize[n] = calculateFibonacciRecur(memoize, n - 1) + calculateFibonacciRecur(memoize, n - 2)
  return memoize[n]

2. Bottom-up with Tabulation

Tabulation is the opposite of the top-down approach and avoids recursion. In this approach, we solve the problem “bottom-up” (i.e. by solving all the related sub-problems first). This is typically done by filling up an n-dimensional table. Based on the results in the table, the solution to the top/original problem is then computed.

Example

def calculateFibonacci(n):
  dp = [0, 1]
  for i in range(2, n + 1):
    dp.append(dp[i - 1] + dp[i - 2])

  return dp[n]

One can also think of dynamic programming as a table-filling algorithm: you know the calculations you have to do, so you pick the best order to do them in and ignore the ones you don't have to fill in.

Great explainer:

https://youtu.be/f2xi3c1S95M

memoization: https://youtu.be/f2xi3c1S95M?t=596

tabulation: https://youtu.be/f2xi3c1S95M?t=893

https://youtu.be/oBt53YbR9Kk

https://youtu.be/aPQY__2H3tE

Be careful while calculating DP's time complexities

The FAST method

The most successful interviewees are those who have developed a repeatable strategy to succeed. This is especially true for dynamic programming. This is the reason for the development of the FAST method.

There are four steps in the FAST method:

First solution
Analyze the first solution
Identify the Subproblems
Turn the solution around

1. First solution

This is an important step for any interview question but is particularly important for dynamic programming.

This step finds the first possible solution. This solution will be brute force and recursive. The goal is to solve the problem without concern for efficiency.

It means that if you need to find the biggest/smallest/longest/shortest something, you should write code that goes through every possibility and then compares them all to find the best one.

Your solution must also meet these restrictions:

The recursive calls must be self-contained. That means no global variables.
You cannot do tail recursion. Your solution must compute the results to each subproblem and then combine them afterwards.
Do not pass in unnecessary variables. Eg. If you can count the depth of your recursion as you return, don’t pass a count variable into your recursive function.

Once you’ve gone through a couple problems, you will likely see how this solution looks almost the same every time.

2. Analyze the first solution

In this step, we will analyze the first solution that you came upwith. This involves determining the time and space complexity of your first solution and asking whether there is obvious room for improvement.

As part of the analytical process, we need to ask whether the first solution fits our rules for problems with dynamic solutions:

Does it have an optimal substructure? Since our solution’s recursive, then there is a strong likelihood that it meets this criteria. If we are recursively solving subproblems of the same problem, then we know that our substructure is optimal, otherwise our algorithm wouldn’t work.
Are there overlapping subproblems? This can be more difficult to determine because it doesn’t always present itself with small examples. It may be necessary to try a medium-sized test case. This will enable you to see if you end up calling the same function with the same input multiple times.

3. Find the Subproblems

If our solution can be made dynamic, the exact subproblems to memoize must be codified. This step requires us to discover the high-level meaning of the subproblems. This will make it easier to understand the solution later. Our recursive solution can be made dynamic by caching the values. This top-down solution facilitates a better understanding of the subproblems which is useful for the next step.

4. Turn the solution around

We now have a top-down solution. This is fine and it would be possible to stop here. However, sometimes it is better to flip it around and to get a bottom-up solution instead. Since we understand our subproblems, we will do that. This involves writing a completely different function (without modifying the existing code). This will iteratively compute the results of successive subproblems until our desired result is reached.

In recursion for example for Fibonacci calculation, if the root node (in the recursion tree) has two children. Each of those children has two children (so four children total in the "grand children" level). Each of those grandchildren has two children, and so on. If we do this n times, we'll have roughlyO(2") nodes. This gives us a runtime of roughly 0(2").

Pro tips

How to avoid duplicates in recursion

Screenshot 2021-11-03 at 09.54.39.png

Brute-force that can work with caching

Divide & Conquer

Account Login - LeetCode

Tower of Hanoi

Towers of Hanoi: A Complete Recursive Visualization

5.10. Tower of Hanoi - Problem Solving with Algorithms and Data Structures

Screenshot 2021-10-12 at 07.16.38.png

""" 
Tower of Hanoi

https://youtu.be/rf6uf3jNjbo
https://runestone.academy/runestone/books/published/pythonds/Recursion/TowerofHanoi.html
https://leetcode.com/discuss/general-discussion/1517167/Tower-of-Hanoi-Algorithm-%2B-Python-code
https://www.notion.so/paulonteri/Recursion-DP-Backtracking-525dddcdd0874ed98372518724fc8753#0fa86da6418247199688a4f435447d86
"""

""" 
Here is a high-level outline of how to move a tower from the starting pole, to the goal pole, using an intermediate pole:
    1. Move a tower of height-1 to an intermediate pole
    2. Move the last/remaining disk to the final pole.
    3. Move the disks height-1 to the first rod and repeat the above steps.
        Move the tower of height-1 from the intermediate pole to the final pole using the original pole.

As long as we always obey the rule that the larger disks remain on the bottom of the stack, 
    we can use the three steps above recursively, 
    treating any larger disks as though they were not even there.

The only thing missing from the outline above is the identification of a base case. 
The simplest Tower of Hanoi problem is a tower of one disk. 
In this case, we need move only a single disk to its final destination. 
A tower of one disk will be our base case. 
"""

def tower_of_hanoi(n, from_rod="A", to_rod="C", aux_rod="B"):
    if n == 1:
        # The simplest Tower of Hanoi problem is a tower of one disk.
        # In this case, we need move only a single disk to its final destination.
        print("Move disk 1 from rod", from_rod, "to rod", to_rod)
        return

    # Move a tower of height-1 to an intermediate pole
    tower_of_hanoi(n-1, from_rod, aux_rod, to_rod)

    # Move the last/remaining disk to the final pole
    print("Move disk", n, "from rod", from_rod, "to rod", to_rod)

    # Move the disks height-1 to the first rod and repeat the above steps
    # Move the tower of height-1 from the intermediate pole to the final pole using the original pole.
    tower_of_hanoi(n-1, aux_rod, to_rod, from_rod)

tower_of_hanoi(1)
print("____________")
tower_of_hanoi(2)
print("____________")
tower_of_hanoi(3)
print("____________")
tower_of_hanoi(4)
print("____________")
tower_of_hanoi(5)

https://runestone.academy/runestone/books/published/pythonds/Recursion/TowerofHanoi.html

Backtracking

Boggle - Coderust: Hacking the Coding Interview

Account Login - LeetCode

Backtracking - InterviewBit

The Backtracking Blueprint: The Legendary 3 Keys To Backtracking Algorithms

A general approach to backtracking questions in Java (Subsets, Permutations, Combination Sum, Palindrome Partioning) - LeetCode Discuss

Java: Backtracking Template -- General Approach - LeetCode Discuss

A general approach to backtracking questions in Java (Subsets, Permutations, Combination Sum, Palindrome Partitioning) - LeetCode Discuss

Backtracking Algorithm tries each possibility until they find the right one. It is a depth-first search of the set of possible solution. During the search, if an alternative doesn't work, then backtrack to the choice point, the place which presented different alternatives, and tries the next alternative.

Screen Recording 2021-10-25 at 18.50.53.mov

Backtracking is an algorithmic technique that involves trying possibilities along a "search path" and cutting off paths of search that will no longer yield a solution. Backtracking is an algorithmic technique for solving problems recursively by trying to build a solution incrementally, one piece at a time, removing those solutions that fail to satisfy the constraints of the problem at any point of time (by time, here, is referred to the time elapsed till reaching any level of the search tree).

Recursion,%20DP%20&%20Backtracking%20525dddcdd0874ed98372518724fc8753/Untitled%201.png

Backtracking is an algorithmic technique that considers searching in every possible combination for solving a computational problem.

It is known for solving problems recursively one step at a time and removing those solutions that do not satisfy the problem constraints at any point in time. It is a refined brute force approach that tries out all the possible solutions and chooses the best possible ones out of them.

Examples:

All Paths From Source to Target

Screenshot 2021-11-12 at 09.00.11.png

Screenshot 2021-11-12 at 09.01.07.png

Screenshot 2021-11-12 at 09.01.23.png

Screenshot 2021-11-12 at 09.01.36.png

Screenshot 2021-11-12 at 09.01.56.png

Screenshot 2021-11-12 at 09.02.21.png

""" 
All Paths From Source to Target

Given a directed acyclic graph (DAG) of n nodes labeled from 0 to n - 1, find all possible paths from node 0 to node n - 1 and return them in any order.
The graph is given as follows: graph[i] is a list of all nodes you can visit from node i (i.e., there is a directed edge from node i to node graph[i][j]).

Example 1:
    Input: graph = [[1,2],[3],[3],[]]
    Output: [[0,1,3],[0,2,3]]
    Explanation: There are two paths: 0 -> 1 -> 3 and 0 -> 2 -> 3.
Example 2:
    Input: graph = [[4,3,1],[3,2,4],[3],[4],[]]
    Output: [[0,4],[0,3,4],[0,1,3,4],[0,1,2,3,4],[0,1,4]]
Example 3:
    Input: graph = [[1],[]]
    Output: [[0,1]]
Example 4:
    Input: graph = [[1,2,3],[2],[3],[]]
    Output: [[0,1,2,3],[0,2,3],[0,3]]
Example 5:
    Input: graph = [[1,3],[2],[3],[]]
    Output: [[0,1,2,3],[0,3]]

Constraints:
    n == graph.length
    2 <= n <= 15
    0 <= graph[i][j] < n
    graph[i][j] != i (i.e., there will be no self-loops).
    All the elements of graph[i] are unique.
    The input graph is guaranteed to be a DAG.

https://leetcode.com/problems/all-paths-from-source-to-target
"""

from typing import List

""" 
As a reminder, backtracking is a general algorithm that incrementally builds candidates to the solutions, 
    and abandons a candidate ("backtrack") as soon as it determines that the candidate cannot possibly lead to a valid solution.
Specifically, for this problem, we could assume ourselves as an agent in a game, we can explore the graph one step at a time.
At any given node, we try out each neighbour node recursively until we reach the target or there is no more node to hop on. 
By trying out, we mark the choice before moving on, and later on we reverse the choice (i.e. backtrack) and start another exploration.

"""

# O(2^N) time | O(2^N) space
# - every time we add a new node into the graph, the number of paths would double.
# We have 2^N paths with building a path taking N time
# We have 2^N paths with each path possibly containing N nodes
class Solution:
    def allPathsSourceTarget(self, graph: List[List[int]]):
        """ 
        - paths = []
        - dfs(node, visiting, path):
            - if node is n-1: add the built path to the paths array
            - if node is in visiting set: return
            - (not needed because graph is acyclic) add node to visiting set
            - for all the child accessible to the node:
                - add node to path
                - dfs(child)
                - remove node from path
        - return paths
        """

        paths = []

        # backtracking
        def dfs(node, curr_path):
            if node == len(graph)-1:
                paths.append(curr_path[:])

            for child in graph[node]:
                curr_path.append(child)
                dfs(child, curr_path)
                curr_path.pop()

        dfs(0, [0])
        return paths

Permutations II **

Screenshot 2021-11-15 at 13.11.30.png

Screenshot 2021-11-15 at 13.15.00.png

Screenshot 2021-11-15 at 13.15.26.png

Screenshot 2021-11-15 at 13.15.44.png

Screenshot 2021-11-15 at 13.16.07.png

Screenshot 2021-11-15 at 13.16.46.png

Screenshot 2021-11-15 at 13.17.02.png

Screenshot 2021-10-13 at 14.57.32.png

""" 
Permutations II

Given a collection of numbers, nums, that might contain duplicates,
 return all possible unique permutations in any order.

Example 1:
    Input: nums = [1,1,2]
    Output:
    [[1,1,2],
    [1,2,1],
    [2,1,1]]
Example 2:
    Input: nums = [1,2,3]
    Output: [[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

https://leetcode.com/problems/permutations-ii
"""

import collections

class Solution:
    def permuteUnique(self, nums):
        result = []
                 # use a counter to ensure each number is considered only once for each position in the array
        self.dfs(collections.Counter(nums), len(nums), [], result)
        return result

    def dfs(self, numbers, length, curr, result):
        if len(curr) == length:
            result.append(curr)

        for num in numbers:
            if numbers[num] == 0:
                continue

            numbers[num] -= 1
            self.dfs(numbers, length, curr+[num], result)

            # backtrack
            numbers[num] += 1

N-Queens

The N Queens Placement Problem Clear Explanation (Backtracking/Recursion)

Backtracking - N-Queens Problem

Screenshot 2021-10-13 at 06.22.48.png

Clever way of dealing with diagonals

Screenshot 2021-10-13 at 06.54.38.png

Screenshot 2021-10-13 at 06.55.10.png

Alternatively

""" 
N-Queens

The n-queens puzzle is the problem of placing n queens on an n x n chessboard such that no two queens attack each other.
Given an integer n, return all distinct solutions to the n-queens puzzle. 
You may return the answer in any order.
Each solution contains a distinct board configuration of the n-queens' placement, where 'Q' and '.' both indicate a queen and an empty space, respectively.

https://leetcode.com/problems/n-queens/
https://www.algoexpert.io/questions/Non-Attacking%20Queens

"""

""" 
Time complexity:
   row: num of placements * time complexity for validating placement == n
    0 : n      * n
    1 : n-2 (remove column & diagonal of prev)    * n
    2 : n-4    * n
    3 : n-6    * n
    ...

    total => n! * n

"""

class Solution:
    def solveNQueens(self, n):

        result = []
        self.solve_n_queens_helper(n, result, set(), 0)
        return result

    def solve_n_queens_helper(self, n, result, placed, row):
        if row == n:
            self.build_solution(n, placed, result)
            return

        for col in range(n):
            # place
            placed.add((row, col))

            if self.is_valid_placement(n, placed):
                self.solve_n_queens_helper(n, result, placed, row+1)

            # remove
            placed.discard((row, col))

    def is_valid_placement(self, n, placed):

        # check columns
        cols = set()
        for item in placed:
            cols.add(item[1])
        if len(cols) < len(placed):
            return False

        # check positive diagonal
        # explanation: https://www.notion.so/paulonteri/Recursion-DP-Backtracking-525dddcdd0874ed98372518724fc8753#d51d8aa004ff49a4a0bf49c755fdf193
        pos_diagonal = set()
        for item in placed:
            row, col = item
            pos_diagonal.add(row - col)
        if len(pos_diagonal) < len(placed):
            return False

        # check negative diagonal
        neg_diagonal = set()
        for item in placed:
            row, col = item
            neg_diagonal.add(row + col)
        if len(neg_diagonal) < len(placed):
            return False

        return True

    def build_solution(self, n, placed, result):
        # result.append(list(placed))
        board = [["." for _ in range(n)]for _ in range(n)]

        for item in placed:
            row, col = item
            board[row][col] = "Q"

        for idx in range(n):
            board[idx] = "".join(board[idx])

        result.append(board)

""" 

"""

class Solution_:
    def solveNQueens(self, n):

        result = []
        board = [["." for _ in range(n)]for _ in range(n)]
        self.solve_n_queens_helper(
            n, board, result, set(), 0, set(), set(), set())
        return result

    def solve_n_queens_helper(self, n, board, result, placed, row, cols_placed, pos_diagonal, neg_diagonal):
        if row == n:
            # print(board)
            board_copy = board[:]
            for idx in range(n):
                board_copy[idx] = "".join(board_copy[idx])
            result.append(board_copy)
            return

        for col in range(n):
            # place
            added = self.add_placement_info(
                row, col, placed, cols_placed, pos_diagonal, neg_diagonal)

            if added:
                board[row][col] = "Q"
                self.solve_n_queens_helper(
                    n, board, result, placed, row+1, cols_placed, pos_diagonal, neg_diagonal)

                # remove
                self.remove_placement_info(
                    row, col, placed, cols_placed, pos_diagonal, neg_diagonal)
                board[row][col] = "."

    def add_placement_info(self, row, col, placed, cols_placed, pos_diagonal, neg_diagonal):
        # explanation: https://www.notion.so/paulonteri/Recursion-DP-Backtracking-525dddcdd0874ed98372518724fc8753#d51d8aa004ff49a4a0bf49c755fdf193
        if col in cols_placed or row-col in pos_diagonal or row+col in neg_diagonal:
            return False
        placed.add((row, col))
        cols_placed.add(col)
        pos_diagonal.add(row - col)
        neg_diagonal.add(row + col)
        return True

    def remove_placement_info(self, row, col, placed,  cols_placed, pos_diagonal, neg_diagonal):
        # explanation: https://www.notion.so/paulonteri/Recursion-DP-Backtracking-525dddcdd0874ed98372518724fc8753#d51d8aa004ff49a4a0bf49c755fdf193
        placed.discard((row, col))
        cols_placed.discard(col)
        pos_diagonal.discard(row - col)
        neg_diagonal.discard(row + col)

Sudoku

"""
Sudoku Solver:

Write a program to solve a Sudoku puzzle by filling the empty cells.

A sudoku solution must satisfy all of the following rules:
    Each of the digits 1-9 must occur exactly once in each row.
    Each of the digits 1-9 must occur exactly once in each column.
    Each of the digits 1-9 must occur exactly once in each of the 9 3x3 sub-boxes of the grid.

Example 1:

    Input:
    board = [["5","3",".",".","7",".",".",".","."],["6",".",".","1","9","5",".",".","."],[".","9","8",".",".",".",".","6","."],["8",".",".",".","6",".",".",".","3"],["4",".",".","8",
        ".","3",".",".","1"],["7",".",".",".","2",".",".",".","6"],[".","6",".",".",".",".","2","8","."],[".",".",".","4","1","9",".",".","5"],[".",".",".",".","8",".",".","7","9"]]
    Output: [["5","3","4","6","7","8","9","1","2"],["6","7","2","1","9","5","3","4","8"],["1","9","8","3","4","2","5","6","7"],["8","5","9","7","6","1","4","2","3"],["4","2","6","8",
        "5","3","7","9","1"],["7","1","3","9","2","4","8","5","6"],["9","6","1","5","3","7","2","8","4"],["2","8","7","4","1","9","6","3","5"],["3","4","5","2","8","6","1","7","9"]]

https://leetcode.com/problems/sudoku-solver/
https://www.algoexpert.io/questions/Solve%20Sudoku
"""

def solveSudoku(board):
    solveSudokuHelper(board, 0, 0)
    return board

def get_valid_nums(board, row, col):

    def get_all_in_3_by_three(board, row, col, invalid):
        end_row = end_col = 8
        if row <= 2:
            end_row = 2
        elif row <= 5:
            end_row = 5
        if col <= 2:
            end_col = 2
        elif col <= 5:
            end_col = 5

        for i in range(end_row-2, end_row+1):
            for j in range(end_col-2, end_col+1):
                num = board[i][j]
                if num != 0:
                    invalid.add(num)

    def get_all_in_row_and_col(board, row, col, invalid):
        for num in board[row]:
            if num != 0:
                invalid.add(num)
        for i in range(9):
            num = board[i][col]
            if num != 0:
                invalid.add(num)

    invalid = set()
    get_all_in_3_by_three(board, row, col, invalid)
    get_all_in_row_and_col(board, row, col, invalid)

    valid = []
    for num in range(1, 10):
        if num not in invalid:
            valid.append(num)
    return valid

def solveSudokuHelper(board, row, col):
    if row == 9:  # Done
        return True

    # # calculate next
    next_row = row
    next_col = col + 1
    if col == 8:
        next_col = 0
        next_row += 1

    # # fill board
    # check if prefilled
    if board[row][col] != 0:
        return solveSudokuHelper(board, next_row, next_col)

    # trial and error (backtracking)
    for num in get_valid_nums(board, row, col):
        board[row][col] = num  # try with num
        # if we have correctly filled the table, there is no need to try out other nums
        if solveSudokuHelper(board, next_row, next_col):
            return True
        # backtrack: if the input was invalid (the else is not needed but it helps in understanding what is happening)
        else:
            board[row][col] = 0

Letter Case Permutations

Generate Parentheses *

""" 
22. Generate Parentheses

Given n pairs of parentheses, write a function to generate all combinations of well-formed parentheses.

Example 1:
    Input: n = 3
    Output: ["((()))","(()())","(())()","()(())","()()()"]
Example 2:
    Input: n = 1
    Output: ["()"]

https://leetcode.com/problems/generate-parentheses
"""

class Solution:
    def generateParenthesis(self, n: int):
        all_parenthesis = []

        def place_brackets(opening, closing, curr_par):
            """ 
            - Only place opening if their count is less than n
            - Only place closing if their count is less than opening
            """
            if opening == n and closing == n:
                all_parenthesis.append("".join(curr_par))

            if opening < n:
                curr_par.append("(")
                place_brackets(opening+1, closing, curr_par)
                curr_par.pop()

            if closing < opening:
                curr_par.append(")")
                place_brackets(opening, closing+1, curr_par)
                curr_par.pop()

        place_brackets(0, 0, [])
        return all_parenthesis

Word Break

Word Break | Dynamic Programming | Leetcode #139

139. Word Break.mp4

Screenshot 2021-11-22 at 20.57.39.png

""" 
Word Break:

Given a string s and a dictionary of strings wordDict, return true if s can be segmented into a space-separated sequence of one or more dictionary words.
Note that the same word in the dictionary may be reused multiple times in the segmentation.

Example 1:
    Input: s = "leetcode", wordDict = ["leet","code"]
    Output: true
    Explanation: Return true because "leetcode" can be segmented as "leet code".
Example 2:
    Input: s = "applepenapple", wordDict = ["apple","pen"]
    Output: true
    Explanation: Return true because "applepenapple" can be segmented as "apple pen apple".
    Note that you are allowed to reuse a dictionary word.
Example 3:
    Input: s = "catsandog", wordDict = ["cats","dog","sand","and","cat"]
    Output: false

abcde
[a,b ab,cde, abc, abcde, e]
=> reason for DP

https://leetcode.com/problems/word-break
https://youtu.be/th4OnoGasMU

"""

"""
------------------------- Problem ---------------------------------
string s
dictionary of strings wordDict
return true if s can be segmented into a space-separated sequence of one or more dictionary words.

------------------------- Examples ---------------------------------
s = "applepenapple", wordDict = ["apple","pen"]
True "apple pen apple"

"bacbacbac" ["bacbac"]
False

"appleappapple" ["apple","app"]
True "apple app apple"

s = "catsandog", wordDict = ["cats","dog","sand","and","cat"]
False "cats and og"

------------------------- Brute force ---------------------------------
Backtracking O(2^n)
idx = 0
find a word that starts with the char at idx:
    - in None return False
    - if we found one, try complete it (for all of them). If we can complete it, we move idx to the next index after the index at the end of the word
repeat the above steps till the end of the end of the string and return True

------------------------- Optimal ---------------------------------

********* Look like a simple Trie problem but it's not ********* 

O(n^3) worst | O(n^2) average
use the memoized brute force

optimal substrcuture: small solutions add up to full

"""

class Solution:
    def wordBreak(self, s: str, wordDict):
        cache = [None] * len(s)
        return self.wordBreakHelper(s, wordDict, 0, cache)

    def wordBreakHelper(self, s, wordDict, idx, cache):
        if idx == len(s):
            return True
        if cache[idx] is not None:
            return cache[idx]

        for word in wordDict:
            if s[idx:idx+len(word)] == word:  # if the word can be completed
                if self.wordBreakHelper(s, wordDict, idx+len(word), cache):
                    cache[idx] = True
                    return cache[idx]

        cache[idx] = False
        return cache[idx]

Word Break II

without caching

with caching

Screenshot 2021-11-14 at 18.49.48.png

""" 
Word Break II

Given a string s and a dictionary of strings wordDict, 
    add spaces in s to construct a sentence where each word is a valid dictionary word. 
Return all such possible sentences in any order.
Note that the same word in the dictionary may be reused multiple times in the segmentation.

Example 1:
    Input: s = "catsanddog", wordDict = ["cat","cats","and","sand","dog"]
    Output: ["cats and dog","cat sand dog"]
Example 2:
    Input: s = "pineapplepenapple", wordDict = ["apple","pen","applepen","pine","pineapple"]
    Output: ["pine apple pen apple","pineapple pen apple","pine applepen apple"]
    Explanation: Note that you are allowed to reuse a dictionary word.
Example 3:
    Input: s = "catsandog", wordDict = ["cats","dog","sand","and","cat"]
    Output: []

https://leetcode.com/problems/word-break-ii
"""

from typing import List

""" 
Time Complexity: O(n * 2^n), where n is the number of characters. In a worst case scenario
Space Complexity: O(n * 2^n)
There seems to be some disagreement online about the complexity of this problem; consider the following example to see the worst case scenario:

s = aaaaaa
wordDict = [a, aa, aaa, aaaa, aaaaa, aaaaaa]

Our memo would look something like: 
{
    "a": ["a"] ----------------------------------------- 2^0 items,
    "aa": ["a a","aa"] ------------------------------ 2^1 items,
    "aaa": ["a a a", "aa a", "a aa", "aaa"] - 2^2 items,
    ...
}
That explains the space.

The time could be explained by the number of executions of the subproblems. Namely, in the worst case we'd have to make n calls of the helper function, and each one of those calls would have 2^n append calls made, leaving us with O(n * 2^n)
"""

class Solution:
    def wordBreak(self, s: str, wordDict: List[str]):
        """ 
        - try out all possible words at each index
            - cache the remaining substrings results 

        - backtrack()
            - base cases
            - res []
            - for each word check if it can start at the current index and end successfully
                - if so, call backtrack again 
                    - if it has results, merge the results of that with the current word
                    - add the merged to res
        """

        cache = {}

        def backtrack(idx):
            if idx == len(s):
                return [[]]
            if idx in cache:
                return cache[idx]

            res = []
            for word in wordDict:
                # check if word can start at the current index and end successfully
                if not s[idx:idx+len(word)] == word:
                    continue

                backtrack_res = backtrack(idx+len(word))
                if not backtrack_res:
                    continue

                # merge the results with the current word
                for sentence in backtrack_res:
                    res.append([word]+sentence)

            cache[idx] = res
            return cache[idx]

        return [" ".join(sentence) for sentence in backtrack(0)]

Remove Invalid Parentheses *

Screenshot 2021-11-03 at 09.19.01.png

Screenshot 2021-11-03 at 09.19.33.png

"""
301. Remove Invalid Parentheses

Given a string s that contains parentheses and letters, remove the minimum number of invalid parentheses to make the input string valid.
Return all the possible results. You may return the answer in any order.s

Example 1:
    Input: s = "()())()"
    Output: ["(())()","()()()"]
Example 2:
    Input: s = "(a)())()"
    Output: ["(a())()","(a)()()"]
Example 3:
    Input: s = ")("
    Output: [""]

https://leetcode.com/problems/remove-invalid-parentheses
https://youtu.be/cp0H_aR3OZo
"""

class Solution:
    def removeInvalidParentheses(self, s):
        result = set()
        invalid_opening, invalid_closing = self.count_invalid(s)

        self.valid_builder(s, result, [], 0, invalid_opening, invalid_closing)
        return list(result)

    def valid_builder(self, s, result, curr, idx, invalid_opening, invalid_closing):
        if idx == len(s):
            if invalid_opening == 0 and invalid_closing == 0 and self.is_valid(curr):
                result.add("".join(curr))
            return
        char = s[idx]

        # can remove opening
        if char == "(" and invalid_opening > 0:
            self.valid_builder(
                s, result, curr, idx+1, invalid_opening-1, invalid_closing)
        # can remove closing
        if char == ")" and invalid_closing > 0:
            self.valid_builder(
                s, result, curr, idx+1, invalid_opening, invalid_closing-1)

        # add regardless
        self.valid_builder(
            s, result, curr+[char], idx+1, invalid_opening, invalid_closing)

    def count_invalid(self, s):
        invalid_closing = 0
        invalid_opening = 0

        # invalid closing
        opening_remaining = 0
        for char in s:
            if char == "(":
                opening_remaining += 1
            elif char == ")":
                if opening_remaining > 0:
                    opening_remaining -= 1
                else:
                    invalid_closing += 1

        # invalid closing
        closing_remaining = 0
        for idx in reversed(range(len(s))):
            if s[idx] == ")":
                closing_remaining += 1
            elif s[idx] == "(":
                if closing_remaining > 0:
                    closing_remaining -= 1
                else:
                    invalid_opening += 1

        return (invalid_opening, invalid_closing)

    def is_valid(self, s):
        opening_count = 0

        for par in s:
            if par == "(":
                opening_count += 1
            elif par == ")":
                if opening_count == 0:
                    return False
                opening_count -= 1

        return opening_count == 0

""" 
Time Complexity :  O(2^N) 
    Since in the worst case we will have only left parentheses in the expression 
        and for every bracket we will have two options i.e. whether to remove it or consider it. 
    Considering that the expression has N parentheses, the time complexity will be O(2^N) 
Space Complexity : O(N) 
    because we are resorting to a recursive solution and for a recursive solution there is always stack space used as internal function states are saved onto a stack during recursion. 
    The maximum depth of recursion decides the stack space used. 
    Since we process one character at a time and the base case for the recursion is when we have processed all of the characters of the expression string, the size of the stack would be O(N). 
    Note that we are not considering the space required to store the valid expressions. We only count the intermediate space here.
"""

class Solution_:
    def removeInvalidParentheses(self, s):
        result = set()

        inv_opening, inv_closing = self.count_invalid(s)
        self.valid_builder(result, list(s), 0, inv_opening, inv_closing)

        return list(result)

    def valid_builder(self,  result, curr, idx, inv_opening, inv_closing):
        if idx == len(curr):
            if inv_opening == 0 and inv_closing == 0 and self.is_valid(curr):
                result.add("".join(curr))
            return
        char = curr[idx]

        # can remove opening
        if char == "(" and inv_opening > 0:
            curr[idx] = ""
            self.valid_builder(
                result, curr, idx+1, inv_opening-1, inv_closing)
            curr[idx] = "("
        # can remove closing
        if char == ")" and inv_closing > 0:
            curr[idx] = ""
            self.valid_builder(
                result, curr, idx+1, inv_opening, inv_closing-1)
            curr[idx] = ")"

        # leave it in / add regardless
        self.valid_builder(
            result, curr, idx+1, inv_opening, inv_closing)

    def count_invalid(self, s):
        inv_closing = 0
        inv_opening = 0

        # invalid closing
        opening_remaining = 0
        for char in s:
            if char == "(":
                opening_remaining += 1
            elif char == ")":
                if opening_remaining > 0:
                    opening_remaining -= 1
                else:
                    inv_closing += 1

        # invalid closing
        closing_remaining = 0
        for idx in reversed(range(len(s))):
            if s[idx] == ")":
                closing_remaining += 1
            elif s[idx] == "(":
                if closing_remaining > 0:
                    closing_remaining -= 1
                else:
                    inv_opening += 1

        return (inv_opening, inv_closing)

    def is_valid(self, s):
        opening_count = 0

        for par in s:
            if par == "(":
                opening_count += 1
            elif par == ")":
                if opening_count == 0:
                    return False
                opening_count -= 1

        return opening_count == 0

Combination Sum III

Screenshot 2021-10-17 at 06.42.45.png

Screenshot 2021-10-17 at 06.43.04.png

Screenshot 2021-10-17 at 06.43.19.png

Screenshot 2021-10-17 at 06.43.36.png

Screenshot 2021-10-17 at 06.43.50.png

Screenshot 2021-11-03 at 10.00.20.png

"""
216. Combination Sum III

Find all valid combinations of k numbers that sum up to n such that the following conditions are true:
    Only numbers 1 through 9 are used.
    Each number is used at most once.
Return a list of all possible valid combinations. The list must not contain the same combination twice, and the combinations may be returned in any order.

Example 1:
    Input: k = 3, n = 7
    Output: [[1,2,4]]
    Explanation:
        1 + 2 + 4 = 7
        There are no other valid combinations.
Example 2:
    Input: k = 3, n = 9
    Output: [[1,2,6],[1,3,5],[2,3,4]]
    Explanation:
        1 + 2 + 6 = 9
        1 + 3 + 5 = 9
        2 + 3 + 4 = 9
        There are no other valid combinations.
Example 3:
    Input: k = 4, n = 1
    Output: []
    Explanation: There are no valid combinations.
        Using 4 different numbers in the range [1,9], 
        the smallest sum we can get is 1+2+3+4 = 10 and since 10 > 1, there are no valid combination.
Example 4:
    Input: k = 3, n = 2
    Output: []
    Explanation: There are no valid combinations.
Example 5:
    Input: k = 9, n = 45
    Output: [[1,2,3,4,5,6,7,8,9]]
    Explanation:
        1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45
        There are no other valid combinations.

https://leetcode.com/problems/combination-sum-iii/

Do after:
- https://leetcode.com/problems/combination-sum
"""

# O(9! * K) time
class Solution(object):
    def combinationSum3(self, k, n):
        res = []
        self.helper(n, res, 1, 0, [0]*k, 0)
        return res

    def helper(self, n, res, start_num, curr_idx, curr, total):
        if total == n and curr_idx == len(curr):
            res.append(curr[:])
            return
        if total >= n or start_num > 9 or curr_idx >= len(curr):
            return

        for number in range(start_num, 10):
            curr[curr_idx] = number
            self.helper(n, res, number+1, curr_idx+1, curr, total+number)
            curr[curr_idx] = 0

Combination Sum

Combination Sum - Backtracking - Leetcode 39 - Python

Screenshot 2021-11-03 at 09.54.39.png

Screenshot 2021-11-03 at 09.58.27.png

""" 
Combination Sum

Given an array of distinct integers candidates and a target integer target, 
    return a list of all unique combinations of candidates where the chosen numbers sum to target. 
You may return the combinations in any order.
The same number may be chosen from candidates an unlimited number of times. 
Two combinations are unique if the frequency of at least one of the chosen numbers is different.
It is guaranteed that the number of unique combinations that sum up to target is less than 150 combinations for the given input.


Example 1:
    Input: candidates = [2,3,6,7], target = 7
    Output: [[2,2,3],[7]]
    Explanation:
        2 and 3 are candidates, and 2 + 2 + 3 = 7. Note that 2 can be used multiple times.
        7 is a candidate, and 7 = 7.
        These are the only two combinations.
Example 2:
    Input: candidates = [2,3,5], target = 8
    Output: [[2,2,2,2],[2,3,3],[3,5]]
Example 3:
    Input: candidates = [2], target = 1
    Output: []
Example 4:
    Input: candidates = [1], target = 1
    Output: [[1]]
Example 5:
    Input: candidates = [1], target = 2
    Output: [[1,1]]

https://leetcode.com/problems/combination-sum

Prerequisite:
- https://leetcode.com/problems/combination-sum-iii
"""

"""

candidates = [2,3,6,7], target = 7
                                                    7[]
                                              5[2]         4[3]
                                           3[2,2] 2[2,3]

                   []rem_target
           /          /     \     \
    [2]5            [3]4  [6]1  [7]0
 /       /    
[2,2]3   [2,3]2  
|        |
[2,2,3]0 [2,3,2]0

"""

class Solution(object):
    def combinationSum(self, candidates, target):
        return self.helper(candidates, 0, target)

    def helper(self, candidates, idx, target):
        # base cases
        if target == 0:
            return [[]]
        if target < 0 or idx >= len(candidates):
            return []
        result = []

        # add number
        # remember to give the current number another chance, rather than moving on (idx instead of idx+1)
        for arr in self.helper(candidates, idx, target-candidates[idx]):
            result.append(arr + [candidates[idx]])

        # skip number
        result += self.helper(candidates, idx+1, target)

        return result

""" 
Let N be the number of candidates, T be the target value, and M be the minimal value among the candidates.

Time Complexity: O(N ^ T/M)
Space Complexity: O(T/M)

    The execution of the backtracking is unfolded as a DFS traversal in a n-ary tree. The total number of steps during the backtracking would be the number of nodes in the tree.
    At each node, it takes a constant time to process, except the leaf nodes which could take a linear time to make a copy of combination. So we can say that the time complexity is linear to the number of nodes of the execution tree.
    Here we provide a loose upper bound on the number of nodes:
        First of all, the fan-out of each node would be bounded to N, i.e. the total number of candidates.
        The maximal depth of the tree, would be T/M, where we keep on adding the smallest element to the combination.
        As we know, the maximal number of nodes in N-ary tree of T/M, height would be : O(N ^ (T/M + 1))
    Note that, the actual number of nodes in the execution tree would be much smaller than the upper bound, since the fan-out of the nodes are decreasing level by level.
"""

class Solution_:
    def combinationSum(self, candidates, target):

        results = []

        def backtrack(remain, comb, start):
            if remain == 0:
                results.append(list(comb))
                return
            elif remain < 0:
                return

            for i in range(start, len(candidates)):
                # add the number into the combination
                comb.append(candidates[i])

                # give the current number another chance, rather than moving on (i instead of i+1)
                backtrack(remain - candidates[i], comb, i)

                # backtrack, remove the number from the combination
                comb.pop()

        backtrack(target, [], 0)

        return results

Expression Add Operators ***

Screenshot 2021-10-22 at 10.19.48.png

Screenshot 2021-10-22 at 10.20.45.png

Screenshot 2021-10-22 at 10.21.09.png

Screenshot 2021-10-22 at 10.21.46.png

Screenshot 2021-10-22 at 10.22.03.png

Screenshot 2021-10-22 at 10.22.29.png

Screenshot 2021-10-22 at 10.23.01.png

Screenshot 2021-10-22 at 10.23.21.png

Screenshot 2021-10-22 at 10.23.50.png

Screenshot 2021-10-22 at 10.24.07.png

Screenshot 2021-10-22 at 10.24.39.png

take note of the above ^

Screenshot 2021-10-22 at 10.24.51.png

""" 
Expression Add Operators

Given a string num that contains only digits and an integer target, 
    return all possibilities to insert the binary operators '+', '-', and/or '*' between the digits of num 
    so that the resultant expression evaluates to the target value.
Note that operands in the returned expressions should not contain leading zeros.

Example 1:
    Input: num = "123", target = 6
    Output: ["1*2*3","1+2+3"]
    Explanation: Both "1*2*3" and "1+2+3" evaluate to 6.
Example 2:
    Input: num = "232", target = 8
    Output: ["2*3+2","2+3*2"]
    Explanation: Both "2*3+2" and "2+3*2" evaluate to 8.
Example 3:
    Input: num = "105", target = 5
    Output: ["1*0+5","10-5"]
    Explanation: Both "1*0+5" and "10-5" evaluate to 5.
        Note that "1-05" is not a valid expression because the 5 has a leading zero.
Example 4:
    Input: num = "00", target = 0
    Output: ["0*0","0+0","0-0"]
    Explanation: "0*0", "0+0", and "0-0" all evaluate to 0.
        Note that "00" is not a valid expression because the 0 has a leading zero.
Example 5:
    Input: num = "3456237490", target = 9191
    Output: []
    Explanation: There are no expressions that can be created from "3456237490" to evaluate to 9191.

https://leetcode.com/problems/expression-add-operators
"""

""" 
https://www.notion.so/paulonteri/Recursion-DP-Backtracking-525dddcdd0874ed98372518724fc8753#83d1fce1c9944b78a65a2c973be09e46
"""

class Solution:
    def addOperators(self, num: str, target: int):
        answers = []

        def dfs(idx, operand_left_section, prev_operation, total, string):
            """ 
            Important info:
                - `operand_left_section` is used to recursively build operands. 
                    - Eg: for 123, it will grow as follows 1 => 12 => 123  \n
                    - if its value is None it means there is no operand_left_section
                - `prev_operation`is used to store the results of the previous operation so that it can be undone in case we need to multiply \n
                - `total` is the result of the running calculation
            """
            # # End (base cases) --------------------------------------------------------------------------------------
            if idx == len(num):
                if total == target and operand_left_section == None:
                    answers.append("".join(string[1:]))
                return

            # # Create operand --------------------------------------------------------------------------------------
            # Extending the current operand by one digit
            operand = int(num[idx])
            if operand_left_section:
                operand += (operand_left_section * 10)
            str_op = str(operand)

            # # Try out all(next) possible operands --------------------------------------------------------------------------------------
            # To avoid cases where we have 1 + 05 or 1 * 05 since 05 won't be a valid operand. Hence this check
            if operand > 0:
                dfs(idx + 1, operand, prev_operation, total, string)

            # # Math -------------------------------------------------------------------------------------------------------------------
            # remember to reset the operand_left_section to None (it is no longer needed, we will start a new one next time)

            # Can subtract or multiply only if there are some previous operations (will not happen at beginning)
            if string:
                # ---
                # Subtraction - negate operand (as prev_operation) so that we don't have to keep track of the signs
                string.append("-")
                string.append(str_op)
                dfs(idx+1, None, -operand, total-operand, string)
                string.pop()
                string.pop()

                # ---
                # Multiplication - undo last operation and multiply
                new_total = total - prev_operation  # undo
                operation = prev_operation * operand  # multiply
                new_total = new_total + operation
                #
                string.append("*")
                string.append(str_op)
                dfs(idx+1, None, operation, new_total, string)
                string.pop()
                string.pop()

            # ---
            # Addition - also used to handle index 0/starting out (no string)
            string.append("+")
            string.append(str_op)
            dfs(idx+1, None, operand, total+operand, string)
            string.pop()
            string.pop()

        dfs(0, None, 0, 0, [])
        return answers

class Solution:
    def addOperators(self, num: 'str', target: 'int') -> 'List[str]':

        N = len(num)
        answers = []
        def recurse(index, prev_operand, current_operand, value, string):

            # Done processing all the digits in num
            if index == N:

                # If the final value == target expected AND
                # no operand is left unprocessed
                if value == target and current_operand == 0:
                    answers.append("".join(string[1:]))
                return

            # Extending the current operand by one digit
            current_operand = current_operand*10 + int(num[index])
            str_op = str(current_operand)

            # To avoid cases where we have 1 + 05 or 1 * 05 since 05 won't be a
            # valid operand. Hence this check
            if current_operand > 0:

                # NO OP recursion
                recurse(index + 1, prev_operand, current_operand, value, string)

            # ADDITION
            string.append('+'); string.append(str_op)
            recurse(index + 1, current_operand, 0, value + current_operand, string)
            string.pop();string.pop()

            # Can subtract or multiply only if there are some previous operands
            if string:

                # SUBTRACTION
                string.append('-'); string.append(str_op)
                recurse(index + 1, -current_operand, 0, value - current_operand, string)
                string.pop();string.pop()

                # MULTIPLICATION
                string.append('*'); string.append(str_op)
                recurse(index + 1, current_operand * prev_operand, 0, value - prev_operand + (current_operand * prev_operand), string)
                string.pop();string.pop()
        recurse(0, 0, 0, 0, [])    
        return answers

Partition to K Equal Sum Subsets *

O(N.N!) time

""" 
Partition to K Equal Sum Subsets

Given an integer array nums and an integer k, 
return true if it is possible to divide this array into k non-empty subsets whose sums are all equal.

Example 1:
    Input: nums = [4,3,2,3,5,2,1], k = 4
    Output: true
    Explanation: 
        It's possible to divide it into 4 subsets (5), (1, 4), (2,3), (2,3) with equal sums.
Example 2:
    Input: nums = [1,2,3,4], k = 3
    Output: false
"""

from typing import List

""" 
Our goal is to break the given array into k subsets of equal sums.
Firstly, we will check if the array sum can be evenly divided into k parts by ensuring that totalArraySum % k is equal to 0.
Now, if the array sum can be evenly divided into k parts, we will try to build those k subsets using backtracking.

O(N.N!) time | O(N) space:
- The idea is that for each recursive call, we will iterate over N elements and make another recursive call. 
    Assume we picked one element, then we iterate over the array and make recursive calls for the next N-1 elements and so on.
    Therefore, in the worst-case scenario, 
        the total number of recursive calls will be N⋅(N−1)⋅(N−2)⋅...⋅2⋅1=N! and in each recursive call we perform an O(N) time operation.
- Another way is to visualize all possible states by drawing a recursion tree. 
    From root node we have NN recursive calls. The first level, therefore, has N nodes. 
    For each of the nodes in the first level, we have (N-1) similar choices. 
    As a result, the second level has N∗(N−1) nodes, and so on. The last level must have N⋅(N−1)⋅(N−2)⋅(N−3)⋅...⋅2⋅1 nodes.

- make a subset with sum totalArraySum/k
    - reduce the needed(k) by one
    - start again with other numbers
-repeat the above till the needed substets == 0
"""

class Solution:
    def canPartitionKSubsets(self, nums: List[int], k: int):
        # get required subset size
        target_sum = sum(nums)/k
        if int(target_sum) != target_sum:
            return False  # cannot have valid subsets

        # nums.sort(reverse=True)
        taken = [False]*len(nums)

        def backtracking(curr_sum, curr_k, idx):
            if curr_sum > target_sum:
                return False
            if curr_k == k:
                return True
            # When current subset sum reaches target sum then one subset is made.
            # Increment count and reset current subset sum to 0.
            if curr_sum == target_sum:
                return backtracking(0, curr_k+1, 0)

            # check if you starting to visit at a current index will give us the subsets
            for i in range(idx, len(nums)):
                # try not picked elements to make some combinations.
                if taken[i]:
                    continue

                # visit (Include this element in current subset)
                taken[i] = True
                if backtracking(curr_sum+nums[i], curr_k, i+1):
                    return True  # if the current index works out, none other can
                # un-visit (Backtrack step)
                taken[i] = False

            # We were not able to make a valid combination after picking
            # each element from the array, hence we can't make k subsets.
            return False

        return backtracking(0, 0, 0)

""" 
Memoization:

O(N.2^N) time | O(N.2^N) space:
- There will be N^2 unique combinations of the taken tuple, 
    in which every combination of the given array will be linearly iterated. 
    And if a combination occurs again then we just return the stored answer for it.
- So for each subset, we are choosing the suitable elements from the array 
    (basically iterate over nums and for each element either use it or skip it, which is O(N.2^N) operation)
- The idea is that we have two choices for each element: include it in the subset OR not include it in the subset. 
    We have N such elements. Therefore, the number of cases for events of including/excluding all numbers is: 2⋅2⋅2⋅...(N times)..⋅2 = 2^N
- Another way is to visualize all possible states by drawing a recursion tree. 
    In the first level, we have 2 choices for the first number, including the first number in the current subset or not. 
    The second level, therefore, has 2 nodes. For each of the nodes in the second level, we have 2 similar choices. 
    As a result, the third level has 2^2 nodes, and so on. 
    The last level must have 2^N nodes.
"""

class Solution_:
    def canPartitionKSubsets(self, nums: List[int], k: int):
        # get required subset size
        target_sum = sum(nums)/k
        if int(target_sum) != target_sum:
            return False  # cannot have valid subsets

        # nums.sort(reverse=True)
        taken = [False]*len(nums)
        cache = {}

        def backtracking(curr_sum, curr_k, idx):
            if curr_sum > target_sum:
                return False
            if curr_k == k:
                return True
            if tuple(taken) in cache:
                return cache[tuple(taken)]
            # When current subset sum reaches target sum then one subset is made.
            # Increment count and reset current subset sum to 0.
            if curr_sum == target_sum:
                cache[tuple(taken)] = backtracking(0, curr_k+1, 0)
                return cache[tuple(taken)]

            # check if you starting to visit at a current index will give us the subsets
            for i in range(idx, len(nums)):
                # try not picked elements to make some combinations.
                if not taken[i]:
                    # visit (Include this element in current subset)
                    taken[i] = True
                    if backtracking(curr_sum+nums[i], curr_k, i+1):
                        return True  # if the current index works out, none other can
                    # un-visit (Backtrack step)
                    taken[i] = False

            # We were not able to make a valid combination after picking
            # each element from the array, hence we can't make k subsets.
            cache[tuple(taken)] = False
            return cache[tuple(taken)]

        return backtracking(0, 0, 0)

These "search paths" can manifest as:

Actual search paths in a graph or searchable structure
Chosen characters placed in a progress string
Moves played in a puzzle, etc.

The 3 core ideas behind backtracking are:

The Choice: What fundamental choice is being made at every step of the algorithm to advance to a solution?
The Constraints: When is a path of decision no longer fruitful? When does the algorithm know for sure that it is wasting time following a certain path? If it is determined a path will no longer yield a solution an algorithm is said to "backtrack" when it returns control to a previous decision that can be advanced from.
The Goal: When do we know that the solution has been found?

Backtracking algorithms are most naturally modeled recursively, though not all recursion is backtracking as backtracking is characterized by the actual act of backtracking when a path is no longer solvable. There must be an element of reflecting on the algorithm's state and deciding to backtrack.

Searching

Search Algorithms

Searching Algorithms - Algorithms for Coding Interviews in Python

Search

General search

Examples

https://leetcode.com/discuss/interview-question/373202

Search a 2D Matrix

Treat is as one long 1D array

Screenshot 2021-10-10 at 15.54.19.png

Screenshot 2021-10-10 at 15.56.00.png

Screenshot 2021-10-10 at 15.59.16.png

Screenshot 2021-10-10 at 15.59.41.png

"""
Search a 2D Matrix:

Write an efficient algorithm that searches for a value in an m x n matrix. This matrix has the following properties:
Integers in each row are sorted from left to right.
The first integer of each row is greater than the last integer of the previous row.

https://leetcode.com/problems/search-a-2d-matrix/
"""
from typing import List
"""
Search In Sorted Matrix:

You're given a two-dimensional array (a matrix) of distinct integers and a target integer.
Each row in the matrix is sorted, and each column is also sorted; the matrix doesn't necessarily have the same height and width.
Write a function that returns an array of the row and column indices of the target integer if it's contained in the matrix, otherwise [-1, -1].

Sample Input:
    matrix = [
    [1, 4, 7, 12, 15, 1000],
    [2, 5, 19, 31, 32, 1001],
    [3, 8, 24, 33, 35, 1002],
    [40, 41, 42, 44, 45, 1003],
    [99, 100, 103, 106, 128, 1004],
    ]
    target = 44
Sample Output:
    [3, 3]

https://www.algoexpert.io/questions/Search%20In%20Sorted%20Matrix
"""

class Solution0:
    def binarySearch(self, target, array):
        left = 0
        right = len(array)-1
        while left <= right:
            mid = (right + left) // 2

            if array[mid] == target:
                return True
            if array[mid] < target:
                left = mid + 1
            else:
                right = mid - 1
        return False

    def searchMatrix(self, matrix: List[List[int]], target: int):

        for row in matrix:
            if row[0] <= target and row[-1] >= target:
                return self.binarySearch(target, row)

        return False

""" 
matrix = 
[
    [1,  3, 5, 7],
    [10,11,16,20],
    [23,30,34,60]
]

target = 13
Output: false

target = 16
Output: true

target = 16
---
if we start at 0,0
    - we do not know if it is in current row, or those below
---
if we start at 0,4
    - we are sure it isn't in current row, we move down
        - at  1,4:
            - we are sure it is in this row or none other
"""

class Solution:
    def searchMatrix(self, matrix: List[List[int]], target: int):

        row = 0
        while row < len(matrix):

            # # check rows
            # check last item in row
            if matrix[row][len(matrix[0])-1] < target:  # move to next row
                row += 1
            elif matrix[row][0] > target:
                return False

            # # found correct row
            # Binary Search on Row
            else:
                left = 0
                right = len(matrix[0])-1
                while left <= right:

                    mid = (right + left) // 2

                    if matrix[row][mid] == target:
                        return True

                    if matrix[row][mid] < target:
                        left = mid + 1
                    else:
                        right = mid - 1

                return False

        return False

def searchInSortedMatrix(matrix, target):

    # start at top right
    row = 0
    col = len(matrix[0]) - 1
    while row < len(matrix) and col >= 0:
        if matrix[row][col] > target:
            col -= 1  # move left
        elif matrix[row][col] < target:
            row += 1  # move down
        else:
            return[row, col]

    return[-1, -1]

"""

matrix = [
  [1, 4, 7, 12, 15, 1000],
  [2, 5, 19, 31, 32, 1001],
  [3, 8, 24, 33, 35, 1002],
  [40, 41, 42, 44, 45, 1003],
  [99, 100, 103, 106, 128, 1004],
]
target = 44

- Start curr at the top right corner
- Check wether you should increase or decrease curr's value
    Move sideways(decrease), downwards (increase)
- 

"""

Intersection of Two Arrays

""" 
Intersection of Two Arrays

Given two integer arrays nums1 and nums2, return an array of their intersection. 
Each element in the result must be unique and you may return the result in any order.

Example 1:
    Input: nums1 = [1,2,2,1], nums2 = [2,2]
    Output: [2]
Example 2:
    Input: nums1 = [4,9,5], nums2 = [9,4,9,8,4]
    Output: [9,4]
    Explanation: [4,9] is also accepted.

https://leetcode.com/problems/intersection-of-two-arrays
"""

"""  
Alternative approach: sort the input arrays and use two pointers
"""

class Solution:
    def intersection(self, nums1, nums2):
        result = set()

        one = set(nums1)
        two = set(nums2)

        for num in one:
            if num in two:
                result.add(num)

        return list(result)

class Solution_:
    def intersection(self, nums1, nums2):
        """
        :type nums1: List[int]
        :type nums2: List[int]
        :rtype: List[int]
        """
        set1 = set(nums1)
        set2 = set(nums2)
        return list(set2 & set1)

Intersection of Two Arrays II

""" 
Intersection of Two Arrays II

Given two integer arrays nums1 and nums2, return an array of their intersection. 
Each element in the result must appear as many times as it shows in both arrays and you may return the result in any order.

Example 1:
    Input: nums1 = [1,2,2,1], nums2 = [2,2]
    Output: [2, 2]
Example 2:
    Input: nums1 = [4,9,5], nums2 = [9,4,9,8,4]
    Output: [9,4]
    Explanation: [4,9] is also accepted.
3:
[4,9,5]
[9,4,9,8,4]
=> [4,9]

https://leetcode.com/problems/intersection-of-two-arrays-ii
"""

""" 
Alternative: use hashmap/collections.Counter
"""

class Solution:
    def intersect(self, nums1, nums2):
        result = []

        nums1.sort()
        nums2.sort()

        one, two = 0, 0
        while one < len(nums1) and two < len(nums2):
            if nums1[one] == nums2[two]:
                result.append(nums1[one])
                one += 1
                two += 1
            elif nums1[one] < nums2[two]:
                one += 1
            else:
                two += 1
        return result

Search Suggestions System

""" 
1268. Search Suggestions System

Given an array of strings products and a string searchWord. We want to design a system that suggests at most three product names from products after each character of searchWord is typed. Suggested products should have common prefix with the searchWord. 
If there are more than three products with a common prefix return the three lexicographically minimums products.
Return list of lists of the suggested products after each character of searchWord is typed.  

Example 1:
    Input: products = ["mobile","mouse","moneypot","monitor","mousepad"], searchWord = "mouse"
    Output: [
        ["mobile","moneypot","monitor"],
        ["mobile","moneypot","monitor"],
        ["mouse","mousepad"],
        ["mouse","mousepad"],
        ["mouse","mousepad"]
        ]
    Explanation: products sorted lexicographically = ["mobile","moneypot","monitor","mouse","mousepad"]
        After typing m and mo all products match and we show user ["mobile","moneypot","monitor"]
        After typing mou, mous and mouse the system suggests ["mouse","mousepad"]
Example 2:
    Input: products = ["havana"], searchWord = "havana"
    Output: [["havana"],["havana"],["havana"],["havana"],["havana"],["havana"]]
Example 3:
    Input: products = ["bags","baggage","banner","box","cloths"], searchWord = "bags"
    Output: [["baggage","bags","banner"],["baggage","bags","banner"],["baggage","bags"],["bags"]]
Example 4:
    Input: products = ["havana"], searchWord = "tatiana"
    Output: [[],[],[],[],[],[],[]]


Constraints
    1 <= products.length <= 1000
    There are no repeated elements in products.
    1 <= Σ products[i].length <= 2 * 10^4
    All characters of products[i] are lower-case English letters.
    1 <= searchWord.length <= 1000
    All characters of searchWord are lower-case English letters.

https://leetcode.com/problems/search-suggestions-system/
"""

"""

- given: products, searchword
- suggests at most 3 (common prefix)
    - after each character is typed

BF: (P.W + P log P) * S
- search arr, get all words with prefix
- sort by lexographic order, return top 3

SOL 1:
- we can store words in trie

P*S
get_words(pref, trie): 
    - heap
    - for each word, add it to a heap, of max size 3
    - return heap

Input
["havana"]
"tatiana"
Output:
[]
Expected
[[],[],[],[],[],[],[]]

"""

from typing import List
import heapq
class Word:
    def __init__(self, word):
        self.word = word

    def __gt__(self, other):
        return other.word > self.word

class Trie:
    def __init__(self):
        self.store = {}
        self.end_char = "*"

    def add(self, word):
        curr_store = self.store

        for char in word:
            if char not in curr_store:
                curr_store[char] = {}
            curr_store = curr_store[char]

        curr_store[self.end_char] = word

    def search_prefix(self, prefix):
        curr_store = self.store

        for char in prefix:
            if char not in curr_store:
                return []
            curr_store = curr_store[char]

        res = []
        self._get_all_words(curr_store, res)
        return res

    def _get_all_words(self, curr_store, result):
        """dfs"""

        for key, value in curr_store.items():
            if key == self.end_char:
                heapq.heappush(result, Word(value))
                if len(result) > 3:
                    heapq.heappop(result)
            else:
                self._get_all_words(value, result)

class Solution:
    def suggestedProducts(self, products: List[str], searchWord: str):

        result = []

        trie = Trie()
        for word in products:
            trie.add(word)

        for i in range(len(searchWord)):
            search_results = trie.search_prefix(searchWord[:i+1])

            if search_results:
                res = [item.word for item in search_results]
                res.sort()
                result.append(res)
            else:
                result.append([])

        return result

Kth Largest Element in an Array

""" 
Kth Largest Element in an Array

Given an integer array nums and an integer k, return the kth largest element in the array.
Note that it is the kth largest element in the sorted order, not the kth distinct element.

Example 1:
Input: nums = [3,2,1,5,6,4], k = 2
Output: 5
Example 2:
Input: nums = [3,2,3,1,2,4,5,5,6], k = 4
Output: 4

https://leetcode.com/problems/kth-largest-element-in-an-array
"""

class Solution:
    def findKthLargest(self, array, k):
        return self.quick_select(array, len(array)-k, 0, len(array)-1)

    def quick_select(self, array, idx, start, end):
        if start == end:
            return array[start]

        # # pick pivot and sort numbers relative to it (like quick sort)
        pivot = start
        # # sort numbers with respect to pivot then put pivot between the large and small numbers
        #   left and right to stop at a place where: left >= pivot & right <= pivot
        left = start + 1
        right = end
        while left <= right:
            # check if can be swapped
            if array[left] > array[pivot] and array[right] < array[pivot]:
                array[left], array[right] = array[right], array[left]

            if array[left] <= array[pivot]:  # no need to swap
                left += 1
            if array[right] >= array[pivot]:  # no need to swap
                right -= 1

        # place pivot at correct position
        # # place the pivot at correct position (right)
        # # place pivot at correct position
        # we know that once the sorting is done, the number at left >= pivot & right <= pivot
        #   smaller values go to the left of array[pivot]
        # # right is at a value < pivot, so ot should be moved left
        array[pivot], array[right] = array[right], array[pivot]

        # after swapping right is the only number we are sure is sorted
        # check if we are at the idx being looked for
        if right == idx:
            return array[right]

        # # proceed search
        elif right < idx:
            return self.quick_select(array, idx, right+1, end)
        else:
            return self.quick_select(array, idx, start, right-1)

x = Solution()
x.findKthLargest([5, 6, 4], 2)

Word Search

"""
Word Search

Given a 2D board and a word, find if the word exists in the grid.
The word can be constructed from letters of sequentially adjacent cells,
where "adjacent" cells are horizontally or vertically neighboring.
The same letter cell may not be used more than once.

Constraints:
    board and word consists only of lowercase and uppercase English letters.
    1 <= board.length <= 200
    1 <= board[i].length <= 200
    1 <= word.length <= 10^3

https://leetcode.com/problems/word-search/
"""

from typing import List

# O(n) time | O(n) space -> because of the recursion call stack |
class Solution:
    def exist(self, board: List[List[str]], word: str):

        # Iterate over each character
        h = 0
        while h < len(board):
            w = 0
            while w < len(board[0]):
                # stop iteration if we find the word
                if board[h][w] == word[0] and self.searchWordOutward(board, word, h, w, 0):
                    return True
                w += 1
            h += 1

        return False

    def searchWordOutward(self, board, word, h, w, word_pos):
        # check if past end of word (found all characters)
        if word_pos >= len(word):
            return True

        if h < 0 or h >= len(board) or \
                w < 0 or w >= len(board[0]):
            return False

        if board[h][w] != word[word_pos]:
            return False

        # remove seen character
        seen_char = board[h][w]
        board[h][w] = ''

        # Expand: move on to next character (word_pos + 1) -> in the order right, left, top, bottom
        found = self.searchWordOutward(board, word, h, w+1, word_pos+1) or \
            self.searchWordOutward(board, word, h, w-1, word_pos+1) or \
            self.searchWordOutward(board, word, h+1, w, word_pos+1) or \
            self.searchWordOutward(board, word, h-1, w, word_pos+1)

        # return seen character
        board[h][w] = seen_char

        return found

"""
Input:
    [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]]
    "ABCCED"
    [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]]
    "SEE"
    [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]]
    "ABCB"
Output:
    true
    true
    false
"""

Linear/Sequential Search

Go through each element one by one. When the element you are searching for is found, return its index.

Binary Search

Binary-search Interview Questions - LeetCode Discuss

Requires a sorted array.

The terminology used in Binary Search:

Target - the value that you are searching for
Index - the current location that you are searching
Left, Right - the indices from which we use to maintain our search Space
Mid - the index that we use to apply a condition to determine if we should search left or right

Searching%20733ff84c808c4c9cb5c40787b2df7b98/binary_search.gif

How does it work?

In its simplest form, Binary Search operates on a contiguous sequence with a specified left and right index. This is called the Search Space. Binary Search maintains the left, right, and middle indices of the search space and compares the search target or applies the search condition to the middle value of the collection; if the condition is unsatisfied or values unequal, the half in which the target cannot lie is eliminated and the search continues on the remaining half until it is successful. If the search ends with an empty half, the condition cannot be fulfilled and the target is not found.

Common types of Binary Search

Simple Binary Search

This is the most basic and elementary form of Binary Search. It is the standard Binary Search Template that most high schools or universities use when they first teach students computer science. It is used to search for an element or condition which can be determined by accessing a single index in the array.

Basic logic:

# Binary Search
# -1 means not found

def search(self, nums, target):
    if not nums:
        return -1
    if len(nums) == 1 and nums[0] == target:
        return 0


    left, right = 0, len(nums) - 1
    # not while left < right: because of cases where the target is on the right pointer
    # like ([1,2,5], 5)
    # the mid can be on the left pointer but never on the right pointer because of the,
    # the floor division -> rounds down results
    while left <= right:
        mid = (left+right) // 2

        if nums[mid] == target:
            return mid

        # # check which half is invalid. Note that mid is already invalid
        # left is invalid (all the numbers to the left are smaller than target)
        elif target > nums[mid]:
            # move left pointer
            # skip mid & all the numbers to the left of it
            left = mid + 1
        else:
            # skip mid & all the numbers to the right of it
            right = mid - 1


    return -1

Key attributes:

Search condition can be determined without comparing to the element's neighbours
No post-processing is required because at each step, you are checking to see if the element has been found. If you reach the end, then you know the element is not found
We allow the right & left pointer be on the same index

Distinguishing Syntax:

Termination: left > right The while loop looks similar to while left <= right:
Searching Left: right = mid-1
Searching Right: left = mid+1
Initial Condition: left = 0, right = length-1

Examples

Guess Number Higher or Lower

"""
Guess Number Higher or Lower: (Binary Search)

We are playing the Guess Game. The game is as follows:
I pick a number from 1 to n. You have to guess which number I picked.
Every time you guess wrong, I will tell you whether the number I picked is higher or lower than your guess.
You call a pre-defined API int guess(int num), which returns 3 possible results:
    -1: The number I picked is lower than your guess (i.e. pick < num).
    1: The number I picked is higher than your guess (i.e. pick > num).
    0: The number I picked is equal to your guess (i.e. pick == num).
Return the number that I picked.

https://leetcode.com/problems/guess-number-higher-or-lower/
"""

#
#
# The guess API is already defined for you.
# @param num, your guess
# @return -1 if my number is lower, 1 if my number is higher, otherwise return 0
# def guess(num: int) -> int:

def guess(num: int):
    pass
#
#

class Solution:
    def guessNumber(self, n):

        if n < 2:
            return n

        left = 1
        right = n

        # we don't use left < right because: the middle pointer will never be at the right pointer,
        # so if the the number we are guessing == n, the right pointer will never be checked (right = n) and,
        # hence never find the guess number
        while left <= right:

            mid = (left+right) // 2
            guess_res = guess(mid)

            if guess_res == 0:
                return mid
            # lower
            elif guess_res == 1:
                left = mid + 1
            else:
                right = mid - 1

class Solution00:
    def guessNumber(self, x: int):

        left = 1
        right = x
        while left <= right:
            mid = (left+right) // 2
            res = guess(mid)
            # print(left, right, mid, res)

            if res == 0:
                return mid

            elif res == -1:
                right = mid - 1

            else:
                left = mid + 1

"""
[0,1,2,3,4,5,6,7,8]
[1,2,3,4,5,6,7,8,9]
6

r = 9
l = 1
m = 5

r = 9
l = 1
m = 5

"""

Sqrt(x) *

"""
Sqrt(x): (Binary Search)

Given a non-negative integer x, compute and return the square root of x.
Since the return type is an integer, the decimal digits are truncated,
 and only the integer part of the result is returned.

Example 1:
    Input: x = 4
    Output: 2

Example 2:
    Input: x = 8
    Output: 2
    Explanation: The square root of 8 is 2.82842..., and since the decimal part is truncated, 2 is returned.
https://leetcode.com/problems/sqrtx/
"""

class Solution:
    def mySqrt(self, x: int):

        left = 1
        right = x
        while left <= right:
            mid = (left+right) // 2
            mid_sq = mid * mid

            if mid_sq == x:
                return mid

            elif mid_sq > x:
                right = mid - 1

            else:
                left = mid + 1

        return right
        # return (left+right) // 2

"""
[0,1,2,3,4,5,6,7,8]
[1,2,3,4,5,6,7,8,9]
9

l = 1,0
r = 9,8
mid = 5,4

l = 1,0
r = 4,3
mid = 3,2

[0,1,2,3,4,5,6,7]
[1,2,3,4,5,6,7,8]
8

l = 1,0
r = 8,7
mid = 4,3

l = 1,0
r = 3,2
mid = 2,1

"""

def mySqrt(self, x):

    if x < 2:
        return x

    left = 1
    right = x

    while left <= right and left ** 2 <= x:
        # Remember:
        # the mid can be on the left pointer, never on the right: floor division -> rounds down results
        # we want to push left as far up as possible:
        # then we can do some rounding down logic later
        mid = (left+right) // 2
        mid_squared = mid ** 2

        if mid_squared == x:
            return mid
        elif mid_squared > x:
            right = mid - 1
        else:
            left = mid + 1

    # from the prompt, we are allowed to round down for example, the square root of 8 is 2.82842..., we return 2
    # this means that the first val we find where (val**2 <= x) is the correct result

    # left will always be larger or equal to the sq root because of the logic in the above while loop
    while left ** 2 > x:
        left -= 1
    return left

    # # Also works
    # mid = (left + right) // 2
    # while mid ** 2 > x:
    #     mid -= 1
    # return mid

#       this would have worked if we were rounding up
#       while not right ** 2 >= x:
#           right += 1

#       return right
# 2147395599

# without comments
def mySqrtWC(self, x: int):
    if x < 2:
        return x

    left = 1
    right = x
    while left <= right and left ** 2 <= x:
        mid = (left+right) // 2
        mid_squared = mid ** 2

        if mid_squared == x:
            return mid
        elif mid_squared > x:
            right = mid - 1
        else:
            left = mid + 1

    # Also works
    mid = (left + right) // 2
    while mid ** 2 > x:
        mid -= 1
    return mid

    # while left ** 2 > x:
    #    left -= 1
    # return left

Root of Number

""" 
Root of Number:

Many times, we need to re-implement basic functions without using any standard library functions already implemented. 
For example, when designing a chip that requires very little memory space.
In this question we’ll implement a function root that calculates the n’th root of a number. 
The function takes a nonnegative number x and a positive integer n, 
and returns the positive n’th root of x within an error of 0.001 (i.e. suppose the real root is y, then the error is: |y-root(x,n)| and must satisfy |y-root(x,n)| < 0.001).
Don’t be intimidated by the question. While there are many algorithms to calculate roots that require prior knowledge in numerical analysis, 
there is also an elementary method which doesn’t require more than guessing-and-checking. Try to think more in terms of the latter.
Make sure your algorithm is efficient, and analyze its time and space complexities.

Examples:

    input:  x = 7, n = 3
    output: 1.913

    input:  x = 9, n = 2
    output: 3
"""

"""
----------------- PROBLEM ----------------- :

calculates the n’th root of a number
takes in nonnegative number x and a positive integer n, and returns the positive n’th root of x within an error of 0.001

suppose the real root is y, then the error is: |y-root(x,n)| and must satisfy |y-root(x,n)| < 0.001).

----------------- EXAMPLES ----------------- :

x = 7, n = 3
1.913

x = 9, n = 2
3

x = 8, n = 3
2

x = 4, n = 2
2

x = 3, n = 2
1.732

r^n = x

0.001 - 8
 for each of them ^n


----------------- BRUTE FORCE ----------------- :
Time complexity : O(1000x) -> O(x)
Space complexity: O(1)

x = 4, n = 2

(0.001, 0.002,.... 1 => 1000) * 4  

x = 8, n = 3

(0.001, 0.002,.... 1 => 1000) * 8

----------------- OPTIMAL ----------------- :

x = 4, n = 2

left    right  mid
0.001 - 4.000  2

x = 8, n = 3

left    right  mid
0.001 - 8.000  4
0.001 - 4.000  2

x = 3, n = 2
left    right  mid
0.001 - 3.000  1.5
1.5   - 3.00   1.5+0.75 = 2.25  
1.5   - 2.25   

---

x = 1.1, n = 2
1.04

left    right  mid   mid^n
0       1.1    0.55  0.3

---

x = 9.1, n = 2
3.01

---
Special case:

x = 0.9, n = 2
0.949

x = 0.5, n = 2
0.707

left    right  mid   mid^n
0.5     1      .75   .5625

break condition:
 - abs(mid^n - x) < 0.001 

"""

def root(x, n):
    left = 0
    right = x
    # special condition
    if x < 1:
        left = x
        right = 1

    while left < right:
        mid = (left+right)/2
        mid_power_n = mid ** n

        # found answer
        if abs(mid_power_n - x) < 0.001:
            return round(mid, 3)

        # is smaller
        elif mid_power_n < x:
            left = mid

        # is larger
        else:
            right = mid

print(root(7, 3))
print(root(3, 2))
print(root(160, 3))
print(root(0.9, 2))
print(root(0.5, 3))

Pow(x, n) **

Pow(x, n) - X to the power of N - Leetcode 50 - Python

""" 
Pow(x, n)

Implement pow(x, n), which calculates x raised to the power n (i.e., xn).

Example 1:
    Input: x = 2.00000, n = 10
    Output: 1024.00000
Example 2:
    Input: x = 2.10000, n = 3
    Output: 9.26100
Example 3:
    Input: x = 2.00000, n = -2
    Output: 0.25000
    Explanation: 2-2 = 1/22 = 1/4 = 0.25

https://leetcode.com/problems/powx-n
https://youtu.be/g9YQyYi4IQQ
"""

""" 
2 ** 6
2*2*2*2*2*2
2**3 * 2**3
(2**2 * 2**1) * (2**2 * 2**1)
(2**1 * 2**1 * 2**1) * (2**1 * 2**1 * 2**1)

2^12 => (2^6)^2
2^6  => (2^3)^2
2^3  => (2^1)^2 * 2

2^10 => (2^5)^2
2^5  => (2^2)^2 * 2
2^2  => (2^1)^2
"""

class Solution:
    def myPow(self, x: float, n: int):
        res = self.my_pow_helper(x, abs(n))

        if n < 0:
            return 1/res
        return res

    def my_pow_helper(self, x, n):
        if x == 0:
            return 0
        if n == 0:
            return 1
        if n == 1:
            return x

        half_n = n // 2
        n_is_odd = n % 2 != 0

        # calculate power
        half_power = self.my_pow_helper(x, half_n)

        if n_is_odd:
            return half_power * half_power * x
        return half_power * half_power

Divide Two Integers ***

Divide Two Integers | Live Coding with Explanation | Leetcode -29

Screenshot 2021-11-29 at 19.48.31.png

Screen Recording 2021-11-29 at 19.50.23.mov

""" 
Divide Two Integers:

Given two integers dividend and divisor, divide two integers without using multiplication, division, and mod operator.
Return the quotient after dividing dividend by divisor.
The integer division should truncate toward zero, which means losing its fractional part. For example, truncate(8.345) = 8 and truncate(-2.7335) = -2.
Note: Assume we are dealing with an environment that could only store integers within the 32-bit signed integer range: [−231, 231 − 1]. For this problem, assume that your function returns 231 − 1 when the division result overflows.



Example 1:
    Input: dividend = 10, divisor = 3
    Output: 3
    Explanation: 10/3 = truncate(3.33333..) = 3.
Example 2:
    Input: dividend = 7, divisor = -3
    Output: -2
    Explanation: 7/-3 = truncate(-2.33333..) = -2.
Example 3:
    Input: dividend = 0, divisor = 1
    Output: 0
Example 4:
    Input: dividend = 1, divisor = 1
    Output: 1

https://leetcode.com/problems/divide-two-integers
"""

class SolutionBF:
    def divide(self, dividend: int, divisor: int):
        is_neg = False
        if divisor < 0:
            divisor = abs(divisor)
            is_neg = not is_neg
        if dividend < 0:
            dividend = abs(dividend)
            is_neg = not is_neg

        count = 0
        while dividend >= divisor:
            dividend -= divisor
            count += 1

        if is_neg:
            return -count
        return count

""" 
dividend = 28, divisor = 3

Repeated Exponential Searches
- Keep on doubling divisor till it cannot be doubled more
3  =3       =3*2^0
6  =3*2     =3*2^1
12 =3*2*2   =3*2^2
24 =3*2*2*2 =3*2^3 => 8 threes

we remained with 28-4
- repeat the above process for 

"""

class Solution:
    def divide(self, dividend: int, divisor: int):
        # Special case: overflow
        MAX_INT = 2147483647        # 2**31 - 1
        MIN_INT = -2147483648       # -2**31
        if dividend == MIN_INT and divisor == -1:
            return MAX_INT

        # handle negatives
        is_neg = False
        if divisor < 0:
            divisor = abs(divisor)
            is_neg = not is_neg
        if dividend < 0:
            dividend = abs(dividend)
            is_neg = not is_neg

        result = 0  # quotient

        # # actual division ----------------------------------------------------
        while dividend >= divisor:

            curr_divisor = divisor
            two_power = 0
            while curr_divisor+curr_divisor <= dividend:
                curr_divisor += curr_divisor  # (double divisor)
                two_power += 1  # record that we doubled the divisor

            result += 2**two_power  # we used the divisor 2**two_power times
            dividend -= curr_divisor  # remaining

         # #  ----------------------------------------------------
        if is_neg:
            return -result
        return result

Random Pick with Weight *

""" 
Random Pick with Weight: 
(answers are so random)

You are given an array of positive integers w where w[i] describes the weight of ith index (0-indexed).
We need to call the function pickIndex() which randomly returns an integer in the range [0, w.length - 1]. 
pickIndex() should return the integer proportional to its weight in the w array. 
For example, for w = [1, 3], the probability of picking the index 0 is 1 / (1 + 3) = 0.25 (i.e 25%) while the probability of picking the index 1 is 3 / (1 + 3) = 0.75 (i.e 75%).
More formally, the probability of picking index i is w[i] / sum(w).

Example 1:
    Input
        ["Solution","pickIndex"]
        [[[1]],[]]
    Output
        [null,0]
    Explanation
        Solution solution = new Solution([1]);
        solution.pickIndex(); // return 0. Since there is only one single element on the array the only option is to return the first element.

Example 2:
Input
    ["Solution","pickIndex","pickIndex","pickIndex","pickIndex","pickIndex"]
    [[[1,3]],[],[],[],[],[]]
Output
    [null,1,1,1,1,0]
Explanation
    Solution solution = new Solution([1, 3]);
    solution.pickIndex(); // return 1. It's returning the second element (index = 1) that has probability of 3/4.
    solution.pickIndex(); // return 1
    solution.pickIndex(); // return 1
    solution.pickIndex(); // return 1
    solution.pickIndex(); // return 0. It's returning the first element (index = 0) that has probability of 1/4.

    Since this is a randomization problem, multiple answers are allowed so the following outputs can be considered correct :
    [null,1,1,1,1,0]
    [null,1,1,1,1,1]
    [null,1,1,1,0,0]
    [null,1,1,1,0,1]
    [null,1,0,1,0,0]
    ......
    and so on.

https://leetcode.com/problems/random-pick-with-weight
"""
import random

"""
Example:

[1,2,3]
[1/5, 2/5, 3/5]

 1 2   3
|-|--|---| => 5

[1,3]
 1  3
|-|---|

[1,1,2]
 1 1 2
|-|-|--|
[0-0.25, 0.25-0.5, 0.5-1]

"""

# Your Solution object will be instantiated and called as such:
# obj = Solution(w)
# param_1 = obj.pickIndex()

class Solution:

    def __init__(self, w):
        self.w = w
        self.total = sum(w)
        self.probability_range = []

        prev_probability = 0
        for num in self.w:
            curr = prev_probability + num/self.total
            self.probability_range.append(curr)
            prev_probability = curr
        # print(self.probability_range)

    def pickIndex(self):
        pick = random.random()

        # binary search
        left = 0
        right = len(self.probability_range)
        while left < right:
            mid = (left+right) // 2
            if self.probability_range[mid] > pick:
                right = mid
            else:
                left = mid + 1
        return left

Find Peak Element

""" 
Find Peak Element

A peak element is an element that is strictly greater than its neighbors.
Given an integer array nums, find a peak element, and return its index. 
If the array contains multiple peaks, return the index to any of the peaks.

You may imagine that nums[-1] = nums[n] = -∞.

You must write an algorithm that runs in O(log n) time.

Example 1:
    Input: nums = [1,2,3,1]
    Output: 2
    Explanation: 3 is a peak element and your function should return the index number 2.
Example 2:
    Input: nums = [1,2,1,3,5,6,4]
    Output: 5
    Explanation: Your function can return either index number 1 where the peak element is 2, or index number 5 where the peak element is 6.

https://leetcode.com/problems/find-peak-element/
"""

""" 
[1,2,3,1]   => 2
[1,2,3,4,5] => 4
[5,4,3,2,1] => 0

Binary search:
    - if the element at mid is in an increasing order:
        - if we move to the right, we might find a peak(decreases) or the array end 
            which are both valid answers
    - the opposite is also True
"""

class Solution:
    def findPeakElement(self, nums):
        if len(nums) == 1:
            return 0

        left = 0
        right = len(nums)-1
        while left <= right:
            mid = (left+right) // 2

            # ends (also is peak)
            if mid == 0:
                if nums[mid+1] < nums[mid]:
                    return mid
                left = mid + 1
            elif mid == len(nums)-1:
                if nums[mid-1] < nums[mid]:
                    return mid
                right = mid

            # is peak but not on ends
            elif nums[mid-1] < nums[mid] and nums[mid+1] < nums[mid]:
                return mid

            # is increasing
            elif nums[mid-1] < nums[mid]:
                left = mid + 1

            # is increasing
            else:
                right = mid

Search a 2D Matrix

Treat is as one long 1D array

Screenshot 2021-10-10 at 15.54.19.png

Screenshot 2021-10-10 at 15.56.00.png

Screenshot 2021-10-10 at 15.59.16.png

Screenshot 2021-10-10 at 15.59.41.png

"""
Search a 2D Matrix:

Write an efficient algorithm that searches for a value in an m x n matrix. This matrix has the following properties:
Integers in each row are sorted from left to right.
The first integer of each row is greater than the last integer of the previous row.

https://leetcode.com/problems/search-a-2d-matrix/
"""
from typing import List
"""
Search In Sorted Matrix:

You're given a two-dimensional array (a matrix) of distinct integers and a target integer.
Each row in the matrix is sorted, and each column is also sorted; the matrix doesn't necessarily have the same height and width.
Write a function that returns an array of the row and column indices of the target integer if it's contained in the matrix, otherwise [-1, -1].

Sample Input:
    matrix = [
    [1, 4, 7, 12, 15, 1000],
    [2, 5, 19, 31, 32, 1001],
    [3, 8, 24, 33, 35, 1002],
    [40, 41, 42, 44, 45, 1003],
    [99, 100, 103, 106, 128, 1004],
    ]
    target = 44
Sample Output:
    [3, 3]

https://www.algoexpert.io/questions/Search%20In%20Sorted%20Matrix
"""

class Solution0:
    def binarySearch(self, target, array):
        left = 0
        right = len(array)-1
        while left <= right:
            mid = (right + left) // 2

            if array[mid] == target:
                return True
            if array[mid] < target:
                left = mid + 1
            else:
                right = mid - 1
        return False

    def searchMatrix(self, matrix: List[List[int]], target: int):

        for row in matrix:
            if row[0] <= target and row[-1] >= target:
                return self.binarySearch(target, row)

        return False

""" 
matrix = 
[
    [1,  3, 5, 7],
    [10,11,16,20],
    [23,30,34,60]
]

target = 13
Output: false

target = 16
Output: true

target = 16
---
if we start at 0,0
    - we do not know if it is in current row, or those below
---
if we start at 0,4
    - we are sure it isn't in current row, we move down
        - at  1,4:
            - we are sure it is in this row or none other
"""

class Solution:
    def searchMatrix(self, matrix: List[List[int]], target: int):

        row = 0
        while row < len(matrix):

            # # check rows
            # check last item in row
            if matrix[row][len(matrix[0])-1] < target:  # move to next row
                row += 1
            elif matrix[row][0] > target:
                return False

            # # found correct row
            # Binary Search on Row
            else:
                left = 0
                right = len(matrix[0])-1
                while left <= right:

                    mid = (right + left) // 2

                    if matrix[row][mid] == target:
                        return True

                    if matrix[row][mid] < target:
                        left = mid + 1
                    else:
                        right = mid - 1

                return False

        return False

def searchInSortedMatrix(matrix, target):

    # start at top right
    row = 0
    col = len(matrix[0]) - 1
    while row < len(matrix) and col >= 0:
        if matrix[row][col] > target:
            col -= 1  # move left
        elif matrix[row][col] < target:
            row += 1  # move down
        else:
            return[row, col]

    return[-1, -1]

"""

matrix = [
  [1, 4, 7, 12, 15, 1000],
  [2, 5, 19, 31, 32, 1001],
  [3, 8, 24, 33, 35, 1002],
  [40, 41, 42, 44, 45, 1003],
  [99, 100, 103, 106, 128, 1004],
]
target = 44

- Start curr at the top right corner
- Check wether you should increase or decrease curr's value
    Move sideways(decrease), downwards (increase)
- 

"""

Advanced Binary Search I

This is an advanced form of binary search that is used to search for an element or condition which requires accessing the current index & its right neighbour's index.

Untitled

Basic logic:

check out the examples

def search(self, nums, target):

    if not nums or len(nums) < 1:
        return -1

    left, right = 0, len(nums) -1 

    while left < right:
        mid = (left+right) // 2

        if nums[mid] == target:
            return mid
        elif target > nums[mid]:
            left = mid + 1
        else:
            right = mid

    # because of left < right : the middle pointer will never be at the right pointer, 
    # so if the the target is at the end of the array, 
    # the right pointer will never be checked (right = nums[-1]) and, hence never find the target
    # example: search([1,2,3], 3) -> will return -1
    if left < len(nums) and nums[left] == target:
        return left

    return -1

Key Attributes:

Most of the time Post-processing required. Loop/Recursion ends when you have 1 element left. Need to assess if the remaining element meets the condition. This is because the while left < right instead of while left <= right * If the target is at the right index, it won't have been found in the initial search(while loop).
Search Condition needs to access the element's immediate right/left neighbour
Use the element's right/left neighbour to determine if the condition is met and decide whether to go left or right
Guarantees Search Space is at least 2 in size at each step
An advanced way to implement Binary Search.

Distinguishing Syntax:

Initial Condition: left = 0, right = length
Termination: left == right
Searching Left: right = mid
Searching Right: left = mid+1

Examples

Find Minimum in Rotated Sorted Array

"""
Find Minimum in Rotated Sorted Array:

Suppose an array of length n sorted in ascending order is rotated between 1 and n times. For example, the array nums = [0,1,2,4,5,6,7] might become:
[4,5,6,7,0,1,2] if it was rotated 4 times.
[0,1,2,4,5,6,7] if it was rotated 7 times.
Notice that rotating an array [a[0], a[1], a[2], ..., a[n-1]] 1 time results in the array [a[n-1], a[0], a[1], a[2], ..., a[n-2]].
Given the sorted rotated array nums, return the minimum element of this array.

https://leetcode.com/problems/find-minimum-in-rotated-sorted-array/

After this: Search in Rotated Sorted Array https://leetcode.com/problems/search-in-rotated-sorted-array/
"""

class Solution:
    # search for the beginning of the unsorted part
    def findMin(self, nums):
        if not nums:
            return None

        left, right = 0, len(nums) - 1
        while left < right:
            mid = (right + left) // 2

            # look for the beginning of the unsorted part
            if nums[mid] > nums[mid+1]:
                return nums[mid+1]
            if nums[mid - 1] > nums[mid]:
                return nums[mid]

            # Binary Search
            if nums[mid] > nums[right]:  # check if right side is unsorted
                left = mid + 1
            else:
                right = mid - 1

        # return smallest number
        return nums[left]

"""
[3,4,5,1,2]
[4,5,6,7,0,1,2]
[11,13,15,17]
[11,13,15,17,10]
[1]
[3,1,2]
"""

Search in Rotated Sorted Array

""" 
Search in Rotated Sorted Array:

There is an integer array nums sorted in ascending order (with distinct values).
Prior to being passed to your function, nums is rotated at an unknown pivot index k (0 <= k < nums.length) 
    such that the resulting array is [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]] (0-indexed). 
    For example, [0,1,2,4,5,6,7] might be rotated at pivot index 3 and become [4,5,6,7,0,1,2].
Given the array nums after the rotation and an integer target, return the index of target if it is in nums, or -1 if it is not in nums.
You must write an algorithm with O(log n) runtime complexity.

Example 1:
    Input: nums = [4,5,6,7,0,1,2], target = 0
    Output: 4
Example 2:
    Input: nums = [4,5,6,7,0,1,2], target = 3
    Output: -1
Example 3:
    Input: nums = [1], target = 0
    Output: -1

https://leetcode.com/problems/search-in-rotated-sorted-array/
https://www.algoexpert.io/questions/Shifted%20Binary%20Search

Prerequisite: Find Minimum in Rotated Sorted Array https://leetcode.com/problems/find-minimum-in-rotated-sorted-array/
"""

class Solution_:
    def search(self, nums, target):

        start_idx = self.get_smallest_num_idx(nums)

        if target >= nums[start_idx] and target <= nums[-1]:
            return self.binary_search(nums, target, start_idx, len(nums)-1)
        return self.binary_search(nums, target, 0, start_idx)

    def get_smallest_num_idx(self, nums):

        left = 0
        right = len(nums)-1
        while left <= right:
            mid = (left+right)//2

            if mid > 0 and nums[mid-1] > nums[mid]:
                return mid
            if mid < len(nums)-1 and nums[mid+1] < nums[mid]:
                return mid+1

            # if right is unsorted
            if nums[mid] > nums[right]:
                left = mid + 1
            else:
                right = mid - 1

        return left

    def binary_search(self, nums, target, left, right):
        while left <= right:
            mid = (left+right) // 2

            if nums[mid] == target:
                return mid

            elif target > nums[mid]:
                left = mid + 1
            else:
                right = mid - 1
        return -1

""" 
- we know that:
    - If a section (left-mid or mid-right) is unsorted then the other must be sorted

"""

class Solution:
    def search(self, nums, target):

        left = 0
        right = len(nums)-1
        while left <= right:
            mid = (left+right)//2
            if nums[mid] == target:
                return mid

            if nums[left] <= nums[mid]:  # left is sorted
                if target >= nums[left] and target <= nums[mid]:  # in left
                    right = mid
                else:
                    left = mid + 1

            else:  # right is sorted
                if target >= nums[mid] and target <= nums[right]:  # in right
                    left = mid
                else:
                    right = mid - 1

        return -1

First Bad Version

"""
First Bad Version:

You are a product manager and currently leading a team to develop a new product.
Unfortunately, the latest version of your product fails the quality check.
Since each version is developed based on the previous version, all the versions after a bad version are also bad.
Suppose you have n versions [1, 2, ..., n] and you want to find out the first bad one, which causes all the following ones to be bad.
You are given an API bool isBadVersion(version) which returns whether version is bad. 
Implement a function to find the first bad version. You should minimize the number of calls to the API.

Example 1:
    Input: n = 5, bad = 4
    Output: 4
    Explanation:
    call isBadVersion(3) -> false
    call isBadVersion(5) -> true
    call isBadVersion(4) -> true
    Then 4 is the first bad version.

Example 2:
    Input: n = 1, bad = 1
    Output: 1

https://leetcode.com/problems/first-bad-version/
"""

# The isBadVersion API is already defined for you.
# @param version, an integer
# @return an integer
# def isBadVersion(version):
def isBadVersion(mid):
    pass

class Solution:
    def firstBadVersion(self, n):
        first_bad = n-1

        left = 1
        right = n
        while left <= right:
            mid = (left+right) // 2

            if isBadVersion(mid):
                first_bad = mid
                right = mid - 1
            else:
                left = mid + 1

        return first_bad

class Solution_:
    def firstBadVersion(self, n):

        left = 1
        right = n
        while left < right:
            mid = (left+right) // 2

            if isBadVersion(mid):
                # in the next loop, this will result in left being brought closer to the bad versions
                # [1,2,3] if bv=2, l=0, r=2, in the next, l=2

                # avoid skipping bad versions
                right = mid
            else:
                # only move left if mid version is good
                # this ensures left never skips any bad version, it will always land on the first bad version
                # skip all good versions
                left = mid + 1

        return left

"""
try to move left to the first bad version - make sure not to pass it (bad version) with right

"""
"""
// [1,2,3]

[0,1,2,3,4,5,6,7,8]
[1,2,3,4,5,6,7,8,9]
6 and above

r = 9
l = 1
m = 5

r = 9
l = 6
m = 7

[0,1,2,3,4,5,6,7,8]
[1,2,3,4,5,6,7,8,9]
2 and above

r = 9
l = 1
m = 5

r = 5
l = 1
m = 2

r = 2
l = 1
m = 1

r = 2
l = 2
m = 2
break

"""

class Solution00:
    def firstBadVersion(self, n):

        left = 1
        right = n

        while left < right:

            mid = (left+right) // 2

            # only move left if mid version is good
            # this ensures left never skips any bad version, it will always land on the first bad version
            if not isBadVersion(mid):
                left = mid + 1

            # try and move right closer and closer to the first bad version
            else:
                right = mid

        return left

Find First and Last Position of Element in Sorted Array/Search For Range

Screenshot 2021-11-02 at 20.11.02.png

""" 
Find First and Last Position of Element in Sorted Array/Search For Range:

Given an array of integers nums sorted in ascending order, find the starting and ending position of a given target value.
If target is not found in the array, return [-1, -1].
You must write an algorithm with O(log n) runtime complexity.

Example 1:
    Input: nums = [5,7,7,8,8,10], target = 8
    Output: [3,4]
Example 2:
    Input: nums = [5,7,7,8,8,10], target = 6
    Output: [-1,-1]
Example 3:
    Input: nums = [], target = 0
    Output: [-1,-1]

https://leetcode.com/problems/find-first-and-last-position-of-element-in-sorted-array/
https://www.algoexpert.io/questions/Search%20For%20Range
"""

""" 

- find the number using binary search
- find start of range using binary search
- find end of range using binary search

[0,1,2,3,4,5]
[5,7,7,8,8,10] 8

[0, 1, 2,   3,  4,  5   6,   7  8   9  10  11  12]
[0, 1, 21, 33, 45, 45, 45, 45, 45, 45, 61, 71, 73] 45

# find end
l, r  m
6, 12 9
10,12 11
10,10 10

"""

""" 
Simplest using pointers to remember last seen
"""

class Solution_P:
    def searchRange(self, nums, target):
        return [
            self.find_start(nums, target),
            self.find_end(nums, target)
        ]

    def find_start(self, nums, target):
        last_seen = -1

        left = 0
        right = len(nums)-1
        while left <= right:
            mid = (left+right)//2

            if nums[mid] > target:
                right = mid - 1
            elif nums[mid] < target:
                left = mid + 1
            else:
                # record that we have seen it &
                #  ignore everything to the right
                last_seen = mid
                right = mid - 1
        return last_seen

    def find_end(self, nums, target):
        last_seen = -1

        left = 0
        right = len(nums)-1
        while left <= right:
            mid = (left+right)//2

            if nums[mid] > target:
                right = mid - 1
            elif nums[mid] < target:
                left = mid + 1
            else:
                # record that we have seen it &
                #  ignore everything to the left
                last_seen = mid
                left = mid + 1
        return last_seen

""" 

"""

class Solution00:
    def searchRange(self, nums, target):

        # # find target
        left = 0
        right = len(nums)-1
        while left <= right:
            mid = (left+right)//2

            if nums[mid] < target:
                left = mid + 1
            elif nums[mid] > target:
                right = mid - 1
            else:
                break

        mid = (left+right)//2
        if mid < 0 or mid >= len(nums) or nums[mid] != target:
            return [-1, -1]

        # # find start of range
        start_left = 0
        start_right = mid
        while start_left < start_right:

            start_mid = (start_left+start_right)//2
            # ensure start_right's value always == target,
            #   when start_left == start_right, that will be the leftmost value with a value of target
            if nums[start_mid] == target:
                start_right = start_mid
            else:
                start_left = start_mid + 1

        # # find end of range
        end_left = mid
        end_right = len(nums)-1
        while end_left <= end_right:
            # print(end_left, end_right)
            end_mid = (end_right+end_left)//2
            # ensure end_left's value always == target,
            #   when end_right == end_left, that will be the rightmost value with a value of target
            if nums[end_mid] == target:
                end_left = end_mid + 1
            else:
                end_right = end_mid - 1

        # #
        return [start_left, end_right]

"""
improvement of above, same time complexity
"""

class Solution:
    def searchRange(self, nums, target):

        # # find start of range
        start_left = 0
        start_right = len(nums)-1
        while start_left < start_right:

            start_mid = (start_left+start_right)//2

            # 1. place start_right in the target subarray
            if nums[start_mid] > target:
                start_right = start_mid
                continue

            # 2. ensure start_right's value always == target,
            #       when start_left == start_right, that will be the leftmost value with a value of target
            if nums[start_mid] == target:
                start_right = start_mid
            else:
                start_left = start_mid + 1

        # # find end of range
        end_left = 0
        end_right = len(nums)-1
        while end_left <= end_right:
            end_mid = (end_right+end_left)//2

            # 1. place end_left in the target subarray
            if nums[end_mid] < target:
                end_left = end_mid + 1
                continue

            # 2. find the first value not equal to target on the end_left pointer
            #       then move the end_right - 1 coz end_left will be +1 position ahead of the last correct value
            if nums[end_mid] == target:
                end_left = end_mid + 1
            else:
                end_right = end_mid - 1

        if end_right < 0 or start_left >= len(nums) or nums[start_left] != target or nums[end_right] != target:
            return [-1, -1]

        # #
        return [start_left, end_right]

Leftmost Column with at Least a One

Screenshot 2021-11-02 at 19.41.04.png

Screenshot 2021-11-02 at 19.44.33.png

Screenshot 2021-11-02 at 19.45.05.png

Screenshot 2021-11-02 at 19.45.26.png

Screen Recording 2021-11-02 at 19.43.05.mov

""" 
Leftmost Column with at Least a One:

A row-sorted binary matrix means that all elements are 0 or 1 and each row of the matrix is sorted in non-decreasing order.
Given a row-sorted binary matrix binaryMatrix, return the index (0-indexed) of the leftmost column with a 1 in it. If such an index does not exist, return -1.
You can't access the Binary Matrix directly. You may only access the matrix using a BinaryMatrix interface:
BinaryMatrix.get(row, col) returns the element of the matrix at index (row, col) (0-indexed).
BinaryMatrix.dimensions() returns the dimensions of the matrix as a list of 2 elements [rows, cols], which means the matrix is rows x cols.
Submissions making more than 1000 calls to BinaryMatrix.get will be judged Wrong Answer. 
Also, any solutions that attempt to circumvent the judge will result in disqualification.
For custom testing purposes, the input will be the entire binary matrix mat. You will not have access to the binary matrix directly.

Example 1:
    Input: mat = [[0,0],[1,1]]
    Output: 0
Example 2:
    Input: mat = [[0,0],[0,1]]
    Output: 1
Example 3:
    Input: mat = [[0,0],[0,0]]
    Output: -1
Example 4:
    Input: mat = [[0,0,0,1],[0,0,1,1],[0,1,1,1]]
    Output: 1

https://leetcode.com/problems/leftmost-column-with-at-least-a-one

Prerequisite:
- https://leetcode.com/problems/first-bad-version
"""

# This is BinaryMatrix's API interface.
# You should not implement it, or speculate about its implementation
class BinaryMatrix(object):
    def get(self, row: int, col: int): pass
    def dimensions(self): pass

""" 
Binary search every row: 
    Let N be the number of rows, and M be the number of columns.
    Time complexity : O(NlogM).

Start at the top right:
similar to Search In Sorted Matrix https://leetcode.com/problems/search-a-2d-matrix

Using the information that the rows are sorted, if we start searching from the right top corner(1st row, last column) and every time when we get a 1, as the row is sorted in non-decreasing order, there is a chance of getting 1 in the left column, so go to previous column in the same row. And if we get 0, there is no chance that in that row we can find a 1, so go to next row. 
"""

class Solution:
    def leftMostColumnWithOne(self, binaryMatrix: 'BinaryMatrix'):
        left_most = -1
        rows, cols = binaryMatrix.dimensions()

        row = 0
        col = cols-1
        while row < rows and col >= 0:
            # find left most at each row
            while col >= 0 and binaryMatrix.get(row, col) == 1:
                left_most = col
                col -= 1

            row += 1

        return left_most

BFS + DFS == 25% of the problems

Trees & Graphs

Articles:

Most graph, tree and string problems simply boil down to a DFS (Depth-first search) / BFS (Breadth-first search)

Have you ever wondered why we don’t use a queue for dfs or stack for bfs? questions like these really give us some insights into the difference between stacks and queues.

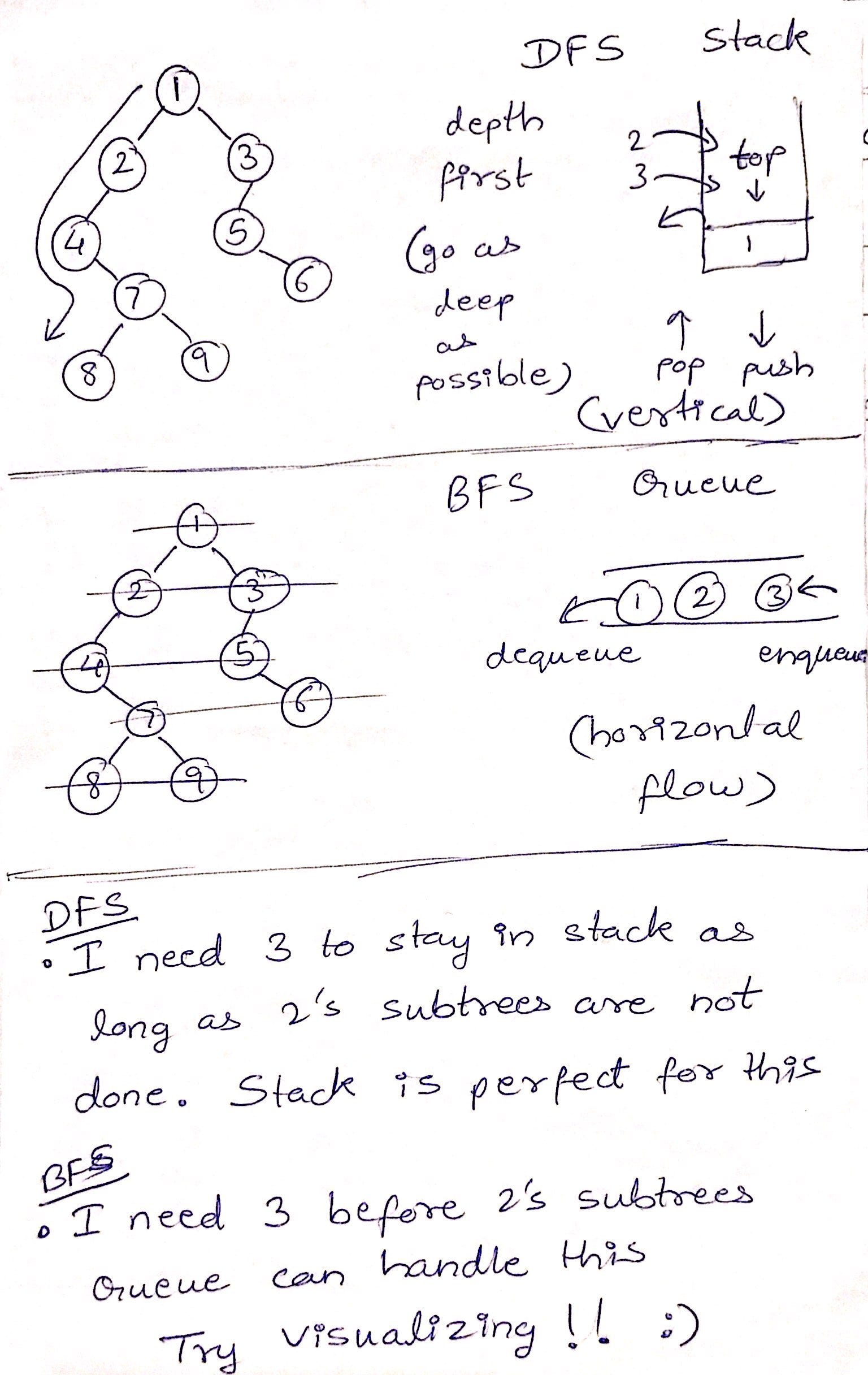
So using a stack I could pop 2 and push its kids and keep doing so eventually exhausting 2’s subtrees, 3 stays calmly in the stack just below the part where the real push-pop action is going, we pop 3 when all subtrees of 2 are done. This feature of the stack is essential for DFS.

While in a queue, I could dequeue 2 and enqueue its subtrees which go behind 3 as it was already sitting in the queue. So the next time I dequeue I get 3 and only after that do I move on to visiting 2’s subtrees, this is essentially a BFS!

For me this revelation was pure bliss. Take a moment to celebrate the history of Computer Science and the geniuses behind these simple yet powerful ideas.

Time Complexity

DFS:

Coding Patterns: Depth First Search (DFS)

DFS → diving as deep as possible before coming back to take a dive again: can use stack

Examples:

Course Schedule/Tasks Scheduling
Alien Dictionary

Basic DFS (use stack)

With recursion

class Node:
    def __init__(self, name):
        self.children = []
        self.name = name

    def depthFirstSearch(self, array):
        self._depthFirstSearchHelper(array)
        return array

    def _depthFirstSearchHelper(self, array):
        array.append(self.name)

        for child in self.children:
            child._depthFirstSearchHelper(array)

With stack

class Node:
    def __init__(self, name):
        self.children = []
        self.name = name

    def depthFirstSearch(self, array):
        stack = [self]

        while len(stack) > 0:
            curr = stack.pop()
            array.append(curr.name)
            for idx in reversed(range(len(curr.children))):
                stack.append(curr.children[idx])

        return array

DFS on graph

look carefully at C

DFS on an adjacency list

With Preorder Traversal

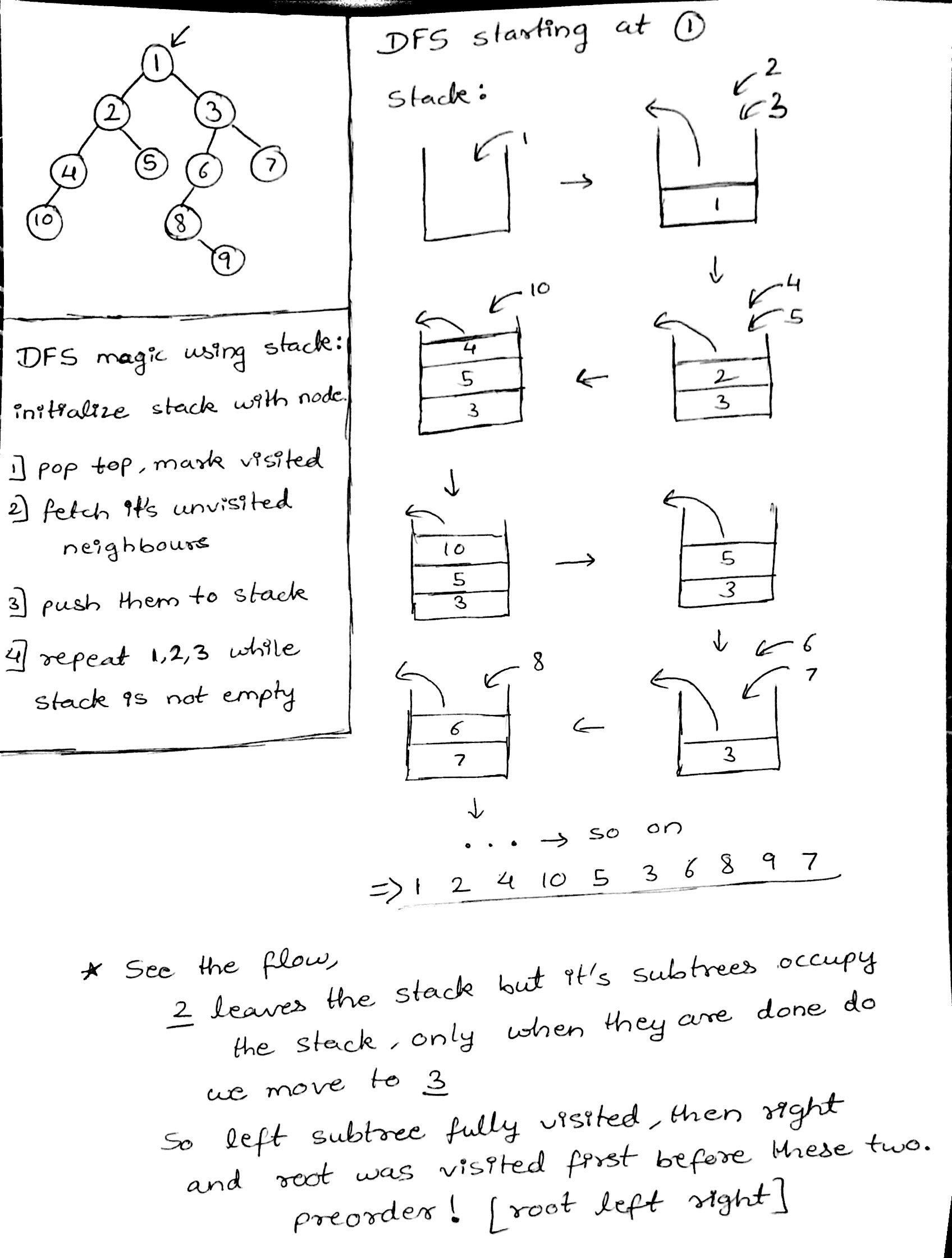
BFS:

Coding Patterns: Breadth First Search (BFS)

Breadth First Search Algorithm | Shortest Path | Graph Theory

Searching%20733ff84c808c4c9cb5c40787b2df7b98/Screenshot_2021-07-18_at_06.28.43.png

These are basically level order traversals.

BFS can be used to find a single-source shortest path in an unweighted graph because, in BFS, we reach a vertex with a minimum number of edges from a source vertex.

Thoughts on BFS:

Problems in which you have to find the shortest path are most likely calling for a BFS.
For graphs having unit edge distances, shortest paths from any point is just a BFS starting at that point, no need for Dijkstra’s algorithm.
Maze solving problems are mostly shortest path problems and every maze is just a fancy graph so you get the flow.

Examples

🌳 Prim's Minimum Spanning Tree Algorithm *

Rotting Oranges

Screenshot 2021-10-25 at 21.24.48.png

""" 
Rotting Oranges

You are given an m x n grid where each cell can have one of three values:
    0 representing an empty cell,
    1 representing a fresh orange, or
    2 representing a rotten orange.
Every minute, any fresh orange that is 4-directionally adjacent to a rotten orange becomes rotten.
Return the minimum number of minutes that must elapse until no cell has a fresh orange. If this is impossible, return -1.

Example 1:
    Input: grid = [[2,1,1],[1,1,0],[0,1,1]]
    Output: 4
Example 2:
    Input: grid = [[2,1,1],[0,1,1],[1,0,1]]
    Output: -1
    Explanation: The orange in the bottom left corner (row 2, column 0) is never rotten, because rotting only happens 4-directionally.
Example 3:
    Input: grid = [[0,2]]
    Output: 0
    Explanation: Since there are already no fresh oranges at minute 0, the answer is just 0.

https://leetcode.com/problems/rotting-oranges
"""

from typing import List
import collections

""" 
BFS
One of the most distinguished code patterns in BFS algorithms is that often we use a queue data structure to keep track of the candidates that we need to visit during the process.

The main algorithm is built around a loop iterating through the queue. At each iteration, we pop out an element from the head of the queue. 
Then we do some particular process with the popped element. More importantly, we then append neighbors of the popped element into the queue, to keep the BFS process running.

O(N) time | O(N) space
"""

class Solution:
    def orangesRotting(self, grid: List[List[int]]):
        minutes_needed = 0

        rotten = collections.deque()

        # # scan the grid to find the initial values for the queue
        for row in range(len(grid)):
            for col in range(len(grid[0])):
                if grid[row][col] == 2:
                    rotten.append((row, col))

        # # run the BFS process on the queue,
        while rotten:
            found_fresh = False

            # empty rotten queue
            for _ in range(len(rotten)):
                rotten_row, rotten_col = rotten.popleft()
                for row, col in self.get_neighbours(grid, rotten_row, rotten_col):
                    # if fresh
                    if grid[row][col] == 1:
                        grid[row][col] = 2
                        rotten.append((row, col))
                        found_fresh = True

            if found_fresh:
                minutes_needed += 1

        for row in range(len(grid)):
            for col in range(len(grid[0])):
                if grid[row][col] == 1:
                    return -1

        return minutes_needed

    def get_neighbours(self, grid, row, col):
        neighbours = []
        if row-1 >= 0:
            neighbours.append((row-1, col))
        if row+1 < len(grid):
            neighbours.append((row+1, col))
        if col-1 >= 0:
            neighbours.append((row, col-1))
        if col+1 < len(grid[0]):
            neighbours.append((row, col+1))
        return neighbours

Word Search

"""
Word Search

Given a 2D board and a word, find if the word exists in the grid.
The word can be constructed from letters of sequentially adjacent cells,
where "adjacent" cells are horizontally or vertically neighboring.
The same letter cell may not be used more than once.

Constraints:
    board and word consists only of lowercase and uppercase English letters.
    1 <= board.length <= 200
    1 <= board[i].length <= 200
    1 <= word.length <= 10^3

https://leetcode.com/problems/word-search/submissions/
"""

from typing import List

# O(n) time | O(n) space -> because of the recursion call stack |
class Solution:
    def exist(self, board: List[List[str]], word: str):

        # Iterate over each character
        h = 0
        while h < len(board):
            w = 0
            while w < len(board[0]):
                # stop iteration if we find the word
                if board[h][w] == word[0] and self.searchWordOutward(board, word, h, w, 0):
                    return True
                w += 1
            h += 1

        return False

    def searchWordOutward(self, board, word, h, w, word_pos):
        # check if past end of word (found all characters)
        if word_pos >= len(word):
            return True

        if h < 0 or h >= len(board) or \
                w < 0 or w >= len(board[0]):
            return False

        if board[h][w] != word[word_pos]:
            return False

        # remove seen character
        seen_char = board[h][w]
        board[h][w] = ''

        # Expand: move on to next character (word_pos + 1) -> in the order right, left, top, bottom
        found = self.searchWordOutward(board, word, h, w+1, word_pos+1) or \
            self.searchWordOutward(board, word, h, w-1, word_pos+1) or \
            self.searchWordOutward(board, word, h+1, w, word_pos+1) or \
            self.searchWordOutward(board, word, h-1, w, word_pos+1)

        # return seen character
        board[h][w] = seen_char

        return found

"""
Input:
    [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]]
    "ABCCED"
    [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]]
    "SEE"
    [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]]
    "ABCB"
Output:
    true
    true
    false
"""

https://leetcode.com/problems/shortest-path-in-a-grid-with-obstacles-elimination/

Coding Interview Problem - Shortest Path With Obstacle Elimination

Leetcode - Shortest Path in a Grid with Obstacles Elimination (Python)

Basic BFS (uses queue)

With queue

class Node:
    def __init__(self, name):
        self.children = []
        self.name = name

    def breadthFirstSearch(self, array):
        queue = [self]
        while len(queue) > 0:
            curr = queue.pop(0)
            array.append(curr.name)
            for child in curr.children:
                queue.append(child)
        return array

With Level order traversal:

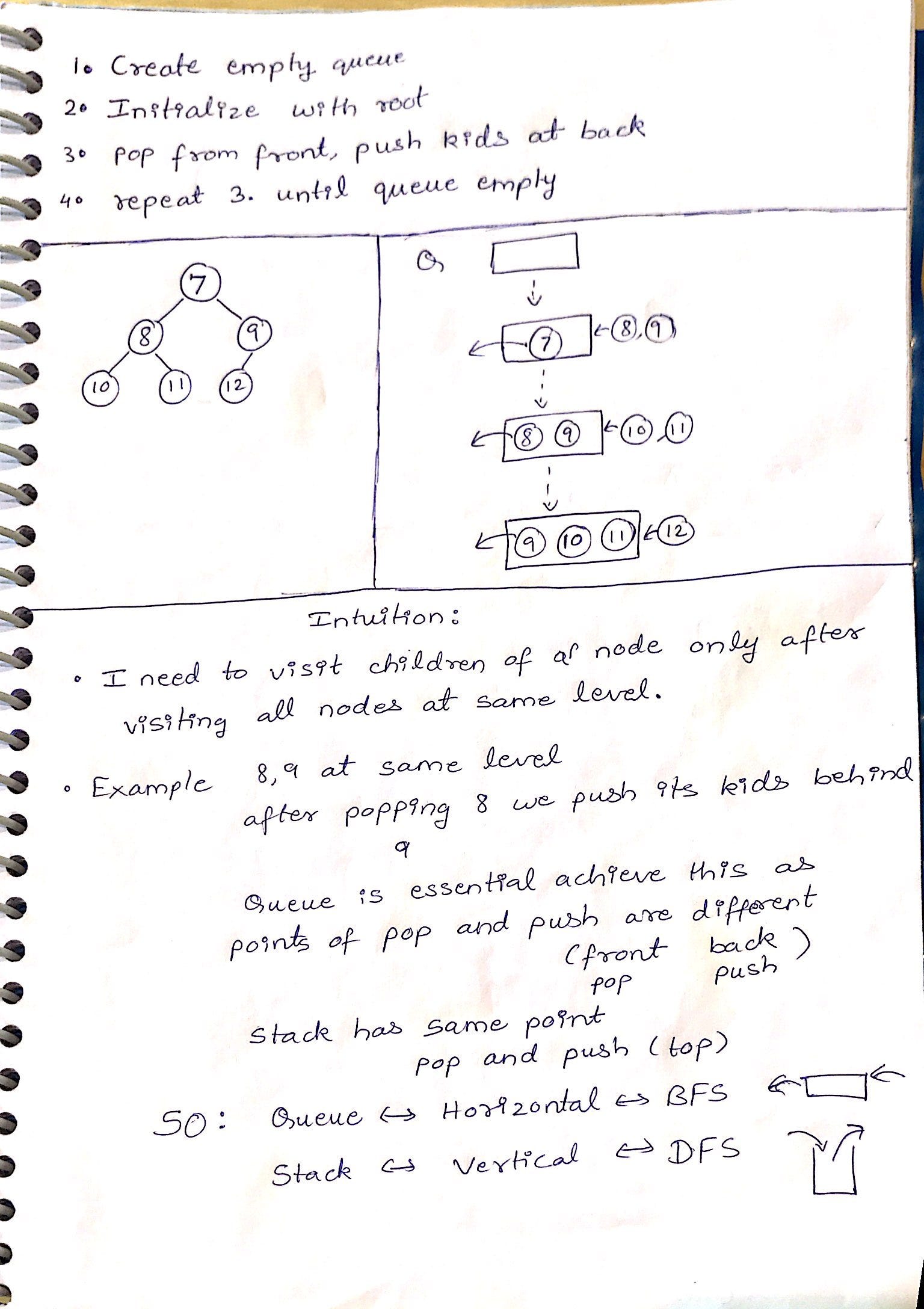
Bidirectional Search *

Bidirectional search is used to find the shortest path between a source and destination node. It operates by essentially running two simultaneous breadth-first searches, one from each node. When their searches collide, we have found a path.

Screenshot 2021-10-06 at 18.26.53.png

Screenshot 2021-10-06 at 18.27.37.png

BFS vs Dijkstra's?

Both are used to find the shortest path

Dijkstra's is only used on positively weighted graphs

Quick Select (used to select index)

Based on Quick Sort. The QuickSort sorting algorithm works by picking a "pivot" number from an array, positioning every other number in the array in sorted order with respect to the pivot (all smaller numbers to the pivot's left; all bigger numbers to the pivot's right), and then repeating the same two steps on both sides of the pivot until the entire array is sorted. Apply the technique used in Quick Sort until the pivot element gets positioned in the kth place in the array, at which point you'll have found the answer to the problem.

Quicksort

Pick a random number from the input array (the first number, for instance) and let that number be the pivot. Iterate through the rest of the array using two pointers, one starting at the left extremity of the array and progressively moving to the right, and the other one starting at the right extremity of the array and progressively moving to the left.

As you iterate through the array, compare the left and right pointer numbers to the pivot. If the left number is greater than the pivot and the right number is less than the pivot, swap them; this will effectively sort these numbers with respect to the pivot at the end of the iteration. If the left number is ever less than or equal to the pivot, increment the left pointer; similarly, if the right number is ever greater than or equal to the pivot, decrement the right pointer. Do this until the pointers pass each other, at which point swapping the pivot with the right number should position the pivot in its final, sorted position, where every number to its left is smaller and every number to its right is greater.

If the pivot is in the kth position, you're done; if it isn't, figure out if the kth smallest number is located to the left or to the right of the pivot.

Repeat the process on the side of the kth smallest number, and keep on repeating the process thereafter until you find the answer.

Time Complexity

"""
Best: O(n) time | O(1) space - where n is the length of the input array 
Average: O(n) time | O(1) space
Worst: O(n^2) time | O(1) space
"""

""" 
Quick Select:

Pick a random number from the input array (the first number, for instance) and let that number be the pivot. 
Iterate through the rest of the array using two pointers, one starting at the left extremity of the array and progressively moving to the right, 
    and the other one starting at the right extremity of the array and progressively moving to the left. 
As you iterate through the array, compare the left and right pointer numbers to the pivot. 
If the left number is greater than the pivot and the right number is less than the pivot, swap them; this will effectively sort these numbers with respect to the pivot at the end of the iteration. 
If the left number is ever less than or equal to the pivot, increment the left pointer; similarly, if the right number is ever greater than or equal to the pivot, decrement the right pointer. 
Do this until the pointers pass each other, at which point swapping the pivot with the right number should position the pivot in its final, sorted position, 
    where every number to its left is smaller and every number to its right is greater.

If the pivot is in the kth position, you're done; if it isn't, figure out if the kth smallest number is located to the left or to the right of the pivot.
Repeat the process on the side of the kth smallest number, and keep on repeating the process thereafter until you find the answer.

https://www.algoexpert.io/questions/Quickselect
https://leetcode.com/problems/kth-largest-element-in-an-array
"""

def quickselect(array, k):
    return quick_select_helper(array, k-1, 0, len(array)-1)

def quick_select_helper(array, idx, start, end):
    if start == end:
        return array[start]

    pivot = start
    # # sort numbers with respect to pivot then put pivot between the large and small numbers
    #   left and right to stop at a place where: left >= pivot & right <= pivot
    left = pivot+1
    right = end
    while left <= right:
        # can be swapped
        if array[left] > array[pivot] and array[right] < array[pivot]:
            array[left], array[right] = array[right], array[left]

        if array[left] <= array[pivot]:  # no need to swap
            left += 1
        if array[right] >= array[pivot]:  # no need to swap
            right -= 1

    # # place the pivot at correct position (right)
    # # place pivot at correct position
    # we know that once the sorting is done, the number at left >= pivot & right <= pivot
    #   smaller values go to the left of array[pivot]
    array[pivot], array[right] = array[right], array[pivot]
    if right == idx:
        return array[right]

    # # proceed search
    if idx < right:
        return quick_select_helper(array, idx, start, right-1)
    else:
        return quick_select_helper(array, idx, right+1, end)

Examples

Kth Largest Element in an Array

""" 
Kth Largest Element in an Array

Given an integer array nums and an integer k, return the kth largest element in the array.
Note that it is the kth largest element in the sorted order, not the kth distinct element.

Example 1:
Input: nums = [3,2,1,5,6,4], k = 2
Output: 5
Example 2:
Input: nums = [3,2,3,1,2,4,5,5,6], k = 4
Output: 4

https://leetcode.com/problems/kth-largest-element-in-an-array
"""

class Solution:
    def findKthLargest(self, array, k):
        return self.quick_select(array, len(array)-k, 0, len(array)-1)

    def quick_select(self, array, idx, start, end):
        if start == end:
            return array[start]

        # # pick pivot and sort numbers relative to it (like quick sort)
        pivot = start
        # # sort numbers with respect to pivot then put pivot between the large and small numbers
        #   left and right to stop at a place where: left >= pivot & right <= pivot
        left = start + 1
        right = end
        while left <= right:
            # check if can be swapped
            if array[left] > array[pivot] and array[right] < array[pivot]:
                array[left], array[right] = array[right], array[left]

            if array[left] <= array[pivot]:  # no need to swap
                left += 1
            if array[right] >= array[pivot]:  # no need to swap
                right -= 1

        # place pivot at correct position
        # # place the pivot at correct position (right)
        # # place pivot at correct position
        # we know that once the sorting is done, the number at left >= pivot & right <= pivot
        #   smaller values go to the left of array[pivot]
        # # right is at a value < pivot, so ot should be moved left
        array[pivot], array[right] = array[right], array[pivot]

        # after swapping right is the only number we are sure is sorted
        # check if we are at the idx being looked for
        if right == idx:
            return array[right]

        # # proceed search
        elif right < idx:
            return self.quick_select(array, idx, right+1, end)
        else:
            return self.quick_select(array, idx, start, right-1)

x = Solution()
x.findKthLargest([5, 6, 4], 2)

Sorting

Sorting Algorithms with Animations

Sorting Algorithms (Selection Sort, Bubble Sort, Merge Sort, and Quicksort)

Selection Sort, Bubble Sort, and Insertion Sort - Algorithms for Coding Interviews in Python

Sorting is any process of arranging items systematically. In computer science, sorting algorithms put elements of a list in a certain order.

Sorting%20c597de5051f1415793ddcf72086aa93d/Untitled.png

Examples

Dutch National Flag Problem

Analyze User Website Visit Pattern *

""" 
1152. Analyze User Website Visit Pattern

You are given two string arrays username and website and an integer array timestamp.
All the given arrays are of the same length and the tuple [username[i], website[i], timestamp[i]] indicates that the user username[i] visited the website website[i] at time timestamp[i].
A pattern is a list of three websites (not necessarily distinct).
    For example, ["home", "away", "love"], ["leetcode", "love", "leetcode"], and ["luffy", "luffy", "luffy"] are all patterns.
The score of a pattern is the number of users that visited all the websites in the pattern in the same order they appeared in the pattern.
    For example, if the pattern is ["home", "away", "love"], the score is the number of users x such that x visited "home" then visited "away" and visited "love" after that.
    Similarly, if the pattern is ["leetcode", "love", "leetcode"], the score is the number of users x such that x visited "leetcode" then visited "love" and visited "leetcode" one more time after that.
    Also, if the pattern is ["luffy", "luffy", "luffy"], the score is the number of users x such that x visited "luffy" three different times at different timestamps.
Return the pattern with the largest score. If there is more than one pattern with the same largest score, return the lexicographically smallest such pattern

Example 1:
    Input: username = ["joe","joe","joe","james","james","james","james","mary","mary","mary"], timestamp = [1,2,3,4,5,6,7,8,9,10], website = ["home","about","career","home","cart","maps","home","home","about","career"]
    Output: ["home","about","career"]
    Explanation: The tuples in this example are:
        ["joe","home",1],["joe","about",2],["joe","career",3],["james","home",4],["james","cart",5],["james","maps",6],["james","home",7],["mary","home",8],["mary","about",9], and ["mary","career",10].
        The pattern ("home", "about", "career") has score 2 (joe and mary).
        The pattern ("home", "cart", "maps") has score 1 (james).
        The pattern ("home", "cart", "home") has score 1 (james).
        The pattern ("home", "maps", "home") has score 1 (james).
        The pattern ("cart", "maps", "home") has score 1 (james).
        The pattern ("home", "home", "home") has score 0 (no user visited home 3 times).
Example 2:
    Input: username = ["ua","ua","ua","ub","ub","ub"], timestamp = [1,2,3,4,5,6], website = ["a","b","a","a","b","c"]
    Output: ["a","b","a"]

Constraints:
    3 <= username.length <= 50
    1 <= username[i].length <= 10
    timestamp.length == username.length
    1 <= timestamp[i] <= 109
    website.length == username.length
    1 <= website[i].length <= 10
    username[i] and website[i] consist of lowercase English letters.
    It is guaranteed that there is at least one user who visited at least three websites.
    All the tuples [username[i], timestamp[i], website[i]] are unique.

https://leetcode.com/problems/analyze-user-website-visit-patterns
"""

from collections import defaultdict
from typing import List

class Pattern:
    def __init__(self, count, websites):
        self.count = count
        self.websites = list(websites)

    def __gt__(self, other):
        if self.count == other.count:
            return self.websites < other.websites
        return self.count > other.count

    def __str__(self):
        return f"{self.count} {self.websites}"

class Solution:
    def mostVisitedPattern(self, username: List[str], timestamp: List[int], website: List[str]):
        """ 
        - store website visit order for each user in a dictionary
        - have a pattern counter
        - generate all patterns (combinations of size 3) for each user and increment their count in the pattern counter
        - return the pattern with the highest count
        """
        username = self.sort_by_timestamp(timestamp, username)
        website = self.sort_by_timestamp(timestamp,  website)

        user_visits = defaultdict(list)
        for idx in range(len(username)):
            user_visits[username[idx]].append(website[idx])

        pattern_counter = defaultdict(int)

        for websites in user_visits.values():
            for combination in self.generate_combinations_size_3(websites):
                pattern_counter[combination] += 1

        pattern_counter_arr = [Pattern(value, key)
                               for key, value in pattern_counter.items()]

        return max(pattern_counter_arr).websites

    def generate_combinations_size_3(self, arr):
        patterns = set()
        for idx_1 in range(len(arr)-2):
            for idx_2 in range(idx_1+1, len(arr)-1):
                for idx_3 in range(idx_2+1, len(arr)):
                    patterns.add((arr[idx_1], arr[idx_2], arr[idx_3]))
        return patterns
        # alternative
        # return (set(combinations(arr, 3)))

    def sort_by_timestamp(self, timestamp, arr):
        # get indexes
        arr_idxs = [[idx, val] for idx, val in enumerate(arr)]
        # sort by position in timestamp
        arr_idxs.sort(key=lambda x: timestamp[x[0]])
        # return sorted arr
        return [item for _, item in arr_idxs]

Sort big file
Peaks and Valleys
https://leetcode.com/problems/sort-list/solution/

Queue Reconstruction by Height *

Screenshot 2021-11-10 at 10.58.54.png

""" 
406. Queue Reconstruction by Height

You are given an array of people, people, which are the attributes of some people in a queue (not necessarily in order). 
Each people[i] = [hi, ki] represents the ith person of height hi with exactly ki other people in front who have a height greater than or equal to hi.
Reconstruct and return the queue that is represented by the input array people. 
The returned queue should be formatted as an array queue, where queue[j] = [hj, kj] is the attributes of the jth person in the queue (queue[0] is the person at the front of the queue).

Example 1:
    Input: people = [[7,0],[4,4],[7,1],[5,0],[6,1],[5,2]]
    Output: [[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]]
    Explanation:
    Person 0 has height 5 with no other people taller or the same height in front.
    Person 1 has height 7 with no other people taller or the same height in front.
    Person 2 has height 5 with two persons taller or the same height in front, which is person 0 and 1.
    Person 3 has height 6 with one person taller or the same height in front, which is person 1.
    Person 4 has height 4 with four people taller or the same height in front, which are people 0, 1, 2, and 3.
    Person 5 has height 7 with one person taller or the same height in front, which is person 1.
    Hence [[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]] is the reconstructed queue.
Example 2:
    Input: people = [[6,0],[5,0],[4,0],[3,2],[2,2],[1,4]]
    Output: [[4,0],[5,0],[2,2],[3,2],[1,4],[6,0]]


Constraints:
    1 <= people.length <= 2000
    0 <= hi <= 106
    0 <= ki < people.length
    It is guaranteed that the queue can be reconstructed.

https://leetcode.com/problems/queue-reconstruction-by-height
"""

from typing import List
"""
https://www.notion.so/paulonteri/Sorting-c597de5051f1415793ddcf72086aa93d#228cc55cb27b4f08a9d7ffdbb64a2d32
[[1, 4], [2, 2], [3, 2], [4, 0], [5, 0], [6, 0]]
[[4, 0], [5, 0], [2, 2], [3, 2], [1, 4], [6, 0]]

[[1, 4], [2, 2], [3, 2], [4, 0], [5, 0], [6, 0]]
[0,       1,      2,      3,      4,      5]
                                 [1,4] skip 4 free positions
                 [2, 2], skip 2 free positions
                         [3, 2], skip 2 free positions
 [4, 0], skip 0 free positions
         [5, 0], skip 0 free positions
                                        [6, 0], skip 0 free positions

Similar solutions:
- https://leetcode.com/problems/queue-reconstruction-by-height/discuss/89407/Python-Documented-solution-in-O(n*n)-time-that-is-easy-to-understand
- https://leetcode.com/problems/queue-reconstruction-by-height/discuss/167308/Python-solution

"""

class Solution:

    def reconstructQueue(self, people: List[List[int]]):
        """ 
        Sort by height then,
        push the shorter people to be after taller/same height ones depending on their position
        """
        # edge cases
        if not people:
            return people

        # -pos to ensure that people with the same hight but different positions are dealt with
        # example; dealing with such -> [[7,0],[7,1]]
        sorted_people = [[height, -pos] for height, pos in people]
        sorted_people.sort()

        queue = [None]*len(people)
        for height, neg_pos in sorted_people:
            self.place_in_queue(queue, height, neg_pos)

        return queue

    def place_in_queue(self, queue, height, neg_pos):
        """
        Place person in the first valid position
        - position must not be occupied
        - position is got by skipping -neg_pos times
        """
        skips = -neg_pos
        for idx, item in enumerate(queue):
            if item is not None:
                continue
            if skips == 0:
                queue[idx] = [height, -neg_pos]
                return

            skips -= 1

Rank from stream

Common operations

`sort()` parameters (key & reverse)

The syntax of the sort() method is:

list.sort(key=..., reverse=...)

key

list.sort(key=len)
sorted(list, key=len)

# take second element for sort
def takeSecond(elem):
    return elem[1]

# random list
random = [(2, 2), (3, 4), (4, 1), (1, 3)]

# sort list with key
random.sort(key=takeSecond)

# print list
print('Sorted list:', random)
# Sorted list: [(4, 1), (2, 2), (1, 3), (3, 4)]

Examples:

Merge Intervals

Sort dictionary

Bubble Sort

Bubble Sort Tutorials & Notes | Algorithms | HackerEarth

Bubble sort in 2 minutes

Traverse the input array, swapping any two numbers that are out of order and keeping track if you make any swap. Once you arrive at the end of the array, check if you have made any swaps; if not, the array is sorted and you are done; otherwise, repeat the steps laid out in this hint until the array is sorted.

# Best: O(n) time | O(1) space -> if already sorted
# Average: O(n^2) time | O(1) space
# Worst: O(n^2) time | O(1) space
def bubbleSort(array):
    if len(array) < 2:
        return array

    is_sorted = False
    while not is_sorted:
        is_sorted = True

        for i in range(len(array)-1):
            if array[i] > array[i+1]:
                is_sorted = False
                # swap
                array[i], array[i+1] = array[i+1], array[i]

    return array

Insertion Sort

Examples

Layman explanation

Have to subarrays (in place):

Take an element from the second and insert it to the first.
Sort the first using something similar to Bubble sort.

Note: seeing the code makes it way easier to understand it

Insertion Sort in Action

Divide the input array into two subarrays in place. - The first subarray should be sorted at all times and should start with a length of 1, while the second subarray should be unsorted. Iterate through the unsorted subarray, inserting all of its elements into the sorted subarray - in the correct position by swapping them into place. Eventually, the entire array will be sorted. Has like a slow bubble sort (for the sorted array).

Explanation for the code: Start with a 'sorted array' of size one at index 0. Insert the element to the right of the sorted array to the sorted array and swap it with other elements till it reaches a balanced position repeat the steps above till you reach the end of the array

# Best: O(n) time | O(1) space -> if already sorted
# Average: O(n^2) time | O(1) space
# Worst: O(n^2) time | O(1) space
def insertionSort(array):

    for i in range(1, len(array)):

        # # insert a new element(array[i]) to the `sorted array`
        # the sorted array will now end at i
        added = i
        while added > 0 and array[added] < array[added-1]:
            # swap
            array[added], array[added-1] = array[added-1], array[added]
            added -= 1

    return array

Selection Sort

Divide the input array into two subarrays in place. The first subarray should be sorted at all times and should start with a length of 0, while the second subarray should be unsorted. Select the smallest (or largest) element in the unsorted subarray and insert it into the sorted subarray with a swap. Repeat this process of finding the smallest (or largest) element in the unsorted subarray and inserting it in its correct position in the sorted subarray with a swap until the entire array is sorted.

Sorting%20c597de5051f1415793ddcf72086aa93d/1_5WXRN62ddiM_Gcf4GDdCZg.gif

# Best: O(n^2) time | O(1) space
# Average: O(n^2) time | O(1) space
# Worst: O(n^2) time | O(1) space
def selectionSort(array):

    # select the smallest element and place it at i
    for i in range(len(array)-1):

        smallest = i
        for idx in range(i+1, len(array)):
            if array[smallest] > array[idx]:
                smallest = idx

        # swap
        array[i], array[smallest] = array[smallest], array[i]

    return array

Merge Sort?

Merge sort is a recursive divide & conquer algorithm that essentially divides a given list into two halves, sorts those halves, and merges them in order. The base case is to merge two lists of size 1 so, eventually, single elements are merged in order; the merge part is where most of the heavy lifting happens.

The time complexity of merge sort is nlog(n).

A recursive merge sort algorithm used to sort an array of 7 integer values.

Sorting%20c597de5051f1415793ddcf72086aa93d/Merge-sort-example-300px.gif

Quick sort

AlgoExpert | Ace the Coding Interviews

Quick sort is the fastest-known, comparison-based sorting algorithm for lists in the average case.It is an algorithm of Divide & Conquer type.

It has 3 steps:

We first select an element which we will call the pivot from the array.
Move all elements that are smaller than the pivot to the left of the pivot; move all elements that are larger than the pivot to the right of the pivot. This is called the partition operation.
Recursively apply the above 2 steps separately to each of the sub-arrays of elements with smaller and bigger values than the last pivot.

Sorting%20c597de5051f1415793ddcf72086aa93d/1_MqYi387Jyd16H2GHWyn46Q.gif

Quick Sort works by picking a "pivot" number from an array, positioning every other number in the array in sorted order with respect to the pivot (all smaller numbers to the pivot's left; all bigger numbers to the pivot's right), and then repeating the same two steps on both sides of the pivot until the entire array is sorted.

Pick a random number from the input array (the first number, for instance) and let that number be the pivot. Iterate through the rest of the array using two pointers, one starting at the left extremity of the array and progressively moving to the right, and the other one starting at the right extremity of the array and progressively moving to the left. As you iterate through the array, compare the left and right pointer numbers to the pivot. If the left number is greater than the pivot and the right number is less than the pivot, swap them; this will effectively sort these numbers with respect to the pivot at the end of the iteration. If the left number is ever less than or equal to the pivot, increment the left pointer; similarly, if the right number is ever greater than or equal to the pivot, decrement the right pointer. Do this until the pointers pass each other, at which point swapping the pivot with the right number should position the pivot in its final, sorted position, where every number to its left is smaller and every number to its right is greater.

Repeat the process mentioned on the respective subarrays located to the left and right of your pivot, and keep on repeating the process thereafter until the input array is fully sorted.

""" 
Quick Sort:

Quick Sort works by picking a "pivot" number from an array, positioning every other number in the array in sorted order with respect to the pivot (all smaller numbers to the pivot's left; 
all bigger numbers to the pivot's right), and then repeating the same two steps on both sides of the pivot until the entire array is sorted.

Pick a random number from the input array (the first number, for instance) and let that number be the pivot. 
Iterate through the rest of the array using two pointers, one starting at the left extremity of the array and progressively moving to the right, 
and the other one starting at the right extremity of the array and progressively moving to the left. 
As you iterate through the array, compare the left and right pointer numbers to the pivot. 
    If the left number is greater than the pivot and the right number is less than the pivot, swap them; this will effectively sort these numbers with respect to the pivot at the end of the iteration. 
    If the left number is ever less than or equal to the pivot, increment the left pointer; 
    similarly, if the right number is ever greater than or equal to the pivot, decrement the right pointer. 
Do this until the pointers pass each other, at which point swapping the pivot with the right number should position the pivot in its final,
 sorted position, where every number to its left is smaller and every number to its right is greater.

Repeat the process mentioned on the respective subarrays located to the left and right of your pivot, and keep on repeating the process thereafter until the input array is fully sorted.
"""

# Average: O(nlog(n)) time | O(log(n)) space
# Worst: O(n^2) time | O(log(n)) space
def quickSort(array):
    quick_sort_helper(array, 0, len(array)-1)
    return array

def quick_sort_helper(array, start, end):
    if start >= end:
        return

    pivot = start
    # # position every number in the array in sorted order with respect to the array[pivot]
    #   left and right to stop at a place where: left >= pivot & right <= pivot
    left = start + 1
    right = end
    while left <= right:
        # # check if can swap
        if array[left] > array[pivot] and array[right] < array[pivot]:
            array[left], array[right] = array[right], array[left]

        # # cannot swap
        elif array[left] <= array[pivot]:  # wait to be swapped
            left += 1
        else:  # if array[right] >= array[pivot]:  # wait to be swapped
            right -= 1

    # # place pivot at correct position
    # we know that once the sorting is done, the number at left >= pivot & right <= pivot
    #   smaller values go to the left of array[pivot]
    array[pivot], array[right] = array[right], array[pivot]

    # # sort to the left & right of array[pivot]
    if (right-1 - start) < (end - right+1):
        quick_sort_helper(array, start, right-1)
        quick_sort_helper(array, right+1, end)
    else:
        quick_sort_helper(array, right+1, end)
        quick_sort_helper(array, start, right-1)

Quick Select

Heap Sort?

Heap sort in 4 minutes

Sorting Algorithms with Animations

Heap sort is the improved version of the Selection sort, which takes advantage of a heap data structure rather than a linear-time search to find the max value item. Using the heap, finding the next largest element takes O(log(n)) time, instead of O(n) for a linear scan as in simple selection sort. This allows heap sort to run in O(n log(n)) time, and this is also the worst case complexity.

Sorting%20c597de5051f1415793ddcf72086aa93d/7073C729230E1A2C3C3C9207B25F6B43.gif

Radix Sort ?

Topological sort

Stacks & Queues

Stacks and Queues

Stacks

Stack data structure playlist

Stacks%20&%20Queues%20c7d2cad790be4a61bac42c8718e031fd/Isaac_Computer_Science_2_Data_Structures_Project_OUTLINE_V6_23.png

Stack is a linear data structure that follows a particular order in which the operations are performed. The order may be LIFO(Last In First Out).

Mainly the following three basic operations are performed in the stack:

.push(): Adds an item in the stack. If the stack is full, then it is said to be an Overflow condition.
.pop(): Removes an item from the stack. The items are popped in the reversed order in which they are pushed. If the stack is empty, then it is said to be an Underflow condition.
.peek(): Returns top element of stack.
**.is_empty():** Returns true if stack is empty, else false.

Often implemented as a linked list to give the above operations a time complexity of O(1)

The last-in, first-out semantics of a stack makes it very useful for creating reverse iterators for sequences that are stored in a way that would make it difficult or impossible to step back from a given element.

Some of the problems require you to implement your own stack class; for others, use the built-in list-type.

s.append(e) pushes an element onto the stack. Not much can go wrong with a call to push.
s[-1] will retrieve but does not remove, the element at the top of the stack.
s.pop(0) will remove and return the element at the top of the stack.
len(s) == 0 tests if the stack is empty.

Examples

DFS

Min Max Stack Construction

"""
Min Max Stack Construction:

Write a MinMaxStack class for a Min Max Stack. The class should support:
Pushing and popping values on and off the stack.
Peeking at the value at the top of the stack.
Getting both the minimum and the maximum values in the stack at any given point in time.
All class methods, when considered independently, should run in constant time and with constant space.

Sample Usage:
    // All operations below are performed sequentially.
    MinMaxStack(): - // instantiate a MinMaxStack
    push(5): -
    getMin(): 5
    getMax(): 5
    peek(): 5
    push(7): -
    getMin(): 5
    getMax(): 7
    peek(): 7
    push(2): -
    getMin(): 2
    getMax(): 7
    peek(): 2
    pop(): 2
    pop(): 7
    getMin(): 5
    getMax(): 5
    peek(): 5

https://www.algoexpert.io/questions/Min%20Max%20Stack%20Construction
"""

# all of the following will be called at valid times
class MinMaxStack:
    def __init__(self):
        self.store = []
        # stores our min & max for every value in the stack
        self.min_max_store = []

    def peek(self):
        return self.store[-1]

    def pop(self):
        self.min_max_store.pop()
        return self.store.pop()

    def push(self, number):
        self.store.append(number)

        # store the current max & min
        max_value = number
        min_value = number
        if len(self.min_max_store) > 0:
            max_value = max(number, self.getMax())
            min_value = min(number, self.getMin())
        self.min_max_store.append({
            "max": max_value,
            "min": min_value
        })

    def getMin(self):
        return self.min_max_store[-1]['min']

    def getMax(self):
        return self.min_max_store[-1]['max']

Screenshot 2021-11-09 at 11.46.34.png

Decode String *

Screenshot 2021-11-09 at 11.43.27.png

Similar to what we have done

Screenshot 2021-11-09 at 11.44.53.png

Screenshot 2021-11-09 at 11.46.44.png

"""
Decode String

Given an encoded string, return its decoded string.
The encoding rule is: k[encoded_string], where the encoded_string inside the square brackets is being repeated exactly k times. 
Note that k is guaranteed to be a positive integer.
You may assume that the input string is always valid; No extra white spaces, square brackets are well-formed, etc.
Furthermore, you may assume that the original data does not contain any digits and that digits are only for those repeat numbers, k.
For example, there won't be input like 3a or 2[4].

https://leetcode.com/problems/decode-string/
"""

# O(n) time | O(n) space
class Solution:
    def decodeString(self, s: str):

        if not s:
            return s

        # before we enter a bracket we store the current word in the prev_multiplier_stack,
        # so as to work on what is in the bracket only first, then
        #  we will restore it to ast it was after the closing bracket,
        #  and add the decoded content(decoded from in the brackets)
        prev_multiplier_stack = []  # add multipliers
        prev_str_stack = []

        current_str = ''

        i = 0
        while i < len(s):
            char = s[i]

            # handle multipliers
            if char.isnumeric():
                # can be one didgit or many:
                # Eg: '384[fsgs]asa'
                num = ''
                while s[i].isnumeric():
                    num += s[i]
                    i += 1
                # store it for easy retrieval
                prev_multiplier_stack.append(int(num))

            # open brackets
            elif char == "[":
                # # we prepare to deal with what is in the brackets first
                # store the current_str in the prev_str_stack
                # will be undone once we hit a closing bracket
                prev_str_stack.append(current_str)
                current_str = ''  # we will now only deal with stuff that is in the brackets []
                i += 1

            # close brackets
            elif char == "]":
                # # leave bracket finally
                # # decode then, return current_string as it was + decoded_chars
                # get the prev(most recently added) multiplier
                multiplier = prev_multiplier_stack.pop()
                # decode
                decoded_chars = current_str * multiplier
                # return current_string as it was, + decoded_chars
                current_str = prev_str_stack.pop() + decoded_chars
                i += 1
                #
                # ignore
                # # made this faster
                # while multiplier > 0:
                #     decoded_chars += current_str
                #     multiplier -= 1
                #
                # # made this faster again
                # decoded_chars = []
                # while multiplier > 0:
                #     decoded_chars.append(current_str)
                #     multiplier -= 1
                # return current_string as it was, + decoded_chars
                # current_str = prev_str_stack.pop() + "".join(decoded_chars)

            # other characters
            else:
                current_str += char
                i += 1

        return current_str

"""
Input:
    "3[a]2[bc]"
    "3[a2[c2[abc]3[cd]ef]]"
    "abc3[cd]xyz"
Output:
    "aaabcbc"
    "acabcabccdcdcdefcabcabccdcdcdefacabcabccdcdcdefcabcabccdcdcdefacabcabccdcdcdefcabcabccdcdcdef"
    "abccdcdcdxyz"
"""

class Solution00:
    def decodeString(self, s: str):
        res = ""

        multiplier_stack = []
        string_stack = []

        i = 0
        curr_string = ""
        while i < len(s):

            # handle numbers
            if s[i].isnumeric():
                curr_num = ""
                while s[i].isnumeric():
                    curr_num += s[i]
                    i += 1

                multiplier_stack.append(int(curr_num))
                continue

            # handle opening brackets
            elif s[i] == "[":
                # # go into bracket
                string_stack.append(curr_string)
                curr_string = ""

            # handle closing brackets
            elif s[i] == "]":
                # # get out of bracket
                # multiply
                prev_multiplier = multiplier_stack.pop()
                multiplied_string = curr_string * prev_multiplier
                # merge with outer bracket
                prev_string = string_stack.pop()
                curr_string = prev_string + multiplied_string

            # handle characters
            else:
                curr_string += s[i]

            i += 1

        return curr_string

Next Greater Element II *

"""
Next Greater Element II 
Given a circular integer array nums (i.e., the next element of nums[nums.length - 1] is nums[0]), 
    return the next greater number for every element in nums.
The next greater number of a number x is the first greater number to its traversing-order next in the array, 
    which means you could search circularly to find its next greater number. If it doesn't exist, return -1 for this number.

Example 1:
    Input: nums = [1,2,1]
    Output: [2,-1,2]
    Explanation: The first 1's next greater number is 2; 
        The number 2 can't find next greater number. 
        The second 1's next greater number needs to search circularly, which is also 2.
Example 2:
    Input: nums = [1,2,3,4,3]
    Output: [2,3,4,-1,4]
https://leetcode.com/problems/next-greater-element-ii
"""

"""
Next Greater Element:

Write a function that takes in an array of integers
 and returns a new array containing,at each index,
 the next element in the input array that's greater than the element at that index in the input array.
In other words, your function should return a new array
 where outputArray[i] is the next element in the input array that's greater than inputArray[i].
If there's no such next greater element for a particular index,
 the value at that index in the output array should be -1.

For example, given array = [1, 2], your function should return [2, -1].
Additionally, your function should treat the input array as a circular array.
 A circular array wraps around itself as if it were connected end-to-end.
 So the next index after the last index in a circular array is the first index.
 This means that, for our problem, given array = [0, 0, 5, 0, 0, 3, 0 0],
  the next greater element after 3 is 5, since the array is circular.

Sample Input
    array = [2, 5, -3, -4, 6, 7, 2]
    Sample Output
    [5, 6, 6, 6, 7, -1, 5]

https://www.algoexpert.io/questions/Next%20Greater%20Element
"""

# O(n) time | O(n) space - where n is the length of the array
def nextGreaterElement00(array):
    res = [-1] * len(array)

    # stack used to store the previous smaller numbers that haven't been replaced
    # stored in the form of {'idx': 0, 'val': 0}
    be_replaced_stack = []

    for i in range(len(array)*2):  # loop through twice because the array is circular
        array_idx = i % len(array)  # prevent out of bound errors

        # check if we have found some values in the be_replaced_stack stack
        #   that is smaller than the current array value array[array_idx]
        #   then replace them (their corresponding values in res)
        while len(be_replaced_stack) > 0 and be_replaced_stack[-1]['val'] < array[array_idx]:

            to_be_replaced = be_replaced_stack.pop()['idx']
            res[to_be_replaced] = array[array_idx]

        # add the current element to the be_replaced_stack so that it can be checked in the futere for replacement
        be_replaced_stack.append({'idx': array_idx, 'val': array[array_idx]})

    return res

# O(n) time | O(n) space - where n is the length of the array
def nextGreaterElement01(array):
    res = [-1] * len(array)

    # stack used to store the previous smaller numbers' indices that haven't been replaced
    be_replaced_stack = []

    for i in range(len(array)*2):  # loop through twice because the array is circular
        array_idx = i % len(array)  # prevent out of bound errors

        # check if we have found some values in the be_replaced_stack stack
        #   that is smaller than the current array value array[array_idx]
        #   then replace them (their corresponding values in res)
        while len(be_replaced_stack) > 0 and array[be_replaced_stack[-1]] < array[array_idx]:
            res[be_replaced_stack.pop()] = array[array_idx]

        # add the current element to the be_replaced_stack so that it can be checked in the futere for replacement
        be_replaced_stack.append(array_idx)

    return res

"""
# we will use a stack to keep track of the past values that have not been replaced
#  once we find a bigger element, we replace them and remove them from the stack
#  then add the big element to the stack in the hope that it will be replaced

array = [0, 1,  2,  3, 4, 5, 6] <= indices
array = [2, 5, -3, -4, 6, 7, 2]

---
num = 2 (index 0)
res = [-1, -1, -1, -1, -1, -1, -1]
stack = [2]

num = 5 (index 1)
res = [5, -1, -1, -1, -1, -1, -1]
stack = [5] -> replaced all smaller values in res and the stack

num = -3
res = [5, -1, -1, -1, -1, -1, -1]
stack = [5, -3]

num = -4 (index 3)
res = [5, -1, -1, -1, -1, -1, -1]
stack = [5, -3, -4]

num = 6 (index 4)
res = [5, 6, 6, 6, -1, -1, -1]
stack = [6] -> replaced all smaller values in res and the stack

num = 7 (index 5)
res = [5, 6, 6, 6, 7, -1, -1]
stack = [7] -> replaced all smaller values in res and the stack

num = 2 (index 6)
res = [5, 6, 6, 6, 7, -1, -1]
stack = [7,2]

num = 2 (index 0)
res = [5, 6, 6, 6, 7, -1, -1]
stack = [7,2,2]
---

"""

# O(n) time | O(n) space - where n is the length of the array
def nextGreaterElement(array):
    res = [-1] * len(array)

    # stack used to store the previous smaller numbers that haven't been replaced
    next_nums_stack = []

    # loop through twice because the array is circular
    for i in reversed(range(len(array)*2)):
        array_idx = i % len(array)  # prevent out of bound errors

        while len(next_nums_stack) > 0:
            # if value at the top of the stack is smaller than the current value in the array,
            #   remove it from the stack till we find something larger
            if next_nums_stack[-1] <= array[array_idx]:
                next_nums_stack.pop()

            # replace the value in the array by the
            #   value at the top of the stack (if stack[-1] is larger)
            else:
                res[array_idx] = next_nums_stack[-1]
                break

        # add the current element to the next_nums_stack so that it can be checked in the futere for replacement
        next_nums_stack.append(array[array_idx])

    return res

Sunset views

def sunsetViews(buildings, direction):
    stack = []

    # order of iteration
    order = range(len(buildings))
    if direction == "WEST":
        order = reversed(order)

    for i in order:
        # remove prev buildings that can be blocked by the current (shorter ones)
        while len(stack) > 0 and buildings[stack[-1]] <= buildings[i]:
            stack.pop()

        stack.append(i)

    if direction == "WEST":
        stack.reverse()
    return stack

Three in One

Simplify Path/Shorten Path

""" 
Simplify Path/Shorten Path:

Given a string path, which is an absolute path (starting with a slash '/') to a file or directory in a Unix-style file system,
 convert it to the simplified canonical path.
In a Unix-style file system, 
    a period '.' refers to the current directory, 
    a double period '..' refers to the directory up a level, 
    and any multiple consecutive slashes (i.e. '//') are treated as a single slash '/'. 
    For this problem, any other format of periods such as '...' are treated as file/directory names.
The canonical path should have the following format:
    The path starts with a single slash '/'.
    Any two directories are separated by a single slash '/'.
    The path does not end with a trailing '/'.
    The path only contains the directories on the path from the root directory to the target file or directory (i.e., no period '.' or double period '..')
Return the simplified canonical path.

Example 1:
    Input: path = "/home/"
    Output: "/home"
    Explanation: Note that there is no trailing slash after the last directory name.
Example 2:
    Input: path = "/../"
    Output: "/"
    Explanation: Going one level up from the root directory is a no-op, as the root level is the highest level you can go.
Example 3:
    Input: path = "/home//foo/"
    Output: "/home/foo"
    Explanation: In the canonical path, multiple consecutive slashes are replaced by a single one.
Example 4:
    Input: path = "/a/./b/../../c/"
    Output: "/c"

https://leetcode.com/problems/simplify-path/
https://www.algoexpert.io/questions/Shorten%20Path
"""

""" 
- have a stack and all all directories we find there
- if we find a '..', remove the directory at the top of the stack
- if we find a '//' or '.' skip it
"""

class Solution0:
    def simplifyPath(self, path):

        stack = []
        start = 0
        end = 0
        while start < len(path):
            # cannot add to stack
            if not (end == len(path)-1 or path[end] == "/"):
                end += 1
                continue

            # # check logic
            substring = path[start:end]
            if end == len(path)-1 and path[end] != "/":
                # deal with cases like "/home"
                substring = path[start:end+1]

            # # path creation logic
            # if we find a '//' or '.' skip it
            if substring == '' or substring == '.':
                pass
            # if we find a '..', remove the directory at the top of the stack
            elif substring == '..':
                if stack:
                    stack.pop()
            # add directory
            else:
                stack.append(substring)

            # # next
            start = end+1
            end = end+1

        return "/" + "/".join(stack)

class Solution:
    def simplifyPath(self, path):
        stack = []

        paths = path.split("/")
        for substring in paths:

            # # path creation logic
            # if we find a '//' or '.' skip it
            if substring == '' or substring == '.':
                pass
            # if we find a '..', remove the directory at the top of the stack
            elif substring == '..':
                if stack:
                    stack.pop()
            # add directory
            else:
                stack.append(substring)

        return "/" + "/".join(stack)

Largest Rectangle in Histogram/Largest Rectangle Under Skyline *

LARGEST RECTANGLE IN HISTOGRAM - Leetcode 84 - Python

Screen Recording 2021-11-23 at 15.29.38.mov

84. Largest Rectangle in a Histogram.mp4

Screenshot 2021-11-23 at 15.28.35.png

""" 
Largest Rectangle in Histogram/Largest Rectangle Under Skyline:

Given an array of integers heights representing the histogram's bar height where the width of each bar is 1, 
return the area of the largest rectangle in the histogram.

Example 1:
    Input: heights = [2,1,5,6,2,3]
    Output: 10
    Explanation: 5*2 The above is a histogram where width of each bar is 1.
    The largest rectangle is shown in the red area, which has an area = 10 units.
Example 2:
    Input: heights = [2,4]
    Output: 4 => 2*2
Example 3:
    heights = [1, 3, 3, 2, 4, 1, 5, 3, 2]
    9

    Below is a visual representation of the sample input.
                 _
             _  | |
       _ _  | | | |_
      | | |_| | | | |_
     _| | | | |_| | | |
    |_|_|_|_|_|_|_|_|_|

https://leetcode.com/problems/largest-rectangle-in-histogram
"""

#
from collections import deque

"""
Brute force:
- for every building, expand outward
"""

"""
- for each height try to find out where it started and calculate the height

- keep track of the largest valid building up to that point:
    - that can still make rectangles
    - the stack will only conttain buildings that can continue expanding to the right

[0,1,2,3,4,5]
[2,1,5,6,2,3]

stack = []

n,  r,s(i,n)
2,[(0,2)]2*1,
1,[(0,1)] # one is in the prev two, 1*2,
5,[(0,1),(2,5)],5*1,1*3
6,[(0,1),(2,5),(3,6)],6*1,5*2,1*4
2,[(0,1),(2,2)],2*3,1*5
3,[(0,1),(2,2),(5,3)],3*1,1*5,2*4

remaining in stack: [(0,1),(2,2),(5,3)]
3*1
2*4
1*5

"""

class RectangleInfo:
    def __init__(self, start_idx, height):
        self.start_idx = start_idx  # far right bound of building
        self.height = height

    def get_area(self, end_idx):
        return (end_idx-self.start_idx + 1) * self.height

class Solution:
    def largestRectangleArea(self, heights):
        max_area = 0
        prev_valid_heights = deque()  # stack

        for idx, curr_height in enumerate(heights):

            # # determine left bound of curr height
            start_idx = idx

            # remove invalid buildings (that cannot be expanded to the right as they are taller than curr_height)
            # - also viewed as expanding as left as possible
            while prev_valid_heights and curr_height < prev_valid_heights[-1].height:
                removed = prev_valid_heights.pop()
                # calculate the area from when the removed was lat valid (using the last valid index)
                max_area = max(max_area, removed.get_area(idx-1))

                # our current rectangle can start from there
                start_idx = removed.start_idx

            prev_valid_heights.append(RectangleInfo(start_idx, curr_height))

        # # empty stack
        while prev_valid_heights:
            removed = prev_valid_heights.pop()
            max_area = max(max_area, removed.get_area(len(heights)-1))

        return max_area

Minimum Remove to Make Valid Parentheses

Screenshot 2021-11-03 at 13.55.19.png

Screen Recording 2021-11-03 at 13.53.53.mov

""" 
Minimum Remove to Make Valid Parentheses:

Given a string s of '(' , ')' and lowercase English characters. 
Your task is to remove the minimum number of parentheses ( '(' or ')', in any positions ) so that the resulting parentheses string is valid and return any valid string.

Formally, a parentheses string is valid if and only if:
    It is the empty string, contains only lowercase characters, or
    It can be written as AB (A concatenated with B), where A and B are valid strings, or
    It can be written as (A), where A is a valid string.


Example 1:
    Input: s = "lee(t(c)o)de)"
    Output: "lee(t(c)o)de"
    Explanation: "lee(t(co)de)" , "lee(t(c)ode)" would also be accepted.
Example 2:
    Input: s = "a)b(c)d"
    Output: "ab(c)d"
Example 3:
    Input: s = "))(("
    Output: ""
    Explanation: An empty string is also valid.
Example 4:
    Input: s = "(a(b(c)d)"
    Output: "a(b(c)d)"

https://leetcode.com/problems/minimum-remove-to-make-valid-parentheses
"""

#

"""
---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
------------- PROBLEM --------------------
- string will have  '(' , ')' and lowercase English characters

- remove the minimum number of parentheses so that the resulting parentheses string is valid
- return any valid string.

------------- EXAMPLES --------------------

a(pp)l)e -> a(pp)le / a(ppl)e -> remove one closing  
a(ppl)e  -> a(ppl)e           -> N/A
a(pple   -> apple             -> remove one opening
a(p(ple  -> apple             -> remove two opening

a(pp()l)e     -> a(pp()l)e                                    -> N/A
lee(t(c)o)de) -> lee(t(c)o)de / lee(t(c)ode)  / lee(t(co)de)  -> remove one closing
a)b(c)d       -> ab(c)d                                       -> remove first closing

a(pp()le 
a(pp()l(e 

"))(("

------------- BRUTE FORCE -------------------- O(n^2) time | O(n) space - where n = len(string)
- count opening and closing then remove the larger randomly and see what works (validate)

------------- OPTIMAL --------------------
------------- 1: O(n) time | O(n) space - where n = len(string)
Two Pass String Builder
- remove any closing bracket that does not have a preceding opening bracket
- remove any excess opening brackets starting at the end

------------- PSEUDOCODE --------------------
------------- 1:
opening_running_count
    (how many unclosed opening brackets we have)

- whenever we meet an opening bracket: opening_running_count += 1
- whenever we meet a closing bracket:
    - if opening_running_count > 0: 
        opening_running_count -= 1
    - else:
        remove it
- remove excess opening brackets starting at the end

"""

class Solution:
    def minRemoveToMakeValid(self, s: str):
        opening_count = 0

        removed_closing = []
        for char in s:
            if char == "(":
                opening_count += 1
                removed_closing.append(char)
            elif char == ")":
                # only add valid ones
                if opening_count > 0:
                    removed_closing.append(char)
                    opening_count -= 1
            else:
                removed_closing.append(char)

        # remove excess opening brackets
        output = [""] * (len(removed_closing) - opening_count)

        curr_idx = len(output) - 1
        for idx in reversed(range(len(removed_closing))):
            # remove
            if removed_closing[idx] == "(" and opening_count > 0:
                opening_count -= 1
            else:
                output[curr_idx] = removed_closing[idx]
                curr_idx -= 1

        return "".join(output)

class _Solution:
    def removeInvalidClosingbrackets(self, s, opening, closing):
        result = []

        opening_count = 0
        for char in s:
            if char == opening:
                opening_count += 1
                result.append(char)
            elif char == closing:
                # only add valid ones
                if opening_count > 0:
                    result.append(char)
                    opening_count -= 1
            else:
                result.append(char)

        return result

    def minRemoveToMakeValid(self, s: str):

        # remove excess brackets
        removed_closing = self.removeInvalidClosingbrackets(s, "(", ")")
        removed_opening = reversed(self.removeInvalidClosingbrackets(reversed(removed_closing),
                                                                     ")", "("))
        return "".join(removed_opening)

""" 
---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
If we put the indexes of the "(" on the stack, then we'll know that all the indexes on the stack at the end are the indexes of the unmatched "(". 
We should also use a set to keep track of the unmatched ")" we come across.
"""

class Solution1:
    def minRemoveToMakeValid(self, s: str):
        indexes_to_remove = set()
        stack = []
        for i, c in enumerate(s):
            if c not in "()":
                continue
            # opening brackets
            if c == "(":
                stack.append(i)

            # closing brackets
            elif not stack:
                indexes_to_remove.add(i)
            else:
                stack.pop()

        # the union of two sets contains all the elements contained in either set (or both sets).
        indexes_to_remove = indexes_to_remove.union(set(stack))

        # build string with skipping invalid parenthesis
        string_builder = []
        for i, c in enumerate(s):
            if i not in indexes_to_remove:
                string_builder.append(c)
        return "".join(string_builder)

Exclusive Time of Functions

Screenshot 2021-09-21 at 10.56.54.png

""" 
Exclusive Time of Functions:

On a single-threaded CPU, we execute a program containing n functions. 
Each function has a unique ID between 0 and n-1.
Function calls are stored in a call stack: when a function call starts, its ID is pushed onto the stack, and when a function call ends, its ID is popped off the stack. 
The function whose ID is at the top of the stack is the current function being executed. 
Each time a function starts or ends, we write a log with the ID, whether it started or ended, and the timestamp.
You are given a list logs, where logs[i] represents the ith log message formatted as a string "{function_id}:{"start" | "end"}:{timestamp}". 
For example, "0:start:3" means a function call with function ID 0 started at the beginning of timestamp 3, and "1:end:2" means a function call with function ID 1 ended at the end of timestamp 2. 
Note that a function can be called multiple times, possibly recursively.
A function's exclusive time is the sum of execution times for all function calls in the program. 
For example, if a function is called twice, one call executing for 2 time units and another call executing for 1 time unit, the exclusive time is 2 + 1 = 3.
Return the exclusive time of each function in an array, where the value at the ith index represents the exclusive time for the function with ID i.

https://leetcode.com/problems/exclusive-time-of-functions/
"""

import collections
'''
*** Fill array with current running job ***
O(n+m) space | where m is the duration

Input: 
    n = 2, 
    logs = ["0:start:0","0:start:2","0:end:5","1:start:6","1:end:6","0:end:7"]
Output: 
    [7,1]
    [0, 1,  2, 3, 4,  5,  6,  0]
    [0, 0,  0, 0, 0,  0,  1,  0]
Explanation:
Function 0 starts at the beginning of time 0, executes for 2 units of time, and recursively calls itself.
Function 0 (recursive call) starts at the beginning of time 2 and executes for 4 units of time.
Function 0 (initial call) resumes execution then immediately calls function 1.
Function 1 starts at the beginning of time 6, executes 1 units of time, and ends at the end of time 6.
Function 0 resumes execution at the beginning of time 6 and executes for 2 units of time.
So function 0 spends 2 + 4 + 1 = 7 units of total time executing, and function 1 spends 1 unit of total time executing.

n = 2, logs = ["0:start:0","0:start:2","0:end:5","1:start:7","1:end:7","0:end:8"]

---
prev_job = []
curr_job = 0

past_process
[0, 1, 2, 3, 4, 5, 6, 7, 8]
[]

---

"0:start:2"
fill past_process with curr_job till idx 1
add curr_job to prev_job
change curr_job to 0

prev_job = [0]
curr_job = 0

past_process
[0,  1, 2, 3, 4, 5, 6, 7, 8]
[0,  ]

---

"0:end:5"
fill past_process with curr_job till idx 5
replace curr_job with prev_job.pop()

prev_job = []
curr_job = 0

past_process
[0,  1, 2, 3, 4, 5,  6, 7, 8]
[0,  0, 0, 0, 0, 0,  ]

---

"1:start:7"
fill past_process with curr_job till idx 6
add curr_job to prev_job
change curr_job to 1

prev_job = [0]
curr_job = 1

past_process
[0,  1, 2, 3, 4, 5,  6,  7, 8]
[0,  0, 0, 0, 0, 0,  0,  ]

---

"1:end:7"
fill past_process with curr_job till idx 7
replace curr_job with prev_job.pop()

prev_job = []
curr_job = 0

past_process
[0,  1, 2, 3, 4, 5,  6,  7,  8]
[0,  0, 0, 0, 0, 0,  0,  1,  ]

---

"0:end:8"
fill past_process with curr_job till idx 8
replace curr_job with prev_job.pop()

prev_job = []
curr_job = None

past_process
[0,  1, 2, 3, 4, 5,  6,  7,  8]
[0,  0, 0, 0, 0, 0,  0,  1,  0]

n = 2, logs = ["0:start:0","1:start:2","1:end:5","0:end:6"]

[0, 1,  2, 3, 4,  5, 6]
[0, 0,  1, 1, 1,  0]
--------------------------
O(n) space
without the space

def time:

    result = [0] * len(n)

    stack = []
    last_job = 0
    for log in logs:
        if start:
            time
            job
            for _ in range((time-last_log)+1):
                prev_job = stack[-1]
                result[prev_job] += 1

            stack.append(job)



        elif end:

'''

"""
--------------------------------------------------------------------------------

"""

class SolutionBF:
    def get_job_info(self, job_str):
        job, kind, time = job_str.split(":")
        return int(job), int(time), kind

    def exclusiveTime(self, n: int, logs):
        task_history = []

        stack = []
        next_placement = 0
        for log in logs:
            job, time, kind = self.get_job_info(log)

            if kind == "start":
                # place last job
                for _ in range((time-next_placement)):
                    prev_job = stack[-1]
                    task_history.append(prev_job)

                # place current job
                task_history.append(job)
                next_placement = time+1

                stack.append(job)

            elif kind == "end":
                # place last job == current job
                prev_job = stack.pop()
                for _ in range((time-next_placement)+1):
                    task_history.append(prev_job)
                next_placement = time+1

        task_counter = collections.Counter(task_history)
        result = [0] * n
        for key in task_counter:
            result[key] = task_counter[key]
        return result

"""
--------------------------------------------------------------------------------

"""

class Solution_:
    def get_job_info(self, job_str):
        job, kind, time = job_str.split(":")
        return int(job), int(time), kind

    def exclusiveTime(self, n: int, logs):
        result = [0] * n

        stack = []
        next_placement = 0
        for log in logs:
            job, time, kind = self.get_job_info(log)

            if kind == "start":
                # place last job
                for _ in range((time-next_placement)):
                    prev_job = stack[-1]
                    result[prev_job] += 1

                # place current job
                result[job] += 1
                next_placement = time+1

                # move to top of stack
                stack.append(job)

            elif kind == "end":
                # place last job == current job
                prev_job = stack.pop()
                for _ in range((time-next_placement)+1):
                    result[prev_job] += 1
                next_placement = time+1

        return result

"""
--------------------------------------------------------------------------------

"""

class Solution:
    def get_job_info(self, job_str):
        job, kind, time = job_str.split(":")
        return int(job), int(time), kind

    def exclusiveTime(self, n: int, logs):
        result = [0] * n

        stack = []
        next_placement = 0
        for log in logs:
            job, time, kind = self.get_job_info(log)

            if kind == "start":
                # place last job
                # record how long the prev job ran (prev job should have continued running from next_placement)
                if stack:
                    prev_job = stack[-1]
                    result[prev_job] += time-next_placement

                # place current job
                # start the current job with one run
                result[job] += 1
                next_placement = time+1

                # move to top of stack
                stack.append(job)

            elif kind == "end":
                # place prev/last job == current job that has ended
                stack.pop()
                # record how long the prev job ran
                result[job] += time-next_placement+1
                next_placement = time+1

        return result

Candy Crush 1D

""" 
1209. Remove All Adjacent Duplicates in String II/Candy Crush 1D

You are given a string s and an integer k, a k duplicate removal consists of choosing k adjacent and equal letters from s and removing them, causing the left and the right side of the deleted substring to concatenate together.
We repeatedly make k duplicate removals on s until we no longer can.
Return the final string after all such duplicate removals have been made. It is guaranteed that the answer is unique.

Example 1:
    Input: s = "abcd", k = 2
    Output: "abcd"
    Explanation: There's nothing to delete.
Example 2:
    Input: s = "deeedbbcccbdaa", k = 3
    Output: "aa"
    Explanation: 
    First delete "eee" and "ccc", get "ddbbbdaa"
    Then delete "bbb", get "dddaa"
    Finally delete "ddd", get "aa"
Example 3:
    Input: s = "pbbcggttciiippooaais", k = 2
    Output: "ps"


Constraints:
    1 <= s.length <= 105
    2 <= k <= 104
    s only contains lower case English letters.


https://leetcode.com/problems/remove-all-adjacent-duplicates-in-string-ii
"""

class Solution:
    def removeDuplicates(self, s: str, k: int):
        """
        Add characters with their frequencies to a stack [(char, freq)]
        - b4 adding a charcater to the stack, check if the character at the top is similar
            - if so, let its frequency be that of the stack top + 1
            - else, add the character to the stack with a freq of 1
        - after adding, check if the next character is similar to the top of the stack
            - if so, add all similar characters to the stack to get the whole sequence of similar characters

        - Try to remove k characters from the stack:
            - if the top of the stack has a frequency of >= k:
                - continue removing k characters from the stack till the above condition is False

        """
        stack = []
        idx = 0
        while idx < len(s):
            # add single character to stack
            self.add_to_stack(stack, s[idx])
            idx += 1
            # try to add similar characters to stack b4 crushing
            while idx < len(s) and stack and s[idx] == stack[-1][0]:
                self.add_to_stack(stack, s[idx])
                idx += 1

            # Candy Crush 1D
            self.remove_duplicates_from_stack(stack, k)

        # after loop
        self.remove_duplicates_from_stack(stack, k)

        return "".join([item[0] for item in stack])

    def remove_duplicates_from_stack(self, stack, k):
        """Candy Crush 1D"""
        while stack and stack[-1][1] >= k:
            # number_of_ks = stack[-1][1]//k
            for _ in range(k):
                stack.pop()

    def add_to_stack(self, stack, char):
        """Add a single character to the stack"""
        if not stack or stack[-1][0] != char:
            stack.append((char, 1))
        else:
            stack.append((char, stack[-1][1]+1))

# https://leetcode.com/discuss/interview-question/380650/Bloomberg-or-Phone-or-Candy-Crush-1D/1143991
def add_to_stack(stack, char):
    if not stack or stack[-1][0] != char:
        stack.append((char, 1))
    else:
        stack.append((char, stack[-1][1]+1))

def candy_crush_1d(s):
    stack = []
    idx = 0
    while idx < len(s):
        # add similar characters to stack b4 crushing
        while idx < len(s) and stack and s[idx] == stack[-1][0]:
            add_to_stack(stack, s[idx])
            idx += 1

        # crush
        if stack and stack[-1][1] >= 3:
            char = stack[-1][0]
            while stack and stack[-1][0] == char:
                stack.pop()

        # add next
        if idx < len(s):
            add_to_stack(stack, s[idx])
            idx += 1

    return "".join([item[0] for item in stack])

S = "aaabbbc"
print(candy_crush_1d(S))

S = "aabbbacd"
print(candy_crush_1d(S))

S = "aaabbbacd"
print(candy_crush_1d(S))

Remove All Adjacent Duplicates in String II/Candy Crush 1D

""" 
1209. Remove All Adjacent Duplicates in String II/Candy Crush 1D

You are given a string s and an integer k, a k duplicate removal consists of choosing k adjacent and equal letters from s and removing them, causing the left and the right side of the deleted substring to concatenate together.
We repeatedly make k duplicate removals on s until we no longer can.
Return the final string after all such duplicate removals have been made. It is guaranteed that the answer is unique.

Example 1:
    Input: s = "abcd", k = 2
    Output: "abcd"
    Explanation: There's nothing to delete.
Example 2:
    Input: s = "deeedbbcccbdaa", k = 3
    Output: "aa"
    Explanation: 
    First delete "eee" and "ccc", get "ddbbbdaa"
    Then delete "bbb", get "dddaa"
    Finally delete "ddd", get "aa"
Example 3:
    Input: s = "pbbcggttciiippooaais", k = 2
    Output: "ps"


Constraints:
    1 <= s.length <= 105
    2 <= k <= 104
    s only contains lower case English letters.


https://leetcode.com/problems/remove-all-adjacent-duplicates-in-string-ii
"""

class Solution:
    def removeDuplicates(self, s: str, k: int):
        """
        Add characters with their frequencies to a stack [(char, freq)]
        - b4 adding a charcater to the stack, check if the character at the top is similar
            - if so, let its frequency be that of the stack top + 1
            - else, add the character to the stack with a freq of 1
        - after adding, check if the next character is similar to the top of the stack
            - if so, add all similar characters to the stack to get the whole sequence of similar characters

        - Try to remove k characters from the stack:
            - if the top of the stack has a frequency of >= k:
                - continue removing k characters from the stack till the above condition is False

        """
        stack = []
        idx = 0
        while idx < len(s):
            # add single character to stack
            self.add_to_stack(stack, s[idx])
            idx += 1
            # try to add similar characters to stack b4 crushing
            while idx < len(s) and stack and s[idx] == stack[-1][0]:
                self.add_to_stack(stack, s[idx])
                idx += 1

            # Candy Crush 1D
            self.remove_duplicates_from_stack(stack, k)

        # after loop
        self.remove_duplicates_from_stack(stack, k)

        return "".join([item[0] for item in stack])

    def remove_duplicates_from_stack(self, stack, k):
        """Candy Crush 1D"""
        while stack and stack[-1][1] >= k:
            # number_of_ks = stack[-1][1]//k
            for _ in range(k):
                stack.pop()

    def add_to_stack(self, stack, char):
        """Add a single character to the stack"""
        if not stack or stack[-1][0] != char:
            stack.append((char, 1))
        else:
            stack.append((char, stack[-1][1]+1)

Monotonic stack

Examples

Next Greater Element II *

"""
Next Greater Element II 
Given a circular integer array nums (i.e., the next element of nums[nums.length - 1] is nums[0]), 
    return the next greater number for every element in nums.
The next greater number of a number x is the first greater number to its traversing-order next in the array, 
    which means you could search circularly to find its next greater number. If it doesn't exist, return -1 for this number.

Example 1:
    Input: nums = [1,2,1]
    Output: [2,-1,2]
    Explanation: The first 1's next greater number is 2; 
        The number 2 can't find next greater number. 
        The second 1's next greater number needs to search circularly, which is also 2.
Example 2:
    Input: nums = [1,2,3,4,3]
    Output: [2,3,4,-1,4]
https://leetcode.com/problems/next-greater-element-ii
"""

"""
Next Greater Element:

Write a function that takes in an array of integers
 and returns a new array containing,at each index,
 the next element in the input array that's greater than the element at that index in the input array.
In other words, your function should return a new array
 where outputArray[i] is the next element in the input array that's greater than inputArray[i].
If there's no such next greater element for a particular index,
 the value at that index in the output array should be -1.

For example, given array = [1, 2], your function should return [2, -1].
Additionally, your function should treat the input array as a circular array.
 A circular array wraps around itself as if it were connected end-to-end.
 So the next index after the last index in a circular array is the first index.
 This means that, for our problem, given array = [0, 0, 5, 0, 0, 3, 0 0],
  the next greater element after 3 is 5, since the array is circular.

Sample Input
    array = [2, 5, -3, -4, 6, 7, 2]
    Sample Output
    [5, 6, 6, 6, 7, -1, 5]

https://www.algoexpert.io/questions/Next%20Greater%20Element
"""

# O(n) time | O(n) space - where n is the length of the array
def nextGreaterElement00(array):
    res = [-1] * len(array)

    # stack used to store the previous smaller numbers that haven't been replaced
    # stored in the form of {'idx': 0, 'val': 0}
    be_replaced_stack = []

    for i in range(len(array)*2):  # loop through twice because the array is circular
        array_idx = i % len(array)  # prevent out of bound errors

        # check if we have found some values in the be_replaced_stack stack
        #   that is smaller than the current array value array[array_idx]
        #   then replace them (their corresponding values in res)
        while len(be_replaced_stack) > 0 and be_replaced_stack[-1]['val'] < array[array_idx]:

            to_be_replaced = be_replaced_stack.pop()['idx']
            res[to_be_replaced] = array[array_idx]

        # add the current element to the be_replaced_stack so that it can be checked in the futere for replacement
        be_replaced_stack.append({'idx': array_idx, 'val': array[array_idx]})

    return res

# O(n) time | O(n) space - where n is the length of the array
def nextGreaterElement01(array):
    res = [-1] * len(array)

    # stack used to store the previous smaller numbers' indices that haven't been replaced
    be_replaced_stack = []

    for i in range(len(array)*2):  # loop through twice because the array is circular
        array_idx = i % len(array)  # prevent out of bound errors

        # check if we have found some values in the be_replaced_stack stack
        #   that is smaller than the current array value array[array_idx]
        #   then replace them (their corresponding values in res)
        while len(be_replaced_stack) > 0 and array[be_replaced_stack[-1]] < array[array_idx]:
            res[be_replaced_stack.pop()] = array[array_idx]

        # add the current element to the be_replaced_stack so that it can be checked in the futere for replacement
        be_replaced_stack.append(array_idx)

    return res

"""
# we will use a stack to keep track of the past values that have not been replaced
#  once we find a bigger element, we replace them and remove them from the stack
#  then add the big element to the stack in the hope that it will be replaced

array = [0, 1,  2,  3, 4, 5, 6] <= indices
array = [2, 5, -3, -4, 6, 7, 2]

---
num = 2 (index 0)
res = [-1, -1, -1, -1, -1, -1, -1]
stack = [2]

num = 5 (index 1)
res = [5, -1, -1, -1, -1, -1, -1]
stack = [5] -> replaced all smaller values in res and the stack

num = -3
res = [5, -1, -1, -1, -1, -1, -1]
stack = [5, -3]

num = -4 (index 3)
res = [5, -1, -1, -1, -1, -1, -1]
stack = [5, -3, -4]

num = 6 (index 4)
res = [5, 6, 6, 6, -1, -1, -1]
stack = [6] -> replaced all smaller values in res and the stack

num = 7 (index 5)
res = [5, 6, 6, 6, 7, -1, -1]
stack = [7] -> replaced all smaller values in res and the stack

num = 2 (index 6)
res = [5, 6, 6, 6, 7, -1, -1]
stack = [7,2]

num = 2 (index 0)
res = [5, 6, 6, 6, 7, -1, -1]
stack = [7,2,2]
---

"""

# O(n) time | O(n) space - where n is the length of the array
def nextGreaterElement(array):
    res = [-1] * len(array)

    # stack used to store the previous smaller numbers that haven't been replaced
    next_nums_stack = []

    # loop through twice because the array is circular
    for i in reversed(range(len(array)*2)):
        array_idx = i % len(array)  # prevent out of bound errors

        while len(next_nums_stack) > 0:
            # if value at the top of the stack is smaller than the current value in the array,
            #   remove it from the stack till we find something larger
            if next_nums_stack[-1] <= array[array_idx]:
                next_nums_stack.pop()

            # replace the value in the array by the
            #   value at the top of the stack (if stack[-1] is larger)
            else:
                res[array_idx] = next_nums_stack[-1]
                break

        # add the current element to the next_nums_stack so that it can be checked in the futere for replacement
        next_nums_stack.append(array[array_idx])

    return res

Queues

https://leetcode.com/problems/shortest-subarray-with-sum-at-least-k/discuss/204290/Monotonic-Queue-Summary

To implement a queue, we again need two basic operations: enqueue() and dequeue()

enqueue() operation appends an element to the end of the queue and dequeue() operation removes an element from the beginning of the queue.

Examples

BFS

Asteroid Collision

""" 
735. Asteroid Collision

We are given an array asteroids of integers representing asteroids in a row.
For each asteroid, the absolute value represents its size, and the sign represents its direction (positive meaning right, negative meaning left). 
Each asteroid moves at the same speed.
Find out the state of the asteroids after all collisions. 
If two asteroids meet, the smaller one will explode. If both are the same size, both will explode. Two asteroids moving in the same direction will never meet.



Example 1:
    Input: asteroids = [5,10,-5]
    Output: [5,10]
    Explanation: The 10 and -5 collide resulting in 10. The 5 and 10 never collide.
Example 2:
    Input: asteroids = [8,-8]
    Output: []
    Explanation: The 8 and -8 collide exploding each other.
Example 3:
    Input: asteroids = [10,2,-5]
    Output: [10]
    Explanation: The 2 and -5 collide resulting in -5. The 10 and -5 collide resulting in 10.
Example 4:
    Input: asteroids = [-2,-1,1,2]
    Output: [-2,-1,1,2]
    Explanation: The -2 and -1 are moving left, while the 1 and 2 are moving right. Asteroids moving the same direction never meet, so no asteroids will meet each other.

Constraints:
    2 <= asteroids.length <= 104
    -1000 <= asteroids[i] <= 1000
    asteroids[i] != 0

https://leetcode.com/problems/asteroid-collision
"""

from collections import deque
from typing import List

class Solution:
    def asteroidCollision(self, asteroids: List[int]):

        stack = deque()
        for asteroid in asteroids:
            if asteroid > 0:
                stack.append(asteroid)
                continue

            while asteroid and stack and stack[-1] > 0:
                if abs(stack[-1]) > abs(asteroid):
                    asteroid = 0
                elif abs(stack[-1]) == abs(asteroid):
                    stack.pop()
                    asteroid = 0
                elif abs(stack[-1]) < abs(asteroid):
                    stack.pop()

            if asteroid and (not stack or stack[-1] < 0):
                stack.append(asteroid)
                asteroid = 0

        return list(stack)

Implement Queue using Stacks

"""
Implement Queue using Stacks:

Implement a first in first out (FIFO) queue using only two stacks.
The implemented queue should support all the functions of a normal queue (push, peek, pop, and empty).
Implement the MyQueue class:
    void push(int x) Pushes element x to the back of the queue.
    int pop() Removes the element from the front of the queue and returns it.
    int peek() Returns the element at the front of the queue.
    boolean empty() Returns true if the queue is empty, false otherwise.
Notes:
You must use only standard operations of a stack, which means only push to top, peek/pop from top, size, and is empty operations are valid.
Depending on your language, the stack may not be supported natively. 
You may simulate a stack using a list or deque (double-ended queue) as long as you use only a stack's standard operations.
Follow-up: 
Can you implement the queue such that each operation is amortized O(1) time complexity? 
In other words, performing n operations will take overall O(n) time even if one of those operations may take longer.

https://leetcode.com/problems/implement-queue-using-stacks
"""

class MyStack:

    def __init__(self):
        self.items = []

    def push(self, x: int):
        self.items.append(x)

    def pop(self):
        return self.items.pop()

    def peek(self):
        return self.items[-1]

    def empty(self):
        return len(self.items) == 0

class MyQueue:

    def __init__(self):
        self.stack = MyStack()
        self.stack_reversed = MyStack()

    def push(self, x: int):
        # Push element x to the back of queue.
        self.stack.push(x)

    def pop(self):
        # Removes the element from in front of queue and returns that element.
        if self.stack_reversed.empty():
            self._reverse_stack()

        return self.stack_reversed.pop()

    def peek(self):
        # Get the front element.
        if self.stack_reversed.empty():
            self._reverse_stack()

        return self.stack_reversed.peek()

    def empty(self):
        # Returns whether the queue is empty.
        return self.stack.empty() and self.stack_reversed.empty()

    def _reverse_stack(self):
        # reverse stack one
        while not self.stack.empty():
            self.stack_reversed.push(self.stack.pop())

# Your MyQueue object will be instantiated and called as such:
# obj = MyQueue()
# obj.push(x)
# param_2 = obj.pop()
# param_3 = obj.peek()
# param_4 = obj.empty()

Design Circular Queue

""" 
622. Design Circular Queue:

Design your implementation of the circular queue. 
The circular queue is a linear data structure in which the operations are performed based on FIFO (First In First Out) principle 
    and the last position is connected back to the first position to make a circle. 
It is also called "Ring Buffer".

One of the benefits of the circular queue is that we can make use of the spaces in front of the queue. 
In a normal queue, once the queue becomes full, we cannot insert the next element even if there is a space in front of the queue. 
But using the circular queue, we can use the space to store new values.

Implementation the MyCircularQueue class:
    MyCircularQueue(k) Initializes the object with the size of the queue to be k.
    int Front() Gets the front item from the queue. If the queue is empty, return -1.
    int Rear() Gets the last item from the queue. If the queue is empty, return -1.
    boolean enQueue(int value) Inserts an element into the circular queue. Return true if the operation is successful.
    boolean deQueue() Deletes an element from the circular queue. Return true if the operation is successful.
    boolean isEmpty() Checks whether the circular queue is empty or not.
    boolean isFull() Checks whether the circular queue is full or not.

You must solve the problem without using the built-in queue data structure in your programming language. 

Example 1:
    Input
        ["MyCircularQueue", "enQueue", "enQueue", "enQueue", "enQueue", "Rear", "isFull", "deQueue", "enQueue", "Rear"]
        [[3], [1], [2], [3], [4], [], [], [], [4], []]
    Output
        [null, true, true, true, false, 3, true, true, true, 4]
    Explanation
        MyCircularQueue myCircularQueue = new MyCircularQueue(3);
        myCircularQueue.enQueue(1); // return True
        myCircularQueue.enQueue(2); // return True
        myCircularQueue.enQueue(3); // return True
        myCircularQueue.enQueue(4); // return False
        myCircularQueue.Rear();     // return 3
        myCircularQueue.isFull();   // return True
        myCircularQueue.deQueue();  // return True
        myCircularQueue.enQueue(4); // return True
        myCircularQueue.Rear();     // return 4
"""

class MyCircularQueue:

    def __init__(self, k: int):
        self.store = [None] * k
        self.start = 0
        self.items_count = 0

    def enQueue(self, value: int):
        if self.isFull():
            return False

        if self.isEmpty():
            self.store[self.start] = value
        else:
            next_idx = self._getEndIdx() + 1
            next_idx %= len(self.store)
            self.store[next_idx] = value

        self.items_count += 1
        return True

    def deQueue(self):
        if self.isEmpty():
            return False

        self.store[self.start] = None
        self.start += 1
        self.start %= len(self.store)

        self.items_count -= 1
        return True

    def Front(self):
        if self.isEmpty():
            return -1
        return self.store[self.start]

    def Rear(self):
        if self.isEmpty():
            return -1
        return self.store[self._getEndIdx()]

    def isEmpty(self):
        return self.items_count == 0

    def isFull(self):
        return self.items_count == len(self.store)

    def _getEndIdx(self):
        return (self.start + self.items_count - 1) % len(self.store)

# Your MyCircularQueue object will be instantiated and called as such:
# obj = MyCircularQueue(k)
# param_1 = obj.enQueue(value)
# param_2 = obj.deQueue()
# param_3 = obj.Front()
# param_4 = obj.Rear()
# param_5 = obj.isEmpty()
# param_6 = obj.isFull()

Animal Shelter

Monotonic Queue

Examples

Sliding Window Maximum

Screenshot 2021-11-23 at 20.53.26.png

""" 
239. Sliding Window Maximum

You are given an array of integers nums, there is a sliding window of size k which is moving from the very left of the array to the very right. 
You can only see the k numbers in the window. Each time the sliding window moves right by one position.
Return the max sliding window.

Example 1:
    Input: nums = [1,3,-1,-3,5,3,6,7], k = 3
    Output: [3,3,5,5,6,7]
    Explanation: 
        Window position                Max
        ---------------               -----
        [1  3  -1] -3  5  3  6  7       3
        1 [3  -1  -3] 5  3  6  7       3
        1  3 [-1  -3  5] 3  6  7       5
        1  3  -1 [-3  5  3] 6  7       5
        1  3  -1  -3 [5  3  6] 7       6
        1  3  -1  -3  5 [3  6  7]      7
Example 2:
    Input: nums = [1], k = 1
    Output: [1]
Example 3:
    Input: nums = [1,-1], k = 1
    Output: [1,-1]
Example 4:
    Input: nums = [9,11], k = 2
    Output: [11]
Example 5:
    Input: nums = [4,-2], k = 2
    Output: [4]

https://leetcode.com/problems/sliding-window-maximum
"""

from typing import List
from collections import deque

class Solution:
    def maxSlidingWindow(self, nums: List[int], k: int):
        """ 
        - have a double-ended-queue
        - for each element in the array:
            - clean deque
                - remove the elements that are out of the window's bounds from the left of the deque
                - remove all elements that are smaller than the element from the right of the deque
            - add the element to the deque
            - the largest element in this window is the leftmost element
        """
        result = []

        de_queue = deque()
        # add first k-1 elements
        for idx in range(k-1):
            while de_queue and nums[de_queue[-1]] <= nums[idx]:
                de_queue.pop()
            de_queue.append(idx)

        for idx in range(k-1, len(nums)):
            # remove not in window
            if de_queue and de_queue[0] <= idx-k:
                de_queue.popleft()

            # remove smaller
            while de_queue and nums[de_queue[-1]] <= nums[idx]:
                de_queue.pop()

            # add the element to the deque & the largest element in this window is the left-most element
            de_queue.append(idx)
            result.append(nums[de_queue[0]])

        return result

`collections.deque()`

How to use a deque in Python

Can be used as both a stack and a queue:

Stack: pop()
Queue: popleft()

Here’s a summary of the main characteristics of deque:

Stores items of any data type
Is a mutable data type
Supports membership operations with the in operator
Supports indexing, like in a_deque[i]
Doesn’t support slicing, like in a_deque[0:2]
Supports built-in functions that operate on sequences and iterables, such as [len()](https://docs.python.org/3/library/functions.html#len), [sorted()](https://realpython.com/python-sort/), [reversed()](https://realpython.com/python-reverse-list/), and more
Doesn’t support in-place sorting
Supports normal and reverse iteration
Supports pickling with [pickle](https://realpython.com/python-pickle-module/)
Ensures fast, memory-efficient, and thread-safe pop and append operations on both ends

Creating deque instances is a straightforward process. You just need to import deque from collections and call it with an optional iterable as an argument:

>>> from collections import deque

>>> # Create an empty deque
>>> deque()
deque([])

>>> # Use different iterables to create deques
>>> deque((1, 2, 3, 4))
deque([1, 2, 3, 4])

>>> deque([1, 2, 3, 4])
deque([1, 2, 3, 4])

>>> deque(range(1, 5))
deque([1, 2, 3, 4])

>>> deque("abcd")
deque(['a', 'b', 'c', 'd'])

>>> numbers = {"one": 1, "two": 2, "three": 3, "four": 4}
>>> deque(numbers.keys())
deque(['one', 'two', 'three', 'four'])

>>> deque(numbers.values())
deque([1, 2, 3, 4])

>>> deque(numbers.items())
deque([('one', 1), ('two', 2), ('three', 3), ('four', 4)])

import collections

# Create a deque
DoubleEnded = collections.deque(["Mon","Tue","Wed"])
print(DoubleEnded)

# Append to the right
print("Adding to the right: ")
DoubleEnded.append("Thu")
print(DoubleEnded)

# append to the left
print("Adding to the left: ")
DoubleEnded.appendleft("Sun")
print(DoubleEnded)

# Remove from the right
print("Removing from the right: ")
DoubleEnded.pop()
print(DoubleEnded)

# Remove from the left
print("Removing from the left: ")
DoubleEnded.popleft()
print(DoubleEnded)

# Reverse the dequeue
print("Reversing the deque: ")
DoubleEnded.reverse()
print(DoubleEnded)

""" 
deque(['Mon', 'Tue', 'Wed'])

Adding to the right: 
deque(['Mon', 'Tue', 'Wed', 'Thu'])

Adding to the left: 
deque(['Sun', 'Mon', 'Tue', 'Wed', 'Thu'])

Removing from the right: 
deque(['Sun', 'Mon', 'Tue', 'Wed'])

Removing from the left: 
deque(['Mon', 'Tue', 'Wed'])

Reversing the deque: 
deque(['Wed', 'Tue', 'Mon'])
"""

If you instantiate deque without providing an iterable as an argument, then you get an empty deque. If you

Heaps

Priority queues

Find the original version of this page (with additional content) on Notion here.

Strings, Arrays & Linked Lists

Array-based problems are the hardest problems by far there are way too many ways of manipulating an array or traversing it and so you have many different ways of actually approaching the problem in a sense you kind of get overloaded by all the possibilities.

Common ways to solve problems

Think of sorting the input array
Think of two pointers

Notes on this:

Pointers
- Fast and slow
- Same speed
- Separate ends
- Both on one end
- Sliding window
Examples:
- https://github.com/paulonteri/leetcode/blob/master/Linked Lists/remove_kth_node_from_end.py
- https://github.com/paulonteri/leetcode/blob/master/Arrays/best_time_to_buy_and_sell_stock.py
- Think of dealing with subarrays
Examples:
- https://github.com/paulonteri/leetcode/blob/master/Arrays/array_of_products.py

Strings

Python Strings

Strings

How to solve DP - String? Template and 4 Steps to be followed. - LeetCode Discuss

Examples

Valid Anagram

"""
Valid Anagram

Given two strings s and t, return true if t is an anagram of s, and false otherwise.

Example 1:

Input: s = "anagram", t = "nagaram"
Output: true
Example 2:

Input: s = "rat", t = "car"
Output: false

https://leetcode.com/problems/valid-anagram/
"""

# 0(n) time | O(n) space
class Solution:
    def isAnagram(self, s: str, t: str):

        len_s = len(s)
        len_t = len(t)

        if len_s != len_t:
            return False

        # chars from s will be added as +1
        # chars from t will be added as -1
        # then we check if each char will have a total of 0
        store = {}

        # add chars to store
        for i in range(len_s):

            # s
            if s[i] not in store:
                store[s[i]] = 1
            else:
                store[s[i]] = store[s[i]] + 1

            # t
            if t[i] not in store:
                store[t[i]] = -1
            else:
                store[t[i]] = store[t[i]] - 1

        # check if each character in the store has a value of 0
        for char in s:
            if store[char] != 0:
                return False

        return True

"""
Example 1:
    Input: s = "anagram", t = "nagaram"
    Output: true

Example 2:
    Input: s = "rat", t = "car"
    Output: false
"""

Group Anagrams

"""
Group Anagrams:

Write a function that takes in an array of strings and groups anagrams together.
Anagrams are strings made up of exactly the same letters, where order doesn't matter. 
For example, "cinema" and "iceman" are anagrams; similarly, "foo" and "ofo" are anagrams.
Your function should return a list of anagram groups in no particular order.

Sample Input
    words = ["yo", "act", "flop", "tac", "foo", "cat", "oy", "olfp"]
Sample Output
    [["yo", "oy"], ["flop", "olfp"], ["act", "tac", "cat"], ["foo"]]

https://www.algoexpert.io/questions/Group%20Anagrams
https://leetcode.com/problems/group-anagrams/
"""

"""
solution for groupAnagrams1:
1. create new array sorted_words with each string sorted in alphabetical order
2. create new array sorted_idxs with sorted_words indexes
3. sort sorted_idxs by the alphabetical order of the words in sorted_words
4. you have the sorted_words in alphabetical order...
- iterate though the sorted indeces grouping words that match together 

words =        ['yo', 'act', 'flop', 'tac', 'foo', 'cat', 'oy', 'olfp']
sorted_words = ['oy', 'act', 'flop', 'act', 'foo', 'act', 'oy', 'flop']
sorted_idxs =  [0, 1, 2, 3, 4, 5, 6, 7]
sorted_idxs =  [1, 3, 5, 2, 7, 4, 0, 6]
"""

# O(w * n * log(n) + n * w * log(w)) time | O(wn) space
#   - where w is the number of words and n is the length of the longest word
def groupAnagrams1(words):

    sorted_words = []
    for word in words:
        sorted_words.append("".join(sorted(word)))

    sorted_idxs = list(range(len(words)))

    sorted_idxs.sort(key=lambda idx: sorted_words[idx])

    anagrams = []
    idx = 0
    while idx < len(sorted_idxs):
        group = [words[sorted_idxs[idx]]]
        idx += 1

        while idx < len(sorted_idxs) and sorted_words[sorted_idxs[idx]] == sorted_words[sorted_idxs[idx-1]]:

            group.append(words[sorted_idxs[idx]])
            idx += 1

        anagrams.append(group)

    return anagrams

"""
solution for groupAnagrams2 & groupAnagrams:
1. create new array sorted_words with each string sorted in alphabetical order

   create a store hashmap b4 2
2. iterate through sorted_words checking if we have seen it before 
   if not:
        add it to the store atoring its index in an array which will be its value in the hasmap
   else:
       add it's index to the array that is it's value in the store
3. for each key in the store genarate its respective strings from the keys in the array

words =        ['yo', 'act', 'flop', 'tac', 'foo', 'cat', 'oy', 'olfp']
sorted_words = ['oy', 'act', 'flop', 'act', 'foo', 'act', 'oy', 'flop']

"""

def groupAnagrams2(words):

    sorted_words = []
    for word in words:
        sorted_words.append("".join(sorted(word)))

    store = {}
    for idx, word in enumerate(sorted_words):
        if word in store:
            store[word] = store[word] + [idx]
        else:
            store[word] = [idx]

    anagrams = []
    for key in store:

        group = []
        for idx in store[key]:
            group.append(words[idx])
        anagrams.append(group)

    return anagrams

# O(w * n * log(n)) time | O(wn) space - where w is the number of words and n is the length of the longest word
def groupAnagrams(words):

    store = {}

    for string in words:
        sorted_string = "".join(sorted(string))

        if sorted_string in store:
            store[sorted_string] = store[sorted_string] + [string]
        else:
            store[sorted_string] = [string]

    return list(store.values())

print(groupAnagrams(['yo', 'act', 'flop', 'tac', 'foo', 'cat', 'oy', 'olfp']))
print(groupAnagrams2(['yo', 'act', 'flop', 'tac', 'foo', 'cat', 'oy', 'olfp']))
print(groupAnagrams1(['yo', 'act', 'flop', 'tac', 'foo', 'cat', 'oy', 'olfp']))

Minimum Window Substring **

Minimum Window Substring - Airbnb Interview Question - Leetcode 76

""" 
76. Minimum Window Substring

Given two strings s and t of lengths m and n respectively, 
return the minimum window substring of s such that every character in t (including duplicates) is included in the window. 
If there is no such substring, return the empty string "".

The testcases will be generated such that the answer is unique.

A substring is a contiguous sequence of characters within the string.

Example 1:
    Input: s = "ADOBECODEBANC", t = "ABC"
    Output: "BANC"
    Explanation: The minimum window substring "BANC" includes 'A', 'B', and 'C' from string t.
Example 2:
    Input: s = "a", t = "a"
    Output: "a"
    Explanation: The entire string s is the minimum window.
Example 3:
    Input: s = "a", t = "aa"
    Output: ""
    Explanation: Both 'a's from t must be included in the window.
    Since the largest window of s only has one 'a', return empty string.

https://leetcode.com/problems/minimum-window-substring

Prerequisites:
- https://leetcode.com/problems/find-all-anagrams-in-a-string/ (https://www.notion.so/paulonteri/Sliding-Window-f6685a15f97a4ca2bb40111e2b264fb2#618e5fb94ea54bee8ff5eb7ab0c155ab)
- https://leetcode.com/problems/permutation-in-string
"""

import collections

""" BF """

class Solution_:

    def minWindow(self, s: str, t: str):
        t_count = collections.Counter(t)
        store = collections.defaultdict(int)

        idx = 0
        while idx < len(s) and not self.hasAllInT(store, t_count):
            store[s[idx]] += 1
            idx += 1

        if not self.hasAllInT(store, t_count):
            return ""

        res = [0, idx-1]
        left = 0
        right = idx-1
        while left <= right and right < len(s):
            # # we have all needed characters
            if left <= right and self.hasAllInT(store, t_count):
                # record size
                res = min(res, [left, right], key=lambda x: x[1]-x[0])

                # reduce size
                store[s[left]] -= 1
                if store[s[left]] == 0:
                    store.pop(s[left])
                left += 1

            # # do not have all needed characters - expand window
            else:
                right += 1
                if right < len(s):
                    store[s[right]] += 1

        return s[res[0]:res[1]+1]

    def hasAllInT(self, store, t_count):

        for char in t_count:
            if char not in store:
                return False
            if store[char] < t_count[char]:
                return False
        return True

""" Optimal """

class Solution:

    def minWindow(self, s: str, t: str):
        t_count = collections.Counter(t)

                 # # window
        window_val_count = collections.defaultdict(int)  # default 0
        # add index 0
                 num_of_valid_chars = self.increase_window(-1, s, t_count, window_val_count, 0)

        res = (0, float("inf"))

        left, right = 0, 0
        while left <= right and right < len(s):

            # we have all characters - decrease window
            if num_of_valid_chars == len(t_count):
                res = min(res, (left, right), key=lambda x: x[1]-x[0])
                num_of_valid_chars = self.decrease_window(
                    left, s, t_count, window_val_count, num_of_valid_chars)
                left += 1

            # do not have all characters - increase window
            else:
                num_of_valid_chars = self.increase_window(
                    right, s, t_count, window_val_count, num_of_valid_chars)
                right += 1

        if res[1] == float('inf'):
            return ""
        return s[res[0]:res[1]+1]

    def decrease_window(self, left, s, t_count, window_val_count, num_of_valid_chars):
        left_char = s[left]
        if left_char not in t_count:
            return num_of_valid_chars

        had_needed = window_val_count[left_char] >= t_count[left_char]

        window_val_count[left_char] -= 1

        # correct valid chars: one is now missing
        if had_needed and window_val_count[left_char] < t_count[left_char]:
            return num_of_valid_chars-1

        return num_of_valid_chars

    def increase_window(self, right, s, t_count, window_val_count, num_of_valid_chars):
        if right+1 >= len(s):
            return num_of_valid_chars

        right_char = s[right+1]
        if right_char not in t_count:
            return num_of_valid_chars

        had_needed = window_val_count[right_char] >= t_count[right_char]

        window_val_count[right_char] += 1

        # correct valid chars: one is now added
        if not had_needed and window_val_count[right_char] >= t_count[right_char]:
            return num_of_valid_chars+1

        return num_of_valid_chars

https://leetcode.com/problems/subdomain-visit-count/

from collections import defaultdict

# O(N) time | O(N) space
# assuming the length of a domain is fixed
class Solution:
    def subdomainVisits(self, cpdomains: List[str]) -> List[str]:
        visited = defaultdict(int)

        for cp_domain in cpdomains:
            str_count, domain = cp_domain.split(" ")
            count = int(str_count)

            split_domain = domain.split(".")
            curr = ""
            for idx in reversed(range(len(split_domain))):
                if idx == len(split_domain)-1:
                    curr += split_domain[idx]
                else:
                    curr = split_domain[idx] + '.' + curr

                visited[curr] += count

        return [f"{value} {key}" for key, value in visited.items()]

Word Pattern II / Pattern Matcher *

""" 
Pattern Matcher:
Word Pattern II:

You're given two non-empty strings. 
The first one is a pattern consisting of only "x"s and / or "y"s; the other one is a normal string of alphanumeric characters. 
Write a function that checks whether the normal string matches the pattern.
A string S0 is said to match a pattern if 
    replacing all "x"s in the pattern with some non-empty substring S1 of S0 and 
    replacing all "y"s in the pattern with some non-empty substring S2 of S0 yields the same string S0.
If the input string doesn't match the input pattern, the function should return an empty array; otherwise, 
    it should return an array holding the strings S1 and S2 that represent "x" and "y" in the normal string, in that order. 
If the pattern doesn't contain any "x"s or "y"s, the respective letter should be represented by an empty string in the final array that you return.
You can assume that there will never be more than one pair of strings S1 and S2 that appropriately represent "x" and "y" in the normal string.

Sample Input
    pattern = "xxyxxy"
    string = "gogopowerrangergogopowerranger"
Sample Output
    ["go", "powerranger"]

https://leetcode.com/problems/word-pattern-ii/
"""

import collections
""" 

- ensure the first letter in the pattern is x
- get the count of x and y

- for lengths of x (x_len => 1 and above):
    - calculate the y_len (length):
        - (len(string) - (x_len * x_count)) / y_count
    - get the x substring:
        - [0 : (x_len - 1)]
    - get the y substring
        - [(x_len * x_count) : (y_len - 1)]
    - build a string following the pattern using the substrings made above and check if it is equivalent to the input string
"""

# O(m) time
def order_pattern(pattern):
    patternLetters = list(pattern)
    if pattern[0] == "x":
        return patternLetters
    else:
        return list(map(lambda char: "x" if char == "y" else "y", patternLetters))

# O(m) time
def get_num_x_b4_y(sorted_pattern):
    num_x_b4_y = 0
    for char in sorted_pattern:
        if char == 'y':
            break
        num_x_b4_y += 1
    return num_x_b4_y

# O(n^2 + m) time | O(n + m) space
def patternMatcher(pattern, string):
    sorted_pattern = order_pattern(pattern)
    num_x_b4_y = get_num_x_b4_y(sorted_pattern)
    count = collections.Counter(sorted_pattern)

    # # missing x or y
    if count['y'] == 0:
        if pattern[0] == 'y':
            return ['', string[:count["x"]]]
        return [string[:count["x"]], '']

    # O(n^2) time
    for x_len in range(1, len(string)):
        # # y details
        y_len = (len(string) - (x_len*count["x"])) / count["y"]
        if y_len != round(y_len):  # skip decimals
            continue
        y_len = round(y_len)
        y_start = x_len*num_x_b4_y

        # # build new string
        new_string = [""]*len(sorted_pattern)
        x_substring = string[0:x_len]
        y_substring = string[y_start:y_start+y_len]
        for idx, char in enumerate(sorted_pattern):
            if char == 'x':
                new_string[idx] = x_substring
            else:
                new_string[idx] = y_substring

        # # validate new string
        if "".join(new_string) == string:
            if pattern[0] == 'y':
                return [y_substring, x_substring]
            return [x_substring, y_substring]

    return []

Underscorify Substring *

""" 
Underscorify Substring:

Write a function that takes in two strings: a main string and a potential substring of the main string. 
The function should return a version of the main string with every instance of the substring in it wrapped between underscores.
If two or more instances of the substring in the main string overlap each other or sit side by side, 
    the underscores relevant to these substrings should only appear on the far left of the leftmost substring 
    and on the far right of the rightmost substring. If the main string doesn't contain the other string at all, 
    the function should return the main string intact.

Sample Input
    string = "testthis is a testtest to see if testestest it works"
    substring = "test"
Sample Output
    "_test_this is a _testtest_ to see if _testestest_ it works"
"""

def merge_positions(positions):
    merged_indices = []
    idx = 0
    while idx < len(positions):
        start, end = positions[idx]
        # # merge overlaps
        # +1 to handle side by side versions too (positions[idx][1]+1)
        while idx+1 < len(positions) and positions[idx][1]+1 >= positions[idx+1][0]:
            end = positions[idx+1][1]
            idx += 1

        merged_indices.append([start, end])
        idx += 1
    return merged_indices

def is_substring_match(string, substring, idx):
    for i, char in enumerate(substring):
        string_idx = idx + i
        if string_idx >= len(string) or string[string_idx] != char:
            return False
    return True

def find_substring_positions(string, substring):
    indices = []
    for idx in range(len(string)):
        if is_substring_match(string, substring, idx):
            indices.append([idx, idx+len(substring)-1])
    return merge_positions(indices)

def underscorifySubstring(string, substring):
    res = []

    substring_positions = find_substring_positions(string, substring)
    substring_pos_idx = 0

    for idx, char in enumerate(string):
        # cannot add an underscore
        if substring_pos_idx >= len(substring_positions):
            res.append(char)
            continue

        # add underscore
        start, end = substring_positions[substring_pos_idx]
        if start == idx and end == idx:  # len(substring) == 1
            res.append('_')
            res.append(char)
            res.append('_')
            substring_pos_idx += 1
        elif end == idx:  # end of substring
            res.append(char)
            res.append('_')
            substring_pos_idx += 1
        elif start == idx:  # beginning of substring
            res.append('_')
            res.append(char)
        else:  # cannot add
            res.append(char)

    return "".join(res)

Write a string sinusoidally

One Edit Distance *

""" 
161. One Edit Distance

Given two strings s and t, return true if they are both one edit distance apart, otherwise return false.
A string s is said to be one distance apart from a string t if you can:
    Insert exactly one character into s to get t.
    Delete exactly one character from s to get t.
    Replace exactly one character of s with a different character to get t.

Example 1:
    Input: s = "ab", t = "acb"
    Output: true
    Explanation: We can insert 'c' into s to get t.
Example 2:
    Input: s = "", t = ""
    Output: false
    Explanation: We cannot get t from s by only one step.
Example 3:
    Input: s = "a", t = ""
    Output: true
Example 4:
    Input: s = "", t = "A"
    Output: true    

https://leetcode.com/problems/one-edit-distance

do https://leetcode.com/problems/edit-distance after this
"""

class Solution:

    def isOneEditDistance(self, s: str, t: str):
        # ensure one edit distance
        if abs(len(t) - len(s)) > 1:
            return False
        if s == t:
            return False
        # ensure t is longer
        if len(t) < len(s):
            return self.isOneEditDistance(t, s)

        edited = False
        s_idx, t_idx = 0, 0
        while s_idx < len(s) or t_idx < len(t):
            # one of them has reached end
            if s_idx == len(s) or t_idx == len(t):
                if edited or t_idx == len(t):
                    return False
                # can remove last element
                return t_idx == len(t)-1

            # same char
            if s[s_idx] == t[t_idx]:
                s_idx += 1
                t_idx += 1

            # try delete from t
            elif self.is_valid_move(s, t, s_idx, t_idx+1) and not edited:
                t_idx += 1
                edited = True

            # try replace
            elif self.is_valid_move(s, t, s_idx+1, t_idx+1) and not edited:
                s_idx += 1
                t_idx += 1
                edited = True
            # try insert
            # if we know len(t) is always longer or equal to len(s),
            #   replaces and deletes will work
            #   insert does the opposite of delete
            else:
                return False

        return edited

    def is_valid_move(self, s, t, s_idx, t_idx):
        if s_idx == len(s) or t_idx == len(t):
            return s_idx == len(s) and t_idx == len(t)

        if s[s_idx] == t[t_idx]:
            return True

        return False

Longest Palindromic Substring

"""
Longest Palindromic Substring:

Given a string s, return the longest palindromic substring in s.
https://leetcode.com/problems/longest-palindromic-substring/
https://www.algoexpert.io/questions/Longest%20Palindromic%20Substring
"""

class Solution:
    def longestPalindrome(self, s: str):
        if len(s) < 2:
            return s

        longest = idx = 1
        left = right = 0
        for idx in range(1, len(s)):

            # check for both even and odd palindromes
            # Examples: even -> zyaaaagh, odd -> zyaaagh
            even, left_even, right_even = self.expandFromMiddle(s, idx-1, idx)
            odd, left_odd, right_odd = self.expandFromMiddle(s, idx-1, idx+1)

            # record the largest palindrome we found
            if even > odd and even > longest:
                longest = even
                left = left_even
                right = right_even
            if odd > even and odd > longest:
                longest = odd
                left = left_odd
                right = right_odd

        return s[left:right+1]

    def expandFromMiddle(self, s, left, right):
        if right >= len(s) or s[left] != s[right]:
            return 0, left, right

        # pointers showing how far we have expanded (which marks how wide the palindrome is)
        exp_left = left
        exp_right = right

        while left >= 0 and right < len(s) and s[left] == s[right]:
            # expand
            exp_left = left
            exp_right = right

            # move on to checking the next
            left -= 1
            right += 1

        # return len of the longest palindrome we found
        return ((exp_right - exp_left) + 1), exp_left, exp_right

Break a Palindrome

LeetCode 1328 - Break a Palindrome

""" 
1328. Break a Palindrome

Given a palindromic string of lowercase English letters palindrome, replace exactly one character with any lowercase English letter so that the resulting string is not a palindrome and that it is the lexicographically smallest one possible.
Return the resulting string. If there is no way to replace a character to make it not a palindrome, return an empty string.
A string a is lexicographically smaller than a string b (of the same length) if in the first position where a and b differ, a has a character strictly smaller than the corresponding character in b. 
For example, "abcc" is lexicographically smaller than "abcd" because the first position they differ is at the fourth character, and 'c' is smaller than 'd'.

Example 1:
    Input: palindrome = "abccba"
    Output: "aaccba"
    Explanation: There are many ways to make "abccba" not a palindrome, such as "zbccba", "aaccba", and "abacba".
    Of all the ways, "aaccba" is the lexicographically smallest.
Example 2:
    Input: palindrome = "a"
    Output: ""
    Explanation: There is no way to replace a single character to make "a" not a palindrome, so return an empty string.
Example 3:
    Input: palindrome = "aa"
    Output: "ab"
Example 4:
    Input: palindrome = "aba"
    Output: "abb"

https://leetcode.com/problems/break-a-palindrome
"""

class Solution:
    def breakPalindrome(self, palindrome: str):
        if len(palindrome) <= 1:
            return ""

        # replace first non-a
        is_odd = len(palindrome) % 2 != 0
        for idx, char in enumerate(palindrome):
            if is_odd and idx == len(palindrome) // 2:
                continue

            if char != "a":
                return palindrome[:idx] + "a" + palindrome[idx+1:]

        # no valid non-a was found so replace the last character
        # eg: aaa->aab, aaaa->aaab, aba->abb
        return palindrome[:-1] + "b"

String Rotation

""" 
String Rotation:

Assume you have a method isSubstring which checks if one word is a substring of another. 
Given two strings, sl and s2, write code to check if s2 is a rotation of sl using only one call to isSubstring 
    (e.g.,"waterbottle" is a rotation of"erbottlewat").
"""

def is_substring(str, substring):
    return substring in str

def string_rotation(s1, s2):
    if len(s1) != len(s2):
        return False
    return is_substring(s1+s1, s2)

Group Shifted Strings *

""" 
249. Group Shifted Strings

We can shift a string by shifting each of its letters to its successive letter.
For example, "abc" can be shifted to be "bcd".
We can keep shifting the string to form a sequence.
For example, we can keep shifting "abc" to form the sequence: "abc" -> "bcd" -> ... -> "xyz".
Given an array of strings strings, group all strings[i] that belong to the same shifting sequence. You may return the answer in any order.

Example 1:
    Input: strings = ["abc","bcd","acef","xyz","az","ba","a","z"]
    Output: [["acef"],["a","z"],["abc","bcd","xyz"],["az","ba"]]
Example 2:
    Input: strings = ["a"]
    Output: [["a"]]

https://leetcode.com/problems/group-shifted-strings
"""

import collections

class Solution:
    def getMovement(self, string):
        movement = []
        for i in range(1, len(string)):
            move = ord(string[i]) - ord(string[i-1])
            if move < 0:  # alphabet is a closed loop
                move += 26
            movement.append(move)
        return tuple(movement)

    def groupStrings(self, strings):
        moves = collections.defaultdict(list)

        for string in strings:
            moves[self.getMovement(string)].append(string)

        return list(moves.values())

Count and Say

Screenshot 2021-11-01 at 16.59.15.png

""" 
Count and Say:

The count-and-say sequence is a sequence of digit strings defined by the recursive formula:
countAndSay(1) = "1"
countAndSay(n) is the way you would "say" the digit string from countAndSay(n-1), which is then converted into a different digit string.
To determine how you "say" a digit string, split it into the minimal number of groups so that each group is a contiguous section all of the same character. Then for each group, say the number of characters, then say the character. To convert the saying into a digit string, replace the counts with a number and concatenate every saying.
For example, the saying and conversion for digit string "3322251":

Given a positive integer n, return the nth term of the count-and-say sequence.

Example 1:
    Input: n = 1
    Output: "1"
    Explanation: This is the base case.
Example 2:
    Input: n = 4
    Output: "1211"
    Explanation:
        countAndSay(1) = "1"
        countAndSay(2) = say "1" = one 1 = "11"
        countAndSay(3) = say "11" = two 1's = "21"
        countAndSay(4) = say "21" = one 2 + one 1 = "12" + "11" = "1211"

https://leetcode.com/problems/count-and-say
"""

class Solution:
    def countAndSay(self, n: int):
        if n == 1:
            return '1'

        res = [1]
        for _ in range(n-1):
            new_res = []

            curr = res[0]
            count = 1
            for idx in range(1, len(res)):
                if res[idx] == curr:
                    count += 1
                else:
                    new_res.append(count)
                    new_res.append(curr)
                    # reset
                    curr = res[idx]
                    count = 1

            new_res.append(count)
            new_res.append(curr)

            res = new_res

        return "".join([str(num) for num in res])

Interconvert Strings & Integers

"""
Interconvert Strings & Integers:

A string is a sequence of characters. A string may encode an integer, e.g., "123" encodes 123. 
In this problem, you are to implement methods that take a string representing an integer and return the corresponding integer, and vice versa. 
Your code should handle negative integers. You cannot use library functions like int in Python.
Implement an integer to string conversion function, and a string to integer conversion function, 
For example, 
 if the input to the first function is the integer 314,
 it should return the string "314" 
 and if the input to the second function is the string "314" it should return the integer 314.

EPI 6.1
"""

""" 
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
int to string
"""

def single_digit_to_char(digit):
    return chr(ord('0')+digit)

def int_to_string(x: int):
    if x == 0:
        return "0"

    is_neg = False
    if x < 0:
        is_neg, x = True, -x

    result = []
    while x > 0:
        result.append(single_digit_to_char(x % 10))
        x = x // 10

    if is_neg:
        result.append('-')
    return "".join(reversed(result))

""" 
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
string to int
"""

def single_char_to_int(character):
    num_mapping = {
        "1": 1,
        "2": 2,
        "3": 3,
        "4": 4,
        "5": 5,
        "6": 6,
        "7": 7,
        "8": 8,
        "9": 9,
        "0": 0,
    }
    return num_mapping[character]

def string_to_int(s: str):

    is_neg = False
    start_idx = 0
    if s and s[0] == "-":
        is_neg, start_idx = True, 1
    if s and s[0] == "+":
        start_idx = 1

    running_sum = 0
    multiplier = 1

    for idx in reversed(range(start_idx, len(s))):
        running_sum += single_char_to_int(s[idx])*multiplier
        multiplier *= 10

    if is_neg:
        return -running_sum
    return running_sum

Letter Case Permutations *

Caesar Cipher Encryptor

"""
Caesar Cipher Encryptor:

Given a non-empty string of lowercase letters and a non-negative integer representing a key,
write a function that returns a new string obtained by shifting every letter in the input string by k positions in the alphabet,
where k is the key.
Note that letters should "wrap" around the alphabet;
 in other words, the letter z shifted by one returns the letter a.

https://www.algoexpert.io/questions/Caesar%20Cipher%20Encryptor
"""

def caesarCipherEncryptor_(string, key):
     key = key % 26  # handle large numbers
   letters = []

    for char in string:
        moved_ord = ord(char) + key

        if moved_ord > ord('z'):
            moved_ord -= 26

        letters.append(chr(moved_ord))

    return "".join(letters)

Minimum Characters For Words

"""
Minimum Characters For Words:

Write a function that takes in an array of words and returns the smallest array of characters needed to form all of the words.
The characters don't need to be in any particular order.
For example, the characters ["y", "r", "o", "u"] are needed to form the words ["your", "you", "or", "yo"].
Note: the input words won't contain any spaces; however, they might contain punctuation and/or special characters.

Sample Input
    words = ["this", "that", "did", "deed", "them!", "a"]
Sample Output
    ["t", "t", "h", "i", "s", "a", "d", "d", "e", "e", "m", "!"]
    // The characters could be ordered differently.

https://www.algoexpert.io/questions/Minimum%20Characters%20For%20Words
"""

from collections import defaultdict

# O(n) time | O(n) space - where n is the length of the word
def get_word_characters(word):
    char_count = defaultdict(int)
    for char in word:
        char_count[char] += 1

    return char_count

# O(n*l) time | O(c) space
# where n is the number of words, l the length of the longest word, c the number of unique charactters
def minimumCharactersForWords(words):
    min_character_count = defaultdict(int)

    for word in words:
        word_char_count = get_word_characters(word)
        for char in word_char_count:
            # update count if we find a word that needs more
            min_character_count[char] = max(
                min_character_count[char], word_char_count[char]
            )

    # convert hash table to list
    min_character_count_list = []
    for char in min_character_count:
        count = min_character_count[char]
        while count > 0:
            min_character_count_list.append(char)
            count -= 1

    return min_character_count_list

"""
- Draw Example(s)
- Test case
- Brute force
- Explain Solution / Algorithm
- Talk about tradeoffs
- Talk through edge cases
- Pseudocode
- Code

[
"this",  -> "t","h","i","s"
"that",  -> "t","t","h","a"
"did"    -> "d","d","i"
]

["t","t","h","i","s","d","d"]

- have an output array that will store the char count
- for each word, calculate the unique character count. Then check

def get_word_characters(word):
    return {}

def minimumCharactersForWords(words):
    min_character_count = {}
    for word in words:
        word_char_count = get_word_characters(word)
        # coompare the word_char_count & min_character_count then update if necessary

    return convert_to_list(min_character_count)

"""

Valid IP Addresses

"""
Valid IP Addresses:

You're given a string of length 12 or smaller, containing only digits. 
Write a function that returns all the possible IP addresses that can be created by inserting three .s in the string.
An IP address is a sequence of four positive integers that are separated by .s, where each individual integer is within the range 0 - 255, inclusive.
An IP address isn't valid if any of the individual integers contains leading 0s. 
 For example, "192.168.0.1" is a valid IP address, but "192.168.00.1" and "192.168.0.01" aren't, because they contain "00" and 01, respectively.
  Another example of a valid IP address is "99.1.1.10"; conversely, "991.1.1.0" isn't valid, because "991" is greater than 255.
Your function should return the IP addresses in string format and in no particular order.
If no valid IP addresses can be created from the string, your function should return an empty list.

Sample Input
    string = "1921680"
Sample Output
    [
    "1.9.216.80",
    "1.92.16.80",
    "1.92.168.0",
    "19.2.16.80",
    "19.2.168.0",
    "19.21.6.80",
    "19.21.68.0",
    "19.216.8.0",
    "192.1.6.80",
    "192.1.68.0",
    "192.16.8.0"
    ]
    // The IP addresses could be ordered differently.
https://www.algoexpert.io/questions/Valid%20IP%20Addresses
"""

def is_valid_ip(string):

    string_as_num = int(string)
    if string_as_num < 0 or string_as_num > 255:
        return False

    # check for leading zeros
    return len(str(string_as_num)) == len(string)

# O(1) time | O(1) space |-> there are a limited/finite/constant number (2^32) of IP Addresses
def validIPAddresses0(string):
    length = len(string)
    all_ip_addresses = []

    ip_address = ['', '', '', '']
    for i_one in range(1, min(length, 4)):
        ip_address[0] = string[:i_one]
        if not is_valid_ip(ip_address[0]):
            continue  # stop current for loop run

        for i_two in range(i_one+1, min(length, i_one+4)):
            ip_address[1] = string[i_one:i_two]
            if not is_valid_ip(ip_address[1]):
                continue  # stop current for loop run (for i_two)

            for i_three in range(i_two+1, min(length, i_two+4)):
                ip_address[2] = string[i_two:i_three]
                ip_address[3] = string[i_three:]
                if is_valid_ip(ip_address[2]) and is_valid_ip(ip_address[3]):
                    all_ip_addresses.append(".".join(ip_address))

    return all_ip_addresses

Valid Palindrome II

""" 
Valid Palindrome II:

Given a string s, return true if the s can be palindrome after deleting at most one character from it.

Example 1:
    Input: s = "aba"
    Output: true
Example 2:
    Input: s = "abca"
    Output: true
    Explanation: You could delete the character 'c'.
Example 3:
    Input: s = "abc"
    Output: false

https://leetcode.com/problems/valid-palindrome-ii
"""

class Solution:
    def validPalindrome(self, s: str):

        left = 0
        right = len(s)-1
        while left < right:
            # left and right are same
            if s[left] == s[right]:
                left += 1
                right -= 1

            # left and right not same
            else:
                return self.isPalindrome(s, left) or self.isPalindrome(s, right)

        return True

    def isPalindrome(self, s, skip):
        # we will start be comparing the left most char & the right most char
        a_pointer = 0
        b_pointer = len(s) - 1

        while a_pointer < b_pointer:
            # skip
            if a_pointer == skip:
                a_pointer += 1
            if b_pointer == skip:
                b_pointer -= 1

            # check if not the same
            if s[a_pointer] != s[b_pointer]:
                return False

            # move on to the next set of chars
            a_pointer += 1
            b_pointer -= 1
        return True

Count Binary Substrings

""" 
696. Count Binary Substrings

Give a binary string s, return the number of non-empty substrings that have the same number of 0's and 1's,
    and all the 0's and all the 1's in these substrings are grouped consecutively.
Substrings that occur multiple times are counted the number of times they occur.

Example 1:
    Input: s = "00110011"
    Output: 6
    Explanation: There are 6 substrings that have equal number of consecutive 1's and 0's: "0011", "01", "1100", "10", "0011", and "01".
        Notice that some of these substrings repeat and are counted the number of times they occur.
        Also, "00110011" is not a valid substring because all the 0's (and 1's) are not grouped together.
Example 2:
    Input: s = "10101"
    Output: 4
    Explanation: There are 4 substrings: "10", "01", "10", "01" that have equal number of consecutive 1's and 0's.

https://leetcode.com/problems/count-binary-substrings
"""

class Solution(object):
    def countBinarySubstrings(self, s):
        ans = 0
        # group sizes (group of zeros or ones)
        prev, cur = 0, 1

        for idx in range(1, len(s)):
            if s[idx-1] != s[idx]:
                # add curr group + the one b4 it
                ans += min(prev, cur)
                # create a new group and move cur to prev
                prev, cur = cur, 1
            else:
                cur += 1

        ans += min(prev, cur)

        return ans

class Solution_:
    def countBinarySubstrings(self, s: str):
        """ 
        - count = 0
        - iterate from index 0 to the 2nd last index
        - for each index:
            - left = index
            - right = index + 1
            - while expand_window(left, right):
                count += 1
                left -= 1
                right += 1
        - return count
        """
        count = 0

        for idx in range(len(s)-1):
            left, right = idx, idx+1

            # check if can start expansion
            left_char, right_char = s[left], s[right]
            expand = left_char + right_char
            if not ("0" in expand and "1" in expand):
                continue

            # expand
            while self.expand_window(s, left, right, left_char, right_char):
                count += 1
                left -= 1
                right += 1

        return count

    def expand_window(self, s, left, right, left_char, right_char):
        """ 
        check if we have a 0 & 1 in left+right
        """
        if left < 0 or right >= len(s):
            return False
        if s[left] != left_char or s[right] != right_char:
            return False

        return True

Reverse Words in a String -

"""
Reverse Words in a String:

Given an input string s, reverse the order of the words.
A word is defined as a sequence of non-space characters.
The words in s will be separated by at least one space.
Return a string of the words in reverse order concatenated by a single space.
Note that s may contain leading or trailing spaces or multiple spaces between two words.
The returned string should only have a single space separating the words. Do not include any extra spaces.

Reverse Words In String:
Write a function that takes in a string of words separated by one or more whitespaces and returns a string that has these words in reverse order.
For example, given the string "tim is great", your function should return "great is tim".
For this problem, a word can contain special characters, punctuation, and numbers.
The words in the string will be separated by one or more whitespaces, and the reversed string must contain the same whitespaces as the original string.
For example, given the string "whitespaces 4" you would be expected to return "4 whitespaces".
Note that you're not allowed to to use any built-in split or reverse methods/functions. However, you are allowed to use a built-in join method/function.
Also note that the input string isn't guaranteed to always contain words.

Sample Input
    string = "AlgoExpert is the best!"
Sample Output
    "best! the is AlgoExpert"

https://leetcode.com/problems/reverse-words-in-a-string/
https://www.algoexpert.io/questions/Reverse%20Words%20In%20String
"""

# O(n) time | O(n) space - where n is the length of the string
def reverseWordsInString(string):
    words = []

    idx = len(string) - 1
    while idx >= 0:
        # white space
        if string[idx] == " ":
            words.append(" ")
            idx -= 1

        # words
        else:
            # get word's beginning
            start = idx
            while start - 1 >= 0 and string[start - 1] != " ":
                start -= 1
            # add word to words array
            words.append(string[start:idx+1])

            idx = start - 1
    return "".join(words)

https://leetcode.com/explore/interview/card/bloomberg/68/array-and-strings/402/ string compression

Strobogrammatic Number

""" 
Strobogrammatic Number

Given a string num which represents an integer, return true if num is a strobogrammatic number.
A strobogrammatic number is a number that looks the same when rotated 180 degrees (looked at upside down).

Example 1:
    Input: num = "69"
    Output: true
Example 2:
    Input: num = "88"
    Output: true
Example 3:
    Input: num = "962"
    Output: false
Example 4:
    Input: num = "1"
    Output: true

https://leetcode.com/problems/strobogrammatic-number
"""

class Solution:
    def isStrobogrammatic(self, num):
        rotated_digits = {'0': '0', '1': '1', '8': '8', '6': '9', '9': '6'}

        rotated = list(num)
        for idx, char in enumerate(rotated):
            if char not in rotated_digits:
                return False

            rotated[idx] = rotated_digits[char]

        rotated.reverse()
        return "".join(rotated) == num

Largest lexicographical string with at most K consecutive elements

screencapture-geeksforgeeks-org-largest-lexicographical-string-with-at-most-k-consecutive-elements-2021-10-22-12_21_18.pdf

Multi String Search *

""" 
Multi String Search:

Write a function that takes in a big string and an array of small strings, all of which are smaller in length than the big string. 
The function should return an array of booleans, where each boolean represents whether the small string at that index in the array of small strings is contained in the big string.
Note that you can't use language-built-in string-matching methods.

Sample Input #1
    bigString = "this is a big string"
    smallStrings = ["this", "yo", "is", "a", "bigger", "string", "kappa"]
Sample Output #1
    [true, false, true, true, false, true, false]
Sample Input #2
    bigString = "abcdefghijklmnopqrstuvwxyz"
    smallStrings = ["abc", "mnopqr", "wyz", "no", "e", "tuuv"]
Sample Output #2
    [true, true, false, true, true, false]

https://www.algoexpert.io/questions/Multi%20String%20Search
"""

endSymbol = "*"

class Trie:
    def __init__(self):
        self.root = {}
        self.endSymbol = endSymbol

    def add(self, word, idx):
        current = self.root
        for letter in word:
            if letter not in current:
                current[letter] = {}
            current = current[letter]
        current[self.endSymbol] = (word, idx)

def find_words(trie, bigString, found_words, idx):
    # # validate
    if idx == len(bigString) or bigString[idx] not in trie:
        return
    char = bigString[idx]
    curr_trie = trie[char]

    # record all words found
    if endSymbol in curr_trie:
        _, i = curr_trie[endSymbol]
        found_words[i] = True

    find_words(curr_trie, bigString, found_words, idx+1)

# O(ns + bs) time | O(ns) space
# b len(big), s len(small), n - no. of small strings, 
def multiStringSearch(bigString, smallStrings):
    found_words = [False] * len(smallStrings)

    # # create trie
    trie = Trie()
    for idx, word in enumerate(smallStrings):
        trie.add(word, idx)

    # # find words
    for idx in range(len(bigString)):
        find_words(trie.root, bigString, found_words, idx)

    return found_words

Questions to ask the interviewer

Is it case sensitive?

Are there special characters?

Is there whitespace? Is it significant?

Tips

Try iterating form the end

Basics

Functions

.count(str) returns how many times the str substring appears in the given string.

.upper() converts the string to uppercase.

.lower() converts the string to lowercase.

.swapcase()

.replace(old, new) replaces all occurrences of old with new.

.find(str)

.split()

.startswith(prefix)

.endswith(suffix)

.isalpha() returns true if a string only contains letters.

.isnumeric() returns true if all characters in a string are numbers.

.isalnum() only returns true if a string contains alphanumeric characters, without symbols.

Are similar to arrays

print(list(enumerate("cold")))  # [(0, 'c'), (1, 'o'), (2, 'l'), (3, 'd')]
print("expensive" not in "The best things in life are free!") # True

Conversion to unicode

print(ord("0")) # 48

print(ord("a")) # 97
print(chr(97)) # a

Convert single digit integer to unicode

print(chr( ord('0') + 2 )) # 9
# or
two_ord = ord('0') + 2
print(chr(two_ord)) # 9

Change a string

Strings are immutable. This means that elements of a string cannot be changed once it has been assigned. We can simply reassign different strings to the same name.

string = "Hello world!"

string[0] = "h"
# TypeError: 'str' object does not support item assignment

string = "hello world!"
print string
# hello world!

Reverse

Need to convert string to list and then reverse().

string = "Hello world!"

string.reverse()
# AttributeError: 'str' object has no attribute 'reverse'

reversed(string) + "apple"
# TypeError: unsupported operand type(s) for +: 'reversed' and 'str'

print string[::-1] 
# !dlrow olleH

.upper() .lower() .swapcase()

print string.upper()
# HELLO WORLD!

print string.lower()
# hello world!

print string.swapcase()
# 'hELLO WORLD!'

.replace()

replaces all occurrences of old with new

str1 = "emre.me.emre.me"

print(str1.replace(".", "-"))
# emre-me-emre-me

.count()

p = "paul is apaul is paul"

p.count("paul")
# 3

.join()

x = ["", "2", "", "3"]

"".join(x) # '23'

Slicing *

A subset of array slicing

word = "0123456789"

print(word[8]) # 8
print(word[-2]) # 8

# Simple slicing
print(word[2:4]) # 23
print(word[2:]) # 23456789
print(word[:4]) # 0123 -> first 4

# reverse
print(word[2:8]) # 23456
print(word[2:-2]) # 23456

# stride
print(word[2:8:2]) # 246
print(word[::2]) # 02468
print(word[::1]) # 0123456789
print(word[::-2]) # 97531
print(word[::-1]) # 9876543210

Sort section of an array using slicing

def sort(self, nums, sort_start):
    nums[sort_start:] = list(sorted(nums[sort_start:]))

You can store all alpha characters in an array of length 26 *

Storing alphanumeric characters in a data structure

Largest lexicographical string with at most K consecutive elements

screencapture-geeksforgeeks-org-largest-lexicographical-string-with-at-most-k-consecutive-elements-2021-10-22-12_21_18.pdf

Time complexity of Arrays,sort(String [])

Given: String[] str, for example: str = {"Hello", "World", "John", "Doe"}
Let n be the number of elements in the str array.
Let m be the average/maximum # of characters for the strings in the str array
Then, calling Arrays.sort(str) on this array would have the performance characteristic of O(m * n log n).

The reason it's O(m*n logn) is that the sorting algorithm itself will run O(n logn) comparison operations in order to perform the sort. And each comparison operation takes O(m) time to finish.

Though that is very much the worst-case scenario: Given, say, Hello and World, even though m = 5 for those two, the comparison completes after only 1 step; the algorithm compares H and W and answers immediately, never even looking at ello or orld. But if the strings are Hello1, Hello2, Hello3 and Hello4, then that's a guaranteed 5 'steps' for every time 2 strings are compared, and there will be O(n logn) comparisons.

If we use a naive sorting algorithm of O(N^2) time, then the total will be O(M * N^2)

Note:

As said above, strings behave much like normal arrays, with the main distinction being that, strings are immutable, meaning that they can't be edited after creation. This also means that simple operations like appending a character to a string are more expensive than they might appear. The canonical example of an operation that's deceptively expensive due to string immutability is the following:

string = "this is a string"
newString = ""

for character in string:
    newString += character

The operation above has a time complexity of O(n^2) where n is the length of string, because each addition of a character to newString creates an entirely new string and is itself an O(n) operation. Therefore, n O(n) operations are performed, leading to an O(n^2) time-complexity operation overall.

StringBuilder

Imagine you were concatenating a list of strings. What would the running time of this code be? For simplicity, assume that the strings are all the same length (call this x) and that there are n strings.

On each concatenation,a new copy of the string is created, and the two strings are copied over,character by character. The first iteration requires us to copy x characters. The second iteration requires copying 2x characters. The third iteration requires 3x,and so on. The total time therefore is O(x + 2x + . . . + nx). This reduces to O(xn^2).

Why is it O(xn^2)? Because 1 + 2 + ... + n equals n(n+1)/2, or O(n^2)

StringBuilder can help you avoid.this problem. StringBuilder simply creates a resizable array of all the strings, copying them back to a string only when necessary.

StringBuilder (Java)

Arrays

Python List

Examples

Hare & Tortoise Algorithm

Contains Duplicate

""" 
Contains Duplicate

Given an integer array nums, 
return true if any value appears at least twice in the array, 
and return false if every element is distinct.

https://leetcode.com/problems/contains-duplicate/
"""

class Solution:
    def containsDuplicate(self, nums):

        store = set()

        for num in nums:
            # we have seen num before
            if num in store:
                return True
            # record that we have just seen num
            store.add(num)

        return False

    def containsDuplicate_(self, nums):
        return not len(set(nums)) == len(nums)

class Solution_:
    def containsDuplicate(self, nums):
        nums.sort()

        for idx in range(1, len(nums)):
            if nums[idx] == nums[idx-1]:
                return True

        return False

When given problems (involving choice) with two arrays, where their indices represent an entity, you can recurse by iterating through each index deciding to include it or not
- 0/1 Knapsack
- Equal Subset Sum Partition

Permutations *
Letter Case Permutations *

Pairs with Specific Difference *

""" 
Pairs with Specific Difference:

Given an array arr of distinct integers and a nonnegative integer k, 
write a function findPairsWithGivenDifference that returns an array of all pairs [x,y] in arr, 
such that x - y = k. If no such pairs exist, return an empty array.

Note: the order of the pairs in the output array should maintain the order of the y element in the original array.

Examples:
    [4,1], 3
    [[4,1]]

    [0,-1,-2,2,1], 1
    [[1, 0], [0, -1], [-1, -2], [2, 1]]

    [1,5,11,7], 4
    [[5,1], [11,7]]

    [1,5,11,7], 6
    [[7,1],[11,5]]

https://www.pramp.com/challenge/XdMZJgZoAnFXqwjJwnpZ

Similar: https://leetcode.com/problems/k-diff-pairs-in-an-array/
"""

""" 

curr - next = k
curr = k + next
"""

def find_pairs_with_given_difference(arr, k):
    res = []
    store = set(arr)

    for num in arr:
        if num+k in store:
            res.append([num+k, num])

    return res

""" 
Works but doesn't obey ordering

curr - next = k
next = curr - k

def find_pairs_with_given_difference(arr, k):
    res = []
    store = set(arr)

    for num in arr:
        if num-k in store:
            res.append([num, num-k])

    return res

"""

print(find_pairs_with_given_difference(
    [0, -1, -2, 2, 1], 1), "required: ", [[1, 0], [0, -1], [-1, -2], [2, 1]])
print(find_pairs_with_given_difference(
    [1, 5, 11, 7], 4), "required: ", [[5, 1], [11, 7]])
print(find_pairs_with_given_difference(
    [1, 5, 11, 7], 6), "required: ",  [[7, 1], [11, 5]])

Three Sum *

Four sum

4SUM (Leetcode) - Code & Whiteboard

Vvveeerrryyyy helpful

4 Sum Problem | Leetcode #18

If ignoring duplicates

https://youtu.be/29LH8QeJMzw

""" 
4Sum:

Given an array nums of n integers, return an array of all the unique quadruplets [nums[a], nums[b], nums[c], nums[d]] such that:
    0 <= a, b, c, d < n
    a, b, c, and d are distinct.
    nums[a] + nums[b] + nums[c] + nums[d] == target
You may return the answer in any order.

Example 1:
    Input: nums = [1,0,-1,0,-2,2], target = 0
    Output: [[-2,-1,1,2],[-2,0,0,2],[-1,0,0,1]]
Example 2:
    Input: nums = [2,2,2,2,2], target = 8
    Output: [[2,2,2,2]]
"""

""" 
[1,0,-1,0,-2,2]

[-2, -1, 0, 0, 1, 2]

- four sum is a combination of two two_sums

- sort the input array so that we can skip duplicates

- have two loops with to iterate through all the possible two number combinations:
    - for the rest of the numbers: find a two sum that = target - (arr[idx_loop_one] + arr[idx_loop_two])

"""

class Solution:

    def fourSum(self, nums, target):
        res = []
        nums.sort()

        for one in range(len(nums)):
            if one > 0 and nums[one] == nums[one-1]:
                continue  # skip duplicates
            for two in range(one+1, len(nums)):
                if two > one+1 and nums[two] == nums[two-1]:
                    continue  # skip duplicates

                # # two sum
                needed = target - (nums[one] + nums[two])
                left = two + 1
                right = len(nums)-1
                while left < right:
                    # skip duplicates
                    if left > two + 1 and nums[left] == nums[left-1]:
                        left += 1
                        continue
                    if right < len(nums)-1 and nums[right] == nums[right+1]:
                        right -= 1
                        continue

                    total = nums[left] + nums[right]
                    if total < needed:
                        left += 1
                    elif total > needed:
                        right -= 1
                    else:
                        res.append(
                            [nums[one], nums[two], nums[left], nums[right]])
                        left += 1
                        right -= 1

        return res

Maximum Product Subarray **

Screenshot 2021-10-16 at 21.03.00.png

Screenshot 2021-10-16 at 21.03.49.png

Screenshot 2021-10-16 at 21.04.14.png

Screenshot 2021-10-16 at 21.04.39.png

Screen Recording 2021-10-16 at 21.05.00.mov

"""
Maximum Product Subarray:

Given an integer array nums, find the contiguous subarray within an array (containing at least one number) which has the largest product.
Example 1:
    Input: [2,3,-2,4]
    Output: 6
    Explanation: [2,3] has the largest product 6.
Example 2:
    Input: [-2,0,-1]
    Output: 0
    Explanation: The result cannot be 2, because [-2,-1] is not a subarray.

https://leetcode.com/problems/maximum-product-subarray/
https://afteracademy.com/blog/max-product-subarray
"""

# O(n) time | O(1) space
class Solution:
    def maxProduct(self, array):

        if not array:
            return -1

        max_product = curr_max = curr_min = array[0]

        for idx in range(1, len(array)):

            temp_curr_max = curr_max
            curr_max = max(
                curr_max * array[idx],
                curr_min * array[idx],  # if array[idx] is negative [-2, 3, -4]
                array[idx]  # helps if array[idx-1] is 0 eg: [0, 2]
            )
            curr_min = min(
                temp_curr_max * array[idx],
                curr_min * array[idx],
                array[idx]
            )

            max_product = max(max_product, curr_max)

        return max_product

sol = Solution()
print(sol.maxProduct([2, 2, 2, 1, -1, 5, 5]))
print(sol.maxProduct([-2, 3, -4]))
print(sol.maxProduct([2]))
print(sol.maxProduct([]))
print(sol.maxProduct([-5]))
print(sol.maxProduct([0, 2, 2, 2, 1, -1, -5, -5]))
print(sol.maxProduct([0, 2]))

"""
Dynamic Programming:

Imagine that we have both max_prod[i] and min_prod[i] i.e. max product ending at i and min product ending at i.

Now if we have a negative number at arr[i+1] and if min_prod[i] is negative,
then the product of the two will be positive and can potentially be the largest product.
So, the key point here is to maintain both the max_prod and min_prod such that at iteration i, they refer to the max and min product ending at index i-1.

In short, One can have three options to make at any position in the array.
- You can get the maximum product by multiplying the current element with the maximum product calculated so far. (might work when current
  element is positive).
- You can get the maximum product by multiplying the current element with minimum product calculated so far. (might work when current
  element is negative).
- The current element might be a starting position for maximum product subarray.
Solution Steps

Initialize maxProduct with arr[0] to store the maximum product so far.
Initialize to variables imax and imin to store the maximum and minimum product till i .
Iterate over the arr and for each negative element of arr, swap imax and imin. (Why?)
Update imax and imin as discussed above and finally return maxProduct
"""

Maximum Subarray **

Subarray Sum Equals K *

Next: Path sum III, Segment trees

Subarray Sum Equals K - Prefix Sums - Leetcode 560 - Python

LeetCode Subarray Sum Equals K Solution Explained - Java

Screenshot 2021-11-13 at 19.53.18.png

"""
Subarray Sum Equals K

Given an array of integers and an integer k,
you need to find the total number of continuous subarrays whose sum equals to k.
Example 1:
    Input: nums = [1,1,1], k = 2
    Output: 2
Example 2:
    Input: nums = [1,2,3], k = 3
    Output: 2

https://leetcode.com/problems/subarray-sum-equals-k/
Do Next: 
- https://leetcode.com/problems/path-sum-iii/
- https://leetcode.com/problems/continuous-subarray-sum
"""

from collections import defaultdict
from typing import List

"""

The idea behind the approach below is as follows: If the cumulative sum(represented by sum[i] for sum up to i^th index) up to two indices is the same,
 the sum of the elements lying in between those indices is zero.
Extending the same thought further, 
 if the cumulative sum up to two indices, say i and j is at a difference of k 
    i.e. if sum[i] - sum[j] = k, 
    the sum of elements lying between indices i and j is k.

If you were at a current sum, 
and you have seen (sum - k) before, it mean that,
we've seen an array of size k: - the distance between those two points is of size k
"""

# O(n) time | O(n) space | n = len(array)
class Solution:
    # check if a total sum in the past plus the current will be equal to k
    # if a (the current sum - a previous sum = k),
    # then elements in the array between must add up to k
    def subarraySum(self, nums: List[int], k: int):
        res = 0

        prev_sums = defaultdict(int)
        # the store has to have 0 to deal with the case where k is in the list
        prev_sums[0] = 1
        curr_sum = 0
        # if (the current sum - a sum in the past = k),
        # then the subarray in between them adds up to k
        for num in nums:

            curr_sum += num
            needed_diff = curr_sum - k

            # check for the needed_diff
            if needed_diff in prev_sums:
                # we add the number of possible times we can get that needed_diff
                res += prev_sums[needed_diff]

             # add the current sum to the store
            prev_sums[curr_sum] += 1

        return res

"""

# only works for arrays with positive integers
class Solution0:
    def subarraySum(self, nums: List[int], k: int):
        res = 0
        total = nums[0]

        start = end = 0
        while start < len(nums):
            if total == k:
                res += 1

            # # edge cases
            # when we cannot increase end or start
            if end == len(nums)-1 or start == len(nums)-1:
                total -= nums[start]
                start += 1
                continue

            if total <= k:
                end += 1
                total += nums[end]
            else:
                total -= nums[start]
                start += 1

        return res

"""

https://leetcode.com/problems/maximum-size-subarray-sum-equals-k/ *

class Solution:
    def maxSubArrayLen(self, nums: List[int], k: int) -> int:
        prefix_sum = longest_subarray = 0
        indices = {}

        for i, num in enumerate(nums):
            prefix_sum += num

            # Check if all of the numbers seen so far sum to k.
            if prefix_sum == k:
                longest_subarray = i + 1

            # If any subarray seen so far sums to k, then
            # update the length of the longest_subarray. 
            if prefix_sum - k in indices:
                longest_subarray = max(longest_subarray, i - indices[prefix_sum - k])

            # Only add the current prefix_sum index pair to the 
            # map if the prefix_sum is not already in the map.
            if prefix_sum not in indices:
                indices[prefix_sum] = i

        return longest_subarray

Continuous Subarray Sum ***

Complete explanation | mathematical | code with proper comments | O(N) | continuous subarray sum - LeetCode Discuss

Math behind the solutions - LeetCode Discuss

Python Solution with explanation - LeetCode Discuss

LeetCode 523. Continuous Subarray Sum Explanation and Solution

523. Continuous Subarray Sum.png

If two sums A and B are giving the same remainder when divided by a number K, then their difference abs(A-B) is always divisible by K. Simply, If you get the same remainder again, it means that you've encountered some sum which is a multiple of K. - Their difference is a multiple of k, that's why they have the same remainder

"""

    [1, 2, 3, 4,]
    [1, 3, 6, 10]
    10-1 =  19  = 2+3+4
    6-1  =   5  = 2+3

if we store the cumulative sum for every point (idx) in the array,
    if (sum2-sum1) % k = 0
    then the numbers between sum2-sum1 add up to a multiple of k

Remember, there's another aspect to this problem. The subarray must have a minimum size of 2.
"""

class SolutionBF:
    def checkSubarraySum(self, nums, k):
        if len(nums) < 2:
            return False

        # 0: -1 is for edge case that current sum mod k == 0
        # for when the current running sum is cleanly divisible by k
        # e.g: nums = [4, 2], k = 3
        sums = {0: -1}  # 0
        cumulative_sum = 0
        for idx, num in enumerate(nums):
            cumulative_sum += num

            for prev_sum in sums:
                if (cumulative_sum-prev_sum) % k == 0 and idx-sums[prev_sum] >= 2:
                    return True

            # if current sum mod k not in dict, store it so as to ensure the further values stay
            if cumulative_sum not in sums:
                sums[cumulative_sum] = idx

        return False

"""
    [1, 2, 3, 4,]  <= array
    [1, 3, 6, 10] <= cumulative sums
    10 -1 =  19  = 2+3+4
    6 -1  =   5  = 2+3

if we store the cumulative sum for every point (idx) in the array,
    if (sum2-sum1) % k = 0
    then the numbers between sum2-sum1 add up to a multiple of k

if you find duplicated sum%k values, then that the sub array between those two indexes will actually be the solution.

---

eg: [15,10,10], k = 10
    15%10 = 5
    25%10 = 5
    35%10 = 5

Did you realize something? No
Let's see- the sums 15 and 25 are giving the remainder 5 when divided by 10 and the difference between 15 and 25 i.;e. 10 is divisible by 10.
Let's check with sums 15 and 35 , both giving the remainder 5 but their difference is divisible by 10.

---

eg: [23, 2, 4, 6, 7], k = 6
    [23,25,29, ...]

    23%6 = 5
    25%6 = 1
    29%6 = 5

The cumulative sums 23 and 29 have the same remainder,
    and their difference is a multiple of 6 (6 (2+4))

Why is getting 5 twice significant here?
    Given any number, let's say 11 and another number 5.
    11%5 = 1

    After adding how much to 11 would we get remainder with 5 equal to 1 again?
    The answer is 5.
    In order to repeat a remainder you need to add the number you are dividing by, in this case 5.

    if 11%5 = 1
    then (11+5)%5 = 1
    (11+10)%5 = 1 and so on

    Therefore as in the above example, because we saw 5 as remainder repeat, that means that, 
        there was a cumulative sum somewhere in the list that added up to 6 (number we are dividing by). 
    That's why we would return true.

---

If two sums A and B are giving the same remainder when divided by a number K, then their difference abs(A-B) is always divisible by K.
Simply, If you get the same remainder again, it means that you've encountered some sum which is a multiple of K.
- Their difference is a multiple of k, that's why they have the same remainder

Additional logic:
(sum2-sum1) % k = 0
sum2%k - sum1%k = 0
sum2%k = sum1%k

https://leetcode.com/problems/continuous-subarray-sum/discuss/688125/Lehman-explanation-of-the-math
https://leetcode.com/problems/continuous-subarray-sum/discuss/1208948/Complete-explanation-or-mathematical-or-code-with-proper-comments-or-O(N)-or-continuous-subarray-sum
https://leetcode.com/problems/continuous-subarray-sum/discuss/338417/Python-Solution-with-explanation
https://www.notion.so/paulonteri/Strings-Arrays-Linked-Lists-81ca9e0553a0494cb8bb74c5c85b89c8#1a8542c704d949a196a82d0d08117435

Remember, there's another aspect to this problem. The subarray must have a minimum size of 2.
"""

class Solution:
    def checkSubarraySum(self, nums, k):
        if len(nums) < 2:
            return False

        # 0: -1 is for edge case that current sum mod k == 0
        # for when the current running sum is cleanly divisible by k
        # e.g: nums = [4, 2], k = 3
        sums = {0: -1}  # 0
        cumulative_sum = 0
        for idx, num in enumerate(nums):
            cumulative_sum += num
            remainder = cumulative_sum % k

            # if current_sum mod k is in dict and index idx - sums[remainder] > 1, we got the Subarray!
            # we use 2 not 1 because the element at sums[remainder] is not in the subarray we are talking about
            if remainder in sums and idx - sums[remainder] >= 2:
                return True

            # if current sum mod k not in dict, store it so as to ensure the further values stay
            if remainder not in sums:
                sums[remainder] = idx

Longest Consecutive Sequence *

""" 
Longest Consecutive Sequence:

Given an unsorted array of integers nums, return the length of the longest consecutive elements sequence.
You must write an algorithm that runs in O(n) time.

Example 1:
    Input: nums = [100,4,200,1,3,2]
    Output: 4
    Explanation: The longest consecutive elements sequence is [1, 2, 3, 4]. Therefore its length is 4.
Example 2:
    Input: nums = [0,3,7,2,5,8,4,6,0,1]
    Output: 9

Constraints:
    0 <= nums.length <= 105
    -109 <= nums[i] <= 109

https://www.algoexpert.io/questions/Largest%20Range
https://leetcode.com/problems/longest-consecutive-sequence/
"""
""" 
Largest Range:

Write a function that takes in an array of integers and 
    returns an array of length 2 representing the largest range of integers contained in that array.
The first number in the output array should be the first number in the range, 
    while the second number should be the last number in the range.
A range of numbers is defined as a set of numbers that come right after each other in the set of real integers. 
For instance, the output array [2, 6] represents the range {2, 3, 4, 5, 6}, which is a range of length 5. 
Note that numbers don't need to be sorted or adjacent in the input array in order to form a range.
You can assume that there will only be one largest range.
Sample Input
    array = [1, 11, 3, 0, 15, 5, 2, 4, 10, 7, 12, 6]
Sample Output
    [0, 7]
"""

# O(nlog(n)) time
def largestRange(nums):
    if len(nums) < 1:
        return []

    nums.sort()
    res = [0, 0]

    idx = 0
    while idx < len(nums) - 1:
        # check if start of consecutive nums
        if not (nums[idx]+1 == nums[idx+1] or nums[idx] == nums[idx+1]):
            idx += 1
            continue

        # find the numbers
        end = idx+1
        while end < len(nums)-1 and (nums[end]+1 == nums[end+1] or nums[end] == nums[end+1]):
            end += 1

        # record
        res = max(res, [idx, end], key=lambda x: nums[x[1]] - nums[x[0]])

        # move pointer
        idx = end

    return [nums[res[0]], nums[res[1]]]

""" 
------------------------------------------------------------------------------------------------------------------------------------------------

- for each number try to build the largest number range from the input array
- the numbers can be stored in a set to improve lookup time

- for each num, if num-1 is in the set:
    - do not check the num because it will be in num-1's range

"""

# O(n) time
class Solution:
    def longestConsecutive(self, nums):
        longest = 0

        store = set(nums)

        for num in store:
            if num-1 in store:
                # do not check the num because it will be in num-1's range
                continue

            # try to build the largest consecutive sequence from the input array
            count = 1
            while num+1 in store:
                count += 1
                num += 1

            longest = max(count, longest)

        return longest

Max Subset Sum No Adjacent *

"""
Max Subset Sum No Adjacent:

Write a function that takes in an array of positive integers and 
 returns the maximum sum of non-adjacent elements in the array.
If the input array is empty, the function should return 0.

https://www.algoexpert.io/questions/Max%20Subset%20Sum%20No%20Adjacent
"""

def maxSubsetSumNoAdjacentBf(array):
    return bfHelper(array, float('inf'), 0, 0)

def bfHelper(array, last_added, curr_sum, idx):
    if idx >= len(array):
        return curr_sum

    not_chosen = bfHelper(array, last_added, curr_sum, idx+1)  # ignore idx
    chosen = -1
    if last_added != idx-1:  # choose idx
        chosen = bfHelper(array, idx, curr_sum + array[idx], idx+1)

    return max(
        not_chosen,
        chosen
    )

# ------------------------------------------------------------------------------------------------------------------------

""" 
          array: [7, 10, 12,          7,    9,    14]
max_sum_at_pos:  [7, 10, 19,         19,   28,    33]
                 [7, 10, 12+7,  10+7/19, 19+9, 19+14]

         array: [30, 25, 50, 55, 100, 120]
max_sum_at_pos: [30, 30, 80, 80, 180, 200]

max_sums[i] = max( 
                    (max_sums[i-1]),            -> i cannot be included
                    (max_sums[i-2] + array[i])  -> i can be included
                )
"""

# 0(n) time | 0(n) space
def maxSubsetSumNoAdjacent(array):

    if len(array) == 0:
        return 0

    # for each index in the input array,
    #  find the maximum possible sum and store it in the max_sums array
    # max_sums[i] = max( (max_sums[i-1]), (max_sums[i-2] + array[i]) )
    max_sums = [array[0]]
    for idx in range(1, len(array)):

        if idx == 1:
            max_sums.append(max(array[0], array[1]))
            continue

        prev_maxsum = max_sums[idx-1]
        curr_plus_before_prev_maxsum = array[idx] + max_sums[idx-2]

        # maximum sum at index
        max_sums.append(
                            max(
            curr_plus_before_prev_maxsum,
            prev_maxsum)
        )

    return max_sums[-1]

# ------------------------------------------------------------------------------------------------------------------------

# 0(n) time | 0(1) space
def maxSubsetSumNoAdjacent1(array):

    if len(array) == 0:
        return 0
    elif len(array) == 1:
        return array[0]

    prev_max = array[0]
    curr_max = max(array[0], array[1])  # at index 1
    # for each index in the input array,
    #  find the maximum possible sum and store it in the max_sums array
    # max sum for array[i] = max( (curr_max), (array[idx] + prev_max) )
    for idx in range(2, len(array)):

        curr_plus_prevmax = array[idx] + prev_max

        prev_max = curr_max
        curr_max = max(curr_plus_prevmax, curr_max)

    return curr_max

Subarrays with Product Less than a Target *

Array Of Products / Product of Array Except Self

"""
Array Of Products:
Product of Array Except Self:

Write a function that takes in a non-empty array of integers and returns an array of the same length,
 where each element in the output array is equal to the product of every other number in the input array.
In other words, the value at output[i] is equal to the product of every number in the input array other than input[i].

Note that you're expected to solve this problem without using division.

https://www.algoexpert.io/questions/Array%20Of%20Products
https://leetcode.com/problems/product-of-array-except-self/
"""

# O(n) time | O(n) space - where n is the length of the input array (O(3n) time)
def arrayOfProducts(array):
    res = array[:]

    # We know that for each element, the product of all other elements
    #  will be equal to the the products of the elements to its right and and the products of the elements to its left
    # we can try to calculate that beforehand

    # multiply left & right products for each element
    left_products = [0]*len(array)
    running_left = 1  # first element will have a product of 1
    for idx in range(len(array)):
        left_products[idx] = running_left
        running_left = array[idx] * running_left

    # calculate products to the right of elements
    right_products = [0]*len(array)
    running_right = 1  # last element will have a product of 1
    for idx in reversed(range(len(array))):
        right_products[idx] = running_right
        running_right = array[idx] * running_right

    # multiply left & right products for each element
    for idx in range(len(array)):
        res[idx] = left_products[idx] * right_products[idx]

    return res

y = [5, 1, 4, 2]
x = [1, 2, 3, 4, 5]
print(arrayOfProducts(x))
print(arrayOfProducts(y))

Squaring a Sorted Array

Intervals Intersection

Drone Flight Planner

"""
Drone Flight Planner:

You’re an engineer at a disruptive drone delivery startup and your CTO asks you
 to come up with an efficient algorithm that calculates the minimum amount of energy required for the company’s drone to complete its flight.
You know that the drone burns 1 kWh (kilowatt-hour is an energy unit) for every mile it ascends, and it gains 1 kWh for every mile it descends.
Flying sideways neither burns nor adds any energy.
Given an array route of 3D points, implement a function calcDroneMinEnergy that computes and returns the minimal amount of energy the drone would need to complete its route.
Assume that the drone starts its flight at the first point in route. That is, no energy was expended to place the drone at the starting point.
For simplicity, every 3D point will be represented as an integer array whose length is 3. Also, the values at indexes 0, 1, and 2 represent the x, y and z coordinates in a 3D point, respectively.

Explain your solution and analyze its time and space complexities.

Example:
    input:  route =[[0,   2, 10],
                    [3,   5,  0],
                    [9,  20,  6],
                    [10, 12, 15],
                    [10, 10,  8]]

    output: 5 # less than 5 kWh and the drone would crash before the finish
            # line. More than `5` kWh and it’d end up with excess energy

"""

# O(n) time | O(1) space
def calc_drone_min_energy(route):

    energy = 0
    min_energy = 0
    for idx in range(1, len(route)):

        energy += route[idx-1][-1] - route[idx][-1]
        min_energy = min(min_energy, energy)

    return abs(min_energy)

x = [[0,  2, 10],
     [3,  5,  0],
     [9, 20,  6],
     [10, 12, 15],
     [10, 10,  8]]
y = [[0,  2,  2],
     [3,  5, 38],
     [9, 20,  6],
     [10, 12, 15],
     [10, 10,  8]]

print(calc_drone_min_energy(x))
print(calc_drone_min_energy(y))
print(calc_drone_min_energy([[0, 1, 19]]))

"""
Since the drone only expends/gains energy when it flies up and down, we can ignore the x and y coordinates and focus only on the altitude - the z coordinate.
We should come up with the initial energy amount needed to enable the flight. 
In other words, at any given point in route, the drone’s level of energy balance mustn’t go below zero. Otherwise, it’ll crash.

get the x and y coordinates out of the way. 
The z coordinate (i.e. the altitude) is the only coordinate that matters.
"""

First Duplicate Value

"""
First Duplicate Value:

Given an array of integers between 1 and n, inclusive, where n is the length of the array,
 write a function that returns the first integer that appears more than once (when the array is read from left to right).
In other words, out of all the integers that might occur more than once in the input array,
 your function should return the one whose first duplicate value has the minimum index.
If no integer appears more than once, your function should return -1.
Note that you're allowed to mutate the input array.

https://www.algoexpert.io/questions/First%20Duplicate%20Value
"""

# 0(n) time | 0(n) space
def firstDuplicateValue1(array):
    store = {}
    for num in array:
        if num in store:
            return num
        store[num] = True
    return -1

"""
integers between 1 and n, inclusive, where n is the length of the array
therefore, the array should look like this if sorted [1,2,3,4,5,.....n] if there are no duplicates

for each number, we can therefore mark it's corresponding index as visited
and if we visit an index more than once, then it's repeated

"""

# 0(n) time | 0(1) space
def firstDuplicateValue(array):

    for num in array:
        val = abs(num)
        index = val - 1
        if array[index] < 0:  # if marked
            return val
        array[index] = -array[index]  # mark
    return -1

Move Zeroes

"""
Move Zeroes:

Given an array nums, write a function to move all 0's to the end of it while maintaining the relative order of the non-zero elements.
Note:
    You must do this in-place without making a copy of the array.
    Minimize the total number of operations.

https://leetcode.com/problems/move-zeroes/
"""

# 0(n) time | 0(1) space
class Solution:
    def moveZeroes(self, nums):

        # # reorder list skipping all zeros (The first one might be replaced by itself if it's not 0)
        next_none_zero = 0  # will mark the next char to be replaced
        for i in range(len(nums)):

            # replace --> if the current char is 0 it will not replace the prev
            if nums[i] != 0:
                nums[next_none_zero] = nums[i]
                next_none_zero += 1

        # from where the next_none_zero last stuck,
        # replace all the nums from the next_none_zero to the end with 0
        while next_none_zero < len(nums):
            nums[next_none_zero] = 0
            next_none_zero += 1

Shortest Unsorted Continuous Subarray *

"""
Shortest Unsorted Continuous Subarray:

Given an integer array nums, you need to find one continuous subarray that if you only sort this subarray in ascending order,
 then the whole array will be sorted in ascending order.
Return the shortest such subarray and output its length.

Example 1:
    Input: nums = [2,6,4,8,10,9,15]
    Output: 5
    Explanation: You need to sort [6, 4, 8, 10, 9] in ascending order to make the whole array sorted in ascending order.
Example 2:
    Input: nums = [1,2,3,4]
    Output: 0
Example 3:
    Input: nums = [1]
    Output: 0

https://leetcode.com/problems/shortest-unsorted-continuous-subarray/
https://www.algoexpert.io/questions/Subarray%20Sort
"""

"""
[2,6,4,8,10,9,15]
- iterate through the array starting from the left:
    - each value should be larger or equal to all on the left
    - keep track of the largest values you see
    - if you find any value smaller that that move the right pointer there (9)
- iterate through the array starting from the right:
    - keep track of the smallest values you see
    - if you find any value larger that that move the left pointer there (6)

return (right - left) + 1
"""

class Solution:
    def findUnsortedSubarray(self, nums):
        left = 0
        right = 0

        minimum = nums[0]
        for idx in range(len(nums)):
            if nums[idx] < minimum:
                right = idx
            minimum = max(nums[idx], minimum)

        maximum = nums[-1]
        for idx in reversed(range(len(nums))):
            if nums[idx] > maximum:
                left = idx
            maximum = min(nums[idx], maximum)

        if right == 0 and left == 0:
            return 0
        return right - left + 1

Longest Peak

"""
Longest Peak:

Write a function that takes in an array of integers and returns the length of the longest peak in the array.
A peak is defined as adjacent integers in the array that are strictly increasing until they reach a tip (the highest value in the peak),
 at which point they become strictly decreasing. At least three integers are required to form a peak.

For example, the integers 1, 4, 10, 2 form a peak, but the integers 4, 0, 10 don't and neither do the integers 1, 2, 2, 0. 
 Similarly, the integers 1, 2, 3 don't form a peak because there aren't any strictly decreasing integers after the 3.

Sample Input
    array = [1, 2, 3, 3, 4, 0, 10, 6, 5, -1, -3, 2, 3]
Sample Output
    6 
    # 0, 10, 6, 5, -1, -3
"""

# O(n) time | O(1) space - where n is the length of the input array
def longestPeak(array):

    def findPeakLength(idx):
        increased_length = 0
        decreased_length = 0

        prev = None
        curr = idx
        if not (curr + 1 < len(array)) or array[curr + 1] <= array[curr]:
            # if next is not increasing
            return 0
        else:
            increased_length += 1
            prev = curr
            curr += 1

        # increasing
        while curr < len(array) and array[curr] > array[prev]:
            if not curr + 1 < len(array):
                return 0  # we won't be able to reach tha decreasing section

            increased_length += 1
            prev = curr
            curr += 1

        # decreasing
        while curr < len(array) and array[curr] < array[prev]:
            decreased_length += 1
            prev = curr
            curr += 1

        if decreased_length > 0:
            return decreased_length + increased_length
        return 0

    longest_len = 0
    for index in range(len(array)):
        longest_len = max(longest_len, findPeakLength(index))

    return longest_len

x = [0, 1, 2, 3, 4, 3, 2]
y = [1, 2, 3, 3, 4, 0, 10, 6, 5, -1, -3, 2, 3]
z = [5, 4, 3, 2, 1, 2, 1]
p = [5, 4, 3, 2, 1, 2, 10, 12]
q = [1, 2, 3, 4, 3, 2, 1]
print(longestPeak(x))
print(longestPeak(y))
print(longestPeak(z))
print(longestPeak(p))
print(longestPeak(q))

Merge Sorted Array *

"""
Merge Sorted Array:

simpler version of Merge K Sorted Lists

Given two sorted integer arrays nums1 and nums2, merge nums2 into nums1 as one sorted array.
Note:
    The number of elements initialized in nums1 and nums2 are m and n respectively.
    You may assume that nums1 has enough space (size that is equal to m + n) to hold additional elements from nums2.
Constraints:
    -10^9 <= nums1[i], nums2[i] <= 10^9
    nums1.length == m + n
    nums2.length == n

https://leetcode.com/problems/merge-sorted-array/
"""

# O(n) time | O(1) space
class Solution:
    def merge(self, nums1, m, nums2, n):

        one = m - 1
        two = n - 1

        # iterate through all the characters in nums1
        for i in reversed(range(m+n)):

            if two < 0:
                return

            # we have to deal with the case where the one pointer goes outside nums1 (-1,-2,...) because
            # many/all of it's values were greater than the ones in nums2
            if nums1[one] < nums2[two] or one < 0:
                nums1[i] = nums2[two]
                two -= 1
            else:
                nums1[i] = nums1[one]
                one -= 1

class Solution0:
    def merge(self, nums1, m, nums2, n):

        one = m - 1
        two = n - 1
        # fill nums1 backwards
        for idx in reversed(range(len(nums1))):

            # handle edge cases
            if two < 0:
                nums1[idx] = nums1[one]
                one -= 1
            elif one < 0:
                nums1[idx] = nums2[two]
                two -= 1

            # fill bey checking which is larger
            elif nums1[one] > nums2[two]:
                nums1[idx] = nums1[one]
                one -= 1
            else:
                nums1[idx] = nums2[two]
                two -= 1

"""
Example:
    Input:
        nums1 = [1,2,3,0,0,0], m = 3
        nums2 = [2,5,6],       n = 3

    Output: [1,2,2,3,5,6]
"""

Max Substring Alphabetically *

"""
Max Substring Alphabetically
Given a string, determine the maximum alphabetically, substring
"""

def maxSubstring(s):

    if len(s) < 1:
        return ""

    # get all characters' indexes
    # sort characters alphabetically
    characters = []  # ['a', 'p', 'p', 'l', 'e']
    idx_store = {}  # {'a': [0], 'p': [1, 2], 'l': [3], 'e': [4]}
    for idx, char in enumerate(s):
        if char not in idx_store:
            characters.append(char)
            idx_store[char] = [idx]
        else:
            idx_store[char].append(idx)

    characters.sort()
    # handle the last character's (from characters array) substrings only
    last_char = characters[-1]

    # get all substrings starting with the last character
    # sort them
    substrings = []  # ['p', 'pp', 'ppl', 'pple', 'p', 'pl', 'ple']
    for idx in idx_store[last_char]:
        right = idx
        while right < len(s):
            substrings.append(s[idx:right+1])
            right += 1

    substrings.sort()
    return substrings[-1]  # pple

print(maxSubstring("apple"))
print(maxSubstring("apsgsxvbbdbsdbsdknnple"))
print(maxSubstring("asazsxs"))
print(maxSubstring("as"))
print(maxSubstring("applze"))
print(maxSubstring("azpple"))
print(maxSubstring("apzzple"))

# Not on Leetcode

Matrices

Maximum Area of a Piece of Cake After Horizontal and Vertical Cuts

Screenshot 2021-10-19 at 08.13.55.png

Screen Recording 2021-10-19 at 08.14.12.mov

Screenshot 2021-10-19 at 08.15.01.png

Screenshot 2021-10-19 at 08.15.13.png

""" 
Maximum Area of a Piece of Cake After Horizontal and Vertical Cuts

You are given a rectangular cake of size h x w and two arrays of integers horizontalCuts and verticalCuts where:
    horizontalCuts[i] is the distance from the top of the rectangular cake to the ith horizontal cut and similarly, and
    verticalCuts[j] is the distance from the left of the rectangular cake to the jth vertical cut.
Return the maximum area of a piece of cake after you cut at each horizontal and vertical position provided in the arrays horizontalCuts and verticalCuts. 
Since the answer can be a large number, return this modulo 109 + 7.

https://leetcode.com/problems/maximum-area-of-a-piece-of-cake-after-horizontal-and-vertical-cuts/
"""

class Solution:
    def maxArea(self, h, w, horizontalCuts, verticalCuts):
        """ 
        Note that: If we were to consider only the horizontal cuts, then we would end up with many pieces of cake with width = w and varying heights. 
        For each new piece, making a vertical cut will change the width, but not the height.
        - when considering the heights, once we find the largest height, that piece is applicable to all the different possible widths
        - when considering the widths, once we find the largest width, that piece is applicable to all heights

        Therefore, we know the largest piece of cake must have a height equal to the tallest height after applying only the horizontal cuts, 
        and it will have a width equal to the widest width after applying only the vertical cuts.
        """

        # Start by sorting the inputs
        horizontalCuts.sort()
        verticalCuts.sort()

        max_height = max(horizontalCuts[0], h - horizontalCuts[-1])
        for i in range(1, len(horizontalCuts)):
            max_height = max(max_height,
                             horizontalCuts[i] - horizontalCuts[i - 1])

        max_width = max(verticalCuts[0], w - verticalCuts[-1])
        for i in range(1, len(verticalCuts)):
            max_width = max(max_width, verticalCuts[i] - verticalCuts[i - 1])

        return (max_height * max_width) % (10**9 + 7)

Candy Crush

"""
Candy Crush:

This question is about implementing a basic elimination algorithm for Candy Crush:
Given a 2D integer array board representing the grid of candy, different positive integers board[i][j] represent different types of candies.
A value of board[i][j] = 0 represents that the cell at position (i, j) is empty.
The given board represents the state of the game following the player's move.

Prerequisite:
- https://leetcode.com/problems/remove-all-adjacent-duplicates-in-string-ii

https://leetcode.com/problems/candy-crush/
"""

from typing import List

class Solution:

    # 1. Check for vertical match
    # 2. Check for horizontal match
    # 3. Gravity
    # 4. repeat till board is clean
    # cells to be crushed will be marked as negative
    def candyCrush(self, board: List[List[int]]):

        h = len(board)
        w = len(board[0])

        toBeCrushed = False

        #  1. Check for vertical match then
        # negate the found (three cells)
        # Note: (don't check the last two as they'll already have been checked)
        for x in range(h-2):
            for y in range(w):

                # check a cell and the two below it then
                # if they are equal, mark them (negate their values)
                if abs(board[x][y]) == abs(board[x+1][y]) == abs(board[x+2][y]) != 0:
                    board[x][y] = board[x+1][y] = board[x+2][y] = - \
                        abs(board[x][y])
                    toBeCrushed = True

        # 2. Check for horizontal match (similar to above)
        for y in range(w-2):
            for x in range(h):

                # check a cell and the two to its right
                # if they are equal, mark them
                if abs(board[x][y]) == abs(board[x][y+1]) == abs(board[x][y+2]) != 0:
                    board[x][y] = board[x][y+1] = board[x][y+2] = - \
                        abs(board[x][y])
                    toBeCrushed = True

        # 3. Gravity
        # iterate through each column, then for each column,
        # move positive values to the bottom then set the rest to 0.
        if toBeCrushed:  # not needed but speeds it up

            # # find negative values then, replace it with the ones above it using two pointers
            # it's easier to iterate from the bottom
            for y in range(w):

                # will stick on negative values till they are replaced
                anchor = h - 1  # starts off at the bottom

                for x in reversed(range(h)):

                    # Replacing the negative values:
                    # check if positive, if positive,
                    #   we replace the last anchored cell[anchor][y] with the current cell([x],[y])
                    #   then we move the anchor up
                    # (skip this on -ve values, wait till we hit a +ve value to replace it)
                    if board[x][y] > 0:
                        # FYI, the first cells, if possitive will be replaced by themselves
                        board[anchor][y] = board[x][y]
                        anchor -= 1  # move anchor up

                # deal with where the anchor last stuck,
                # all the values of cells from the anchor upwards to be marked as 0
                while anchor >= 0:
                    board[anchor][y] = 0
                    anchor -= 1

        # Repeat till the board is clean
        if toBeCrushed:
            return self.candyCrush(board)
        else:
            return board

"""
Example:

Input:
board =
[[110,5,112,113,114],[210,211,5,213,214],[310,311,3,313,314],[410,411,412,5,414],[5,1,512,3,3],[610,4,1,613,614],[710,1,2,713,714],[810,1,2,1,1],[1,1,2,2,2],[4,1,4,4,1014]]

Output:
[[0,0,0,0,0],[0,0,0,0,0],[0,0,0,0,0],[110,0,0,0,114],[210,0,0,0,214],[310,0,0,113,314],[410,0,0,213,414],[610,211,112,313,614],[710,311,412,613,714],[810,411,512,713,1014]]
"""

"""
Full Question:

This question is about implementing a basic elimination algorithm for Candy Crush.

Given a 2D integer array board representing the grid of candy, different positive integers board[i][j] represent different types of candies. A value of board[i][j] = 0 represents that the cell at position (i, j) is empty. The given board represents the state of the game following the player's move. Now, you need to restore the board to a stable state by crushing candies according to the following rules:

If three or more candies of the same type are adjacent vertically or horizontally, "crush" them all at the same time - these positions become empty.
After crushing all candies simultaneously, if an empty space on the board has candies on top of itself, then these candies will drop until they hit a candy or bottom at the same time. (No new candies will drop outside the top boundary.)
After the above steps, there may exist more candies that can be crushed. If so, you need to repeat the above steps.
If there does not exist more candies that can be crushed (ie. the board is stable), then return the current board.
You need to perform the above rules until the board becomes stable, then return the current board.

Note:

The length of board will be in the range [3, 50].
The length of board[i] will be in the range [3, 50].
Each board[i][j] will initially start as an integer in the range [1, 2000].
"""

Set Matrix Zeroes

"""
Set Matrix Zeroes:

Given an m x n matrix. If an element is 0, set its entire row and column to 0. Do it in-place.

Follow up:
A straight forward solution using O(mn) space is probably a bad idea.
A simple improvement uses O(m + n) space, but still not the best solution.
Could you devise a constant space solution?

Example 1:
    Input: matrix =
        [
        [1,1,1],
        [1,0,1],
        [1,1,1]]
    Output:
        [
        [1,0,1],
        [0,0,0],
        [1,0,1]
        ]
Example 2:
    Input: matrix =
    [
    [0,1,2,0],
    [3,4,5,2],
    [1,3,1,5]
    ]
    Output:
    [
    [0,0,0,0],
    [0,4,5,0],
    [0,3,1,0]
    ]

# Input: valid matrix
# Output: None
# Constraints:
    - edit array in-place

https://leetcode.com/problems/set-matrix-zeroes/
"""

class Solution:
    def setZeroes(self, matrix):
        flag = "&"

        # # Find Matrix Zeroes
        first_col = first_row = False
        for row in range(len(matrix)):
            for col in range(len(matrix[0])):
                if matrix[row][col] == 0:

                    # mark first row and col to be erased
                    matrix[row][0] = flag  # mark first col of row
                    matrix[0][col] = flag  # mark first row of col

                    if col == 0:
                        first_col = True
                    if row == 0:
                        first_row = True

        # # Set Matrix Zeroes
        # # do not set matrix zeros for the first row & column as they are used as guides for marking
        # deal with rows
        for row in range(1, len(matrix)):
            if matrix[row][0] == flag:
                for col in range(len(matrix[0])):
                    matrix[row][col] = 0
        # deal with cols
        for col in range(1, len(matrix[0])):
            if matrix[0][col] == flag:
                for row in range(len(matrix)):
                    matrix[row][col] = 0

        # # Set Matrix Zeroes for the first row & col
        if first_col:
            for i in range(len(matrix)):
                matrix[i][0] = 0
        if first_row:
            for i in range(len(matrix[0])):
                matrix[0][i] = 0

        return matrix

Spiral Matrix

"""
Spiral Matrix:

Given a matrix of m x n elements (m rows, n columns), return all elements of the matrix in spiral order.
Given an m x n matrix, return all elements of the matrix in spiral order.
Example 1:
    Input: matrix = [[1,2,3],[4,5,6],[7,8,9]]
    Output: [1,2,3,6,9,8,7,4,5]
Example 2:
    Input: matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
    Output: [1,2,3,4,8,12,11,10,9,5,6,7]

https://leetcode.com/problems/spiral-matrix/
"""

# O(n) time | 0(n) space
def spiralTraverse1(array):
    result = []

    rowBegin = columnBegin = 0
    rowEnd = len(array) - 1
    columnEnd = len(array[0]) - 1

    isTop = True
    isRight = isLeft = isBottom = False

    while (rowBegin <= rowEnd and (isBottom or isTop)) or \
            (columnBegin <= columnEnd and (isRight or isLeft)):
        # the `and (isRight or isLeft)` helps prevent addition of an extra element after the traversal is complete
        # print(result)
        if isTop:
            for col in range(columnBegin, columnEnd + 1):
                result.append(array[rowBegin][col])
            rowBegin += 1
            isTop = False
            isRight = True
        elif isRight:
            for row in range(rowBegin, rowEnd+1):
                result.append(array[row][columnEnd])
            columnEnd -= 1
            isBottom = True
            isRight = False
        elif isBottom:
            for col in reversed(range(columnBegin, columnEnd+1)):
                result.append(array[rowEnd][col])
            rowEnd -= 1
            isLeft = True
            isBottom = False
        elif isLeft:
            for row in reversed(range(rowBegin, rowEnd + 1)):
                result.append(array[row][columnBegin])
            columnBegin += 1
            isTop = True
            isLeft = False
    return result

def spiralTraverse(array):
    output = []

    left = 0
    right = len(array[0]) - 1
    top = 0
    bottom = len(array) - 1
    while left <= right or top <= bottom:

        # top
        if top <= bottom:
            for idx in range(left, right+1):
                output.append(array[top][idx])
            top += 1

        # right
        if left <= right:
            for idx in range(top, bottom+1):
                output.append(array[idx][right])
            right -= 1

        # bottom
        if top <= bottom:
            for idx in reversed(range(left, right+1)):
                output.append(array[bottom][idx])
            bottom -= 1

        # left
        if left <= right:
            for idx in reversed(range(top, bottom+1)):
                output.append(array[idx][left])
            left += 1

    return output

# O(n) time | 0(n) space
def spiralTraverse0(array):
    result = []

    top = left = 0
    bottom = len(array) - 1
    right = len(array[0]) - 1

    while (top <= bottom) and (left <= right):

        # top
        for col in range(left, right + 1):
            result.append(array[top][col])

        # right
        for row in range(top + 1, bottom+1):
            result.append(array[row][right])

        # bottom
        for col in reversed(range(left, right)):
            # Handle the edge case when there's a single row
            # in the middle of the matrix. In this case, we don't
            # want to double-count the values in this row, which
            # we've already counted in the first for loop above.
            if top == bottom:
                break
            result.append(array[bottom][col])

        # left
        for row in reversed(range(top + 1, bottom)):
            # Handle the edge case when there's a single column
            # in the middle of the matrix. In this case, we don't
            # want to double-count the values in this column, which
            # we've already counted in the second for loop above.
            if left == right:
                break
            result.append(array[row][left])

        top += 1
        bottom -= 1
        left += 1
        right -= 1

    return result

Tips:

Array problems often have simple brute-force solutions that use O(n) space, but there are subtler solutions that use the array itself to reduce space complexity to O(1).
Instead of deleting an entry (which requires moving all entries to its right), consider overwriting it.
Be comfortable with writing code that operates on subarrays.
It’s incredibly easy to make off-by-1 errors when operating on arrays—reading past the last element of an array is a common error that has catastrophic consequences.
Don’t worry about preserving the integrity of the array (sortedness, keeping equal entries together, etc.) until it is time to return.
An array can serve as a good data structure when you know the distribution of the elements in advance. For example, a Boolean array of length W is a good choice for representing a subset of {0, 1, . . . , W − 1}. (When using a Boolean array to represent a subset of {1, 2, 3, . . . , n}, allocate an array of size n + 1 to simplify indexing.) .
When operating on 2D arrays, use parallel logic for rows and for columns.
Sometimes it’s easier to simulate the specification than to analytically solve for the result. For example, rather than writing a formula for the i-th entry in the spiral order for an n × n matrix, just compute the output from the beginning.
The basic operations are: len(A), A.append(42), A.remove(2), and A.insert(3, 28), A.reverse() (in-place), reversed(A) (returns an iterator), A.sort() (in-place), sorted(A) (returns a copy), del A[i] (deletes the i-th element), and del A[i:j] (removes the slice).
Understand how copy works, i.e., the difference between B = A and B = list(A). Understand what a deep copy is, and how it differs from a shallow copy, i.e., how copy.copy(A) differs from copy.deepcopy(A).

Functions

.append(item) adds an item to the end of the list.

.insert(index, item) adds an item at the given index in the list.

.remove(item) removes an item from the list.

.pop(index) removes the item at the given index.

.count(item) returns a count of how many times an item occurs in the list.

.reverse() reverses items in the list in place reversed(list) (returns an iterator).

.sort() sorts the list in place. By default, the list is sorted ascending. You can specify sort(reverse=True), to sort descending. sorted(list) (returns a copy)

max(list) returns the maximum value.

min(list) returns the minimum value.

del list[i] (deletes the i-th element), and del list[i:j] (removes the slice).

Find index [1,2,3,4].index(3)) → 2 *

Untitled

# Python list methods
my_list = [3, 8, 1, 6, 0, 8, 4]

# Output: 1
print(my_list.index(8))

# Output: 2
print(my_list.count(8))

my_list.sort()

# Output: [0, 1, 3, 4, 6, 8, 8]
print(my_list)

my_list.reverse()

# Output: [8, 8, 6, 4, 3, 1, 0]
print(my_list)

# Deleting list items
my_list = ['p', 'r', 'o', 'b', 'l', 'e', 'm']

# delete one item
del my_list[2]

print(my_list) # ['p', 'r', 'b', 'l', 'e', 'm']

# delete multiple items
del my_list[1:5]

print(my_list) # ['p', 'm']

# delete entire list
del my_list

print(my_list) # Error: List not defined

my_list = ['p','r','o','b','l','e','m']
my_list.remove('p')

# Output: ['r', 'o', 'b', 'l', 'e', 'm', 'p']
print(my_list)

# Demonstration of list insert() method
odd = [1, 9]
odd.insert(1,3)

print(odd) # [1, 3, 9]

odd[2:2] = [5, 7]

print(odd) # [1, 3, 5, 7, 9]

List comprehensions

cubes = [i**3 for i in range(5)] # [0, 1, 8, 27, 64]
print([i*2 for i in range(5)]) # [0, 2, 4, 6, 8]

evens=[i**2 for i in range(10) if i**2 % 2 == 0] # [0, 4, 16, 36, 64]

Slicing

list[::2] returns every other element from the list (indices 0, 2, .. )

# substitute
word = "0123456789"
temp_w = list(word)
temp_w[2:4] = "t"
print(temp_w)

Tuple

Python Tuple

Unlike lists, tuples are immutable.

# Changing tuple values
my_tuple = (4, 2, 3, [6, 5])

# TypeError: 'tuple' object does not support item assignment
# my_tuple[1] = 9

# However, item of mutable element can be changed
my_tuple[3][0] = 9    # Output: (4, 2, 3, [9, 5])
print(my_tuple)

# Tuples can be reassigned
my_tuple = ('p', 'r', 'o', 'g', 'r', 'a', 'm', 'i', 'z')

# Output: ('p', 'r', 'o', 'g', 'r', 'a', 'm', 'i', 'z')
print(my_tuple)

Pro tips

Store multiple items in a dict or other hashable manner:

Use a tuple
Example:

Multiplying lists can just create several copies to the same list

Python list multiplication: [[...]]*3 makes 3 lists which mirror each other when modified

Strings,%20Arrays%20&%20Linked%20Lists%2081ca9e0553a0494cb8bb74c5c85b89c8/Screenshot_2021-08-03_at_21.06.43.png

Strings,%20Arrays%20&%20Linked%20Lists%2081ca9e0553a0494cb8bb74c5c85b89c8/Screenshot_2021-08-03_at_21.07.40.png

Sets

Linked Lists

Examples

Check/Store unique nodes (not necessarily with unique values)

Not necessarily with unique values → meaning we can have two different nodes with the same value

Hare & Tortoise Algorithm

Reverse linked list

Untitled

"""
Reverse Linked List

https://leetcode.com/problems/reverse-linked-list/submissions/
https://www.algoexpert.io/questions/Reverse%20Linked%20List
"""

# Definition for singly-linked list.
class ListNode:
    def __init__(self, val=0, next=None):
        self.val = val
        self.next = next

# O(n) time | O(1) space
class Solution:
    def reverseList(self, head: ListNode):

        current = head
        prev = None

        while current is not None:
            # store next because we will loose track of it
            nxt = current.next

            # reverse pointer (point backwords)
            current.next = prev

            # # move on to next node
            # in the next iteration, the current current will be the prev
            prev = current
            # in the next iteration, the current current.next will be the current
            current = nxt

        return prev

def reverseLinkedList(self, head):
    prev = None
    curr = head
    while curr is not None:
        nxt = curr.next
        curr.next = prev
        prev = curr
        curr = nxt
    return prev

Reverse Linked List II

"""
Reverse Linked List II:

Given the head of a singly linked list and two integers left and right where left <= right,
 reverse the nodes of the list from position left to position right, and return the reversed list.
Follow up: Could you do it in one pass?
Example 1:
    Input: head = [1,2,3,4,5], left = 2, right = 4
    Output: [1,4,3,2,5]
Example 2:
    Input: head = [5], left = 1, right = 1
    Output: [5]
https://leetcode.com/problems/reverse-linked-list-ii/
"""

class Solution:
    def reverseBetween(self, head: ListNode, left: int, right: int):
        if left == right:
            return head

        before_sublist = after_sublist = None
        sublist_start = sublist_end = None

        prev = None
        curr = head
        count = 1
        while curr:
            if count == left-1:
                before_sublist = curr
            elif count == left:
                sublist_start = curr
            elif count == right:
                sublist_end = curr
            elif count == right+1:
                after_sublist = curr

            # reverse sublist
            nxt = curr.next
            if count > left and count <= right:
                curr.next = prev

            prev = curr
            curr = nxt
            count += 1

        # correct start and end of sublist
        if before_sublist is None:
            sublist_start.next = after_sublist
            return sublist_end  # new head
        else:
            before_sublist.next = sublist_end
            sublist_start.next = after_sublist
            return head

"""

"""

class Solution_:
    def reverseBetween(self, head: ListNode, left: int, right: int):
        prev = None
        curr = head

        # # find where reversing begins
        for _ in range(left-1):  # the 1st node is at pos 1
            prev = curr
            curr = curr.next

        # we cannot use before_reverse.next when left is at 1, coz there is no before_reverse so we use start_reverse
        # store the last non reversed(not to be reversed) node
        start_reverse = curr
        # will be the tail of the last reversed list
        before_reverse = prev

        # # reverse a section
        for _ in range(left, right+1):
            nxt = curr.next
            curr.next = prev
            prev = curr
            curr = nxt

        # # merge the reversed section (fix the reversed list position in the larger list)
        # the (left - 1) node to point to right
        if before_reverse and before_reverse.next:
            # before_reverse.next = last reversed node (prev)
            before_reverse.next = prev

        else:
            # if we started reversing from 1, then the last item reversed will be put at 1 (head)
            head = prev

        # the first reversed (left) node to point to the node at (right + 1)
        start_reverse.next = curr

        return head

Reorder List *

Screenshot 2021-10-17 at 16.19.34.png

Screenshot 2021-10-17 at 16.19.56.png

Screenshot 2021-10-17 at 16.20.19.png

Screenshot 2021-10-17 at 16.20.34.png

Screenshot 2021-10-17 at 16.20.58.png

Screenshot 2021-10-17 at 16.21.14.png

""" 
Reorder List

You are given the head of a singly linked-list. The list can be represented as:
    L0 → L1 → … → Ln - 1 → Ln
Reorder the list to be on the following form:
    L0 → Ln → L1 → Ln - 1 → L2 → Ln - 2 → …
You may not modify the values in the list's nodes. Only nodes themselves may be changed.

Example 1:
    Input: head = [1,2,3,4]
    Output: [1,4,2,3]
Example 2:
    Input: head = [1,2,3,4,5]
    Output: [1,5,2,4,3]

https://leetcode.com/problems/reorder-list
"""

""" 
This problem is a combination of these three easy problems:
    Middle of the Linked List.
    Reverse Linked List.
    Merge Two Sorted Lists.
"""

class Solution:
    def reorderList(self, head: ListNode):
        if not head:
            return

        # find the middle of linked list [Problem 876]
        # in 1->2->3->4->5->6 find 4
        slow = fast = head
        while fast and fast.next:
            slow = slow.next
            fast = fast.next.next

        # reverse the second part of the list [Problem 206]
        # convert 1->2->3->4->5->6 into 1->2->3->4 and 6->5->4
        # reverse the second half in-place
        prev, curr = None, slow
        while curr:
            curr.next, prev, curr = prev, curr, curr.next

        # merge two sorted linked lists [Problem 21]
        # merge 1->2->3->4 and 6->5->4 into 1->6->2->5->3->4
        first, second = head, prev
        while second.next:
            first.next, first = second, first.next
            second.next, second = first, second.next

Find the start of linked list cycle

def detectCycle(self, head):

    # # find cycle
    fast = head
    slow = head
    while True:
        if fast is None or fast.next is None:  # find invalid
            return None

        slow = slow.next
        fast = fast.next.next
        if slow == fast:
            break

    # # find start of cycle
    # the (dist) head to the start of the cycle ==
    #   the (dist) meeting point to the start of the cycle
    one = head
    two = fast
    while one != two:
        one = one.next
        two = two.next
    return one

Merge K Sorted Lists

Rotate List/Shift Linked List

""" 
Rotate List/Shift Linked List:

Given the head of a linked list, rotate the list to the right by k places.

Example 1:
    Input: head = [1,2,3,4,5], k = 2
    Output: [4,5,1,2,3]
Example 2:
    Input: head = [0,1,2], k = 4
    Output: [2,0,1]

Constraints:
    The number of nodes in the list is in the range [0, 500].
    -100 <= Node.val <= 100
    0 <= k <= 2 * 109

https://leetcode.com/problems/rotate-list/
https://www.algoexpert.io/questions/Shift%20Linked%20List
"""

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next

"""
- find length of list
- find end of list
- k %= length
- we'll have to pluck of the list from position length - k to the end
    and place it a the beginning of the list
    - get to node (length - k):
        - hold k in a pointer (new_head)
        - node (length - k) to point to null
        - end to point to head
    - return new_head

0 -> 1 -> 2 -> 3 -> 4 -> 5 

2
4 -> 5 -> 0 -> 1 -> 2 -> 3

5
1 -> 2 -> 3 -> 4 -> 5 -> 0

"""

class Solution:
    def rotateRight(self, head, k):
        if not head:
            return

        # # get tail and length
        tail = None
        length = 0
        curr = head
        while curr:
            tail = curr
            curr = curr.next
            length += 1

        # # validate k
        k %= length
        if k == 0:
            return head

        # # find new ending (length - k)
        new_tail = head
        for _ in range(length - k - 1):
            new_tail = new_tail.next

        # # rotate
        new_head = new_tail.next
        new_tail.next = None
        tail.next = head

        return new_head

Merge Two Sorted Lists/Merge Linked Lists *

"""
Merge Two Sorted Lists/Merge Linked Lists:

Merge two sorted linked lists and return it as a sorted list. 
The list should be made by splicing together the nodes of the first two lists.

https://www.algoexpert.io/questions/Merge%20Linked%20Lists
https://leetcode.com/problems/merge-two-sorted-lists/
"""

"""
Have two pointers, one at l1 and another at l2
we will be merging l1 into l2
compare which one is smaller, add the appropriate and move the pointers forward and move the 
"""

# Definition for singly-linked list.
class ListNode:
    def __init__(self, val=0, next=None):
        self.val = val
        self.next = next

class Solution:
    def mergeTwoLists(self, l1: ListNode, l2: ListNode):
        if l1 is None and l2 is None:
            return None
        elif l1 is None:
            return l2
        elif l2 is None:
            return l1

        one = l1
        two = l2

        # deal with head (larger one to be two and head)
        if one.val < two.val:
            temp_one = one
            one = two
            two = temp_one
        head = two

        prev_two = None
        # add ***one into two***
        while one is not None and two is not None:
            if one.val < two.val:
                nxt = one.next
                self.insertBetween(prev_two, two, one)
                prev_two = one
                one = nxt
            else:
                prev_two = two
                two = two.next

        while one is not None:  # add remaining one into two
            prev_two.next = one
            prev_two = prev_two.next
            one = one.next

        return head

    def insertBetween(self, left, right, new):
        left.next = new
        new.next = right

Insert into a Sorted Circular Linked List

Screenshot 2021-10-16 at 06.35.32.png

Screenshot 2021-10-16 at 06.35.56.png

Screenshot 2021-10-16 at 06.36.20.png

Screenshot 2021-10-16 at 06.36.50.png

Screenshot 2021-10-16 at 06.37.01.png

Screenshot 2021-10-16 at 06.37.27.png

""" 
Insert into a Sorted Circular Linked List:

Given a Circular Linked List node, which is sorted in ascending order, write a function to insert a value insertVal into the list such that it remains a sorted circular list.
The given node can be a reference to any single node in the list and may not necessarily be the smallest value in the circular list.
If there are multiple suitable places for insertion, you may choose any place to insert the new value. After the insertion, the circular list should remain sorted.
If the list is empty (i.e., the given node is null), you should create a new single circular list and return the reference to that single node. Otherwise, you should return the originally given node.

Example 1:
    Input: head = [3,4,1], insertVal = 2
    Output: [3,4,1,2]
    Explanation: In the figure above, there is a sorted circular list of three elements. 
                    You are given a reference to the node with value 3, and we need to insert 2 into the list. 
                    The new node should be inserted between node 1 and node 3. After the insertion, the list should look like this, and we should still return node 3.
Example 2:
    Input: head = [], insertVal = 1
    Output: [1]
    Explanation: The list is empty (given head is null). We create a new single circular list and return the reference to that single node.
Example 3:
    Input: head = [1], insertVal = 0
    Output: [1,0]

https://leetcode.com/problems/insert-into-a-sorted-circular-linked-list
"""

# Definition for a Node.
class Node:
    def __init__(self, val=None, next=None):
        self.val = val
        self.next = next

class Solution:
    def insert(self, head: 'Node', insertVal: int):
        node = Node(insertVal)

        # empty list
        if not head:
            node.next = node
            return node

        smallest = head
        largest = head
        curr = head.next
        while curr != head:
            # the or equal is to ensure the largest is the last node in such [3,3,3]
            if curr.val < smallest.val:
                smallest = curr
            if curr.val >= largest.val:
                largest = curr
            curr = curr.next

        # only one node or all nodes have a similar value
        if smallest.val == largest.val:
            largest.next = node
            node.next = smallest

        # is the largest or smallest value
        elif insertVal <= smallest.val or insertVal >= largest.val:
            largest.next = node
            node.next = smallest

        else:
            prev = None
            curr = None
            while curr != smallest:
                if curr is None:
                    curr = smallest
                    prev = largest

                if insertVal < curr.val:
                    prev.next = node
                    node.next = curr
                    break

                prev = curr
                curr = curr.next

        return head

Test for overlapping lists

Remove Kth Node From End

"""
Remove Kth Node From End:

Write a function that takes in the head of a Singly Linked List and an integer k and removes the kth node from the end of the list.
The removal should be done in place, meaning that the original data structure should be mutated (no new structure should be created).
Furthermore, the input head of the linked list should remain the head of the linked list after the removal is done,
 even if the head is the node that's supposed to be removed.
In other words, if the head is the node that's supposed to be removed, your function should simply mutate its value and next pointer.
Note that your function doesn't need to return anything.
You can assume that the input Linked List will always have at least two nodes and, more specifically, at least k nodes.
Each LinkedList node has an integer value as well as a next node pointing to the next node in the list or to None / null if it's the tail of the list.
https://www.algoexpert.io/questions/Remove%20Kth%20Node%20From%20End
"""

class LinkedList:
    def __init__(self, value):
        self.value = value
        self.next = None

# O(n) time | O(n) space
def removeKthNodeFromEnd(head, k):

    # find node positions
    positions = {}
    curr = head
    count = 1
    while curr is not None:
        positions[count] = curr
        curr = curr.next
        count += 1

    if k == 1:  # if node is the tail:
        before_to_delete = positions[(count-(k))-1]
        before_to_delete.next = None
    else:
        after_to_delete = positions[(count-(k))+1]
        to_delete = positions[count-(k)]
        to_delete.value = after_to_delete.value
        to_delete.next = after_to_delete.next

    return head

# O(n) time | O(1) space
def removeKthNodeFromEnd1(head, k):

    right = head
    left = head
    prev_left = None

    counter = 1
    # create length k space between right and left
    while counter <= k:
        right = right.next
        counter += 1

    # find end (move right past end)
    while right is not None:
        prev_left = left
        left = left.next
        right = right.next

    # delete
    if left.next is None:  # tail
        prev_left.next = None
    else:
        nxt = left.next
        left.value = nxt.value
        left.next = nxt.next

    return head

def removeKthNodeFromEnd4(head, k):
    left = right = head
    before_left = None

    counter = 1
    while counter <= k:
        right = right.next
        counter += 1

    while right is not None:
        right = right.next
        before_left = left
        left = left.next

    if before_left is None:  # remove head
        left.value = left.next.value
        left.next = left.next.next
    else:
        before_left.next = before_left.next.next

def removeKthNodeFromEnd01(head, k):
    left = right = head

    counter = 1
    while counter <= k:  # not counter < k to ensure we say on the node_at_k.prev
        right = right.next
        counter += 1

    # if left is head
    if right is None:
        left.value = left.next.value
        left.next = left.next.next

    else:
        while right.next is not None:
            left = left.next
            right = right.next

        left.next = left.next.next

"""
Remove Nth Node From End of List:

Given the head of a linked list, remove the nth node from the end of the list and return its head.
Follow up: Could you do this in one pass?
https://leetcode.com/problems/remove-nth-node-from-end-of-list/
"""

# Definition for singly-linked list.
class ListNode:
    def __init__(self, val=0, next=None):
        self.val = val
        self.next = next

class Solution:
    def removeNthFromEnd(self, head: ListNode, n: int):

        # keep distance
        left = head
        right = head.next
        count = 1
        while count != n:
            count += 1
            right = right.next

        # find end
        prev_left = None
        while right is not None:
            prev_left = left
            left = left.next
            right = right.next

        # remove
        if count == 1 and prev_left is None and right is None:  # list has single element
            return None
        elif prev_left is None:  # remove head
            return head.next

        prev_left.next = left.next
        return head

Add Two Numbers II

"""
Add Two Numbers II:

You are given two non-empty linked lists representing two non-negative integers.
The most significant digit comes first and each of their nodes contain a single digit. Add the two numbers and return it as a linked list.
You may assume the two numbers do not contain any leading zero, except the number 0 itself.

Follow up:
What if you cannot modify the input lists? In other words, reversing the lists is not allowed.

https://leetcode.com/problems/add-two-numbers-ii/
"""
# can also reverse

# Definition for singly-linked list.
class ListNode:
    def __init__(self, val=0, next=None):
        self.val = val
        self.next = next

# 0(max(n+m)) time | 0(n+m) space
class Solution:
    def addTwoNumbers(self, l1: ListNode, l2: ListNode):

        result = ListNode(-1)

        stack_one = []
        stack_two = []

        # fill up the stacks
        item_one = l1
        while item_one:
            stack_one.append(item_one.val)
            item_one = item_one.next
        item_two = l2
        while item_two:
            stack_two.append(item_two.val)
            item_two = item_two.next

        len_one = len(stack_one)
        len_two = len(stack_two)
        max_len = max(len_one, len_two)

        # addition
        i = 0
        carry = 0
        node_after_head = None
        while i <= max_len:  # iterate till max_len in order to handle carries

            # get values
            val_one = 0
            if i < len_one:
                val_one = stack_one.pop()
            val_two = 0
            if i < len_two:
                val_two = stack_two.pop()

            # arithmetic
            total = val_one + val_two + carry
            carry = 0
            if total > 9:
                total -= 10  # eg: when total = 19 : add (19-10) and carry 1
                carry = 1

            # add nodes to the result
            # if we are still adding or we have one left carry(eg: 99 + 99)
            if i < max_len or total > 0:
                node = ListNode(total)
                if node_after_head:
                    node.next = node_after_head
                    result.next = node
                    node_after_head = node
                else:
                    result.next = node
                    node_after_head = node
            i += 1

        # skip the first node (start at node_after_head)
        return result.next

"""
Example:

Input: (7 -> 2 -> 4 -> 3) + (5 -> 6 -> 4)
Output: 7 -> 8 -> 0 -> 7

input:
    [7,2,4,3]
    [5,6,4]
    [9,8,7,6,6,7,8,9]
    [9,8,7,6,6,7,8,9]
    [1,2,3,4,5,5,6,9]
    [1,2,3,4,5,5,6,9]
output:
    [7,8,0,7]
    [7,8,0,7]
    [1,9,7,5,3,3,5,7,8]
    [2,4,6,9,1,1,3,8]
    [1,5]
"""

class Solution00:
    def reverseLinkedList(self, head):
        prev = None
        curr = head
        while curr is not None:
            nxt = curr.next
            curr.next = prev
            prev = curr
            curr = nxt
        return prev

    def addTwoNumbers(self, l1: ListNode, l2: ListNode):
        one = self.reverseLinkedList(l1)
        two = self.reverseLinkedList(l2)

        res = ListNode()
        curr = res
        carry = 0
        while one is not None or two is not None or carry > 0:
            total = carry
            carry = 0
            if one is not None:
                total += one.val
                one = one.next
            if two is not None:
                total += two.val
                two = two.next

            curr.next = ListNode(total % 10)
            curr = curr.next
            carry = total // 10

        return self.reverseLinkedList(res.next)

class Solution01:

    def stackFromLinkedList(self, head):
        stack = []
        curr = head
        while curr is not None:
            stack.append(curr.val)
            curr = curr.next

        return stack

    def addTwoNumbers(self, l1: ListNode, l2: ListNode):
        res = ListNode()
        node_after_res = None

        stack_one = self.stackFromLinkedList(l1)
        stack_two = self.stackFromLinkedList(l2)

        carry = 0
        idx, len_one, len_two = 0, len(stack_one), len(stack_two)
        while idx < len_one or idx < len_two or carry > 0:
            total = carry
            if idx < len_one:
                total += stack_one.pop()
            if idx < len_two:
                total += stack_two.pop()

            carry = total // 10

            # make sure node comes between res & node_after_res,
            #  making it the new node_after_res
            node = ListNode(total % 10)
            if node_after_res:
                node.next = node_after_res
            res.next = node
            node_after_res = node

            idx += 1

        return res.next

""" 
Input: l1 = [7,2,4,3], l2 = [5,6,4]
Output: [7,8,0,7]

h -> 7
h -> 0 -> 7
h -> 8 -> 0 -> 7
"""

Palindrome Linked List

Copy List with Random Pointer *

"""
Copy List with Random Pointer:

A linked list is given such that each node contains an additional random pointer which could point to any node in the list or null.
Return a deep copy of the list.
The Linked List is represented in the input/output as a list of n nodes. Each node is represented as a pair of [val, random_index] where:
val: an integer representing Node.val
random_index: the index of the node (range from 0 to n-1) where random pointer points to, or null if it does not point to any node.

https://leetcode.com/problems/copy-list-with-random-pointer/
"""

# Definition for a Node.
class Node:
    def __init__(self, x: int, next: 'Node' = None, random: 'Node' = None):
        self.val = int(x)
        self.next = next
        self.random = random

class Solution:
    def copyRandomList(self, head: 'Node'):
        if not head:
            return None

        # create new nodes
        node = head
        while node:
            # create the node's holder & store it at random
            node.random = Node(node.val, None, node.random)
            node = node.next

        # populate random field of the new node
        node = head
        while node:
            temp_node = node.random
            if temp_node.random:
                temp_node.random = temp_node.random.random
            node = node.next

        # build new list
        head_copy, node = head.random, head
        while node:
            if node.next:
                node.random.next = node.next.random
            node = node.next

        return head_copy

class Solution_:
    def copyRandomList(self, head: 'Node'):
        if not head:
            return None

        # create new nodes
        node = head
        while node:
            # create the node's holder & store it at random
            node.random = Node(node.val, None, node.random)
            node = node.next

        # populate random field of the new node
        node = head
        while node:
            temp_node = node.random
            if temp_node.random:
                temp_node.next = temp_node.random
                temp_node.random = temp_node.random.random
            node = node.next

        # restore original list and build new list
        head_copy, node = head.random, head
        while node:
            nodes_random = node.random.next
            node.random.next = None

            if node.next:
                node.random.next = node.next.random

            node.random = nodes_random

            node = node.next

        return head_copy

class Solution__:
    def copyRandomList(self, head: 'Node'):

        # create new nodes
        node = head
        while node:
            node.random = Node(node.val, None, node.random)
            node = node.next

        # populate random field of the new node
        node = head
        while node:
            new_node = node.random
            new_node.random = new_node.random.random if new_node.random else None
            node = node.next

        # restore original list and build new list
        head_copy, node = head.random if head else None, head
        while node:
            node.random.next = node.next.random if node.next else None
            node.random = node.random.next
            node = node.next
        return head_copy

""" 
"""

class Solution___:
    def copyRandomList(self, head):

        result = Node(-1)

        curr = result
        store = {}
        while head is not None:
            # create node
            if head not in store:
                new_node = Node(head.val)
                store[head] = new_node  # add node to store
            else:
                new_node = store[head]

            # create random
            if head.random is not None:
                if head.random not in store:
                    new_random = Node(head.random.val)
                    new_node.random = new_random
                    store[head.random] = new_random  # add node to store
                else:
                    new_node.random = store[head.random]

            # next
            curr.next = new_node
            curr = new_node

            head = head.next

        return result.next

class Solution00:
    def getOrCreateNodeCopy(self, store, node):
        # we store the original node as a key and,
        #   the new node (copy) as its value
        if node not in store:
            store[node] = Node(node.val)

        return store[node]

    def copyRandomList(self, head: 'Node'):
        res = Node(-1)
        store = {}
        copy = res
        old = head
        while old is not None:
            # create old & old.random copies
            node = self.getOrCreateNodeCopy(store, old)
            if old.random is not None:
                node.random = self.getOrCreateNodeCopy(store, old.random)

            copy.next = node
            copy = node

            old = old.next

        return res.next

Flatten a Multilevel Doubly Linked List - LeetCode

Tips

if it involves returning a new LL it might be easier to have a temp head (hd) then at the end return hd.next

Have a pseudo head and pseudo tail in a Doubly Linked List, so that we don't need to check the null node during the add and remove.

Honourable mentions

Find the original version of this page (with additional content) on Notion here.

TODO

Copy List with Random Pointer *

Find the original version of this page (with additional content) on Notion here.

Trees & Graphs

Tree Algorithms

General Trees

Tree question pattern ||2021 placement - LeetCode Discuss

DFS, BFS & Bidirectional Search

Searching

Examples

Youngest Common Ancestor

"""
Youngest Common Ancestor:

You're given three inputs, all of which are instances of an AncestralTree class that have an ancestor property pointing to their youngest ancestor.
The first input is the top ancestor in an ancestral tree (i.e., the only instance that has no ancestor--its ancestor property points to None / null),
 and the other two inputs are descendants in the ancestral tree.
Write a function that returns the youngest common ancestor to the two descendants.
Note that a descendant is considered its own ancestor.
So in the simple ancestral tree below, the youngest common ancestor to nodes A and B is node A.
https://www.algoexpert.io/questions/Youngest%20Common%20Ancestor
"""

# This is an input class. Do not edit.
# class AncestralTree:
#     def __init__(self, name):
#         self.name = name
#         self.ancestor = None

# O(d) time | O(d) space - where d is the depth (height) of the ancestral tree
def getYoungestCommonAncestor00(topAncestor, descendantOne, descendantTwo):
    set_one = set()
    set_two = set()

    while descendantOne is not None or descendantTwo is not None:
        if descendantOne is not None:
            if descendantOne in set_two:
                return descendantOne
            # we do this before doing the two checks because any of them has to be ahead
            set_one.add(descendantOne)
            descendantOne = descendantOne.ancestor

        if descendantTwo is not None:
            if descendantTwo in set_one:
                return descendantTwo
            set_two.add(descendantTwo)
            descendantTwo = descendantTwo.ancestor

# O(d) time | O(1) space - where d is the depth (height) of the ancestral tree
def getYoungestCommonAncestor01(topAncestor, descendantOne, descendantTwo):
    depth_one = getNodeDepth(topAncestor, descendantOne)
    depth_two = getNodeDepth(topAncestor, descendantTwo)

    # put nodes at the same depth
    one = descendantOne
    two = descendantTwo
    if depth_one > depth_two:
        one = moveNodeUp(descendantOne, (depth_one-depth_two))
    else:
        two = moveNodeUp(descendantTwo, (depth_two-depth_one))

    # move nodes upward together
    while one != two:
        one = one.ancestor
        two = two.ancestor

    return one  # or two (they are now equal)

def getNodeDepth(topAncestor, node):
    depth = 0
    while node is not topAncestor:
        depth += 1
        node = node.ancestor
    return depth

def moveNodeUp(node, dist):
    while dist > 0:
        node = node.ancestor
        dist -= 1
    return node

Lowest Common Manager

"""
Lowest Common Manager:

You're given three inputs, all of which are instances of an OrgChart class that have a directReports property pointing to their direct reports.
The first input is the top manager in an organizational chart (i.e., the only instance that isn't anybody else's direct report),
 and the other two inputs are reports in the organizational chart. The two reports are guaranteed to be distinct.
Write a function that returns the lowest common manager to the two reports.

Sample Input
    // From the organizational chart below.
    topManager = Node A
    reportOne = Node E
    reportTwo = Node I
            A
        /     \
        B       C
        /   \   /   \
    D     E F     G
    /   \
    H     I
Sample Output
    Node B

https://www.algoexpert.io/questions/Lowest%20Common%20Manager
"""

# This is an input class. Do not edit.
class OrgChart:
    def __init__(self, name):
        self.name = name
        self.directReports = []

def getLowestCommonManager1(top_manager, report_one, report_two):
    common_manager = [None]
    getManagers(top_manager, report_one, report_two, common_manager)
    return common_manager[0]

def getManagers(curr, report_one, report_two, common_manager):

    count = 0

    # one of them is the common ancestor edge case
    if curr == report_one or curr == report_two:
        count = 1

    for report in curr.directReports:
        count += getManagers(report, report_one, report_two, common_manager)

    if common_manager[0] == None and count == 2:
        common_manager[0] = curr

    return count

""" """

class TreeInfo:
    def __init__(self, lowest_common_manager=None):
        self.lowest_common_manager = lowest_common_manager

def getLowestCommonManager(topManager, reportOne, reportTwo):
    treeInfo = TreeInfo()
    getLowestCommonManagerHelper(topManager, reportOne, reportTwo, treeInfo)
    return treeInfo.lowest_common_manager

def getLowestCommonManagerHelper(curr, reportOne, reportTwo, treeInfo):
    if not curr:
        return False

    found = curr == reportOne or curr == reportTwo
    for child in curr.directReports:
        child_found = getLowestCommonManagerHelper(child,
                                                   reportOne, reportTwo, treeInfo)
        if found and child_found:
            treeInfo.lowest_common_manager = curr
            return False
        found = found or child_found
    return found

Bidirectional Search

Graphs/Networks

Graph Search Algorithms in 100 Seconds - And Beyond with JS

Graphs

Graph Data Structure: Directed, Acyclic, etc | Interview Cake

List of graph algorithms for coding interview - LeetCode Discuss

Graph For Beginners [Problems | Pattern | Sample Solutions] - LeetCode Discuss

Topological Sort (for graphs) *

A tree is actually a type of graph, but not all graphs are trees. Simply put, a tree is a connected graph without cycles.

Examples

It can be helpful to go through 2D array problems

Accounts Merge

""" 
Accounts Merge:

Given a list of accounts where each element accounts[i] is a list of strings, where the first element accounts[i][0] is a name, 
and the rest of the elements are emails representing emails of the account.
Now, we would like to merge these accounts. 
Two accounts definitely belong to the same person if there is some common email to both accounts. 
Note that even if two accounts have the same name, they may belong to different people as people could have the same name. 
A person can have any number of accounts initially, but all of their accounts definitely have the same name.
After merging the accounts, return the accounts in the following format: the first element of each account is the name, and the rest of the elements are emails in sorted order. The accounts themselves can be returned in any order.

Example 1:

    Input: 
        accounts = [["John","[email protected]","[email protected]"],["John","[email protected]","[email protected]"],["Mary","[email protected]"],["John","[email protected]"]]
    Output: 
        [["John","[email protected]","[email protected]","[email protected]"],["Mary","[email protected]"],["John","[email protected]"]]
    Explanation:
    The first and second John's are the same person as they have the common email "[email protected]".
    The third John and Mary are different people as none of their email addresses are used by other accounts.
    We could return these lists in any order, for example the answer [['Mary', '[email protected]'], ['John', '[email protected]'], 
    ['John', '[email protected]', '[email protected]', '[email protected]']] would still be accepted.
Example 2:
    Input: 
        accounts = [["Gabe","[email protected]","[email protected]","[email protected]"],["Kevin","[email protected]","[email protected]","[email protected]"],["Ethan","[email protected]","[email protected]","[email protected]"],["Hanzo","[email protected]","[email protected]","[email protected]"],["Fern","[email protected]","[email protected]","[email protected]"]]
    Output: 
        [["Ethan","[email protected]","[email protected]","[email protected]"],["Gabe","[email protected]","[email protected]","[email protected]"],["Hanzo","[email protected]","[email protected]","[email protected]"],["Kevin","[email protected]","[email protected]","[email protected]"],["Fern","[email protected]","[email protected]","[email protected]"]]

https://leetcode.com/problems/accounts-merge
"""
import collections

"""
-------------------- Problem --------------------
accounts[i][0] is a name, and the rest of the elements are emails 
Two accounts definitely belong to the same person if there is some common email to both accounts
Note that even if two accounts have the same name, they may belong to different people as people could have the same name. 
A person can have any number of accounts initially, but all of their accounts definitely have the same name.

-------------------- Examples --------------------
accounts = [
["John","[email protected]","[email protected]"],                  ["John","[email protected]","[email protected]"],
["Mary","[email protected]"],   
["John","[email protected]"]]

Output: [
["John","[email protected]","[email protected]","[email protected]"],
["Mary","[email protected]"],
["John","[email protected]"]]

-------------------- Brute force --------------------
O(n^2) time | O(n) space
- for every account, look for duplicates

-------------------- Optimal --------------------

- build undirected cyclic graph of the emails
- dfs/bfs returning all connected emails
- add name to connected emails

[["D","[email protected]","[email protected]","[email protected]","[email protected]"],["D","[email protected]","[email protected]"],["D","[email protected]","[email protected]"],["D","[email protected]","[email protected]"],["D","[email protected]","[email protected]"]]

[
["D","[email protected]","[email protected]","[email protected]","[email protected]"],
["D","[email protected]","[email protected]"],
["D","[email protected]","[email protected]"],
["D","[email protected]","[email protected]"]
["D","[email protected]","[email protected]"],
["D","[email protected]","[email protected]"]

]

(only using the number part of the email)
# use the first email as the original key and let the others point to it

--- idx 0 ["D","[email protected]","[email protected]","[email protected]","[email protected]"]
0:[1,9,8]*
1:[0]*
9:[0]*
8:[0]*
--- ["D","[email protected]","[email protected]"]
0:[1,9,8]
1:[0]
9:[0]
8:[0]
3:[4]*
4:[3]*
--- ["D","[email protected]","[email protected]"]
0:[1,9,8]
1:[0]
9:[0]
8:[0]
3:[4]
4:[3,5]*
5:[4]*
--- ["D","[email protected]","[email protected]"]
0:[1,9,8]
1:[0]
9:[0]
8:[0]
3:[4]
4:[3,5]
5:[4]
6:[8]*
8:[6]*
--- ["D","[email protected]","[email protected]"],
0:[1,9,8]
1:[0]
9:[0]
8:[0]
3:[4,2]*
4:[3,5]
5:[4]
6:[8]
8:[6]
2:[3]*
--- ["D","[email protected]","[email protected]"]
0:[1,9,8]
1:[0,2] *
9:[0]
8:[0]
3:[4,2]
4:[3,5]
5:[4]
6:[8]
8:[6]
2:[3,1] *
---
after dfs
[0,1,2,3,4,5,9,8]
[6,8]

"""

class Solution:
    def accountsMerge(self, accounts):
        result = []

        email_to_name = {}
        graph = collections.defaultdict(list)  # Adjacency List
        for account in accounts:
            name = account[0]
            main_email = account[1]

            # add emails to graph
            for idx in range(1, len(account)):
                # point to each other
                graph[main_email].append(account[idx])
                graph[account[idx]].append(main_email)
                # save name
                email_to_name[account[idx]] = name

        visited = set()
        for node in graph:
            emails_found = set()
            self.dfs(graph, node, visited, emails_found)
            if emails_found:
                sorted_emails = sorted(list(emails_found))
                name = email_to_name[sorted_emails[0]]
                result.append([name]+sorted_emails)
        return result

    def dfs(self, graph, node, visited, emails_found):
        if node in visited:
            return
        visited.add(node)

        # add node to emails_found
        emails_found.add(node)

        for email in graph[node]:
            self.dfs(graph, email, visited, emails_found)

Word Ladder **

127. Word Ladder.mp4

Screenshot 2021-11-22 at 20.27.21.png

Screenshot 2021-11-22 at 20.27.56.png

Screenshot 2021-11-22 at 20.28.19.png

Screenshot 2021-11-22 at 20.28.41.png

Screenshot 2021-11-22 at 20.29.24.png

Screenshot 2021-11-22 at 20.29.45.png

Screenshot 2021-11-22 at 20.29.58.png

Screenshot 2021-11-22 at 20.30.15.png

Screenshot 2021-11-22 at 20.30.33.png

""" 
127. Word Ladder

A transformation sequence from word beginWord to word endWord using a dictionary wordList is a sequence of words beginWord -> s1 -> s2 -> ... -> sk such that:
    Every adjacent pair of words differs by a single letter.
    Every si for 1 <= i <= k is in wordList. Note that beginWord does not need to be in wordList.
    sk == endWord
Given two words, beginWord and endWord, and a dictionary wordList, return the number of words in the shortest transformation sequence from beginWord to endWord, 
    or 0 if no such sequence exists.

Example 1:
    Input: beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log","cog"]
    Output: 5
    Explanation: One shortest transformation sequence is "hit" -> "hot" -> "dot" -> "dog" -> cog", which is 5 words long.
Example 2:
    Input: beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log"]
    Output: 0
    Explanation: The endWord "cog" is not in wordList, therefore there is no valid transformation sequence.

Constraints:
    1 <= beginWord.length <= 10
    endWord.length == beginWord.length
    1 <= wordList.length <= 5000
    wordList[i].length == beginWord.length
    beginWord, endWord, and wordList[i] consist of lowercase English letters.
    beginWord != endWord
    All the words in wordList are unique.

https://leetcode.com/problems/word-ladder
"""
from collections import defaultdict, deque
from typing import List

""" 
https://www.notion.so/paulonteri/Trees-Graphs-edc3401e06c044f29a2d714d20ffe185#6f533b3f9c35463492e9378f632ef22b
"""

# N is the number of words, W is the length of the longest word,
# Preprocess: process N words taking W time for each (N*W), forming each word takes W time. Total (N*W^2) time
# BSF: might visit N words and at each word we need to examine need to examine M different combinations (creating them will take W^2 time). Total (N*W^2) time
class Solution:
    def ladderLength(self, beginWord: str, endWord: str, wordList: List[str]):

        # preprocess words (record all words  with a certain pattern/transformation)
        word_transfms = defaultdict(list)
        for word in wordList:
            for word_transfm in self.get_word_transf(word):
                word_transfms[word_transfm].append(word)

        # BFS (find shortest path)
        visited = set()
        queue = deque()
        queue.append((beginWord, 1))
        while queue:
            word, dist = queue.popleft()

            # reached end
            if word == endWord:
                return dist

            # add neighbours to queue
            for word_transfm in self.get_word_transf(word):
                for next_word in word_transfms[word_transfm]:
                    if next_word in visited:
                        continue
                    queue.append((next_word, dist+1))

            visited.add(word)
        return 0

    def get_word_transf(self, word):
        word_transformations = []
        for idx in range(len(word)):
            word_transformations.append(word[:idx]+"*"+word[idx+1:])
        return word_transformations

Course Schedule/Tasks Scheduling

Minimum Passes Of Matrix

""" 
Minimum Passes Of Matrix:

Write a function that takes in an integer matrix of potentially unequal height and width and 
    returns the minimum number of passes required to convert all negative integers in the matrix to positive integers.
A negative integer in the matrix can only be converted to a positive integer if one or more of its adjacent elements is positive. 
An adjacent element is an element that is to the left, to the right, above, or below the current element in the matrix. 
Converting a negative to a positive simply involves multiplying it by -1.
Note that the 0 value is neither positive nor negative, meaning that a 0 can't convert an adjacent negative to a positive.
A single pass through the matrix involves converting all the negative integers that can be converted at a particular point in time. 
For example, consider the following input matrix:
    [ 
    [0, -2, -1], 
    [-5, 2, 0], 
    [-6, -2, 0],
    ]

    After a first pass, only 3 values can be converted to positives:

    [ 
    [0, 2, -1], 
    [5, 2, 0], 
    [-6, 2, 0],
    ]

    After a second pass, the remaining negative values can all be converted to positives:

    [ 
    [0, 2, 1], 
    [5, 2, 0], 
    [6, 2, 0],
    ]

Note that the input matrix will always contain at least one element. If the negative integers in the input matrix can't all be converted to positives, regardless of how many passes are run, your function should return -1.

Sample Input
    matrix = [
    [0, -1, -3, 2, 0],
    [1, -2, -5, -1, -3],
    [3, 0, 0, -4, -1],
    ]
Sample Output
    3

https://www.algoexpert.io/questions/Minimum%20Passes%20Of%20Matrix
"""

""" 
- res = 0
- add all positive numbers to a queue
- for each number in the queue:
    - remove it from the queue
    - convert all positive neighbours to positive and add them to the next queue
    - if a number was converted, increment res by one
    - repeat these steps until the queue is empty
"""

def minimumPassesOfMatrix(matrix):
    number = removeNegatives(matrix)

    for row in range(len(matrix)):
        for col in range(len(matrix[0])):
            # negative not removed
            if matrix[row][col] < 0:
                return -1

    return number

def removeNegatives(matrix):
    res = 0
    queue = []

    # create initial queue
    for row in range(len(matrix)):
        for col in range(len(matrix[0])):
            if matrix[row][col] > 0:
                queue.append((row, col))

    # remove negatives
    while queue:
        has_negative = False
        for _ in range(len(queue)):
            row, col = queue.pop(0)

            # left
            if col-1 >= 0 and matrix[row][col-1] < 0:
                has_negative = True
                matrix[row][col-1] = matrix[row][col-1] * -1
                queue.append((row, col-1))

            # right
            if col+1 < len(matrix[0]) and matrix[row][col+1] < 0:
                has_negative = True
                matrix[row][col+1] = matrix[row][col+1] * -1
                queue.append((row, col+1))

            # above
            if row-1 >= 0 and matrix[row-1][col] < 0:
                has_negative = True
                matrix[row-1][col] = matrix[row-1][col] * -1
                queue.append((row-1, col))

            # below
            if row+1 < len(matrix) and matrix[row+1][col] < 0:
                has_negative = True
                matrix[row+1][col] = matrix[row+1][col] * -1
                queue.append((row+1, col))

        if has_negative:
            res += 1

    return res

Cycle In Graph

"""
Cycle In Graph:

You're given a list of edges representing an unweighted, directed graph with at least one node.
Write a function that returns a boolean representing whether the given graph contains a cycle.
For the purpose of this question, a cycle is defined as any number of vertices, including just one vertex, that are connected in a closed chain.
A cycle can also be defined as a chain of at least one vertex in which the first vertex is the same as the last.

The given list is what's called an adjacency list, and it represents a graph.
The number of vertices in the graph is equal to the length of edges, where each index i in edges contains vertex i's outbound edges, in no particular order.
Each individual edge is represented by a positive integer that denotes an index (a destination vertex) in the list that this vertex is connected to.
Note that these edges are directed, meaning that you can only travel from a particular vertex to its destination,
 not the other way around (unless the destination vertex itself has an outbound edge to the original vertex).
Also note that this graph may contain self-loops. A self-loop is an edge that has the same destination and origin;
 in other words, it's an edge that connects a vertex to itself. For the purpose of this question, a self-loop is considered a cycle.

Sample Input
    edges = [
    [1, 3],
    [2, 3, 4],
    [0],
    [],
    [2, 5],
    [],
    ]
Sample Output
    true 
    // There are multiple cycles in this graph: 
    // 1) 0 -> 1 -> 2 -> 0
    // 2) 0 -> 1 -> 4 -> 2 -> 0
    // 3) 1 -> 2 -> 0 -> 1
    // These are just 3 examples; there are more.

https://www.algoexpert.io/questions/Cycle%20In%20Graph
"""

# ----------------------------------------------------------------------------------------------------------------------------------------------------------------

def cycleInGraph0(edges):
    # # start dfs at each vertex -> loop can start anywhere
    # handles case where vertex 0 = []
    for i in range(len(edges)):
        # can be optimised by storing each vertex's result in a hash table
        if dfs0(edges, set(), i):
            return True

    return False

# we use the visited set to keep track of the vertices currently in the recursive stack
def dfs0(edges, visited, vertex):
    if vertex in visited:
        return True

    # backtracking
    visited.add(vertex)
    found_cycle = False
    for nxt in edges[vertex]:
        found_cycle = found_cycle or dfs0(edges, visited, nxt)

        # note
    visited.discard(vertex)

    return found_cycle

# ----------------------------------------------------------------------------------------------------------------------------------------------------------------

# O(v + e) time | O(v) space - where v is the number of vertices and e is the number of edges in the graph
# time -> basic DFS (we have to consider all the vertices & edges)
def cycleInGraph(edges):
    # # start dfs at each vertex -> loop can start anywhere
    # handles case where vertex 0 = []
    cache = {}
    for i in range(len(edges)):
        if dfs(edges, cache, set(), i):
            return True

    return False

# we use the visited set to keep track of the vertices currently in the recursive stack
def dfs(edges, cache, visited, vertex):
    if vertex in cache:
        return cache[vertex]
    if vertex in visited:  # repeated (found cycle)
        return True

    # backtracking
    visited.add(vertex)
    found_cycle = False
    for nxt in edges[vertex]:
        found_cycle = found_cycle or dfs(edges, cache, visited, nxt)

        # note
    visited.discard(vertex)

    cache[vertex] = found_cycle
    return cache[vertex]

"""
edges = [
  [1, 3],
  [2, 3, 4],
  [0],
  [],
  [2, 5],
  [],
]

if starting at 0

visited = {}
vertex = 0

visited = {0}
vertex = 1

visited = {0,1}
vertex = 2

visited = {0,1,2}
vertex = 0

"""

Remove Islands

"""
Remove Islands:

You're given a two-dimensional array (a matrix) of potentially unequal height and width containing only 0s and 1s.
The matrix represents a two-toned image, where each 1 represents black and each 0 represents white. An island is defined as any number of 1s that are horizontally or vertically adjacent (but not diagonally adjacent) and that don't touch the border of the image. In other words, a group of horizontally or vertically adjacent 1s isn't an island if any of those 1s are in the first row, last row, first column, or last column of the input matrix.
Note that an island can twist. In other words, it doesn't have to be a straight vertical line or a straight horizontal line; it can be L-shaped, for example.
You can think of islands as patches of black that don't touch the border of the two-toned image.
Write a function that returns a modified version of the input matrix, where all of the islands are removed. You remove an island by replacing it with 0s.
Naturally, you're allowed to mutate the input matrix.

https://www.algoexpert.io/questions/Remove%20Islands
"""

# O(wh) time | O(wh) space - where w and h
# are the width and height of the input matrix
def removeIslands(matrix):

    for row in range(1, len(matrix)-1):
        for col in range(1, len(matrix[0])-1):

            if matrix[row][col] == 1 and isIsland(matrix, row, col):
                removeOneIsland(matrix, row, col)

    return matrix

def isIsland(matrix, row, col):

    # check if not island
    if matrix[row][col] != 1 or \
        row <= 0 or col <= 0 or \
            row >= len(matrix)-1 or col >= len(matrix[0])-1:
        return False

    matrix[row][col] = -1  # mark

    # check if still island

    up = True
    if row - 1 >= 0 and matrix[row-1][col] == 1:
        up = isIsland(matrix, row-1, col)
    down = True
    if row + 1 < len(matrix) and matrix[row+1][col] == 1:
        down = isIsland(matrix, row+1, col)

    left = True
    if col - 1 >= 0 and matrix[row][col-1] == 1:
        left = isIsland(matrix, row, col-1)
    right = True
    if col + 1 < len(matrix[0]) and matrix[row][col+1] == 1:
        right = isIsland(matrix, row, col+1)

    matrix[row][col] = 1  # unmark

    return left and right and down and up

def removeOneIsland(matrix, row, col):

    if matrix[row][col] == 1:

        matrix[row][col] = 0  # remove

        # down
        if matrix[row+1][col] == 1:
            removeOneIsland(matrix, row+1, col)
        # left
        if matrix[row][col-1] == 1:
            removeOneIsland(matrix, row, col-1)
        # right
        if matrix[row][col+1] == 1:
            removeOneIsland(matrix, row, col+1)

# Solution:
# 1. iterate through every element in the matrix
# 2. chsck if valid island
# 3. if valid island, remove the island

def checkIfIsland(matrix, row, col):
    is_at_end = row <= 0 or col <= 0 or \
        row >= len(matrix)-1 or col >= len(matrix[0])-1

    if is_at_end or matrix[row][col] != 1:
        return False

    matrix[row][col] = -1  # mark

    right = left = up = down = True
    # checks to ensure we don't run into a loop
    if matrix[row][col+1] == 1:  # right
        right = checkIfIsland(matrix, row, col+1)
    if matrix[row][col-1] == 1:  # left
        left = checkIfIsland(matrix, row, col-1)
    if matrix[row+1][col] == 1:  # up
        up = checkIfIsland(matrix, row+1, col)
    if matrix[row-1][col] == 1:  # down
        down = checkIfIsland(matrix, row-1, col)

    matrix[row][col] = 1  # unmark

    return left and right and up and down

def removeAnIsland(matrix, row, col):

    if matrix[row][col] == 1:

        matrix[row][col] = 0  # remove

        # checks to ensure we don't run into a loop
        # down
        if matrix[row+1][col] == 1:
            removeAnIsland(matrix, row+1, col)
        # left
        if matrix[row][col-1] == 1:
            removeAnIsland(matrix, row, col-1)
        # right
        if matrix[row][col+1] == 1:
            removeAnIsland(matrix, row, col+1)

def removeIslands2(matrix):

    for row in range(len(matrix)):
        for col in range(len(matrix[0])):
            if checkIfIsland(matrix, row, col):
                removeAnIsland(matrix, row, col)

    return matrix

"""

Sample Input
    matrix =
    [
    [1, 0, 0, 0, 0, 0],
    [0, 1, 0, 1, 1, 1],
    [0, 0, 1, 0, 1, 0],
    [1, 1, 0, 0, 1, 0],
    [1, 0, 1, 1, 0, 0],
    [1, 0, 0, 0, 0, 1]
    ]
Sample Output
    [
    [1, 0, 0, 0, 0, 0],
    [0, 0, 0, 1, 1, 1],
    [0, 0, 0, 0, 1, 0],
    [1, 1, 0, 0, 1, 0],
    [1, 0, 0, 0, 0, 0],
    [1, 0, 0, 0, 0, 1]
    ]
    // The islands that were removed can be clearly seen here:
    // [
    //   [ ,  ,  ,  ,  , ],
    //   [ , 1,  ,  ,  , ],
    //   [ ,  , 1,  ,  , ],
    //   [ ,  ,  ,  ,  , ],
    //   [ ,  , 1, 1,  , ],
    //   [ ,  ,  ,  ,  , ]
    // ]

matrix = [[1, 0, 0, 0, 0, 0],
          [0, 0, 0, 1, 1, 1],
          [0, 0, 0, 0, 1, 0],
          [1, 1, 0, 0, 1, 0],
          [1, 0, 0, 0, 0, 0],
          [1, 0, 0, 0, 0, 1]
          ]

matrix_2 = [
    [1, 0, 0, 0, 0, 0],
    [0, 1, 0, 1, 1, 1],
    [0, 0, 1, 0, 1, 0],
    [1, 1, 0, 0, 1, 0],
    [1, 0, 1, 1, 0, 0],
    [1, 0, 0, 0, 0, 1]
]

"""

mx = [
    [1, 0, 0, 0, 0, 0],
    [0, 1, 0, 1, 1, 1],
    [0, 0, 1, 0, 1, 0],
    [1, 1, 0, 0, 1, 0],
    [1, 0, 1, 1, 0, 0],
    [1, 0, 0, 0, 0, 1]
]

print(removeIslands(mx))

River Sizes

"""
River Sizes:

You're given a two-dimensional array (a matrix) of potentially unequal height and width containing only 0s and 1s.
Each 0 represents land, and each 1 represents part of a river.
A river consists of any number of 1s that are either horizontally or vertically adjacent (but not diagonally adjacent).
The number of adjacent 1s forming a river determine its size.
Note that a river can twist. In other words, it doesn't have to be a straight vertical line or a straight horizontal line; it can be L-shaped, for example.
Write a function that returns an array of the sizes of all rivers represented in the input matrix. 
The sizes don't need to be in any particular order.

Sample Input
    matrix = [
    [1, 0, 0, 1, 0],
    [1, 0, 1, 0, 0],
    [0, 0, 1, 0, 1],
    [1, 0, 1, 0, 1],
    [1, 0, 1, 1, 0],
    ]
Sample Output
    [1, 2, 2, 2, 5] // The numbers could be ordered differently.

// The rivers can be clearly seen here:
// [
//   [1,  ,  , 1,  ],
//   [1,  , 1,  ,  ],
//   [ ,  , 1,  , 1],
//   [1,  , 1,  , 1],
//   [1,  , 1, 1,  ],
// ]

https://www.algoexpert.io/questions/River%20Sizes
"""

"""
Solution:
1. iterate through every element in the array
2. if we find a river (1) map out it's length while marking the river's elements as visited (-1)
"""

# O(wh) time | O(wh) space
def riverSizes(matrix):
    river_sizes = []
    for row in range(len(matrix)):
        for col in range(len(matrix[0])):

            if matrix[row][col] == 1:  # if river
                river_sizes.append(findRiverSize(matrix, row, col))

    return river_sizes

def findRiverSize(matrix, row, col):
    if row < 0 or col < 0 or row >= len(matrix) or col >= len(matrix[0]) \
            or matrix[row][col] != 1:  # not river (base case)
        return 0

    matrix[row][col] = -1  # mark point as visited

    left = findRiverSize(matrix, row, col-1)
    right = findRiverSize(matrix, row, col+1)
    down = findRiverSize(matrix, row+1, col)
    up = findRiverSize(matrix, row-1, col)

    return 1 + right + left + down + up  # visit neighbours

matrix = [
    [1, 0, 0, 1, 0],
    [1, 0, 1, 0, 0],
    [0, 0, 1, 0, 1],
    [1, 0, 1, 0, 1],
    [1, 0, 1, 1, 0],
]
x = [
    [1, 0, 0, 1, 0, 1, 0, 0, 1, 1, 1, 0],
    [1, 0, 1, 0, 0, 1, 1, 1, 1, 0, 1, 0],
    [0, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1, 1],
    [1, 0, 1, 0, 1, 1, 0, 0, 0, 1, 0, 0],
    [1, 0, 1, 1, 0, 0, 0, 1, 1, 1, 0, 1]
]  # [2, 1, 21, 5, 2, 1]
print(riverSizes(matrix))
print(riverSizes([[1, 1, 1, 0, 1, 1, 0, 0, 0, 1, 0]]))
print(riverSizes(x))
# print(findRiverSize(x, 0, 5))

Single Cycle Check

"""
Single Cycle Check:

You're given an array of integers where each integer represents a jump of its value in the array.
For instance, the integer 2 represents a jump of two indices forward in the array;
    the integer -3 represents a jump of three indices backward in the array.
If a jump spills past the array's bounds, it wraps over to the other side. 
For instance, a jump of -1 at index 0 brings us to the last index in the array. 
Similarly, a jump of 1 at the last index in the array brings us to index 0.

Write a function that returns a boolean representing whether the jumps in the array form a single cycle.
A single cycle occurs if, starting at any index in the array and following the jumps,
    every element in the array is visited exactly once before landing back on the starting index.

Sample Input
    array = [2, 3, 1, -4, -4, 2]
Sample Output
    true

https://www.algoexpert.io/questions/Single%20Cycle%20Check
"""

# 0(n) time | 0(n) space
def hasSingleCycle(array):

    visited = {}  # visited indexes
    idx = 0
    while True:

        # # jump logic (find where we are visiting)
        idx = getNextIdx(idx, array)

        # if we have been at this index before (which will eventually happen):
        if idx in visited:
            # if len(visited) is the same as len(array),
            #   then we must have done one complete loop including every element
            #   will handle cycles that do not cover all elements in the array
            return len(visited) == len(array)

        # # visit index
        visited[idx] = True

""" 
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
"""

def hasSingleCycle00(array):
    indices = [0] * len(array)

    i = 0
    for _ in range(len(array)*2):
        # mark current index as visted
        indices[i] = indices[i] + 1

        # move to next index
        i += array[i]
        if i > len(array) - 1:  # too large
            i = i % len(array)
        while i < 0:
            i += len(array)

    # look for invalid
    for num in indices:
        if num != 2:
            return False

    return True

""" 
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

after len(array)-1 visits, we should land at index 0
"""

# 0(n) time | 0(1) space
def hasSingleCycle2(array):
    # after len(array)-1 visits, we should land at index 0

    num_elements_visited = 0
    idx = 0
    while num_elements_visited < len(array):
        if num_elements_visited > 0 and idx == 0:
            return False

        num_elements_visited += 1
        idx = getNextIdx(idx, array)

    return idx == 0

def getNextIdx(idx, array):

    # # jump logic (find where we are visiting)
    idx = idx + array[idx]
    while idx >= len(array) or idx < 0:
        if idx >= len(array):
            idx -= len(array)
        if idx < 0:
            idx += len(array)

    return idx

""" 
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
"""

def hasSingleCycle0(array):

    counter = 0

    idx = 0
    while counter < len(array):
        if array[idx] == float("-inf"):
            return False

        idx_val = array[idx]
        # mark as visited
        array[idx] = float("-inf")

        # jump
        idx += idx_val
        counter += 1

        while idx < 0:
            idx += len(array)
        while idx > len(array) - 1:
            idx -= len(array)

    return idx == 0

"""

[0, 1, 2,  3,  4, 5]
[2, 1, 1,  1,  1, 1]
[2, 3, 1, -4, -4, 2]

"""

Clone Graph

"""
Clone Graph:

Given a reference of a node in a connected undirected graph.
Return a deep copy (clone) of the graph.
Each node in the graph contains a val (int) and a list (List[Node]) of its neighbors.
    class Node {
        public int val;
        public List<Node> neighbors;
    }

Test case format:

For simplicity sake, each node's value is the same as the node's index (1-indexed). For example, the first node with val = 1, the second node with val = 2, and so on. 

The graph is represented in the test case using an adjacency list.
Adjacency list is a collection of unordered lists used to represent a finite graph. Each list describes the set of neighbors of a node in the graph.

The given node will always be the first node with val = 1. You must return the copy of the given node as a reference to the cloned graph.

https://leetcode.com/problems/clone-graph/
"""

from typing import List

# Definition for a Node.
class Node:
    def __init__(self, val=0, neighbors=None):
        self.val = val
        self.neighbors = neighbors if neighbors is not None else []

class Solution:
    def cloneGraph(self, node: 'Node'):
        if node is None:
            return None

        created_nodes = []  # node 1 will be at index 0,  2 at 1...

        return self.createNode(node, created_nodes)

    def createNode(self, node: Node, created_nodes):
        # ensure we have the index: node 1 will be at index 0,  2 at 1...
        while len(created_nodes) < node.val:
            created_nodes.append(None)
        # check if created: no need to create it again
        if created_nodes[node.val-1] is not None:
            return created_nodes[node.val-1]

        # # create new node
        new_node = Node(node.val)
        # add to created_nodes
        created_nodes[node.val-1] = new_node

        # create neighbors
        if node.neighbors:
            neighbors = []
            for neighbour in node.neighbors:
                neighbors.append(self.createNode(neighbour, created_nodes))
            new_node.neighbors = neighbors

        return new_node

"""
1. create new node
2. add children to node
    - create child

node
node.neighnours = [createNode(child1), createNode(child2)
"""

Youngest Common Ancestor

"""
Youngest Common Ancestor:

You're given three inputs, all of which are instances of an AncestralTree class that have an ancestor property pointing to their youngest ancestor.
The first input is the top ancestor in an ancestral tree (i.e., the only instance that has no ancestor--its ancestor property points to None / null),
 and the other two inputs are descendants in the ancestral tree.
Write a function that returns the youngest common ancestor to the two descendants.
Note that a descendant is considered its own ancestor.
So in the simple ancestral tree below, the youngest common ancestor to nodes A and B is node A.

https://www.algoexpert.io/questions/Youngest%20Common%20Ancestor
"""

# This is an input class. Do not edit.
class AncestralTree:
    def __init__(self, name):
        self.name = name
        self.ancestor = None

# 0(d) time | 0(d) space - where d is the depth (height) of the ancestral tree
def getYoungestCommonAncestor1(topAncestor, descendantOne, descendantTwo):

    store_one = {}
    store_two = {}
    while descendantOne != topAncestor or descendantTwo != topAncestor:
        # # move up
        # one
        if descendantOne != topAncestor:
            if descendantOne.name in store_two:  # if seen by other descendant
                return descendantOne
            else:
                store_one[descendantOne.name] = True
            descendantOne = descendantOne.ancestor  # move up

        # two
        if descendantTwo != topAncestor:
            if descendantTwo.name in store_one:  # if seen by other descendant
                return descendantTwo
            else:
                store_two[descendantTwo.name] = True
            descendantTwo = descendantTwo.ancestor  # move up

    return topAncestor  # will always be an ancestor

# 0(d) time | 0(1) space
def getYoungestCommonAncestor(topAncestor, descendantOne, descendantTwo):

    dist_top_one = 0
    dist_top_two = 0
    curr_one = descendantOne
    curr_two = descendantTwo
    # calculate height from top
    while curr_one != topAncestor or curr_two != topAncestor:
        if curr_one != topAncestor:
            dist_top_one += 1
            curr_one = curr_one.ancestor
        if curr_two != topAncestor:
            dist_top_two += 1
            curr_two = curr_two.ancestor

    # level nodes
    while dist_top_one != dist_top_two:  # move the lower pointer upwards
        if dist_top_one > dist_top_two:
            dist_top_one -= 1
            descendantOne = descendantOne.ancestor
        else:
            dist_top_two -= 1
            descendantTwo = descendantTwo.ancestor

    # find common ancestor
    while descendantOne != topAncestor or descendantTwo != topAncestor:
        if descendantTwo == descendantOne:
            return descendantOne

        descendantOne = descendantOne.ancestor
        descendantTwo = descendantTwo.ancestor

    return topAncestor  # will always be an ancestor

"""
Sample Input
// The nodes are from the ancestral tree below.
    topAncestor = node A
    descendantOne = node E
    descendantTwo = node I
            A
        /     \
       B       C
     /  \     /  \
    D     E F     G
 /   \
 H     I
Sample Output
    node B

Solution:
1. try to get the (pointers to the) nodes to be at the same level
    - for example pointer two should move up to D
    - this can be done by calculating the distance to the top ancestor,
        then moving the lower pointer upwards
2. iterate upwards and return when they are at the same node

"""

Shortest Distance from All Buildings *

Screenshot 2021-10-09 at 15.48.18.png

Screenshot 2021-10-09 at 15.49.29.png

""" 
Shortest Distance from All Buildings

You are given an m x n grid grid of values 0, 1, or 2, where:
    each 0 marks an empty land that you can pass by freely,
    each 1 marks a building that you cannot pass through, and
    each 2 marks an obstacle that you cannot pass through.

You want to build a house on an empty land that reaches all buildings in the shortest total travel distance. 
You can only move up, down, left, and right.

Return the shortest travel distance for such a house. 
If it is not possible to build such a house according to the above rules, return -1.

The total travel distance is the sum of the distances between the houses of the friends and the meeting point.

The distance is calculated using Manhattan Distance, where distance(p1, p2) = |p2.x - p1.x| + |p2.y - p1.y|.

Example 1:
    Input: 
        grid = 
        [
            [1,0,2,0,1],
            [0,0,0,0,0],
            [0,0,1,0,0]
        ]
    Output: 
        7
    Explanation: 
        Given three buildings at (0,0), (0,4), (2,2), and an obstacle at (0,2).
        The point (1,2) is an ideal empty land to build a house, as the total travel distance of 3+3+1=7 is minimal.
        So return 7.
Example 2:
    Input: grid = [[1,0]]
    Output: 1
Example 3:
    Input: grid = [[1]]
    Output: -1
https://leetcode.com/problems/shortest-distance-from-all-buildings
"""

""" 
1. BFS from free space to all houses
2. BFS from houses to free spaces 

"""

# Let N and M be the number of rows and columns in grid respectively.
# O(N^2 . M^2) time | O(N . M) time
class Solution:
    def shortestDistance(self, grid):
        """ 
        BFS from Houses to Empty Land
        """
        houses_reached = [
            [0 for _ in range(len(grid[0]))] for _ in range(len(grid))]

        # # count houses
        houses_count = 0
        for row in range(len(grid)):
            for col in range(len(grid[0])):
                if grid[row][col] == 1:
                    houses_count += 1

        # # bfs on each house
        for row in range(len(grid)):
            for col in range(len(grid[0])):
                # check if house
                if grid[row][col] == 1:
                    self.bfs(row, col, grid, houses_reached)

        # # find suitable free space
        largest = float('-inf')
        for row in range(len(grid)):
            for col in range(len(grid[0])):
                # check if valid free space
                if houses_reached[row][col] == houses_count and grid[row][col] < 0:
                    largest = max(largest, grid[row][col])

        if largest == float('-inf'):
            return -1
        return largest * -1

    def bfs(self, row, col, grid, houses_reached):
        visited = [
            [False for _ in range(len(grid[0]))] for _ in range(len(grid))]
        queue = []

        # initialise queue
        queue.append((row-1, col, -1))
        queue.append((row+1, col, -1))
        queue.append((row, col-1, -1))
        queue.append((row, col+1, -1))

        while queue:
            c_row, c_col, distance = queue.pop(0)
            if c_row < 0 or c_row >= len(grid):
                continue
            if c_col < 0 or c_col >= len(grid[0]):
                continue
            if visited[c_row][c_col]:
                continue
            if grid[c_row][c_col] > 0:
                continue

            visited[c_row][c_col] = True

            # # record distance
            grid[c_row][c_col] += distance
            houses_reached[c_row][c_col] += 1

            # # move outward
            new_distance = distance - 1
            queue.append((c_row-1, c_col, new_distance))
            queue.append((c_row+1, c_col, new_distance))
            queue.append((c_row, c_col-1, new_distance))
            queue.append((c_row, c_col+1, new_distance))

Min Cost to Connect All Points

Prim's Algorithm - Minimum Spanning Tree - Min Cost to Connect all Points - Leetcode 1584 - Python

Screenshot 2021-10-19 at 07.17.51.png

""" 
1584. Min Cost to Connect All Points

You are given an array points representing integer coordinates of some points on a 2D-plane, where points[i] = [xi, yi].
The cost of connecting two points [xi, yi] and [xj, yj] is the manhattan distance between them: |xi - xj| + |yi - yj|, where |val| denotes the absolute value of val.
Return the minimum cost to make all points connected. All points are connected if there is exactly one simple path between any two points.

Example 1:
    Input: points = [[0,0],[2,2],[3,10],[5,2],[7,0]]
    Output: 20
Explanation:
    We can connect the points as shown above to get the minimum cost of 20.
    Notice that there is a unique path between every pair of points.
Example 2:
    Input: points = [[3,12],[-2,5],[-4,1]]
    Output: 18
Example 3:
    Input: points = [[0,0],[1,1],[1,0],[-1,1]]
    Output: 4
Example 4:
    Input: points = [[-1000000,-1000000],[1000000,1000000]]
    Output: 4000000
Example 5:
    Input: points = [[0,0]]
    Output: 0

https://leetcode.com/problems/min-cost-to-connect-all-points
https://www.notion.so/paulonteri/Trees-Graphs-edc3401e06c044f29a2d714d20ffe185#2ac2c79816464704a3851de16d494dff
"""

import collections
import heapq

""" 
Prim's Minimum Spanning Tree Algorithm: https://www.notion.so/paulonteri/Trees-Graphs-edc3401e06c044f29a2d714d20ffe185#596bc798759a4edabe22a895aadeb12c
https://youtu.be/f7JOBJIC-NA
"""

class Solution_:
    def minCostConnectPoints(self, points):
        total = 0

        # # Create adjacency list
        # Will store  nodes in the form => `parent: [[cost_to_1, node_1], [cost_to_2, node_2], ...]`
        graph = collections.defaultdict(list)
        for idx in range(len(points)):
            x1, y1 = points[idx]
            for idx2 in range(idx + 1, len(points)):
                x2, y2 = points[idx2]
                cost = abs(x1 - x2) + abs(y1 - y2)

                graph[str(x1)+str(y1)].append([cost, str(x2)+str(y2)])
                graph[str(x2)+str(y2)].append([cost, str(x1)+str(y1)])

        # # Prim's Minimum Spanning Tree Algorithm
        visited = set()
        priority_queue = []
        first_node = str(points[0][0])+str(points[0][1])
        heapq.heappush(priority_queue, (0, first_node))  # start from node 0
        while len(visited) < len(graph):
            cost, node = heapq.heappop(priority_queue)
            # skip visited
            if node in visited:
                continue
            visited.add(node)

            # record cost
            total += cost
            # add neighbours
            for neighbour in graph[node]:
                if neighbour[1] not in visited:
                    heapq.heappush(priority_queue, neighbour)

        return total

class Solution:
    def minCostConnectPoints(self, points):

        total = 0

        # # Create adjacency list
        # Will use the array indices as id's
        # Will store  nodes in the form => `parent: [[cost_to_1, node_1], [cost_to_2, node_2], ...]`
        graph = collections.defaultdict(list)
        for idx in range(len(points)):
            x1, y1 = points[idx]
            for idx2 in range(idx + 1, len(points)):
                x2, y2 = points[idx2]
                cost = abs(x1 - x2) + abs(y1 - y2)

                graph[idx].append([cost, idx2])
                graph[idx2].append([cost, idx])

        # # Prim's Minimum Spanning Tree Algorithm
        visited = set()
        priority_queue = []
        heapq.heappush(priority_queue, (0, 0))  # start from node 0
        while len(visited) < len(graph):
            cost, node = heapq.heappop(priority_queue)
            # skip visited
            if node in visited:
                continue
            visited.add(node)

            # record cost
            total += cost
            # add neighbours
            for neighbour in graph[node]:
                if neighbour[1] not in visited:
                    heapq.heappush(priority_queue, neighbour)

        return total

Connecting Cities With Minimum Cost

""" 
1584. Min Cost to Connect All Points

You are given an array points representing integer coordinates of some points on a 2D-plane, where points[i] = [xi, yi].
The cost of connecting two points [xi, yi] and [xj, yj] is the manhattan distance between them: |xi - xj| + |yi - yj|, where |val| denotes the absolute value of val.
Return the minimum cost to make all points connected. All points are connected if there is exactly one simple path between any two points.

Example 1:
    Input: points = [[0,0],[2,2],[3,10],[5,2],[7,0]]
    Output: 20
Explanation:
    We can connect the points as shown above to get the minimum cost of 20.
    Notice that there is a unique path between every pair of points.
Example 2:
    Input: points = [[3,12],[-2,5],[-4,1]]
    Output: 18
Example 3:
    Input: points = [[0,0],[1,1],[1,0],[-1,1]]
    Output: 4
Example 4:
    Input: points = [[-1000000,-1000000],[1000000,1000000]]
    Output: 4000000
Example 5:
    Input: points = [[0,0]]
    Output: 0

https://leetcode.com/problems/min-cost-to-connect-all-points
https://www.notion.so/paulonteri/Trees-Graphs-edc3401e06c044f29a2d714d20ffe185#2ac2c79816464704a3851de16d494dff
"""

import collections
import heapq

""" 
Prim's Minimum Spanning Tree Algorithm: https://www.notion.so/paulonteri/Trees-Graphs-edc3401e06c044f29a2d714d20ffe185#596bc798759a4edabe22a895aadeb12c
https://youtu.be/f7JOBJIC-NA
"""

class Solution_:
    def minCostConnectPoints(self, points):
        total = 0

        # # Create adjacency list
        # Will store  nodes in the form => `parent: [[cost_to_1, node_1], [cost_to_2, node_2], ...]`
        graph = collections.defaultdict(list)
        for idx in range(len(points)):
            x1, y1 = points[idx]
            for idx2 in range(idx + 1, len(points)):
                x2, y2 = points[idx2]
                cost = abs(x1 - x2) + abs(y1 - y2)

                graph[str(x1)+str(y1)].append([cost, str(x2)+str(y2)])
                graph[str(x2)+str(y2)].append([cost, str(x1)+str(y1)])

        # # Prim's Minimum Spanning Tree Algorithm
        visited = set()
        priority_queue = []
        first_node = str(points[0][0])+str(points[0][1])
        heapq.heappush(priority_queue, (0, first_node))  # start from node 0
        while len(visited) < len(graph):
            cost, node = heapq.heappop(priority_queue)
            # skip visited
            if node in visited:
                continue
            visited.add(node)

            # record cost
            total += cost
            # add neighbours
            for neighbour in graph[node]:
                if neighbour[1] not in visited:
                    heapq.heappush(priority_queue, neighbour)

        return total

class Solution:
    def minCostConnectPoints(self, points):

        total = 0

        # # Create adjacency list
        # Will use the array indices as id's
        # Will store  nodes in the form => `parent: [[cost_to_1, node_1], [cost_to_2, node_2], ...]`
        graph = collections.defaultdict(list)
        for idx in range(len(points)):
            x1, y1 = points[idx]
            for idx2 in range(idx + 1, len(points)):
                x2, y2 = points[idx2]
                cost = abs(x1 - x2) + abs(y1 - y2)

                graph[idx].append([cost, idx2])
                graph[idx2].append([cost, idx])

        # # Prim's Minimum Spanning Tree Algorithm
        visited = set()
        priority_queue = []
        heapq.heappush(priority_queue, (0, 0))  # start from node 0
        while len(visited) < len(graph):
            cost, node = heapq.heappop(priority_queue)
            # skip visited
            if node in visited:
                continue
            visited.add(node)

            # record cost
            total += cost
            # add neighbours
            for neighbour in graph[node]:
                if neighbour[1] not in visited:
                    heapq.heappush(priority_queue, neighbour)

        return total

Terminology & Definitions

a directed, weighted, acyclic graph with 6 vertices and 8 edges

Vertex/Node

A vertex (also called a node) is a fundamental part of a graph. It can have a name (a key), it may also have additional information (the payload). Our graph has 6 vertices: V = {a, b, c, d, e, f}

Edge/Arc

An edge (also called an “arc”) is another fundamental part of a graph. An edge connects two vertices to show that there is a relationship between them. Our graph has 8 edges: E = {(a, b, 45), (a, c, 52), (a, d, 7), (b, c, 11), (b, f, 5), (d, e, 17), (e, f, 6), (f, c, 21)}

Weighted or Unweighted

If a graph is weighted, each edge has a “weight.” The weight could, for example, represent the distance between two locations, or the cost or time it takes to travel between the locations.

Directed or Undirected

In directed graphs, edges point from the node at one end to the node at the other end. In undirected graphs, the edges simply connect the nodes at each end.

Our example above is a directed graph.

Cyclic or Acyclic

A graph is cyclic if it has a cycle, an unbroken series of nodes with no repeating nodes or edges that connects back to itself. Graphs without cycles are acyclic. Our example above is an acyclic graph.

Connected vs Disconnected

If G is an undirected graph, vertices u and v are said to be connected if G contains a path from u to v; otherwise, u and v are said to be disconnected.

A graph is said to be connected if every pair of vertices in the graph is connected. A connected component is a maximal set of vertices C such that each pair of vertices in C is connected in G. E

Topological ordering

Topological Sort (for graphs) *

A directed acyclic graph (DAG) is a directed graph in which there are no cycles, i.e., paths that contain one or more edges and which begin and end at the same vertex.

Vertices in a directed acyclic graph that have no incoming edges are referred to as sources.

Vertices that have no outgoing edges are referred to as sinks.

Indegree → count of incoming edges of each vertex/node or how many parents it has (used to determine sources)

A topological ordering of the vertices in a DAG is an ordering of the vertices in which each edge is from a vertex earlier in the ordering to a vertex later in the ordering.

Representing Graphs in Code

There are a few ways to represent graphs in the code. We’ll look at the most common three, and the basic tradeoffs.

Let’s take this graph as an example:

Edge List

A list of all the edges in the graph: graph = [[4, 5], [2, 4], [2, 3], [1, 2], [0, 2], [0, 1]] Since node 0 has edges to nodes 1 and 2, [0, 1] and [0, 2] are in the edge list.

This is well suited to performant lookups of an edge, or listing all edges, but is slow with many other query types. For example, to find all vertices adjacent to a given vertex, every edge must be examined.

Adjacency List (Use of indexes & dicts) *

A list where the index represents the node and the value at that index is a list of the node’s neighbours: Since node 2 has edges to nodes 0, 1, 3 and 4, graph[2] has the adjacency list [0, 1, 3, 4].

We could also use a dictionary where the keys represent the node and the values are the lists of neighbours. This would be useful if the nodes were represented by strings, objects, or otherwise didn’t map cleanly to list indices.

graph = [ [1, 2], [0, 2], [0, 1, 3, 4], [2], [2, 5], [4] ]

graph = { 0: [1, 2], 1: [0, 2], 2: [0, 1, 3, 4], 3: [2], 4: [2, 5], 5: [4] }

This representation allows for constant-time lookup of adjacent vertices, which is useful in many query and pathfinding scenarios. It is slower for edge lookups, as the whole list of vertices adjacent to u must be examined for v, in order to find edge uv.

Adjacency lists are the typical choice for general purpose use, though edge lists or adjacency matrices have their own strengths, which may match a specific use case.

Pros:

Saves on space (memory): the representation takes as many memory words as there are nodes and edge.

Cons:

It can take up to O(n) time to determine if a pair of nodes (i,j) is an edge: one would have to search the linked list L[i], which takes time proportional to the length of L[i].

Adjacency Matrix *

A matrix of 0 and 1 indicates whether node x connects to node y (0 means no, 1 means yes).

Since node 4 has edges to nodes 2 and 5, graph[4][2] and graph[4][5] have value 1.

Pros:

Simple to implement
O(1) edge lookups. Easy and fast to tell if a pair (i,j) is an edge: simply check if A[i][j] is 1 or 0

Cons:

No matter how few edges the graph has, the matrix takes O(n2) in memory

graph = [ [0, 1, 1, 0, 0, 0], [1, 0, 1, 0, 0, 0], [1, 1, 0, 1, 1, 0], [0, 0, 1, 0, 0, 0], [0, 0, 1, 0, 0, 1], [0, 0, 0, 0, 1, 0] ]

Adjacency matrices perform strongly with edge lookups, with a constant-time lookup given a pair of vertex Id. They tend to be slow for other operations. For example, listing everything adjacent to a vertex requires checking every single vertex in the graph. They also typically require more space than other models, especially with sparse graphs (graphs with “few” edges)

Other

DFS & BFS time complexity: *

Bipartite graph/Look for even cycle using graph colouring

Possible Bipartition | Bipartite graph | Graph coloring | Leetcode #886

Bipartite graph - Wikipedia

What is a bipartite graph?

Examples

Is Graph Bipartite?

Screenshot 2021-10-10 at 09.23.09.png

""" 
785. Is Graph Bipartite?

There is an undirected graph with n nodes, where each node is numbered between 0 and n - 1. 
You are given a 2D array graph, where graph[u] is an array of nodes that node u is adjacent to. 
More formally, for each v in graph[u], there is an undirected edge between node u and node v. The graph has the following properties:
    There are no self-edges (graph[u] does not contain u).
    There are no parallel edges (graph[u] does not contain duplicate values).
    If v is in graph[u], then u is in graph[v] (the graph is undirected).
    The graph may not be connected, meaning there may be two nodes u and v such that there is no path between them.

A graph is bipartite if the nodes can be partitioned into two independent sets 
 A and B such that every edge in the graph connects a node in set A and a node in set B.

Return true if and only if it is bipartite.

https://leetcode.com/problems/is-graph-bipartite
https://www.notion.so/paulonteri/Trees-Graphs-edc3401e06c044f29a2d714d20ffe185#dc05cd22189b412f8a0a8c1d1a827bde
"""

class Solution:
    def isBipartite(self, graph):

        colours = [None] * len(graph)
        visited = [False] * len(graph)

        for node in range(len(graph)):
            if not self.dfs(graph, node, colours, visited):
                return False
        return True

    def dfs(self, graph, node, colours, visited):
        if visited[node]:
            return True
        if colours[node] is None:
            # https://www.notion.so/paulonteri/Trees-Graphs-edc3401e06c044f29a2d714d20ffe185#596387a8e4254e1690f5eca7996ab9a1
            # if we do not know the colour then we can group it with the nodes in which we do not know the colours
            colours[node] = True

        visited[node] = True

        # Check colours & Dfs
        for child in graph[node]:
            if colours[child] is None:
                colours[child] = not colours[node]
            # check for correct colours
            if colours[child] == colours[node]:
                return False

            # Dfs
            if not self.dfs(graph, child, colours, visited):
                return False

        return True

Screenshot 2021-10-10 at 07.41.53.png

https://encrypted-tbn0.gstatic.com/images?q=tbn:ANd9GcTxVsY_1LCKk5csP6iyLxE_PorhQYoAipU5a-zz2uoT9Q&s

A Bipartite Graph is a graph whose vertices can be divided into two independent sets, U and V such that every edge (u, v) either connects a vertex from U to V or a vertex from V to U. In other words, for every edge (u, v), either u belongs to U and v to V, or u belongs to V and v to U. We can also say that there is no edge that connects vertices of same set.

Equivalently, a bipartite graph is a graph that does not contain any odd-length cycles.

Graph colouring:
- the graph on the left has an even cycle
- the graph on the right failed to make an even cycle (at 4/5)

Graph colouring: - the graph on the left has an even cycle - the graph on the right failed to make an even cycle (at 4/5)

Binary Trees

Binary Tree

Binary Tree Data Structure | Interview Cake

Binary Tree Bootcamp: Full, Complete, & Perfect Trees. Preorder, Inorder, & Postorder Traversal.

Binary Trees study guide - LeetCode Discuss

General

Implementation

class BinaryTree:
    def __init__(self, data):
        self.left = None
        self.right = None
        self.root = data

    def insert_left(self, value):
        if self.left is None:
            self.left = BinaryTree(value)
        else:
            new_node = BinaryTree(value)
            new_node.left = self.left
            self.left = new_node

    def insert_right(self, value):
        if self.right is None:
            self.right = BinaryTree(value)
        else:
            new_node = BinaryTree(value)
            new_node.left = self.left
            self.left = new_node

    def get_right_child(self):
        return self.right

    def get_left_child(self):
        return self.left

    def set_root_value(self, value):
        self.root = value

    def get_root_value(self):
        return self.root

Binary Tree

Examples:

Symmetric Tree **

""" 
101. Symmetric Tree

Given the root of a binary tree, check whether it is a mirror of itself (i.e., symmetric around its center).

https://leetcode.com/problems/symmetric-tree/

        1
       / \
      2   2  
     / \  / \
    3  4  4  3      
True
"""

# Definition for a binary tree node.
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Solution_:
    def isSymmetric(self, root):

        queue = [(root, 0, 0)]
        store = set()
        while queue:
            node, depth, horizontal = queue.pop(0)

            # # add children
            if node.left:
                queue.append((node.left, depth+1, horizontal-1))
            if node.right:
                queue.append((node.right, depth+1, horizontal+1))

            # # visit
            curr = (node.val, depth, horizontal)
            opposite_curr = (node.val, depth, horizontal*-1)
            #
            if opposite_curr in store:
                store.remove(opposite_curr)
            else:
                store.add(curr)

        return len(store) == 1

""" 
"""

class Solution:
    def isSymmetric(self, root):
        queue = [root.left, root.right]

        while queue:
            one = queue.pop(0)
            two = queue.pop(0)

            if one == None or two == None:
                if one == None and two == None:
                    continue
                else:
                    return False
            if one.val != two.val:
                return False

            # # add children
            # the left child of one will match with the right child of two (diagram)
            queue.append(one.left)
            queue.append(two.right)
            # the right child of one will match with the left child of two (diagram)
            queue.append(one.right)
            queue.append(two.left)

        return True

Binary Tree Zigzag Level Order Traversal

"""
Binary Tree Zigzag Level Order Traversal:

Given a binary tree, return the zigzag level order traversal of its nodes' values.
 (ie, from left to right, then right to left for the next level and alternate between).

https://leetcode.com/problems/binary-tree-zigzag-level-order-traversal/
"""

# Definition for a binary tree node.
from collections import deque

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Solution:
    def zigzagLevelOrder(self, root: TreeNode):
        res = []
        self.zigzagHelper(root, res, 1)
        return res

    def zigzagHelper(self, root, res, level):
        if not root:
            return

        if len(res) < level:
            # add array for level
            res.append([])

        if level % 2 == 0:  # right to left
            res[level-1].insert(0, root.val)
        else:  # left to right
            res[level-1].append(root.val)

        self.zigzagHelper(root.left, res, level+1)
        self.zigzagHelper(root.right, res, level+1)

""" 
Using a double ended queue makes the time complexity better
(collections.dequeue)
"""

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def zigzagLevelOrder(self, root):
        """
        :type root: TreeNode
        :rtype: List[List[int]]
        """
        if root is None:
            return []

        results = []

        def dfs(node, level):
            if level >= len(results):
                results.append(deque([node.val]))
            else:
                if level % 2 == 0:
                    results[level].append(node.val)
                else:
                    results[level].appendleft(node.val)

            for next_node in [node.left, node.right]:
                if next_node is not None:
                    dfs(next_node, level+1)

        # normal level order traversal with DFS
        dfs(root, 0)

        return results

Binary Tree Paths

"""
Binary Tree Paths

Given the root of a binary tree, return all root-to-leaf paths in any order.

https://leetcode.com/problems/binary-tree-paths
"""

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right

class Solution:
    def binaryTreePaths(self, root):
        paths = []
        if not root:
            return paths

        stack = [(root, [str(root.val)])]
        while stack:
            node, path = stack.pop()

            # leaf node
            if not node.left and not node.right:
                paths.append("->".join(path))
                continue

            if node.left:
                stack.append((node.left, path+[str(node.left.val)]))
            if node.right:
                stack.append((node.right, path+[str(node.right.val)]))

        return paths

Binary Tree Diameter *

Screenshot 2021-10-10 at 06.12.45.png

Screenshot 2021-10-10 at 06.13.17.png

Screenshot 2021-10-10 at 06.13.53.png

Screenshot 2021-10-10 at 06.14.17.png

Screenshot 2021-10-10 at 06.14.31.png

"""
Binary Tree Diameter:
Diameter of Binary Tree:

Write a function that takes in a Binary Tree and returns its diameter. 
The diameter of a binary tree is defined as the length of its longest path, even if that path doesn't pass through the root of the tree.
A path is a collection of connected nodes in a tree, where no node is connected to more than two other nodes. 
The length of a path is the number of edges between the path's first node and its last node.
Each BinaryTree node has an integer value, a left child node, and a right child node. Children nodes can either be BinaryTree nodes themselves or None / null.

https://www.algoexpert.io/questions/Binary%20Tree%20Diameter
https://leetcode.com/problems/diameter-of-binary-tree/
"""

"""
Sample Input
tree =        1
            /  \
           3     2
             \ 
        7     4
       /       \
      8         5
     /           \
    9             6
Sample Output
    6 // 9 -> 8 -> 7 -> 3 -> 4 -> 5 -> 6
    // There are 6 edges between the
    // first node and the last node
    // of this tree's longest path.

Sample Input
tree =  1

Sample Output
    0
"""

""" 
The key observation to make is: 
    the longest path has to be between two leaf nodes. 
We can prove this with contradiction. 
Imagine that we have found the longest path, and it is not between two leaf nodes. 
We can extend that path by 1, by adding the child node of one of the end nodes (as at least one must have a child, given that they aren't both leaves). 
This contradicts the fact that our path is the longest path. Therefore, the longest path must be between two leaf nodes.

Moreover, we know that in a tree, nodes are only connected with their parent node and 2 children. 
Therefore we know that the longest path in the tree would consist of a node, its longest left branch, and its longest right branch. 
So, our algorithm to solve this problem will find the node where the sum of its longest left and right branches is maximized. 
This would hint at us to apply Depth-first search (DFS) to count each node's branch lengths, 
 because it would allow us to dive deep into the leaves first, and then start counting the edges upwards.

"""

# Definition for a binary tree node.
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Solution:
    def diameterOfBinaryTree(self, root):
        if not root:
            return 0
        diameter = 0

        def diameter_helper(root):
            if not root:
                return 0
            nonlocal diameter

            left = diameter_helper(root.left)
            right = diameter_helper(root.right)

            diameter = max(left + right,  # Connect left & right branches
                           diameter)

            # Create a branch that will be used to calculate longest_path by the root's parent node

            # we do not add the curr node's height/depth to any of the calculations/results for the longest_diameter,
            #   it is only considered from its parent node
            #   because if tree = 1 (node), longest_diameter = 0
            return max(left, right) + 1

        diameter_helper(root)
        return diameter

""""""

# This is an input class. Do not edit.

class BinaryTree:
    def __init__(self, value, left=None, right=None):
        self.value = value
        self.left = left
        self.right = right

# ---------------------------------------------------------------------------------------------------------------------

def binaryTreeDiameter3(tree):
    max_diameter = [-1]
    depths(tree, max_diameter)
    return max_diameter[0]

def depths(node, max_diameter):
    if node is None:
        return 0

    # calculate diameter
    left = depths(node.left, max_diameter)
    right = depths(node.right, max_diameter)
    max_diameter[0] = max(max_diameter[0], left+right)

    return max(left, right) + 1  # add node to depth

# ---------------------------------------------------------------------------------------------------------------------

def binaryTreeDiameter(tree):
    return binaryTreeDiameterHelper(tree, 0).longest_diameter

class Result:
    def __init__(self, longest_path, longest_diameter):
        self.longest_path = longest_path
        self.longest_diameter = longest_diameter

    def __str__(self):  # for debugging
        return f"{self.longest_path} {self.longest_diameter}"

def binaryTreeDiameterHelper(tree, depth):
    if tree is None:
        return Result(0, 0)

    left = binaryTreeDiameterHelper(tree.left, depth+1)
    right = binaryTreeDiameterHelper(tree.right, depth+1)

    curr_diameter = left.longest_path + right.longest_path
    prev_longest_diameter = max(left.longest_diameter, right.longest_diameter)

    curr_longest_diameter = max(
        curr_diameter,
        prev_longest_diameter,
    )

    # we do not add the curr node's height/depth to any of the calculations/results for the longest_diameter,
    #   it is only considered from its parent node
    #   because if tree = 1 (node), longest_diameter = 0
    nxt_longest_path = max(left.longest_path, right.longest_path) + 1
    return Result(nxt_longest_path, curr_longest_diameter)

Binary Tree Maximum Path Sum **

"""
Max Path Sum In Binary Tree:
Binary Tree Maximum Path Sum:

A path in a binary tree is a sequence of nodes where each pair of adjacent nodes in the sequence has an edge connecting them. 
A node can only appear in the sequence at most once. Note that the path does not need to pass through the root.
The path sum of a path is the sum of the node's values in the path.
Given the root of a binary tree, return the maximum path sum of any path.

Write a function that takes in a Binary Tree and returns its max path sum.
A path is a collection of connected nodes in a tree, where no node is connected to more than two other nodes;
 a path sum is the sum of the values of the nodes in a particular path.
Each BinaryTree node has an integer value, a left child node, and a right child node.
Children nodes can either be BinaryTree nodes themselves or None / null.

Sample Input
    tree = 1
        /     \
      2       3
    /   \   /   \
    4     5 6     7
Sample Output
    18 // 5 + 2 + 1 + 3 + 7

https://www.algoexpert.io/questions/Max%20Path%20Sum%20In%20Binary%20Tree
https://leetcode.com/problems/binary-tree-maximum-path-sum
"""

# Definition for a binary tree node.
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Solution_:
    def maxPathSum(self, root):
        if not root:
            return 0
        maximum = float('-inf')

        def max_path(root):
            nonlocal maximum
            if not root:
                return float('-inf')

            left = max_path(root.left)
            right = max_path(root.right)

            # longest continuous branch/straight line.
            curr_branch = max(
                root.val,
                root.val + left,
                root.val + right
            )

            # longest branch/triangle we have seen so far
            maximum = max(
                maximum,
                curr_branch,
                root.val + left + right,  # as triangle
            )

            return curr_branch

        max_path(root)
        return maximum

""""""

class Solution:
    def maxPathSum(self, root):
        if not root:
            return 0
        return self.max_path(root)[0]

    def max_path(self, root):
        if not root:
            return float("-inf"), float("-inf")

        left = self.max_path(root.left)
        right = self.max_path(root.right)

        max_as_path = max(root.val,
                          root.val + left[1],
                          root.val + right[1],)

        maximum = max(max_as_path,  # Max as path
                      root.val + left[1] + right[1],  # Max as tree
                      left[0],  # Prev max
                      right[0])  # Prev max

        return maximum, max_as_path

""" 
"""

class TreeInfo:

    def __init__(self, max_as_branch, max_as_branch_or_triangle):
        self.max_as_branch = max_as_branch
        # max continuous path as branch/tree
        self.max_as_branch_or_triangle = max_as_branch_or_triangle

# O(n) time
# O(log(n)) space - because it is a binary tree
def maxPathSum(tree):
    res = maxPathSumHelper(tree)
    return res.max_as_branch_or_triangle

def maxPathSumHelper(tree):
    if not tree:
        # handle negatives with float('-inf')
        # return TreeInfo(float('-inf'), float('-inf')) # <- also works.
        return TreeInfo(0, float('-inf'))

    left = maxPathSumHelper(tree.left)
    right = maxPathSumHelper(tree.right)

    # longest continuous branch/straight line.
    curr_max_as_branch = max(
        tree.value,
        tree.value + left.max_as_branch,
        tree.value + right.max_as_branch
    )

    # longest branch/triangle we have seen so far note: curr_max_as_branch is automatically included
    curr_max_as_branch_or_triangle = max(
        curr_max_as_branch,
        tree.value + left.max_as_branch + right.max_as_branch,  # curr_max_as_triangle
        left.max_as_branch_or_triangle,
        right.max_as_branch_or_triangle
    )

    return TreeInfo(curr_max_as_branch, curr_max_as_branch_or_triangle)

Smallest String Starting From Leaf - LeetCode

Smallest String Starting From Leaf - LeetCode

Path Sum II

Simple Python Solution: top-down DFS - LeetCode Discuss

Path Sum II

"""
Path Sum II

Given a binary tree and a sum, find all root-to-leaf paths where each path's sum equals the given sum.
Note: A leaf is a node with no children.
https://leetcode.com/problems/path-sum-ii/
"""

class Solution:
    def pathSum(self, root, targetSum):
        if not root:
            return []

        targetSum -= root.val
        if targetSum == 0:
            if not root.left and not root.right: # leaf
                return [[root.val]]

        left = self.pathSum(root.left, targetSum)
        right = self.pathSum(root.right, targetSum)

        res = []
        for arr in right:
            res.append([root.val]+arr)
        for arr in left:
            res.append([root.val]+arr)

        return res


"""
- iterate leaves checking if they add up to the path sum
- if so, return an array of an array containing the leaf [[leaf,]]
    - and keep on adding the parent elements tto the array as you bubble up
    - if a parent has both of its children returning arrays, combine the inner arrays


"""

Path Sum III **

Screenshot 2021-11-13 at 20.04.00.png

Screenshot 2021-11-13 at 19.57.50.png

Screenshot 2021-11-13 at 19.58.15.png

Screenshot 2021-11-13 at 19.58.32.png

Screenshot 2021-11-13 at 19.59.47.png

Screenshot 2021-11-13 at 20.00.42.png

Screenshot 2021-11-13 at 20.01.04.png

Screen Recording 2021-11-13 at 20.01.46.mov

""" 
437. Path Sum III

Given the root of a binary tree and an integer targetSum, 
    return the number of paths where the sum of the values along the path equals targetSum.
The path does not need to start or end at the root or a leaf, but it must go downwards 
    (i.e., traveling only from parent nodes to child nodes).

Example 1:
    Input: root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
    Output: 3
    Explanation: The paths that sum to 8 are shown.
Example 2:
    Input: root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
    Output: 3

Prerequisite:
- https://leetcode.com/problems/subarray-sum-equals-k

https://leetcode.com/problems/path-sum-iii
"""

from typing import Optional
from collections import defaultdict

# Definition for a binary tree node
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

""" 

The idea behind the approach below is as follows: 
- If the cumulative sum(represented by sum[i] in an array for sum up to i^th index) up to two indices is the same,
    the sum of the elements lying in between those indices is zero.
- Extending the same thought further, 
    if the cumulative sum up to two indices, say i and j is at a difference of k 
        i.e. if sum[i] - sum[j] = k, 
    the sum of elements lying between indices i and j is k.

https://www.notion.so/paulonteri/Strings-Arrays-Linked-Lists-81ca9e0553a0494cb8bb74c5c85b89c8#2c097c6a479142b6bb1f584f122d3e9b
"""

class Solution:
    def pathSum(self, root: Optional[TreeNode], targetSum: int):
        sums = defaultdict(int)
        sums[0] = 1

        return self.path_sum_helper(targetSum, sums, root, 0)

    def path_sum_helper(self, targetSum, sums, node, running_sum):
        if not node:
            return 0

        total = 0
        cur_sum = running_sum + node.val

        # check if the needed is in the sums dict
        needed = cur_sum - targetSum
        if needed in sums:
            total += sums[needed]

        # add the current sum to the sums dict
        sums[cur_sum] += 1

        total += self.path_sum_helper(targetSum, sums, node.left, cur_sum)
        total += self.path_sum_helper(targetSum, sums, node.right, cur_sum)

        # remove the current sum to the sums dict
        sums[cur_sum] -= 1
        if sums[cur_sum] == 0:
            sums.pop(cur_sum)

        return total

Populating Next Right Pointers in Each Node *

Screenshot 2021-11-02 at 10.59.29.png

Remember that we are dealing with a perfect tree

""" 
116. Populating Next Right Pointers in Each Node

You are given a perfect binary tree where all leaves are on the same level, and every parent has two children. The binary tree has the following definition:
    struct Node {
    int val;
    Node *left;
    Node *right;
    Node *next;
    }

Populate each next pointer to point to its next right node. 
If there is no next right node, the next pointer should be set to NULL.
Initially, all next pointers are set to NULL.

https://leetcode.com/problems/populating-next-right-pointers-in-each-node
EPI 9.16
"""
import collections

# Definition for a Node.
class Node:
    def __init__(self, val: int = 0, left: 'Node' = None, right: 'Node' = None, next: 'Node' = None):
        self.val = val
        self.left = left
        self.right = right
        self.next = next

class Solution:
    def connect(self, root: 'Node'):
        if not root:
            return

        queue = [root]
        while queue:
            curr = queue.pop(0)

            if curr.left:
                curr.left.next = curr.right
                queue.append(curr.left)

            if curr.right:
                if curr.next:
                    curr.right.next = curr.next.left
                queue.append(curr.right)

        return root

""" 
"""

class Solution_:
    def connect(self, root: 'Node'):
        if not root:
            return None

        prev_nodes = collections.defaultdict(lambda: None)
        queue = [(root, 0)]

        while queue:
            curr, depth = queue.pop(0)

            curr.next = prev_nodes[depth]
            prev_nodes[depth] = curr

            # next
            if curr.right:
                queue.append((curr.right, depth+1))
            if curr.left:
                queue.append((curr.left, depth+1))

        return root

Flatten Binary Tree to Linked List **

Screenshot 2021-10-09 at 06.59.22.png

Screenshot 2021-10-09 at 06.59.49.png

Solution 1

Screenshot 2021-10-09 at 07.04.47.png

Screenshot 2021-10-09 at 07.02.09.png

Screenshot 2021-10-09 at 07.02.36.png

Screenshot 2021-10-09 at 07.02.56.png

Screenshot 2021-10-09 at 07.03.12.png

Screenshot 2021-10-09 at 07.01.34.png

# Definition for a binary tree node.
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Solution_:
    def flatten(self, root):
        if not root:
            return None

        right = root.right

        if root.left:
            # place the left subtree between the root & root.right
            root.right = root.left
            left_ending = self.flatten(root.left)
            left_ending.right = right

            # remove left
            root.left = None

        furthest = self.flatten(root.right)

        return furthest or root

"""
our algorithm will return the tail node of the flattened out tree.

For a given node, we will recursively flatten out the left and the right subtrees 
    and store their corresponding tail nodes in left_ending and right_ending respectively.

Next, we will make the following connections 
(only if there is a left child for the current node, else the left_ending would be null)
(Place the left subtree between the root & root.right)
    left_ending.right = node.right
    node.right = node.left
    node.left = None

Next we have to return the tail of the final, flattened out tree rooted at node. 
So, if the node has a right child, then we will return the right_ending, else, we'll return the left_ending
"""

class Solution:
    def flatten(self, root):
        if not root:
            return None

        left_ending = self.flatten(root.left)
        right_ending = self.flatten(root.right)

        # If there was a left subtree, we shuffle the connections
        #   around so that there is nothing on the left side anymore.
        if left_ending:
            # Place the left subtree between the root & root.right
            left_ending.right = root.right
            root.right = root.left
            # Remove left
            root.left = None

        # We need to return the "rightmost" node after we are done wiring the new connections.
        # 2. For a node with only a left subtree, the rightmost node will be left_ending because it has been moved to the right subtree
        # 3. For a leaf node, we simply return the node
        return right_ending or left_ending or root

Solution 2

Screenshot 2021-10-09 at 07.06.16.png

class Solution:
    def flatten(self, root):
        if not root:
            return None

        stack = [root]

        while stack:
            node = stack.pop()

            if node.right:
                stack.append(node.right)
            if node.left:
                stack.append(node.left)

            node.left = None
            if stack:
                node.right = stack[-1]  # Peek

Approach 3: O(1) Iterative Solution (Greedy & similar to Morris Traversal)

similar to Morris Traversal

Screenshot 2021-10-09 at 07.25.23.png

Screenshot 2021-10-09 at 07.28.07.png

Screenshot 2021-10-09 at 07.29.18.png

Screenshot 2021-10-09 at 07.29.42.png

Screenshot 2021-10-09 at 07.30.24.png

Screenshot 2021-10-09 at 07.31.43.png

Screenshot 2021-10-09 at 07.32.03.png

Screenshot 2021-10-09 at 07.32.25.png

Screenshot 2021-10-09 at 07.32.57.png

""" 
O(1) Iterative Solution (Greedy & similar to Morris Traversal)
"""

class Solution:
    def flatten(self, root):
        if not root:
            return None

        curr = root
        while curr:

            # If there was a left subtree, we shuffle the connections
            #   around so that there is nothing on the left side anymore.
            if curr.left:
                l_right_most = self.find_right_most(curr.left)

                # place the left subtree between the root & root.right
                l_right_most.right = curr.right
                curr.right = curr.left

                # remove left
                curr.left = None

            curr = curr.right

    def find_right_most(self, root):
        curr = root
        while curr.right:
            curr = curr.right
        return curr

Find Successor

"""
Find Successor:

Write a function that takes in a Binary Tree (where nodes have an additional pointer to their parent node)
 as well as a node contained in that tree and returns the given node's successor.
A node's successor is the next node to be visited (immediately after the given node) 
 when traversing its tree using the in-order tree-traversal technique.
A node has no successor if it's the last node to be visited in the in-order traversal.
If a node has no successor, your function should return None / null.
Each BinaryTree node has an integer value, a parent node, a left child node, and a right child node.
Children nodes can either be BinaryTree nodes themselves or None / null.

Sample Input
    tree = 
                1
             /   \
            2     3
          /   \ 
         4     5
        /       
        6  
    node = 5   
Sample Output
    1
    // This tree's in-order traversal order is:
    // 6 -> 4 -> 2 -> 5 -> 1 -> 3 
    // 1 comes immediately after 5.

https://www.algoexpert.io/questions/Find%20Successor
"""

# This is an input class. Do not edit.
class BinaryTree:
    def __init__(self, value, left=None, right=None, parent=None):
        self.value = value
        self.left = left
        self.right = right
        self.parent = parent

def findSuccessor(tree, node):
    if tree is None:
        return

    left = findSuccessor(tree.left, node)
    if tree == node:
        return findSuccessorHelper(tree, node)
    right = findSuccessor(tree.right, node)

    return left or right

def findSuccessorHelper(tree, node):

    # if has a right child
    # will be left most node of right child
    if tree.right is not None:
        # find left most in right subtree
        left_most = tree.right
        while left_most.left is not None:
            left_most = left_most.left
        return left_most

    # no right child -> successor is ancestor:
    # find ancestor where child is left child
    else:

        # find where we first branched left
        while tree is not None:
            if tree.parent is not None and tree == tree.parent.left:
                return tree.parent

            tree = tree.parent

    return None

"""
If a node has a right subtree:
- its successor is the futhest left node in the right subtree
else: 
- its successor is the first point where we turned left
-    i.e if tree == tree.parent.left, return tree.parent

Sample Input
tree = 
              1
            /   \
           2     3
         /   \ 
        4     5
       /     /  \
      6     7   8

node = 5   
output = 8

node = 8   
output = 1

node = 2   
output = 7

node = 1   
output = 3

"""

Subtree of Another Tree *

Check subtree

Screenshot 2021-11-02 at 11.45.39.png

Screenshot 2021-11-02 at 11.46.00.png

"""
Subtree of Another Tree:

Given two non-empty binary trees s and t, check whether tree t has exactly the same structure and node values with a subtree of s.
A subtree of s is a tree consists of a node in s and all of this node's descendants.
The tree s could also be considered as a subtree of itself.

https://leetcode.com/problems/subtree-of-another-tree/
"""

# Definition for a binary tree node.
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Solution:
    def isSubtree(self, s: TreeNode, t: TreeNode):
        return self.traverse(s, t)

    def traverse(self, s, t):
        if self.checkSubTreeFunction(s, t) == True:
            return True
        if s is None:
            return False

        return self.traverse(s.left, t) or self.traverse(s.right, t)

    def checkSubTreeFunction(self, s, t):
        if s == None and t == None:
            return True
        elif s == None or t == None or s.val != t.val:
            return False

        return self.checkSubTreeFunction(s.left, t.left) and self.checkSubTreeFunction(s.right, t.right)

Construct Binary Tree from Preorder and Inorder Traversal

[1/3] CONSTRUCT BINARY TREE FROM PREORDER/INORDER TRAVERSAL - Code & Whiteboard

Construct Binary Tree from Inorder and Preorder Traversal - Leetcode 105 - Python

LeetCode 105. Construct Binary Tree from Preorder and Inorder Traversal (Algorithm Explained)

Screenshot 2021-11-02 at 12.35.33.png

Screenshot 2021-10-04 at 05.43.02.png

"""
Construct Binary Tree from Preorder and Inorder Traversal:

Given two integer arrays preorder and inorder where
preorder is the preorder traversal of a binary tree and inorder is the inorder traversal of the same tree,
construct and return the binary tree.

Example 1:
    Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
    Output: [3,9,20,null,null,15,7]
Example 2:
    Input: preorder = [-1], inorder = [-1]
    Output: [-1]

https://leetcode.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal/
"""

from typing import List

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

# ---------------------------------------------------------------------------------------------------------------------

""" 
- The root will be the first element in the preorder sequence
- Next, locate the index of the root node in the inorder sequence
    - this will help you know the number of nodes to its left & the number to its right
- repeat this recursively
"""

class SolutionBF(object):
    def buildTree(self, preorder, inorder):
        return self.dfs(preorder, inorder)

    def dfs(self, preorder, inorder):
        if len(preorder) == 0:
            return None

        root = TreeNode(preorder[0])

        mid = inorder.index(preorder[0])

        root.left = self.dfs(preorder[1: mid+1], inorder[: mid])
        root.right = self.dfs(preorder[mid+1:], inorder[mid+1:])
        return root

class SolutionBF0:
    def buildTree(self, preorder, inorder):

        if len(inorder) == 0:
            # the remaining preorder values do not belong in this subtree
            return None

        if len(preorder) == 1:
            return TreeNode(preorder[0])

        ino_index = inorder.index(preorder.pop(0))  # remove from preorder
        node = TreeNode(inorder[ino_index])

        node.left = self.buildTree(preorder, inorder[:ino_index])
        node.right = self.buildTree(preorder, inorder[ino_index+1:])

        return node

class SolutionBF00:
    def buildTree(self, preorder, inorder):

        preorder_pos = 0

        def buildTreeHelper(preorder, inorder):
            nonlocal preorder_pos

            # we do not have valid nodes to be placed
            if preorder_pos >= len(preorder):
                return

            # # create node
            # node
            inorder_idx = inorder.index(preorder[preorder_pos])
            preorder_pos += 1
            node = TreeNode(inorder[inorder_idx])

            # children -> will pass only valid children below -> (inorder[:inorder_idx] & inorder[inorder_idx+1:] does that)
            node.left = buildTreeHelper(preorder, inorder[:inorder_idx])
            node.right = buildTreeHelper(preorder, inorder[inorder_idx+1:])

            return node
        return buildTreeHelper(preorder, inorder)
#         def buildTreeHelper2( preorder, inorder):
#             nonlocal preorder_pos

#             if preorder_pos >= len(preorder):
#                 return

#             # # create node
#             # node
#             inorder_idx = inorder.index( preorder[preorder_pos] )
#             preorder_pos += 1
#             node = TreeNode(inorder[inorder_idx ])

#             left = inorder[:inorder_idx]
#             right = inorder[inorder_idx+1:]
#             if left:
#                 node.left = buildTreeHelper(preorder, left)
#             if right:
#                 node.right = buildTreeHelper(preorder, right)

#             return node
#       return buildTreeHelper2(preorder, inorder)

# ---------------------------------------------------------------------------------------------------------------------

""" 
- The root will be the first element in the preorder sequence
- Next, locate the index of the root node in the inorder sequence
    - this will help you know the number of nodes to its left & the number to its right
- repeat this recursively

- iterate through the preorder array and check if the current can be placed in the current tree(or recursive call)

- We use the remaining inorder traversal to determine(restrict) whether
    the current preorder node is in the left or right
"""

class Solution:
    def buildTree(self, preorder, inorder):
        preorder_pos = 0
        inorder_idxs = {val: idx for idx, val in enumerate(inorder)}

        def helper(inorder_left, inorder_right):
            nonlocal preorder_pos

            if preorder_pos == len(preorder):
                return
            if inorder_left > inorder_right:
                return

            val = preorder[preorder_pos]
            preorder_pos += 1

            node = TreeNode(val)

            inorder_idx = inorder_idxs[val]
            # start with left !
            node.left = helper(inorder_left, inorder_idx-1)
            node.right = helper(inorder_idx+1, inorder_right)

            return node

        return helper(0, len(inorder)-1)

Construct Binary Tree from Inorder and Postorder Traversal

""" 
106. Construct Binary Tree from Inorder and Postorder Traversal

Given two integer arrays inorder and postorder where 
    inorder is the inorder traversal of a binary tree and 
    postorder is the postorder traversal of the same tree, 
construct and return the binary tree.

Example 1:
    Input: inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
    Output: [3,9,20,null,null,15,7]
Example 2:
    Input: inorder = [-1], postorder = [-1]
    Output: [-1]

https://leetcode.com/problems/construct-binary-tree-from-inorder-and-postorder-traversal
"""

# Definition for a binary tree node.
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Solution:
    def buildTree(self, inorder, postorder):
        postorder_idx = len(postorder)-1
        inorder_idxs = {val: idx for idx, val in enumerate(inorder)}

        def helper(inorder_left, inorder_right):
            nonlocal postorder_idx

            if postorder_idx < 0:
                return None
            if inorder_left > inorder_right:
                return None

            val = postorder[postorder_idx]
            postorder_idx -= 1

            # create node
            node = TreeNode(val)

            inorder_idx = inorder_idxs[val]
            # start with right !
            node.right = helper(inorder_idx+1, inorder_right)
            node.left = helper(inorder_left, inorder_idx-1)

            return node
        return helper(0, len(inorder)-1)

Preorder/Postorder

Binary Tree Inorder Traversal - Iterative **

Screenshot 2021-11-02 at 13.07.38.png

Screen Recording 2021-10-23 at 13.36.24.mov

"""
Binary Tree Inorder Traversal:

Given the root of a binary tree, return the inorder traversal of its nodes' values.

https://leetcode.com/problems/binary-tree-inorder-traversal/

https://www.enjoyalgorithms.com/blog/iterative-binary-tree-traversals-using-stack
https://www.educative.io/edpresso/how-to-perform-an-iterative-inorder-traversal-of-a-binary-tree
https://www.techiedelight.com/inorder-tree-traversal-iterative-recursive

After this:
- https://leetcode.com/problems/binary-search-tree-iterator
"""

# Definition for a binary tree node.
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

""" 
 - add all left nodes to stack
 - visit left most node
 - move to the right
"""

class Solution_:
    def inorderTraversal(self, root: TreeNode):
        if not root:
            return None
        result = []

        stack = []
        curr = root
        while stack or curr:
            # add all left
            # put the left most value(s) to the top of the stack
            while curr and curr.left:
                stack.append(curr)
                curr = curr.left

            # the top of the stack has the left most unvisited value
            #  visit node
            if not curr:
                curr = stack.pop()
            result.append(curr.val)

            # - has no unvisited left
            # - itself is visited
            # so the next to be visited is right
            curr = curr.right

        return result

"""

class Solution:
    def inorderTraversal(self, root: TreeNode):
        output = []

        stack = []
        curr = root
        while curr is not None or len(stack) > 0:

            # add all left
            while curr is not None:
                stack.append(curr)
                curr = curr.left

            # visit node
            temp = stack.pop()
            output.append(temp.val)

            curr = temp.right

        return output
"""

#         10
#       /    \
#      4      17
#    /   \      \
#   2     5     19
#  /           /
#  1           18

class Solution:
    def inorderTraversal(self, root: TreeNode):
        if not root:
            return None
        result = []

        stack = []
        curr = root
        while stack or curr:
            # put the left most value(s) to the top of the stack
            while curr:
                stack.append(curr)
                curr = curr.left

            # the top of the stack has the left most unvisited value
            #  visit node
            curr = stack.pop()
            result.append(curr.val)

            # - has no unvisited left
            # - itself is visited
            # so the next to be visited is right
            # eg: after 4 is 5 in the example above
            curr = curr.right

        return result

""" 
------------------------------------------------------------------------------------------------------------
"""

class Solution1:
    def inorderTraversal(self, root):
        output = []
        self.inorderTraversalHelper(root, output)
        return output

    def inorderTraversalHelper(self, root, output):
        if not root:
            return

        self.inorderTraversalHelper(root.left, output)
        output.append(root.val)
        self.inorderTraversalHelper(root.right, output)

Morris Inorder Tree Traversal - Inorder with O(1) space ***

https://youtu.be/wGXB9OWhPTg

Screenshot 2021-10-04 at 05.34.34.png

Screenshot 2021-10-08 at 08.27.31.png

Screenshot 2021-10-04 at 05.34.52.png

Screenshot 2021-10-08 at 08.49.59.png

Screenshot 2021-10-08 at 08.50.43.png

Screenshot 2021-10-08 at 08.50.57.png

""" 
Morris Inorder Tree Traversal - Inorder with O(1) space

https://leetcode.com/problems/binary-tree-inorder-traversal
EPI 9.11
"""

# Definition for a binary tree node.
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Solution:
    def inorderTraversal(self, root):
        res = []

        curr = root
        while curr is not None:

            # has no left child - so is the next valid
            if not curr.left:
                res.append(curr.val)
                curr = curr.right

            # place the curr node as the right child of its predecessor
            #   which is the rightmost node in the left subtree
            else:
                predecessor = self.get_inorder_predecessor(curr)

                # # move node down the tree
                left = curr.left
                curr.left = None  # prevent loop

                predecessor.right = curr

                # # continue to left subtree
                curr = left

        return res

    def get_inorder_predecessor(self, node):
        curr = node.left

        while curr.right is not None:
            curr = curr.right

        return curr

536. Construct Binary Tree from String

Serialize and Deserialize Binary Tree **

Screenshot 2021-11-02 at 13.15.43.png

""" 
Serialize and Deserialize Binary Tree

Serialization is the process of converting a data structure or object into a sequence of bits so that it can be stored in a file or memory buffer, 
    or transmitted across a network connection link to be reconstructed later in the same or another computer environment.
Design an algorithm to serialize and deserialize a binary tree. 
There is no restriction on how your serialization/deserialization algorithm should work. 
You just need to ensure that a binary tree can be serialized to a string and this string can be deserialized to the original tree structure.
Clarification: The input/output format is the same as how LeetCode serializes a binary tree. 
You do not necessarily need to follow this format, so please be creative and come up with different approaches yourself.

Example 1:
    Input: root = [1,2,3,null,null,4,5]
    Output: [1,2,3,null,null,4,5]
Example 2:
    Input: root = []
    Output: []
Example 3:
    Input: root = [1]
    Output: [1]
Example 4:
    Input: root = [1,2]
    Output: [1,2]

https://leetcode.com/problems/serialize-and-deserialize-binary-tree/

Prerequisites:
- https://leetcode.com/problems/serialize-and-deserialize-bst
- https://leetcode.com/problems/construct-binary-search-tree-from-preorder-traversal
"""

# Definition for a binary tree node.
class TreeNode(object):
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None

class Codec:

    def serialize(self, root):
        preorder_result = []

        # def preorder(node):
        #     if not node:
        #         preorder_result.append(str(None))
        #         return

        #     preorder_result.append(str(node.val))
        #     preorder(node.left)
        #     preorder(node.right)
        def preorder(node):
            if not node:
                preorder_result.append(str(None))
                return

            preorder_result.append(str(node.val))
            preorder(node.left)
            preorder(node.right)

        preorder(root)
        return " ".join(preorder_result)

    def deserialize(self, data):

        idx = 0
        def reverse_preorder(arr):
            nonlocal idx
            if idx > len(arr):
                return None
            if arr[idx] == 'None':
                idx += 1
                return None

            node = TreeNode(int(arr[idx]))
            idx += 1

            node.left = reverse_preorder(arr)
            node.right = reverse_preorder(arr)

            return node

        return reverse_preorder(data.split(" "))

# Your Codec object will be instantiated and called as such:
# ser = Codec()
# deser = Codec()
# ans = deser.deserialize(ser.serialize(root))

Construct Binary Tree from String

Screenshot 2021-11-27 at 11.50.38.png

Screenshot 2021-11-27 at 11.51.39.png

Screenshot 2021-11-27 at 11.52.13.png

Screenshot 2021-11-27 at 11.52.53.png

Screenshot 2021-11-27 at 11.53.24.png

Screenshot 2021-11-27 at 11.54.03.png

Screenshot 2021-11-27 at 11.54.41.png

Screenshot 2021-11-27 at 11.54.59.png

Screenshot 2021-11-27 at 11.55.35.png

Screenshot 2021-11-27 at 11.56.58.png

Screenshot 2021-11-27 at 11.57.33.png

Screenshot 2021-11-27 at 11.57.57.png

Screenshot 2021-11-27 at 11.58.15.png

Screenshot 2021-11-27 at 11.58.34.png

""" 
536. Construct Binary Tree from String

You need to construct a binary tree from a string consisting of parenthesis and integers.
The whole input represents a binary tree. It contains an integer followed by zero, one or two pairs of parenthesis.
The integer represents the root's value and a pair of parenthesis contains a child binary tree with the same structure.
You always start to construct the left child node of the parent first if it exists.

https://leetcode.com/problems/construct-binary-tree-from-string
"""

""" 
"4( 2( 3) ( 1) ) (6(5))"

- tree startes at number
- new opening bracket means new subtree
- unclosable closing brackets means we return

- record number as value then idx + 1
- left: if opening bracket, start new tree at idx + 1
    - skip closing bracket move idx += 1
- right: if opening bracket, start new tree at idx + 1
     - skip closing bracket move idx += 1
- else:
    return 

"""

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Solution:
    def str2tree(self, s: str):

        idx = 0

        def build_tree():
            nonlocal idx
            # base cases
            if idx >= len(s):
                return None

            start_idx = idx
            # get number
            while idx < len(s) and (s[idx].isnumeric() or s[idx] == '-'):
                idx += 1
            node = TreeNode(s[start_idx:idx])

            # subtrees
            if idx < len(s) and s[idx] == "(":
                idx += 1
                node.left = build_tree()
                idx += 1

            if idx < len(s) and s[idx] == "(":
                idx += 1
                node.right = build_tree()
                idx += 1

            return node

        return build_tree()

Flatten Binary Tree to Linked List **

Screenshot 2021-10-09 at 06.59.22.png

Screenshot 2021-10-09 at 06.59.49.png

Solution 1

Screenshot 2021-10-09 at 07.04.47.png

Screenshot 2021-10-09 at 07.02.09.png

Screenshot 2021-10-09 at 07.02.36.png

Screenshot 2021-10-09 at 07.02.56.png

Screenshot 2021-10-09 at 07.03.12.png

Screenshot 2021-10-09 at 07.01.34.png

# Definition for a binary tree node.
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Solution_:
    def flatten(self, root):
        if not root:
            return None

        right = root.right

        if root.left:
            # place the left subtree between the root & root.right
            root.right = root.left
            left_ending = self.flatten(root.left)
            left_ending.right = right

            # remove left
            root.left = None

        furthest = self.flatten(root.right)

        return furthest or root

"""
our algorithm will return the tail node of the flattened out tree.

For a given node, we will recursively flatten out the left and the right subtrees 
    and store their corresponding tail nodes in left_ending and right_ending respectively.

Next, we will make the following connections 
(only if there is a left child for the current node, else the left_ending would be null)
(Place the left subtree between the root & root.right)
    left_ending.right = node.right
    node.right = node.left
    node.left = None

Next we have to return the tail of the final, flattened out tree rooted at node. 
So, if the node has a right child, then we will return the right_ending, else, we'll return the left_ending
"""

class Solution:
    def flatten(self, root):
        if not root:
            return None

        left_ending = self.flatten(root.left)
        right_ending = self.flatten(root.right)

        # If there was a left subtree, we shuffle the connections
        #   around so that there is nothing on the left side anymore.
        if left_ending:
            # Place the left subtree between the root & root.right
            left_ending.right = root.right
            root.right = root.left
            # Remove left
            root.left = None

        # We need to return the "rightmost" node after we are done wiring the new connections.
        # 2. For a node with only a left subtree, the rightmost node will be left_ending because it has been moved to the right subtree
        # 3. For a leaf node, we simply return the node
        return right_ending or left_ending or root

Solution 2

Screenshot 2021-10-09 at 07.06.16.png

class Solution:
    def flatten(self, root):
        if not root:
            return None

        stack = [root]

        while stack:
            node = stack.pop()

            if node.right:
                stack.append(node.right)
            if node.left:
                stack.append(node.left)

            node.left = None
            if stack:
                node.right = stack[-1]  # Peek

Approach 3: O(1) Iterative Solution (Greedy & similar to Morris Traversal)

similar to Morris Traversal

Screenshot 2021-10-09 at 07.25.23.png

Screenshot 2021-10-09 at 07.28.07.png

Screenshot 2021-10-09 at 07.29.18.png

Screenshot 2021-10-09 at 07.29.42.png

Screenshot 2021-10-09 at 07.30.24.png

Screenshot 2021-10-09 at 07.31.43.png

Screenshot 2021-10-09 at 07.32.03.png

Screenshot 2021-10-09 at 07.32.25.png

Screenshot 2021-10-09 at 07.32.57.png

""" 
O(1) Iterative Solution (Greedy & similar to Morris Traversal)
"""

class Solution:
    def flatten(self, root):
        if not root:
            return None

        curr = root
        while curr:

            # If there was a left subtree, we shuffle the connections
            #   around so that there is nothing on the left side anymore.
            if curr.left:
                l_right_most = self.find_right_most(curr.left)

                # place the left subtree between the root & root.right
                l_right_most.right = curr.right
                curr.right = curr.left

                # remove left
                curr.left = None

            curr = curr.right

    def find_right_most(self, root):
        curr = root
        while curr.right:
            curr = curr.right
        return curr

Lowest Common Ancestor of a Binary Tree

"""
Lowest Common Ancestor of a Binary Tree:

Given a binary tree, find the lowest common ancestor (LCA) of two given nodes in the tree.
According to the definition of LCA on Wikipedia: 
“The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has 
    both p and q as descendants (where we allow a node to be a descendant of itself).”
https://leetcode.com/problems/lowest-common-ancestor-of-a-binary-tree/
"""

# Definition for a binary tree node.
class TreeNode:
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None

class Solution:
    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode'):
        return self.lowestCommonAncestorHelper(root, p, q)

    def lowestCommonAncestorHelper(self,  curr: TreeNode, p: TreeNode, q: TreeNode):
        if curr is None:
            return None

        left = self.lowestCommonAncestorHelper(curr.left, p, q)
        right = self.lowestCommonAncestorHelper(curr.right, p, q)

        # found common ancestor
        if left == True and right == True:
            return curr
        elif (curr.val == p.val or curr.val == q.val) and (left == True or right == True):
            return curr

        # found p/q in current subtree
        elif curr.val == p.val or curr.val == q.val or left == True or right == True:
            return True

        # return the common ancestor
        return left or right

Lowest Common Ancestor of a Binary Tree III

""" 
Lowest Common Ancestor of a Binary Tree III:

Given two nodes of a binary tree p and q, return their lowest common ancestor (LCA).
Each node will have a reference to its parent node. The definition for Node is below:
    class Node {
        public int val;
        public Node left;
        public Node right;
        public Node parent;
    }
According to the definition of LCA on Wikipedia: 
    "The lowest common ancestor of two nodes p and q in a tree T is the lowest node 
        that has both p and q as descendants (where we allow a node to be a descendant of itself)."

Example 1:
    Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
    Output: 3
    Explanation: The LCA of nodes 5 and 1 is 3.
Example 2:
    Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
    Output: 5
    Explanation: The LCA of nodes 5 and 4 is 5 since a node can be a descendant of itself according to the LCA definition.
Example 3:
    Input: root = [1,2], p = 1, q = 2
    Output: 1

https://leetcode.com/problems/lowest-common-ancestor-of-a-binary-tree-iii/
"""

# Definition for a Node.
class Node:
    def __init__(self, val):
        self.val = val
        self.left = None
        self.right = None
        self.parent = None

class Solution:
    def lowestCommonAncestor(self, p: 'Node', q: 'Node'):

        # # balance distance from root
        # calculate heights
        curr_p, curr_q = p, q
        height_p, height_q = 0, 0
        while curr_p.parent is not None or curr_q.parent is not None:
            if curr_p.parent is not None:
                height_p += 1
                curr_p = curr_p.parent
            if curr_q.parent is not None:
                height_q += 1
                curr_q = curr_q.parent

        # two should be the lower one
        one, two = p, q
        if height_p > height_q:
            one, two = q, p

        # move two up
        for _ in range(abs(height_p-height_q)):
            two = two.parent

        # # find common ancestor
        while one != two:
            one = one.parent
            two = two.parent

        return one

""" 
Other solutions:
https://leetcode.com/problems/lowest-common-ancestor-of-a-binary-tree-iii/discuss/932499/Simple-Python-Solution-with-O(1)-space-complexity
https://leetcode.com/problems/lowest-common-ancestor-of-a-binary-tree-iii/discuss/1142138/Python-Solution-with-Two-Pointers
"""

Vertical Order Traversal of a Binary Tree

Screenshot 2021-11-02 at 13.19.01.png

Screenshot 2021-11-02 at 13.19.23.png

Screenshot 2021-11-02 at 13.19.38.png

Screenshot 2021-11-09 at 11.59.40.png

Screenshot 2021-11-09 at 12.00.28.png

Screenshot 2021-11-09 at 12.00.50.png

"""
Vertical Order Traversal of a Binary Tree:

Given the root of a binary tree, calculate the vertical order traversal of the binary tree.
For each node at position (x, y), its left and right children will be at positions (x - 1, y - 1) and (x + 1, y - 1) respectively.
The vertical order traversal of a binary tree is a list of non-empty reports for each unique x-coordinate from left to right. 
Each report is a list of all nodes at a given x-coordinate. The report should be primarily sorted by y-coordinate from highest y-coordinate to lowest. 
If any two nodes have the same y-coordinate in the report, the node with the smaller value should appear earlier.
Return the vertical order traversal of the binary tree.

https://leetcode.com/problems/vertical-order-traversal-of-a-binary-tree/
"""

"""
https://leetcode.com/problems/vertical-order-traversal-of-a-binary-tree/solution/999715

think the main time complexity is within sorting, in addition to the last solution, 
you can optimize and record both row and column min and max then there is no need for sorting for row and column, 
just need to sort the values with duplicate indices, which can greatly reduced time complexity,

int minRow = 0;
int maxRow = 0;
int minCol = 0;
int maxCol = 0;
"""

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Solution:
    def verticalTraversal(self, root: TreeNode):
        if not root:
            return root

        node_positions = {}
        self.getNodesPositions(root, node_positions)

        # sort by x
        node_positions_vals = sorted(node_positions, key=lambda x: x)
        for idx, key in enumerate(node_positions_vals):
            node_positions_vals[idx] = node_positions[key]

        # sort by y
        for items_list in node_positions_vals:
            items_list.sort(key=lambda x: x[0])
            for idx in range(len(items_list)):
                items_list[idx] = items_list[idx][1]  # remove y

        return node_positions_vals

    # get each node's position
    # x will represent 'columns' and y 'rows'
    def getNodesPositions(self, node, node_positions, x=0, y=0):
        if node is None:
            return None

        if x not in node_positions:
            node_positions[x] = []

        node_positions[x] = node_positions[x]+[[y, node.val]]
        self.getNodesPositions(node.left, node_positions, x-1, y+1)
        self.getNodesPositions(node.right, node_positions, x+1, y+1)

""" 
Solution 2: BFS with queue
- explained in EPI
"""

Binary Tree Vertical Order Traversal

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right

""" 
Better solution:
- use BFS
- instead of sorting keep track of the range of the column index (i.e. [min_column, max_column]) and iterate through it
"""
class Solution:
    def verticalOrder(self, root: TreeNode):
        if not root:
            return root

        node_positions = {}
        self.getNodesPositions(root, node_positions)
        # print(node_positions)

        # sort by x
        node_positions_vals = sorted(node_positions, key=lambda x: x)
        for idx, key in enumerate(node_positions_vals):
            node_positions_vals[idx] = node_positions[key]
        # print(node_positions_vals)

        # sort by y
        for items_list in node_positions_vals:
            # print(items_list)
            items_list.sort(key=lambda x: x[0])
            # print(items_list)
            for idx in range(len(items_list)):
                items_list[idx] = items_list[idx][1]  # remove y
        # print(node_positions_vals)
        return node_positions_vals

    # get each node's position
    # x will represent 'columns' and y 'rows'
    def getNodesPositions(self, node, node_positions, x=0, y=0):
        if node is None:
            return None

        if x not in node_positions:
            node_positions[x] = []

        node_positions[x] = node_positions[x]+[[y, node.val]]
        self.getNodesPositions(node.left, node_positions, x-1, y+1)
        self.getNodesPositions(node.right, node_positions, x+1, y+1)

Find Nodes Distance K *

Screenshot 2021-11-02 at 13.23.31.png

""" 
Find Nodes Distance K:

You're given the root node of a Binary Tree, a target value of a node that's contained in the tree, and a positive integer k. 
Write a function that returns the values of all the nodes that are exactly distance k from the node with target value.
The distance between two nodes is defined as the number of edges that must be traversed to go from one node to the other. 
For example, the distance between a node and its immediate left or right child is 1. The same holds in reverse: the distance between a node and its parent is 1. In a tree of three nodes where the root node has a left and right child, the left and right children are distance 2 from each other.

Each BinaryTree node has an integer value, a left child node, and a right child node. Children nodes can either be BinaryTree nodes themselves or None / null.

Note that all BinaryTree node values will be unique, and your function can return the output values in any order.

Sample Input
tree = 1
     /   \
    2     3
  /   \     \
 4     5     6
           /   \
          7     8
target = 3
k = 2
Sample Output
[2, 7, 8] // These values could be ordered differently.

https://www.algoexpert.io/questions/Find%20Nodes%20Distance%20K
"""
""" 
All Nodes Distance K in Binary Tree

Given the root of a binary tree, the value of a target node target, and an integer k, 
    return an array of the values of all nodes that have a distance k from the target node.
You can return the answer in any order.
Example 1:
    Input: root = [3,5,1,6,2,0,8,null,null,7,4], target = 5, k = 2
    Output: [7,4,1]
    Explanation: The nodes that are a distance 2 from the target node (with value 5) have values 7, 4, and 1.

https://leetcode.com/problems/all-nodes-distance-k-in-binary-tree/
"""

# Definition for a binary tree node.
class TreeNode:
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None

"""
- a graph representation of this will make it easier

- find/record parents
- find target
- dfs from target
"""

class Solution:
    def distanceK(self, root: TreeNode, target: TreeNode, k: int):
        res = []
        parents = {}
        self.recordParents(root, parents, None)
        self.findNodesDistanceK(target, parents, k, res, target)
        return res

    def findNodesDistanceK(self, root, parents, k, res, prev):
        if root is None:
            return

        if k == 0:
            res.append(root.val)
            return

        if root.left != prev:  # left
            self.findNodesDistanceK(root.left, parents, k-1, res, root)
        if root.right != prev:  # right
            self.findNodesDistanceK(root.right, parents, k-1, res, root)
        if parents[root.val] != prev:  # parent
            self.findNodesDistanceK(parents[root.val], parents, k-1, res, root)

    def recordParents(self, root, parents, parent):
        if root is None:
            return

        parents[root.val] = parent
        self.recordParents(root.left, parents, root)
        self.recordParents(root.right, parents, root)

Random node
Find Bottom Left Tree Value - LeetCode

Boundary of Binary Tree

Screenshot 2021-11-23 at 18.07.13.png

Screenshot 2021-11-23 at 18.07.26.png

Screenshot 2021-11-23 at 18.07.44.png

Screenshot 2021-11-23 at 18.06.58.png

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
public class Solution {

    public boolean isLeaf(TreeNode t) {
        return t.left == null && t.right == null;
    }

    public void addLeaves(List<Integer> res, TreeNode root) {
        if (isLeaf(root)) {
            res.add(root.val);
        } else {
            if (root.left != null) {
                addLeaves(res, root.left);
            }
            if (root.right != null) {
                addLeaves(res, root.right);
            }
        }
    }

    public List<Integer> boundaryOfBinaryTree(TreeNode root) {
        ArrayList<Integer> res = new ArrayList<>();
        if (root == null) {
            return res;
        }
        if (!isLeaf(root)) {
            res.add(root.val);
        }
        TreeNode t = root.left;
        while (t != null) {
            if (!isLeaf(t)) {
                res.add(t.val);
            }
            if (t.left != null) {
                t = t.left;
            } else {
                t = t.right;
            }

        }
        addLeaves(res, root);
        Stack<Integer> s = new Stack<>();
        t = root.right;
        while (t != null) {
            if (!isLeaf(t)) {
                s.push(t.val);
            }
            if (t.right != null) {
                t = t.right;
            } else {
                t = t.left;
            }
        }
        while (!s.empty()) {
            res.add(s.pop());
        }
        return res;
    }
}

Screenshot 2021-11-23 at 18.06.33.png

Screenshot 2021-11-23 at 18.06.46.png

Definition of terms

The depth of a node n is the number of nodes on the search path from the root to n, not including n itself. The height of a binary tree is the maximum depth of any node in that tree. A level of a tree is all nodes at the same depth.

Balanced vs. Unbalanced

A balanced binary tree, also referred to as a height-balanced binary tree, is defined as a binary tree in which the height of the left and right subtree of any node differ by not more than 1. One way to think about it is that a "balanced" tree really means something more like "not terribly imbalanced:" It's balanced enough to ensure 0(logn) times for insert and find,but it's not necessarily as balanced as it could be.

While many trees are balanced, not all are. Ask your interviewer for clarification here. Note that balancing a tree does not mean the left and right subtrees are exactly the same size (like you see under "perfect binary trees").

Two common types of balanced trees are red-black trees and AVL trees.

Complete Binary Trees

Screenshot 2021-10-06 at 18.20.21.png

A complete binary tree is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible (This terminology is not universal, e.g., some authors use complete binary tree where we write perfect binary tree.)

Full Binary Trees

Screenshot 2021-10-06 at 18.21.20.png

A full binary tree is a binary tree in which every node other than the leaves has two children.

Perfect binary tree

A perfect binary tree is a full binary tree in which all leaves are at the same depth, and in which every parent has two children. (every level of the tree is completely full)

Binary trees have a few interesting properties when they're perfect:

The number of total nodes on each "level" doubles as we move down the tree.
The number of nodes on the last level is equal to the sum of the number of nodes on all other levels (plus 1). In other words, about half of our nodes are on the last level.

Populating Next Right Pointers in Each Node *

Screenshot 2021-11-02 at 10.59.29.png

Remember that we are dealing with a perfect tree

""" 
116. Populating Next Right Pointers in Each Node

You are given a perfect binary tree where all leaves are on the same level, and every parent has two children. The binary tree has the following definition:
    struct Node {
    int val;
    Node *left;
    Node *right;
    Node *next;
    }

Populate each next pointer to point to its next right node. 
If there is no next right node, the next pointer should be set to NULL.
Initially, all next pointers are set to NULL.

https://leetcode.com/problems/populating-next-right-pointers-in-each-node
EPI 9.16
"""
import collections

# Definition for a Node.
class Node:
    def __init__(self, val: int = 0, left: 'Node' = None, right: 'Node' = None, next: 'Node' = None):
        self.val = val
        self.left = left
        self.right = right
        self.next = next

class Solution:
    def connect(self, root: 'Node'):
        if not root:
            return

        queue = [root]
        while queue:
            curr = queue.pop(0)

            if curr.left:
                curr.left.next = curr.right
                queue.append(curr.left)

            if curr.right:
                if curr.next:
                    curr.right.next = curr.next.left
                queue.append(curr.right)

        return root

""" 
"""

class Solution_:
    def connect(self, root: 'Node'):
        if not root:
            return None

        prev_nodes = collections.defaultdict(lambda: None)
        queue = [(root, 0)]

        while queue:
            curr, depth = queue.pop(0)

            curr.next = prev_nodes[depth]
            prev_nodes[depth] = curr

            # next
            if curr.right:
                queue.append((curr.right, depth+1))
            if curr.left:
                queue.append((curr.left, depth+1))

        return root

Binary Tree Traversals (Inorder, Preorder and Postorder)

We can use DFS to do pre-order, in-order and post-order traversal. There is a common feature among these three traversal orders: we never trace back unless we reach the deepest node. That is also the largest difference between DFS and BFS, BFS never go deeper unless it has already visited all nodes at the current level. Typically, we implement DFS using recursion.

Pre-order Traversal (nlr)

In this traversal mode, one starts from the root, move to left child, then right child.

In-order Traversal (lnr)

Screen Recording 2021-10-23 at 13.31.41.mov

In this traversal mode, one starts visiting with the left child, followed by root and then the right child.

Check out how to do it iteratively.

Post-order Traversal (lrn)

In this traversal mode, one starts from the left child, move to the right child, and terminate at the root.

Examples

Binary Search Tree Iterator

Screenshot 2021-10-23 at 13.34.15.png

"""
Binary Search Tree Iterator:

Implement the BSTIterator class that represents an iterator over the in-order traversal of a binary search tree (BST):
BSTIterator(TreeNode root) Initializes an object of the BSTIterator class. 
The root of the BST is given as part of the constructor. The pointer should be initialized to a non-existent number smaller than any element in the BST.
boolean hasNext() Returns true if there exists a number in the traversal to the right of the pointer, otherwise returns false.
int next() Moves the pointer to the right, then returns the number at the pointer.
Notice that by initializing the pointer to a non-existent smallest number, the first call to next() will return the smallest element in the BST.
You may assume that next() calls will always be valid. That is, there will be at least a next number in the in-order traversal when next() is called.

Example 1:
     7
    / \
    3  15
       / \
       9  20
    Input
    ["BSTIterator", "next", "next", "hasNext", "next", "hasNext", "next", "hasNext", "next", "hasNext"]
    [[[7, 3, 15, null, null, 9, 20]], [], [], [], [], [], [], [], [], []]
Output
    [null, 3, 7, true, 9, true, 15, true, 20, false]

    Explanation
    BSTIterator bSTIterator = new BSTIterator([7, 3, 15, null, null, 9, 20]);
    bSTIterator.next();    // return 3
    bSTIterator.next();    // return 7
    bSTIterator.hasNext(); // return True
    bSTIterator.next();    // return 9
    bSTIterator.hasNext(); // return True
    bSTIterator.next();    // return 15
    bSTIterator.hasNext(); // return True
    bSTIterator.next();    // return 20
    bSTIterator.hasNext(); // return False
"""

from typing import Optional
""" 
----
Solution 1:
store the inorder traversal in an array and return them index by index

---
Solution 2:
controlled iteration

check Binary Tree Inorder Traversal (Iterative)
https://www.notion.so/paulonteri/Trees-Graphs-edc3401e06c044f29a2d714d20ffe185#8c489e8b02804929ab535f25f945a31b

[3,7,9,15,20]

"""

# Definition for a binary tree node.
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class BSTIterator:

    def __init__(self, root: Optional[TreeNode]):
        self.curr = root
        self.stack = []

    def next(self):
        # put the left most value(s) to the top of the stack
        while self.curr:
            self.stack.append(self.curr)
            self.curr = self.curr.left
        # the left-most node is at the top of the stack
        node = self.stack.pop()
        # the next (only next unvisited valid node) will be at the right
        self.curr = node.right

        return node.val

    def hasNext(self):
        return self.curr or self.stack

# Your BSTIterator object will be instantiated and called as such:
# obj = BSTIterator(root)
# param_1 = obj.next()
# param_2 = obj.hasNext()

Inorder Successor in BST

Screenshot 2021-10-05 at 10.50.47.png

Screenshot 2021-10-05 at 10.51.39.png

Screenshot 2021-10-05 at 10.51.57.png

Screenshot 2021-10-05 at 10.52.16.png

""" 
Inorder Successor in BST:
FIND THE FIRST KEY GREATER THAN A GIVEN VALUE IN A BST:

Given the root of a binary search tree and a node p in it, return the in-order successor of that node in the BST. 
If the given node has no in-order successor in the tree, return null.

The successor of a node p is the node with the smallest key greater than p.val.

https://leetcode.com/problems/inorder-successor-in-bst
epi 14.2
"""

# Definition for a binary tree node.
class TreeNode:
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None

class Solution:
    def inorderSuccessor(self, root: 'TreeNode', p: 'TreeNode'):
        nxt = None

        curr = root
        while curr is not None:
                          # successor will be the next larger value compared to the element
            if curr.val > p.val:
                nxt = curr
                # try to reduce the value
                curr = curr.left
            else:
                # try to increase the value
                curr = curr.right

        return nxt

Inorder Successor in BST II

Example 1:

https://camo.githubusercontent.com/c516e4fd7889308d123f51537c2892bdfba09cafa68775b01f0f82b00892de64/68747470733a2f2f6173736574732e6c656574636f64652e636f6d2f75706c6f6164732f323031392f30312f32332f3238355f6578616d706c655f312e504e47

Input: tree = [2,1,3], node = 1
Output: 2
Explanation: 1's in-order successor node is 2. Note that both the node and the return value is of Node type.

Example 2:

https://camo.githubusercontent.com/99e689e63ae1e3a208844a949e1529dbbd9b4204c64dd6ff88af27aee0c8946f/68747470733a2f2f6173736574732e6c656574636f64652e636f6d2f75706c6f6164732f323031392f30312f32332f3238355f6578616d706c655f322e504e47

Input: tree = [5,3,6,2,4,null,null,1], node = 6
Output: null
Explanation: There is no in-order successor of the current node, so the answer is null.

Example 3:

https://camo.githubusercontent.com/dc36f2d972da5a61aa3e91c1ede841a46f21d21851c546dacd020236814dd01c/68747470733a2f2f6173736574732e6c656574636f64652e636f6d2f75706c6f6164732f323031392f30322f30322f3238355f6578616d706c655f33342e504e47

Input: tree = [15,6,18,3,7,17,20,2,4,null,13,null,null,null,null,null,null,null,null,9], node = 15
Output: 17

Example 4:

https://camo.githubusercontent.com/dc36f2d972da5a61aa3e91c1ede841a46f21d21851c546dacd020236814dd01c/68747470733a2f2f6173736574732e6c656574636f64652e636f6d2f75706c6f6164732f323031392f30322f30322f3238355f6578616d706c655f33342e504e47

Input: tree = [15,6,18,3,7,17,20,2,4,null,13,null,null,null,null,null,null,null,null,9], node = 13
Output: 15

Example 5:

Input: tree = [0], node = 0
Output: null

Screenshot 2021-10-07 at 06.08.39.png

Screenshot 2021-10-07 at 06.09.03.png

Screenshot 2021-10-07 at 06.09.29.png

""" 
510. Inorder Successor in BST II

Given a node in a binary search tree, return the in-order successor of that node in the BST. 
If that node has no in-order successor, return null.

The successor of a node is the node with the smallest key greater than node.val.

You will have direct access to the node but not to the root of the tree. 
Each node will have a reference to its parent node. Below is the definition for Node:
    class Node {
        public int val;
        public Node left;
        public Node right;
        public Node parent;
    }

"""

""" 
Node has a right child, and hence its successor is somewhere lower in the tree. 
To find the successor, go to the right once and then as many times to the left as you could.

Node has no right child, then its successor is somewhere upper in the tree. 
To find the successor, go up till the node that is left child of its parent. The answer is the parent. 
Beware that there could be no successor (= null successor) in such a situation.
"""

# Definition for a Node.
class Node:
    def __init__(self, val):
        self.val = val
        self.left = None
        self.right = None
        self.parent = None

class Solution:
    def inorderSuccessor(self, node):
        curr = node

        if curr.right:
            # get left most child in right subtree
            curr = curr.right
            while curr and curr.left:
                curr = curr.left
            return curr

        else:
            # find where the tree last branched left
            while curr:
                if curr.parent and curr.parent.left == curr:
                    return curr.parent
                curr = curr.parent

        return None

BST Traversal

"""
BST Traversal:

Write three functions that take in a Binary Search Tree (BST) and an empty array,
 traverse the BST, add its nodes' values to the input array, and return that array.
The three functions should traverse the BST using the in-order, pre-order, and post-order tree-traversal techniques, respectively.

Each BST node has an integer value, a left child node, and a right child node.
A node is said to be a valid BST node if and only if it satisfies the BST property:
 its value is strictly greater than the values of every node to its left; its value is less than or equal to the values of every node to its right;
  and its children nodes are either valid BST nodes themselves or None / null.

https://www.algoexpert.io/questions/BST%20Traversal
"""

# In  ->  lnr
# Pre ->  nlr
# Post -> lrn

def inOrderTraverse(node, array):
    if node is None:
        return

    # before we get to the append we inOrderTraverse() on the left, then we find anther left, we inOrderTraverse on the left again and again
    #  till we are at the final left for a given tree/sub-tree
    # we finally append its value then call inOrderTraverse() on its right child and the process repeats istself again and again

    # we will keep on going till the furthest left before any other step like array.append(node.value) or inOrderTraverse(node.right, array)
    inOrderTraverse(node.left, array)
    array.append(node.value)
    inOrderTraverse(node.right, array)

    return array

def preOrderTraverse(node, array):
    if node is None:
        return

    array.append(node.value)
    preOrderTraverse(node.left, array)
    preOrderTraverse(node.right, array)

    return array

def postOrderTraverse(node, array):
    if node is None:
        return

    postOrderTraverse(node.left, array)
    postOrderTraverse(node.right, array)
    array.append(node.value)

    return array

Find Kth Largest Value In BST

"""
Find Kth Largest Value In BST:

Write a function that takes in a Binary Search Tree (BST) and a positive integer k and returns the kth largest integer contained in the BST.
You can assume that there will only be integer values in the BST and that k is less than or equal to the number of nodes in the tree.
Also, for the purpose of this question, duplicate integers will be treated as distinct values.
In other words, the second largest value in a BST containing values {5, 7, 7} will be 7—not 5.
Each BST node has an integer value, a left child node, and a right child node.
A node is said to be a valid BST node if and only if it satisfies the BST property: 
    its value is strictly greater than the values of every node to its left; its value is less than or equal to the values of every node to its right;
     and its children nodes are either valid BST nodes themselves or None / null.
Sample Input
    tree =   15
        /     \
        5      20
        /   \   /   \
    2     5 17   22
    /   \         
    1     3       
    k = 3
Sample Output
    17
https://www.algoexpert.io/questions/Find%20Kth%20Largest%20Value%20In%20BST
"""

# This is an input class. Do not edit.
class BST:
    def __init__(self, value, left=None, right=None):
        self.value = value
        self.left = left
        self.right = right

class TreeInfo:
    def __init__(self, visits_remaining):
        self.visits_remaining = visits_remaining
        self.last_visited = None

# O(h + k) time | O(h) space - where h is the height of the tree and k is the input parameter
#   we have to go to the largest element, at the furthest/deepest right (h) first before looking for k
def findKthLargestValueInBst(tree, k):
    tree_info = TreeInfo(k)
    reverseInOrderTraverse(tree, tree_info)
    return tree_info.last_visited.value

def reverseInOrderTraverse(tree, tree_info):
    if not tree:
        return

    reverseInOrderTraverse(tree.right, tree_info)
    # # visit node
    # tree_info was updated in the above function call
    if tree_info.visits_remaining > 0:
        tree_info.visits_remaining -= 1
        tree_info.last_visited = tree
    else:
        return
    reverseInOrderTraverse(tree.left, tree_info)

Reconstruct Binary Search Tree from Preorder Traversal with Less than, greater than patterns

"""
Construct Binary Search Tree from Preorder Traversal:

Return the root node of a binary search tree that matches the given preorder traversal.
(Recall that a binary search tree is a binary tree where for every node, any descendant of node.left has a value < node.val,
 and any descendant of node.right has a value > node.val.  Also recall that a preorder traversal displays the value of the node first,
 then traverses node.left, then traverses node.right.)
It's guaranteed that for the given test cases there is always possible to find a binary search tree with the given requirements.

https://leetcode.com/problems/construct-binary-search-tree-from-preorder-traversal/
"""
"""
Reconstruct BST:

The pre-order traversal of a Binary Tree is a traversal technique that starts at the tree's root node and visits nodes in the following order:
    Current node
    Left subtree
    Right subtree
Given a non-empty array of integers representing the pre-order traversal of a Binary Search Tree (BST),
    write a function that creates the relevant BST and returns its root node.
The input array will contain the values of BST nodes in the order in which these nodes would be visited with a pre-order traversal.
Each BST node has an integer value, a left child node, and a right child node.
A node is said to be a valid BST node if and only if it satisfies the BST property: 
    its value is strictly greater than the values of every node to its left;
    its value is less than or equal to the values of every node to its right;
    and its children nodes are either valid BST nodes themselves or None / null.
Sample Input
    preOrderTraversalValues = [10, 4, 2, 1, 5, 17, 19, 18]
Sample Output
            10 
        /    \
        4      17
    /   \      \
    2     5     19
    /           /
    1           18 
https://www.algoexpert.io/questions/Reconstruct%20BST
"""

from typing import List
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

"""
use pointers to keep track of valid values for each subtree
"""

class SolutionBF:
    def bstFromPreorderHelper(self, preorder, start, end):
        if start > end:
            return None
        if start == end:
            return TreeNode(preorder[start])

        node = TreeNode(preorder[start])

        left_start = start + 1
        left_end = left_start
        while left_end <= end and preorder[left_end] < preorder[start]:
            left_end += 1
        left_end -= 1  # last valid value

        node.left = self.bstFromPreorderHelper(preorder, left_start, left_end)
        node.right = self.bstFromPreorderHelper(preorder, left_end+1, end)

        return node

    def bstFromPreorder(self, preorder):
        return self.bstFromPreorderHelper(preorder, 0, len(preorder)-1)

# ----------------------------------------------------------------------------------------------------------------------

"""
We will start by creating the root node while keeping track of the max and min values at any time:
- if value is less than node & greater than min: pass ot to left
- if value is greater than node & less than max: pass to right

Then proceed to the left: passing the max to be the root's value & min to be -inf
                   right: passing the min to be thr root's value & max to be inf


"""

"""
Sample Input
    preOrderTraversalValues = [10, 4, 2, 1, 5, 17, 16, 19, 18]
Sample Output
        10 
      /    \
     4      17 
   /   \   /  \
  2     5 16  19
 /           /
1           18 

keep track of the largest and smallest node that can be placed
left -> pass current node as largest
right -> pass curr node as smallest

if it does not satisfy the constraints we go back up the tree till where it will match
else, insert it

"""

class Solution:
    def bstFromPreorder(self, preorder: List[int]):
        # if not preorder
        return self.bstFromPreorderHelper(preorder, [0], float('-inf'), float('inf'))

    def bstFromPreorderHelper(self, preorder, curr, minimum, maximum):
        if curr[0] >= len(preorder):  # validate curr position on preoder array
            return None

        value = preorder[curr[0]]  # get value from preoder array
        if value < minimum or value > maximum:  # check whether it can be added
            return None

        node = TreeNode(value)  # create Node

        # add left and right
        curr[0] = curr[0] + 1  # move pointer forward
        node.left = self.bstFromPreorderHelper(preorder, curr, minimum, value)
        node.right = self.bstFromPreorderHelper(preorder, curr, value, maximum)

        return node

Same BSTs *

"""
Same BSTs:

An array of integers is said to represent the Binary Search Tree (BST) obtained by inserting each integer in the array, from left to right, into the BST.
Write a function that takes in two arrays of integers and determines whether these arrays represent the same BST. Note that you're not allowed to construct any BSTs in your code.
A BST is a Binary Tree that consists only of BST nodes. 
A node is said to be a valid BST node if and only if it satisfies the BST property:
 its value is strictly greater than the values of every node to its left;
 its value is less than or equal to the values of every node to its right; 
 and its children nodes are either valid BST nodes themselves or None / null.

Sample Input
    arrayOne = [10, 15, 8, 12, 94, 81, 5, 2, 11]
    arrayTwo = [10, 8, 5, 15, 2, 12, 11, 94, 81]
Sample Output
    true // both arrays represent the BST below
            10
        /     \
        8      15
      /       /   \
    5        12     94
    /       /     /
    2       11    81

https://www.algoexpert.io/questions/Same%20BSTs 
"""

# O(n^2) time | O(n^2) space - where n is the number of nodes in each array, respectively
def sameBsts(arrayOne, arrayTwo):
    return sameBstsHelper(arrayOne, arrayTwo)

def sameBstsHelper(arrayOne, arrayTwo):
    # must be same length
    if len(arrayOne) != len(arrayTwo):
        return False

    # we didn't find anything wrong
    if len(arrayOne) == 0:  # any -> arrayOne/arrayTwo
        return True

    # must have same head
    if arrayOne[0] != arrayTwo[0]:
        return False

    # # split into right and left
    # elements larger or equal to than idx 0
    right_one = []
    right_two = []
    # elements smaller than idx 0
    left_one = []
    left_two = []
    for idx in range(1, len(arrayOne)):  # any -> arrayOne/arrayTwo

        # one
        if arrayOne[idx] < arrayOne[0]:
            left_one.append(arrayOne[idx])
        else:
            right_one.append(arrayOne[idx])

        # two
        if arrayTwo[idx] < arrayTwo[0]:
            left_two.append(arrayTwo[idx])
        else:
            right_two.append(arrayTwo[idx])

    left = sameBstsHelper(left_one, left_two)
    right = sameBstsHelper(right_one, right_two)

    return left and right

"""
# ----------------------------------------------------------------------------------------------------------------------

# check roots
- `build bst `(find all the roots at every point in the tree) and validate that they are same
"""

# O(n^2) time | O(d) space
# where n is the number of nodes in each array, respectively,
# and d is the depth of the BST that they represent
def sameBsts(array_one, array_two):
    return buildTrees(array_one, array_two, 0, 0, float('-inf'), float('inf'))

def buildTrees(array_one, array_two, idx_one, idx_two, minimum, maximum):
    # no extra elements to add (reached end)
    if idx_one == None or idx_two == None:
        return idx_one == idx_two

    # validate roots (roots should be same)
    if array_one[idx_one] != array_two[idx_two]:
        return False
    curr = array_one[idx_one]

    left_one = findNextValidSmaller(array_one, idx_one, minimum)
    left_two = findNextValidSmaller(array_two, idx_two, minimum)
    right_one = findNextValidLargerOrEqual(array_one, idx_one, maximum)
    right_two = findNextValidLargerOrEqual(array_two, idx_two, maximum)

    left = buildTrees(
        # the curr is the largest there will ever be
        array_one, array_two, left_one, left_two, minimum, curr)
    right = buildTrees(
        # curr is the smallest
        array_one, array_two, right_one, right_two, curr, maximum)

    return left and right

def findNextValidSmaller(array, starting_idx, running_minimum):
    # used to find the next left root
    # Find the index of the first smaller value after the startingIdx.
    # Make sure that this value is greater than or equal to the minVal,
    # which is the value of the previous parent node in the BST.
    # If it isn't, then that value is located in the left subtree of the
    # previous parent node.
    for idx in range(starting_idx + 1, len(array)):
        if array[idx] < array[starting_idx] and array[idx] >= running_minimum:
            return idx
    return None

def findNextValidLargerOrEqual(array, starting_idx, running_maximum):
    # used to find the next right root
    # Find the index of the first bigger/equal value after the startingIdx.
    # Make sure that this value is smaller than maxVal, which is the value
    # of the previous parent node in the BST.
    # If it isn't, then that value is located in the right subtree of the previous parent node.
    for idx in range(starting_idx + 1, len(array)):
        if array[idx] >= array[starting_idx] and array[idx] < running_maximum:
            return idx
    return None

Serialize and Deserialize BST *

Screenshot 2021-11-02 at 13.47.27.png

""" 
Serialize and Deserialize BST

Serialization is converting a data structure or object into a sequence of bits so that it can be stored in a file 
    or memory buffer, or transmitted across a network connection link to be reconstructed later in the same or another computer environment.
Design an algorithm to serialize and deserialize a binary search tree. 
There is no restriction on how your serialization/deserialization algorithm should work. 
You need to ensure that a binary search tree can be serialized to a string, and this string can be deserialized to the original tree structure.
The encoded string should be as compact as possible.

Example 1:
    Input: root = [2,1,3]
    Output: [2,1,3]
Example 2:
    Input: root = []
    Output: []

After this:
- https://leetcode.com/problems/serialize-and-deserialize-binary-tree

https://leetcode.com/problems/serialize-and-deserialize-bst
"""

""" 
Alternative solutions:
-  using preorder traversal (here we use postorder) https://leetcode.com/problems/construct-binary-search-tree-from-preorder-traversal
"""

# Definition for a binary tree node.
class TreeNode:
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None

class Codec:
    def serialize(self, root):
        """
        Encodes a tree to a single postorder string.
        """
        postorder_result = []

        def postorder(node):
            if not node:
                return
            postorder(node.left)
            postorder(node.right)
            postorder_result.append(node.val)

        postorder(root)
        return ' '.join(map(str,  postorder_result))

    def deserialize(self, data):
        """
        Decodes your encoded data to tree.
        """
        def reverse_postorder(lower, upper):
            """ 
            Reverse of postorder: postorder is `lrn`, here we do `nrl`
            """
            if not data:
                return None
            if data[-1] < lower or data[-1] > upper:
                return None

            node = TreeNode(data.pop())
            node.right = reverse_postorder(node.val, upper)
            node.left = reverse_postorder(lower, node.val)

            return node

        data = [int(x) for x in data.split(' ') if x]
        return reverse_postorder(float('-inf'), float('inf'))

# Your Codec object will be instantiated and called as such:
# Your Codec object will be instantiated and called as such:
# ser = Codec()
# deser = Codec()
# tree = ser.serialize(root)
# ans = deser.deserialize(tree)
# return ans

Subtree of Another Tree *

Check subtree

Screenshot 2021-11-02 at 11.45.39.png

Screenshot 2021-11-02 at 11.46.00.png

"""
Subtree of Another Tree:

Given two non-empty binary trees s and t, check whether tree t has exactly the same structure and node values with a subtree of s.
A subtree of s is a tree consists of a node in s and all of this node's descendants.
The tree s could also be considered as a subtree of itself.

https://leetcode.com/problems/subtree-of-another-tree/
"""

# Definition for a binary tree node.
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Solution:
    def isSubtree(self, s: TreeNode, t: TreeNode):
        return self.traverse(s, t)

    def traverse(self, s, t):
        if self.checkSubTreeFunction(s, t) == True:
            return True
        if s is None:
            return False

        return self.traverse(s.left, t) or self.traverse(s.right, t)

    def checkSubTreeFunction(self, s, t):
        if s == None and t == None:
            return True
        elif s == None or t == None or s.val != t.val:
            return False

        return self.checkSubTreeFunction(s.left, t.left) and self.checkSubTreeFunction(s.right, t.right)

Construct Binary Tree from Preorder and Inorder Traversal

[1/3] CONSTRUCT BINARY TREE FROM PREORDER/INORDER TRAVERSAL - Code & Whiteboard

Construct Binary Tree from Inorder and Preorder Traversal - Leetcode 105 - Python

LeetCode 105. Construct Binary Tree from Preorder and Inorder Traversal (Algorithm Explained)

Screenshot 2021-11-02 at 12.35.33.png

Screenshot 2021-10-04 at 05.43.02.png

"""
Construct Binary Tree from Preorder and Inorder Traversal:

Given two integer arrays preorder and inorder where
preorder is the preorder traversal of a binary tree and inorder is the inorder traversal of the same tree,
construct and return the binary tree.

Example 1:
    Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
    Output: [3,9,20,null,null,15,7]
Example 2:
    Input: preorder = [-1], inorder = [-1]
    Output: [-1]

https://leetcode.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal/
"""

from typing import List

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

# ---------------------------------------------------------------------------------------------------------------------

""" 
- The root will be the first element in the preorder sequence
- Next, locate the index of the root node in the inorder sequence
    - this will help you know the number of nodes to its left & the number to its right
- repeat this recursively
"""

class SolutionBF(object):
    def buildTree(self, preorder, inorder):
        return self.dfs(preorder, inorder)

    def dfs(self, preorder, inorder):
        if len(preorder) == 0:
            return None

        root = TreeNode(preorder[0])

        mid = inorder.index(preorder[0])

        root.left = self.dfs(preorder[1: mid+1], inorder[: mid])
        root.right = self.dfs(preorder[mid+1:], inorder[mid+1:])
        return root

class SolutionBF0:
    def buildTree(self, preorder, inorder):

        if len(inorder) == 0:
            # the remaining preorder values do not belong in this subtree
            return None

        if len(preorder) == 1:
            return TreeNode(preorder[0])

        ino_index = inorder.index(preorder.pop(0))  # remove from preorder
        node = TreeNode(inorder[ino_index])

        node.left = self.buildTree(preorder, inorder[:ino_index])
        node.right = self.buildTree(preorder, inorder[ino_index+1:])

        return node

class SolutionBF00:
    def buildTree(self, preorder, inorder):

        preorder_pos = 0

        def buildTreeHelper(preorder, inorder):
            nonlocal preorder_pos

            # we do not have valid nodes to be placed
            if preorder_pos >= len(preorder):
                return

            # # create node
            # node
            inorder_idx = inorder.index(preorder[preorder_pos])
            preorder_pos += 1
            node = TreeNode(inorder[inorder_idx])

            # children -> will pass only valid children below -> (inorder[:inorder_idx] & inorder[inorder_idx+1:] does that)
            node.left = buildTreeHelper(preorder, inorder[:inorder_idx])
            node.right = buildTreeHelper(preorder, inorder[inorder_idx+1:])

            return node
        return buildTreeHelper(preorder, inorder)
#         def buildTreeHelper2( preorder, inorder):
#             nonlocal preorder_pos

#             if preorder_pos >= len(preorder):
#                 return

#             # # create node
#             # node
#             inorder_idx = inorder.index( preorder[preorder_pos] )
#             preorder_pos += 1
#             node = TreeNode(inorder[inorder_idx ])

#             left = inorder[:inorder_idx]
#             right = inorder[inorder_idx+1:]
#             if left:
#                 node.left = buildTreeHelper(preorder, left)
#             if right:
#                 node.right = buildTreeHelper(preorder, right)

#             return node
#       return buildTreeHelper2(preorder, inorder)

# ---------------------------------------------------------------------------------------------------------------------

""" 
- The root will be the first element in the preorder sequence
- Next, locate the index of the root node in the inorder sequence
    - this will help you know the number of nodes to its left & the number to its right
- repeat this recursively

- iterate through the preorder array and check if the current can be placed in the current tree(or recursive call)

- We use the remaining inorder traversal to determine(restrict) whether
    the current preorder node is in the left or right
"""

class Solution:
    def buildTree(self, preorder, inorder):
        preorder_pos = 0
        inorder_idxs = {val: idx for idx, val in enumerate(inorder)}

        def helper(inorder_left, inorder_right):
            nonlocal preorder_pos

            if preorder_pos == len(preorder):
                return
            if inorder_left > inorder_right:
                return

            val = preorder[preorder_pos]
            preorder_pos += 1

            node = TreeNode(val)

            inorder_idx = inorder_idxs[val]
            # start with left !
            node.left = helper(inorder_left, inorder_idx-1)
            node.right = helper(inorder_idx+1, inorder_right)

            return node

        return helper(0, len(inorder)-1)

Construct Binary Tree from Inorder and Postorder Traversal

""" 
106. Construct Binary Tree from Inorder and Postorder Traversal

Given two integer arrays inorder and postorder where 
    inorder is the inorder traversal of a binary tree and 
    postorder is the postorder traversal of the same tree, 
construct and return the binary tree.

Example 1:
    Input: inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
    Output: [3,9,20,null,null,15,7]
Example 2:
    Input: inorder = [-1], postorder = [-1]
    Output: [-1]

https://leetcode.com/problems/construct-binary-tree-from-inorder-and-postorder-traversal
"""

# Definition for a binary tree node.
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Solution:
    def buildTree(self, inorder, postorder):
        postorder_idx = len(postorder)-1
        inorder_idxs = {val: idx for idx, val in enumerate(inorder)}

        def helper(inorder_left, inorder_right):
            nonlocal postorder_idx

            if postorder_idx < 0:
                return None
            if inorder_left > inorder_right:
                return None

            val = postorder[postorder_idx]
            postorder_idx -= 1

            # create node
            node = TreeNode(val)

            inorder_idx = inorder_idxs[val]
            # start with right !
            node.right = helper(inorder_idx+1, inorder_right)
            node.left = helper(inorder_left, inorder_idx-1)

            return node
        return helper(0, len(inorder)-1)

Preorder/Postorder

Binary Tree Inorder Traversal - Iterative **

Screenshot 2021-11-02 at 13.07.38.png

Screen Recording 2021-10-23 at 13.36.24.mov

"""
Binary Tree Inorder Traversal:

Given the root of a binary tree, return the inorder traversal of its nodes' values.

https://leetcode.com/problems/binary-tree-inorder-traversal/

https://www.enjoyalgorithms.com/blog/iterative-binary-tree-traversals-using-stack
https://www.educative.io/edpresso/how-to-perform-an-iterative-inorder-traversal-of-a-binary-tree
https://www.techiedelight.com/inorder-tree-traversal-iterative-recursive

After this:
- https://leetcode.com/problems/binary-search-tree-iterator
"""

# Definition for a binary tree node.
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

""" 
 - add all left nodes to stack
 - visit left most node
 - move to the right
"""

class Solution_:
    def inorderTraversal(self, root: TreeNode):
        if not root:
            return None
        result = []

        stack = []
        curr = root
        while stack or curr:
            # add all left
            # put the left most value(s) to the top of the stack
            while curr and curr.left:
                stack.append(curr)
                curr = curr.left

            # the top of the stack has the left most unvisited value
            #  visit node
            if not curr:
                curr = stack.pop()
            result.append(curr.val)

            # - has no unvisited left
            # - itself is visited
            # so the next to be visited is right
            curr = curr.right

        return result

"""

class Solution:
    def inorderTraversal(self, root: TreeNode):
        output = []

        stack = []
        curr = root
        while curr is not None or len(stack) > 0:

            # add all left
            while curr is not None:
                stack.append(curr)
                curr = curr.left

            # visit node
            temp = stack.pop()
            output.append(temp.val)

            curr = temp.right

        return output
"""

#         10
#       /    \
#      4      17
#    /   \      \
#   2     5     19
#  /           /
#  1           18

class Solution:
    def inorderTraversal(self, root: TreeNode):
        if not root:
            return None
        result = []

        stack = []
        curr = root
        while stack or curr:
            # put the left most value(s) to the top of the stack
            while curr:
                stack.append(curr)
                curr = curr.left

            # the top of the stack has the left most unvisited value
            #  visit node
            curr = stack.pop()
            result.append(curr.val)

            # - has no unvisited left
            # - itself is visited
            # so the next to be visited is right
            # eg: after 4 is 5 in the example above
            curr = curr.right

        return result

""" 
------------------------------------------------------------------------------------------------------------
"""

class Solution1:
    def inorderTraversal(self, root):
        output = []
        self.inorderTraversalHelper(root, output)
        return output

    def inorderTraversalHelper(self, root, output):
        if not root:
            return

        self.inorderTraversalHelper(root.left, output)
        output.append(root.val)
        self.inorderTraversalHelper(root.right, output)

Morris Inorder Tree Traversal - Inorder with O(1) space ***

https://youtu.be/wGXB9OWhPTg

Screenshot 2021-10-04 at 05.34.34.png

Screenshot 2021-10-08 at 08.27.31.png

Screenshot 2021-10-04 at 05.34.52.png

Screenshot 2021-10-08 at 08.49.59.png

Screenshot 2021-10-08 at 08.50.43.png

Screenshot 2021-10-08 at 08.50.57.png

""" 
Morris Inorder Tree Traversal - Inorder with O(1) space

https://leetcode.com/problems/binary-tree-inorder-traversal
EPI 9.11
"""

# Definition for a binary tree node.
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Solution:
    def inorderTraversal(self, root):
        res = []

        curr = root
        while curr is not None:

            # has no left child - so is the next valid
            if not curr.left:
                res.append(curr.val)
                curr = curr.right

            # place the curr node as the right child of its predecessor
            #   which is the rightmost node in the left subtree
            else:
                predecessor = self.get_inorder_predecessor(curr)

                # # move node down the tree
                left = curr.left
                curr.left = None  # prevent loop

                predecessor.right = curr

                # # continue to left subtree
                curr = left

        return res

    def get_inorder_predecessor(self, node):
        curr = node.left

        while curr.right is not None:
            curr = curr.right

        return curr

536. Construct Binary Tree from String

Serialize and Deserialize Binary Tree **

Screenshot 2021-11-02 at 13.15.43.png

""" 
Serialize and Deserialize Binary Tree

Serialization is the process of converting a data structure or object into a sequence of bits so that it can be stored in a file or memory buffer, 
    or transmitted across a network connection link to be reconstructed later in the same or another computer environment.
Design an algorithm to serialize and deserialize a binary tree. 
There is no restriction on how your serialization/deserialization algorithm should work. 
You just need to ensure that a binary tree can be serialized to a string and this string can be deserialized to the original tree structure.
Clarification: The input/output format is the same as how LeetCode serializes a binary tree. 
You do not necessarily need to follow this format, so please be creative and come up with different approaches yourself.

Example 1:
    Input: root = [1,2,3,null,null,4,5]
    Output: [1,2,3,null,null,4,5]
Example 2:
    Input: root = []
    Output: []
Example 3:
    Input: root = [1]
    Output: [1]
Example 4:
    Input: root = [1,2]
    Output: [1,2]

https://leetcode.com/problems/serialize-and-deserialize-binary-tree/

Prerequisites:
- https://leetcode.com/problems/serialize-and-deserialize-bst
- https://leetcode.com/problems/construct-binary-search-tree-from-preorder-traversal
"""

# Definition for a binary tree node.
class TreeNode(object):
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None

class Codec:

    def serialize(self, root):
        preorder_result = []

        # def preorder(node):
        #     if not node:
        #         preorder_result.append(str(None))
        #         return

        #     preorder_result.append(str(node.val))
        #     preorder(node.left)
        #     preorder(node.right)
        def preorder(node):
            if not node:
                preorder_result.append(str(None))
                return

            preorder_result.append(str(node.val))
            preorder(node.left)
            preorder(node.right)

        preorder(root)
        return " ".join(preorder_result)

    def deserialize(self, data):

        idx = 0
        def reverse_preorder(arr):
            nonlocal idx
            if idx > len(arr):
                return None
            if arr[idx] == 'None':
                idx += 1
                return None

            node = TreeNode(int(arr[idx]))
            idx += 1

            node.left = reverse_preorder(arr)
            node.right = reverse_preorder(arr)

            return node

        return reverse_preorder(data.split(" "))

# Your Codec object will be instantiated and called as such:
# ser = Codec()
# deser = Codec()
# ans = deser.deserialize(ser.serialize(root))

Construct Binary Tree from String

Screenshot 2021-11-27 at 11.50.38.png

Screenshot 2021-11-27 at 11.51.39.png

Screenshot 2021-11-27 at 11.52.13.png

Screenshot 2021-11-27 at 11.52.53.png

Screenshot 2021-11-27 at 11.53.24.png

Screenshot 2021-11-27 at 11.54.03.png

Screenshot 2021-11-27 at 11.54.41.png

Screenshot 2021-11-27 at 11.54.59.png

Screenshot 2021-11-27 at 11.55.35.png

Screenshot 2021-11-27 at 11.56.58.png

Screenshot 2021-11-27 at 11.57.33.png

Screenshot 2021-11-27 at 11.57.57.png

Screenshot 2021-11-27 at 11.58.15.png

Screenshot 2021-11-27 at 11.58.34.png

""" 
536. Construct Binary Tree from String

You need to construct a binary tree from a string consisting of parenthesis and integers.
The whole input represents a binary tree. It contains an integer followed by zero, one or two pairs of parenthesis.
The integer represents the root's value and a pair of parenthesis contains a child binary tree with the same structure.
You always start to construct the left child node of the parent first if it exists.

https://leetcode.com/problems/construct-binary-tree-from-string
"""

""" 
"4( 2( 3) ( 1) ) (6(5))"

- tree startes at number
- new opening bracket means new subtree
- unclosable closing brackets means we return

- record number as value then idx + 1
- left: if opening bracket, start new tree at idx + 1
    - skip closing bracket move idx += 1
- right: if opening bracket, start new tree at idx + 1
     - skip closing bracket move idx += 1
- else:
    return 

"""

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Solution:
    def str2tree(self, s: str):

        idx = 0

        def build_tree():
            nonlocal idx
            # base cases
            if idx >= len(s):
                return None

            start_idx = idx
            # get number
            while idx < len(s) and (s[idx].isnumeric() or s[idx] == '-'):
                idx += 1
            node = TreeNode(s[start_idx:idx])

            # subtrees
            if idx < len(s) and s[idx] == "(":
                idx += 1
                node.left = build_tree()
                idx += 1

            if idx < len(s) and s[idx] == "(":
                idx += 1
                node.right = build_tree()
                idx += 1

            return node

        return build_tree()

Flatten Binary Tree to Linked List **

Screenshot 2021-10-09 at 06.59.22.png

Screenshot 2021-10-09 at 06.59.49.png

Solution 1

Screenshot 2021-10-09 at 07.04.47.png

Screenshot 2021-10-09 at 07.02.09.png

Screenshot 2021-10-09 at 07.02.36.png

Screenshot 2021-10-09 at 07.02.56.png

Screenshot 2021-10-09 at 07.03.12.png

Screenshot 2021-10-09 at 07.01.34.png

# Definition for a binary tree node.
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Solution_:
    def flatten(self, root):
        if not root:
            return None

        right = root.right

        if root.left:
            # place the left subtree between the root & root.right
            root.right = root.left
            left_ending = self.flatten(root.left)
            left_ending.right = right

            # remove left
            root.left = None

        furthest = self.flatten(root.right)

        return furthest or root

"""
our algorithm will return the tail node of the flattened out tree.

For a given node, we will recursively flatten out the left and the right subtrees 
    and store their corresponding tail nodes in left_ending and right_ending respectively.

Next, we will make the following connections 
(only if there is a left child for the current node, else the left_ending would be null)
(Place the left subtree between the root & root.right)
    left_ending.right = node.right
    node.right = node.left
    node.left = None

Next we have to return the tail of the final, flattened out tree rooted at node. 
So, if the node has a right child, then we will return the right_ending, else, we'll return the left_ending
"""

class Solution:
    def flatten(self, root):
        if not root:
            return None

        left_ending = self.flatten(root.left)
        right_ending = self.flatten(root.right)

        # If there was a left subtree, we shuffle the connections
        #   around so that there is nothing on the left side anymore.
        if left_ending:
            # Place the left subtree between the root & root.right
            left_ending.right = root.right
            root.right = root.left
            # Remove left
            root.left = None

        # We need to return the "rightmost" node after we are done wiring the new connections.
        # 2. For a node with only a left subtree, the rightmost node will be left_ending because it has been moved to the right subtree
        # 3. For a leaf node, we simply return the node
        return right_ending or left_ending or root

Solution 2

Screenshot 2021-10-09 at 07.06.16.png

class Solution:
    def flatten(self, root):
        if not root:
            return None

        stack = [root]

        while stack:
            node = stack.pop()

            if node.right:
                stack.append(node.right)
            if node.left:
                stack.append(node.left)

            node.left = None
            if stack:
                node.right = stack[-1]  # Peek

Approach 3: O(1) Iterative Solution (Greedy & similar to Morris Traversal)

similar to Morris Traversal

Screenshot 2021-10-09 at 07.25.23.png

Screenshot 2021-10-09 at 07.28.07.png

Screenshot 2021-10-09 at 07.29.18.png

Screenshot 2021-10-09 at 07.29.42.png

Screenshot 2021-10-09 at 07.30.24.png

Screenshot 2021-10-09 at 07.31.43.png

Screenshot 2021-10-09 at 07.32.03.png

Screenshot 2021-10-09 at 07.32.25.png

Screenshot 2021-10-09 at 07.32.57.png

""" 
O(1) Iterative Solution (Greedy & similar to Morris Traversal)
"""

class Solution:
    def flatten(self, root):
        if not root:
            return None

        curr = root
        while curr:

            # If there was a left subtree, we shuffle the connections
            #   around so that there is nothing on the left side anymore.
            if curr.left:
                l_right_most = self.find_right_most(curr.left)

                # place the left subtree between the root & root.right
                l_right_most.right = curr.right
                curr.right = curr.left

                # remove left
                curr.left = None

            curr = curr.right

    def find_right_most(self, root):
        curr = root
        while curr.right:
            curr = curr.right
        return curr

Binary Search Trees

General

Examples:

Implementation

# Binary Search Tree Implementation in Python
# Blog post: https://emre.me/data-structures/binary-search-trees/

class Node:
    def __init__(self, key, val, left=None, right=None, parent=None):
        self.key = key
        self.payload = val
        self.leftChild = left
        self.rightChild = right
        self.parent = parent

    def has_left_child(self):
        return self.leftChild

    def has_right_child(self):
        return self.rightChild

    def is_left_child(self):
        return self.parent and self.parent.leftChild == self

    def is_right_child(self):
        return self.parent and self.parent.rightChild == self

    def is_root(self):
        return not self.parent

    def is_leaf(self):
        return not (self.rightChild or self.leftChild)

    def has_any_children(self):
        return self.rightChild or self.leftChild

    def has_both_children(self):
        return self.rightChild and self.leftChild

    def splice_out(self):
        if self.is_leaf():
            if self.is_left_child():
                self.parent.leftChild = None
            else:
                self.parent.rightChild = None
        elif self.has_any_children():
            if self.has_left_child():
                if self.is_left_child():
                    self.parent.leftChild = self.leftChild
                else:
                    self.parent.rightChild = self.leftChild
                self.leftChild.parent = self.parent
            else:
                if self.is_left_child():
                    self.parent.leftChild = self.rightChild
                else:
                    self.parent.rightChild = self.rightChild
                self.rightChild.parent = self.parent

    def find_successor(self):
        successor = None
        if self.has_right_child():
            successor = self.rightChild.find_min()
        else:
            if self.parent:
                if self.is_left_child():
                    successor = self.parent
                else:
                    self.parent.rightChild = None
                    successor = self.parent.find_successor()
                    self.parent.rightChild = self
        return successor

    def find_min(self):
        current = self
        while current.has_left_child():
            current = current.leftChild
        return current

    def replace_node_data(self, key, value, lc, rc):
        self.key = key
        self.payload = value
        self.leftChild = lc
        self.rightChild = rc
        if self.has_left_child():
            self.leftChild.parent = self
        if self.has_right_child():
            self.rightChild.parent = self

class BinarySearchTree:

    def __init__(self):
        self.root = None
        self.size = 0

    def length(self):
        return self.size

    def __len__(self):
        return self.size

    def put(self, key, val):
        if self.root:
            self._put(key, val, self.root)
        else:
            self.root = Node(key, val)
        self.size = self.size + 1

    def _put(self, key, val, current_node):
        if key < current_node.key:
            if current_node.has_left_child():
                self._put(key, val, current_node.leftChild)
            else:
                current_node.leftChild = Node(key, val, parent=current_node)
        else:
            if current_node.has_right_child():
                self._put(key, val, current_node.rightChild)
            else:
                current_node.rightChild = Node(key, val, parent=current_node)

    def __setitem__(self, k, v):
        self.put(k, v)

    def get(self, key):
        if self.root:
            res = self._get(key, self.root)
            if res:
                return res.payload
            else:
                return None
        else:
            return None

    def _get(self, key, current_node):
        if not current_node:
            return None
        elif current_node.key == key:
            return current_node
        elif key < current_node.key:
            return self._get(key, current_node.leftChild)
        else:
            return self._get(key, current_node.rightChild)

    def __getitem__(self, key):
        return self.get(key)

    def __contains__(self, key):
        if self._get(key, self.root):
            return True
        else:
            return False

    def delete(self, key):
        if self.size > 1:
            node_to_remove = self._get(key, self.root)
            if node_to_remove:
                self.remove(node_to_remove)
                self.size = self.size - 1
            else:
                raise KeyError('Error, key not in tree')
        elif self.size == 1 and self.root.key == key:
            self.root = None
            self.size = self.size - 1
        else:
            raise KeyError('Error, key not in tree')

    def __delitem__(self, key):
        self.delete(key)

    def remove(self, current_node):
        if current_node.is_leaf():  # leaf
            if current_node == current_node.parent.leftChild:
                current_node.parent.leftChild = None
            else:
                current_node.parent.rightChild = None
        elif current_node.has_both_children():  # interior
            successor = current_node.find_successor()
            successor.splice_out()
            current_node.key = successor.key
            current_node.payload = successor.payload

        else:  # this node has one child
            if current_node.has_left_child():
                if current_node.is_left_child():
                    current_node.leftChild.parent = current_node.parent
                    current_node.parent.leftChild = current_node.leftChild
                elif current_node.is_right_child():
                    current_node.leftChild.parent = current_node.parent
                    current_node.parent.rightChild = current_node.leftChild
                else:
                    current_node.replace_node_data(current_node.leftChild.key,
                                                   current_node.leftChild.payload,
                                                   current_node.leftChild.leftChild,
                                                   current_node.leftChild.rightChild)
            else:
                if current_node.is_left_child():
                    current_node.rightChild.parent = current_node.parent
                    current_node.parent.leftChild = current_node.rightChild
                elif current_node.is_right_child():
                    current_node.rightChild.parent = current_node.parent
                    current_node.parent.rightChild = current_node.rightChild
                else:
                    current_node.replace_node_data(current_node.rightChild.key,
                                                   current_node.rightChild.payload,
                                                   current_node.rightChild.leftChild,
                                                   current_node.rightChild.rightChild)

Find Kth Largest Value In BST

"""
Find Kth Largest Value In BST:

Write a function that takes in a Binary Search Tree (BST) and a positive integer k and returns the kth largest integer contained in the BST.
You can assume that there will only be integer values in the BST and that k is less than or equal to the number of nodes in the tree.
Also, for the purpose of this question, duplicate integers will be treated as distinct values.
In other words, the second largest value in a BST containing values {5, 7, 7} will be 7—not 5.
Each BST node has an integer value, a left child node, and a right child node.
A node is said to be a valid BST node if and only if it satisfies the BST property: 
    its value is strictly greater than the values of every node to its left; its value is less than or equal to the values of every node to its right;
     and its children nodes are either valid BST nodes themselves or None / null.
Sample Input
    tree =   15
        /     \
        5      20
        /   \   /   \
    2     5 17   22
    /   \         
    1     3       
    k = 3
Sample Output
    17
https://www.algoexpert.io/questions/Find%20Kth%20Largest%20Value%20In%20BST
"""

# This is an input class. Do not edit.
class BST:
    def __init__(self, value, left=None, right=None):
        self.value = value
        self.left = left
        self.right = right

class TreeInfo:
    def __init__(self, visits_remaining):
        self.visits_remaining = visits_remaining
        self.last_visited = None

# O(h + k) time | O(h) space - where h is the height of the tree and k is the input parameter
#   we have to go to the largest element, at the furthest/deepest right (h) first before looking for k
def findKthLargestValueInBst(tree, k):
    tree_info = TreeInfo(k)
    reverseInOrderTraverse(tree, tree_info)
    return tree_info.last_visited.value

def reverseInOrderTraverse(tree, tree_info):
    if not tree:
        return

    reverseInOrderTraverse(tree.right, tree_info)
    # # visit node
    # tree_info was updated in the above function call
    if tree_info.visits_remaining > 0:
        tree_info.visits_remaining -= 1
        tree_info.last_visited = tree
    else:
        return
    reverseInOrderTraverse(tree.left, tree_info)

Reconstruct Binary Search Tree from Preorder Traversal with Less than, greater than patterns

"""
Construct Binary Search Tree from Preorder Traversal:

Return the root node of a binary search tree that matches the given preorder traversal.
(Recall that a binary search tree is a binary tree where for every node, any descendant of node.left has a value < node.val,
 and any descendant of node.right has a value > node.val.  Also recall that a preorder traversal displays the value of the node first,
 then traverses node.left, then traverses node.right.)
It's guaranteed that for the given test cases there is always possible to find a binary search tree with the given requirements.

https://leetcode.com/problems/construct-binary-search-tree-from-preorder-traversal/
"""
"""
Reconstruct BST:

The pre-order traversal of a Binary Tree is a traversal technique that starts at the tree's root node and visits nodes in the following order:
    Current node
    Left subtree
    Right subtree
Given a non-empty array of integers representing the pre-order traversal of a Binary Search Tree (BST),
    write a function that creates the relevant BST and returns its root node.
The input array will contain the values of BST nodes in the order in which these nodes would be visited with a pre-order traversal.
Each BST node has an integer value, a left child node, and a right child node.
A node is said to be a valid BST node if and only if it satisfies the BST property: 
    its value is strictly greater than the values of every node to its left;
    its value is less than or equal to the values of every node to its right;
    and its children nodes are either valid BST nodes themselves or None / null.
Sample Input
    preOrderTraversalValues = [10, 4, 2, 1, 5, 17, 19, 18]
Sample Output
            10 
        /    \
        4      17
    /   \      \
    2     5     19
    /           /
    1           18 
https://www.algoexpert.io/questions/Reconstruct%20BST
"""

from typing import List
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

"""
use pointers to keep track of valid values for each subtree
"""

class SolutionBF:
    def bstFromPreorderHelper(self, preorder, start, end):
        if start > end:
            return None
        if start == end:
            return TreeNode(preorder[start])

        node = TreeNode(preorder[start])

        left_start = start + 1
        left_end = left_start
        while left_end <= end and preorder[left_end] < preorder[start]:
            left_end += 1
        left_end -= 1  # last valid value

        node.left = self.bstFromPreorderHelper(preorder, left_start, left_end)
        node.right = self.bstFromPreorderHelper(preorder, left_end+1, end)

        return node

    def bstFromPreorder(self, preorder):
        return self.bstFromPreorderHelper(preorder, 0, len(preorder)-1)

# ----------------------------------------------------------------------------------------------------------------------

"""
We will start by creating the root node while keeping track of the max and min values at any time:
- if value is less than node & greater than min: pass ot to left
- if value is greater than node & less than max: pass to right

Then proceed to the left: passing the max to be the root's value & min to be -inf
                   right: passing the min to be thr root's value & max to be inf


"""

"""
Sample Input
    preOrderTraversalValues = [10, 4, 2, 1, 5, 17, 16, 19, 18]
Sample Output
        10 
      /    \
     4      17 
   /   \   /  \
  2     5 16  19
 /           /
1           18 

keep track of the largest and smallest node that can be placed
left -> pass current node as largest
right -> pass curr node as smallest

if it does not satisfy the constraints we go back up the tree till where it will match
else, insert it

"""

class Solution:
    def bstFromPreorder(self, preorder: List[int]):
        # if not preorder
        return self.bstFromPreorderHelper(preorder, [0], float('-inf'), float('inf'))

    def bstFromPreorderHelper(self, preorder, curr, minimum, maximum):
        if curr[0] >= len(preorder):  # validate curr position on preoder array
            return None

        value = preorder[curr[0]]  # get value from preoder array
        if value < minimum or value > maximum:  # check whether it can be added
            return None

        node = TreeNode(value)  # create Node

        # add left and right
        curr[0] = curr[0] + 1  # move pointer forward
        node.left = self.bstFromPreorderHelper(preorder, curr, minimum, value)
        node.right = self.bstFromPreorderHelper(preorder, curr, value, maximum)

        return node

Same BSTs *

"""
Same BSTs:

An array of integers is said to represent the Binary Search Tree (BST) obtained by inserting each integer in the array, from left to right, into the BST.
Write a function that takes in two arrays of integers and determines whether these arrays represent the same BST. Note that you're not allowed to construct any BSTs in your code.
A BST is a Binary Tree that consists only of BST nodes. 
A node is said to be a valid BST node if and only if it satisfies the BST property:
 its value is strictly greater than the values of every node to its left;
 its value is less than or equal to the values of every node to its right; 
 and its children nodes are either valid BST nodes themselves or None / null.

Sample Input
    arrayOne = [10, 15, 8, 12, 94, 81, 5, 2, 11]
    arrayTwo = [10, 8, 5, 15, 2, 12, 11, 94, 81]
Sample Output
    true // both arrays represent the BST below
            10
        /     \
        8      15
      /       /   \
    5        12     94
    /       /     /
    2       11    81

https://www.algoexpert.io/questions/Same%20BSTs 
"""

# O(n^2) time | O(n^2) space - where n is the number of nodes in each array, respectively
def sameBsts(arrayOne, arrayTwo):
    return sameBstsHelper(arrayOne, arrayTwo)

def sameBstsHelper(arrayOne, arrayTwo):
    # must be same length
    if len(arrayOne) != len(arrayTwo):
        return False

    # we didn't find anything wrong
    if len(arrayOne) == 0:  # any -> arrayOne/arrayTwo
        return True

    # must have same head
    if arrayOne[0] != arrayTwo[0]:
        return False

    # # split into right and left
    # elements larger or equal to than idx 0
    right_one = []
    right_two = []
    # elements smaller than idx 0
    left_one = []
    left_two = []
    for idx in range(1, len(arrayOne)):  # any -> arrayOne/arrayTwo

        # one
        if arrayOne[idx] < arrayOne[0]:
            left_one.append(arrayOne[idx])
        else:
            right_one.append(arrayOne[idx])

        # two
        if arrayTwo[idx] < arrayTwo[0]:
            left_two.append(arrayTwo[idx])
        else:
            right_two.append(arrayTwo[idx])

    left = sameBstsHelper(left_one, left_two)
    right = sameBstsHelper(right_one, right_two)

    return left and right

"""
# ----------------------------------------------------------------------------------------------------------------------

# check roots
- `build bst `(find all the roots at every point in the tree) and validate that they are same
"""

# O(n^2) time | O(d) space
# where n is the number of nodes in each array, respectively,
# and d is the depth of the BST that they represent
def sameBsts(array_one, array_two):
    return buildTrees(array_one, array_two, 0, 0, float('-inf'), float('inf'))

def buildTrees(array_one, array_two, idx_one, idx_two, minimum, maximum):
    # no extra elements to add (reached end)
    if idx_one == None or idx_two == None:
        return idx_one == idx_two

    # validate roots (roots should be same)
    if array_one[idx_one] != array_two[idx_two]:
        return False
    curr = array_one[idx_one]

    left_one = findNextValidSmaller(array_one, idx_one, minimum)
    left_two = findNextValidSmaller(array_two, idx_two, minimum)
    right_one = findNextValidLargerOrEqual(array_one, idx_one, maximum)
    right_two = findNextValidLargerOrEqual(array_two, idx_two, maximum)

    left = buildTrees(
        # the curr is the largest there will ever be
        array_one, array_two, left_one, left_two, minimum, curr)
    right = buildTrees(
        # curr is the smallest
        array_one, array_two, right_one, right_two, curr, maximum)

    return left and right

def findNextValidSmaller(array, starting_idx, running_minimum):
    # used to find the next left root
    # Find the index of the first smaller value after the startingIdx.
    # Make sure that this value is greater than or equal to the minVal,
    # which is the value of the previous parent node in the BST.
    # If it isn't, then that value is located in the left subtree of the
    # previous parent node.
    for idx in range(starting_idx + 1, len(array)):
        if array[idx] < array[starting_idx] and array[idx] >= running_minimum:
            return idx
    return None

def findNextValidLargerOrEqual(array, starting_idx, running_maximum):
    # used to find the next right root
    # Find the index of the first bigger/equal value after the startingIdx.
    # Make sure that this value is smaller than maxVal, which is the value
    # of the previous parent node in the BST.
    # If it isn't, then that value is located in the right subtree of the previous parent node.
    for idx in range(starting_idx + 1, len(array)):
        if array[idx] >= array[starting_idx] and array[idx] < running_maximum:
            return idx
    return None

Serialize and Deserialize BST *

Screenshot 2021-11-02 at 13.47.27.png

""" 
Serialize and Deserialize BST

Serialization is converting a data structure or object into a sequence of bits so that it can be stored in a file 
    or memory buffer, or transmitted across a network connection link to be reconstructed later in the same or another computer environment.
Design an algorithm to serialize and deserialize a binary search tree. 
There is no restriction on how your serialization/deserialization algorithm should work. 
You need to ensure that a binary search tree can be serialized to a string, and this string can be deserialized to the original tree structure.
The encoded string should be as compact as possible.

Example 1:
    Input: root = [2,1,3]
    Output: [2,1,3]
Example 2:
    Input: root = []
    Output: []

After this:
- https://leetcode.com/problems/serialize-and-deserialize-binary-tree

https://leetcode.com/problems/serialize-and-deserialize-bst
"""

""" 
Alternative solutions:
-  using preorder traversal (here we use postorder) https://leetcode.com/problems/construct-binary-search-tree-from-preorder-traversal
"""

# Definition for a binary tree node.
class TreeNode:
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None

class Codec:
    def serialize(self, root):
        """
        Encodes a tree to a single postorder string.
        """
        postorder_result = []

        def postorder(node):
            if not node:
                return
            postorder(node.left)
            postorder(node.right)
            postorder_result.append(node.val)

        postorder(root)
        return ' '.join(map(str,  postorder_result))

    def deserialize(self, data):
        """
        Decodes your encoded data to tree.
        """
        def reverse_postorder(lower, upper):
            """ 
            Reverse of postorder: postorder is `lrn`, here we do `nrl`
            """
            if not data:
                return None
            if data[-1] < lower or data[-1] > upper:
                return None

            node = TreeNode(data.pop())
            node.right = reverse_postorder(node.val, upper)
            node.left = reverse_postorder(lower, node.val)

            return node

        data = [int(x) for x in data.split(' ') if x]
        return reverse_postorder(float('-inf'), float('inf'))

# Your Codec object will be instantiated and called as such:
# Your Codec object will be instantiated and called as such:
# ser = Codec()
# deser = Codec()
# tree = ser.serialize(root)
# ans = deser.deserialize(tree)
# return ans

Validate Binary Search Tree (with Less than, greater than patterns)

"""
Validate Binary Search Tree

Given a binary tree, determine if it is a valid binary search tree (BST).
Assume a BST is defined as follows:
The left subtree of a node contains only nodes with keys less than the node's key.
The right subtree of a node contains only nodes with keys greater than the node's key.
Both the left and right subtrees must also be binary search trees.

Example 1:

    2
    / \
    1   3

    Input: [2,1,3]
    Output: true

Example 2:

    5
    / \
    1   4
        / \
        3   6

    Input: [5,1,4,null,null,3,6]
    Output: false
    Explanation: The root node's value is 5 but its right child's value is 4.

https://leetcode.com/problems/validate-binary-search-tree/
"""

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right

#  O(n) time | O(d) space | where d is the depth of the tree (because of the callstack)
def validateBst(node, maximum=float('inf'), minimum=float('-inf')):
    if node is None:
        return True  # we didn't find an invalid node

    if node.value >= maximum or node.value < minimum:  # validate with max & min
        return False

    # for every left child, it's maximum will be the value of it's parent and
    # for every right child, it's minimum will be the value of it's parent
    return validateBst(node.left, maximum=node.value, minimum=minimum) \
        and validateBst(node.right, maximum=maximum, minimum=node.value)

Min Height BST

"""
Min Height BST:
Write a function that takes in a non-empty sorted array of distinct integers, constructs a BST from the integers, and returns the root of the BST.
The function should minimize the height of the BST.
You've been provided with a BST class that you'll have to use to construct the BST.
Each BST node has an integer value, a left child node, and a right child node.
A node is said to be a valid BST node if and only if it satisfies the BST property:
 its value is strictly greater than the values of every node to its left; its value is less than or equal to the values of every node to its right;
  and its children nodes are either valid BST nodes themselves or None / null.
A BST is valid if and only if all of its nodes are valid BST nodes.
Note that the BST class already has an insert method which you can use if you want.

Sample Input
array = [1, 2, 5, 7, 10, 13, 14, 15, 22]
Sample Output
         10
       /     \
      2      14
    /   \   /   \
   1     5 13   15
          \       \
           7      22
// This is one example of a BST with min height
// that you could create from the input array.
// You could create other BSTs with min height
// from the same array; for example:
         10
       /     \
      5      15
    /   \   /   \
   2     7 13   22
 /           \
1            14
https://www.algoexpert.io/questions/Min%20Height%20BST
"""

# ----------------------------------------------------------------------------------------------------------------------

# O(nlog(n)) time | O(n) space - where n is the length of the array
def minHeightBst00(array):
    return minHeightBstHelper00(array, None, 0, len(array)-1)

def minHeightBstHelper00(array, node, left, right):
    if left > right:
        return None

    mid = (left+right) // 2

    if node is None:
        node = BST(array[mid])
    else:
        node.insert(array[mid])

    minHeightBstHelper00(array, node, left, mid-1)  # left
    minHeightBstHelper00(array, node, mid+1, right)  # right

    return node

# ----------------------------------------------------------------------------------------------------------------------

# O(n) time | O(n) space - where n is the length of the array
def minHeightBst01(array):
    return minHeightBstHelper01(array, 0, len(array)-1)

def minHeightBstHelper01(array, left, right):
    if left > right:
        return None

    mid = (left+right) // 2

    node = BST(array[mid])
    node.left = minHeightBstHelper01(array, left, mid-1)
    node.right = minHeightBstHelper01(array, mid+1, right)

    return node

"""
Sample Input
array = [1, 2, 5, 7, 10, 13, 14, 15, 22]
Sample Output
         10
       /     \
      2      14
    /   \   /   \
   1     5 13   15
          \       \
           7      22
// This is one example of a BST with min height
// that you could create from the input array.
// You could create other BSTs with min height
// from the same array; for example:
         10
       /     \
      5      15
    /   \   /   \
   2     7 13   22
 /           \
1            14

                [1, 2, 5, 7, 10, 13, 14, 15, 22]->10
            [1, 2, 5, 7]->2                      [13, 14, 15, 22]->
        [1]->1    [5, 7]->5   
                    [7][7]->7
"""

Balance a Binary Search Tree

""" 
1382. Balance a Binary Search Tree

Given the root of a binary search tree, return a balanced binary search tree with the same node values. 
If there is more than one answer, return any of them.
A binary search tree is balanced if the depth of the two subtrees of every node never differs by more than 1.

https://leetcode.com/problems/balance-a-binary-search-tree

similar to Min Height BST
"""

# Definition for a binary tree node.
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

""" 
1. convert tree to sorted array using inorder traversal
2. build the tree from the sorted array
    - the root will be the middle of the array
    - the left of the middle will be passed to a recursive function to build the left children
    - the right of the middle will be passed to a recursive function to build the right children

"""

class Solution:
    def balanceBST(self, root: TreeNode):
        array = []
        self.inOrderTraverse(root, array)
        return self.buildTree(array, 0, len(array)-1)

    def buildTree(self, array, start, end):
        if start > end:
            return None

        mid = (start+end) // 2

        curr = array[mid]
        curr.left = self.buildTree(array, start, mid-1)
        curr.right = self.buildTree(array, mid+1, end)

        return curr

    def inOrderTraverse(self, root, array):
        stack = []
        curr = root
        while curr or stack:
            # if has a left child, move left
            while curr and curr.left:
                stack.append(curr)
                curr = curr.left

            # curr is either the left most value or None
            # if none take the left-most from the top of stack
            if curr is None:
                curr = stack.pop()

            array.append(curr)
            # we are at the left most value so the only possible next place to go is right
            curr = curr.right

Lowest Common Ancestor of a Binary Search Tree *

Screenshot 2021-10-08 at 12.21.29.png

"""
Lowest Common Ancestor of a Binary Search Tree:

Given a binary search tree (BST), find the lowest common ancestor (LCA) of two given nodes in the BST.
According to the definition of LCA on Wikipedia: 
“The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants
 (where we allow a node to be a descendant of itself).”
https://leetcode.com/problems/lowest-common-ancestor-of-a-binary-search-tree/
"""

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def lowestCommonAncestor(self, root, p, q):
        curr = root

        while True:
            if curr.val < p.val and curr.val < q.val:
                curr = curr.right

            elif curr.val > p.val and curr.val > q.val:
                curr = curr.left

            else:
                break

        return curr

"""
First Approach:
- take advantage of BST's properties: skip all valid ancestors
"""

Find Closest Value In BST

"""
Find Closest Value In BST:

Write a function that takes in a Binary Search Tree (BST) and
 a target integer value and returns the closest value to that target value contained in the BST.
You can assume that there will only be one closest value.
Each BST node has an integer value, a left child node, and a right child node.
A node is said to be a valid BST node if and only if it satisfies the BST property:
 its value is strictly greater than the values of every node to its left; its value is less than or
  equal to the values of every node to its right; and its children nodes are either valid BST nodes themselves or None / null.

https://www.algoexpert.io/questions/Find%20Closest%20Value%20In%20BST
"""

# This is the class of the input tree. Do not edit.
class BST:
    def __init__(self, value):
        self.value = value
        self.left = None
        self.right = None

# O(log(n)) time | O(1) space
# worst: O(n) time | O(1) space -> tree with one branch
def findClosestValueInBst(tree, target):
    curr = tree
    closest = float('inf')

    while curr is not None:

        # update closest
        if abs(curr.value-target) < abs(closest-target):
            closest = curr.value

        # move downwards
        if curr.left is None or (curr.right is not None and target >= curr.value):
            # target >= node.value: every value to the left will be further away from that target than the node.value
            curr = curr.right
        else:
            # target < node.value: every value to the right will be further away from that target than the node.value
            curr = curr.left

    return closest

"""
Sample Input
tree =   10
       /     \
      5      15
    /   \   /   \
   2     5 13   22
 /           \
1            14
    target = 12

t = 12
    11
   / \
10    20

Sample Output
    13

# Input: tree & target
# Output: closest(int)

# # First Approach:
start at head
# at every node:
    - update closest value
    - target >= node.value: every value to the left will be further away from that target than the node.value
        - move to the right
    - target < node.value: every value to the right will be further away from that target than the node.value
        - move to the left
"""

# Average: O(log(n)) time | O(1) space
# Worst: O(n) time | O(1) space
def findClosestValueInBst2(tree, target):
    closest = float('inf')
    curr = tree

    while curr is not None:

        # # update closest
        if abs(curr.value - target) < abs(closest - target):
            closest = curr.value

        # # move on to next node

        if curr.value == target:
            break  # no need to go on
        elif curr.value < target:
            # 05:55
            # because the curr node's value is less than the target,
            #   all values to the left of curr will be futher away from the target (BST property -> are less then curr)
            curr = curr.right
        else:
            # curr node's value is greater than the target, all values to the right of curr,
            #  will be further away from target as they are larger than curr
            curr = curr.left

    return closest

Inorder Successor in BST

Screenshot 2021-10-05 at 10.50.47.png

Screenshot 2021-10-05 at 10.51.39.png

Screenshot 2021-10-05 at 10.51.57.png

Screenshot 2021-10-05 at 10.52.16.png

""" 
Inorder Successor in BST:
FIND THE FIRST KEY GREATER THAN A GIVEN VALUE IN A BST:

Given the root of a binary search tree and a node p in it, return the in-order successor of that node in the BST. 
If the given node has no in-order successor in the tree, return null.

The successor of a node p is the node with the smallest key greater than p.val.

https://leetcode.com/problems/inorder-successor-in-bst
epi 14.2
"""

# Definition for a binary tree node.
class TreeNode:
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None

class Solution:
    def inorderSuccessor(self, root: 'TreeNode', p: 'TreeNode'):
        nxt = None

        curr = root
        while curr is not None:
                          # successor will be the next larger value compared to the element
            if curr.val > p.val:
                nxt = curr
                # try to reduce the value
                curr = curr.left
            else:
                # try to increase the value
                curr = curr.right

        return nxt

Inorder Successor in BST II

Example 1:

https://camo.githubusercontent.com/c516e4fd7889308d123f51537c2892bdfba09cafa68775b01f0f82b00892de64/68747470733a2f2f6173736574732e6c656574636f64652e636f6d2f75706c6f6164732f323031392f30312f32332f3238355f6578616d706c655f312e504e47

Input: tree = [2,1,3], node = 1
Output: 2
Explanation: 1's in-order successor node is 2. Note that both the node and the return value is of Node type.

Example 2:

https://camo.githubusercontent.com/99e689e63ae1e3a208844a949e1529dbbd9b4204c64dd6ff88af27aee0c8946f/68747470733a2f2f6173736574732e6c656574636f64652e636f6d2f75706c6f6164732f323031392f30312f32332f3238355f6578616d706c655f322e504e47

Input: tree = [5,3,6,2,4,null,null,1], node = 6
Output: null
Explanation: There is no in-order successor of the current node, so the answer is null.

Example 3:

https://camo.githubusercontent.com/dc36f2d972da5a61aa3e91c1ede841a46f21d21851c546dacd020236814dd01c/68747470733a2f2f6173736574732e6c656574636f64652e636f6d2f75706c6f6164732f323031392f30322f30322f3238355f6578616d706c655f33342e504e47

Input: tree = [15,6,18,3,7,17,20,2,4,null,13,null,null,null,null,null,null,null,null,9], node = 15
Output: 17

Example 4:

https://camo.githubusercontent.com/dc36f2d972da5a61aa3e91c1ede841a46f21d21851c546dacd020236814dd01c/68747470733a2f2f6173736574732e6c656574636f64652e636f6d2f75706c6f6164732f323031392f30322f30322f3238355f6578616d706c655f33342e504e47

Input: tree = [15,6,18,3,7,17,20,2,4,null,13,null,null,null,null,null,null,null,null,9], node = 13
Output: 15

Example 5:

Input: tree = [0], node = 0
Output: null

Screenshot 2021-10-07 at 06.08.39.png

Screenshot 2021-10-07 at 06.09.03.png

Screenshot 2021-10-07 at 06.09.29.png

""" 
510. Inorder Successor in BST II

Given a node in a binary search tree, return the in-order successor of that node in the BST. 
If that node has no in-order successor, return null.

The successor of a node is the node with the smallest key greater than node.val.

You will have direct access to the node but not to the root of the tree. 
Each node will have a reference to its parent node. Below is the definition for Node:
    class Node {
        public int val;
        public Node left;
        public Node right;
        public Node parent;
    }

"""

""" 
Node has a right child, and hence its successor is somewhere lower in the tree. 
To find the successor, go to the right once and then as many times to the left as you could.

Node has no right child, then its successor is somewhere upper in the tree. 
To find the successor, go up till the node that is left child of its parent. The answer is the parent. 
Beware that there could be no successor (= null successor) in such a situation.
"""

# Definition for a Node.
class Node:
    def __init__(self, val):
        self.val = val
        self.left = None
        self.right = None
        self.parent = None

class Solution:
    def inorderSuccessor(self, node):
        curr = node

        if curr.right:
            # get left most child in right subtree
            curr = curr.right
            while curr and curr.left:
                curr = curr.left
            return curr

        else:
            # find where the tree last branched left
            while curr:
                if curr.parent and curr.parent.left == curr:
                    return curr.parent
                curr = curr.parent

        return None

Binary Search Tree Iterator

Screenshot 2021-10-23 at 13.34.15.png

"""
Binary Search Tree Iterator:

Implement the BSTIterator class that represents an iterator over the in-order traversal of a binary search tree (BST):
BSTIterator(TreeNode root) Initializes an object of the BSTIterator class. 
The root of the BST is given as part of the constructor. The pointer should be initialized to a non-existent number smaller than any element in the BST.
boolean hasNext() Returns true if there exists a number in the traversal to the right of the pointer, otherwise returns false.
int next() Moves the pointer to the right, then returns the number at the pointer.
Notice that by initializing the pointer to a non-existent smallest number, the first call to next() will return the smallest element in the BST.
You may assume that next() calls will always be valid. That is, there will be at least a next number in the in-order traversal when next() is called.

Example 1:
     7
    / \
    3  15
       / \
       9  20
    Input
    ["BSTIterator", "next", "next", "hasNext", "next", "hasNext", "next", "hasNext", "next", "hasNext"]
    [[[7, 3, 15, null, null, 9, 20]], [], [], [], [], [], [], [], [], []]
Output
    [null, 3, 7, true, 9, true, 15, true, 20, false]

    Explanation
    BSTIterator bSTIterator = new BSTIterator([7, 3, 15, null, null, 9, 20]);
    bSTIterator.next();    // return 3
    bSTIterator.next();    // return 7
    bSTIterator.hasNext(); // return True
    bSTIterator.next();    // return 9
    bSTIterator.hasNext(); // return True
    bSTIterator.next();    // return 15
    bSTIterator.hasNext(); // return True
    bSTIterator.next();    // return 20
    bSTIterator.hasNext(); // return False
"""

from typing import Optional
""" 
----
Solution 1:
store the inorder traversal in an array and return them index by index

---
Solution 2:
controlled iteration

check Binary Tree Inorder Traversal (Iterative)
https://www.notion.so/paulonteri/Trees-Graphs-edc3401e06c044f29a2d714d20ffe185#8c489e8b02804929ab535f25f945a31b

[3,7,9,15,20]

"""

# Definition for a binary tree node.
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class BSTIterator:

    def __init__(self, root: Optional[TreeNode]):
        self.curr = root
        self.stack = []

    def next(self):
        # put the left most value(s) to the top of the stack
        while self.curr:
            self.stack.append(self.curr)
            self.curr = self.curr.left
        # the left-most node is at the top of the stack
        node = self.stack.pop()
        # the next (only next unvisited valid node) will be at the right
        self.curr = node.right

        return node.val

    def hasNext(self):
        return self.curr or self.stack

# Your BSTIterator object will be instantiated and called as such:
# obj = BSTIterator(root)
# param_1 = obj.next()
# param_2 = obj.hasNext()

Convert Binary Search Tree to Sorted Doubly Linked List

Screenshot 2021-09-22 at 05.45.52.png

""" 
Convert Binary Search Tree to Sorted Doubly Linked List:

Convert a Binary Search Tree to a sorted Circular Doubly-Linked List in place.
You can think of the left and right pointers as synonymous to the predecessor and successor pointers in a doubly-linked list. 
For a circular doubly linked list, the predecessor of the first element is the last element, and the successor of the last element is the first element.
We want to do the transformation in place. After the transformation, the left pointer of the tree node should point to its predecessor, 
 and the right pointer should point to its successor. You should return the pointer to the smallest element of the linked list.

            4
           / \
          2   5
         / \
        1   3


        1 2 3 4 5

https://leetcode.com/problems/convert-binary-search-tree-to-sorted-doubly-linked-list
"""

"""

            4
           / \
          2   5
         / \
        1   3


        1 2 3 4 5



prev = None
curr = 1
---
prev = 1
curr = 2

prev.right = curr
curr.left = prev

 r -->  <-- l r -->  <-- l 
1            2           3
---
prev = 2
curr = 3

2.right = 3
3.left = 2

O(tree depth), so O(n) worst case and O(log(n)) space
"""

# Definition for a Node.
class Node:
    def __init__(self, val, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class TreeInfo:
    def __init__(self):
        self.smallest = None
        self.prev = None
        self.largest = None

class Solution:
    def treeToDoublyList(self, root: 'Node'):
        tree_info = TreeInfo()
        self.in_order_traversal(root, tree_info)

        if tree_info.smallest and tree_info.largest:
            tree_info.smallest.left = tree_info.largest
            tree_info.largest.right = tree_info.smallest

        return tree_info.smallest

    def in_order_traversal(self, root, tree_info):
        if not root:
            return

        self.in_order_traversal(root.left, tree_info)

        # visit node
        if tree_info.smallest is None:  # first node
            tree_info.smallest = root
            tree_info.prev = root
            tree_info.largest = root
        else:
            # pointers
            tree_info.prev.right = root
            root.left = tree_info.prev
            # update info
            tree_info.prev = root
            tree_info.largest = root

        self.in_order_traversal(root.right, tree_info)

Delete Node in a BST

Delete Node in a BST - LeetCode

DELETE NODE IN A BST (Leetcode) - Code & Whiteboard

Binary Search Tree Removal

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right

class Solution:

    def findMinVal(self, root):
        curr = root
        while curr.left:
            curr = curr.left
        return curr

    def deleteNode(self, root: TreeNode, key: int) -> TreeNode:
        if not root:
            return None

        elif key < root.val:
            root.left = self.deleteNode(root.left, key)

        elif key > root.val:
            root.right = self.deleteNode(root.right, key)

        else:
            """
            Removal Cases:
                - No Children
                - Right Child
                - Left Child
                - Both
                    - replace with max of left or
                    - replace with min of right

            """
            if not root.right and not root.left:
                root = None

            elif not root.left:
                root = root.right

            elif not root.right:
                root = root.left

            else:
                temp = self.findMinVal(root.right)
                root.val = temp.val
                root.right = self.deleteNode(root.right, temp.val)

        return root

The Binary Search Tree (BST) is a Binary Tree with the following properties.

Keys that are less than the parent are found in the left subtree
Keys that are greater than or equal to the parent are found in the right subtree
Both the left and right subtrees must also be binary search trees.

Binary Search Tree Operations

Key lookup, insertion, and deletion take time proportional to the height of the tree, which can in worst-case be O(n), if insertions and deletions are naively implemented. However, there are implementations of insert and delete which guarantee that the tree has height O(log n). These require storing and updating additional data at the tree nodes. Red-black trees are an example of height-balanced BSTs and are widely used in data structure libraries.

When we are talking about the average case, it is the time it takes for the operation on a balanced tree, and when we are talking about the worst case, it is the time it takes for the given operation on a non-balanced tree.

These are discussed in more depth below.

Operations

Implementation

Full Implementation

Implementation

# Binary Search Tree Implementation in Python
# Blog post: https://emre.me/data-structures/binary-search-trees/

class Node:
    def __init__(self, key, val, left=None, right=None, parent=None):
        self.key = key
        self.payload = val
        self.leftChild = left
        self.rightChild = right
        self.parent = parent

    def has_left_child(self):
        return self.leftChild

    def has_right_child(self):
        return self.rightChild

    def is_left_child(self):
        return self.parent and self.parent.leftChild == self

    def is_right_child(self):
        return self.parent and self.parent.rightChild == self

    def is_root(self):
        return not self.parent

    def is_leaf(self):
        return not (self.rightChild or self.leftChild)

    def has_any_children(self):
        return self.rightChild or self.leftChild

    def has_both_children(self):
        return self.rightChild and self.leftChild

    def splice_out(self):
        if self.is_leaf():
            if self.is_left_child():
                self.parent.leftChild = None
            else:
                self.parent.rightChild = None
        elif self.has_any_children():
            if self.has_left_child():
                if self.is_left_child():
                    self.parent.leftChild = self.leftChild
                else:
                    self.parent.rightChild = self.leftChild
                self.leftChild.parent = self.parent
            else:
                if self.is_left_child():
                    self.parent.leftChild = self.rightChild
                else:
                    self.parent.rightChild = self.rightChild
                self.rightChild.parent = self.parent

    def find_successor(self):
        successor = None
        if self.has_right_child():
            successor = self.rightChild.find_min()
        else:
            if self.parent:
                if self.is_left_child():
                    successor = self.parent
                else:
                    self.parent.rightChild = None
                    successor = self.parent.find_successor()
                    self.parent.rightChild = self
        return successor

    def find_min(self):
        current = self
        while current.has_left_child():
            current = current.leftChild
        return current

    def replace_node_data(self, key, value, lc, rc):
        self.key = key
        self.payload = value
        self.leftChild = lc
        self.rightChild = rc
        if self.has_left_child():
            self.leftChild.parent = self
        if self.has_right_child():
            self.rightChild.parent = self

class BinarySearchTree:

    def __init__(self):
        self.root = None
        self.size = 0

    def length(self):
        return self.size

    def __len__(self):
        return self.size

    def put(self, key, val):
        if self.root:
            self._put(key, val, self.root)
        else:
            self.root = Node(key, val)
        self.size = self.size + 1

    def _put(self, key, val, current_node):
        if key < current_node.key:
            if current_node.has_left_child():
                self._put(key, val, current_node.leftChild)
            else:
                current_node.leftChild = Node(key, val, parent=current_node)
        else:
            if current_node.has_right_child():
                self._put(key, val, current_node.rightChild)
            else:
                current_node.rightChild = Node(key, val, parent=current_node)

    def __setitem__(self, k, v):
        self.put(k, v)

    def get(self, key):
        if self.root:
            res = self._get(key, self.root)
            if res:
                return res.payload
            else:
                return None
        else:
            return None

    def _get(self, key, current_node):
        if not current_node:
            return None
        elif current_node.key == key:
            return current_node
        elif key < current_node.key:
            return self._get(key, current_node.leftChild)
        else:
            return self._get(key, current_node.rightChild)

    def __getitem__(self, key):
        return self.get(key)

    def __contains__(self, key):
        if self._get(key, self.root):
            return True
        else:
            return False

    def delete(self, key):
        if self.size > 1:
            node_to_remove = self._get(key, self.root)
            if node_to_remove:
                self.remove(node_to_remove)
                self.size = self.size - 1
            else:
                raise KeyError('Error, key not in tree')
        elif self.size == 1 and self.root.key == key:
            self.root = None
            self.size = self.size - 1
        else:
            raise KeyError('Error, key not in tree')

    def __delitem__(self, key):
        self.delete(key)

    def remove(self, current_node):
        if current_node.is_leaf():  # leaf
            if current_node == current_node.parent.leftChild:
                current_node.parent.leftChild = None
            else:
                current_node.parent.rightChild = None
        elif current_node.has_both_children():  # interior
            successor = current_node.find_successor()
            successor.splice_out()
            current_node.key = successor.key
            current_node.payload = successor.payload

        else:  # this node has one child
            if current_node.has_left_child():
                if current_node.is_left_child():
                    current_node.leftChild.parent = current_node.parent
                    current_node.parent.leftChild = current_node.leftChild
                elif current_node.is_right_child():
                    current_node.leftChild.parent = current_node.parent
                    current_node.parent.rightChild = current_node.leftChild
                else:
                    current_node.replace_node_data(current_node.leftChild.key,
                                                   current_node.leftChild.payload,
                                                   current_node.leftChild.leftChild,
                                                   current_node.leftChild.rightChild)
            else:
                if current_node.is_left_child():
                    current_node.rightChild.parent = current_node.parent
                    current_node.parent.leftChild = current_node.rightChild
                elif current_node.is_right_child():
                    current_node.rightChild.parent = current_node.parent
                    current_node.parent.rightChild = current_node.rightChild
                else:
                    current_node.replace_node_data(current_node.rightChild.key,
                                                   current_node.rightChild.payload,
                                                   current_node.rightChild.leftChild,
                                                   current_node.rightChild.rightChild)

Insert Operation

We have a Node() and BinarySearchTree() classes, we are ready to insert elements to this BinarySearchTree() class.

We are going to implement a put(self, key, val) method. This method will check to see if the tree already has a root. If there is not a root then put() will create a new Node() and install it as the root of the tree. If a root node is already in place then put() calls the private, recursive, helper function _put() to search the tree according to the Binary Search Tree properties that we explained in the first paragraph of this article.

Code

def put(self, key, val):
    if self.root:
        self._put(key, val, self.root)
    else:
        self.root = Node(key, val)
    self.size = self.size + 1

def _put(self, key, val, current_node):
    if key < current_node.key:
        if current_node.has_left_child():
            self._put(key, val, current_node.leftChild)
        else:
            current_node.leftChild = Node(key, val, parent=current_node)
    else:
        if current_node.has_right_child():
            self._put(key, val, current_node.rightChild)
        else:
            current_node.rightChild = Node(key, val, parent=current_node)

def __setitem__(self, k, v):
    self.put(k, v)

Lookup (Search) Operation

Once the tree is constructed, the next task is to implement the retrieval of a value for a given key. The get() method is even easier than the put() method because it simply searches the tree recursively until it gets to a non-matching leaf node or finds a matching key. When a matching key is found, the value stored in the payload of the node is returned.

Code

def get(self, key):
    if self.root:
        result = self._get(key, self.root)
        if result:
            return result.payload
        else:
            return None
    else:
        return None

def _get(self, key, current_node):
    if not current_node:
        return None
    elif current_node.key == key:
        return current_node
    elif key < current_node.key:
        return self._get(key, current_node.leftChild)
    else:
        return self._get(key, current_node.rightChild)

def __getitem__(self, key):
    return self.get(key)

def __contains__(self, key):
    if self._get(key, self.root):
        return True
    else:
        return False

Delete Operation

delete() operation is the most challenging operation in the Binary Search Tree.

Screenshot 2021-11-09 at 12.46.07.png

The first task is to find the node to delete by searching the tree. If the tree has more than one node we search using the _get() method to find the Node() that needs to be removed. If the tree only has a single node, that means we are removing the root of the tree, but we still must check to make sure the key of the root matches the key that is to be deleted. In either case if the key is not found the delete() method raises an error.

Once we have found the node containing the key we want to delete, there are three cases that we must consider:

The node to be deleted has no children
The node to be deleted has only one child
The node to be deleted has two children

1. The node to be deleted has **no** children

The node to be deleted has no children

2. The node to be deleted has **only one** child

The node to be deleted has only one child

https://www.notion.so

Handling the first case is pretty easy ↑
← If a node has only a single child, then we can simply promote the child to take the place of its parent.The decision proceeds as follows:
1. If the current node is a left child then we only need to update the parent reference of the left child to point to the parent of the current node, and then update the left child reference of the parent to point to the current node’s left child.
2. If the current node is a right child then we only need to update the parent reference of the left child to point to the parent of the current node, and then update the right child reference of the parent to point to the current node’s left child.
3. If the current node has no parent, it must be the root. In this case we will just replace the key, payload, leftChild, and rightChild data by calling the replace_node_data() method on the root.
If a node has two children, we search the tree for a node that can be used to replace the one scheduled for deletion. What we need is a node that will preserve the binary search tree relationships for both of the existing left and right subtrees. The node that will do this is the node that has the next-largest key in the tree. We call this node the successor. There are three cases to consider when looking for a successor:
1. If the node has a right child, then the successor is the smallest key in the right subtree
2. If the node has no right child and is the left child of its parent, then the parent is the successor
3. If the node is the right child of its parent, and itself has no right child, then the successor to this node is the successor of its parent, excluding this node.

3. The node to be deleted has **two** children

The node to be deleted has two children

Screenshot 2021-11-09 at 12.25.04.png

Screenshot 2021-11-09 at 12.25.22.png

Screenshot 2021-11-09 at 12.23.26.png

Screenshot 2021-11-09 at 12.22.53.png

Screenshot 2021-11-09 at 12.23.11.png

Delete Node in a BST

Delete Node in a BST - LeetCode

DELETE NODE IN A BST (Leetcode) - Code & Whiteboard

Binary Search Tree Removal

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right

class Solution:

    def findMinVal(self, root):
        curr = root
        while curr.left:
            curr = curr.left
        return curr

    def deleteNode(self, root: TreeNode, key: int) -> TreeNode:
        if not root:
            return None

        elif key < root.val:
            root.left = self.deleteNode(root.left, key)

        elif key > root.val:
            root.right = self.deleteNode(root.right, key)

        else:
            """
            Removal Cases:
                - No Children
                - Right Child
                - Left Child
                - Both
                    - replace with max of left or
                    - replace with min of right

            """
            if not root.right and not root.left:
                root = None

            elif not root.left:
                root = root.right

            elif not root.right:
                root = root.left

            else:
                temp = self.findMinVal(root.right)
                root.val = temp.val
                root.right = self.deleteNode(root.right, temp.val)

        return root

Prim's Minimum Spanning Tree Algorithm

Dijkstra's Algorithm vs Prim's Algorithm

Examples

Min Cost to Connect All Points

Prim's Algorithm - Minimum Spanning Tree - Min Cost to Connect all Points - Leetcode 1584 - Python

Screenshot 2021-10-19 at 07.17.51.png

""" 
1584. Min Cost to Connect All Points

You are given an array points representing integer coordinates of some points on a 2D-plane, where points[i] = [xi, yi].
The cost of connecting two points [xi, yi] and [xj, yj] is the manhattan distance between them: |xi - xj| + |yi - yj|, where |val| denotes the absolute value of val.
Return the minimum cost to make all points connected. All points are connected if there is exactly one simple path between any two points.

Example 1:
    Input: points = [[0,0],[2,2],[3,10],[5,2],[7,0]]
    Output: 20
Explanation:
    We can connect the points as shown above to get the minimum cost of 20.
    Notice that there is a unique path between every pair of points.
Example 2:
    Input: points = [[3,12],[-2,5],[-4,1]]
    Output: 18
Example 3:
    Input: points = [[0,0],[1,1],[1,0],[-1,1]]
    Output: 4
Example 4:
    Input: points = [[-1000000,-1000000],[1000000,1000000]]
    Output: 4000000
Example 5:
    Input: points = [[0,0]]
    Output: 0

https://leetcode.com/problems/min-cost-to-connect-all-points
https://www.notion.so/paulonteri/Trees-Graphs-edc3401e06c044f29a2d714d20ffe185#2ac2c79816464704a3851de16d494dff
"""

import collections
import heapq

""" 
Prim's Minimum Spanning Tree Algorithm: https://www.notion.so/paulonteri/Trees-Graphs-edc3401e06c044f29a2d714d20ffe185#596bc798759a4edabe22a895aadeb12c
https://youtu.be/f7JOBJIC-NA
"""

class Solution_:
    def minCostConnectPoints(self, points):
        total = 0

        # # Create adjacency list
        # Will store  nodes in the form => `parent: [[cost_to_1, node_1], [cost_to_2, node_2], ...]`
        graph = collections.defaultdict(list)
        for idx in range(len(points)):
            x1, y1 = points[idx]
            for idx2 in range(idx + 1, len(points)):
                x2, y2 = points[idx2]
                cost = abs(x1 - x2) + abs(y1 - y2)

                graph[str(x1)+str(y1)].append([cost, str(x2)+str(y2)])
                graph[str(x2)+str(y2)].append([cost, str(x1)+str(y1)])

        # # Prim's Minimum Spanning Tree Algorithm
        visited = set()
        priority_queue = []
        first_node = str(points[0][0])+str(points[0][1])
        heapq.heappush(priority_queue, (0, first_node))  # start from node 0
        while len(visited) < len(graph):
            cost, node = heapq.heappop(priority_queue)
            # skip visited
            if node in visited:
                continue
            visited.add(node)

            # record cost
            total += cost
            # add neighbours
            for neighbour in graph[node]:
                if neighbour[1] not in visited:
                    heapq.heappush(priority_queue, neighbour)

        return total

class Solution:
    def minCostConnectPoints(self, points):

        total = 0

        # # Create adjacency list
        # Will use the array indices as id's
        # Will store  nodes in the form => `parent: [[cost_to_1, node_1], [cost_to_2, node_2], ...]`
        graph = collections.defaultdict(list)
        for idx in range(len(points)):
            x1, y1 = points[idx]
            for idx2 in range(idx + 1, len(points)):
                x2, y2 = points[idx2]
                cost = abs(x1 - x2) + abs(y1 - y2)

                graph[idx].append([cost, idx2])
                graph[idx2].append([cost, idx])

        # # Prim's Minimum Spanning Tree Algorithm
        visited = set()
        priority_queue = []
        heapq.heappush(priority_queue, (0, 0))  # start from node 0
        while len(visited) < len(graph):
            cost, node = heapq.heappop(priority_queue)
            # skip visited
            if node in visited:
                continue
            visited.add(node)

            # record cost
            total += cost
            # add neighbours
            for neighbour in graph[node]:
                if neighbour[1] not in visited:
                    heapq.heappush(priority_queue, neighbour)

        return total

Connecting Cities With Minimum Cost

""" 
1584. Min Cost to Connect All Points

You are given an array points representing integer coordinates of some points on a 2D-plane, where points[i] = [xi, yi].
The cost of connecting two points [xi, yi] and [xj, yj] is the manhattan distance between them: |xi - xj| + |yi - yj|, where |val| denotes the absolute value of val.
Return the minimum cost to make all points connected. All points are connected if there is exactly one simple path between any two points.

Example 1:
    Input: points = [[0,0],[2,2],[3,10],[5,2],[7,0]]
    Output: 20
Explanation:
    We can connect the points as shown above to get the minimum cost of 20.
    Notice that there is a unique path between every pair of points.
Example 2:
    Input: points = [[3,12],[-2,5],[-4,1]]
    Output: 18
Example 3:
    Input: points = [[0,0],[1,1],[1,0],[-1,1]]
    Output: 4
Example 4:
    Input: points = [[-1000000,-1000000],[1000000,1000000]]
    Output: 4000000
Example 5:
    Input: points = [[0,0]]
    Output: 0

https://leetcode.com/problems/min-cost-to-connect-all-points
https://www.notion.so/paulonteri/Trees-Graphs-edc3401e06c044f29a2d714d20ffe185#2ac2c79816464704a3851de16d494dff
"""

import collections
import heapq

""" 
Prim's Minimum Spanning Tree Algorithm: https://www.notion.so/paulonteri/Trees-Graphs-edc3401e06c044f29a2d714d20ffe185#596bc798759a4edabe22a895aadeb12c
https://youtu.be/f7JOBJIC-NA
"""

class Solution_:
    def minCostConnectPoints(self, points):
        total = 0

        # # Create adjacency list
        # Will store  nodes in the form => `parent: [[cost_to_1, node_1], [cost_to_2, node_2], ...]`
        graph = collections.defaultdict(list)
        for idx in range(len(points)):
            x1, y1 = points[idx]
            for idx2 in range(idx + 1, len(points)):
                x2, y2 = points[idx2]
                cost = abs(x1 - x2) + abs(y1 - y2)

                graph[str(x1)+str(y1)].append([cost, str(x2)+str(y2)])
                graph[str(x2)+str(y2)].append([cost, str(x1)+str(y1)])

        # # Prim's Minimum Spanning Tree Algorithm
        visited = set()
        priority_queue = []
        first_node = str(points[0][0])+str(points[0][1])
        heapq.heappush(priority_queue, (0, first_node))  # start from node 0
        while len(visited) < len(graph):
            cost, node = heapq.heappop(priority_queue)
            # skip visited
            if node in visited:
                continue
            visited.add(node)

            # record cost
            total += cost
            # add neighbours
            for neighbour in graph[node]:
                if neighbour[1] not in visited:
                    heapq.heappush(priority_queue, neighbour)

        return total

class Solution:
    def minCostConnectPoints(self, points):

        total = 0

        # # Create adjacency list
        # Will use the array indices as id's
        # Will store  nodes in the form => `parent: [[cost_to_1, node_1], [cost_to_2, node_2], ...]`
        graph = collections.defaultdict(list)
        for idx in range(len(points)):
            x1, y1 = points[idx]
            for idx2 in range(idx + 1, len(points)):
                x2, y2 = points[idx2]
                cost = abs(x1 - x2) + abs(y1 - y2)

                graph[idx].append([cost, idx2])
                graph[idx2].append([cost, idx])

        # # Prim's Minimum Spanning Tree Algorithm
        visited = set()
        priority_queue = []
        heapq.heappush(priority_queue, (0, 0))  # start from node 0
        while len(visited) < len(graph):
            cost, node = heapq.heappop(priority_queue)
            # skip visited
            if node in visited:
                continue
            visited.add(node)

            # record cost
            total += cost
            # add neighbours
            for neighbour in graph[node]:
                if neighbour[1] not in visited:
                    heapq.heappush(priority_queue, neighbour)

        return total

Minimum Spanning Tree

A minimum spanning tree (or MST for short) is a tree that spans the whole graph connecting all nodes together while minimising the total edge cost. It's important to note that your spanning tree cannot contain any cycles, otherwise it's not a tree.

Screenshot 2021-10-19 at 06.00.31.png

Screenshot 2021-10-19 at 06.00.49.png

Given a connected and undirected graph, a spanning tree of that graph is a subgraph that is a tree and connects all the vertices together. A single graph can have many different spanning trees. A minimum spanning tree (MST) or minimum weight spanning tree for a weighted, connected, undirected graph is a spanning tree with a weight less than or equal to the weight of every other spanning tree. The weight of a spanning tree is the sum of weights given to each edge of the spanning tree.

Screenshot 2021-10-19 at 06.01.22.png

Screenshot 2021-10-19 at 06.01.53.png

By nature, it's a greedy algorithm that always selects the next best edge to add to the MST and it works very well on dense graphs with lots of edges.

Prim's Minimum Spanning Tree Algorithm

Screenshot 2021-10-19 at 06.28.47.png

Lazy Prim's Minimum Spanning Tree Algorithm

Maintain a Priority Queue that sorts edges based on minimum edge cost. This PQ is used to tell you which node to go to next and what edge was used to get there. Then the algorithm begins and we start on any starting node s and mark s as visited and iterate over all its edges and add them to the PQ. From this point on, while the PQ is not empty and an MST has not been formed, dequeue the next best edge from the PQ. If the dequeued edge is not outdated which it could be if we visit the node it points to via another path before getting to this edge then mark the current node as visited and add the selected edge to the PQ. If you selected a stale outdated edge simply poll again. Then repeat the process of iterating over the current node's edges and adding them to the PQ. While doing this care not to add edges that point to already visited nodes, this will reduce the number of outdated edges in the PQ.

Screen Recording 2021-10-19 at 06.15.29.mov

Eager Prim's Minimum Spanning Tree Algorithm

Eager Prim's Minimum Spanning Tree Algorithm | Graph Theory

The lazy implementation of Prim’s inserts E edges into the PQ. This results in each poll operation on the PQ to be O(log(E)). In the eager version, we maintain the idea that instead of adding edges to the PQ which could later become stale, that instead, we should track (node, edge) key-value pairs that can easily be updated and polled to determine the next best edge to add to the MST.

For this all to make sense there's a key realisation that needs to happen and that is: for any MST with directed edges, each node is paired with exactly one of its incoming edges (except for the start node). One way to see this is on an MST with possibly multiple edges leaving a node, but only ever one edge entering a node.

Screenshot 2021-10-19 at 06.34.57.png

Screenshot 2021-10-19 at 06.35.14.png

In the eager version, we are trying to determine which of a node's incoming edges we should select to include in the MST. The main difference coming from the lazy version is that instead of adding edges to the PQ as we iterate over the edges of node we’re going to relax (update) the destination node’s most promising incoming edge.

Think of an IPQ as the data structure you'd get if a hashtable and a priority queue had a baby together. It supports sorted key-value pair update and poll operations in logarithmic time.

Indexed Priority Queue | Data Structure

Screenshot 2021-10-19 at 06.39.10.png

Screen Recording 2021-10-19 at 06.40.30.mov

Examples (do not add more here, add above)

Min Cost to Connect All Points

Prim's Algorithm - Minimum Spanning Tree - Min Cost to Connect all Points - Leetcode 1584 - Python

Screenshot 2021-10-19 at 07.17.51.png

""" 
1584. Min Cost to Connect All Points

You are given an array points representing integer coordinates of some points on a 2D-plane, where points[i] = [xi, yi].
The cost of connecting two points [xi, yi] and [xj, yj] is the manhattan distance between them: |xi - xj| + |yi - yj|, where |val| denotes the absolute value of val.
Return the minimum cost to make all points connected. All points are connected if there is exactly one simple path between any two points.

Example 1:
    Input: points = [[0,0],[2,2],[3,10],[5,2],[7,0]]
    Output: 20
Explanation:
    We can connect the points as shown above to get the minimum cost of 20.
    Notice that there is a unique path between every pair of points.
Example 2:
    Input: points = [[3,12],[-2,5],[-4,1]]
    Output: 18
Example 3:
    Input: points = [[0,0],[1,1],[1,0],[-1,1]]
    Output: 4
Example 4:
    Input: points = [[-1000000,-1000000],[1000000,1000000]]
    Output: 4000000
Example 5:
    Input: points = [[0,0]]
    Output: 0

https://leetcode.com/problems/min-cost-to-connect-all-points
https://www.notion.so/paulonteri/Trees-Graphs-edc3401e06c044f29a2d714d20ffe185#2ac2c79816464704a3851de16d494dff
"""

import collections
import heapq

""" 
Prim's Minimum Spanning Tree Algorithm: https://www.notion.so/paulonteri/Trees-Graphs-edc3401e06c044f29a2d714d20ffe185#596bc798759a4edabe22a895aadeb12c
https://youtu.be/f7JOBJIC-NA
"""

class Solution_:
    def minCostConnectPoints(self, points):
        total = 0

        # # Create adjacency list
        # Will store  nodes in the form => `parent: [[cost_to_1, node_1], [cost_to_2, node_2], ...]`
        graph = collections.defaultdict(list)
        for idx in range(len(points)):
            x1, y1 = points[idx]
            for idx2 in range(idx + 1, len(points)):
                x2, y2 = points[idx2]
                cost = abs(x1 - x2) + abs(y1 - y2)

                graph[str(x1)+str(y1)].append([cost, str(x2)+str(y2)])
                graph[str(x2)+str(y2)].append([cost, str(x1)+str(y1)])

        # # Prim's Minimum Spanning Tree Algorithm
        visited = set()
        priority_queue = []
        first_node = str(points[0][0])+str(points[0][1])
        heapq.heappush(priority_queue, (0, first_node))  # start from node 0
        while len(visited) < len(graph):
            cost, node = heapq.heappop(priority_queue)
            # skip visited
            if node in visited:
                continue
            visited.add(node)

            # record cost
            total += cost
            # add neighbours
            for neighbour in graph[node]:
                if neighbour[1] not in visited:
                    heapq.heappush(priority_queue, neighbour)

        return total

class Solution:
    def minCostConnectPoints(self, points):

        total = 0

        # # Create adjacency list
        # Will use the array indices as id's
        # Will store  nodes in the form => `parent: [[cost_to_1, node_1], [cost_to_2, node_2], ...]`
        graph = collections.defaultdict(list)
        for idx in range(len(points)):
            x1, y1 = points[idx]
            for idx2 in range(idx + 1, len(points)):
                x2, y2 = points[idx2]
                cost = abs(x1 - x2) + abs(y1 - y2)

                graph[idx].append([cost, idx2])
                graph[idx2].append([cost, idx])

        # # Prim's Minimum Spanning Tree Algorithm
        visited = set()
        priority_queue = []
        heapq.heappush(priority_queue, (0, 0))  # start from node 0
        while len(visited) < len(graph):
            cost, node = heapq.heappop(priority_queue)
            # skip visited
            if node in visited:
                continue
            visited.add(node)

            # record cost
            total += cost
            # add neighbours
            for neighbour in graph[node]:
                if neighbour[1] not in visited:
                    heapq.heappush(priority_queue, neighbour)

        return total

Connecting Cities With Minimum Cost

""" 
1584. Min Cost to Connect All Points

You are given an array points representing integer coordinates of some points on a 2D-plane, where points[i] = [xi, yi].
The cost of connecting two points [xi, yi] and [xj, yj] is the manhattan distance between them: |xi - xj| + |yi - yj|, where |val| denotes the absolute value of val.
Return the minimum cost to make all points connected. All points are connected if there is exactly one simple path between any two points.

Example 1:
    Input: points = [[0,0],[2,2],[3,10],[5,2],[7,0]]
    Output: 20
Explanation:
    We can connect the points as shown above to get the minimum cost of 20.
    Notice that there is a unique path between every pair of points.
Example 2:
    Input: points = [[3,12],[-2,5],[-4,1]]
    Output: 18
Example 3:
    Input: points = [[0,0],[1,1],[1,0],[-1,1]]
    Output: 4
Example 4:
    Input: points = [[-1000000,-1000000],[1000000,1000000]]
    Output: 4000000
Example 5:
    Input: points = [[0,0]]
    Output: 0

https://leetcode.com/problems/min-cost-to-connect-all-points
https://www.notion.so/paulonteri/Trees-Graphs-edc3401e06c044f29a2d714d20ffe185#2ac2c79816464704a3851de16d494dff
"""

import collections
import heapq

""" 
Prim's Minimum Spanning Tree Algorithm: https://www.notion.so/paulonteri/Trees-Graphs-edc3401e06c044f29a2d714d20ffe185#596bc798759a4edabe22a895aadeb12c
https://youtu.be/f7JOBJIC-NA
"""

class Solution_:
    def minCostConnectPoints(self, points):
        total = 0

        # # Create adjacency list
        # Will store  nodes in the form => `parent: [[cost_to_1, node_1], [cost_to_2, node_2], ...]`
        graph = collections.defaultdict(list)
        for idx in range(len(points)):
            x1, y1 = points[idx]
            for idx2 in range(idx + 1, len(points)):
                x2, y2 = points[idx2]
                cost = abs(x1 - x2) + abs(y1 - y2)

                graph[str(x1)+str(y1)].append([cost, str(x2)+str(y2)])
                graph[str(x2)+str(y2)].append([cost, str(x1)+str(y1)])

        # # Prim's Minimum Spanning Tree Algorithm
        visited = set()
        priority_queue = []
        first_node = str(points[0][0])+str(points[0][1])
        heapq.heappush(priority_queue, (0, first_node))  # start from node 0
        while len(visited) < len(graph):
            cost, node = heapq.heappop(priority_queue)
            # skip visited
            if node in visited:
                continue
            visited.add(node)

            # record cost
            total += cost
            # add neighbours
            for neighbour in graph[node]:
                if neighbour[1] not in visited:
                    heapq.heappush(priority_queue, neighbour)

        return total

class Solution:
    def minCostConnectPoints(self, points):

        total = 0

        # # Create adjacency list
        # Will use the array indices as id's
        # Will store  nodes in the form => `parent: [[cost_to_1, node_1], [cost_to_2, node_2], ...]`
        graph = collections.defaultdict(list)
        for idx in range(len(points)):
            x1, y1 = points[idx]
            for idx2 in range(idx + 1, len(points)):
                x2, y2 = points[idx2]
                cost = abs(x1 - x2) + abs(y1 - y2)

                graph[idx].append([cost, idx2])
                graph[idx2].append([cost, idx])

        # # Prim's Minimum Spanning Tree Algorithm
        visited = set()
        priority_queue = []
        heapq.heappush(priority_queue, (0, 0))  # start from node 0
        while len(visited) < len(graph):
            cost, node = heapq.heappop(priority_queue)
            # skip visited
            if node in visited:
                continue
            visited.add(node)

            # record cost
            total += cost
            # add neighbours
            for neighbour in graph[node]:
                if neighbour[1] not in visited:
                    heapq.heappush(priority_queue, neighbour)

        return total

Dijkstra's Algorithm

Dijkstra's Shortest Path Algorithm | Graph Theory

Dijkstra's Shortest Path Algorithm - A Detailed and Visual Introduction

Dijkstra's Algorithm

Dijkstra's Algorithm vs Prim's Algorithm

Graphs in Python: Dijkstra's Algorithm

With Dijkstra's Algorithm, you can find the shortest path between nodes in a graph. Particularly, you can find the shortest path from a node (called the "source node") to all other nodes in the graph, producing a shortest-path tree.

Dr.Edsger Dijkstra at ETH Zurich in 1994

Dijkstra's Algorithm can only work with graphs that have positive weights. This is because, during the process, the weights of the edges have to be added to find the shortest path.

If there is a negative weight in the graph, then the algorithm will not work properly. Once a node has been marked as "visited", the current path to that node is marked as the shortest path to reach that node. And negative weights can alter this if the total weight can be decremented after this step has occurred.

Screen Recording 2021-10-22 at 20.17.10.mov

Screenshot 2021-11-02 at 17.56.18.png

Screenshot 2021-11-02 at 17.57.10.png

Screenshot 2021-11-02 at 17.55.22.png

function dijkstra(G, S)
        ...

    while Q IS NOT EMPTY
        U <- Extract MIN from Q

        for each unvisited neighbour V of U

            tempDistance <- distance[U] + edge_weight(U, V)

            if tempDistance < distance[V]
                distance[V] <- tempDistance
                previous[V] <- U

    return distance[], previous[]

Time & Space complexity

O((v + e) * log(v)) time | O(v) space - where v is the number of vertices and e is the number of edges in the input graph

Examples:

Cheapest Flights Within K Stops

Screenshot 2021-10-22 at 18.37.07.png

Screenshot 2021-10-22 at 18.37.50.png

Screenshot 2021-10-22 at 18.38.09.png

Screenshot 2021-10-22 at 18.38.35.png

Screenshot 2021-10-22 at 18.39.52.png

Screenshot 2021-10-22 at 18.40.22.png

Screenshot 2021-10-22 at 18.41.01.png

Screenshot 2021-10-22 at 18.41.53.png

""" 
Cheapest Flights Within K Stops

There are n cities connected by some number of flights. 
You are given an array flights where flights[i] = [fromi, toi, pricei] indicates that there is a flight from city fromi to city toi with cost pricei.
You are also given three integers src, dst, and k, return the cheapest price from src to dst with at most k stops. If there is no such route, return -1.

Example 1:
    Input: n = 3, flights = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 1
    Output: 200
    Explanation: The graph is shown.
    The cheapest price from city 0 to city 2 with at most 1 stop costs 200, as marked red in the picture.
Example 2:
    Input: n = 3, flights = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 0
    Output: 500
    Explanation: The graph is shown.
    The cheapest price from city 0 to city 2 with at most 0 stop costs 500, as marked blue in the picture.

https://leetcode.com/problems/cheapest-flights-within-k-stops
"""

import collections
import heapq

class Solution:
    def findCheapestPrice(self, n, flights, src, dst, k):

        # Build graph
        graph = collections.defaultdict(list)
        for from_node, to_node, price in flights:
            graph[from_node].append((price, to_node))

        # Dijkstra's Algorithm
        heap = [(0, src, 0)]
        visited = set()
        city_stops = [float('inf')] * n  # shortest distance/price to node
        while heap:
            price, city, stops = heapq.heappop(heap)

            if city == dst:
                return price
            if stops == k+1:
                continue
            # # Note: in Dijkstra's Algorithm, we never revisit nodes
            # Remember that our algorithm stops whenever we pass k stops/visits - we need to consider this & look for a path that will give us less stops
            # Therefore, if we ever encounter a node that has already been processed before
            #   but the number of stops from the source is lesser than what was recorded before,
            #   we will add it to the heap so that it gets considered again!
            # That's the only change we need to make to make Dijkstra's compliant with the limitation on the number of stops.
            #   if city in visited:   <- normal Dijkstra's Algorithm
            #   if city in visited and stops > city_stops[city]:    <- modified Dijkstra's Algorithm
            if city in visited and stops > city_stops[city]:
                continue

            visited.add(city)
            city_stops[city] = stops

            for neighbour_cost, neighbour in graph[city]:
                heapq.heappush(
                    heap, (price+neighbour_cost,  neighbour, stops+1,)
                )

        return -1

Union find (disjoint set)

Union Find Introduction

Disjoint Set | UNION and FIND

Disjoint Set Union (DSU)/Union-Find - A Complete Guide - LeetCode Discuss

Examples:

Making A Large Island

""" 
Making A Large Island

You are given an n x n binary matrix grid. You are allowed to change at most one 0 to be 1.
Return the size of the largest island in grid after applying this operation.
An island is a 4-directionally connected group of 1s.

Example 1:
    Input: grid = [[1,0],[0,1]]
    Output: 3
    Explanation: Change one 0 to 1 and connect two 1s, then we get an island with area = 3.
Example 2:
    Input: grid = [[1,1],[1,0]]
    Output: 4
    Explanation: Change the 0 to 1 and make the island bigger, only one island with area = 4.
Example 3:
    Input: grid = [[1,1],[1,1]]
    Output: 4
    Explanation: Can't change any 0 to 1, only one island with area = 4.

https://leetcode.com/problems/making-a-large-island
"""
from collections import defaultdict
from typing import List

# O(N^2) time | O(N^2) space
# we traverse the graph twice in the worst case, for time, and only store row*col nodes, for space
class Solution:
    def largestIsland(self, grid: List[List[int]]):
        """ 
        * Based on union find: https://www.notion.so/paulonteri/Trees-Graphs-edc3401e06c044f29a2d714d20ffe185#02cd6da5a64447feab03037d22d40b38

        - Group nodes into different islands
            - store the island sizes
            - record the island_id for each node
        - For each 0, try to merge its surrounding islands
        """
        island_sizes, child_to_island_id = self.create_islands(grid)

        largest_island = 0
        if island_sizes:
            largest_island = max(island_sizes.values())

        for row in range(len(grid)):
            for col in range(len(grid[0])):
                if grid[row][col] != 0:
                    continue
                """ 
                Try to connect the surrounding islands
                if we have seen the island before, we don't need to do anything
                """
                seen_island_ids = set()

                top_island, top = self.get_node_island_and_size(grid, row-1, col, island_sizes, child_to_island_id)
                seen_island_ids.add(top_island)

                bottom_island, bottom = self.get_node_island_and_size(grid, row+1, col, island_sizes, child_to_island_id)
                # is part of an island we saw above (in this case part of top_island)
                if bottom_island in seen_island_ids:
                    bottom = 0
                seen_island_ids.add(bottom_island)

                left_island, left = self.get_node_island_and_size(grid, row, col-1, island_sizes, child_to_island_id)
                if left_island in seen_island_ids:
                    left = 0
                seen_island_ids.add(left_island)

                right_island, right = self.get_node_island_and_size(grid, row, col+1, island_sizes, child_to_island_id)
                if right_island in seen_island_ids:
                    right = 0
                seen_island_ids.add(right_island)

                # merge all neighbouring islands + the current node (1)
                largest_island = max(largest_island, 1+top+bottom+left+right)

        return largest_island

    def get_node_island_and_size(self, grid, row, col, island_sizes, child_to_island_id):
        """ Returns the node's island_id and size """
        if row < 0 or col < 0 or row >= len(grid) or col >= len(grid[0]):
            return None, 0
        if grid[row][col] == 0:
            return None, 0
        island_id = child_to_island_id[(row, col)]
        return island_id, island_sizes[island_id]

    def create_islands(self, grid: List[List[int]]):
        """
        Creates islands
        - returns:
            - a dict of { `island_id` -> `island_size` }
            - a dict of {`child/node` -> `island_id` }
        """
        island_sizes = defaultdict(int)
        child_to_island_id = {}

        def group_into_island(row, col, island_id):
            if row < 0 or col < 0 or row >= len(grid) or col >= len(grid[0]):
                return
            if (row, col) in child_to_island_id:
                return  # skip if part of an island
            if grid[row][col] == 0:
                return

            island_sizes[island_id] += 1
            child_to_island_id[(row, col)] = island_id

            group_into_island(row-1, col, island_id)
            group_into_island(row, col-1, island_id)
            group_into_island(row+1, col, island_id)
            group_into_island(row, col+1, island_id)

        curr_id = -1
        for row in range(len(grid)):
            for col in range(len(grid[0])):
                group_into_island(row, col, curr_id)
                curr_id -= 1

        return island_sizes, child_to_island_id

Screenshot 2021-10-27 at 07.03.26.png

Screen Recording 2021-10-27 at 07.07.23.mov

The Disjoint set uses chaining to define a set. The chaining is defined as a parent-child relationship.

Screenshot 2021-10-27 at 07.16.15.png

Screenshot 2021-10-27 at 07.21.09.png

Every node points to its parent and absolute roots have no parent

Find:

check if the two nodes share an absolute root and return True

Union:

make the absolute root of one point to the absolutte root of another

Segment tree

Segment Trees Tutorials & Notes | Data Structures | HackerEarth

Understanding Range Queries and Updates: Segment Tree, Lazy Propagation and MO's Algorithm

Sum of given range | Segment tree construction and update | Simplest explanation

What is a segment tree?

Introduction

Segment Tree

A segment tree is a very flexible data structure, because it is used to solve numerous range query problems like finding minimum, maximum, sum, greatest common divisor, least common denominator in array in logarithmic time.

Screenshot 2021-11-12 at 11.17.08.png

Let’s say we have an array A of size N. A segment of the array is a contiguous part of an array in form A[i:j] A segment tree is essentially a binary tree in whose nodes we store the information about the segments of a linear data structure such as an array. Do not worry about what kind of information as of now. We shall take a look at that later.

The root node of the segment tree would contain the information about segment A[0:N-1]
The left child of the root node would contain the information about segment A[0:(N-1)/2] and similarly,
The right child of the root node would contain the information about segment A[ 1+((N-1)/2) : (N-1) ] and so on.

In simpler terms the root node contains information about the whole array, its left child contains a similar kind of information about the left half of the array, and the right child of the root node will contain the information about the right half of the array and so on. Thus at each step (level of the tree), we divide the segment into two halves and the further children nodes contain the information about these two halves. This continues till we reach the leaf nodes which contain the element of the array A itself. The i-th leaf node contains A[i]. Thus we can say that there will be N leaf *nodes and the height of the tree will be log *N to the base 2.

Note: Once a segment tree is built for an array, its structure cannot be changed. We are allowed to update the values of the nodes but we cannot change the structure of the Segment Tree. That is to say, we cannot add more elements to the array and expect the segment tree to update. In that case, we will have to create a new segment tree altogether. However, we are allowed to update the values of the array and the segment tree shall be updated accordingly.

Segment Trees allow for the following two operations:

Update: This operation allows us to update the values of array A and reflect the corresponding changes in the segment tree.
Query: This operation allows us to perform a range query on the array. For example, let's say we have an array of size 15 and we wish to find the maximum element in the segment of an array with start index as 3 and end index 9. This is an example of a range query.

Thus we can say that a segment tree comes in handy when we have a lot of range-based queries to be performed on an array along with value updates on the same array. The process of creation of a segment tree takes some time but once it's done, the operation of range queries becomes very fast.

What kind of information does a segment tree hold?

Now that we have a basic understanding of the structure of the segment tree let us have a look at what kind of information does a segment tree hold. Consider an array A = [1, 4, 5, 8, 0, 13]

Now a segment tree is always associated with a piece of certain information that is directly linked with the kind of range queries we wish to perform. A couple of them are as follows:

Find the sum/product of elements of an array in the range A[i:j]
Find the maximum/minimum element in the range A[i:j]
Find the count of even/odd/prime etc, numbers in the range A[i:j]

There can be many others depending upon the usage. Let us have a look at how we can make use of a segment tree to find the sum of elements in a given range.

Construction

Screenshot 2021-11-12 at 10.23.54.png

Screenshot 2021-11-12 at 10.24.51.png

Screenshot 2021-11-12 at 10.25.31.png

Screenshot 2021-11-12 at 10.26.25.png

Screenshot 2021-11-12 at 10.27.04.png

Screen Recording 2021-11-12 at 12.03.56.mov

Let’s say we have an array A = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] ****and we wish to find the sum of elements in a given range. Then each node would store the sum of its children nodes, except the leaf nodes which store the array elements. Then the segment tree for the same would look something like this:

Untitled

The red node being the root node, the blue nodes being the internal nodes and the green nodes being the leaf nodes. Each node contains information about a particular segment of the array. In this example,

Root node contains the sum of all the elements of the array
The left child of the root node contains the information about the sum of the left half of the array i.e. [1, 2, 3, 4, 5]. Its left child in turn contains the sum of the segment [1, 2, 3] and the right child contains the sum of the segment [4, 5] and so on.
The right child of the root node contains the information about the sum of the left half of the array i.e. [6, 7, 8, 9, 10]. Its left child in turn contains the sum of the segment [6, 7, 8] and the right child contains the sum of the segment [9, 10] and so on.

If we wanted to compute, let's say, the maximum element then we would be storing the maximum element in each segment in the corresponding nodes. Thus before building the Segment Tree one must figure out the intent behind building the tree and the type of values to be stored in the tree’s nodes.

Thus we can also notice that a segment tree is always going to be a full binary tree i.e. each node either has 2 or 0 children.

The total number of leaf nodes is at least N. Total number of internal nodes = N-1. So, the total number of nodes = 2N-1. But generally, to build a segment tree over an array of size N, we use a tree of 4N nodes**. (Why?)

Array representation of above segment tree will be

Tree[] = {1,2,3,4,5,6,7,8,9,dummy,dummy,10,11,dummy,dummy};

Since we use the array representation of the segment tree, so a bit of space is wasted as you can see in the above example. This wasted space can be removed but in that case, its implementation would be more complex. Considering these waste spaces, for the smooth working of data structure, a tree of size 4*N is used, which is still of linear space complexity.

4*N size is enough for an array of size N. Why?

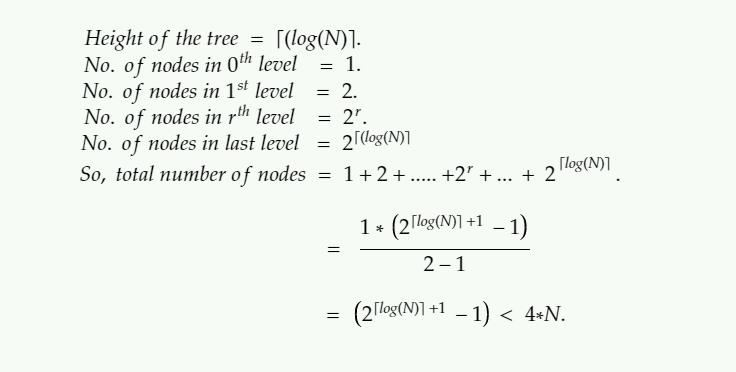
void build(int node, int start, int end)
{
    if(start == end)
    {
        // Leaf node will have a single element
        tree[node] = A[start];
    }
    else
    {
        int mid = (start + end) / 2;

        // Recurse on the left child
        build(2*node, start, mid);
        // Recurse on the right child
        build(2*node+1, mid+1, end);

        // Internal node will have the sum of both of its children
        tree[node] = tree[2*node] + tree[2*node+1];
    }
}

void Build_Tree(int node, int st, int end)
{
    if(st == end)
    {
        /*Leaf node will store the single array element*/
        tree[node] = A[st];
        return ;
    }
    int mid = (st+end)/2;

    /*Call recursion for left child*/
    Build_Tree(node*2, st, mid);

    /*Call recursion for right child*/  
    Build_Tree(node*2+1, mid+1, end);

    /*Update the current node as minimum of both children*/
    tree[node] = min(tree[2*node], tree[2*node+1]);
    return;
}

Screenshot 2021-11-12 at 11.28.39.png

In the above function, node represents the current node of the tree being processed and variables st and end represent the range (segment) of that current node. Recall that segment tree is a binary tree, left child, given by 2node, contains the range A[st : mid] and right child, which is given by 2node+1, contains the range A [mid+1: end] where mid=(st+end)/2.

Since the build function is being called once for each node (total maximum 4N node), so the time complexity of the build() is O(N)*.

Update the Tree

Screen Recording 2021-11-12 at 12.05.24.mov

Now, we want to modify the array element as A[a] = b and hence we have to modify the segment tree. Looking at the tree, one can clearly observe that index to be updated lies only in one segment of each level so we need to update only log(N) nodes. Starting from the root node we will recursively call the update function for the node which contains required index till we reach the leaf node representing that index. Then we will update that node, and in backtracking all the ancestors till root will be updated as minimum of its children.

Code for the same is:

void update(int node, int start, int end, int idx, int val)
{
    if(start == end)
    {
        // Leaf node
        A[idx] += val;
        tree[node] += val;
    }
    else
    {
        int mid = (start + end) / 2;
        if(start <= idx and idx <= mid)
        {
            // If idx is in the left child, recurse on the left child
            update(2*node, start, mid, idx, val);
        }
        else
        {
            // if idx is in the right child, recurse on the right child
            update(2*node+1, mid+1, end, idx, val);
        }
        // Internal node will have the sum of both of its children
        tree[node] = tree[2*node] + tree[2*node+1];
    }
}

void update(int node, int st, int end, int idx, int value)
{
    if(st == end)
    {
        /*Update leaf node*/
        tree[node] = value;
        A[idx] = value;
        return ;
    }

    int mid = (st+end)/2;
    /*if index lies in the left child call update() for left child*/
    if(idx<=mid)
      update(2*node, st, mid, idx, value);

    /*else index would lie in the right child, call update() for the right child*/
    else
        update(2*node+1, mid+1, end, idx, value);

    /*after updating the children,update the current node as smallest of its children */
    tree[node] = min(tree[2*node], tree[2*node+1]);
    return ;
}

TIme complexity of update function is O(log(N)).

P.S. Often we don’t need to write one special build() function for building the segment tree. It can be done using the update function as well. For that we need to initialize the tree nodes with such a value that will never affect our answer.

Range query

Screen Recording 2021-11-12 at 12.05.58.mov

We are given two integers l and r, we need to find the smallest element in this range (l and r inclusive).

To accomplish the task, we will traverse the segment tree and use the pre-computed values of the intervals. Let’s consider that currently, we are at a vertex that covers the interval A[st, st+1, st+2, . . ., end]. Then there are three possibilities:

Range represented by the node lies completely inside the given query range: In this case, we will just return the value stored at that node in the segment tree.
The range represented by the node lies completely outside the given query range: In this case, the query function should return such a value that will not affect our answer. For example, if we want to find the minimum element, our function should return infinity (INT_MAX).
Range represented by the node lies partially inside and partially outside the given query range: As in this case, our answer depends on both the children so we will make two recursive calls one for each child. Let’s say partial answer from left child is ans1 and that from right child is ans2, so our answer would be min(ans1, ans2).

int query(int node, int start, int end, int l, int r)
{
    if(r < start or end < l)
    {
        // range represented by a node is completely outside the given range
        return 0;
    }
    if(l <= start and end <= r)
    {
        // range represented by a node is completely inside the given range
        return tree[node];
    }
    // range represented by a node is partially inside and partially outside the given range
    int mid = (start + end) / 2;
    int p1 = query(2*node, start, mid, l, r);
    int p2 = query(2*node+1, mid+1, end, l, r);
    return (p1 + p2);
}

int range_min_query(int node, int st, int end, int l, int r)
{
    /*if range of the current node lies inside the query range*/
    if(l <= st && end <= r )
    {
        return tree[node];
    }
    /*If current range is completely outside the query range*/
    if(st>r || end<l)
    return INT_MAX;

  /*If query range intersects both the children*/
    int mid = (st+end)/2;
    int ans1 = range_min_query(2*node, st, mid, l, r);
    int ans2 = range_min_query(2*node+1, mid+1, end, l, r); 
    return min(ans1, ans2); 
}

Time Complexity: Since at any level at most 4 nodes will be visited and the total number of levels in the tree is log(N). The upper bound of all the visited nodes would be 4log(N). Hence, the time complexity of each query would be O(log(N).*

Range Sum Query - Mutable

Screenshot 2021-11-12 at 10.33.38.png

Screenshot 2021-11-12 at 10.34.36.png

Tries

Topological sort

Topological Sort (for graphs) *

Morris Traversal

→ Morris Traversal

Find the original version of this page (with additional content) on Notion here.

Trie (Keyword Tree)

Introduction

Explore - LeetCode

Trie (Keyword Tree) Tutorials & Notes | Data Structures | HackerEarth

Article on Trie. General Template and List of problems. - LeetCode Discuss

Simple Trie

Screenshot 2021-08-31 at 09.42.21.png

class Trie:
    def __init__(self):
        self.root = {}
        self.endSymbol = endSymbol

    def add(self, word):
        current = self.root
        for letter in word:
            if letter not in current:
                current[letter] = {}
            current = current[letter]
        current[self.endSymbol] = word

    def remove(self, word):
        self.delete(self.root, word, 0)

    def delete(self, dicts, word, i):
        if i == len(word):
            if '*' in dicts:
                del dicts['*']
                if len(dicts) == 0:
                    return True
                else:
                    return False
            else:
                return False
        else:
            if word[i] in dicts and self.delete(dicts[word[i]], word, i + 1):
                if len(dicts[word[i]]) == 0:
                    del dicts[word[i]]
                    return True
                else:
                    return False

            else:
                return False

Examples

Design Add and Search Words Data Structure

""" 
211. Design Add and Search Words Data Structure:

Design a data structure that supports adding new words and finding if a string matches any previously added string.
Implement the WordDictionary class:
    WordDictionary() Initializes the object.
    void addWord(word) Adds word to the data structure, it can be matched later.
    bool search(word) Returns true if there is any string in the data structure that matches word or false otherwise. word may contain dots '.' where dots can be matched with any letter.


Example:
    Input
        ["WordDictionary","addWord","addWord","addWord","search","search","search","search"]
        [[],["bad"],["dad"],["mad"],["pad"],["bad"],[".ad"],["b.."]]
    Output
        [null,null,null,null,false,true,true,true]
    Explanation
        WordDictionary wordDictionary = new WordDictionary();
        wordDictionary.addWord("bad");
        wordDictionary.addWord("dad");
        wordDictionary.addWord("mad");
        wordDictionary.search("pad"); // return False
        wordDictionary.search("bad"); // return True
        wordDictionary.search(".ad"); // return True
        wordDictionary.search("b.."); // return True

https://leetcode.com/problems/design-add-and-search-words-data-structure
"""

class WordDictionary:

    def __init__(self):
        self.root = {}
        self.end_symbol = "*"

    def addWord(self, word: str):
        curr_root = self.root
        for char in word:
            if char not in curr_root:
                curr_root[char] = {}
            curr_root = curr_root[char]
        curr_root[self.end_symbol] = True

    def search(self, word: str):
        return self.search_helper(word, 0, self.root)

    def search_helper(self, word, idx, curr_root):
        # end of word
        if idx == len(word):
            return self.end_symbol in curr_root
        # no matching char
        if word[idx] != "." and word[idx] not in curr_root:
            return False

        if word[idx] == ".":
            for letter in curr_root:
                if letter != self.end_symbol and self.search_helper(word, idx+1, curr_root[letter]):
                    return True
            return False
        else:
            return self.search_helper(word, idx+1, curr_root[word[idx]])

# Your WordDictionary object will be instantiated and called as such:
# obj = WordDictionary()
# obj.addWord(word)
# param_2 = obj.search(word)

Boggle Board/Word Search II

""" 
Word Search II

Given an m x n board of characters and a list of strings words, return all words on the board.
Each word must be constructed from letters of sequentially adjacent cells, 
    where adjacent cells are horizontally or vertically neighboring. 
The same letter cell may not be used more than once in a word.
https://leetcode.com/problems/word-search-ii/
"""

"""
Boggle Board:
You're given a two-dimensional array (a matrix) of potentially unequal height and width containing letters;
 this matrix represents a boggle board. You're also given a list of words.
Write a function that returns an array of all the words contained in the boggle board. The final words don't need to be in any particular order.
A word is constructed in the boggle board by connecting adjacent (horizontally, vertically, or diagonally) letters,
 without using any single letter at a given position more than once; while a word can of course have repeated letters,
 those repeated letters must come from different positions in the boggle board in order for the word to be contained in the board.
Note that two or more words are allowed to overlap and use the same letters in the boggle board.

Sample Input
    board = [
    ["t", "h", "i", "s", "i", "s", "a"],
    ["s", "i", "m", "p", "l", "e", "x"],
    ["b", "x", "x", "x", "x", "e", "b"],
    ["x", "o", "g", "g", "l", "x", "o"],
    ["x", "x", "x", "D", "T", "r", "a"],
    ["R", "E", "P", "E", "A", "d", "x"],
    ["x", "x", "x", "x", "x", "x", "x"],
    ["N", "O", "T", "R", "E", "-", "P"],
    ["x", "x", "D", "E", "T", "A", "E"],
    ],
    words = [
    "this", "is", "not", "a", "simple", "boggle",
    "board", "test", "REPEATED", "NOTRE-PEATED",
    ]
Sample Output
    ["this", "is", "a", "simple", "boggle", "board", "NOTRE-PEATED"]
    // The words could be ordered differently.

https://www.algoexpert.io/questions/Boggle%20Board
"""

""" 
------------------------------------------------------------------------------------------------------------------------------
"""

def boggleBoardBF(board, words):
    found_words = []

    for row in range(len(board)):
        for col in range(len(board[row])):

            # look for each word
            for idx in range(len(words)):
                if words[idx] != '-1':
                    if find_word(board, words, found_words, idx, 0, row, col):
                        found_words.append(words[idx])
                        # mark word as visted
                        words[idx] = '-1'

    return found_words

def find_word(board, words, found_words, curr_word_idx,  curr_char_idx, row, col):
    # had found word
    if words[curr_word_idx] == '-1':
        return False

    word = words[curr_word_idx]

    # found word
    if curr_char_idx >= len(word):
        return True

    # out of bounds
    if row < 0 or col < 0 or row >= len(board) or col >= len(board[0]):
        return False

    # was visited
    if board[row][col] == '000':
        return False

    curr_char = board[row][col]

    # cannot make word
    if curr_char != word[curr_char_idx]:
        return False

    # mark as visited
    board[row][col] = '000'

    # explore
    top = find_word(board, words, found_words, curr_word_idx,
                    curr_char_idx+1, row+1, col)
    bottom = find_word(board, words, found_words, curr_word_idx,
                       curr_char_idx+1, row-1, col)
    left = find_word(board, words, found_words, curr_word_idx,
                     curr_char_idx+1, row, col-1)
    right = find_word(board, words, found_words, curr_word_idx,
                      curr_char_idx+1, row, col+1)
    top_left = find_word(board, words, found_words, curr_word_idx,
                         curr_char_idx+1, row+1, col-1)
    top_right = find_word(board, words, found_words, curr_word_idx,
                          curr_char_idx+1, row+1, col+1)
    bottom_left = find_word(board, words, found_words, curr_word_idx,
                            curr_char_idx+1, row-1, col-1)
    bottom_right = find_word(board, words, found_words, curr_word_idx,
                             curr_char_idx+1, row-1, col+1)

    # unmark
    board[row][col] = curr_char

    return top or bottom or left or right or top_left or top_right or bottom_left or bottom_right

""" 
------------------------------------------------------------------------------------------------------------------------------

use a Trie
"""

""" 
------------------------------------------------------------------------------------------------------------------------------

use a Trie
"""

endSymbol = "*"

class Trie:
    def __init__(self):
        self.root = {}
        self.endSymbol = endSymbol

    def add(self, word):
        current = self.root
        for letter in word:
            if letter not in current:
                current[letter] = {}
            current = current[letter]
        current[self.endSymbol] = word

    def remove(self, word):
        self.delete(self.root, word, 0)

    def delete(self, dicts, word, i):
        if i == len(word):
            if '*' in dicts:
                del dicts['*']
                if len(dicts) == 0:
                    return True
                else:
                    return False
            else:
                return False
        else:
            if word[i] in dicts and self.delete(dicts[word[i]], word, i + 1):
                if len(dicts[word[i]]) == 0:
                    del dicts[word[i]]
                    return True
                else:
                    return False

            else:
                return False

class Solution:
    def findWords(self, board, words):
        trie = Trie()
        for word in words:
            trie.add(word)

        found_words = {}

        for row in range(len(board)):
            for col in range(len(board[row])):
                self.explore(trie, row, col, trie.root, board, found_words)

        return list(found_words.keys())

    def get_neighbours(self, i, j, board):
        neighbours = []
        if i > 0:
            neighbours.append([i - 1, j])
        if i < len(board) - 1:
            neighbours.append([i + 1, j])
        if j > 0:
            neighbours.append([i, j - 1])
        if j < len(board[0]) - 1:
            neighbours.append([i, j + 1])
        return neighbours

    def explore(self, main_trie, row, col, trie, board, found_words):
        mark = -1

        # # validate
        if board[row][col] not in trie:
            return
        if board[row][col] == mark:
            return

        char = board[row][col]
        curr_trie = trie[char]

        # # record all words found
        if endSymbol in curr_trie:
            word = curr_trie[endSymbol]
            found_words[word] = True
            main_trie.remove(word)

        # # continue search
        board[row][col] = mark  # visit - mark visited
        for neighbour in self.get_neighbours(row, col, board):
            self.explore(
                main_trie, neighbour[0], neighbour[1], curr_trie, board, found_words)
        board[row][col] = char  # univisit - remove mark

""" 
---------------------------------------------------------
"""

def get_neighbours(i, j, board):

    neighbours = []

    if i > 0 and j > 0:
        neighbours.append([i - 1, j - 1])
    if i > 0 and j < len(board[0]) - 1:
        neighbours.append([i - 1, j + 1])
    if i < len(board) - 1 and j < len(board[0]) - 1:
        neighbours.append([i + 1, j + 1])
    if i < len(board) - 1 and j > 0:
        neighbours.append([i + 1, j - 1])
    if i > 0:
        neighbours.append([i - 1, j])
    if i < len(board) - 1:
        neighbours.append([i + 1, j])
    if j > 0:
        neighbours.append([i, j - 1])
    if j < len(board[0]) - 1:
        neighbours.append([i, j + 1])
    return neighbours

def explore(row, col, trie, board, found_words):
    mark = -1

    # # validate
    if board[row][col] not in trie:
        return
    if board[row][col] == mark:
        return

    char = board[row][col]
    curr_trie = trie[char]

    # # record all words found
    if "*" in curr_trie:
        found_words[curr_trie["*"]] = True

    # # continue search
    board[row][col] = mark  # visit - mark visited
    for neighbour in get_neighbours(row, col, board):
        explore(neighbour[0], neighbour[1], curr_trie, board, found_words)
    board[row][col] = char  # univisit - remove mark

def boggleBoard(board, words):
    trie = Trie()
    for word in words:
        trie.add(word)

    found_words = {}

    for row in range(len(board)):
        for col in range(len(board[row])):
            explore(row, col, trie.root, board, found_words)

    return list(found_words.keys())

""" 
------------------------------------------------------------------------------------------------------------------------------
"""

Find the original version of this page (with additional content) on Notion here.

_Object-Oriented Analysis and Design

GitHub - knightsj/object-oriented-design: 面向对象设计的设计原则和设计模式

Python Design Patterns

Python Object Oriented Programming

How to Ace Object-Oriented Design Interviews

GitHub - tssovi/grokking-the-object-oriented-design-interview

Grokking the Object Oriented Design Interview - Learn Interactively

One Stop OOP Guide | Useful and Short topics for interviews | Object Oriented Programming (C++) - LeetCode Discuss

Introduction

Examples

GitHub - tuvo1106/ctci_6th_edition: Practice problems and solutions for Cracking the Coding Interview

GitHub - w-hat/ctci-solutions: Python solutions to Cracking the Coding Interview (6th edition)

use botom up design - design smallest components to the largest

Simple Examples

Design Underground System

"""
Design Underground System:

Implement the class UndergroundSystem that supports three methods:
    1. checkIn(int id, string stationName, int t)
        A customer with id card equal to id, gets in the station stationName at time t.
        A customer can only be checked into one place at a time.
    2. checkOut(int id, string stationName, int t)
        A customer with id card equal to id, gets out from the station stationName at time t.
    3. getAverageTime(string startStation, string endStation) 
        Returns the average time to travel between the startStation and the endStation.
        The average time is computed from all the previous traveling from startStation to endStation that happened
        directly.
        Call to getAverageTime is always valid.
You can assume all calls to checkIn and checkOut methods are consistent. 
That is, if a customer gets in at time t1 at some station, then it gets out at time t2 with t2 > t1. 
All events happen in chronological order.

https://leetcode.com/problems/design-underground-system
"""

class CustomerCheckIn:
    def __init__(self, station_name, time):
        self.station_name = station_name
        self.time = time

class RouteHistory:
    def __init__(self):
        self.total_time = 0
        self.trips = 0

    def add_trip_time(self, time):
        self.total_time += time
        self.trips += 1

    def get_avg_time(self):
        return self.total_time / self.trips

class UndergroundSystem:

    def __init__(self):
        self.check_ins = {}
        self.route_histories = {}

    def checkIn(self, id: int, stationName: str, t: int):
        self.check_ins[id] = CustomerCheckIn(stationName, t)

    def checkOut(self, id: int, stationName: str, t: int):
        check_in = self.check_ins[id]
        self.check_ins.pop(id)

        route = (check_in.station_name, stationName)

        if route not in self.route_histories:
            self.route_histories[route] = RouteHistory()

        self.route_histories[route].add_trip_time(t-check_in.time)

    def getAverageTime(self, startStation: str, endStation: str):
        route = (startStation, endStation)
        return self.route_histories[route].get_avg_time()

# Your UndergroundSystem object will be instantiated and called as such:
# obj = UndergroundSystem()
# obj.checkIn(id,stationName,t)
# obj.checkOut(id,stationName,t)
# param_3 = obj.getAverageTime(startStation,endStation)
""" 

"""

class UndergroundSystem_:

    def __init__(self):
        self.checkin_details = {}
        self.route_total_time = {}

    def checkIn(self, id: int, stationName: str, t: int) -> None:
        # save journey start details for each passenger
        # save cutomer checkin details
        self.checkin_details[id] = {
            "station": stationName,
            "time": t
        }

    def checkOut(self, id: int, stationName: str, t: int) -> None:
        checkin = self.checkin_details[id]
        # time taken = end time - start time
        time_taken = t - checkin["time"]

        # path = start station + end station
        path = checkin["station"] + stationName

        # increase total time and count
        if path in self.route_total_time:
            prev_total = self.route_total_time[path]

            self.route_total_time[path] = {
                "total": prev_total["total"] + time_taken,
                "count": prev_total["count"] + 1
            }

        # create entry in route_total_time: record total time and the count as 1
        else:
            self.route_total_time[path] = {
                "total": time_taken,
                "count": 1
            }

        # end customer journey
        self.checkin_details.pop(id)

    def getAverageTime(self, startStation: str, endStation: str) -> float:
        path = startStation + endStation
        # calculate average
        return self.route_total_time[path]["total"] / self.route_total_time[path]["count"]

"""
Input:
    ["UndergroundSystem","checkIn","checkIn","checkIn","checkOut","checkOut","checkOut","getAverageTime",
    "getAverageTime","checkIn","getAverageTime","checkOut","getAverageTime"]
    [[],[45,"Leyton",3],[32,"Paradise",8],[27,"Leyton",10],[45,"Waterloo",15],[27,"Waterloo",20],[32,"Cambridge",22],
    ["Paradise","Cambridge"],["Leyton","Waterloo"],[10,"Leyton",24],["Leyton","Waterloo"],[10,"Waterloo",38],
    ["Leyton","Waterloo"]]
Output:
    [null,null,null,null,null,null,null,14.00000,11.00000,null,11.00000,null,12.00000]
"""

Design an Ordered Stream

Screen Recording 2021-11-13 at 20.38.32.mov

""" 
1656. Design an Ordered Stream

There is a stream of n (idKey, value) pairs arriving in an arbitrary order, where idKey is an integer between 1 and n and value is a string. 
No two pairs have the same id.
Design a stream that returns the values in increasing order of their IDs by returning a chunk (list) of values after each insertion. 
The concatenation of all the chunks should result in a list of the sorted values.
Implement the OrderedStream class:
    OrderedStream(int n) Constructs the stream to take n values.
    String[] insert(int idKey, String value) Inserts the pair (idKey, value) into the stream, then returns the largest possible chunk of currently inserted values that appear next in the order.


Example:
    Input
        ["OrderedStream", "insert",     "insert",     "insert",      "insert",     "insert"]
        [[5],             [3, "ccccc"], [1, "aaaaa"], [2, "bbbbb"],  [5, "eeeee"], [4, "ddddd"]]
    Output
        [null,            [],           ["aaaaa"],    ["bbbbb", "ccccc"], [],      ["ddddd", "eeeee"]
    Explanation
        // Note that the values ordered by ID is ["aaaaa", "bbbbb", "ccccc", "ddddd", "eeeee"].
        OrderedStream os = new OrderedStream(5);
        os.insert(3, "ccccc"); // Inserts (3, "ccccc"), returns [].
        os.insert(1, "aaaaa"); // Inserts (1, "aaaaa"), returns ["aaaaa"].
        os.insert(2, "bbbbb"); // Inserts (2, "bbbbb"), returns ["bbbbb", "ccccc"].
        os.insert(5, "eeeee"); // Inserts (5, "eeeee"), returns [].
        os.insert(4, "ddddd"); // Inserts (4, "ddddd"), returns ["ddddd", "eeeee"].
        // Concatentating all the chunks returned:
        // [] + ["aaaaa"] + ["bbbbb", "ccccc"] + [] + ["ddddd", "eeeee"] = ["aaaaa", "bbbbb", "ccccc", "ddddd", "eeeee"]
        // The resulting order is the same as the order above.


Constraints:
    1 <= n <= 1000
    1 <= id <= n
    value.length == 5
    value consists only of lowercase letters.
    Each call to insert will have a unique id.
    Exactly n calls will be made to insert.

https://leetcode.com/problems/design-an-ordered-stream
"""

""" 
["init", "insert",   "insert",     "insert",     "insert",     "insert"]
[[5],  [3, "ccccc"], [1, "aaaaa"], [2, "bbbbb"], [5, "eeeee"], [4, "ddddd"]]
Output
[null,           [], ["aaaaa"],     ["bbbbb", "ccccc"], [], ["ddddd", "eeeee"]]

"""

class OrderedStream:

    def __init__(self, n: int):
        self.store = [None] * (n+1)
        self.pointer = 1

    def insert(self, idKey: int, value: str):
        self.store[idKey] = value

        pointer_start = self.pointer
        while self.pointer < len(self.store) and self.store[self.pointer] is not None:
            self.pointer += 1

        if pointer_start != self.pointer:
            return self.store[pointer_start:self.pointer]
        return []

# Your OrderedStream object will be instantiated and called as such:
# obj = OrderedStream(n)
# param_1 = obj.insert(idKey,value)

Thought it was related to this:

Count Unhappy Friends

""" 
1583. Count Unhappy Friends

You are given a list of preferences for n friends, where n is always even.
For each person i, preferences[i] contains a list of friends sorted in the order of preference. 
In other words, a friend earlier in the list is more preferred than a friend later in the list. Friends in each list are denoted by integers from 0 to n-1.
All the friends are divided into pairs. The pairings are given in a list pairs, where pairs[i] = [xi, yi] denotes xi is paired with yi and yi is paired with xi.
However, this pairing may cause some of the friends to be unhappy. A friend x is unhappy if x is paired with y and there exists a friend u who is paired with v but:
    x prefers u over y, and
    u prefers x over v.
Return the number of unhappy friends.

Example 1:
    Input: n = 4, preferences = [[1, 2, 3], [3, 2, 0], [3, 1, 0], [1, 2, 0]], pairs = [[0, 1], [2, 3]]
    Output: 2
    Explanation:
        Friend 1 is unhappy because:
        - 1 is paired with 0 but prefers 3 over 0, and
        - 3 prefers 1 over 2.
        Friend 3 is unhappy because:
        - 3 is paired with 2 but prefers 1 over 2, and
        - 1 prefers 3 over 0.
        Friends 0 and 2 are happy.
Example 2:
    Input: n = 2, preferences = [[1], [0]], pairs = [[1, 0]]
    Output: 0
    Explanation: Both friends 0 and 1 are happy.
Example 3:
    Input: n = 4, preferences = [[1, 3, 2], [2, 3, 0], [1, 3, 0], [0, 2, 1]], pairs = [[1, 3], [0, 2]]
    Output: 4


Constraints:
    2 <= n <= 500
    n is even.
    preferences.length == n
    preferences[i].length == n - 1
    0 <= preferences[i][j] <= n - 1
    preferences[i] does not contain i.
    All values in preferences[i] are unique.
    pairs.length == n/2
    pairs[i].length == 2
    xi != yi
    0 <= xi, yi <= n - 1
    Each person is contained in exactly one pair.

https://leetcode.com/problems/count-unhappy-friends
"""

""" 
n - even
[
0 [1, 3, 2], u
1 [2, 3, 0],
2 [1, 3, 0],
3 [0, 2, 1]
], 

pairs = [[1, 3], [0, 2]]

{ 
1:3,
3:1,
0:2,
2:0
}

# x unhappy
x -> y
u -> v

# if there exists such a condition
x -> u (x prefers u than what it currently has)
u -> x (prefers x than what it has)

- count = 0
- store the preferences in a dict/list:
    { 
    x1: { u1: pref_u1, u2: pref_u2 }
    x2: { u1: pref_u1, u2: pref_u2 }
    }
- store the friendships in a dict/list:
    {
    x1:u1,
    u1:x1
    }
- for each x in the pairings:
    - if not with the highest priority friend
        - if can_get_higher_prio(x):
            count += 1


can_get_higher_prio(x):
    - check if for all the higher priority friends u1, u2, u2
        - any of them is matched with a friend they prefer less than x 

https://www.notion.so/paulonteri/_Object-Oriented-Analysis-and-Design-1a01887a9271475da7b3cd3f4efc9e0d#3b876eef896b482ea279ebdfbd918590
"""

from typing import List
class Solution:
    def unhappyFriends(self, n: int, preferences: List[List[int]], pairs: List[List[int]]):
        count = 0

        pref_lookup = [{} for _ in range(n)]
        friendships_lookup = [-1 for _ in range(n)]

        # store the preferences in a dict
        for person, preferences_list in enumerate(preferences):
            for priority, other_person in enumerate(preferences_list):
                pref_lookup[person][other_person] = priority
        # store the friendships in a dict
        for x, y in pairs:
            friendships_lookup[x] = y
            friendships_lookup[y] = x

        for person, paired_with in enumerate(friendships_lookup):
            if pref_lookup[person][paired_with] == 0:
                continue
            if self.can_get_higher_prio(pref_lookup, friendships_lookup, person, paired_with):
                count += 1

        return count

    def can_get_higher_prio(self, pref_lookup, friendships_lookup, person, paired_with):
        """ 
        - check if for all the higher priority friends u1, u2, u2 of person
            - if any of them is matched with a friend they prefer less than x:
                - return True
        - return False
        """

        for other_friend in pref_lookup[person]:
            # other_friend is of a lower priority
            if pref_lookup[person][other_friend] > pref_lookup[person][paired_with]:
                continue
            # person is not under other_friend's priorities
            if person not in pref_lookup[other_friend]:
                continue

            # check other_friend's preference with person vs preference with who they were paired with
            pref_w_person = pref_lookup[other_friend][person]
            pref_w_paired_with = pref_lookup[other_friend][friendships_lookup[other_friend]]

            if pref_w_paired_with > pref_w_person:
                return True

        return False

LRU Cache

LRU Cache - Twitch Interview Question - Leetcode 146

Screenshot 2021-10-23 at 13.23.26.png

from collections import OrderedDict
class LRUCache(OrderedDict):

    def __init__(self, capacity):
        """
        :type capacity: int
        """
        self.capacity = capacity

    def get(self, key):
        """
        :type key: int
        :rtype: int
        """
        if key not in self:
            return - 1

        self.move_to_end(key)
        return self[key]

    def put(self, key, value):
        """
        :type key: int
        :type value: int
        :rtype: void
        """
        if key in self:
            self.move_to_end(key)
        self[key] = value
        if len(self) > self.capacity:
            self.popitem(last = False)

# Your LRUCache object will be instantiated and called as such:
# obj = LRUCache(capacity)
# param_1 = obj.get(key)
# obj.put(key,value)

Screenshot 2021-10-23 at 13.25.16.png

Screenshot 2021-11-09 at 06.27.01.png

"""
LRU Cache: Leecode 146

Design a data structure that follows the constraints of a Least Recently Used (LRU) cache.
Implement the LRUCache class:
    LRUCache(int capacity) Initialize the LRU cache with positive size capacity.
    int get(int key) Return the value of the key if the key exists, otherwise return -1.
    void put(int key, int value) Update the value of the key if the key exists. Otherwise, add the key-value pair to the cache. If the number of keys exceeds the capacity from this operation, evict the least recently used key.

Follow up:
Could you do get and put in O(1) time complexity?

https://leetcode.com/problems/lru-cache
"""

from collections import OrderedDict
from typing import Dict

class Node:
    def __init__(self, key, value):
        self.key = key
        self.value = value
        self.next = None
        self.prev = None

# special Doubly Linked List
class DLL:
    # head & tail will help in easily finding the beginning and end
    def __init__(self, head: Node, tail: Node):
        head.next = tail
        tail.prev = head
        self.head = head
        self.tail = tail

    def remove_between_head_and_tail(self, node: Node):
        # special remove function for our cache
        pr = node.prev
        nxt = node.next
        pr.next = nxt
        nxt.prev = pr

    def add_after_head(self, node: Node):
        after_head = self.head.next

        # update head
        self.head.next = node
        # update node that was after head
        after_head.prev = node
        # node
        node.next = after_head
        node.prev = self.head

    # ignore this
    # it is used for testing only
    def print_all(self):
        curr = self.head
        elements = []

        while curr is not None:
            pr = None
            nxt = None

            if curr.prev:
                pr = curr.prev
            if curr.next:
                nxt = curr.next
            elements.append([curr.key, curr.value, {"prev": pr, "next": nxt}])

        print(elements)
        return elements

# Your LRUCache object will be instantiated and called as such:
# obj = LRUCache(capacity)
# param_1 = obj.get(key)
# obj.put(key,value)

# SOLUTION:
# get O(1) time | put O(1)
class LRUCache:

    def __init__(self, capacity: int):
        self.capacity = capacity
        self.count = 0
        # used to store all the key value pairs
        self.store: Dict[int, Node] = {}
        # actual cache
        self.cache = DLL(Node(-1, -1), Node(-1, -1))

    def get(self, key: int):
        if not key in self.store:
            return -1
        else:
            node = self.store[key]
            # move to front (make most recent)
            self.cache.remove_between_head_and_tail(node)
            self.cache.add_after_head(node)
            return node.value

    def put(self, key: int, value: int):
        # have key in store
        if key in self.store:
            node = self.store[key]
            # update
            node.value = value
            # move to front (make most recent)
            self.cache.remove_between_head_and_tail(node)
            self.cache.add_after_head(node)
        # new key
        else:
            # create
            node = Node(key, value)
            self.store[key] = node
            self.cache.add_after_head(node)
            self.count += 1

        # check for excess
        if self.count > self.capacity:
            before_last = self.cache.tail.prev
            self.cache.remove_between_head_and_tail(before_last)
            self.store.pop(before_last.key)
            self.count -= 1

"""
Input:
    ["LRUCache","put","put","put","put","get","get"]
    [[2],       [2,1],[1,1],[2,3],[4,1],[1],   [2]]

    ["LRUCache","put","put","get","put","get","put","get","get","get"]
    [[2],      [1,10],[2,20],[1], [3,30],[2], [4,40],[1],  [3],[4]]
Output:
    [null,null,null,null,null,-1,3]

    [null,null,null,10,null,-1,null,-1,30,40]
"""

""" 
Ordered dictionary
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
"""

class LRUCache2(OrderedDict):

    def __init__(self, capacity):
        """
        :type capacity: int
        """
        self.capacity = capacity

    def get(self, key):
        """
        :type key: int
        :rtype: int
        """
        if key not in self:
            return - 1

        self.move_to_end(key)
        return self[key]

    def put(self, key, value):
        """
        :type key: int
        :type value: int
        :rtype: void
        """
        if key in self:
            self.move_to_end(key)
        self[key] = value
        if len(self) > self.capacity:
            self.popitem(last=False)

# Your LRUCache object will be instantiated and called as such:
# obj = LRUCache(capacity)
# param_1 = obj.get(key)
# obj.put(key,value)

Range Sum Query - Immutable

"""
Range Sum Query - Immutable

Given an integer array nums, handle multiple queries of the following type:
Calculate the sum of the elements of nums between indices left and right inclusive where left <= right.
Implement the NumArray class:
    NumArray(int[] nums) Initializes the object with the integer array nums.
    int sumRange(int left, int right) Returns the sum of the elements of nums between indices left and right inclusive (i.e. nums[left] + nums[left + 1] + ... + nums[right]).


Example 1:
    Input
        ["NumArray", "sumRange", "sumRange", "sumRange"]
        [[[-2, 0, 3, -5, 2, -1]], [0, 2], [2, 5], [0, 5]]
    Output
        [null, 1, -1, -3]
    Explanation
        NumArray numArray = new NumArray([-2, 0, 3, -5, 2, -1]);
        numArray.sumRange(0, 2); // return (-2) + 0 + 3 = 1
        numArray.sumRange(2, 5); // return 3 + (-5) + 2 + (-1) = -1
        numArray.sumRange(0, 5); // return (-2) + 0 + 3 + (-5) + 2 + (-1) = -3

https://leetcode.com/problems/range-sum-query-immutable
"""

class NumArray:
    """ 
    Pre-compute the cumulative sums to give O(1) lookup
    """

    def __init__(self, nums):
        self.cumulative_sums = [0]*len(nums)

        running_sum = 0
        for idx, num in enumerate(nums):
            running_sum += num
            self.cumulative_sums[idx] = running_sum

    def sumRange(self, left: int, right: int):
        left_val = 0
        if left > 0:
            left_val = self.cumulative_sums[left-1]
        return self.cumulative_sums[right] - left_val

# Your NumArray object will be instantiated and called as such:
# obj = NumArray(nums)
# param_1 = obj.sumRange(left,right)

Range Sum Query 2D - Immutable

Screenshot 2021-10-24 at 07.34.42.png

Screenshot 2021-10-24 at 07.35.22.png

Screenshot 2021-10-24 at 07.35.43.png

Screenshot 2021-10-24 at 07.36.37.png

Summed-area table - Wikipedia

Computer Vision - The Integral Image

Screenshot 2021-10-24 at 07.38.21.png

Screenshot 2021-10-24 at 07.38.34.png

""" 
Range Sum Query 2D - Immutable

Given a 2D matrix matrix, handle multiple queries of the following type:
Calculate the sum of the elements of matrix inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).
Implement the NumMatrix class:
    NumMatrix(int[][] matrix) Initializes the object with the integer matrix matrix.
    int sumRegion(int row1, int col1, int row2, int col2) Returns the sum of the elements of matrix inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).


Example 1:
    Input
        ["NumMatrix", "sumRegion", "sumRegion", "sumRegion"]
        [[[[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]], [2, 1, 4, 3], [1, 1, 2, 2], [1, 2, 2, 4]]
    Output
        [null, 8, 11, 12]
    Explanation
        NumMatrix numMatrix = new NumMatrix([[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]);
        numMatrix.sumRegion(2, 1, 4, 3); // return 8 (i.e sum of the red rectangle)
        numMatrix.sumRegion(1, 1, 2, 2); // return 11 (i.e sum of the green rectangle)
        numMatrix.sumRegion(1, 2, 2, 4); // return 12 (i.e sum of the blue rectangle)


Constraints:
    m == matrix.length
    n == matrix[i].length
    1 <= m, n <= 200
    -105 <= matrix[i][j] <= 105
    0 <= row1 <= row2 < m
    0 <= col1 <= col2 < n
    At most 104 calls will be made to sumRegion.

https://leetcode.com/problems/range-sum-query-2d-immutable
    https://www.notion.so/paulonteri/Object-Oriented-Analysis-and-Design-1a01887a9271475da7b3cd3f4efc9e0d#4925b17f4f7142b88467b45d66602384
"""

class NumMatrix:
    """ 
    Pre-compute the cumulative sums for each row to give O(R) lookup 
    where R in the number of rows requested
    """

    def __init__(self, matrix):
        self.row_sums = [
            [0 for _ in range(len(matrix[0]))]for _ in range(len(matrix))
        ]

        for row_idx in range(len(matrix)):
            running_sum = 0
            for col_idx, num in enumerate(matrix[row_idx]):
                running_sum += num
                self.row_sums[row_idx][col_idx] = running_sum

    def sumRegion(self, row1: int, col1: int, row2: int, col2: int):
        total = 0

        for row_idx in range(row1, row2+1):
            total += self._get_row_sum(self.row_sums[row_idx], col1, col2)

        return total

    def _get_row_sum(self, row, left, right):
        left_val = 0
        if left > 0:
            left_val = row[left-1]
        return row[right] - left_val

# Your NumMatrix object will be instantiated and called as such:
# obj = NumMatrix(matrix)
# param_1 = obj.sumRegion(row1,col1,row2,col2)

""" 

"""

class NumMatrix2:
    """ 
    Here we use the technique of integral image, which is introduced to speed up block computation.
    https://www.notion.so/paulonteri/Object-Oriented-Analysis-and-Design-1a01887a9271475da7b3cd3f4efc9e0d#4925b17f4f7142b88467b45d66602384
    """

    def __init__(self, matrix):

        # build integral image by recurrence relationship
        self.integral_image = [
            [0 for _ in range(len(matrix[0]))] for _ in range(len(matrix))
        ]

        for row in range(len(matrix)):

            running_sum = 0
            for col in range(len(matrix[0])):
                running_sum += matrix[row][col]
                self.integral_image[row][col] = running_sum
                # add top row
                if row > 0:
                    self.integral_image[row][col] += self.integral_image[row-1][col]

    def sumRegion(self, row1: int, col1: int, row2: int, col2: int):

        bottom_right = self.integral_image[row2][col2]
        #
        bottom_left = 0
        if col1 > 0:
            bottom_left = self.integral_image[row2][col1-1]
        #
        top_right = 0
        if row1 > 0:
            top_right = self.integral_image[row1-1][col2]
        #
        top_left = 0
        if col1 > 0 and row1 > 0:
            top_left = self.integral_image[row1 - 1][col1-1]

        # calculate area
        return bottom_right - bottom_left - top_right + top_left

# Your NumMatrix object will be instantiated and called as such:
# obj = NumMatrix(matrix)
# param_1 = obj.sumRegion(row1,col1,row2,col2)

Insert Delete GetRandom O(1) - LeetCode

LFU Cache

LFU CACHE (Leetcode) - Code & Whiteboard

Python concise solution detailed explanation: Two dict + Doubly linked list - LeetCode Discuss

LFU Cache - LeetCode

Design Browser History *

Use a special DLL to manage the history.
Have a current_page pointer pointing to a node in the DLL
back(steps):
- self.current_page = self.current_page.prev for the number of steps
forward(steps):
- self.current_page = self.current_page.nxt for the number of steps
visit(url):
- self.history.remove_all_after_node(self.current_page) <- clear forward history
- DLL.add_node(url)

""" 
1472. Design Browser History

You have a browser of one tab where you start on the homepage and you can visit another url, get back in the history number of steps or move forward in the history number of steps.
Implement the BrowserHistory class:
    BrowserHistory(string homepage) Initializes the object with the homepage of the browser.
    void visit(string url) Visits url from the current page. It clears up all the forward history.
    string back(int steps) Move steps back in history. If you can only return x steps in the history and steps > x, you will return only x steps. Return the current url after moving back in history at most steps.
    string forward(int steps) Move steps forward in history. If you can only forward x steps in the history and steps > x, you will forward only x steps. Return the current url after forwarding in history at most steps.


Example:
    Input:
    ["BrowserHistory","visit","visit","visit","back","back","forward","visit","forward","back","back"]
    [["leetcode.com"],["google.com"],["facebook.com"],["youtube.com"],[1],[1],[1],["linkedin.com"],[2],[2],[7]]
    Output:
    [null,null,null,null,"facebook.com","google.com","facebook.com",null,"linkedin.com","google.com","leetcode.com"]

    Explanation:
        BrowserHistory browserHistory = new BrowserHistory("leetcode.com");
        browserHistory.visit("google.com");       // You are in "leetcode.com". Visit "google.com"
        browserHistory.visit("facebook.com");     // You are in "google.com". Visit "facebook.com"
        browserHistory.visit("youtube.com");      // You are in "facebook.com". Visit "youtube.com"
        browserHistory.back(1);                   // You are in "youtube.com", move back to "facebook.com" return "facebook.com"
        browserHistory.back(1);                   // You are in "facebook.com", move back to "google.com" return "google.com"
        browserHistory.forward(1);                // You are in "google.com", move forward to "facebook.com" return "facebook.com"
        browserHistory.visit("linkedin.com");     // You are in "facebook.com". Visit "linkedin.com"
        browserHistory.forward(2);                // You are in "linkedin.com", you cannot move forward any steps.
        browserHistory.back(2);                   // You are in "linkedin.com", move back two steps to "facebook.com" then to "google.com". return "google.com"
        browserHistory.back(7);                   // You are in "google.com", you can move back only one step to "leetcode.com". return "leetcode.com"


Constraints:
    1 <= homepage.length <= 20
    1 <= url.length <= 20
    1 <= steps <= 100
    homepage and url consist of  '.' or lower case English letters.
    At most 5000 calls will be made to visit, back, and forward.

https://leetcode.com/problems/design-browser-history
"""

class Node:
    def __init__(self, val, nxt, prev):
        self.val = val
        self.prev = prev
        self.nxt = nxt

class DLL:
    def __init__(self, head_val):
        self.head = Node(head_val, None, None)
        self.tail = Node("", None, self.head)
        self.head.nxt = self.tail

    def add_node(self, val):
        prev = self.tail.prev

        node = Node(val, self.tail, prev)

        self.tail.prev = node
        prev.nxt = node

        return node

    def remove_all_after_node(self, node):
        node.nxt = self.tail
        self.tail.prev = node

    # for debugging
    def print_all(self):
        curr = self.head
        res = []
        while curr:
            res.append(curr.val)
            curr = curr.nxt
        print(res)

class BrowserHistory:
    """ 
    - Use a special DLL to manage the history.
    - Have a `current_page` pointer pointing to a node in the DLL
    - `back(steps)`:
        - `self.current_page = self.current_page.prev` for the number of steps
    - `forward(steps)`:
        - `self.current_page = self.current_page.nxt` for the number of steps
    - `visit(url)`:
        - `self.history.remove_all_after_node(self.current_page)` <- clear forward history
        - `DLL.add_node(url)`
    """

    def __init__(self, homepage: str):
        self.history = DLL(homepage)
        self.current_page = self.history.head

    def visit(self, url: str):
        # clear forward history
        self.history.remove_all_after_node(self.current_page)
        # add url to history
        self.current_page = self.history.add_node(url)

    def back(self, steps: int):
        while self.current_page.prev and steps > 0:
            self.current_page = self.current_page.prev
            steps -= 1

        return self.current_page.val

    def forward(self, steps: int):
        # move forward by the steps
        # if greater than the size of the history, fallback to the last page

        # stop the loop at the end of the history (just before the tail)
        while self.current_page.nxt.nxt and steps > 0:
            self.current_page = self.current_page.nxt
            steps -= 1

        return self.current_page.val

# Your BrowserHistory object will be instantiated and called as such:
# obj = BrowserHistory(homepage)
# obj.visit(url)
# param_2 = obj.back(steps)
# param_3 = obj.forward(steps)

Design A Leaderboard - LeetCode

Screenshot 2021-11-09 at 12.53.09.png

Screenshot 2021-11-09 at 12.54.12.png

Screenshot 2021-11-09 at 12.53.55.png

Screenshot 2021-11-09 at 12.54.43.png

Code 2

from sortedcontainers import SortedDict

class Leaderboard:

    def __init__(self):
        self.scores = {}
        self.sortedScores = SortedDict()

    def addScore(self, playerId: int, score: int) -> None:

        # The scores dictionary simply contains the mapping from the
        # playerId to their score. The sortedScores contain a BST with 
        # key as the score and value as the number of players that have
        # that score.     
        if playerId not in self.scores:
            self.scores[playerId] = score
            self.sortedScores[-score] = self.sortedScores.get(-score, 0) + 1
        else:
            preScore = self.scores[playerId]
            val = self.sortedScores.get(-preScore)
            if val == 1:
                del self.sortedScores[-preScore]
            else:
                self.sortedScores[-preScore] = val - 1    

            newScore = preScore + score;
            self.scores[playerId] = newScore
            self.sortedScores[-newScore] = self.sortedScores.get(-newScore, 0) + 1

    def top(self, K: int) -> int:
        count, total = 0, 0;

        for key, value in self.sortedScores.items():
            times = self.sortedScores.get(key)
            for _ in range(times): 
                total += -key;
                count += 1;

                # Found top-K scores, break.
                if count == K:
                    break;

            # Found top-K scores, break.
            if count == K:
                break;

        return total;

    def reset(self, playerId: int) -> None:
        preScore = self.scores[playerId]
        if self.sortedScores[-preScore] == 1:
            del self.sortedScores[-preScore]
        else:
            self.sortedScores[-preScore] -= 1
        del self.scores[playerId];

Read N Characters Given Read4

""" 
157. Read N Characters Given Read4

Given a file and assume that you can only read the file using a given method read4, 
implement a method to read n characters.

Method read4:
    The API read4 reads four consecutive characters from file, then writes those characters into the buffer array buf4.
    The return value is the number of actual characters read.
    Note that read4() has its own file pointer, much like FILE *fp in C.

Definition of read4
    Parameter:  char[] buf4
    Returns:    int

buf4[] is a destination, not a source. The results from read4 will be copied to buf4[].

Below is a high-level example of how read4 works:

    File file("abcde"); // File is "abcde", initially file pointer (fp) points to 'a'
    char[] buf4 = new char[4]; // Create buffer with enough space to store characters
    read4(buf4); // read4 returns 4. Now buf4 = "abcd", fp points to 'e'
    read4(buf4); // read4 returns 1. Now buf4 = "e", fp points to end of file
    read4(buf4); // read4 returns 0. Now buf4 = "", fp points to end of file


Method read:
    By using the read4 method, implement the method read that reads n characters from file and store it in the buffer array buf. 
    Consider that you cannot manipulate file directly.
    The return value is the number of actual characters read.

Definition of read:
    Parameters: char[] buf, int n
    Returns:    int

buf[] is a destination, not a source. You will need to write the results to buf[].

Note:
    Consider that you cannot manipulate the file directly. The file is only accessible for read4 but not for read.
    The read function will only be called once for each test case.
    You may assume the destination buffer array, buf, is guaranteed to have enough space for storing n characters.


Example 1:
    Input: file = "abc", n = 4
    Output: 3
    Explanation: 
        After calling your read method, buf should contain "abc". We read a total of 3 characters from the file, so return 3.
    Note that "abc" is the file's content, not buf. buf is the destination buffer that you will have to write the results to.
Example 2:
    Input: file = "abcde", n = 5
    Output: 5
    Explanation: 
        After calling your read method, buf should contain "abcde". We read a total of 5 characters from the file, so return 5.
Example 3:
    Input: file = "abcdABCD1234", n = 12
    Output: 12
    Explanation: 
        After calling your read method, buf should contain "abcdABCD1234". We read a total of 12 characters from the file, so return 12.
Example 4:
    Input: file = "leetcode", n = 5
    Output: 5
    Explanation: 
        After calling your read method, buf should contain "leetc". We read a total of 5 characters from the file, so return 5.
"""
import math

def read4(buf4): return -1

"""
The read4 API is already defined for you.

    @param buf4, a list of characters
    @return an integer
    def read4(buf4):

# Below is an example of how the read4 API can be called.
file = File("abcdefghijk") # File is "abcdefghijk", initially file pointer (fp) points to 'a'
buf4 = [' '] * 4 # Create buffer with enough space to store characters
read4(buf4) # read4 returns 4. Now buf = ['a','b','c','d'], fp points to 'e'
read4(buf4) # read4 returns 4. Now buf = ['e','f','g','h'], fp points to 'i'
read4(buf4) # read4 returns 3. Now buf = ['i','j','k',...], fp points to end of file
"""

class Solution:
    def read(self, buf, n):
        """
        :type buf: Destination buffer (List[str])
        :type n: Number of characters to read (int)
        :rtype: The number of actual characters read (int)
        """

        buf4 = [""] * 4
        idx = 0
        for _ in range(math.ceil(n/4)):
            # # read characters
            num_read = read4(buf4)

            max_read = num_read
            # ensure we do not read more than required
            # if (idx + num_read - 1) > (n - 1):  # -1 to use indices
            if idx + num_read > n:
                max_read = n-idx

            # # add the read characters to buf
            for num in range(max_read):
                buf[idx] = buf4[num]
                idx += 1

        return idx

Read N Characters Given Read4 II - Call multiple times

""" 
Read N Characters Given Read4 II - Call multiple times:

Given a file and assume that you can only read the file using a given method read4, 
implement a method read to read n characters. Your method read may be called multiple times.

Method read4:
    The API read4 reads four consecutive characters from file, then writes those characters into the buffer array buf4.
    The return value is the number of actual characters read.
    Note that read4() has its own file pointer, much like FILE *fp in C.

Definition of read4:
    Parameter:  char[] buf4
    Returns:    int

buf4[] is a destination, not a source. The results from read4 will be copied to buf4[].

Below is a high-level example of how read4 works:
    File file("abcde"); // File is "abcde", initially file pointer (fp) points to 'a'
    char[] buf4 = new char[4]; // Create buffer with enough space to store characters
    read4(buf4); // read4 returns 4. Now buf4 = "abcd", fp points to 'e'
    read4(buf4); // read4 returns 1. Now buf4 = "e", fp points to end of file
    read4(buf4); // read4 returns 0. Now buf4 = "", fp points to end of file


Method read:
    By using the read4 method, implement the method read that reads n characters from file and store it in the buffer array buf. Consider that you cannot manipulate file directly.
    The return value is the number of actual characters read.

Definition of read:
    Parameters: char[] buf, int n
    Returns:    int

buf[] is a destination, not a source. You will need to write the results to buf[].

Note:
    Consider that you cannot manipulate the file directly. The file is only accessible for read4 but not for read.
    The read function may be called multiple times.
    Please remember to RESET your class variables declared in Solution, as static/class variables are persisted across multiple test cases. Please see here for more details.
    You may assume the destination buffer array, buf, is guaranteed to have enough space for storing n characters.
    It is guaranteed that in a given test case the same buffer buf is called by read.


Example 1:
    Input: file = "abc", queries = [1,2,1]
    Output: [1,2,0]
    Explanation: The test case represents the following scenario:
    File file("abc");
    Solution sol;
    sol.read(buf, 1); // After calling your read method, buf should contain "a". We read a total of 1 character from the file, so return 1.
    sol.read(buf, 2); // Now buf should contain "bc". We read a total of 2 characters from the file, so return 2.
    sol.read(buf, 1); // We have reached the end of file, no more characters can be read. So return 0.
    Assume buf is allocated and guaranteed to have enough space for storing all characters from the file.
Example 2:
    Input: file = "abc", queries = [4,1]
    Output: [3,0]
    Explanation: The test case represents the following scenario:
    File file("abc");
    Solution sol;
    sol.read(buf, 4); // After calling your read method, buf should contain "abc". We read a total of 3 characters from the file, so return 3.
    sol.read(buf, 1); // We have reached the end of file, no more characters can be read. So return 0.

https://leetcode.com/problems/read-n-characters-given-read4-ii-call-multiple-times
# https://leetcode.com/problems/read-n-characters-given-read4-ii-call-multiple-times/discuss/49607/The-missing-clarification-you-wish-the-question-provided
# https://leetcode.com/problems/read-n-characters-given-read4-ii-call-multiple-times/discuss/49601/What-is-the-difference-between-call-once-and-call-multiple-times
"""
from collections import deque

# The read4 API is already defined for you.
def read4(buf4): return -1

class Solution:
    def __init__(self):
        self.read_items_queue = deque()
        self.buf4 = [""] * 4

    def read(self, buf, n):

        prev_read_count = 4
        idx = 0
        # # if we haven't read all the characters yet there are more to be read
        #   more to be read: have items in queue or did not reach end of file (read4)
        while idx < n and (self.read_items_queue or prev_read_count):

            # we have prev characters
            if self.read_items_queue:
                buf[idx] = self.read_items_queue.popleft()
                idx += 1

            # add more characters to the queue
            prev_read_count = read4(self.buf4)
            self.read_items_queue += self.buf4[:prev_read_count]

        return idx

""" 

"""

class Solution_:
    def __init__(self):
        self.queue = []
        self.buf4 = [""] * 4

    def read(self, buf, n):

        num_read = 4
        idx = 0

        while idx < n:

            # we have prev characters
            if self.queue:
                buf[idx] = self.queue.pop(0)
                idx += 1

            # the last time we read we found that we have no more characters
            elif num_read < 4:
                return idx

            # add more characters to the queue
            else:
                num_read = read4(self.buf4)
                self.queue += self.buf4[:num_read]

        return idx

Deck of cards

Design Interview Question: Design a Deck of Cards [Logicmojo.com]

Deck of Cards | Object Oriented Designs

Python OOP - Deck of Cards

# PROBLEM --------------------------------------------------------
""" 
Deck of Cards: 
Design the data structures for a generic deck of cards. 
Explain how you would subclass the data structures to implement blackjack.
"""
from enum import Enum
import random

# SOLUTION --------------------------------------------------------
""" 
# Gather requirements ---------------------------------------

First, we need to recognize that a "generic" deck of cards can mean many things. 
Generic could mean a standard deck of cards that can play a poker-like game, or it could even stretch to Uno or Baseball cards. 
It is important to ask your interviewer what she means by generic.
Let's assume that your interviewer clarifies that the deck is a standard 52-card set, like you might see used in a blackjack or poker game. 

The game might also have a player

# High level design ---------------------------------------

- Card: we have cards:
    - We have 4 groups (suit) of cards:
        - Clubs
        - Diamonds
        - Hearts
        - Spades
    - The cards also have a label (face value):
        - (2-10)
        - Jack
        - Queen
        - King
        - Ace
        # - Jokers
- Deck: We have a deck of cards that is comprised of all of the above groups of cards:
    - cards # will have a list of 54 cards
    - shuffle() => None
    - draw() => Card
- Player: We can have a player that has a hand of cards:
    - name: string
    - hand: have a list of cards
    - draw(deck) => None
    - show_hand() => None
    - discard() => Card

"""

# Constants & Enums ----------------------------------------------------

class Suit(Enum):
    # name = value
    CLUBS = "Clubs"
    DIAMONDS = "Diamonds"
    HEARTS = "Hearts"
    SPADES = "Spades"

class FaceValue(Enum):
    ACE = 1
    TWO = 2
    THREE = 3
    FOUR = 4
    FIVE = 5
    SIX = 6
    SEVEN = 7
    EIGHT = 8
    NINE = 9
    TEN = 10
    JACK = 11
    QUEEN = 12
    KING = 13

# Classes ----------------------------------------------------

class Card:
    def __init__(self, suit, face_value):
        self.suit = suit
        self.face_value = face_value

    def __str__(self):
        return f"{self.face_value.name} of {self.suit.name}"

    def get_value(self):
        return self.face_value.value

class Deck:
    def __init__(self):
        self.cards = []
        self._create_deck()

    def draw(self):
        """Return the top card"""
        return self.cards.pop()

    def shuffle(self, num=1):
        """Shuffle the deck"""
        length = len(self.cards)
        for _ in range(num):
            # This is the fisher yates shuffle algorithm
            for i in range(length-1, 0, -1):
                randi = random.randint(0, i)
                if i == randi:
                    continue
                self.cards[i], self.cards[randi] = self.cards[randi], self.cards[i]

    def show_cards(self):
        for card in self.cards:
            print(card)

    def _create_deck(self):
        """Generate 52 cards"""
        for suit in Suit:
            for face_value in FaceValue:
                self.cards.append(Card(suit, face_value))

class Player:
    def __init__(self, name):
        self.name = name
        self.hand = []

    def draw(self, deck):
        """Pick card from the deck"""
        self.hand.append(deck.draw())

    def show_hand(self):
        for card in self.hand:
            print(card)

    def discard(self):
        return self.hand.pop()

# Test making a Deck
deck = Deck()
deck.shuffle()
deck.show_cards()

bob = Player("Bob")
print(bob.name)
bob.draw(deck)
bob.draw(deck)
bob.draw(deck)
bob.show_hand()

Movie Ticket Booking System

Movie Ticket Booking System || Object Oriented Design || Case Study - LeetCode Discuss

Parking lot

Parking Lot Design | Object Oriented Design Interview Question

Object Oriented Design Interview Question Design a Car Parking Lot

System Design Interview Question: DESIGN A PARKING LOT - asked at Google, Facebook

""" 
Parking Lot: Design a parking lot using object-oriented principles.

https://youtu.be/tVRyb4HaHgw
"""
from datetime import datetime
from typing import List
from abc import ABC, abstractmethod

""" 

# Gather requirements ---------------------------------------

The wording of this question is vague, just as it would be in an actual interview. 
- Can have 10000 - 3000 parking lots
- Will have 4 entries and 4 exits
    - will print ticket
- Parking spot is assigned at the gate
    - Should be the closest to the gate
- Will have a limit on capacity
- Diffrent parking spots
    - Handicap
    - Compact
    - Large
    - Motorcycle
- Will have hourly rates
- Can pay via Cash or Credit Card
- Will have monitoring system
- Should be able to be used on diffrent parking lot systems

# High level design ---------------------------------------

## ParkingSpot:
- id: int
- location: int[2]
- reserved: bool
- is_reserved: bool

    ### HandicapParkingSpot:
    ### CompactParkingSpot:
    ### LargeParkingSpot:
    ### MotorcycleParkingSpot:
- type: Enum(Handicap, Compact, Large, Motorcycle) not used as it will violate the open/closed principle - adding new types will require changes to the code

## ParkingTicket:
- id: int
- parking_spot: ParkingSpot (has type and id)
- issued_at: datetime

## RateCalculator:
- rate_per_hour: float

## ParkingSpotAssigner: # https://youtu.be/tVRyb4HaHgw?t=996
- assign_spot(Terminal): ParkingSpot 

## PaymentCalculator:
- calculate_payment(ParkingTicket): int

## PaymentProcessor:
    - process_payment(amount:float): None
    ### CashPaymentProcessor:
    ### CreditCardPaymentProcessor:

## Terminal:
- id: int
- location: int[2]
- get_id(): => int

    ### EntryTerminal:
    - closest_spots: ParkingSpot[] <-- will actually be a priority list/ mean heap
    - enter(Vehicle): ParkingTicket
        assign spot using ParkingSpotAssigner
        _create_ticket(ParkingSpot)
    - _create_ticket(ParkingSpot): ParkingTicket
    - remove_parking_spot_from_closest_spots(ParkingSpot): None
    - add_parking_spot_to_closest_spots(ParkingSpot): None
    ### ExitTerminal:
    - exit(ParkingTicket): bool
        calculate payment using PaymentCalculator
        charge payment using PaymentProcessor
        free ParkingSpot

## Monitor/Logger:
## ParkingLotSystem: <- will be singleton
- entry_terminals: EntryTerminals[]
- exit_terminals: ExitTerminals[]
- available_spots: ParkingSpot[]
- reserved_spots: ParkingSpot[]
- _create_parking_spots(n:int): None
- _create_terminals(number_of_entry_terminals: int, number_of_exit_terminals: int): None
- park_vehicle(terminal:EntryTerminal): ParkingTicket
- remove_vehicle(terminal:ExitTerminal): ParkingTicket
- get_entry_terminals(): EntryTerminal[]
- is_full(): bool

## Vehicle:? - no need to use it
-> not needed
-> is an actor
-> not needed as this is not a simulation

"""

# TODO: remove vehicle

# ParkingSpot

class ParkingSpot(ABC):
    def __init__(self, id, x_location, y_location):
        self.id = id
        self.reserved = False
        self.location = [x_location, y_location]

    def is_reserved(self):
        return self.reserved

    @abstractmethod
    def occupy_spot(self):
        pass

class HandicapParkingSpot(ParkingSpot):
    def __init_(self, id, x_location, y_location):
        return super().__init__(id, x_location, y_location)

    def occupy_spot(self):
        pass

class CompactParkingSpot(ParkingSpot):
    def __init_(self, id, x_location, y_location):
        return super().__init__(id, x_location, y_location)

    def occupy_spot(self):
        pass

class LargeParkingSpot(ParkingSpot):
    def __init_(self, id, x_location, y_location):
        return super().__init__(id, x_location, y_location)

    def occupy_spot(self):
        pass

class MotorcycleParkingSpot(ParkingSpot):
    def __init_(self, id, x_location, y_location):
        return super().__init__(id, x_location, y_location)

    def occupy_spot(self):
        pass

# ParkingTicket

class ParkingTicket:
    def __init__(self, id, parking_spot: 'ParkingSpot'):
        self.id = id
        self.parking_spot = parking_spot
        self.issued_at = datetime.now()

# RateCalculator

class RateCalculator:
    def __init__(self, rate_per_hour):
        self.rate_per_hour = rate_per_hour

    def calculate_rate(self, parking_ticket: 'ParkingTicket'):
        pass

# ParkingSpotAssigner

class ParkingSpotAssigner:
    def __init__(self):
        pass

    def assign_spot(self, terminal: 'Terminal'):
        pass

# PaymentCalculator

class PaymentCalculator:

    def calculate_payment(self, parking_ticket: 'ParkingTicket'):
        pass

# PaymentProcessor

class PaymentProcessor(ABC):
    def __init__(self, amount: float):
        self.amount = amount

    @abstractmethod
    def process_payment(self, amount: float):
        pass

class CashPaymentProcessor(PaymentProcessor):
    def __init__(self, amount: float):
        super().__init__(amount)

    def process_payment(self, amount: float):
        pass

class CreditCardPaymentProcessor(PaymentProcessor):
    def __init__(self, amount: float):
        super().__init__(amount)

    def process_payment(self, amount: float):
        pass

# Terminal

class Terminal(ABC):
    def __init__(self, id: int, location: List[int],):
        self.id = id
        self.location = location

    def get_id(self):
        return self.id

class EntryTerminal(Terminal):
    def __init__(self, id: int, location: List[int], parking_spots: 'List[ParkingSpot]'):
        super().__init__(id, location)
        self.closest_spots = []  # should be a priority queue

    def enter(self):
        pass

    def _create_ticket(self, parking_spot: 'ParkingSpot'):
        pass

    def remove_parking_spot_from_closest_spots(self, parking_spot: 'ParkingSpot'):
        pass

    def add_parking_spot_to_closest_spots(self, parking_spot: 'ParkingSpot'):
        pass

class ExitTerminal(Terminal):
    def __init__(self, id: int, location: List[int], parking_spots: 'List[ParkingSpot]'):
        super().__init__(id, location)

    def exit(self):
        pass

# Monitor/Logger

class Logger:
    pass

# ParkingLotSystem

class ParkingLotSystem:
    def __init__(self, number_of_parking_spots: int, number_of_entry_terminals: int, number_of_exit_terminals: int):
        self.available_spots = []
        self.reserved_spots = []
        self._create_parking_spots(number_of_parking_spots)
        self.entry_terminals = []
        self.exit_terminals = []
        self._create_terminals(number_of_entry_terminals,
                               number_of_exit_terminals)

    def park_vehicle(self, terminal: 'EntryTerminal'):
        pass

    def remove_vehicle(self, terminal: 'ExitTerminal'):
        pass

    def is_full(self):
        pass

    def get_entry_terminals(self):
        pass

    def _create_parking_spots(self, number_of_parking_spots: int):
        pass

    def _create_terminals(self, number_of_entry_terminals: int, number_of_exit_terminals: int):
        pass

Design file system

"""
# Gather requirements ---------------------------------------

- Have files
- Have folders
    - can contain files and folders
- Files and folders have
    - name
    - time_last_accessed
    - time_created
    - time_last_modified
    - path
    - delete()

- Can delete file & folder
- Can change name

# High level design ---------------------------------------

## FileAndFolderStructure
- name
- parent
- time_last_accessed
- time_created
- time_last_modified
- path(): str
- size(): float
- change_name(): str
- delete(): None
- get_time_last_accessed(): str
- get_time_created(): str
- get_time_last_modified(): str

    ### File
    - file_size
    ### Folder
    - children{,}
    - delete_child()
    - add_child(FileAndFolderStructure): bool
    - is_empty(): bool

"""

from abc import ABC, abstractmethod
from datetime import datetime

class FileAndFolderStructure(ABC):
    def __init__(self, name: str, parent: 'Folder|None'):
        self.name = name
        self.parent = parent
        self.time_last_accessed = datetime.now()
        self.time_created = datetime.now()
        self.time_last_modified = datetime.now()

    @abstractmethod
    def size(self):
        pass

    @abstractmethod
    def delete(self):
        pass

    @property
    def path(self):
        if not self.parent:
            return ""  # root dir
        else:
            return self.parent.path + "/" + self.name

    def change_name(self, name):
        self.name = name
        return self.name

    def get_time_last_accessed(self):
        return self.time_last_accessed

    def get_time_created(self):
        return self.time_created

    def get_time_last_modified(self):
        return self.time_last_modified

class File(FileAndFolderStructure):

    def __init__(self, name: str, parent: 'Folder', file_size):
        super().__init__(name, parent)
        self.file_size = file_size

    def size(self):
        return self.file_size

    def delete(self):
        self.parent.delete_child(self)

class Folder(FileAndFolderStructure):
    def __init__(self, name: str, parent: 'Folder|None'):
        super().__init__(name, parent)
        self.children = set()

    def size(self):
        total_size = 0
        for child in self.children:
            total_size += child.size()
        return total_size

    def delete(self):
        for child in self.children:
            child.delete()
        if self.parent:
            self.parent.delete_child(self)

    def add_child(self, child: 'FileAndFolderStructure'):
        self.children.add(child)
        return True

    def delete_child(self, child: 'FileAndFolderStructure'):
        if child in self.children:
            self.children.remove(child)
            return True
        return False

    def is_empty(self):
        return len(self.children) == 0

root = Folder("root", None)

pictures = Folder("pictures", root)

paul_png = File("paul.png", pictures, 22)

print(root.path)  #
print(pictures.path)  # /pictures/paul.png
print(paul_png.name)  # paul.png
print(paul_png.path)  # /pictures/paul.png

Design Unix File Search API / Linux Find Command

# Design Unix File Search API / Linux Find Command
""" 
As for what I would expect (not necessarily all of these):
    - Obviously coming straight to the right design (encapsulating the Filtering logic into its own interface etc...), with an explanation on why this approach is good. I'm obviously open to alternate approaches as long as they are as flexible and elegant.
    - Implement boolean logic: AND/OR/NOT, here I want to see if the candidate understands object composition
    - Support for symlinks. Rather than seeing the implementation (which I don't really care about) I want to understand the tradeoffs of adding yet another parameter to the find method VS other options (eg. Constructor). Keep adding params to a method is usually bad.
    - How to handle the case where the result is really big (millions of files), and you may not be able to put all of them into a List.
"""
from abc import ABC, abstractmethod
from collections import deque
from typing import List

# File
# - no need to implement different files & directories as that will not be used in this system

class File:
    def __init__(self, name, size):
        self.name = name
        self.size = size
        self.children = []
        self.is_directory = False if '.' in name else True
        self.children = []
        self.extension = name.split(".")[1] if '.' in name else ""

    def __repr__(self):
        return "{"+self.name+"}"

# Filters

class Filter(ABC):
    def __init__(self):
        pass

    @abstractmethod
    def apply(self, file):
        pass

class MinSizeFilter(Filter):
    def __init__(self, size):
        self.size = size

    def apply(self, file):
        return file.size > self.size

class ExtensionFilter(Filter):
    def __init__(self, extension):
        self.extension = extension

    def apply(self, file):
        return file.extension == self.extension

# LinuxFindCommand

class LinuxFind():
    def __init__(self):
        self.filters: List[Filter] = []

    def add_filter(self, given_filter):
        # validate given_filter is a filter
        if isinstance(given_filter, Filter):
            self.filters.append(given_filter)

    def apply_OR_filtering(self, root):
        found_files = []

        # bfs
        queue = deque()
        queue.append(root)
        while queue:
            # print(queue)
            curr_root = queue.popleft()
            if curr_root.is_directory:
                for child in curr_root.children:
                    queue.append(child)
            else:
                for filter in self.filters:
                    if filter.apply(curr_root):
                        found_files.append(curr_root)
                        print(curr_root)
                        break
        return found_files

    def apply_AND_filtering(self, root):
        found_files = []

        # bfs
        queue = deque()
        queue.append(root)
        while queue:
            curr_root = queue.popleft()
            if curr_root.is_directory:
                for child in curr_root.children:
                    queue.append(child)
            else:
                is_valid = True
                for filter in self.filters:
                    if not filter.apply(curr_root):
                        is_valid = False
                        break
                if is_valid:
                    found_files.append(curr_root)
                    print(curr_root)

        return found_files

f1 = File("root_300", 300)

f2 = File("fiction_100", 100)
f3 = File("action_100", 100)
f4 = File("comedy_100", 100)
f1.children = [f2, f3, f4]

f5 = File("StarTrek_4.txt", 4)
f6 = File("StarWars_10.xml", 10)
f7 = File("JusticeLeague_15.txt", 15)
f8 = File("Spock_1.jpg", 1)
f2.children = [f5, f6, f7, f8]

f9 = File("IronMan_9.txt", 9)
f10 = File("MissionImpossible_10.rar", 10)
f11 = File("TheLordOfRings_3.zip", 3)
f3.children = [f9, f10, f11]

f11 = File("BigBangTheory_4.txt", 4)
f12 = File("AmericanPie_6.mp3", 6)
f4.children = [f11, f12]

greater5_filter = MinSizeFilter(5)
txt_filter = ExtensionFilter("txt")

my_linux_find = LinuxFind()
my_linux_find.add_filter(greater5_filter)
my_linux_find.add_filter(txt_filter)

print(my_linux_find.apply_OR_filtering(f1))
print(my_linux_find.apply_AND_filtering(f1))

package linux_find_command;

// https://www.programmersought.com/article/31817103996/

/*
As for what I would expect (not necessarily all of these):
    - Obviously coming straight to the right design (encapsulating the Filtering logic into its own interface etc...), with an explanation on why this approach is good. I'm obviously open to alternate approaches as long as they are as flexible and elegant.
    - Implement boolean logic: AND/OR/NOT, here I want to see if the candidate understands object composition
    - Support for symlinks. Rather than seeing the implementation (which I don't really care about) I want to understand the tradeoffs of adding yet another parameter to the find method VS other options (eg. Constructor). Keep adding params to a method is usually bad.
    - How to handle the case where the result is really big (millions of files), and you may not be able to put all of them into a List.
*/

// "static void main" must be defined in a public class.
public class LinuxFindCommand {
    public static void main(String[] args) {
      new LinuxFindCommand().test();
    }

    private void test() {
      SearchParams params = new SearchParams();
      params.extension = "xml";
      params.minSize = 2;
      params.maxSize = 100;

      File xmlFile = new File();
      xmlFile.setContent("aaa.xml".getBytes());
      xmlFile.name = "aaa.xml";

      File txtFile = new File();
      txtFile.setContent("bbb.txt".getBytes());
      txtFile.name = "bbb.txt";

      File jsonFile = new File();
      jsonFile.setContent("ccc.json".getBytes());
      jsonFile.name = "ccc.json";

      Directory dir1 = new Directory();
      dir1.addEntry(txtFile);
      dir1.addEntry(xmlFile);

      Directory dir0 = new Directory();
      dir0.addEntry(jsonFile);
      dir0.addEntry(dir1);

      FileSearcher searcher = new FileSearcher();
      System.out.println(searcher.search(dir0, params));
    }

    // Files

    public interface IEntry {

      String getName();

      void setName(String name);

      int getSize();

      boolean isDirectory();
    }


    private abstract class Entry implements IEntry {
      protected String name;

      @Override
      public String getName() {
        return name;
      }

      @Override
      public void setName(String name) {
        this.name = name;
      }

    }


    public class File extends Entry {
      private byte[] content;

      public String getExtension() {
        return name.substring(name.indexOf(".") + 1);
      }

      public void setContent(byte[] content) {
        this.content = content;
      }

      public byte[] getContent() {
        return content;
      }

      @Override
      public int getSize() {
        return content.length;
      }

      @Override
      public boolean isDirectory() {
        return false;
      }

      @Override
      public String toString() {
        return "File{" +
          "name='" + name + '\'' +
          '}';
      }
    }

    public class Directory extends Entry {
        private List<Entry> entries = new ArrayList<>();

      @Override
      public int getSize() {
        int size = 0;
        for (Entry entry  : entries) {
          size += entry.getSize();
        }

        return size;
      }

      @Override
      public boolean isDirectory() {
        return true;
      }

      public void addEntry(Entry entry) {
        this.entries.add(entry);
      }
    }

    //  Filters

    public class SearchParams {
      String extension;
      Integer minSize;
      Integer maxSize;
      String name;
    }

    public interface IFilter {

        boolean isValid(SearchParams params, File file);

    }

    public class ExtensionFilter implements IFilter {

      @Override
      public boolean isValid(SearchParams params, File file) {
        if (params.extension == null) {
          return true;
        }

        return file.getExtension().equals(params.extension);
      }

    }

    public class MinSizeFilter implements IFilter {

      @Override
      public boolean isValid(SearchParams params, File file) {
        if (params.minSize == null) {
          return true;
        }

        return file.getSize() >= params.minSize;
      }

    }

    public class MaxSizeFilter implements IFilter {

      @Override
      public boolean isValid(SearchParams params, File file) {
        if (params.maxSize == null) {
          return true;
        }

        return file.getSize() <= params.maxSize;
      }

    }

    public class NameFilter implements IFilter {

      @Override
      public boolean isValid(SearchParams params, File file) {
        if (params.name == null) {
        return true;
        }

        return file.getName().equals(params.name);
      }

    }

    public class FileFilter {
      private final List<IFilter> filters = new ArrayList<>();

      public FileFilter() {
        filters.add(new NameFilter());
        filters.add(new MaxSizeFilter());
        filters.add(new MinSizeFilter());
        filters.add(new ExtensionFilter());
      }

      public boolean isValid(SearchParams params, File file) {
        for (IFilter filter : filters) {
          if (!filter.isValid(params, file)) {
            return false;
          }
        }

        return true;
      }

    }

    // Searcher

    public class FileSearcher {
      private FileFilter filter = new FileFilter();

      public List<File> search(Directory dir, SearchParams params) {
        List<File> files = new ArrayList<>();

        Queue<Directory> queue = new LinkedList<>();
        queue.add(dir);

        while (!queue.isEmpty()) {
          Directory folder = queue.poll();

          for (IEntry entry : folder.entries) {
            if (entry.isDirectory()) {
            queue.add((Directory) entry);
            } else {
            File file = (File) entry;
            if (filter.isValid(params, file)) {
              files.add(file);
            }
            }
          }
        }

        return files;
        }
    }

  }

Design elevator

""" 
# Design an elevator
https://youtu.be/siqiJAJWUVg
https://thinksoftware.medium.com/elevator-system-design-a-tricky-technical-interview-question-116f396f2b1c
"""

"""
## Requirements collection ------------------------------------------------------------

- elevator system
    - can have around 200 floors
    - with 50 elevator cars
    - minimise wait time of system/passenger
    - high throughput
    - reduce power usage / cost
    - can have operational zones: like floor 20-30
        - we will assume that this system we are building will work for one specific zone only
            it can then be replicated for the other zones
- elevator cars
    - has three states: UP, DOWN & IDLE
    - can transfer passengers from one floor to another
    - can only open door whn idle
    - max_load
    - max_speed
- emergency alarms
- VIP
- monitoring systems

## Use cases  ------------------------------------------------------------------s

1. Calling the elevator
2. Move/Stop elevators
3. Directions
4. Floor
5. Emergency call
5. Emergency floor

## High level design ------------------------------------------------------------------

### Door
- is_open
- open()
- close()

### ElevatorCarMotion
- move(floor: int)
- stop()

### ElevatorCar
- door: Door

### Floor
- button_panel: ButttonPanel

### Button
- is_pressed()
- press()

    #### HallButton
    - press()
    #### ElevatorButton
    - press()

### ButttonPanel
- botton: HallButton

### Dispatcher https://www.youtube.com/watch?v=siqiJAJWUVg&t=1205s
=> can use first-come-first-serve with queue
    send nearest (idle) or (moving in same direction towards passenger) elevator to passenger
=> shortest seek time first
    - use pq or array of floors
    - find closest passengers
=> scan

### Monitor/Logger

### ElevatorSystem

### Passenger?
=> not needed
=> is an actor
=> not needed as this is not a simulation

"""

Design hashtable

Data Structures: Hash Tables

Hash Tables - Beau teaches JavaScript

- use a hashfunction to tranform key to an index in array
    -  hashfunction
        - convert string to interger?
- the array has a linked list at each index
    - each node can point back to the original list
    - wehn we run out of space in the array, we implement resizing

## Collision handling
- Chaining
    - store in linked list

Object-oriented programming (OOP) is a style of programming that focuses on using objects to design and build applications. Contrary to procedure-oriented programming where programs are designed as blocks of statements to manipulate data, OOP organises the program to combine data and functionality and wrap it inside something called an “Object”.

Basic concepts of OOP:

Objects: Objects represent a real-world entity and the basic building block of OOP. For example, an Online Shopping System will have objects such as shopping cart, customer, product item, etc.
Class: Class is the prototype or blueprint of an object. It is a template definition of the attributes and methods of an object. For example, in the Online Shopping System, the Customer object will have attributes like shipping address, credit card, etc., and methods for placing an order, cancelling an order, etc.

Screenshot 2021-11-08 at 05.22.57.png

The four principles of object-oriented programming are encapsulation, abstraction, inheritance, and polymorphism.

Encapsulation: Encapsulation is the mechanism of binding the data together and hiding it from the outside world. Encapsulation is achieved when each object keeps its state private so that other objects don’t have direct access to its state. Instead, they can access this state only through a set of public functions.
Abstraction: Abstraction can be thought of as the natural extension of encapsulation. It means hiding all but the relevant data about an object in order to reduce the complexity of the system. In a large system, objects talk to each other, which makes it difficult to maintain a large codebase; abstraction helps by hiding internal implementation details of objects and only revealing operations that are relevant to other objects.
Inheritance: Inheritance is the mechanism of creating new classes from existing ones.
Polymorphism: Polymorphism (from Greek, meaning “many forms”) is the ability of an object to take different forms and thus, depending upon the context, to respond to the same message in different ways. Take the example of a chess game; a chess piece can take many forms, like bishop, castle, or knight and all these pieces will respond differently to the ‘move’ message

Theory

GitHub - knightsj/object-oriented-design: 面向对象设计的设计原则和设计模式

Constructors in Python

__init__() function. This special function gets called whenever a new object of that class is instantiated. This type of function is also called constructor in Object-Oriented Programming (OOP). We normally use it to initialise all the variables.

class ComplexNumber:
    def __init__(self, r=0, i=0):
        self.real = r
        self.imag = i

    def get_data(self):
        print(f'{self.real}+{self.imag}j')

# Create a new ComplexNumber object
num1 = ComplexNumber(2, 3)

# Call get_data() method
# Output: 2+3j
num1.get_data()

# Create another ComplexNumber object
# and create a new attribute 'attr'
num2 = ComplexNumber(5)
num2.attr = 10

# Output: (5, 0, 10)
print((num2.real, num2.imag, num2.attr))

# but c1 object doesn't have attribute 'attr'
# AttributeError: 'ComplexNumber' object has no attribute 'attr'
print(num1.attr)

Output

2+3j
(5, 0, 10)
Traceback (most recent call last):
  File "<string>", line 27, in <module>
    print(num1.attr)
AttributeError: 'ComplexNumber' object has no attribute 'attr'

In the above example, we defined a new class to represent complex numbers. It has two functions, __init__() to initialize the variables (defaults to zero) and get_data() to display the number properly.

An interesting thing to note in the above step is that attributes of an object can be created on the fly. We created a new attribute attr for object num2 and read it as well. But this does not create that attribute for object num1.

Inheritance

Inheritance is a way of creating a new class for using details of an existing class without modifying it. The newly formed class is a derived class (or child class). Similarly, the existing class is a base class (or parent class).

We use the super() function inside the init() method. This allows us to run the init() method of the parent class inside the child class.

# parent class
class Bird:

    def __init__(self):
        print("Bird is ready")

    def whoisThis(self):
        print("Bird")

    def swim(self):
        print("Swim faster")

# child class
class Penguin(Bird):

    def __init__(self):
        # call super() function
        super().__init__() # *************
        print("Penguin is ready")

    def whoisThis(self):
        print("Penguin")

    def run(self):
        print("Run faster")

peggy = Penguin()
peggy.whoisThis()
peggy.swim()
peggy.run()

Screenshot 2021-10-11 at 21.30.49.png

class Polygon:
    def __init__(self, no_of_sides):
        self.n = no_of_sides
        self.sides = [0 for i in range(no_of_sides)]

    def inputSides(self):
        self.sides = [float(input("Enter side "+str(i+1)+" : ")) for i in range(self.n)]

    def dispSides(self):
        for i in range(self.n):
            print("Side",i+1,"is",self.sides[i])

class Triangle(Polygon):
    def __init__(self):
        **super().__init__(self,3)**

    def findArea(self):
        a, b, c = self.sides
        # calculate the semi-perimeter
        s = (a + b + c) / 2
        area = (s*(s-a)*(s-b)*(s-c)) ** 0.5
        print('The area of the triangle is %0.2f' %area)

>>> t = Triangle()

>>> t.inputSides()
Enter side 1 : 3
Enter side 2 : 5
Enter side 3 : 4

>>> t.dispSides()
Side 1 is 3.0
Side 2 is 5.0
Side 3 is 4.0

>>> t.findArea()
The area of the triangle is 6.00

Method Overriding in Python

In the above example, notice that __init__() method was defined in both classes, Triangle as well in Polygon. When this happens, the method in the derived class overrides that in the base class. This is to say, __init__() in Triangle gets preference over the __init__ in Polygon.

Generally, when overriding a base method, we tend to extend the definition rather than simply replace it. The same is being done by calling the method in the base class from the one in the derived class (calling Polygon.__init__() from __init__() in Triangle).

A better option would be to use the built-in function super(). So, super().__init__(3) is equivalent to Polygon.__init__(self,3) and is preferred.

Composition vs Inheritance

Encapsulation

Encapsulation: Encapsulation is the mechanism of binding the data together and hiding it from the outside world. Encapsulation is achieved when each object keeps its state private so that other objects don’t have direct access to its state. Instead, they can access this state only through a set of public functions.

Using OOP in Python, we can restrict access to methods and variables. This prevents data from direct modification which is called encapsulation. In Python, we denote private attributes using underscore as the prefix i.e single _ or double __.

class Computer:

    def __init__(self):
        self.__maxprice = 900

    def sell(self):
        print("Selling Price: {}".format(self.__maxprice))

    def setMaxPrice(self, price):
        self.__maxprice = price

c = Computer()
c.sell() # Selling Price: 900

# change the price
c.__maxprice = 1000
c.sell() # Selling Price: 900

# using setter function
c.setMaxPrice(1000)
c.sell() # Selling Price: 1000

In the above program, we defined a Computer class.

We used __init__() method to store the maximum selling price of the Computer. We tried to modify the price. However, we can't change it because Python treats the __maxprice as private attributes. As shown, to change the value, we have to use a setter function i.e setMaxPrice() which takes price as a parameter.

Abstraction

Abstraction: Abstraction can be thought of as the natural extension of encapsulation. It means hiding all but the relevant data about an object in order to reduce the complexity of the system. In a large system, objects talk to each other, which makes it difficult to maintain a large codebase; abstraction helps by hiding internal implementation details of objects and only revealing operations that are relevant to other objects.

Abstract Classes

Python Abstract Class

Beginner's guide to abstract base class in Python

In object-oriented programming, an abstract class is a class that cannot be instantiated. However, you can create classes that inherit from an abstract class. Typically, you use an abstract class to create a blueprint for other classes.

Similarly, an abstract method is an method without an implementation. An abstract class may or may not include abstract methods.

Python doesn’t directly support abstract classes. But it does offer a module that allows you to define abstract classes.

To define an abstract class, you use the abc (abstract base class) module.

The abc module provides you with the infrastructure for defining abstract base classes.

from abc import ABC, abstractmethod

class AbstractClassName(ABC):
    @abstractmethod
    def abstract_method_name(self):
        pass

Example

from abc import ABC, abstractmethod

class Employee(ABC):
    def __init__(self, first_name, last_name):
        self.first_name = first_name
        self.last_name = last_name

    @property
    def full_name(self):
        return f"{self.first_name} {self.last_name}"

    @abstractmethod
    def get_salary(self):
        pass

class FulltimeEmployee(Employee):
    def __init__(self, first_name, last_name, salary):
        super().__init__(first_name, last_name)
        self.salary = salary

    def get_salary(self):
        return self.salary

class HourlyEmployee(Employee):
    def __init__(self, first_name, last_name, worked_hours, rate):
        super().__init__(first_name, last_name)
        self.worked_hours = worked_hours
        self.rate = rate

    def get_salary(self):
        return self.worked_hours * self.rate

Polymorphism *

Polymorphism (from Greek, meaning “many forms”) is the ability of an object to take different forms and thus, depending upon the context, to respond to the same message in different ways. Take the example of a chess game; a chess piece can take many forms, like bishop, castle, or knight and all these pieces will respond differently to the ‘move’ message

Polymorphism is an ability (in OOP) to use a common interface for multiple forms (data types).

Suppose, we need to color a shape, there are multiple shape options (rectangle, square, circle). However we could use the same method to color any shape. This concept is called Polymorphism.

Polymorphism means "many forms", it means to have different functions in different situation, just like functions keys on keyboard, same key but with different functions in different pages. B,C,D inherits from A and have same function but performs differently when is called.

class Parrot:

    def fly(self):
        print("Parrot can fly")

    def swim(self):
        print("Parrot can't swim")

class Penguin:

    def fly(self):
        print("Penguin can't fly")

    def swim(self):
        print("Penguin can swim")

# common interface
def flying_test(bird):
    bird.fly()

#instantiate objects
blu = Parrot()
peggy = Penguin()

# passing the object
flying_test(blu)
flying_test(peggy)

Class & Static attributes

Screenshot 2021-10-17 at 18.02.19.png

class Parrot:

    # class attribute
    species = "bird"
    names = []

    # instance attribute
    def __init__(self, name, age):
        self.name = name
        self.names.append(self.name)
        self.age = age

# instantiate the Parrot class
blu = Parrot("Blu", 10)
woo = Parrot("Woo", 15)

# access the class attributes
print("Blu is a {}".format(blu.species))  # Blu is a bird
print("Woo is also a {}".format(woo.species))  # Woo is also a bird

# access the class attributes
print(Parrot.names)  # ['Blu', 'Woo']
print("Blu is a {}".format(blu.names))  # Blu is a ['Blu', 'Woo']
print("Woo is also a {}".format(woo.names))  # Woo is also a ['Blu', 'Woo']

# access the instance attributes
print("{} is {} years old".format(blu.name, blu.age)) # Blu is 10 years old
print("{} is {} years old".format(woo.name, woo.age)) # Woo is 15 years old

Class & Static methods

Python Tutorial - Static and Class Methods - techwithtim.net

class myClass:
    count = 0

    def __init__(self, x):
        self.x = x

    @staticmethod
    def staticMethod():
        return "i am a static method"
        # Notice staticMethod does not require the self parameter
        # use as function without access to items in the class eg: instance variables
        # eg: used in creating libraries like math, random, etc

    @classmethod
    def classMethod(cls):
        cls.count += 1
        return cls.count
        # The classMethod can access and modify class variables. It takes the class name as a required parameter

print(myClass.staticMethod())  # i am a static method
print(myClass.classMethod())  # 1
print(myClass.classMethod())  # 2

Private and Public Classes

class _Private:
    def __init__(self, name):
        self.name = name

class NotPrivate:
    def __init__(self, name):
        self.name = name
        # Even though we decalre something private we can still call and us it
        self.priv = _Private(name)

    def _dispaly(self):  # Private
        print("Hello")

    def display(self):  # Public
        print("Hi")

Operator Overloading

Overloading the numerical operators

Python Operator Overloading

class Point:
    def __init__(self, x=0, y=0):
        self.x = x
        self.y = y

    def __str__(self):
        return "({0},{1})".format(self.x, self.y)

    def __add__(self, other):
        x = self.x + other.x
        y = self.y + other.y
        return Point(x, y)

p1 = Point(1, 2)
p2 = Point(2, 3)

print(p1+p2) # (3,5)

What actually happens is that, when you use p1 + p2, Python calls p1.**add**(p2) which in turn is Point.**add**(p1,p2). After this, the addition operation is carried out the way we specified.

Overloading Comparison Operators

# overloading the less than operator
class Point:
    def __init__(self, x=0, y=0):
        self.x = x
        self.y = y

    def __str__(self):
        return "({0},{1})".format(self.x, self.y)

    def __lt__(self, other):
        self_mag = (self.x ** 2) + (self.y ** 2)
        other_mag = (other.x ** 2) + (other.y ** 2)
        return self_mag < other_mag

p1 = Point(1,1)
p2 = Point(-2,-3)
p3 = Point(1,-1)

# use less than
print(p1<p2) # True
print(p2<p3) # False
print(p1<p3) # False

Singleton

Python Design Patterns - Singleton

class Singleton:
   __instance = None

   @staticmethod 
   def getInstance():
      """ Static access method. """
      if Singleton.__instance == None:
         Singleton()
      return Singleton.__instance

   def __init__(self):
      """ Virtually private constructor. """
      if Singleton.__instance != None:
         raise Exception("This class is a singleton!")
      else:
         Singleton.__instance = self

s = Singleton()
print s

s = Singleton.getInstance()
print s

s = Singleton.getInstance()
print s

Quick tips

hash

Typically used in hashing. For example while storing a class in a dictionary(hashmap)

from typing import List

class ContactNames:
    def __init__(self, names: List):
        # names is a list of strings
        self.names = names

    def __hash__(self):
        # https://www.programiz.com/python-programming/methods/built-in/hash
        # Conceptually we want to hash the set of names,
        # Since the set type is mutable, it cannot be hashed. Therefore, we use a frozenset. (https://www.notion.so/paulonteri/Hash-Tables-220d9f0e409044c58ec6c2b0e7fe0ab5#a33b73089b544532bddb600fff546306)
        # return hash(self.names) # -> TypeError: unhashable type: 'list'
        return hash(frozenset(self.names)) # we use the built-in hash() function

    def __eq__(self, other):
        return set(self.names) == set(other.names)

    def __str__(self):
        # only used for the testing below
        return " ".join(self.names)

# # Testing if it works
number_store = {}

paul = ContactNames(["Paul", "O"])
number_store[paul] = "999"

paul_similar = ContactNames(["Paul", "O"])

print(number_store[paul])  # 999
print(number_store[paul_similar])  # 999
print(number_store[ContactNames(["Paul", "O"])])  # 999
print(len(number_store))  # 1 -> only has paul

kim = ContactNames(["Kim", "Jackson", "Model"])
number_store[kim] = "444"

print(len(number_store))  # 2 -> only has paul & kim

for key in number_store:
    print(key, ": ", number_store[key])

"""
Additional notes:

The time complexity of computing the hash is O(n), where n is the number of strings in the contact names.
    Hash codes are often cached for performance, with the caveat that the cache must be cleared
     if object fields that are referenced by the hash function are uPdated.
"""

Use a class within itself

Use self

class Tree:
    def __init__(self, name):
        self.children = []
        self.name = name

    def depthFirstSearch(self, array):
                 # using itself -> by passing down self
        self._depthFirstSearchHelper(array, self)
        return array

    def _depthFirstSearchHelper(self, array, root):
        if not root:
            return

        array.append(root.name)

        for child in root.children:
            self._depthFirstSearchHelper(array, child)

Quick tip (Bad code vs Good code)

Bad code

class Tree:
    def __init__(self, name):
        self.children = []
        self.name = name

    def depthFirstSearch(self, array):
        self._depthFirstSearchHelper(array, self)
        return array

    def _depthFirstSearchHelper(self, array, root):
        if not root:
            return

        array.append(root.name)

        for child in root.children:
            self._depthFirstSearchHelper(array, child)

Good code

class Node:
    def __init__(self, name):
        self.children = []
        self.name = name

    def depthFirstSearch(self, array):
        self._depthFirstSearchHelper(array)
        return array

    def _depthFirstSearchHelper(self, array):
        array.append(self.name)

        for child in self.children:
            child._depthFirstSearchHelper(array)

Comparing two classes eq greater gt

Screenshot 2021-10-17 at 17.57.43.png

Examples:

'K' Closest Points to the Origin

Creating a coordinates class

Examples:

'K' Closest Points to the Origin (similar)

nonlocal

Python Global, Local and Nonlocal variables

The nonlocal keyword is used to work with variables inside nested functions, where the variable should not belong to the inner function.

Use the keyword nonlocal to declare that the variable is not local.

class Solution:
    def buildTree(self, preorder: List[int], inorder: List[int]):
        preorder_pos = 0
        inorder_idxs = {val: idx for idx, val in enumerate(inorder)}

        def helper(preorder: List[int], inorder: List[int], inorder_left, inorder_right):
            nonlocal preorder_pos

Enum

>>> from enum import Enum
>>> class Suit(Enum):
...     CLUBS = "Clubs"
...     DIAMONDS = "Diamonds"
...     HEARTS = "Hearts"
...     SPADES = "Spades"
... 

>>> for i in Suit.__members__:
...     print(i)
... 
CLUBS
DIAMONDS
HEARTS
SPADES
>>>

Python Operator Overloading

TODO: Abstract Base Class *

Abstract Base Class (abc) in Python - GeeksforGeeks

Object Oriented Design

A class is an encapsulation of data and methods that operate on that data. Classes match the way we think about computation. They provide encapsulation, which reduces the conceptual burden of writing code, and enable code reuse, through the use of inheritance and polymorphism. However, naive use of object-oriented constructs can result in code that is hard to maintain.

A design pattern is a general repeatable solution to a commonly occurring problem. It is not a complete design that can be coded up directly—rather, it is a description of how to solve a problem that arises in many different situations. In the context of object-oriented programming, design patterns address both reuse and maintainability. In essence, design patterns make some parts of a system vary independently from the other parts.

Adnan’s Design Pattern course material, available freely online, contains lecture notes, homeworks, and labs that may serve as a good resource on the material in this chapter.

Design patterns

1. Template method vs Strategy

Explain the difference between the template method pattern and the strategy pattern with a concrete example.

Solution:

Both the template method and strategy pattems are similar in that:

both are behavioral pattems,
both are used to make algorithms reusable,
and both are general and very widely used.

However, they differ in the following key way:

In the template method, a skeleton algorithm is provided in a superclass. Subclasses can override methods to specialize the algorithm.
The strategy pattern is typically applied when a family of algorithms implements a common interface. These algorithms can then be selected by clients.

As a concrete example, consider a sorting algorithm like quicksort. TWo of the key steps in quicksort are pivot selection and partitioning. Quicksort is a good example of a template method - subclasses can implement their own pivot selection algorithm, e.g., using randomized median finding or selecting an element at random, and their own partitioning method, e.t.c

Since there may be multiple ways in which to sort elements, e.g., student objects may be compared by GPA, major, name, and combinations thereof, it's natural to make the comparison operation used by the sorting algorithm an argument to quicksort. One way to do this is to pass quicksort an object that implements a compare method. These objects constitute an example of the strategy pattem, as do the objects implementing pivot selection and partitioning.

There are some other smaller differences between the two pattems. For example, in the template method pattern, the superclass algorithm may have "hooks" - calls to placeholder methods that can be overridden by subclasses to provide additional functionality. Sometimes a hook is not implemented, thereby forcing the subclasses to implement that functionality; some times it offers a "no-operation" or some baseline functionality. There is no analog to a hook in a strategy pattern.

2. Observer pattern

The observer pattem defines a one-to-many dependency between objects so that when one object changes state all its dependents are notified and updated automatically.

The observed object must implement the following methods.

Register an observer.
Remove an observer.
Notify all currently registered observers.

The observer object must implement the following method.

Update the observer. (Update is sometimes refeffed to as notify.)

As a concrete example, consider a service that logs user requests, and keeps track of the 10 most visited pages. There may be multiple client applications that use this information, e.g., a leaderboard display, ad placement algorithms, recorunendation system, etc. Instead of having the clients poll the service, the service, which is the observed object, provides clients with register and remove capabilities. As soon as its state changes, the service enumerates through registered observers, calling each observer's update method.

Though most readily understood in the context of a single program, where the observed and observer are objects, the observer pattern is also applicable to distributed computing.

3. Push vs Pull Observer pattern

In the observer pattem, subjects push information to their observers. There is another way to update data - the observers may "pull" the information they need from the subject. Compare and contrast these two approaches.

Solution: Both push and pull observer designs are valid and have tradeoffr depending on the needs of the project. With the push design, the subject notifies the observer that its data is ready and includes the relevant information that the observer is subscribing to, whereas with the pull design, it is the observer's job to retrieve that information from the subject. The pull design places a heavier load on the observers, but it also allows the observer to query the subject only as often as is needed. One important consideration is that by the time the observer retrieves the information from the subject, the data could have changed. This could be a positive or negative result depending on the application. The pull design places less responsibility on the subject for tracking exactly which information the observer needs, as long as the subject knows when to notify the observer. This design also requires that the subject make its data publicly accessible by the observers. This design would likely work better when the observers are running with varied frequency and it suits them best to get the data they need on demand. The push design leaves all of the information transfer in the subject's control. The subject calls update for each observer and passes the relevant information along with this call. This design seems more object-oriented, because the subject is pushing its own data out, rather than making its data accessible for the observers to pull. It is also somewhat simpler and safer in that the subject always knows when the data is being pushed out to observers, so you don't have to worry about an observer pulling data in the middle of an update to the data, which would require synchronization.

4. Sigletons and Flyweights

The singleton pattern ensures a class has only one instance, and provides a global point of access to it. The flyweight pattern minimizes memory use by sharing as much data as possible with other similar objects. It is a way to use objects in large numbers when a simple repeated representation would use an unacceptable amount of memory.

A common example of a singleton is a logger. There may be many clients who want to listen to the logged data (console, hle, messaging service, etc.), so all code should log to a single place.

A common example of a flyweight is string inteming-a method of storing only one copy of each distinct string value. Inteming strings makes some string processing tasks more time- or space-efficient at the cost of requiring more time when the string is created or intemed. The distinct values are usually stored in a hash table. Since multiple clients may refer to the same flyweight object for safety flyweights should be immutable.

There is a superficial similarity between singleton and flyweight both keep a single copy of an object. There are several key differences between the two:

o Flyweights are used to save memory. Singletons are used to ensure all clients see the same object.

o A singleton is used where there is a single shared object, e.g., a database corurection, server configurations, a logger, etc. A flyweight is used where there is a family of shared objects, e.g., objects describing character fonts, or nodes shared across multiple binary search trees.

o Flyweight objects are invariable immutable. Singleton objects are usually not immutablll e.g, requests can be added to the database connection object.

o The singleton pattem is a creational pattern, whereas the flyweight is a structural pattem. In summary a singleton is like a global variable, whereas a flyweight is like a pointer to a canonical representation.

Sometimes, but not always, a singleton object is used to meate flyweights---dients ask the singleton for an object with specified fields, and the singleton checks its intemal pool of flyweights to see if one exists. If such an object already exists, it returns that, otherwise it creates a new flyweight, add it to its pool, and then retums it. (L:r essence the singleton serves as a gateway to a static factory.)

5. Adapters

The adapter pattern allows the interface of an existing class to be used from another interface. It is often used to make existing classes work with others without modifying their source code.

There are two ways to build an adapter: via subclassing (the class adapter pattern) and composition (the object adapter pattern). In the class adapter pattem, the adapter inherits both the interface that is expected and the interface that is pre-existing. In the object adapter pattern, the adapter contains an instance of the class it wraps and the adapter makes calls to the instance of the wrapped object.

Here are some remarks on the class adapter pattem. o The class adapter pattern allows re-use of implementation code in both the target and adaptee.

This is an advantage in that the adapter doesn't have to contain boilerplate pass-throughs or

cut-and-paste reimplementation of code in either the target or the adaptee. o The class adapter pattem has the disadvantages of inheritance (changes in base class may cause unforeseen misbehaviors in derived classes, etc.). The disadvantages of inheritance are made worse by the use of two base classes, which also precludes its use in languages like Java

(prior to |ava 1.8) that do not support multiple inheritance. o The class adapter can be used in place of either the target or the adaptee. This can be advantage

if there is a need for a two-way adapter. The ability to substitute the adapter for adaptee can be a disadvantage otherwise as it dilutes the purpose of the adapter and may lead to incorrect behavior if the adapter is used in an unexpected manner.

o The class adapter allows details of the behavior of the adaptee to be changed by overriding the adaptee's methods. Class adapters, as members of the class hierarchy, are tied to specific adaptee and target concrete classes.

As a concrete example of an object adapter, suppose we have legacy code that returns objects of type stack. Newer code expects inputs of type deque, which is more general than stack (but does not subclass stack). We could create a new type, stack-adapter, which implements the deque methods, and can be used anywhere deque is required. The stack-adapter class has a field of type stack-this is referred to as object composition. It implements the deque methods with code that uses methods on the composed stack object. Deque methods that are not supported by the underlying stack throw unsupported operation exceptions. Lr this scenario, the stack-adapter is an example of an object adapter.

Here are some conunents on the object adapter pattem. o The object adapter pattern is "purer" in its approach to the purpose of making the adaptee

behave like the target. By implementing the interface of the target only, the object adapter is

only useful as a target. o Use of an interface for the target allows the adaptee to be used in place of any prospective

target that is referenced by clients using that interface. o Use of composition for the adaptee similarly allows flexibility in the choice of the concrete

classes. If adaptee is a concrete class, any subclass of adaptee will work equally well within the object adapter pattem, If adaptee is an interface, any concrete class implementing that interface will work.

o A disadvantage is that if target is not based on an interface, target and all its clients may need to change to allow the object adapter to be substituted.

6. Creational patterns

Explain what each of these creational pattems is: builder, static factory, factory method, and abstract factory. Solution: The idea behind the builder pattem is to build a complex object in phases. It avoids mutability and inconsistent state by using an mutable inner class that has a build method that retums the desired object, Its key benefits are that it breaks down the construction process/ and can give names to steps. Compared to a constructor, it deals far better with optional parameters and when the parameter list is very long.

A static factory is a function for construction of objects. Its key benefits are as follow: the function's niune c€u:r make what it's doing much clearer compared to a call to a constructor. The function is not obliged to create a new object-in particulaq, it can retum a flyweight. It can also return a subtype that's more optimized, e.g., it can choose to construct an object that uses an integer in place of a Boolean array if the array size is not more than the integer word size.

A factory method defines interface for creating an object, but lets subclasses decide which class to instantiate. The classic example is a maze game with two modes-one with regular rooms, and one with magic rooms. The program below uses a template method, as described in Problem 22.1 on Page 333, to combine the logic common to the two versions of the game.

A drawback of the factory method pattern is that it makes subclassing challenging. An abstract factory provides an interface for creating families of related objects without sPecify- ing their concrete classes. For example, a class DocumentCreator could provide interfaces to create

anumberof products,suchascreateletterO andcreateResumeO. Concreteimplementationsof this class could choose to irnplement these products in different ways, e.9., with modern or classic fonts, right-flush or right-ragged layout, etc. Client code gets a DocumentCreator object and calls its factory methods. Use of this pattem makes it possible to interchange concrete implementations without changing the code that uses them, even at runtime. The price for this flexibility is more

planning and upfront coding, as well as and code that may be harder to understand, because of the added indirections.

SOLID

Python Open-closed Principle

OO Analysis and Design

OO Analysis and Design is a structured method for analyzing and designing a system by applying object-oriented concepts. This design process consists of an investigation into the objects constituting the system. It starts by first identifying the objects of the system and then figuring out the interactions between various objects.

The process of OO analysis and design can be described as:

Identifying the objects in a system
Defining relationships between objects
Establishing the interface of each object and,
Making a design, which can be converted to executables using OO languages.

We need a standard method/tool to document all this information; for this purpose we use UML. UML can be considered as the successor of object-oriented (OO) analysis and design. UML is powerful enough to represent all the concepts that exist in object-oriented analysis and design. UML diagrams are a representation of object-oriented concepts only.

Tips for OOD Interview

Clarify the scenario, write out user cases

Use case is a description of sequences of events that, taken together, lead to a system doing something useful. Who is going to use it and how they are going to use it. The system may be very simple or very complicated.

Special system requirements such as multi-threading, read or write oriented.

Define objects

Map identity to class: one scenario for one class, each core object in this scenario for one class.

Consider the relationships among classes: certain class must have unique instance, one object has many other objects (composition), one object is another object (inheritance).

Identify attributes for each class: change noun to variable and action to methods.

Use design patterns such that it can be reused in multiple applications.

UML

Screenshot 2021-11-08 at 05.31.51.png

UML stands for Unified Modeling Language and is used to model the Object-Oriented Analysis of a software system. UML is a way of visualizing and documenting a software system by using a collection of diagrams, which helps engineers, businesspeople, and system architects understand the behavior and structure of the system being designed.

Benefits of using UML:

Helps develop a quick understanding of a software system.
UML modeling helps in breaking a complex system into discrete pieces that can be easily understood.
UML’s graphical notations can be used to communicate design decisions.
Since UML is independent of any specific platform or language or technology, it is easier to abstract out concepts.
It becomes easier to hand the system over to a new team.

Types of UML Diagrams: The current UML standards call for 14 different kinds of diagrams. These diagrams are organized into two distinct groups: structural diagrams and behavioral or interaction diagrams. As the names suggest, some UML diagrams analyze and depict the structure of a system or process, whereas others describe the behavior of the system, its actors, and its building components. The different types are broken down as follows:

Structural UML diagrams

Class diagram
Object diagram
Package diagram
Component diagram
Composite structure diagram
Deployment diagram
Profile diagram

Behavioral UML diagrams

Use case diagram
Activity diagram
Sequence diagram
State diagram
Communication diagram
Interaction overview diagram
Timing diagram

In this course, we will be focusing on the following UML diagrams:

Use Case Diagram: Used to describe a set of user scenarios, this diagram, illustrates the functionality provided by the system.
Class Diagram: Used to describe structure and behavior in the use cases, this diagram provides a conceptual model of the system in terms of entities and their relationships.
Activity Diagram: Used to model the functional flow-of-control between two or more class objects.
Sequence Diagram: Used to describe interactions among classes in terms of an exchange of messages over time.

Use Case Diagrams

Use case diagrams describe a set of actions (called use cases) that a system should or can perform in collaboration with one or more external users of the system (called actors). Each use case should provide some observable and valuable result to the actors.

Use Case Diagrams describe the high-level functional behavior of the system.
It answers what system does from the user point of view.
Use case answers ‘What will the system do?’ and at the same time tells us ‘What will the system NOT do?’.

A use case illustrates a unit of functionality provided by the system. The primary purpose of the use case diagram is to help development teams visualize the functional requirements of a system, including the relationship of “actors” to the essential processes, as well as the relationships among different use cases.

To illustrate a use case on a use case diagram, we draw an oval in the middle of the diagram and put the name of the use case in the center of the oval. To show an actor (indicating a system user) on a use-case diagram, we draw a stick figure to the left or right of the diagram.

Screenshot 2021-11-08 at 05.35.29.png

The different components of the use case diagram are:

System boundary: A system boundary defines the scope and limits of the system. It is shown as a rectangle that spans all use cases of the system.
Actors: An actor is an entity who performs specific actions. These roles are the actual business roles of the users in a given system. An actor interacts with a use case of the system. For example, in a banking system, the customer is one of the actors.
Use Case: Every business functionality is a potential use case. The use case should list the discrete business functionality specified in the problem statement.
Include: Include relationship represents an invocation of one use case by another use case. From a coding perspective, it is like one function being called by another function.
Extend: This relationship signifies that the extended use case will work exactly like the base use case, except that some new steps will be inserted in the extended use case

Class diagrams

Class diagram is the backbone of object-oriented modeling - it shows how different entities (people, things, and data) relate to each other. In other words, it shows the static structures of the system.

A class diagram describes the attributes and operations of a class and also the constraints imposed on the system. Class diagrams are widely used in the modeling of object-oriented systems because they are the only UML diagrams that can be mapped directly to object-oriented languages.

The purpose of the class diagram can be summarized as:

Analysis and design of the static view of an application
To describe the responsibilities of a system
To provide a base for component and deployment diagrams and,
Forward and reverse engineering.

A class is depicted in the class diagram as a rectangle with three horizontal sections, as shown in the figure below.

The upper section shows the class’s name (Flight), the middle section contains the properties of the class, and the lower section contains the class’s operations (or “methods”).

Screenshot 2021-11-08 at 05.40.28.png

These are the different types of relationships between classes:

Association: If two classes in a model need to communicate with each other, there must be a link between them. This link can be represented by an association. Associations can be represented in a class diagram by a line between these classes with an arrow indicating the navigation direction.

By default, associations are always assumed to be bi-directional; this means that both classes are aware of each other and their relationship. In the diagram below, the association between Pilot and FlightInstance is bi-directional, as both classes know each other.
By contrast, in a uni-directional association, two classes are related - but only one class knows that the relationship exists. In the below example, only Flight class knows about Aircraft; hence it is a uni-directional association

Multiplicity Multiplicity indicates how many instances of a class participate in the relationship. It is a constraint that specifies the range of permitted cardinalities between two classes. For example, in the diagram below, one FlightInstance will have two Pilots, while a Pilot can have many FlightInstances. A ranged multiplicity can be expressed as “0…*” which means “zero to many" or as “2…4” which means “two to four”.

We can indicate the multiplicity of an association by adding multiplicity adornments to the line denoting the association. The below diagram, demonstrates that a FlightInstance has exactly two Pilots but a Pilot can have many FlightInstances.

Screenshot 2021-11-08 at 05.42.30.png

Aggregation: Aggregation is a special type of association used to model a “whole to its parts” relationship. In a basic aggregation relationship, the lifecycle of a PART class is independent of the WHOLE class’s lifecycle. In other words, aggregation implies a relationship where the child can exist independently of the parent. In the above diagram, Aircraft can exist without Airline.

Composition: The composition aggregation relationship is just another form of the aggregation relationship, but the child class’s instance lifecycle is dependent on the parent class’s instance lifecycle. In other words, Composition implies a relationship where the child cannot exist independent of the parent. In the above example, WeeklySchedule is composed in Flight which means when Flight lifecycle ends, WeeklySchedule automatically gets destroyed.

Generalization: Generalization is the mechanism for combining similar classes of objects into a single, more general class. Generalization identifies commonalities among a set of entities. In the above diagram, Crew, Pilot, and Admin, all are Person.

Dependency: A dependency relationship is a relationship in which one class, the client, uses or depends on another class, the supplier. In the above diagram, FlightReservation depends on Payment.

Abstract class: An abstract class is identified by specifying its name in italics. In the above diagram, both Person and Account classes are abstract classes.

Screenshot 2021-11-08 at 05.46.37.png

Sequence diagram

Screenshot 2021-11-08 at 05.48.58.png

Sequence diagrams describe interactions among classes in terms of an exchange of messages over time and are used to explore the logic of complex operations, functions or procedures. In this diagram, the sequence of interactions between the objects is represented in a step-by-step manner.

Sequence diagrams show a detailed flow for a specific use case or even just part of a particular use case. They are almost self-explanatory; they show the calls between the different objects in their sequence and can explain, at a detailed level, different calls to various objects.

A sequence diagram has two dimensions: The vertical dimension shows the sequence of messages in the chronological order that they occur; the horizontal dimension shows the object instances to which the messages are sent.

A sequence diagram is straightforward to draw. Across the top of your diagram, identify the class instances (objects) by putting each class instance inside a box (see above figure). If a class instance sends a message to another class instance, draw a line with an open arrowhead pointing to the receiving class instance and place the name of the message above the line. Optionally, for important messages, you can draw a dotted line with an arrowhead pointing back to the originating class instance; label the returned value above the dotted line.

Activity Diagrams

We use Activity Diagrams to illustrate the flow of control in a system. An activity diagram shows the flow of control for a system functionality; it emphasizes the condition of flow and the sequence in which it happens. We can also use an activity diagram to refer to the steps involved in the execution of a use case.

Activity diagrams illustrate the dynamic nature of a system by modeling the flow of control from activity to activity. An activity represents an operation on some class in the system that results in a change in the state of the system. Typically, activity diagrams are used to model workflow or business processes and internal operations.

Following is an activity diagram for a user performing online shopping:

Sample activity diagram for online shopping

What is the difference between Activity diagram and Sequence diagram?

Activity diagram captures the process flow. It is used for functional modeling. A functional model represents the flow of values from external inputs, through operations and internal data stores, to external outputs.Sequence diagram tracks the interaction between the objects. It is used for dynamic modeling, which is represented by tracking states, transitions between states, and the events that trigger these transitions.

Design patterns

Design Patterns and Refactoring

The 3 Types of Design Patterns All Developers Should Know (with code examples of each)

The 7 Most Important Software Design Patterns

5 Design Patterns Every Engineer Should Know

Examples:

Singleton
Observer Pattern (Pub/Sub)
Facade
Bridge/Adapter Pattern
Strategy Pattern

Creational Patterns

Structural Patterns

Behavioral Patterns

Object Oriented Design Case Studies

""" 
- System requirements
- Use case diagrams
        - Actors
        - Use cases
        - Use case diagrams
- Class diagrams
        - Main classes
        - Class diagrams
- Activity diagrams
- Code

"""

Amazon System Design Interview: Design Parking Garage

Design a Library Management System

Design a Library Management System

Solution

Design an ATM

Design an ATM

Solution

Design a parking lot

Design a Parking Lot

Solution

xx

Find the original version of this page (with additional content) on Notion here.

_Patterns for Coding Questions

Grokking the Coding Interview: Patterns for Coding Questions - Learn Interactively

Posts by Category

Leetcode Patterns

14 Patterns to Ace Any Coding Interview Question | Hacker Noon

Data Structure Visualization

GitHub - Arjiit/LeetCode-Patterns: Set of Patterns to solve many algorithmic questions of similar type on LeetCode

Grokking-the-Coding-Interview-Patterns/Pattern 02: Two Pointers.md at main · Chanda-Abdul/Grokking-the-Coding-Interview-Patterns

GitHub - cl2333/Grokking-the-Coding-Interview-Patterns-for-Coding-Questions

GitHub - MahdiMashrur/Awesome-Coding-Interview-Question-Patterns: The most common question-patterns for any coding-interview

Seven (7) Essential Data Structures for a Coding Interview and associated common questions

https://youtu.be/qGvosafaXUE

20% of the material you study will be relevant to 80% of the interview questions and vice versa. That being said, there are a lot of small things you should know as well, not just how to manipulate data structures.

Pointers

Cyclic Sort

Subsets, Permutations & Combinations *

Merge Intervals

Bit Manipulation

Parenthesis

Advanced Binary Search

Suffix Trees & Arrays

Heap Tricks *

DP

Trees & Graphs (Additional content)

_Other

Find the original version of this page (with additional content) on Notion here.

Strings, Arrays & Linked Lists 81ca9e0553a0494cb8bb74c5c85b89c8 ↵

Untitled Database a6aee36cf3b9470ea0f88713ab30a9e6 ↵

adds all elements of a list to another list

Methods: https://www.programiz.com/python-programming/methods/list/extend

Find the original version of this page (with additional content) on Notion here.

adds an element to the end of the list

Methods: https://www.programiz.com/python-programming/methods/list/append

Find the original version of this page (with additional content) on Notion here.

inserts an item at the defined index

Methods: https://www.programiz.com/python-programming/methods/list/insert

Find the original version of this page (with additional content) on Notion here.

removes all items from the list

Methods: https://www.programiz.com/python-programming/methods/list/clear

Find the original version of this page (with additional content) on Notion here.

removes an item from the list

Methods: https://www.programiz.com/python-programming/methods/list/remove

Find the original version of this page (with additional content) on Notion here.

returns a shallow copy of the list

Methods: https://www.programiz.com/python-programming/methods/list/copy

Find the original version of this page (with additional content) on Notion here.

returns and removes an element at the given index

Methods: https://www.programiz.com/python-programming/methods/list/pop

Find the original version of this page (with additional content) on Notion here.

returns the count of the number of items passed as an argument

Methods: https://www.programiz.com/python-programming/methods/list/count

Find the original version of this page (with additional content) on Notion here.

returns the index of the first matched item

Methods: https://www.programiz.com/python-programming/methods/list/index

Find the original version of this page (with additional content) on Notion here.

reverse the order of items in the list

Methods: https://www.programiz.com/python-programming/methods/list/reverse

Find the original version of this page (with additional content) on Notion here.

sort items in a list in ascending order

Methods: https://www.programiz.com/python-programming/methods/list/sort

Find the original version of this page (with additional content) on Notion here.

Ended: Untitled Database a6aee36cf3b9470ea0f88713ab30a9e6

Ended: Strings, Arrays & Linked Lists 81ca9e0553a0494cb8bb74c5c85b89c8

Trees & Graphs edc3401e06c044f29a2d714d20ffe185 ↵

Operations afa24885f0c94372b3f16d911d3c5e13 ↵

Delete

Average: O(log n) Worst Case: O(n)

Find the original version of this page (with additional content) on Notion here.

Insert

Average: O(log n) Worst Case: O(n)

Find the original version of this page (with additional content) on Notion here.

Lookup

Average: O(log n) Worst Case: O(n)

Find the original version of this page (with additional content) on Notion here.

Maximum

Average: O(log n) Worst Case: O(n)

Find the original version of this page (with additional content) on Notion here.

Minimum

Average: O(log n) Worst Case: O(n)

Find the original version of this page (with additional content) on Notion here.

Predecessor

Average: O(log n) Worst Case: O(n)

Find the original version of this page (with additional content) on Notion here.

Successor

Average: O(log n) Worst Case: O(n)

Find the original version of this page (with additional content) on Notion here.

Ended: Operations afa24885f0c94372b3f16d911d3c5e13

Ended: Trees & Graphs edc3401e06c044f29a2d714d20ffe185

Object Oriented Analysis and Design 1a01887a9271475da7b3cd3f4efc9e0d ↵

Design a Library Management System

Introduction

grokking-the-object-oriented-design-interview/design-a-library-management-system.md at master · tssovi/grokking-the-object-oriented-design-interview

A Library Management System is a software built to handle the primary housekeeping functions of a library. Libraries rely on library management systems to manage asset collections as well as relationships with their members. Library management systems help libraries keep track of the books and their checkouts, as well as members’ subscriptions and profiles.

Library management systems also involve maintaining the database for entering new books and recording books that have been borrowed with their respective due dates.

System requirements

Always clarify requirements at the beginning of the interview. Be sure to ask questions to find the exact scope of the system that the interviewer has in mind.

We will focus on the following set of requirements while designing the Library Management System:

Any library member should be able to search books by their title, author, subject category as well by the publication date.
Each book will have a unique identification number and other details including a rack number which will help to physically locate the book.
There could be more than one copy of a book, and library members should be able to check-out and reserve any copy. We will call each copy of a book, a book item.
The system should be able to retrieve information like who took a particular book or what are the books checked-out by a specific library member.
There should be a maximum limit (5) on how many books a member can check-out.
There should be a maximum limit (10) on how many days a member can keep a book.
The system should be able to collect fines for books returned after the due date.
Members should be able to reserve books that are not currently available.
The system should be able to send notifications whenever the reserved books become available, as well as when the book is not returned within the due date.
Each book and member card will have a unique barcode. The system will be able to read barcodes from books and members’ library cards.

Use case diagram

Main Actors

We have three main actors in our system:

Librarian: Mainly responsible for adding and modifying books, book items, and users. The Librarian can also issue, reserve, and return book items.
Member: All members can search the catalog, as well as check-out, reserve, renew, and return a book.
System: Mainly responsible for sending notifications for overdue books, canceled reservations, etc.

Use cases

Here are the top use cases of the Library Management System:

Add/Remove/Edit book: To add, remove or modify a book or book item.
Search catalog: To search books by title, author, subject or publication date.
Register new account/cancel membership: To add a new member or cancel the membership of an existing member.
Check-out book: To borrow a book from the library.
Reserve book: To reserve a book which is not currently available.
Renew a book: To reborrow an already checked-out book.
Return a book: To return a book to the library which was issued to a member.

Use case diagram

Screenshot 2021-11-08 at 14.39.25.png

Screenshot 2021-11-08 at 14.39.31.png

Class diagram

Main classes

Here are the main classes of our Library Management System:

Account
- Member
- Librarian
LibraryCard
Library
Catalog
Author
Book
BookItem
BookReservation
BookLending
Rack
Fine
Notification

In more detail:

Library: The central part of the organization for which this software has been designed. It has attributes like ‘Name’ to distinguish it from any other libraries and ‘Address’ to describe its location.
Book: The basic building block of the system. Every book will have ISBN, Title, Subject, Publishers, etc.
BookItem: Any book can have multiple copies, each copy will be considered a book item in our system. Each book item will have a unique barcode.
Account: We will have two types of accounts in the system, one will be a general member, and the other will be a librarian.
LibraryCard: Each library user will be issued a library card, which will be used to identify users while issuing or returning books.
BookReservation: Responsible for managing reservations against book items.
BookLending: Manage the checking-out of book items.
Catalog: Catalogs contain list of books sorted on certain criteria. Our system will support searching through four catalogs: Title, Author, Subject, and Publish-date.
Fine: This class will be responsible for calculating and collecting fines from library members.
Author: This class will encapsulate a book author.
Rack: Books will be placed on racks. Each rack will be identified by a rack number and will have a location identifier to describe the physical location of the rack in the library.
Notification: This class will take care of sending notifications to library members.

Class diagrams

Screenshot 2021-11-08 at 14.53.07.png

Screenshot 2021-11-08 at 05.46.37.png

Activity diagrams

Check-out a book: Any library member or librarian can perform this activity. Here are the set of steps to check-out a book:

Screenshot 2021-11-08 at 14.58.44.png

Return a book: Any library member or librarian can perform this activity. The system will collect fines from members if they return books after the due date. Here are the steps for returning a book:

Screenshot 2021-11-08 at 15.00.43.png

Renew a book: While renewing (re-issuing) a book, the system will check for fines and see if any other member has not reserved the same book, in that case the book item cannot be renewed. Here are the different steps for renewing a book:

Screenshot 2021-11-08 at 15.01.01.png

Code

Here is the code for the use cases mentioned above:

Check-out a book,
Return a book, and
Renew a book.

Note: This code only focuses on the design part of the use cases. Since you are not required to write a fully executable code in an interview, you can assume parts of the code to interact with the database, payment system, etc.

Enums and Constants:

Here are the required enums, data types, and constants:

class BookFormat(Enum):
  HARDCOVER, PAPERBACK, AUDIO_BOOK, EBOOK, NEWSPAPER, MAGAZINE, JOURNAL = 1, 2, 3, 4, 5, 6, 7

class BookStatus(Enum):
  AVAILABLE, RESERVED, LOANED, LOST = 1, 2, 3, 4

class ReservationStatus(Enum):
  WAITING, PENDING, CANCELED, NONE = 1, 2, 3, 4

class AccountStatus(Enum):
  ACTIVE, CLOSED, CANCELED, BLACKLISTED, NONE = 1, 2, 3, 4, 5

# ------

class Address:
  def __init__(self, street, city, state, zip_code, country):
    self.__street_address = street
    self.__city = city
    self.__state = state
    self.__zip_code = zip_code
    self.__country = country

class Person(ABC):
  def __init__(self, name, address, email, phone):
    self.__name = name
    self.__address = address
    self.__email = email
    self.__phone = phone

class Constants:
  self.MAX_BOOKS_ISSUED_TO_A_USER = 5
  self.MAX_LENDING_DAYS = 10

public enum BookFormat {
  HARDCOVER,
  PAPERBACK,
  AUDIO_BOOK,
  EBOOK,
  NEWSPAPER,
  MAGAZINE,
  JOURNAL
}

public enum BookStatus {
  AVAILABLE,
  RESERVED,
  LOANED,
  LOST
}

public enum ReservationStatus{
  WAITING,
  PENDING,
  CANCELED,
  NONE
}

public enum AccountStatus{
  ACTIVE,
  CLOSED,
  CANCELED,
  BLACKLISTED,
  NONE
}

public class Address {
  private String streetAddress;
  private String city;
  private String state;
  private String zipCode;
  private String country;
}

public class Person {
  private String name;
  private Address address;
  private String email;
  private String phone;
}

public class Constants {
  public static final int MAX_BOOKS_ISSUED_TO_A_USER = 5;
  public static final int MAX_LENDING_DAYS = 10;
}

Account, Member, and Librarian:

These classes represent various people that interact with our system:

# For simplicity, we are not defining getter and setter functions. The reader can
# assume that all class attributes are private and accessed through their respective
# public getter methods and modified only through their public methods function.

from abc import ABC, abstractmethod

class Account(ABC):
  def __init__(self, id, password, person, status=AccountStatus.Active):
    self.__id = id
    self.__password = password
    self.__status = status
    self.__person = person

  def reset_password(self):
    None

class Librarian(Account):
  def __init__(self, id, password, person, status=AccountStatus.Active):
    super().__init__(id, password, person, status)

  def add_book_item(self, book_item):
    None

  def block_member(self, member):
    None

  def un_block_member(self, member):
    None

class Member(Account):
  def __init__(self, id, password, person, status=AccountStatus.Active):
    super().__init__(id, password, person, status)
    self.__date_of_membership = datetime.date.today()
    self.__total_books_checkedout = 0

  def get_total_books_checkedout(self):
    return self.__total_books_checkedout

  def reserve_book_item(self, book_item):
    None

  def increment_total_books_checkedout(self):
    None

  def renew_book_item(self, book_item):
    None

  def checkout_book_item(self, book_item):
    if self.get_total_books_checked_out() >= Constants.MAX_BOOKS_ISSUED_TO_A_USER:
      print("The user has already checked-out maximum number of books")
      return False
    book_reservation = BookReservation.fetch_reservation_details(book_item.get_barcode())
    if book_reservation != None and book_reservation.get_member_id() != self.get_id():
      # book item has a pending reservation from another user
      print("self book is reserved by another member")
      return False
    elif book_reservation != None:
      # book item has a pending reservation from the give member, update it
      book_reservation.update_status(ReservationStatus.COMPLETED)

    if not book_item.checkout(self.get_id()):
      return False

    self.increment_total_books_checkedout()
    return True

  def check_for_fine(self, book_item_barcode):
    book_lending = BookLending.fetch_lending_details(book_item_barcode)
    due_date = book_lending.get_due_date()
    today = datetime.date.today()
    # check if the book has been returned within the due date
    if today > due_date:
      diff = today - due_date
      diff_days = diff.days
      Fine.collect_fine(self.get_member_id(), diff_days)

  def return_book_item(self, book_item):
    self.check_for_fine(book_item.get_barcode())
    book_reservation = BookReservation.fetch_reservation_details(book_item.get_barcode())
    if book_reservation != None:
      # book item has a pending reservation
      book_item.update_book_item_status(BookStatus.RESERVED)
      book_reservation.send_book_available_notification()
    book_item.update_book_item_status(BookStatus.AVAILABLE)

  def renew_book_item(self, book_item):
    self.check_for_fine(book_item.get_barcode())
    book_reservation = BookReservation.fetch_reservation_details(book_item.get_barcode())
    # check if self book item has a pending reservation from another member
    if book_reservation != None and book_reservation.get_member_id() != self.get_member_id():
      print("self book is reserved by another member")
      self.decrement_total_books_checkedout()
      book_item.update_book_item_state(BookStatus.RESERVED)
      book_reservation.send_book_available_notification()
      return False
    elif book_reservation != None:
      # book item has a pending reservation from self member
      book_reservation.update_status(ReservationStatus.COMPLETED)
    BookLending.lend_book(book_item.get_bar_code(), self.get_member_id())
    book_item.update_due_date(datetime.datetime.now().AddDays(Constants.MAX_LENDING_DAYS))
    return True

// For simplicity, we are not defining getter and setter functions. The reader can
// assume that all class attributes are private and accessed through their respective
// public getter methods and modified only through their public methods function.

public abstract class Account {
  private String id;
  private String password;
  private AccountStatus status;
  private Person person;

  public boolean resetPassword();
}

public class Librarian extends Account {
  public boolean addBookItem(BookItem bookItem);

  public boolean blockMember(Member member);

  public boolean unBlockMember(Member member);
}

public class Member extends Account {
  private Date dateOfMembership;
  private int totalBooksCheckedout;

  public int getTotalBooksCheckedout();

  public boolean reserveBookItem(BookItem bookItem);

  private void incrementTotalBooksCheckedout();

  public boolean checkoutBookItem(BookItem bookItem) {
    if (this.getTotalBooksCheckedOut() >= Constants.MAX_BOOKS_ISSUED_TO_A_USER) {
      ShowError("The user has already checked-out maximum number of books");
      return false;
    }
    BookReservation bookReservation = BookReservation.fetchReservationDetails(bookItem.getBarcode());
    if (bookReservation != null && bookReservation.getMemberId() != this.getId()) {
      // book item has a pending reservation from another user
      ShowError("This book is reserved by another member");
      return false;
    } else if (bookReservation != null) {
      // book item has a pending reservation from the give member, update it
      bookReservation.updateStatus(ReservationStatus.COMPLETED);
    }

    if (!bookItem.checkout(this.getId())) {
      return false;
    }

    this.incrementTotalBooksCheckedout();
    return true;
  }

  private void checkForFine(String bookItemBarcode) {
    BookLending bookLending = BookLending.fetchLendingDetails(bookItemBarcode);
    Date dueDate = bookLending.getDueDate();
    Date today = new Date();
    // check if the book has been returned within the due date
    if (today.compareTo(dueDate) > 0) {
      long diff = todayDate.getTime() - dueDate.getTime();
      long diffDays = diff / (24 * 60 * 60 * 1000);
      Fine.collectFine(memberId, diffDays);
    }
  }

  public void returnBookItem(BookItem bookItem) {
    this.checkForFine(bookItem.getBarcode());
    BookReservation bookReservation = BookReservation.fetchReservationDetails(bookItem.getBarcode());
    if (bookReservation != null) {
      // book item has a pending reservation
      bookItem.updateBookItemStatus(BookStatus.RESERVED);
      bookReservation.sendBookAvailableNotification();
    }
    bookItem.updateBookItemStatus(BookStatus.AVAILABLE);
  }

  public bool renewBookItem(BookItem bookItem) {
    this.checkForFine(bookItem.getBarcode());
    BookReservation bookReservation = BookReservation.fetchReservationDetails(bookItem.getBarcode());
    // check if this book item has a pending reservation from another member
    if (bookReservation != null && bookReservation.getMemberId() != this.getMemberId()) {
      ShowError("This book is reserved by another member");
      member.decrementTotalBooksCheckedout();
      bookItem.updateBookItemState(BookStatus.RESERVED);
      bookReservation.sendBookAvailableNotification();
      return false;
    } else if (bookReservation != null) {
      // book item has a pending reservation from this member
      bookReservation.updateStatus(ReservationStatus.COMPLETED);
    }
    BookLending.lendBook(bookItem.getBarCode(), this.getMemberId());
    bookItem.updateDueDate(LocalDate.now().plusDays(Constants.MAX_LENDING_DAYS));
    return true;
  }
}

BookReservation, BookLending, and Fine:

These classes represent a book reservation, lending, and fine collection, respectively.

class BookReservation:
  def __init__(self, creation_date, status, book_item_barcode, member_id):
    self.__creation_date = creation_date
    self.__status = status
    self.__book_item_barcode = book_item_barcode
    self.__member_id = member_id

  def fetch_reservation_details(self, barcode):
    None

class BookLending:
  def __init__(self, creation_date, due_date, book_item_barcode, member_id):
    self.__creation_date = creation_date
    self.__due_date = due_date
    self.__return_date = None
    self.__book_item_barcode = book_item_barcode
    self.__member_id = member_id

  def lend_book(self, barcode, member_id):
    None

  def fetch_lending_details(self, barcode):
    None

class Fine:
  def __init__(self, creation_date, book_item_barcode, member_id):
    self.__creation_date = creation_date
    self.__book_item_barcode = book_item_barcode
    self.__member_id = member_id

  def collect_fine(self, member_id, days):
    None

public class BookReservation {
  private Date creationDate;
  private ReservationStatus status;
  private String bookItemBarcode;
  private String memberId;

  public static BookReservation fetchReservationDetails(String barcode);
}

public class BookLending {
  private Date creationDate;
  private Date dueDate;
  private Date returnDate;
  private String bookItemBarcode;
  private String memberId;

  public static boolean lendBook(String barcode, String memberId);
  public static BookLending fetchLendingDetails(String barcode);
}

public class Fine {
  private Date creationDate;
  private double bookItemBarcode;
  private String memberId;

  public static void collectFine(String memberId, long days) {}
}

BookItem:

Encapsulating a book item, this class will be responsible for processing the reservation, return, and renewal of a book item.

from abc import ABC, abstractmethod

class Book(ABC):
  def __init__(self, ISBN, title, subject, publisher, language, number_of_pages):
    self.__ISBN = ISBN
    self.__title = title
    self.__subject = subject
    self.__publisher = publisher
    self.__language = language
    self.__number_of_pages = number_of_pages
    self.__authors = []

class BookItem(Book):
  def __init__(self, barcode, is_reference_only, borrowed, due_date, price, book_format, status, date_of_purchase, publication_date, placed_at):
    self.__barcode = barcode
    self.__is_reference_only = is_reference_only
    self.__borrowed = borrowed
    self.__due_date = due_date
    self.__price = price
    self.__format = book_format
    self.__status = status
    self.__date_of_purchase = date_of_purchase
    self.__publication_date = publication_date
    self.__placed_at = placed_at

  def checkout(self, member_id):
    if self.get_is_reference_only():
      print("self book is Reference only and can't be issued")
      return False
    if not BookLending.lend_book(self.get_bar_code(), member_id):
      return False
    self.update_book_item_status(BookStatus.LOANED)
    return True

class Rack:
  def __init__(self, number, location_identifier):
    self.__number = number
    self.__location_identifier = location_identifier

public abstract class Book {
  private String ISBN;
  private String title;
  private String subject;
  private String publisher;
  private String language;
  private int numberOfPages;
  private List<Author> authors;
}

public class BookItem extends Book {
  private String barcode;
  private boolean isReferenceOnly;
  private Date borrowed;
  private Date dueDate;
  private double price;
  private BookFormat format;
  private BookStatus status;
  private Date dateOfPurchase;
  private Date publicationDate;
  private Rack placedAt;

  public boolean checkout(String memberId) {
    if(bookItem.getIsReferenceOnly()) {
      ShowError("This book is Reference only and can't be issued");
      return false;
    }
    if(!BookLending.lendBook(this.getBarCode(), memberId)){
      return false;
    }
    this.updateBookItemStatus(BookStatus.LOANED);
    return true;
  }
}

public class Rack {
  private int number;
  private String locationIdentifier;
}

Search interface and Catalog:

The Catalog class will implement the Search interface to facilitate searching of books.

from abc import ABC, abstractmethod

class Search(ABC):
  def search_by_title(self, title):
    None

  def search_by_author(self, author):
    None

  def search_by_subject(self, subject):
    None

  def search_by_pub_date(self, publish_date):
    None

class Catalog(Search):
  def __init__(self):
    self.__book_titles = {}
    self.__book_authors = {}
    self.__book_subjects = {}
    self.__book_publication_dates = {}

  def search_by_title(self, query):
    # return all books containing the string query in their title.
    return self.__book_titles.get(query)

  def search_by_author(self, query):
    # return all books containing the string query in their author's name.
    return self.__book_authors.get(query)

public interface Search {
  public List<Book> searchByTitle(String title);
  public List<Book> searchByAuthor(String author);
  public List<Book> searchBySubject(String subject);
  public List<Book> searchByPubDate(Date publishDate);
}

public class Catalog implements Search {
  private HashMap<String, List<Book>> bookTitles;
  private HashMap<String, List<Book>> bookAuthors;
  private HashMap<String, List<Book>> bookSubjects;
  private HashMap<String, List<Book>> bookPublicationDates;

  public List<Book> searchByTitle(String query) {
    // return all books containing the string query in their title.
    return bookTitles.get(query);
  }

  public List<Book> searchByAuthor(String query) {
    // return all books containing the string query in their author's name.
    return bookAuthors.get(query);
  }
}

Full code

# https://paulonteri.notion.site/Design-a-Library-Management-System-d6f0c5b09f314a80870d7c8f582de630

from abc import ABC, abstractmethod
from datetime import datetime
from enum import Enum

# # Enums and Constants: Here are the required enums, data types, and constants:

class BookFormat(Enum):
    HARDCOVER, PAPERBACK, AUDIO_BOOK, EBOOK, NEWSPAPER, MAGAZINE, JOURNAL = 1, 2, 3, 4, 5, 6, 7

class BookStatus(Enum):
    AVAILABLE, RESERVED, LOANED, LOST = 1, 2, 3, 4

class ReservationStatus(Enum):
    WAITING, PENDING, CANCELED, NONE = 1, 2, 3, 4

class AccountStatus(Enum):
    ACTIVE, CLOSED, CANCELED, BLACKLISTED, NONE = 1, 2, 3, 4, 5

class Address:
    # used by person and library
    def __init__(self, street, city, state, zip_code, country):
        self.__street_address = street
        self.__city = city
        self.__state = state
        self.__zip_code = zip_code
        self.__country = country

class Person(ABC):
    # used by account
    def __init__(self, name, address: Address, email, phone):
        self.__name = name
        self.__address = address
        self.__email = email
        self.__phone = phone

class Constants:
    MAX_BOOKS_ISSUED_TO_A_USER = 5
    MAX_LENDING_DAYS = 10

# # Account, Member, and Librarian: These classes represent various people that interact with our system:
# For simplicity, we are not defining getter and setter functions. The reader can
# assume that all class attributes are private and accessed through their respective
# public getter methods and modified only through their public methods function.

class Account(ABC):
    def __init__(self, id, password, person: Person, status=AccountStatus.ACTIVE):
        self.__id = id
        self.__password = password
        self.__status = status
        self.__person = person  # Person

    def reset_password(self):
        None

class Librarian(Account):
    def __init__(self, id, password, person: Person, status=AccountStatus.ACTIVE):
        super().__init__(id, password, person, status)

    def add_book_item(self, book_item):
        None

    def block_member(self, member):
        None

    def un_block_member(self, member):
        None

class Member(Account):
    def __init__(self, id, password, person: Person, status=AccountStatus.ACTIVE):
        super().__init__(id, password, person, status)
        self.__date_of_membership = datetime.date.today()
        self.__total_books_checkedout = 0

    def get_total_books_checkedout(self):
        return self.__total_books_checkedout

    def reserve_book_item(self, book_item):
        None

    def increment_total_books_checkedout(self):
        None

    # def renew_book_item(self, book_item):
    #     None

    def checkout_book_item(self, book_item: 'BookItem'):
        if self.get_total_books_checked_out() >= Constants.MAX_BOOKS_ISSUED_TO_A_USER:
            print("The user has already checked-out maximum number of books")
            return False
        book_reservation = BookReservation.fetch_reservation_details(
            book_item.get_barcode())
        if book_reservation != None and book_reservation.get_member_id() != self.get_id():
            # book item has a pending reservation from another user
            print("self book is reserved by another member")
            return False
        elif book_reservation != None:
            # book item has a pending reservation from the give member, update it
            book_reservation.update_status(ReservationStatus.COMPLETED)

        if not book_item.checkout(self.get_id()):
            return False

        self.increment_total_books_checkedout()
        return True

    def check_for_fine(self, book_item_barcode):
        book_lending = BookLending.fetch_lending_details(book_item_barcode)
        due_date = book_lending.get_due_date()
        today = datetime.date.today()
        # check if the book has been returned within the due date
        if today > due_date:
            diff = today - due_date
            diff_days = diff.days
            Fine.collect_fine(self.get_member_id(), diff_days)

    def return_book_item(self, book_item: 'BookItem'):
        self.check_for_fine(book_item.get_barcode())
        book_reservation = BookReservation.fetch_reservation_details(
            book_item.get_barcode())
        if book_reservation != None:
            # book item has a pending reservation
            book_item.update_book_item_status(BookStatus.RESERVED)
            book_reservation.send_book_available_notification()
        book_item.update_book_item_status(BookStatus.AVAILABLE)

    def renew_book_item(self, book_item: 'BookItem'):
        self.check_for_fine(book_item.get_barcode())
        book_reservation = BookReservation.fetch_reservation_details(
            book_item.get_barcode())
        # check if self book item has a pending reservation from another member
        if book_reservation != None and book_reservation.get_member_id() != self.get_member_id():
            print("self book is reserved by another member")
            self.decrement_total_books_checkedout()
            book_item.update_book_item_state(BookStatus.RESERVED)
            book_reservation.send_book_available_notification()
            return False
        elif book_reservation != None:
            # book item has a pending reservation from self member
            book_reservation.update_status(ReservationStatus.COMPLETED)
        BookLending.lend_book(book_item.get_bar_code(), self.get_member_id())
        book_item.update_due_date(
            datetime.datetime.now().AddDays(Constants.MAX_LENDING_DAYS))
        return True

# # BookReservation, BookLending, and Fine: These classes represent a book reservation, lending, and fine collection, respectively.

class BookReservation:
    def __init__(self, creation_date, status, book_item_barcode, member_id):
        self.__creation_date = creation_date
        self.__status = status
        self.__book_item_barcode = book_item_barcode
        self.__member_id = member_id

    def fetch_reservation_details(self, barcode):
        None

class BookLending:
    def __init__(self, creation_date, due_date, book_item_barcode, member_id):
        self.__creation_date = creation_date
        self.__due_date = due_date
        self.__return_date = None
        self.__book_item_barcode = book_item_barcode
        self.__member_id = member_id

    def lend_book(self, barcode, member_id):
        None

    def fetch_lending_details(self, barcode):
        None

class Fine:
    def __init__(self, creation_date, book_item_barcode, member_id):
        self.__creation_date = creation_date
        self.__book_item_barcode = book_item_barcode
        self.__member_id = member_id

    def collect_fine(self, member_id, days):
        None

# # BookItem: Encapsulating a book item, this class will be responsible for processing the reservation, return, and renewal of a book item.

class Book(ABC):
    def __init__(self, ISBN, title, subject, publisher, language, number_of_pages):
        self.__ISBN = ISBN
        self.__title = title
        self.__subject = subject
        self.__publisher = publisher
        self.__language = language
        self.__number_of_pages = number_of_pages
        self.__authors = []

class BookItem(Book):
    def __init__(self, barcode, is_reference_only, borrowed, due_date, price, book_format, status, date_of_purchase, publication_date, placed_at):
        self.__barcode = barcode
        self.__is_reference_only = is_reference_only
        self.__borrowed = borrowed
        self.__due_date = due_date
        self.__price = price
        self.__format = book_format
        self.__status = status
        self.__date_of_purchase = date_of_purchase
        self.__publication_date = publication_date
        self.__placed_at = placed_at

    def checkout(self, member_id):
        # Check if this book can be borrowed
        if self.get_is_reference_only():
            print("self book is Reference only and can't be issued")
            return False
        # Failed to lend book
        if not BookLending.lend_book(self.get_bar_code(), member_id):
            return False
        # Successfully lent book
        self.update_book_item_status(BookStatus.LOANED)
        return True

class Rack:
    def __init__(self, number, location_identifier):
        self.__number = number
        self.__location_identifier = location_identifier

# Search interface and Catalog: The Catalog class will implement the Search interface to facilitate searching of books.

class Search(ABC):
    def search_by_title(self, title):
        None

    def search_by_author(self, author):
        None

    def search_by_subject(self, subject):
        None

    def search_by_pub_date(self, publish_date):
        None

class Catalog(Search):
    def __init__(self):
        self.__book_titles = {}
        self.__book_authors = {}
        self.__book_subjects = {}
        self.__book_publication_dates = {}

    def search_by_title(self, query):
        # return all books containing the string query in their title.
        return self.__book_titles.get(query)

    def search_by_author(self, query):
        # return all books containing the string query in their author's name.
        return self.__book_authors.get(query)

// https://paulonteri.notion.site/Design-a-Library-Management-System-d6f0c5b09f314a80870d7c8f582de630

// Enums and Constants: Here are the required enums, data types, and constants:
public enum BookFormat {
  HARDCOVER,
  PAPERBACK,
  AUDIO_BOOK,
  EBOOK,
  NEWSPAPER,
  MAGAZINE,
  JOURNAL
}

public enum BookStatus { AVAILABLE, RESERVED, LOANED, LOST }

public enum ReservationStatus { WAITING, PENDING, CANCELED, NONE }

public enum AccountStatus { ACTIVE, CLOSED, CANCELED, BLACKLISTED, NONE }

public class Address {
  private String streetAddress;
  private String city;
  private String state;
  private String zipCode;
  private String country;
}

public class Person {
  private String name;
  private Address address;
  private String email;
  private String phone;
}

public class Constants {
  public static final int MAX_BOOKS_ISSUED_TO_A_USER = 5;
  public static final int MAX_LENDING_DAYS = 10;
}

// For simplicity, we are not defining getter and setter functions. The reader
// can assume that all class attributes are private and accessed through their
// respective public getter methods and modified only through their public
// methods function.

public abstract class Account {
  private String id;
  private String password;
  private AccountStatus status;
  private Person person;

  public boolean resetPassword();
}

public class Librarian extends Account {
  public boolean addBookItem(BookItem bookItem);

  public boolean blockMember(Member member);

  public boolean unBlockMember(Member member);
}

public class Member extends Account {
  private Date dateOfMembership;
  private int totalBooksCheckedout;

  public int getTotalBooksCheckedout();

  public boolean reserveBookItem(BookItem bookItem);

  private void incrementTotalBooksCheckedout();

  public boolean checkoutBookItem(BookItem bookItem) {
    if (this.getTotalBooksCheckedOut() >=
        Constants.MAX_BOOKS_ISSUED_TO_A_USER) {
      ShowError("The user has already checked-out maximum number of books");
      return false;
    }
    BookReservation bookReservation =
        BookReservation.fetchReservationDetails(bookItem.getBarcode());
    if (bookReservation != null &&
        bookReservation.getMemberId() != this.getId()) {
      // book item has a pending reservation from another user
      ShowError("This book is reserved by another member");
      return false;
    } else if (bookReservation != null) {
      // book item has a pending reservation from the give member, update it
      bookReservation.updateStatus(ReservationStatus.COMPLETED);
    }

    if (!bookItem.checkout(this.getId())) {
      return false;
    }

    this.incrementTotalBooksCheckedout();
    return true;
  }

  private void checkForFine(String bookItemBarcode) {
    BookLending bookLending = BookLending.fetchLendingDetails(bookItemBarcode);
    Date dueDate = bookLending.getDueDate();
    Date today = new Date();
    // check if the book has been returned within the due date
    if (today.compareTo(dueDate) > 0) {
      long diff = todayDate.getTime() - dueDate.getTime();
      long diffDays = diff / (24 * 60 * 60 * 1000);
      Fine.collectFine(memberId, diffDays);
    }
  }

  public void returnBookItem(BookItem bookItem) {
    this.checkForFine(bookItem.getBarcode());
    BookReservation bookReservation =
        BookReservation.fetchReservationDetails(bookItem.getBarcode());
    if (bookReservation != null) {
      // book item has a pending reservation
      bookItem.updateBookItemStatus(BookStatus.RESERVED);
      bookReservation.sendBookAvailableNotification();
    }
    bookItem.updateBookItemStatus(BookStatus.AVAILABLE);
  }

  public bool renewBookItem(BookItem bookItem) {
    this.checkForFine(bookItem.getBarcode());
    BookReservation bookReservation =
        BookReservation.fetchReservationDetails(bookItem.getBarcode());
    // check if this book item has a pending reservation from another member
    if (bookReservation != null &&
        bookReservation.getMemberId() != this.getMemberId()) {
      ShowError("This book is reserved by another member");
      member.decrementTotalBooksCheckedout();
      bookItem.updateBookItemState(BookStatus.RESERVED);
      bookReservation.sendBookAvailableNotification();
      return false;
    } else if (bookReservation != null) {
      // book item has a pending reservation from this member
      bookReservation.updateStatus(ReservationStatus.COMPLETED);
    }
    BookLending.lendBook(bookItem.getBarCode(), this.getMemberId());
    bookItem.updateDueDate(
        LocalDate.now().plusDays(Constants.MAX_LENDING_DAYS));
    return true;
  }
}

//

public class BookReservation {
  private Date creationDate;
  private ReservationStatus status;
  private String bookItemBarcode;
  private String memberId;

  public static BookReservation fetchReservationDetails(String barcode);
}

public class BookLending {
  private Date creationDate;
  private Date dueDate;
  private Date returnDate;
  private String bookItemBarcode;
  private String memberId;

  public static boolean lendBook(String barcode, String memberId);
  public static BookLending fetchLendingDetails(String barcode);
}

public class Fine {
  private Date creationDate;
  private double bookItemBarcode;
  private String memberId;

  public static void collectFine(String memberId, long days) {}
}

//

public abstract class Book {
  private String ISBN;
  private String title;
  private String subject;
  private String publisher;
  private String language;
  private int numberOfPages;
  private List<Author> authors;
}

public class BookItem extends Book {
  private String barcode;
  private boolean isReferenceOnly;
  private Date borrowed;
  private Date dueDate;
  private double price;
  private BookFormat format;
  private BookStatus status;
  private Date dateOfPurchase;
  private Date publicationDate;
  private Rack placedAt;

  public boolean checkout(String memberId) {
    if (bookItem.getIsReferenceOnly()) {
      ShowError("This book is Reference only and can't be issued");
      return false;
    }
    if (!BookLending.lendBook(this.getBarCode(), memberId)) {
      return false;
    }
    this.updateBookItemStatus(BookStatus.LOANED);
    return true;
  }
}

public class Rack {
  private int number;
  private String locationIdentifier;
}

//

public interface Search {
  public List<Book> searchByTitle(String title);
  public List<Book> searchByAuthor(String author);
  public List<Book> searchBySubject(String subject);
  public List<Book> searchByPubDate(Date publishDate);
}

public class Catalog implements Search {
  private HashMap<String, List<Book>> bookTitles;
  private HashMap<String, List<Book>> bookAuthors;
  private HashMap<String, List<Book>> bookSubjects;
  private HashMap<String, List<Book>> bookPublicationDates;

  public List<Book> searchByTitle(String query) {
    // return all books containing the string query in their title.
    return bookTitles.get(query);
  }

  public List<Book> searchByAuthor(String query) {
    // return all books containing the string query in their author's name.
    return bookAuthors.get(query);
  }
}

Find the original version of this page (with additional content) on Notion here.

Design a Parking Lot

Is incomplete

A parking lot or car park is a dedicated cleared area that is intended for parking vehicles. In most countries where cars are a major mode of transportation, parking lots are a feature of every city and suburban area. Shopping malls, sports stadiums, megachurches, and similar venues often feature parking lots over large areas.

Screenshot 2021-11-08 at 05.59.02.png

System Requirements

We will focus on the following set of requirements while designing the parking lot:

The parking lot should have multiple floors where customers can park their cars.
The parking lot should have multiple entry and exit points.
Customers can collect a parking ticket from the entry points and can pay the parking fee at the exit points on their way out.
Customers can pay the tickets at the automated exit panel or to the parking attendant.
Customers can pay via both cash and credit cards.
Customers should also be able to pay the parking fee at the customer’s info portal on each floor. If the customer has paid at the info portal, they don’t have to pay at the exit.
The system should not allow more vehicles than the maximum capacity of the parking lot. If the parking is full, the system should be able to show a message at the entrance panel and on the parking display board on the ground floor.
Each parking floor will have many parking spots. The system should support multiple types of parking spots such as Compact, Large, Handicapped, Motorcycle, etc.
The Parking lot should have some parking spots specified for electric cars. These spots should have an electric panel through which customers can pay and charge their vehicles.
The system should support parking for different types of vehicles like car, truck, van, motorcycle, etc.
Each parking floor should have a display board showing any free parking spot for each spot type.
The system should support a per-hour parking fee model. For example, customers have to pay $4 for the first hour, $3.5 for the second and third hours, and $2.5 for all the remaining hours.

Use case diagrams

Actors

Here are the main actors in our system:

Admin: Mainly responsible for adding and modifying parking floors, parking spots, entrance, and exit panels, adding/removing parking attendants, etc.
Parking attendant: All customers can get a parking ticket and pay for it.
Customer: Parking attendants can do all the activities on the customer’s behalf, and can take cash for ticket payment.
System: To display messages on different info panels, as well as assigning and removing a vehicle from a parking spot

Use cases

Here are the top use cases for Parking Lot:

Add/Remove/Edit parking floor: To add, remove or modify a parking floor from the system. Each floor can have its own display board to show free parking spots.
Add/Remove/Edit parking spot: To add, remove or modify a parking spot on a parking floor.
Add/Remove a parking attendant: To add or remove a parking attendant from the system.
Take ticket: To provide customers with a new parking ticket when entering the parking lot.
Scan ticket: To scan a ticket to find out the total charge.
Credit card payment: To pay the ticket fee with credit card.
Cash payment: To pay the parking ticket through cash.
Add/Modify parking rate: To allow admin to add or modify the hourly parking rate.

Use case diagram

Screenshot 2021-11-08 at 14.20.53.png

Class diagram

Here are the main classes of our Parking Lot System:

ParkingLot
ParkingFloor
ParkingSpot
Account
- ParkingAttendant
- Admin
- ~~Customer~~ ← not there
Vehicle
- Car
- Truck
- ...
EntrancePanel and ExitPanel

Activity diagrams

Code

Find the original version of this page (with additional content) on Notion here.

Design an ATM

Introduction

Is incomplete

grokking-the-object-oriented-design-interview/design-an-atm.md at master · tssovi/grokking-the-object-oriented-design-interview

An automated teller machine (ATM) is an electronic telecommunications instrument that provides the clients of a financial institution with access to financial transactions in a public space without the need for a cashier or bank teller. ATMs are necessary as not all the bank branches are open every day of the week, and some customers may not be in a position to visit a bank each time they want to withdraw or deposit money.

Find the original version of this page (with additional content) on Notion here.

Composition vs Inheritance 9c1dc560a2724a8ea8a3797540ee10ef ↵

Difference

Composition: has-a relation Inheritance: is-a relation

Find the original version of this page (with additional content) on Notion here.

Difference

Composition: declare implementation Inheritance: extends implementation

Find the original version of this page (with additional content) on Notion here.

advantages

Composition: won't break encapsulation, easy to test, fits java for no multiple inheritance allowed Inheritance: easy to understand relationship

Find the original version of this page (with additional content) on Notion here.

Ended: Composition vs Inheritance 9c1dc560a2724a8ea8a3797540ee10ef

Overloading Comparison Operators 81101d971d0e4dad92625b304e846520 ↵

Equal to

p1 < p2: p1 == p2 p1.lt(p2): p1.eq(p2)

Find the original version of this page (with additional content) on Notion here.

Greater than

p1 < p2: p1 > p2 p1.lt(p2): p1.gt(p2)

Find the original version of this page (with additional content) on Notion here.

Greater than or equal to

p1 < p2: p1 >= p2 p1.lt(p2): p1.ge(p2)

Find the original version of this page (with additional content) on Notion here.

Less than or equal to

p1 < p2: p1 <= p2 p1.lt(p2): p1.le(p2)

Find the original version of this page (with additional content) on Notion here.

Not equal to

p1 < p2: p1 != p2 p1.lt(p2): p1.ne(p2)

Find the original version of this page (with additional content) on Notion here.

Ended: Overloading Comparison Operators 81101d971d0e4dad92625b304e846520

Python Operator Overloading 0e8809af87164a039f103691140df730 ↵

Addition

Expression: p1 + p2 Internally: p1.add(p2)

Find the original version of this page (with additional content) on Notion here.

Bitwise AND

Expression: p1 & p2 Internally: p1.and(p2)

Find the original version of this page (with additional content) on Notion here.

Bitwise Left Shift

Expression: p1 << p2 Internally: p1.lshift(p2)

Find the original version of this page (with additional content) on Notion here.

Bitwise NOT

Expression: ~p1 Internally: p1.invert()

Find the original version of this page (with additional content) on Notion here.

Bitwise OR

Expression: p1 | p2 Internally: p1.or(p2)

Find the original version of this page (with additional content) on Notion here.

Bitwise Right Shift

Expression: p1 >> p2 Internally: p1.rshift(p2)

Find the original version of this page (with additional content) on Notion here.

Bitwise XOR

Expression: p1 ^ p2 Internally: p1.xor(p2)

Find the original version of this page (with additional content) on Notion here.

Division

Expression: p1 / p2 Internally: p1.truediv(p2)

Find the original version of this page (with additional content) on Notion here.

Floor Division

Expression: p1 // p2 Internally: p1.floordiv(p2)

Find the original version of this page (with additional content) on Notion here.

Multiplication

Expression: p1 * p2 Internally: p1.mul(p2)

Find the original version of this page (with additional content) on Notion here.

Power

Expression: p1 ** p2 Internally: p1.pow(p2)

Find the original version of this page (with additional content) on Notion here.

Remainder (modulo)

Expression: p1 % p2 Internally: p1.mod(p2)

Find the original version of this page (with additional content) on Notion here.

Subtraction

Expression: p1 - p2 Internally: p1.sub(p2)

Find the original version of this page (with additional content) on Notion here.

Ended: Python Operator Overloading 0e8809af87164a039f103691140df730

Ended: Object Oriented Analysis and Design 1a01887a9271475da7b3cd3f4efc9e0d

Patterns for Coding Questions e3f5361611c147ebb2fb3eff37a743fd ↵

Advanced Binary Search

Coding Patterns: Modified Binary Search

Also known as Advanced Binary Search

The full content can be found here.

Find the original version of this page (with additional content) on Notion here.

Bit Manipulation

Introduction

Algorithms: Bit Manipulation

Coding Patterns: Bitwise XOR

Bit Manipulation - InterviewBit

Basics of Bit Manipulation Tutorials & Notes | Basic Programming | HackerEarth

Bit Manipulation Tricks

Binary Computation and Bitwise Operators

Binary | Tech Interview Handbook

📌 TIPS | HACKS WHICH YOU CAN'T IGNORE AS A CODER ✨🎩 - LeetCode Discuss

Bit Manipulation Course

Bitwise Operators in Python - Real Python

https://youtu.be/NLKQEOgBAnw

XOR is a logical bitwise operator that returns 0 (false) if both bits are the same and returns 1 (true) otherwise. In other words, it only returns 1 if exactly one bit is set to 1 out of the two bits in comparison.

XOR

Conversion to binary and back

>>> bin(5)
'0b101'

>>> int('101',2)
5

Important properties of XOR to remember

Following are some important properties of XOR to remember:

Taking XOR of a number with itself returns 0, e.g.,
- 1 ^ 1 = 0
- 29 ^ 29 = 0
Taking XOR of a number with 0 returns the same number, e.g.,
- 1 ^ 0 = 1
- 31 ^ 0 = 31
XOR is Associative & Commutative, which means:
- (a ^ b) ^ c = a ^ (b ^ c)
- a ^ b = b ^ a

Check if right most bit is a one

Remember that a single one can be assumed to have zeros till the left end

Screen Recording 2021-11-11 at 15.40.32.mov

Examples:

Number of 1 Bits

""" 
191. Number of 1 Bits

Write a function that takes an unsigned integer and returns the number of '1' bits it has (also known as the Hamming weight).
Note:
    Note that in some languages, such as Java & Python, there is no unsigned integer type. 
    In this case, the input will be given as a signed integer type. It should not affect your implementation, as the integer's internal binary representation is the same, whether it is signed or unsigned.
    In Java, the compiler represents the signed integers using 2's complement notation.
    Therefore, in Example 3, the input represents the signed integer. -3.


Example 1:
    Input: n = 00000000000000000000000000001011
    Output: 3
    Explanation: The input binary string 00000000000000000000000000001011 has a total of three '1' bits.
Example 2:
    Input: n = 00000000000000000000000010000000
    Output: 1
    Explanation: The input binary string 00000000000000000000000010000000 has a total of one '1' bit.
Example 3:
    Input: n = 11111111111111111111111111111101
    Output: 31
    Explanation: The input binary string 11111111111111111111111111111101 has a total of thirty one '1' bits.

https://leetcode.com/problems/number-of-1-bits
"""
from collections import Counter

""" 
https://youtu.be/5Km3utixwZs
"""

# O(1) time | O(1) space
# It will run a maximum of 32 times, since the input is 32 bits long.
class Solution:
    def hammingWeight(self, n: int):
        count = 0

        while n:
            # check if right most number is 1 by running an & operation with 1
            if n & 1 == 1:
                count += 1

            # logical right shift to remove the right-most 1
            n = n >> 1

        return count

class Solution_:
    def hammingWeight(self, n: int):
        # convert to binary string and count the number of 1's
        return Counter(bin(n))['1']

Counting Bits

""" 
338. Counting Bits

Given an integer n, return an array ans of length n + 1 such that for each i (0 <= i <= n), 
ans[i] is the number of 1's in the binary representation of i.

Example 1:
    Input: n = 2
    Output: [0,1,1]
    Explanation:
    0 --> 0
    1 --> 1
    2 --> 10
Example 2:
    Input: n = 5
    Output: [0,1,1,2,1,2]
    Explanation:
        0 --> 0
        1 --> 1
        2 --> 10
        3 --> 11
        4 --> 100
        5 --> 101

Constraints:
    0 <= n <= 105

https://leetcode.com/problems/counting-bits

Prerequisites:
- https://leetcode.com/problems/number-of-1-bits
"""

class Solution:
    def countBits(self, n: int):
        bits = [None] * (n+1)
        bits[0] = 0

        for num in range(1, n+1):
            bits[num] = self.get_bits(bits, num)

        return bits

    def get_bits(self, bits, num):
        count = 0

        # # check if has 1 at right end
        if num & 1:
            count += 1

        # #right shift:
        # remove the number at the right end
        num = num >> 1

        # # get the number of ones remaining after shifting
        # right shift == floor dividing by two, so will be smaller & have been precalculated
        return count + bits[num]

Numbers used in examples in binary form

>>> bin(2)
'0b10'
>>> bin(3)
'0b11'
>>> bin(4)
'0b100'
>>> bin(5)
'0b101'
>>> 2 & 1

Examples

>>> 2 & 1 # 10 & 01
0

>>> 3 & 1
1

>>> 4 & 1
0

>>> 5 & 1
1

Bit shifting

Algorithms: Bit Manipulation

Screenshot 2021-11-11 at 15.09.39.png

A bit shift moves each digit in a number's binary representation left or right. There are three main types of shifts:

Left Shifts

When shifting left, the most-significant bit is lost, and a 0 bit is inserted on the other end.

The left shift operator is usually written as "<<". **0010 << 1 → 0100**

0010 << 1  →  0100
0010 << 2  →  1000

A single left shift multiplies a binary number by 2:

0010 << 1  →  0100

0010 is 2
0100 is 4

Logical Right Shifts

This does not exist in python!

How to get the logical right binary shift in python

When shifting right with a logical right shift, the least-significant bit is lost and a 0 is inserted on the other end.

1011 >>> 1  →  0101
1011 >>> 3  →  0001

For positive numbers, a single logical right shift divides a number by 2, throwing out any remainders.

0101 >>> 1  →  0010

0101 is 5
0010 is 2

Arithmetic Right Shifts

Examples

Number of 1 Bits

""" 
191. Number of 1 Bits

Write a function that takes an unsigned integer and returns the number of '1' bits it has (also known as the Hamming weight).
Note:
    Note that in some languages, such as Java & Python, there is no unsigned integer type. 
    In this case, the input will be given as a signed integer type. It should not affect your implementation, as the integer's internal binary representation is the same, whether it is signed or unsigned.
    In Java, the compiler represents the signed integers using 2's complement notation.
    Therefore, in Example 3, the input represents the signed integer. -3.


Example 1:
    Input: n = 00000000000000000000000000001011
    Output: 3
    Explanation: The input binary string 00000000000000000000000000001011 has a total of three '1' bits.
Example 2:
    Input: n = 00000000000000000000000010000000
    Output: 1
    Explanation: The input binary string 00000000000000000000000010000000 has a total of one '1' bit.
Example 3:
    Input: n = 11111111111111111111111111111101
    Output: 31
    Explanation: The input binary string 11111111111111111111111111111101 has a total of thirty one '1' bits.

https://leetcode.com/problems/number-of-1-bits
"""
from collections import Counter

""" 
https://youtu.be/5Km3utixwZs
"""

# O(1) time | O(1) space
# It will run a maximum of 32 times, since the input is 32 bits long.
class Solution:
    def hammingWeight(self, n: int):
        count = 0

        while n:
            # check if right most number is 1 by running an & operation with 1
            if n & 1 == 1:
                count += 1

            # logical right shift to remove the right-most 1
            n = n >> 1

        return count

class Solution_:
    def hammingWeight(self, n: int):
        # convert to binary string and count the number of 1's
        return Counter(bin(n))['1']

Counting Bits

""" 
338. Counting Bits

Given an integer n, return an array ans of length n + 1 such that for each i (0 <= i <= n), 
ans[i] is the number of 1's in the binary representation of i.

Example 1:
    Input: n = 2
    Output: [0,1,1]
    Explanation:
    0 --> 0
    1 --> 1
    2 --> 10
Example 2:
    Input: n = 5
    Output: [0,1,1,2,1,2]
    Explanation:
        0 --> 0
        1 --> 1
        2 --> 10
        3 --> 11
        4 --> 100
        5 --> 101

Constraints:
    0 <= n <= 105

https://leetcode.com/problems/counting-bits

Prerequisites:
- https://leetcode.com/problems/number-of-1-bits
"""

class Solution:
    def countBits(self, n: int):
        bits = [None] * (n+1)
        bits[0] = 0

        for num in range(1, n+1):
            bits[num] = self.get_bits(bits, num)

        return bits

    def get_bits(self, bits, num):
        count = 0

        # # check if has 1 at right end
        if num & 1:
            count += 1

        # #right shift:
        # remove the number at the right end
        num = num >> 1

        # # get the number of ones remaining after shifting
        # right shift == floor dividing by two, so will be smaller & have been precalculated
        return count + bits[num]

When shifting right with an arithmetic right shift, the least-significant bit is lost and the most-significant bit is copied. Languages handle arithmetic and logical right shifting in different ways. Java provides two right shift operators: >> does an arithmetic right shift and >>> does a logical right shift. **1011 >> 1 → 1101**

1011 >> 1  →  1101
1011 >> 3  →  1111

0011 >> 1  →  0001
0011 >> 2  →  0000

The first two numbers had a 1 as the most significant bit, so more 1's were inserted during the shift. The last two numbers had a 0 as the most significant bit, so the shift inserted more 0's. If a number is encoded using two's complement, then an arithmetic right shift preserves the number's sign, while a logical right shift makes the number positive.

Python uses this by default

# Arithmetic shift
1011 >> 1  →  1101
    1011 is -5
    1101 is -3

# Logical shift
1111 >>> 1  →  0111
    1111 is -1
    0111 is  7

Simple problems

todo:

Single Number

""" 
Single Number:

Given a non-empty array of integers nums, every element appears twice except for one. Find that single one.
You must implement a solution with a linear runtime complexity and use only constant extra space.

https://leetcode.com/problems/single-number/
"""

""" 
4^4=0          -> cancel out each other
4^0=4
4^7^6^6^4^7=0  -> contains all the pairs
4^7^6^4^7=6    -> missing pair of 6

"""

class Solution:
    def singleNumber(self, nums):

        res = 0
        for num in nums:
            res ^= num
        return res

Missing Number

""" 
Missing Number:

Given an array nums containing n distinct numbers in the range [0, n], return the only number in the range that is missing from the array.
Follow up: Could you implement a solution using only O(1) extra space complexity and O(n) runtime complexity?

Example 1:
    Input: nums = [3,0,1]
    Output: 2
    Explanation: n = 3 since there are 3 numbers, so all numbers are in the range [0,3]. 2 is the missing number in the range since it does not appear in nums.
Example 2:
    Input: nums = [0,1]
    Output: 2
    Explanation: n = 2 since there are 2 numbers, so all numbers are in the range [0,2]. 2 is the missing number in the range since it does not appear in nums.
Example 3:
    Input: nums = [9,6,4,2,3,5,7,0,1]
    Output: 8
    Explanation: n = 9 since there are 9 numbers, so all numbers are in the range [0,9]. 8 is the missing number in the range since it does not appear in nums.
Example 4:
    Input: nums = [0]
    Output: 1
    Explanation: n = 1 since there is 1 number, so all numbers are in the range [0,1]. 1 is the missing number in the range since it does not appear in nums.

https://leetcode.com/problems/missing-number/
"""

""" 
Sum formulae:

(sum of all possible numbers) - (sum of given number) = missing_number
"""

class Solution0:
    def missingNumber(self, nums):

        possible = sum(range(len(nums)+1))
        given = sum(nums)

        return possible - given

""" 
Bitwise XOR 
4^4=0          -> cancel out each other
4^0=4
4^7^6^6^4^7=0  -> contains all the pairs
4^7^6^4^7=6    -> missing pair of 6

- XOR all the possible numbers with the given numbers, 
    the result will be the missing as it won't have a partner to cancel it out

example: [3,0,1]
- > all possible: 0^1^2^3
- > given: 3^0^1
- > 0^1^2^3 ^ 3^0^1 = 2 (it won't be canceled out)
"""

class Solution:
    def missingNumber(self, nums):

        res = 0
        for i in range(1, len(nums)+1):
            res ^= i

        for num in nums:
            res ^= num

        return res

Number of 1 Bits

""" 
191. Number of 1 Bits

Write a function that takes an unsigned integer and returns the number of '1' bits it has (also known as the Hamming weight).
Note:
    Note that in some languages, such as Java & Python, there is no unsigned integer type. 
    In this case, the input will be given as a signed integer type. It should not affect your implementation, as the integer's internal binary representation is the same, whether it is signed or unsigned.
    In Java, the compiler represents the signed integers using 2's complement notation.
    Therefore, in Example 3, the input represents the signed integer. -3.


Example 1:
    Input: n = 00000000000000000000000000001011
    Output: 3
    Explanation: The input binary string 00000000000000000000000000001011 has a total of three '1' bits.
Example 2:
    Input: n = 00000000000000000000000010000000
    Output: 1
    Explanation: The input binary string 00000000000000000000000010000000 has a total of one '1' bit.
Example 3:
    Input: n = 11111111111111111111111111111101
    Output: 31
    Explanation: The input binary string 11111111111111111111111111111101 has a total of thirty one '1' bits.

https://leetcode.com/problems/number-of-1-bits
"""
from collections import Counter

""" 
https://youtu.be/5Km3utixwZs
"""

# O(1) time | O(1) space
# It will run a maximum of 32 times, since the input is 32 bits long.
class Solution:
    def hammingWeight(self, n: int):
        count = 0

        while n:
            # check if right most number is 1 by running an & operation with 1
            if n & 1 == 1:
                count += 1

            # logical right shift to remove the right-most 1
            n = n >> 1

        return count

class Solution_:
    def hammingWeight(self, n: int):
        # convert to binary string and count the number of 1's
        return Counter(bin(n))['1']

Counting Bits

""" 
338. Counting Bits

Given an integer n, return an array ans of length n + 1 such that for each i (0 <= i <= n), 
ans[i] is the number of 1's in the binary representation of i.

Example 1:
    Input: n = 2
    Output: [0,1,1]
    Explanation:
    0 --> 0
    1 --> 1
    2 --> 10
Example 2:
    Input: n = 5
    Output: [0,1,1,2,1,2]
    Explanation:
        0 --> 0
        1 --> 1
        2 --> 10
        3 --> 11
        4 --> 100
        5 --> 101

Constraints:
    0 <= n <= 105

https://leetcode.com/problems/counting-bits

Prerequisites:
- https://leetcode.com/problems/number-of-1-bits
"""

class Solution:
    def countBits(self, n: int):
        bits = [None] * (n+1)
        bits[0] = 0

        for num in range(1, n+1):
            bits[num] = self.get_bits(bits, num)

        return bits

    def get_bits(self, bits, num):
        count = 0

        # # check if has 1 at right end
        if num & 1:
            count += 1

        # #right shift:
        # remove the number at the right end
        num = num >> 1

        # # get the number of ones remaining after shifting
        # right shift == floor dividing by two, so will be smaller & have been precalculated
        return count + bits[num]

Sum of Two Integers

https://leetcode.com/problems/sum-of-two-integers

Blind-75 - Sum of Two Integers - Leetcode 371 - Java

Find the original version of this page (with additional content) on Notion here.

Cyclic Sort

Coding Patterns: Cyclic Sort

Cyclic Sort - Explained - LeetCode Discuss

This pattern describes an interesting approach to deal with problems involving arrays containing numbers in a given range. For example, take the following problem:

You are given an unsorted array containing numbers taken from the range 1 to ‘n’. The array can have duplicates, which means that some numbers will be missing. Find all the missing numbers.

To efficiently solve this problem, we can use the fact that the input array contains numbers in the range of 1 to ‘n’. For example, to efficiently sort the array, we can try placing each number in its correct place, i.e., placing ‘1’ at index ‘0’, placing ‘2’ at index ‘1’, and so on. Once we are done with the sorting, we can iterate the array to find all indices that are missing the correct numbers. These will be our required numbers.

Untitled

This pattern describes an interesting approach to deal with problems involving arrays containing numbers in a given range. The Cyclic Sort pattern iterates over the array one number at a time, and if the current number you are iterating is not at the correct index, you swap it with the number at its correct index.

How do I identify this pattern?

They will be problems involving a sorted array with numbers in a given range
If the problem asks you to find the missing/duplicate/smallest number in an sorted/rotated array

Cyclic Sort

""" 
Cyclic Sort:

We are given an array containing ‘n’ objects. 
Each object, when created, was assigned a unique number from 1 to ‘n’ based on their creation sequence. 
This means that the object with sequence number ‘3’ was created just before the object with sequence number ‘4’.
Write a function to sort the objects in-place on their creation sequence number in O(n) and without any extra space. 
For simplicity, let’s assume we are passed an integer array containing only the sequence numbers, though each number is actually an object.

There are no duplicates

Example 1:
    Input: [3, 1, 5, 4, 2]
    Output: [1, 2, 3, 4, 5]
Example 2:
    Input: [2, 6, 4, 3, 1, 5]
    Output: [1, 2, 3, 4, 5, 6]
Example 3:
    Input: [1, 5, 6, 4, 3, 2]
    Output: [1, 2, 3, 4, 5, 6]
"""

"""
As we know, the input array contains numbers in the range of 1 to ‘n’. We can use this fact to devise an efficient way to sort the numbers. 
Since all numbers are unique, we can try placing each number at its correct place, i.e., placing ‘1’ at index ‘0’, placing ‘2’ at index ‘1’, and so on.
"""

def cyclic_sort(nums):

    idx = 0
    while idx < len(nums):
        if nums[idx] != idx+1:
            # nums[num-1], nums[idx] = nums[idx], nums[num-1]
            nums[nums[idx]-1], nums[idx] = nums[idx], nums[nums[idx]-1]
            continue

        idx += 1

    return nums

Find the Missing Number

"""
Find the Missing Number:

We are given an array containing ‘n’ distinct numbers taken from the range 0 to ‘n’.
Since the array has only ‘n’ numbers out of the total ‘n+1’ numbers, find the missing number.

Example 1:
    Input: [4, 0, 3, 1]
    Output: 2
Example 2:
    Input: [8, 3, 5, 2, 4, 6, 0, 1]
    Output: 7

"""

""" 
Since the input array contains unique numbers from the range 0 to ‘n’, 
    we can use a similar strategy as discussed in Cyclic Sort to place the numbers on their correct index.
Once we have every number in its correct place, 
    we can iterate the array to find the index which does not have the correct number, and that index will be our missing number.
"""

def find_missing_number(nums):
    idx = 0
    while idx < len(nums):
        num_in_range = nums[idx] >= 0 and nums[idx] < len(nums)
        if num_in_range and nums[idx] != idx:
            # nums[num-1], nums[idx] = nums[idx], nums[num-1]
            nums[nums[idx]], nums[idx] = nums[idx], nums[nums[idx]]
            continue
        idx += 1

    for idx in range(len(nums)):
        if nums[idx] != idx:
            return idx

    return -1

First Missing Positive

https://leetcode.com/problems/first-missing-positive/

Find All Numbers Disappeared in an Array

""" 
Find All Numbers Disappeared in an Array:

Given an array nums of n integers where nums[i] is in the range [1, n], 
return an array of all the integers in the range [1, n] that do not appear in nums.

Example 1:
    Input: nums = [4,3,2,7,8,2,3,1]
    Output: [5,6]
Example 2:
    Input: nums = [1,1]
    Output: [2]

Constraints:
    n == nums.length
    1 <= n <= 105
    1 <= nums[i] <= n

 Could you do it without extra space and in O(n) runtime? You may assume the returned list does not count as extra space.
"""

class Solution:
    def findDisappearedNumbers(self, nums):
        result = []

        idx = 0
        while idx < len(nums):
            num = nums[idx]
            if num-1 != idx and nums[num-1] != num:
                nums[num-1], nums[idx] = nums[idx], nums[num-1]
                continue
                            idx += 1

        for idx in range(len(nums)):
            if nums[idx]-1 != idx:
                result.append(idx+1)

        return result

Find the original version of this page (with additional content) on Notion here.

DP

Patterns

How to solve DP - String? Template and 4 Steps to be followed. - LeetCode Discuss

Based on:

0/1 Knapsack (Dynamic Programming)

Levenshtein Distance *

Staircase

Jump Game

Palindromes

Longest Increasing Subsequence

Kadane's Algorithm

Find the original version of this page (with additional content) on Notion here.

Heap Tricks *

K-Way Merge

Top/Smallest/Frequent K elements *

Two Heaps

Other

Find the original version of this page (with additional content) on Notion here.

Merge Intervals

Introduction

Interval | Tech Interview Handbook

This pattern describes an efficient technique to deal with overlapping intervals. In a lot of problems involving intervals, we either need to find overlapping intervals or merge intervals if they overlap.

Given two intervals (‘a’ and ‘b’), there will be six different ways the two intervals can relate to each other:

Understanding the above six cases will help us in solving all intervals related problems.

Helpers

image-1635410969251.jpg5977164209775688851.jpg

Draw number line
Sort the intervals

Simple examples

Conflicting Appointments

"""
Given an array of intervals representing ‘N’ appointments, find out if a person can attend all the appointments.

Example 1:
        Appointments: [[1,4], [2,5], [7,9]]
        Output: false
        Explanation: Since [1,4] and [2,5] overlap, a person cannot attend both of these appointments.
Example 2:
        Appointments: [[6,7], [2,4], [8,12]]
        Output: true
        Explanation: None of the appointments overlap, therefore a person can attend all of them.
Example 3:
        Appointments: [[4,5], [2,3], [3,6]]
        Output: false
        Explanation: Since [4,5] and [3,6] overlap, a person cannot attend both of these appointments.
"""

def can_attend_all_appointments(intervals):
  intervals.sort(key=lambda x: x[0])

  start, end = 0, 1
  for i in range(1, len(intervals)):
    if intervals[i][start] < intervals[i-1][end]:
      # please note the comparison above, it is "<" and not "<="
      # while merging we needed "<=" comparison, as we will be merging the two
      # intervals having condition "intervals[i][start] == intervals[i - 1][end]" but
      # such intervals don't represent conflicting appointments as one starts right
      # after the other
      return False
  return True

Merge Intervals

Untitled

Problem

""" 
Merge Intervals:

Given a list of intervals, merge all the overlapping intervals to produce a list that has only mutually exclusive intervals.

Example 1:
    Intervals: [[1,4], [2,5], [7,9]]
    Output: [[1,5], [7,9]]
    Explanation: Since the first two intervals [1,4] and [2,5] overlap, we merged them into one [1,5].
Example 2:
    Intervals: [[6,7], [2,4], [5,9]]
    Output: [[2,4], [5,9]]
    Explanation: Since the intervals [6,7] and [5,9] overlap, we merged them into one [5,9].
Example 3:
    Intervals: [[1,4], [2,6], [3,5]]
    Output: [[1,6]]
    Explanation: Since all the given intervals overlap, we merged them into one.
"""

Screenshot 2021-08-18 at 10.19.11.png

Solution

Let’s take the example of two intervals (‘a’ and ‘b’) such that a.start <= b.start. There are four possible scenarios:

Merge%20Intervals%20579d83afac224dcaa70b8b68dcbcf2d9/Screenshot_2021-08-18_at_09.49.39%201.png

Our goal is to merge the intervals whenever they overlap. For the above-mentioned three overlapping scenarios (2, 3, and 4), this is how we will merge them:

Earliest end vs latest end

The diagram above clearly shows a merging approach. Our algorithm will look like this:

Sort the intervals on the start time to ensure a.start <= b.start
If ‘a’ overlaps ‘b’ (i.e. b.start <= a.end), we need to merge them into a new interval ‘c’ such that:
We will keep repeating the above two steps to merge ‘c’ with the next interval if it overlaps with ‘c’.

    c.start = a.start
    c.end = max(a.end, b.end)

""" 
Solution:

[[6,7], [2,4], [5,9]]

sort
[[2,4], [5,9], [6,7]]
merge
[[2,4], [5,9]]

- so that its easier to know what comes b4 what, we should ***sort the intervals by their starting interval***
- we can then check if a particular interval overlaps the next ones by checking if its ***ending interval > the next's starting interval***
    - the new merged interval will have the start as the first's starting interval and the ending to be the max(the next's ending interval, the first's starting interval)

"""

class Interval:
    def __init__(self, start, end):
        self.start = start
        self.end = end

def merge(intervals):
    merged = []
    intervals.sort(key=lambda x: x.start)

    i = 0
    while i < len(intervals)-1:
        start = intervals[i].start
        end = intervals[i].end
        while i < len(intervals)-1 and end >= intervals[i+1].start:
            i += 1
            end = max(end, intervals[i].end)

        merged.append(Interval(start, end))

    return merged

"""
Leetcode 56: Merge Intervals

Given a collection of intervals, merge all overlapping intervals.

Example:
    Input:
        [[8,10],[15,18], [1,3],[2,6]]
        [[1,3],[2,6],[8,10],[15,18]]
        [[1,3]]
        []
        [[1,4],[4,5]]
        [[1,4],[2,3]]
    Output:
        [[1,6],[8,10],[15,18]]
        [[1,6],[8,10],[15,18]]
        [[1,3]]
        []
        [[1,5]]
        [[1,4]]
https://leetcode.com/problems/merge-intervals
"""

from typing import List

""" 
[[6,7], [2,4], [5,9]]

**0 1 2 3 4 5 6 7 8 9

    2---4
          5-------9
            6-7**

- have a res arrray
- sort the intervals by their start value:
- for each interval (curr_interval):
    - if it overlaps the next, merge the next into it (update the curr_intervals end)
        - skip the next (move the index forward)
        - repeat this until we no longer find an overlap
    - add it to res
- return res
"""

class Solution:
    def merge(self, intervals: List[List[int]]):

        merged = []
        intervals.sort(key=lambda x: x[0])

        i = 0
        while i < len(intervals):
            start = intervals[i][0]
            end = intervals[i][1]
            while i < len(intervals)-1 and end >= intervals[i+1][0]:
                i += 1
                end = max(end, intervals[i][1])

            merged.append([start, end])
            i += 1

        return merged

class Solution2:
    def merge(self, intervals: List[List[int]]):

        # sort
        intervals.sort(key=lambda item: item[0])

        i = 0
        # no need to check the last array
        while (i + 1) < len(intervals):

            curr_a = intervals[i]
            next_a = intervals[i+1]

            # check for overlap
            if curr_a[1] >= next_a[0]:

                # merge
                # we use max coz of such a case: [[1,4],[2,3]]
                # make the last element of the first array be the furthest(largest value)
                intervals[i][1] = max(curr_a[1], next_a[1])

                # delete the second array
                intervals.pop(i+1)

            else:
                i += 1

        return intervals

Time & Space complexity

The time complexity of the above algorithm is O(N ∗ log N), where ‘N’ is the total number of intervals. We are iterating the intervals only once which will take O(N), in the beginning though, since we need to sort the intervals, our algorithm will take O(N ∗ log N).

The space complexity of the above algorithm will be O(N) as we need to return a list containing all the merged intervals.

Intervals Intersection *

Problem

Screenshot 2021-08-19 at 11.16.52.png

"""
Interval List Intersections:

You are given two lists of closed intervals, firstList and secondList, 
    where firstList[i] = [starti, endi] and secondList[j] = [startj, endj]. 
Each list of intervals is pairwise disjoint and in sorted order.
Return the intersection of these two interval lists.

A closed interval [a, b] (with a < b) denotes the set of real numbers x with a <= x <= b.
The intersection of two closed intervals is a set of real numbers that are either empty or represented as a closed interval. 
For example, the intersection of [1, 3] and [2, 4] is [2, 3].

Example:
    Input: arr1=[[1, 3], [5, 6], [7, 9]], arr2=[[2, 3], [5, 7]]
    Output: [2, 3], [5, 6], [7, 7]
    Explanation: The output list contains the common intervals between the two lists.
Example:
    Input: arr1=[[1, 3], [5, 7], [9, 12]], arr2=[[5, 10]]
    Output: [5, 7], [9, 10]
    Explanation: The output list contains the common intervals between the two lists.
Example 1:
    Input: firstList = [[0,2],[5,10],[13,23],[24,25]], secondList = [[1,5],[8,12],[15,24],[25,26]]
    Output: [[1,2],[5,5],[8,10],[15,23],[24,24],[25,25]]
Example 2:
    Input: firstList = [[1,3],[5,9]], secondList = []
    Output: []
Example 3:
    Input: firstList = [], secondList = [[4,8],[10,12]]
    Output: []
Example 4:
    Input: firstList = [[1,7]], secondList = [[3,10]]
    Output: [[3,7]]
"""

"""
Intervals Intersection:

Given two lists of intervals, find the intersection of these two lists. 
Each list consists of disjoint intervals sorted on their start time.

Example 1:
        Input: arr1=[[1, 3], [5, 6], [7, 9]], 
                        arr2=[[2, 3], [5, 7]]
        Output: [2, 3], [5, 6], [7, 7]
        Explanation: The output list contains the common intervals between the two lists.
Example 2:
        Input: arr1=[[1, 3], [5, 7], [9, 12]], arr2=[[5, 10]]
        Output: [5, 7], [9, 10]
        Explanation: The output list contains the common intervals between the two lists.

https://leetcode.com/problems/interval-list-intersections/
https://www.educative.io/courses/grokking-the-coding-interview/JExVVqRAN9D
"""

Solution

Untitled

image-1635411919648.jpg5374943471934743018.jpg

"""
Solution:

---

# Note: Each list of intervals is pairwise disjoint and in sorted order.

- check if start of two <= end of one and end of two >= start of one: => ensure they are together (are not before or after each other)
- if so:
    ***intersection = [max(start_one, start_two), min(end_one, end_two)]***
        - futhest start, first end (end that is in both intervals)
- move the pointer of the interval with the ***least ending forward***
    - list with the smaller might have another intersection in the current bigger intersection
    - because the bigger one might still be in another intersection

firstList =  [[0,2],[5,10],[13,23],[24,25]], 
secondList = [[1,5],[8,12],[15,24],[25,26]]

one,two,res
0,0,[] => intersection = [max(0,1), min(2,5)]
1,0,[[1,2], ] => intersection = [max(5,1), min(10,5)]
1,1,[[1,2],[5,5] ] => intersection = [max(5,8), min(10,12)]
2,1,[[1,2],[5,5],[8,10] ] => intersection = None
2,2,[[1,2],[5,5],[8,10] ] => intersection = [max(13,15), min(23,24)]
3,2,[[1,2],[5,5],[8,10],[15,23] ] => intersection = [max(24,15), min(25,24)]
3,3,[[1,2],[5,5],[8,10],[15,23],[24,24] ] => intersection = [max(24,25), min(25,26)]
3,3,[[1,2],[5,5],[8,10],[15,23],[24,24],[25,25] ]

"""

class Solution:
    def getIntersection(self, l_one, l_two):
        # futhest start, first end -> ensures interval is in both intervals
        return [max(l_one[0], l_two[0]), min(l_one[1], l_two[1])]

    def intervalIntersection(self, firstList, secondList):
        if not firstList or not secondList:
            return []

        res = []
        one = 0
        two = 0
        while one <= len(firstList)-1 and two <= len(secondList)-1:
            l_one = firstList[one]
            l_two = secondList[two]

            if l_two[0] <= l_one[1] and l_two[1] >= l_one[0]:  # if has interval
                res.append(self.getIntersection(l_one, l_two))

            # move forward the pointer of list with the least ending
            #   so that we can continue evaluating the one with the furthest end in the next loop
            if two == len(secondList)-1 or l_one[1] < l_two[1]:
                one += 1
            else:
                two += 1

        return res

[Python] Two Pointer Approach + Thinking Process Diagrams - LeetCode Discuss

Partition Labels

Find the original version of this page (with additional content) on Notion here.

Parenthesis

Valid Parentheses / Balanced Brackets

"""
Valid Parentheses / Balanced Brackets

Given a string s containing just the characters '(', ')', '{', '}', '[' and ']', determine if the input string is valid.
An input string is valid if:
    Open brackets must be closed by the same type of brackets.
    Open brackets must be closed in the correct order.

https://leetcode.com/problems/valid-parentheses/
https://www.algoexpert.io/questions/Balanced%20Brackets
"""

class Solution(object):
    def isValid(self, s):

        myStack = []

        match = {
            "(": ")",
            "[": "]",
            "{": "}"
        }

        for par in s:
            if par == "(" or par == "{" or par == "[":
                myStack.append(par)

            elif len(myStack) == 0 or match[myStack.pop()] != par:
                return False

        return len(myStack) == 0

def balancedBrackets(string):
    opening_brackets = "([{"
    matching_brackets = {")": "(", "]": "[", "}": "{"}
    stack = []
    for char in string:

        if char not in matching_brackets and char in opening_brackets:  # opening bracket
            stack.append(char)

        # closing brackets
        elif char in matching_brackets and(not stack or matching_brackets[char] != stack.pop(-1)):
            return False

    return len(stack) == 0

print(balancedBrackets("([])(){}(())()()"))
print(balancedBrackets("([])(){}(()))()()"))

Minimum Add to Make Parentheses Valid

""" 
921. Minimum Add to Make Parentheses Valid

A parentheses string is valid if and only if:
    It is the empty string,
    It can be written as AB (A concatenated with B), where A and B are valid strings, or
    It can be written as (A), where A is a valid string.
You are given a parentheses string s. 
In one move, you can insert a parenthesis at any position of the string.
For example, if s = "()))", you can insert an opening parenthesis to be "(()))" or a closing parenthesis to be "())))".
Return the minimum number of moves required to make s valid.

Example 1:

Input: s = "())"
Output: 1
Example 2:

Input: s = "((("
Output: 3
Example 3:

Input: s = "()"
Output: 0
Example 4:

Input: s = "()))(("
Output: 4

https://leetcode.com/problems/minimum-add-to-make-parentheses-valid
"""

class Solution:
    def minAddToMakeValid(self, s: str):
        invalid_closing = 0
        invalid_opening = 0

        # invalid closing
        opening_remaining = 0
        for char in s:
            if char == "(":
                opening_remaining += 1
            else:
                if opening_remaining > 0:
                    opening_remaining -= 1
                else:
                    invalid_closing += 1

        # invalid closing
        closing_remaining = 0
        for idx in reversed(range(len(s))):
            if s[idx] == ")":
                closing_remaining += 1
            else:
                if closing_remaining > 0:
                    closing_remaining -= 1
                else:
                    invalid_opening += 1

        return invalid_opening + invalid_closing

Longest Valid Parentheses **

Screenshot 2021-10-17 at 11.26.43.png

Screen Recording 2021-10-17 at 11.27.12.mov

Screenshot 2021-11-03 at 18.22.53.png

Screen Recording 2021-11-03 at 18.23.28.mov

""" 
Longest Valid Parentheses:

Given a string containing just the characters '(' and ')', 
find the length of the longest valid (well-formed) parentheses substring.

https://leetcode.com/problems/longest-valid-parentheses/
https://paulonteri.notion.site/Parenthesis-b2a79fe0baaf47459a53183b2f99115c
"""

from collections import deque

class Solution:
    def longestValidParentheses(self, s: str):
        """Store the longest streak we had so far at each index so that we can look back"""
        if not s:
            return 0

        opening_brackets = 0
        longest_so_far = [0]*(len(s)+1)
        for idx, char in enumerate(s):
            # opening brackets
            if char == '(':
                opening_brackets += 1

            # closing brackets
            else:
                if opening_brackets <= 0:
                    continue
                opening_brackets -= 1
                length = 2  # create streak

                # # "()"
                if s[idx-1] == "(" and idx > 1:
                    # add what is outside the brackets. Eg: (())() - at the last idx
                    length += longest_so_far[idx-2]

                # #"))"
                elif s[idx-1] == ")":
                    # continue streak
                    length += longest_so_far[idx-1]
                    # add what is outside the brackets. Eg: ()(()) - at the last idx
                    if idx-length >= 0:
                        length += longest_so_far[idx-length]

                longest_so_far[idx] = length

        return max(longest_so_far)

""" 
"((())())"
['(', '(', '(', ')', ')', '(', ')', ')']
[  0,  1,    2,  3,   4,   5,   6,   7]

idx,res,c_l,stack
0    0   0  [0]
1    0   0  [0,0]
2    0   0  [0,0,0]
3    2   2  [0,0]
4    4   4  [0]
5    4   0  [4,0]
6    6   6  [0]
7    8   8  []

"""

class Solution__:
    def longestValidParentheses(self, s: str):
        """ 
        Whenever we see a new open parenthesis, reset the streak
            we push the current longest streak to the prev_streak_stack.
            and reset the current length
        Whenever we see a close parenthesis, extend the streak
            If there is no matching open parenthesis for a close parenthesis, 
                reset the current count.
            else:
                we pop the top value, and add the value (which was the previous longest streak up to that point) to the current one (because they are now contiguous) 
                and add 2 to count for the matching open and close parenthesis. 

        Use this example to understand `"(()())"`
        """
        res = 0

        prev_streak_stack, curr_length = [], 0
        for char in s:

            # # saves streak that might be continued or broken by the next closing brackets
            if char == '(':
                prev_streak_stack.append(curr_length)  # save prev streak
                curr_length = 0  # reset streak

            # # create/increase or reset streak
            elif char == ')':

                if prev_streak_stack:
                    curr_length = curr_length + prev_streak_stack.pop() + 2
                    res = max(res, curr_length)

                else:
                    curr_length = 0

        return res

""" 

"""

class Solution_:
    def longestValidParentheses(self, s: str):
        """ 
        use stack to store left most invalid positions (followed by opening brackets)
            note that an unclosed opening brackets is also invalid
        """
        result = 0

        # stack contains left most invalid positions
        stack = deque([-1])

        for idx, bracket in enumerate(s):
            if bracket == "(":
                stack.append(idx)

            else:
                stack.pop()

                # the top of the stack should now contain the left most invalid index
                if stack:
                    result = max(result, idx-stack[-1])
                # if not, the element removed was not an opening bracket but the left most invalid index
                # which means that this closing bracket is invalid and should be added to the top of the stack
                else:
                    stack.append(idx)

        return result

Maximum Nesting Depth of Two Valid Parentheses Strings - LeetCode

Find the original version of this page (with additional content) on Notion here.

Pointers

Sliding Window

Two Pointers

Hare & Tortoise Algorithm

Find cycle in list

Find the original version of this page (with additional content) on Notion here.

Subsets, Permutations & Combinations *

Introduction

Screenshot 2021-10-30 at 22.28.17.png

Subsets

A general approach to backtracking questions in Java (Subsets, Permutations, Combination Sum, Palindrome Partioning) - LeetCode Discuss

Coding Patterns: Subsets

A huge number of coding interview problems involve dealing with Permutations and Combinations of a given set of elements. This pattern describes an efficient Breadth-First Search (BFS) approach to handle all these problems.

Simple problems

Subsets

To generate all possible subsets, we can use the Breadth First Search (BFS) approach. Starting with an empty set, we will iterate through all numbers one-by-one, and add them to existing sets to create subsets.

Start with an empty set: [[ ]]
Add num (1) to existing sets: [[ ], [1]]
Add num (2) to existing sets: [[ ], [1], [2], [1, 2]]
Add num (3) to existing sets: [[ ], [1], [2], [1, 2], [3], [1, 3], [2, 3], [1, 2, 3]]

Screenshot 2021-10-30 at 22.25.43.png

Screenshot 2021-08-21 at 21.53.45.png

"""
Subsets/Powerset:

Write a function that takes in an array of unique integers and returns its powerset.
The powerset P(X) of a set X is the set of all subsets of X. 
For example, the powerset of [1,2] is [[], [1], [2], [1,2]].
Note that the sets in the powerset do not need to be in any particular order.

https://www.algoexpert.io/questions/Powerset
# https://leetcode.com/problems/subsets/
"""

"""
To generate all subsets of the given set, we can use the Breadth First Search (BFS) approach. 
We can start with an empty set, iterate through all numbers one-by-one, and add them to existing sets to create new subsets.
"""

class Solution:
    def subsets(self, nums: List[int]) -> List[List[int]]:
        powerset = [[]]

        for num in nums:
            # take all existing subsets and add num to them
            for i in range(len(powerset)):
                powerset.append(powerset[i] + [num])

        return powerset

Time Complexity: O(2^N) since, in each step, number of subsets doubles.

Each number can eitther be in a previous subsets or not. If we had an array of len 10, the number of subtrees at each level of the recursive tree will be: $1 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 == 2 pow 10$

Space Complexity: O(2^N)

Since, in each step, the number of subsets doubles as we add each element to all the existing subsets, therefore, we will have a total of **O(2^N)** subsets, where ‘N’ is the total number of elements in the input set. And since we construct a new subset from an existing set, therefore, the time complexity of the above algorithm will be O(N*2^N)

All the additional space used by our algorithm is for the output list. Since we will have a total of O(2^N) subsets, and each subset can take up to O(N) space, therefore, the space complexity of our algorithm will be O(N*2^N)

Subsets With Duplicates/Subsets II

Screenshot 2021-08-22 at 05.34.07.png

"""
Subsets II

Given a collection of integers that might contain duplicates, nums, return all possible subsets (the power set).
Note: The solution set must not contain duplicate subsets.

Example:

    Input: [1,2,2]

    Output:
        [
        [2],
        [1],
        [1,2,2],
        [2,2],
        [1,2],
        []
        ]
https://leetcode.com/problems/subsets-ii/
"""

"""
- Sort all numbers of the given set. This will ensure that all duplicate numbers are next to each other.
- When we process a duplicate ( instead of adding the current number (which is a duplicate) to all the existing subsets,
         only add it to the subsets which were created in the previous step.
"""

class Solution:
    def subsetsWithDup(self, nums: List[int]):
        subsets = [[]]
        nums.sort()

        last_added = 0
        for idx, num in enumerate(nums):

            # handle duplicates
            if idx > 0 and num == nums[idx-1]:
                added = 0
                for i in range(len(subsets)-last_added, len(subsets)):
                    subsets.append(subsets[i] + [num])
                    added += 1

                last_added = added


            # handle non-duplicates
            else:
                last_added = 0
                for i in range(len(subsets)):
                    subsets.append(subsets[i] + [num])
                    last_added += 1



        return subsets

Permutations

Problem

"""
Permutations

Given an array nums of distinct integers, return all the possible permutations. You can return the answer in any order.

Example 1:
    Input: nums = [1,2,3]
    Output: [[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

https://leetcode.com/problems/permutations/
https://www.algoexpert.io/questions/Permutations
"""

Solution

Screen Recording 2021-10-30 at 22.34.05.mov

Screenshot 2021-08-22 at 10.24.50.png

Solution one

"""
[
[1,2,3],
[1,3,2],
[2,1,3],
[2,3,1],
[3,1,2],
[3,2,1]
]

                     []
          /               |    \
        [1]              [2]
        / \              / \     
    [1,2]  [1,3]     [2,1] [2,3]
      |        |       |      |
[1,2,3]     [1,3,2]  [2,1,3]  [2,3,1]

                                                  ([], [], [1,2,3])

        ([], [1], [2,3])                           ([], [2], [1,3])              ([], [3], [1,2])

([], [1, 2], [3]) ([], [1, 3], [3])

[[1,2,3,4],[1,2,4,3],[1,3,2,4],[1,3,4,2],[1,4,2,3],[1,4,3,2],[2,1,3,4],[2,1,4,3],[2,3,1,4],[2,3,4,1],[2,4,1,3],[2,4,3,1],[3,1,2,4],[3,1,4,2],[3,2,1,4],[3,2,4,1],[3,4,1,2],[3,4,2,1],[4,1,2,3],[4,1,3,2],[4,2,1,3],[4,2,3,1],[4,3,1,2],[4,3,2,1]]

# try placing each number at the beginning if the list, then add all the others at all the possible positions

- have result = []
- have a function perm(arr, curr_subset, result)
    - for each num in arr
        - place num in a copy of curr_subset
        - remove the num in a copy of arr
        - pass both copies to perm()
    - do the above step till arr is empty
        - then add curr_subset to result
- return result
"""

def _getPermutationsHelper(array, result, curr):
    if not array:
        return result.append(curr)

    for i in range(len(array)):
        _getPermutationsHelper(array[:i]+array[i+1:], result, curr+[array[i]])

def _getPermutations(array):
    result = []
    if not array:
        return result
    _getPermutationsHelper(array, result, [])
    return result

Solution two

"""

# remove all the elements from nums then insert them back in all positions possible

# place one each number at the beginning of a different list, then insert all the rest in different orders

- have a recursive function perm(nums_array)
    - with base cases:
        returns [[]] once nums_array is empty
- for each number in the list (iterate through the list)
    - remove it from the list
    - pass the rest of the numbers to the perm() recursive function
    - add it to all the lists returned by perm()
"""

def getPermutations0(array):
    if len(array) == 1:
        return [array[:]]

    result = []
    for _ in range(len(array)):
        # use the first index by default instead of keeping track of indices down the recursive tree
        num = array.pop(0)

        for arr in getPermutations(array):
            arr.append(num)
            result.append(arr)

        array.append(num)

    return result

# look below for an alternative

""" 
Improvement of above
"""

def ___getPermutations(array):
    if len(array) < 1:
        return array
    return ___getPermutationsHelper(array, 0)

def ___getPermutationsHelper(array, pos):
    if pos == len(array)-1:
        return [[array[pos]]]

    result = []
    for i in range(pos, len(array)):
        # add the number(array[i]) to the permutation
        # place the element of interest at the first position (pos)
        #  Example: for getPermutationsHelper([1,2,3,4], 0), while in this for loop
        #       when at value 1 (i=0), we want 1 to be at pos(0), so that we can iterate through [2,3,4] next without adding 1 again
        #       when at 2, we want 2 to be at pos(0), so that we can iterate through [1,3,4] next ([2,1,3,4])
        #       when at 3, we want it to be at pos(0), so that we can iterate through [2,1,4] next ([3,2,1,4])
        #   so we have to manually place it there (via swapping with the element at pos), then we return it just before the loop ends
        # and move pos forward

        # # num = array[i] (num of interest)
        # place the num at pos because it will be ignored down the recursive tree
        array[i], array[pos] = array[pos], array[i]

        for subset in ___getPermutationsHelper(array, pos+1):
            subset.append(array[pos])
            result.append(subset)

        # return num to its original position
        array[i], array[pos] = array[pos], array[i]

    return result

Solution three (most optimal)

""" 

perm(1,2,3)
                            [1,2,3]
                /             |                \
          [1,2,3]           [2,1,3]           [3,2,1]
          /  \              /      \              /   \
    [1,2,3] [1,3,2]    [2,1,3] [2,3,1]   [3,2,1] [3,1,2]

Try to get all possible arrangements of nums

"""

def getPermutations(array):
    if len(array) < 1:
        return array

    result = []
    getPermutationsHelper(result, array, 0)

    return result

def getPermutationsHelper(result, array, pos):
    if pos == len(array):
        result.append(array[:]) # found one arrangement
        return

    for i in range(pos, len(array)):
        # # add the number(array[i]) to the permutation
        # place the element of interest at the first position (pos)
        #  Example: for getPermutationsHelper([1,2,3,4], 0), while in this for loop
        #       when at value 1 (i=0), we want 1 to be at pos(0), so that we can iterate through [2,3,4] next without adding 1 again
        #       when at 2, we want 2 to be at pos(0), so that we can iterate through [1,3,4] next ([2,1,3,4])
        #       when at 3, we want it to be at pos(0), so that we can iterate through [2,1,4] next ([3,2,1,4])
        #   so we have to manually place it there (via swapping with the element at pos), then we return it just before the loop ends
        # and move pos forward

        # # num = array[i] (num of interest) -> it is array[i]'s turn to be at pos
        # place the num at pos because it will be ignored down the recursive tree
        array[i], array[pos] = array[pos], array[i]

        getPermutationsHelper(result, array, pos+1)

        # return num to its original position
        array[i], array[pos] = array[pos], array[i]

Time & Space complexity

Screenshot 2021-11-08 at 20.53.17.png

Time complexity: O(n x n!) as there are n! permutations and n for the cost of list slicing.

N * (N-1) * ... * ! == 3 * 2 * 1 == N!

We know that there are a total of N! permutations of a set with ‘N’ numbers. In the algorithm above, we are iterating through all of these permutations with the help of the two ‘for’ loops. In each iteration, we go through all the current permutations to insert a new number in them on line 17 (line 23 for C++ solution). To insert a number into a permutation of size ‘N’ will take O(N), which makes the overall time complexity of our algorithm O(N*N!).
If we had an array of len 10, the number of subtrees at each level of the recursive tree will be: $10 * 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1 == 10!$
- Space complexity: O(N*N!) as we have to store all n! permutations and for each permutation, we store a slice of the input.

Permutations with duplicates

Letter Case Permutations/String Permutations by changing case

"""
Letter Case Permutation/String Permutations by changing case:

Given a string s, we can transform every letter individually to be lowercase or uppercase to create another string.
Return a list of all possible strings we could create. You can return the output in any order. 

Example 1:
    Input: s = "a1b2"
    Output: ["a1b2","a1B2","A1b2","A1B2"]
Example 2:
    Input: s = "3z4"
    Output: ["3z4","3Z4"]
Example 3:
    Input: s = "12345"
    Output: ["12345"]
Example 4:
    Input: s = "0"
    Output: ["0"]

https://leetcode.com/problems/letter-case-permutation/
"""

""" 
Brute force:

- result = []
- have a perm(s,idx,curr_perm) helper function
    - for the character at idx:
        perm(s, idx+1, curr_perm+[character])
        - if is not a number:
            perm(s, idx+1, curr_perm+[character.swapcase()])
    - once we reach idx == len(s):
        - result.append(curr_perm)

---

Optimal:

- result = []
- arr = list(s)
- have a perm(arr,idx) helper function
    - for the character at idx:
            perm(arr,idx+1)
            - if is not a number:
                arr[idx] = arr[idx].swapcase()
                perm(arr,idx+1)
                arr[idx] = arr[idx].swapcase()
    - once we reach idx == len(s):
        - result.append(arr[:])

https://leetcode.com/problems/letter-case-permutation/discuss/379928/Python-clear-solution
"""

class Solution:
    def letterCasePermutationHelper(self, result, arr, idx):
        if idx == len(arr):
            result.append("".join(arr))
            return

        # case 1: do nothing
        self.letterCasePermutationHelper(result, arr, idx+1)

        # case 2: change case
        if arr[idx].isalpha():
            arr[idx] = arr[idx].swapcase()
            self.letterCasePermutationHelper(result, arr, idx+1)
            arr[idx] = arr[idx].swapcase()

    def letterCasePermutation(self, s):
        result = []
        if len(s) < 1:
            return result

        self.letterCasePermutationHelper(result, list(s), 0)
        return result

More examples

Combinations

Combination Sum

Find the original version of this page (with additional content) on Notion here.

Suffix Trees & Arrays

Suffix Trees Tutorials & Notes | Data Structures | HackerEarth

Find the original version of this page (with additional content) on Notion here.

Trees & Graphs (Additional content)

Dijkstra's Algorithm

Prim's Minimum Spanning Tree Algorithm

Bipartite graph/Look for even cycle using graph coloring

Less than, Greater than in BST

Topological Sort (for graphs) *

Union find (disjoint set)

Iterative traversals on Trees

Segment Trees: Range queries and Updates

Find the original version of this page (with additional content) on Notion here.

_Other

Find the original version of this page (with additional content) on Notion here.

Bit Manipulation 8c5610224bc34e8d90ac23914734bdce ↵

XOR 985656fb96144a739ce8ac8e2c447fa0 ↵

0

A xor B: 1 B: 1

Find the original version of this page (with additional content) on Notion here.

0

A xor B: 0 B: 0

Find the original version of this page (with additional content) on Notion here.

1

A xor B: 1 B: 0

Find the original version of this page (with additional content) on Notion here.

1

A xor B: 0 B: 1

Find the original version of this page (with additional content) on Notion here.

Ended: XOR 985656fb96144a739ce8ac8e2c447fa0

Ended: Bit Manipulation 8c5610224bc34e8d90ac23914734bdce

DP f1cdccd481ba461ea65ea993e984da07 ↵

0/1 Knapsack (Dynamic Programming)

0/1 Knapsack problem

Dynamic Programming - Knapsack Problem

Coding Patterns: 0/1 Knapsack (DP)

Introduction

Given the weights and profits of ‘N’ items, we are asked to put these items in a knapsack that has a capacity ‘C’. The goal is to get the maximum profit from the items in the knapsack. Each item can only be selected once, as we don’t have multiple quantities of any item.

Let’s take Merry’s example, who wants to carry some fruits in the knapsack to get maximum profit. Here are the weights and profits of the fruits: Items: { Apple, Orange, Banana, Melon } Weights: { 2, 3, 1, 4 } Profits: { 4, 5, 3, 7 } Knapsack capacity: 5 Let’s try to put different combinations of fruits in the knapsack, such that their total weight is not more than 5: Apple + Orange (total weight 5) => 9 profit Apple + Banana (total weight 3) => 7 profit Orange + Banana (total weight 4) => 8 profit Banana + Melon (total weight 5) => 10 profit This shows that Banana + Melon is the best combination, as it gives us the maximum profit and the total weight does not exceed the capacity.

Problem Statement

Given two integer arrays to represent weights and profits of ‘N’ items, we need to find a subset of these items which will give us maximum profit such that their cumulative weight is not more than a given number ‘C’. Write a function that returns the maximum profit. Each item can only be selected once, which means either we put an item in the knapsack or skip it.

"""
0/1 Knapsack:

Given two integer arrays to represent weights and profits of ‘N’ items, 
    we need to find a subset of these items which will give us maximum profit 
    such that their cumulative weight is not more than a given number ‘C’. 
Write a function that returns the maximum profit.
Each item can only be selected once, which means either we put an item in the knapsack or skip it.

https://www.educative.io/courses/grokking-dynamic-programming-patterns-for-coding-interviews/RM1BDv71V60
"""

Brute force (complete search)

Basic bruteforce

def solve_knapsack_helper(profits, weights, capacity, total_profits):
    if len(profits) == 0 or capacity < 0:
        return -1

    highest = -1
    for idx, weight in enumerate(weights):
        rem_profits = profits[:idx] + profits[idx+1:]
        rem_weights = weights[:idx] + weights[idx+1:]
        highest = max(
            highest,
            solve_knapsack_helper(rem_profits, rem_weights, capacity-weight, total_profits+profits[idx])
        )

    return max(total_profits, highest)

def solve_knapsack(profits, weights, capacity):
    return solve_knapsack_helper(profits, weights, capacity, 0)

All green boxes have a total weight that is less than or equal to the capacity (7), and all the red ones have a weight that is more than 7. The best solution we have is with items [B, D] having a total profit of 22 and a total weight of 7.

Improved Bruteforce

When given problems (involving choice) with two arrays, where their indices represent an entity, you can recurse by iterating through each index deciding to include it or not

(in reverse) When given problems (involving choice) with two arrays, where their indices represent an entity, you can recurse by iterating through each index deciding to include it or not

""" 
Brute force:
A basic brute-force solution could be to try all combinations of the given items,
    allowing us to choose the one with maximum profit and a weight that doesn’t exceed ‘C.’ 

The algorithm’s time complexity is exponential O(2^n)
The space complexity is O(n). This space will be used to store the recursion stack. 
Since our recursive algorithm works in a depth-first fashion, 
    which means, we can’t have more than ‘n’ recursive calls on the call stack at any time.
"""

# "iterate" through all the elements & at each element, 
#   see which will give max - choosing or excluding the element
# has some backtracking
def knapsack_recursive(profits, weights, capacity, idx, curr_profit):
    if capacity < 0:  # we made an invalid choice & went beyond the capacity
        return -1
    if idx == len(weights):  # no more to choose
        return curr_profit

         # can only be selected once
    if_chosen = knapsack_recursive(profits, weights, capacity - weights[idx], idx + 1, curr_profit + profits[idx])

    if_excluded = knapsack_recursive(profits, weights, capacity, idx + 1, curr_profit)

    return max(curr_profit, if_chosen, if_excluded)
        # return max(if_chosen, if_excluded) # -> this also works 

def solve_knapsack(profits, weights, capacity):
    return knapsack_recursive(profits, weights, capacity, 0, 0)

# ----------------------------

# avoids backtracking
def knapsack_recursive_2(profits, weights, capacity, idx):
    if capacity <= 0 or idx >= len(profits):
        return 0

    if_chosen = 0
    if weights[idx] <= capacity:  # avoid backtracking
        if_chosen = profits[idx] + knapsack_recursive_2(profits, weights, capacity - weights[idx], idx + 1)
    if_excluded = knapsack_recursive_2(profits, weights, capacity, idx + 1)

    return max(if_chosen, if_excluded)

def solve_knapsack_2(profits, weights, capacity):
    return knapsack_recursive_2(profits, weights, capacity, 0)

We have overlapping sub-problems

Let’s visually draw the recursive calls to see if there are any overlapping sub-problems. As we can see, in each recursive call, profits and weights arrays remain constant, and only capacity and currentIndex change. For simplicity, let’s denote capacity with ‘c’ and idx/currentIndex with ‘i’:

Denoted capacity with c and idx/currentIndex with i

Denoted capacity with c and idx/currentIndex with i

We can clearly see that ‘c:4, i:3’ has been called twice; hence we have an overlapping sub-problems pattern. As we discussed above, overlapping sub-problems can be solved through Memoization. Let's look at how we can do that next.

Top-down Dynamic Programming with Memoization

We can use memoization to overcome the overlapping sub-problems. To reiterate, memoization is when we store the results of all the previously solved sub-problems and return the results from memory if we encounter a problem that has already been solved.

Since we have two changing values (capacity and idx) in our recursive function knapsack_recursive(), we can use a two-dimensional array to store the results of all the solved sub-problems. As mentioned above, we need to store results for every sub-array (i.e., for every possible index ‘i’) and for every possible capacity ‘c’.

"""
Top-down Dynamic Programming with Memoization:

We can use memoization to overcome the overlapping sub-problems from the brute force solution.
Since we have two changing values (`capacity` and `idx`) in our recursive function `knapsack_recursive()`,
 we can use a two-dimensional array to store the results of all the solved sub-problems.
As mentioned above, we need to store results for every sub-array (i.e., for every possible index ‘i’) and for every possible capacity ‘c’.
"""

# -----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

def knapsack_recursive(profits, weights, cache, capacity, idx, curr_profit):
    if capacity < 0:
        return -1
    if idx == len(weights):
        return curr_profit

    # if we have already solved a similar problem, return the result from memory/cache
    if cache[idx][capacity]:
        return cache[idx][capacity]

    if_chosen = knapsack_recursive(profits, weights, cache, capacity - weights[idx], idx + 1, curr_profit + profits[idx])
    if_excluded = knapsack_recursive(profits, weights, cache, capacity, idx + 1, curr_profit)

    # store result in cache
    cache[idx][capacity] = max(if_chosen, if_excluded)
    return cache[idx][capacity]

def solve_knapsack(profits, weights, capacity):
    cache = [[False] * (capacity+1)] * len(weights) # use a two-dimensional array to store the results of all the solved sub-problems
    return knapsack_recursive(profits, weights, cache, capacity, 0, 0)

Time & space complexity

Since our memoization array cache[profits.length/weights.length][capacity+1] stores the results for all subproblems, we can conclude that we will not have more than N*C subproblems (where ‘N’ is the number of items and ‘C’ is the knapsack capacity).

This means that our time complexity will be O(N*C).

The above algorithm will use O(N*C) space for the memoization array. Other than that, we will use O(N) space for the recursion call-stack. So the total space complexity will be O(N∗C + N), which is asymptotically equivalent to O(N*C)

Bottom-up Dynamic Programming

0/1 Knapsack Problem Dynamic Programming

0/1 Knapsack problem | Dynamic Programming

Let’s try to populate our dp[][] array from the above solution, working in a bottom-up fashion. Essentially, we want to find the maximum profit for every sub-array and for every possible capacity. This means, dp[i][c] will represent the maximum knapsack profit for capacity c calculated from the first i items.

How to work this out

Formulae discussed below

Screenshot 2021-11-01 at 10.34.06.png

So, for each item at index i $(0 <= i < items.length)$ and capacity c $(0 <= c <= capacity)$, we have two options:

Exclude the item at index i. In this case, we will take whatever profit we get from the sub-array excluding this item => dp[i-1][c] (the top of curr i in the chart)
Include the item at index i if its weight is not more than the capacity. In this case, we include its profit plus whatever profit we get from the remaining capacity and from remaining items => profits[i] + dp[i-1][c-weights[i]]

Finally, our optimal solution will be maximum of the above two values:

dp[i][c] = max( dp[i-1][c], # **exclude item:** take prev/top profit
                                    profits[i] + dp[i-1][c-weights[i]] # **include item:** include its profit plus whatever profit we get from the remaining capacity
                                )

# dp[i][c] = max(exclude curr,   include curr + fill the remaining capacity)

0%201%20Knapsack%20(Dynamic%20Programming)%20b70111b897a547b6afdc2fc5cec2fbb6/Screenshot_2021-08-01_at_08.16.30.png

Decide whether not to **include curr item (v=4,w=3) and have a value/profit of 4** (the prev best val) or **include it and have a value/profit of 6** → 2+4, **include its profit plus whatever profit we get from the remaining capacity** (move w steps back in the top row(2) + curr val(4))

Decide whether not to include curr item (v=4,w=3) and have a value/profit of 4 (the prev best val) or include it and have a value/profit of 6 → 2+4, include its profit plus whatever profit we get from the remaining capacity (move w steps back in the top row(2) + curr val(4))

Start at 0 to the max

Code

def solve_knapsack(profits, weights, capacity):

    table = [[0 for _ in range(capacity+1)] for _ in range(len(profits))]

    for item in range(len(profits)):
        for cap in range(capacity + 1):
            excluded = 0
            included = 0
            prev_items = item - 1

            # # exclude item -> take prev largest
            if prev_items >= 0:
                excluded = table[prev_items][cap]

            # # include item
            if weights[item] <= cap:
                included = profits[item]

                # fill remaining capacity -> add prev items that can fit in the remaining capacity
                rem_cap = cap - weights[item]
                if rem_cap >= 0 and prev_items >= 0:
                    included += table[prev_items][rem_cap]

            # # record max
            table[item][cap] = max(included, excluded)

    return table[-1][-1]

How to find the selected items?

0/1 Knapsack problem | Dynamic Programming

Equal Subset Sum Partition

Introduction

""" 
Given a set of positive numbers, find if we can partition it into two subsets such that the sum of elements in both the subsets is equal.

Example 1
    Input: {1, 2, 3, 4}
    Output: True
    Explanation: The given set can be partitioned into two subsets with equal sum: {1, 4} & {2, 3}
Example 2
    Input: {1, 1, 3, 4, 7}
    Output: True
    Explanation: The given set can be partitioned into two subsets with equal sum: {1, 3, 4} & {1, 7}
Example 3
    Input: {2, 3, 4, 6}
    Output: False
    Explanation: The given set cannot be partitioned into two subsets with equal sum.

https://www.educative.io/courses/grokking-dynamic-programming-patterns-for-coding-interviews/3jEPRo5PDvx
"""

Given a set of positive numbers, find if we can partition it into two subsets such that the sum of elements in both the subsets is equal.

Example 1

Input: {1, 2, 3, 4}
Output: True
# Explanation: The given set can be partitioned into two subsets with equal sum: {1, 4} & {2, 3}

Example 2

Input: {1, 1, 3, 4, 7}
Output: True
# Explanation: The given set can be partitioned into two subsets with equal sum: {1, 3, 4} & {1, 7}

Example 3

Input: {2, 3, 4, 6}
Output: False
# Explanation: The given set cannot be partitioned into two subsets with equal sum.

Solution

""" 
We know that if we can partition it into equal subsets that each set’s sum will have to be sum/2. 
If the sum is an odd number we cannot possibly have two equal sets.
This changes the problem into finding if a subset of the input array has a sum of sum/2.
We know that if we find a subset that equals sum/2, 
    the rest of the numbers must equal sum/2 so we’re good since they will both be equal to sum/2. 
We can solve this using dynamic programming similar to the knapsack problem.

We basically need to find two groups of numbers that will each be equal to sum(input_array) / 2
Finding one such group (with its sum = sum(input_array)/2) will imply that there will be another with a similar sum
We can use the 0/1 knapsack pattern
"""

Brute force

Code

# ----------------------------------------------------------------------------------------------------------------------------------------------------------------
""" 
Brute Force 1:
While using recursion, `iterate` through the input array,
choosing whether to include each number in one of two arrays: "one" & "two" stop once the sum of elements in each of the arrays are equal to sum(input_array) / 2
"""

def can_partition_helper_bf1(num, total, res, idx, one, two):
    # base cases
    if sum(one) == total/2 and sum(two) == total/2:
        res.append([one, two])
        return

    if sum(one) > total/2 or sum(two) > total/2:
        return

    if idx >= len(num):
        return

    can_partition_helper_bf1(num, total, res, idx+1, one+[num[idx]], two)  # one
    can_partition_helper_bf1(num, total, res, idx+1, one, two+[num[idx]])  # two

def can_partition_bf1(num):
    res = []
    total = sum(num)
    can_partition_helper_bf1(num, total, res, 0, [], [])
    return len(res) > 0

# ----------------------------------------------------------------------------------------------------------------------------------------------------------------
""" 
Brute Force 2:
While using recursion, `iterate` through the input array,
choosing whether to include each number in one of two sums: "one" & "two" stop once each of the sums are equal to sum(input_array) / 2

Basically Brute Force 1 without remembering the numbers
"""

def can_partition_helper_bf2(num, total,  idx, one, two):
    # base cases
    if one == total/2 and two == total/2:
        return True

    if one > total/2 or two > total/2:
        return False
    if idx >= len(num):
        return False

    in_one = can_partition_helper_bf2(num, total,  idx+1, one+num[idx], two)
    in_two = can_partition_helper_bf2(num, total,  idx+1, one, two+num[idx])

    return in_one or in_two

def can_partition_bf2(num):
    total = sum(num)
    return can_partition_helper_bf2(num, total,  0, 0, 0)

# ----------------------------------------------------------------------------------------------------------------------------------------------------------------
""" 
Brute Force 3:

We basically need to find one group of numbers that will be equal to sum(input_array) / 2
Finding one such group (with its sum = sum(input_array)/2) will imply that there will be another with a similar sum

While using recursion, `iterate` through the input array,
choosing whether to include each number in the sum stop once the sum is equal to sum(input_array) / 2

Basically Brute Force 2 but dealing with one sum
"""

def can_partition_helper_bf3_0(num, total,  idx, one):
    # base cases
    if one == total/2:
        return True

    if one > total/2:
        return False
    if idx >= len(num):
        return False

    included = can_partition_helper_bf3_0(num, total,  idx+1, one+num[idx])
    excluded = can_partition_helper_bf3_0(num, total,  idx+1, one)

    return included or excluded

# O(2^n) time | O(n) space
def can_partition_bf3_0(num):
    total = sum(num)
    return can_partition_helper_bf3_0(num, total,  0, 0)

# -----------------------------------

def can_partition_helper_bf3(num, total, idx):
    # base cases
    if total == 0:
        return True

    if total < 0:
        return False
    if idx >= len(num):
        return False

    included = can_partition_helper_bf3(num, total-num[idx], idx+1)
    excluded = can_partition_helper_bf3(num, total, idx+1)

    return included or excluded

# O(2^n) time | O(n) space
def can_partition_bf3(num):
    total = sum(num)
    return can_partition_helper_bf3(num, total/2,  0)

Time complexity

The time complexity for Brute Force 3 is exponential O(2^n), where ‘n’ represents the total number. The space complexity is O(n), this memory will be used to store the recursion stack.

Top-down Dynamic Programming with Memoization

We can use memoization to overcome the overlapping sub-problems. Since we need to store the results for every subset and for every possible sum, therefore we will be using a two-dimensional array to store the results of the solved sub-problems. The first dimension of the array will represent different subsets and the second dimension will represent different ‘sums’ that we can calculate from each subset. These two dimensions of the array can also be inferred from the two changing values (total and idx) in our recursive function

Code

"""
Top-down Dynamic Programming with Memoization:

We can use memoization to overcome the overlapping sub-problems. 
Since we need to store the results for every subset and for every possible sum,
 therefore we will be using a two-dimensional array to store the results of the solved sub-problems.
The first dimension of the array will represent different subsets and the second dimension will represent different ‘sums’ that we can calculate from each subset.
These two dimensions of the array can also be inferred from the two changing values (total and idx) in our recursive function.
"""

def can_partition_helper_memo(num, cache, total, idx):
    if total == 0:
        return True
    if total < 0 or idx >= len(num):
        return False

    if cache[idx][total] == True or cache[idx][total] == False:
        return cache[idx][total]

    included = can_partition_helper_memo(num, cache, total-num[idx], idx+1)
    excluded = can_partition_helper_memo(num, cache, total, idx+1)

    cache[idx][total] = included or excluded
    return cache[idx][total]

def can_partition_memo(num):
    half_total = int(sum(num)/2)  # convert to int for use in range
    if half_total != sum(num)/2:  # ensure it wasn't a decimal number
        # if its a an odd number, we can't have two subsets with equal sum
        return False

    cache = [[-1 for _ in range(half_total+1)] for _ in range(len(num))]

    return can_partition_helper_memo(num, cache, half_total,  0)

Time complexity

The above algorithm has a time and space complexity of O(N*S), where ‘N’ represents total numbers and ‘S’ is the total sum of all the numbers.

Bottom-up Dynamic Programming

Screenshot 2021-11-01 at 10.40.27.png

0%201%20Knapsack%20(Dynamic%20Programming)%20b70111b897a547b6afdc2fc5cec2fbb6/Screen_Recording_2021-08-04_at_11.12.59.mov

dp[n][total] means whether the specific sum 'total' can be gotten from the first 'n' numbers.

If we can find such numbers from 0-'n' whose sum is total, dp[n][total] is true, otherwise, it is false.

dp[0][0] is true since with 0 elements a subset-sum of 0 is possible (both empty sets).

dp[n][total] is true if dp[n-1][total] is true (meaning that we skipped this element, and took the sum of the previous result) or dp[n-1][total- element’s value(num[n])] assuming this isn’t out of range (meaning that we added this value to our subset-sum so we look at the sum — the current element’s value).

This means dp[n][total] will be ‘true’ if we can make sum ‘total’ from the first ‘n’ numbers.

For each n and sum, we have two options:

Exclude the n. In this case, we will see if we can get the total from the subset excluding this n: dp[n-1][total]
Include the n if its value is not more than ‘total’. In this case, we will see if we can find a subset to get the remaining sum: dp[n-1][total-num[n]]

Code

"""
dp[n][total] means whether the specific sum 'total' can be gotten from the first 'n' numbers. 
If we can find such numbers from 0-'n' whose sum is total, dp[n][total] is true, otherwise it is false.

dp[0][0] is true since with 0 elements a subset-sum of 0 is possible (both empty sets).

dp[n][total] is true if dp[n-1][total] is true (meaning that we skipped this element, and took the sum of the previous result) 
 or dp[n-1][total- element’s value(num[n])] assuming this isn’t out of range (meaning that we added this value to our subset-sum so we look at the sum — the current element’s value).
This means, dp[n][total] will be ‘true’ if we can make sum ‘total’ from the first ‘n’ numbers.

For each n and sum, we have two options:
1. Exclude the n. In this case, we will see if we can get total from the subset excluding this n: dp[n-1][total]
2. Include the n if its value is not more than ‘total’. 
        In this case, we will see if we can find a subset to get the remaining sum: dp[n-1][total-num[n]]

"""

def can_partition_bu(num):
    half_total = int(sum(num)/2)  # convert to int for use in range
    if half_total != sum(num)/2:  # ensure it wasn't a decimal number
        # if its a an odd number, we can't have two subsets with equal sum
        return False

    dp = [[False for _ in range(half_total+1)] for _ in range(len(num))]  # type: ignore

    for n in range(len(num)):
        for total in range(half_total+1):
            if total == 0:  # '0' sum can always be found through an empty set
                dp[n][total] = True
                continue

            included = False
            excluded = False

            # # exclude
            if n-1 >= 0:
                excluded = dp[n-1][total]

            # # include
            if n <= total:
                rem_total = total - num[n]
                included = rem_total == 0  # fills the whole total
                if n-1 >= 0:
                    # prev n can fill the remaining total
                    included = included or dp[n-1][rem_total]

            dp[n][total] = included or excluded

    return dp[-1][-1]

Time complexity

The above algorithm has a time and space complexity of O(N*S), where ‘N’ represents total numbers and ‘S’ is the total sum of all the numbers.

Honourable mentions

Find the original version of this page (with additional content) on Notion here.

Jump Game

Jump Game - Greedy - Leetcode 55

Jump Game II - Greedy - Leetcode 45 - Python

Greedy solution to Jump Game II, Video Stitching & Minimum Number of Taps to Open to Water a Garden - LeetCode Discuss

Find the original version of this page (with additional content) on Notion here.

Kadane's Algorithm

Maximum Subarray

Screenshot 2021-11-01 at 15.29.36.png

Screen Recording 2021-11-01 at 15.30.10.mov

"""
Maximum Subarray:

Given an integer array nums, find the contiguous subarray (containing at least one number) which has the largest sum and return its sum.
Follow up: If you have figured out the O(n) solution, try coding another solution using the divide and conquer approach, which is more subtle

Example 1:
    Input: nums = [-2,1,-3,4,-1,2,1,-5,4]
    Output: 6
    Explanation: [4,-1,2,1] has the largest sum = 6.
Example 2:
    Input: nums = [1]
    Output: 1
Example 3:
    Input: nums = [5,4,-1,7,8]
    Output: 23

https://leetcode.com/problems/maximum-subarray/
"""

from typing import List

# O(n) time | O(1) space
class Solution:
    def maxSubArray(self, nums: List[int]):
        # # # find the maximum subarray per given element:
        # # ***check which one is larger:***
        # # ***adding the element to the current subarray or starting a new subarray at the element***

        # the max subarray we found's sum
        max_sa_sum = float("-inf")

        # sum of the current subarray that we are working with
        curr_subarray = float("-inf")
        for num in nums:

            # check if adding the num to the current subarray will be
            # a longer sum than starting a new subarray at the element
            # then the current subarray should be the longer/larger of the two
            curr_subarray = max(num, curr_subarray + num)

            # record the largest (sum) we found
            max_sa_sum = max(curr_subarray, max_sa_sum)

        return max_sa_sum

"""
Inputs:
    [-2,1,-3,4,-1,2,1,-5,4]
    [-2]
    [1]
    [-2,-3,-1,-5]
    [1,2,3,4,5,6,7,8,9,0]
Outputs:
    6
    -2
    1
    -1
    45
"""

Find the original version of this page (with additional content) on Notion here.

Levenshtein Distance *

Levenshtein Distance

Edit Distance | Dynamic Programming | LeetCode 72 | C++, Java, Python

Minimum edit distance | Dynamic programming | Backtracking

Edit Distance Between 2 Strings - The Levenshtein Distance ("Edit Distance" on LeetCode)

Introduction

Basic concept

""" 
Levenshtein Distance/Edit Distance:

Given two strings word1 and word2, return the minimum number of operations required to convert word1 to word2.
You have the following three operations permitted on a word:
    Insert a character
    Delete a character
    Replace a character


Example 1:
    Input: word1 = "horse", word2 = "ros"
    Output: 3
    Explanation: 
    horse -> rorse (replace 'h' with 'r')
    rorse -> rose (remove 'r')
    rose -> ros (remove 'e')
Example 2:
    Input: word1 = "intention", word2 = "execution"
    Output: 5
    Explanation: 
    intention -> inention (remove 't')
    inention -> enention (replace 'i' with 'e')
    enention -> exention (replace 'n' with 'x')
    exention -> exection (replace 'n' with 'c')
    exection -> execution (insert 'u')

https://leetcode.com/problems/edit-distance/
https://www.notion.so/paulonteri/Levenshtein-Distance-6eee820d93bb4de8a4be93cd42abd596#79d2868f016b40068d01c6a7b02c9c7c
"""

Solutions

Recursion (Brute force)

x to y https://youtu.be/ZkgBinDx9Kg

class Solution:
    def minDistanceHelper(self,  word1, word2, one, two, curr):
        # # base cases
        # end of both words
        if one == len(word1) and two == len(word2):
            return curr
        # end of any word
        if one == len(word1):
            return curr + len(word2) - two
        if two == len(word2):
            return curr + len(word1) - one

        # # operations required to convert word1 to word2
        # no operation needed
        if word1[one] == word2[two]:
            return self.minDistanceHelper(word1, word2, one+1, two+1, curr)

        # insert -> insert word2[two] into word1
        insert = self.minDistanceHelper(word1, word2, one, two+1, curr+1)
        # delete -> delete char at word1[one] (move to next char at word1)
        delete = self.minDistanceHelper(word1, word2, one+1, two, curr+1)
        # replace -> replace word1[one] with word2[two]
        replace = self.minDistanceHelper(word1, word2, one+1, two+1, curr+1)

        return min(insert, delete, replace)

    def minDistance(self, word1, word2):
        return self.minDistanceHelper(word1, word2, 0, 0, 0)

Brute-force that can work with caching

class Solution:
    def minDistanceHelper(self,  word1, word2, one, two):
        # # base cases
        # end of both words
        if one == len(word1) and two == len(word2):
            return 0
        # end of any word
        if one == len(word1):
            return len(word2) - two
        if two == len(word2):
            return len(word1) - one

        # # operations required to convert word1 to word2
        # no operation needed
        if word1[one] == word2[two]:
            return self.minDistanceHelper(word1, word2, one+1, two+1)

        # insert -> insert word2[two] into word1
        insert = self.minDistanceHelper(word1, word2, one, two+1)
        # delete -> delete char at word1[one] (move to next char at word1)
        delete = self.minDistanceHelper(word1, word2, one+1, two)
        # replace -> replace word1[one] with word2[two]
        replace = self.minDistanceHelper(word1, word2, one+1, two+1)
        return 1 + min(insert, delete, replace)

    def minDistance(self, word1, word2):
        return self.minDistanceHelper(word1, word2, 0, 0)

Memoization (Top Down Dynamic programming)

Improvement of the brute-force solution

Screenshot 2021-08-26 at 17.22.23.png

class Solution:
    def minDistanceHelper(self, dp, word1, word2, one, two):
        # # base cases
        # end of both words
        if one == len(word1) and two == len(word2):
            return 0
        # end of any word
        if one == len(word1):
            return len(word2) - two
        if two == len(word2):
            return len(word1) - one

        # # check cache
        if dp[one][two]:
            return dp[one][two]

        # # operations required to convert word1 to word2
        # no operation needed
        if word1[one] == word2[two]:
            dp[one][two] = self.minDistanceHelper(dp, word1, word2, one+1, two+1)
        else:
            # insert -> insert word2[two] into word1
            insert = self.minDistanceHelper(dp, word1, word2, one, two+1)
            # delete -> delete char at word1[one] (move to next char at word1)
            delete = self.minDistanceHelper(dp, word1, word2, one+1, two)
            # replace -> replace word1[one] with word2[two]
            replace = self.minDistanceHelper(dp, word1, word2, one+1, two+1)
            dp[one][two] = 1 + min(insert, delete, replace)

        return dp[one][two]

    def minDistance(self, word1, word2):
        dp = [[False for _ in range(len(word2)+1)] for _ in range(len(word1)+1)]
        return self.minDistanceHelper(dp, word1, word2, 0, 0)

Tabulation (Bottom Up Dynamic programming)

arrows show how to get results of certain actions

Screenshot 2021-08-26 at 17.32.14.png

x to y

Screenshot 2021-08-27 at 10.20.59.png

class Solution:
    def minDistance(self, word1, word2):

        dp = [[0 for _ in range(len(word1)+1)] for _ in range(len(word2)+1)]

        # # fill the values we know
        for i in range(len(dp[0])):
            dp[0][i] = i
        for i in range(len(dp)):
            dp[i][0] = i

        for two in range(1, len(dp)):
            for one in range(1, len(dp[0])):
                left = dp[two][one-1]  # delete
                top = dp[two-1][one]  # insert
                diagonal = dp[two-1][one-1]  # replace/skip

                if word1[one-1] == word2[two-1]:
                    dp[two][one] = dp[two-1][one-1]  # skip
                else:
                    dp[two][one] = min(left, top, diagonal) + 1

        return dp[-1][-1]

Find the original version of this page (with additional content) on Notion here.

Longest Increasing Subsequence

Find the original version of this page (with additional content) on Notion here.

Palindromes

Coding Patterns: Palindromes (DP)

# 0(n) time | O(1) space - where n = len(string)
def isPalindrome(string):

    left = 0
    right = len(string) - 1
    while left <= right:
        if string[left] != string[right]:
            return False

        left += 1
        right -= 1

    return True

Find the original version of this page (with additional content) on Notion here.

Staircase

Coding Patterns: Staircase (DP)

Find the original version of this page (with additional content) on Notion here.

Ended: DP f1cdccd481ba461ea65ea993e984da07

Heap Tricks e3f1996b84f54cc7a09f289d0d74f0cb ↵

K-Way Merge

Introduction

This pattern helps us solve problems that involve a list of sorted arrays.

Whenever we are given ‘K’ sorted arrays, we can use a Heap to efficiently perform a sorted traversal of all the elements of all arrays. We can push the smallest (first) element of each sorted array in a Min Heap to get the overall minimum. While inserting elements to the Min Heap we keep track of which array the element came from. We can, then, remove the top element from the heap to get the smallest element and push the next element from the same array, to which this smallest element belonged, to the heap. We can repeat this process to make a sorted traversal of all elements.

Untitled

When to use

Whenever you’re given ‘K’ sorted arrays, you can use a Heap to efficiently perform a sorted traversal of all the elements of all arrays. You can push the smallest element of each array in a Min Heap to get the overall minimum. After getting the overall minimum, push the next element from the same array to the heap. Then, repeat this process to make a sorted traversal of all elements.

Merge K Sorted Lists

Problem

"""
Merge K Sorted Lists:

You are given an array of k linked-lists lists, each linked-list is sorted in ascending order.
Merge all the linked-lists into one sorted linked-list and return it.

Example 1:
    Input: lists = [[1,4,5],[1,3,4],[2,6]]
    Output: [1,1,2,3,4,4,5,6]
    Explanation: The linked-lists are:
    [
    1->4->5,
    1->3->4,
    2->6
    ]
    merging them into one sorted list:
    1->1->2->3->4->4->5->6
Example 2:
    Input: lists = []
    Output: []
Example 3:
    Input: lists = [[]]
    Output: []
Example 4:
    Input: L1=[2, 6, 8], L2=[3, 6, 7], L3=[1, 3, 4]
    Output: [1, 2, 3, 3, 4, 6, 6, 7, 8]
Example 5:
    Input: L1=[5, 8, 9], L2=[1, 7]
    Output: [1, 5, 7, 8, 9]

https://leetcode.com/problems/merge-k-sorted-lists/
https://www.educative.io/courses/grokking-the-coding-interview/Y5n0n3vAgYK
"""

Solution

from typing import List
import heapq

"""
Solution:

[[1,4,5],[1,3,4],[2,6]]
Output: [1,1,2,3,4,4,5,6]

# Non-optimal Solution:
    using pointers ->
    Time complexity : O(kN) where k is the number of linked lists.
    Almost every selection of node in final linked costs O(k) time. There are N nodes in the final linked list.
There are NN nodes in the final linked list.
- for each list, create a pointer to the head of the list
- compare the values of the pointers, and add the smaller value to the result list

# Optimal Solution:
    using heap ->
    Time complexity : O(klogk) where k is the number of linked lists.
- add the first element of each list to a heap (keep track of the list((index or node) and the value))
- while the heap is not empty:
    - pop the smallest element from the heap and add it to the result list
    - add the next element of the list to the heap
- return the result list
"""

# Definition for singly-linked list.
class ListNode:
    def __init__(self, val=0, next=None):
        self.val = val
        self.next = next

# --------

class Solution0:
    def mergeKLists(self, lists: List[ListNode]):

        heap = []  # added in the form [val, random_unique_key, node]
        for i in range(len(lists)):
            if lists[i] is not None:
                heap.append([lists[i].val, i, lists[i]])
        heapq.heapify(heap)

        res = ListNode()
        curr = res
        while len(heap) > 0:
            # remove the smallest element
            smallest_arr = heapq.heappop(heap)
            curr.next = ListNode(smallest_arr[0])
            curr = curr.next

            # add the next node in the list that contains the smallest_arr[2] element
            nxt = smallest_arr[2].next
            if nxt is not None:
                heapq.heappush(heap, [nxt.val, smallest_arr[1], nxt])

        return res.next

# --------

class HeapElement:
    def __init__(self, val, node):
        self.val = val
        self.node = node

    def __gt__(self, other):  # (greater than) will be used in comparisons by the heap
        return self.val > other.val

class Solution:
    def mergeKLists(self, lists: List[ListNode]):

        # add the first element of each list to a heap
        heap = []
        for i in range(len(lists)):
            if lists[i] is not None:
                heap.append(HeapElement(lists[i].val,  lists[i]))
        heapq.heapify(heap)

        res = ListNode()
        curr = res
        while len(heap) > 0:
            # remove the smallest element
            smallest = heapq.heappop(heap)

            # add to res
            curr.next = ListNode(smallest.val)
            curr = curr.next

            # add the next node in the list that contains the smallest[2] element
            if smallest.node.next is not None:
                heapq.heappush(heap, HeapElement(smallest.node.next.val,
                                                 smallest.node.next)
                               )

        return res.next  # skip the one used initialise res

Non-optimal Solution

Kth Smallest Number in M Sorted Lists

"""
Kth Smallest Number in M Sorted Lists:

Given ‘M’ sorted arrays, find the K’th smallest number among all the arrays.

Example 1:
    Input: L1=[2, 6, 8], L2=[3, 6, 7], L3=[1, 3, 4], K=5
    Output: 4
    Explanation: The 5th smallest number among all the arrays is 4, this can be verified from
        the merged list of all the arrays: [1, 2, 3, 3, 4, 6, 6, 7, 8]
Example 2:
    Input: L1=[5, 8, 9], L2=[1, 7], K=3
    Output: 7
    Explanation: The 3rd smallest number among all the arrays is 7.
"""

"""
L1=[2, 6, 8], L2=[3, 6, 7], L3=[1, 3, 4], K=5

- initialise heap with the first element of each list
- pop the smallest element from the heap and replace it with the next element from the list it came from
    - repeat until the K'th time and return the number
"""

import heapq

class HeapElement:
    def __init__(self, val, val_idx, list_idx):
        self.val = val
        self.val_idx = val_idx
        self.list_idx = list_idx

    def __gt__(self, other):
        return self.val > other.val

    def get_list(self, arr):
        return arr[self.list_idx]

def find_Kth_smallest(lists, k):

    heap = []
    for i in range(len(lists)):
        if len(lists[i]) > 0:
            heapq.heappush(heap, HeapElement(lists[i][0], 0, i))

    number = -1
    for _ in range(k):
        if len(heap) == 0:
            return -1
        smallest = heapq.heappop(heap)

        # record number
        number = smallest.val

        # replace with next element from the list
        if smallest.val_idx + 1 < len(smallest.get_list(lists)):
            element = HeapElement(
                smallest.get_list(lists)[smallest.val_idx + 1],
                smallest.val_idx + 1,
                smallest.list_idx
            )
            heapq.heappush(heap, element)
    return number

print("Kth smallest number is: " +
      str(find_Kth_smallest([[2, 6, 8], [3, 6, 7], [1, 3, 4]], 5)))
print("Kth smallest number is: " +
      str(find_Kth_smallest([[2, 6, 8], [3, 6, 7], [1, 3, 4]], 2)))
print("Kth smallest number is: " +
      str(find_Kth_smallest([[2, 6, 8], [3, 6, 7], [1, 3, 4]], 1)))
print("Kth smallest number is: " +
      str(find_Kth_smallest([[2, 6, 8], [3, 6, 7], [1, 3, 4]], 200)))

Find the original version of this page (with additional content) on Notion here.

Top/Smallest/Frequent K elements *

Introduction

14 Patterns to Ace Any Coding Interview Question | Hacker Noon

Untitled

When to use

Any problem that asks us to find the top/smallest/frequent ‘K’ elements among a given set falls under this pattern.

The best data structure that comes to mind to keep track of ‘K’ elements is Heap. This pattern will make use of the Heap to solve multiple problems dealing with ‘K’ elements at a time from a set of given elements.

Simple examples

Top 'K' Numbers

Problem

""" 
Top 'K' Numbers:

Given an unsorted array of numbers, find the ‘K’ largest numbers in it.

Example 1:
    Input: [3, 1, 5, 12, 2, 11], K = 3
    Output: [5, 12, 11]
Example 2:
    Input: [5, 12, 11, -1, 12], K = 3
    Output: [12, 11, 12]
"""

Solution

""" 
Solution:

get rid of all smaller numbers

A brute force solution could be to sort the array and return the largest K numbers. 
The time complexity of such an algorithm will be O(N*logN) as we need to use a sorting algorithm.

If we iterate through the array one element at a time and keep ‘K’ largest numbers in a heap such that
 each time we find a larger number than the smallest number in the heap, we do two things:
    - Take out the smallest number from the heap, and
    - Insert the larger number into the heap.
This will ensure that we always have ‘K’ largest numbers in the heap. 

As discussed above, 
 it will take us O(logK) to extract the minimum number from the min-heap. 
So the overall time complexity of our algorithm will be O(K*logK+(N-K)*logK) since, 
 first, we insert ‘K’ numbers in the heap and then iterate through the remaining numbers and at every step, 
 in the worst case, we need to extract the minimum number and insert a new number in the heap. 
This algorithm is better than O(N*logN).
"""

the time complexity of this algorithm is O(K*logK+(N-K)*logK)O(K∗logK+(N−K)∗logK), which is asymptotically equal to O(N*logK)O(N∗logK)import heapq

def find_k_largest_numbers(nums, k):
    res = []
    for num in nums:
        heapq.heappush(res, num)
        while len(res) > k:
            heapq.heappop(res)
    return res

Given array: [3, 1, 5, 12, 2, 11], and K=3

First, let’s insert ‘K’ elements in the min-heap.
After the insertion, the heap will have three numbers [3, 1, 5] with ‘1’ being the root as it is the smallest element.
We’ll iterate through the remaining numbers and perform the above-mentioned two steps if we find a number larger than the root of the heap.
The 4th number is ‘12’ which is larger than the root (which is ‘1’), so let’s take out ‘1’ and insert ‘12’. Now the heap will have [3, 5, 12] with ‘3’ being the root as it is the smallest element.
The 5th number is ‘2’ which is not bigger than the root of the heap (‘3’), so we can skip this as we already have top three numbers in the heap.
The last number is ‘11’ which is bigger than the root (which is ‘3’), so let’s take out ‘3’ and insert ‘11’. Finally, the heap has the largest three numbers: [5, 12, 11]

Screen Recording 2021-08-17 at 05.40.47.mov

Time & Space complexity

The time complexity of this algorithm is O(K*logK+(N-K)logK), which is asymptotically equal to O(N∗logK) and is better than normal sorting O(N∗logN)

The space complexity will be O(K) since we need to store the top ‘K’ numbers in the heap.

Kth Smallest Number

This problem follows the Top ‘K’ Numbers pattern but has two differences:

Here we need to find the Kth smallest number, whereas in Top ‘K’ Numbers we were dealing with ‘K’ largest numbers.
In this problem, we need to find only one number (Kth smallest) compared to finding all ‘K’ largest numbers.

We can follow the same approach as discussed in the ‘Top K Elements’ problem. To handle the first difference mentioned above, we can use a max-heap instead of a min-heap. As we know, the root is the biggest element in the max heap. So, since we want to keep track of the ‘K’ smallest numbers, we can compare every number with the root while iterating through all numbers, and if it is smaller than the root, we’ll take the root out and insert the smaller number.

'K' Closest Points to the Origin

Problem

""" 
'K' Closest Points to the Origin:

Given an array of points in a 2D2D plane, find ‘K’ closest points to the origin.

Example 1:
    Input: points = [[1,2],[1,3]], K = 1
    Output: [[1,2]]
    Explanation: The Euclidean distance between (1, 2) and the origin is sqrt(5).
    The Euclidean distance between (1, 3) and the origin is sqrt(10).
    Since sqrt(5) < sqrt(10), therefore (1, 2) is closer to the origin.
Example 2:
    Input: point = [[1, 3], [3, 4], [2, -1]], K = 2
    Output: [[1, 3], [2, -1]]

https://leetcode.com/problems/k-closest-points-to-origin/
https://www.educative.io/courses/grokking-the-coding-interview/3YxNVYwNR5p
"""

The Euclidean distance of a point P(x,y) from the origin can be calculated through the following formula:

$\sqrt{x^2 + y^2}$

Solution

This solution uses the Top 'K' Numbers pattern

import heapq
import math

class Point:
    def __init__(self, x, y):
        self.x = x
        self.y = y

    # used for max-heap sorting
    # can also use less than __lt__
    def __gt__(self, other: 'Point'):
        # return self.distance_from_origin() > other.distance_from_origin()
        # we sort this way to ensure we have the k closest/smallest
        return self.distance_from_origin() < other.distance_from_origin()

    def distance_from_origin(self):
        return math.sqrt((self.x * self.x) + (self.y * self.y))

def find_closest_points(points, k):
    result = []
    for point in points:
        heapq.heappush(result, point)
        while len(result) > k:
            heapq.heappop(result)

    return result

Connect Ropes

""" 
Connect Ropes;

Example 1:
    Input: [1, 3, 11, 5]
    Output: 33
    Explanation: First connect 1+3(=4), then 4+5(=9), and then 9+11(=20). So the total cost is 33 (4+9+20)
Example 2:
    Input: [3, 4, 5, 6]   *
    Output: 36
    Explanation: First connect 3+4(=7), then 5+6(=11), 7+11(=18). Total cost is 36 (7+11+18)
Example 3:
    Input: [1, 3, 11, 5, 2]
    Output: 42
    Explanation: First connect 1+2(=3), then 3+3(=6), 6+5(=11), 11+11(=22). Total cost is 42 (3+6+11+22)
"""

Solution

""" 
Solution:

In this problem, following a greedy approach to connect the smallest ropes first will ensure the lowest cost. 
We can use a Min Heap to find the smallest ropes following a similar approach as discussed in Kth Smallest Number. 
Once we connect two ropes, we need to insert the resultant rope back in the Min Heap so that we can connect it with the remaining ropes.
"""

import heapq

def minimum_cost_to_connect_ropes(ropeLengths):
    minHeap = []
    # add all ropes to the min heap
    for i in ropeLengths:
        heapq.heappush(minHeap, i)

    # go through the values of the heap, in each step take top (lowest) rope lengths from the min heap
    # connect them and push the result back to the min heap.
    # keep doing this until the heap is left with only one rope
    result = 0
    while len(minHeap) > 1:
        temp = heapq.heappop(minHeap) + heapq.heappop(minHeap)
        result += temp
        heapq.heappush(minHeap, temp)

    return result

Time & space complexity

Time complexity

Given ‘N’ ropes, we need O(NlogN) to insert all the ropes in the heap. In each step, while processing the heap, we take out two elements from the heap and insert one. This means we will have a total of ‘N’ steps, having a total time complexity of O(NlogN).

Space complexity

The space complexity will be O(N) because we need to store all the ropes in the heap.

Top 'K' Frequent Numbers

""" 
Top 'K' Frequent Numbers:

Given an unsorted array of numbers, find the top ‘K’ frequently occurring numbers in it.

Example 1:
    Input: [1, 3, 5, 12, 11, 12, 11], K = 2
    Output: [12, 11]
    Explanation: Both '11' and '12' appeared twice.
Example 2:
    Input: [5, 12, 11, 3, 11], K = 2
    Output: [11, 5] or [11, 12] or [11, 3]
    Explanation: Only '11' appeared twice, all other numbers appeared once.
"""
from typing import List

from collections import Counter
from heapq import heappop, heappush

""" 
- have a min heap (smallest number at the top)
- get the count of all nums in the array
- all the counts plus corresponding numbers to the heap
    - the heap will contain a max of k elements
- return the numbers in the heap
"""

# O(N∗logK) time | O(N) space
class Solution:
    def topKFrequent(self, nums: List[int], k: int):
        min_heap = []

        for number, count in Counter(nums).items():
            heappush(min_heap, (count, number))
            if len(min_heap) > k:
                heappop(min_heap)

        return [item[1] for item in min_heap]

Frequency Sort

Similar to Top 'K' Frequent Numbers

"""
Given a string, sort it based on the decreasing frequency of its characters.

Example 1:
        Input: "Programming"
        Output: "rrggmmPiano"
        Explanation: 'r', 'g', and 'm' appeared twice, so they need to appear before any other character.
Example 2:
        Input: "abcbab"
        Output: "bbbaac"
        Explanation: 'b' appeared three times, 'a' appeared twice, and 'c' appeared only once.

"""

"""
- get the character count of each character
- sort the characters by count (using a heap)
- build a new string following the sorted charcters and filling it up with the count
"""

Kth Largest Number in a Stream

""" 
Kth Largest Number in a Stream:

Design a class to efficiently find the Kth largest element in a stream of numbers.
The class should have the following two things:
    The constructor of the class should accept an integer array containing initial numbers from the stream and an integer ‘K’.
    The class should expose a function add(int num) which will store the given number and return the Kth largest number.

Example 1:
    Input: [3, 1, 5, 12, 2, 11], K = 4
    1. Calling add(6) should return '5'.
    2. Calling add(13) should return '6'.
    2. Calling add(4) should still return '6'.
"""

""" 
Input: [3, 1, 5, 12, 2, 11], K = 4

sorted_input => [1,2,3,5,11,12]

1. Calling add(6) should return '5'.
[1,2,3,5,6,11,12]

2. Calling add(13) should return '6'.
[1,2,3,5,6,11,12,13]

2. Calling add(4) should still return '6'.
[1,2,3,4,5,6,11,12,13]

- if we find a way to store the k largest numbers,
    we can be knowing the kth largest easily
- we can use a heap for this
"""

import heapq

class KthLargestNumberInStream:
    def __init__(self, nums, k):
        self.nums = nums
        self.k = k

    def add(self, num):
        heapq.heappush(self.nums, num)

        while len(self.nums) > self.k:
            heapq.heappop(self.nums)

        return self.nums[0]

'K' Closest Numbers

Problem

"""
'K' Closest Numbers:

Given a sorted number array and two integers ‘K’ and ‘X’, find ‘K’ closest numbers to ‘X’ in the array.
Return the numbers in the sorted order. ‘X’ is not necessarily present in the array.

Example 1:
        Input: [5, 6, 7, 8, 9], K = 3, X = 7
        Output: [6, 7, 8]
Example 2:
        Input: [2, 4, 5, 6, 9], K = 3, X = 6
        Output: [4, 5, 6]
Example 3:
        Input: [2, 4, 5, 6, 9], K = 3, X = 10
        Output: [5, 6, 9]
"""

Solution

"""
SOLUTION:

O(N∗logK):
- for each number in the array, calculate its abolute difference with X 
- store the difference in a max-heap(largest on top) maintaining K numbers in the heap
- return the heap

O(logN + KlogK)
- Since the array is sorted, we can first find the number closest to ‘X’ through Binary Search. Let’s say that number is ‘Y’.
- The ‘K’ closest numbers to ‘Y’ will be adjacent to ‘Y’ in the array. We can search in both directions of ‘Y’ to find the closest numbers.
- We can use a heap to efficiently search for the closest numbers. We will take ‘K’ numbers in both directions of ‘Y’ 
        and push them in a Min Heap sorted by their absolute difference from ‘X’. 
        This will ensure that the numbers with the smallest difference from ‘X’ (i.e., closest to ‘X’) can be extracted easily from the Min Heap.
- Finally, we will extract the top ‘K’ numbers from the Min Heap to find the required numbers.
"""

import heapq

# O(logN + KlogK) time | O(K) space
def find_closest_elements(arr, K, X):

    closest_idx = binary_search(arr, X)
    close = []
    for idx in range(max(0, closest_idx-K), min(len(arr), closest_idx+K+1)):
        num = arr[idx]
        heapq.heappush(close, [-abs(X-num), num])
        if len(close) > K:
            heapq.heappop(close)

    result = []
    for item in close:
        result.append(item[1])

    return result

def binary_search(arr, num):
    left = 0
    right = len(arr)-1
    while left < right:
        mid = (left+right) // 2
        if arr[mid] == num:
            return mid
        elif arr[mid] > num:
            right = mid-1
        else:
            left = mid+1

    return left

Alternate Solution using Two Pointers

After finding the number closest to ‘X’ through Binary Search, we can use the Two Pointers approach to find the ‘K’ closest numbers. Let’s say the closest number is ‘Y’. We can have a left pointer to move back from ‘Y’ and a right pointer to move forward from ‘Y’. At any stage, whichever number pointed out by the left or the right pointer gives the smaller difference from ‘X’ will be added to our result list.

To keep the resultant list sorted we can use a Queue. So whenever we take the number pointed out by the left pointer, we will append it at the beginning of the list and whenever we take the number pointed out by the right pointer we will append it at the end of the list.

Time & Space complexity

The time complexity of the above algorithm is O(logN + KlogK). We need O(logN) for Binary Search and O(KlogK) to insert the numbers in the Min Heap, as well as to sort the output array.

The space complexity will be O(K), as we need to put a maximum of K numbers in the heap.

Top K Frequent Words

from typing import List
import collections
import heapq

class Word:
    def __init__(self, word, count):
        self.word = word
        self.count = count

    def __gt__(self, other):
        if self.count == other.count:
            return self.word < other.word
        return self.count > other.count

class Solution:
    def topKFrequent(self, words: List[str], k: int):
        word_count = collections.Counter(words)

        heap = []
        for word, count in word_count.items():
            heapq.heappush(heap, Word(word, count))
            if len(heap) > k:
                heapq.heappop(heap)

        top_k_words = []
        while heap:
            top_k_words.append(heapq.heappop(heap).word)
        top_k_words.reverse()
        return top_k_words

Others

Sort K-Sorted Array

"""
Sort K-Sorted Array:

Write a function that takes in a non-negative integer k and a k-sorted array of integers and
    returns the sorted version of the array. Your function can either sort the array in place
    or create an entirely new array.
A k-sorted array is a partially sorted array in which all elements are at most k positions away from their sorted position.
For example, the array [3, 1, 2, 2] is k-sorted with k = 3, because each element in the array is at most 3 positions away from its sorted position.
Note that you're expected to come up with an algorithm that can sort the k-sorted array faster than in O(nlog(n)) time.

Sample Input
    array = [3, 2, 1, 5, 4, 7, 6, 5]
    k = 3
Sample Output
    [1, 2, 3, 4, 5, 5, 6, 7]

https://www.algoexpert.io/questions/Sort%20K-Sorted%20Array
"""
import heapq

"""
 - have a min-heap with k elements

 - iterate through the input array and at each index:
    - remove and record the value at the top of the heap at the index
    - add the element at index + k to the heap
"""

# O(nlog(k)) time | O(k) space
def sortKSortedArray(array, k):

    # have a min-heap with k elements
    heap = array[:k+1]
    heapq.heapify(heap)

    for idx in range(len(array)):
        # remove and record the value at the top of the heap at the index
        array[idx] = heapq.heappop(heap)

        # add the element at index + k+1 to the heap
        if idx+k+1 < len(array):
            heapq.heappush(heap, array[idx+k+1])

    return array

Find the original version of this page (with additional content) on Notion here.

Two Heaps

Introduction

Heaps & Priority Queues

In many problems, where we are given a set of elements such that we can divide them into two parts. To solve the problem, we are interested in knowing the smallest element in one part and the biggest element in the other part. This pattern is an efficient approach to solve such problems.

This pattern uses two Heaps to solve these problems; A Min Heap to find the smallest element and a Max Heap to find the biggest element.

Ways to identify the Two Heaps pattern

Useful in situations like Priority Queue, Scheduling
If the problem states that you need to find the smallest/largest/median elements of a set
Sometimes, useful in problems featuring a binary tree data structure

Find Median from Data Stream / Find the Median of a Number Stream

Problem

""" 
Design a class to calculate the median of a number stream. The class should have the following two methods:

insertNum(int num): stores the number in the class
findMedian(): returns the median of all numbers inserted in the class
If the count of numbers inserted in the class is even, the median will be the average of the middle two numbers.

Example 1:
    1. insertNum(3)
    2. insertNum(1)
    3. findMedian() -> output: 2
    4. insertNum(5)
    5. findMedian() -> output: 3
    6. insertNum(4)
    7. findMedian() -> output: 3.5

https://www.educative.io/courses/grokking-the-coding-interview/3Yj2BmpyEy4
https://www.algoexpert.io/questions/Continuous%20Median
"""

Solution

Screenshot 2021-11-11 at 11.52.46.png

Screenshot 2021-11-11 at 11.54.26.png

Screenshot 2021-11-11 at 11.53.29.png

Screenshot 2021-11-11 at 11.54.11.png

As we know, the median is the middle value in an ordered integer list. So a brute force solution could be to maintain a sorted list of all numbers inserted in the class so that we can efficiently return the median whenever required. Inserting a number in a sorted list will take O(N) time if there are ‘N’ numbers in the list. This insertion will be similar to the Insertion sort. Can we do better than this? Can we utilize the fact that we don’t need the fully sorted list - we are only interested in finding the middle element?

Assume ‘x’ is the median of a list. This means that half of the numbers in the list will be smaller than (or equal to) ‘x’ and half will be greater than (or equal to) ‘x’. This leads us to an approach where we can divide the list into two halves: one half to store all the smaller numbers (let’s call it smallNumList) and one half to store the larger numbers (let’s call it largNumList). The median of all the numbers will either be the largest number in the smallNumList or the smallest number in the largNumList. If the total number of elements is even, the median will be the average of these two numbers

The best data structure that comes to mind to find the smallest or largest number among a list of numbers is a Heap.

"""
Solution:

Assume ‘x’ is the median of a list. This means that half of the numbers in the list will be smaller than (or equal to) ‘x’ and half will be greater than (or equal to) ‘x’.
- we basically have to keep track of the middle number(s) at every point

- we can divide the set of numbers into two sorted halves (small & large numbers)
    - the if total count of numbers is even, the median will be (the smallest large number + largest small number) / 2
    - otherwise the median will be the middle number

larger = []
smaller = []

1. insertNum(3)
larger = [3]
smaller = []

2. insertNum(1)
larger = [3]
smaller = [1]

3. findMedian() -> output: 2
(3+1)/2

4. insertNum(5)
larger = [3,5]
smaller = [1]

5. findMedian() -> output: 3
(3)

6. insertNum(4)
larger = [3,4,5]
smaller = [1]
---
larger = [4,5]
smaller = [3,1]

7. findMedian() -> output: 3.5
(3+4)/2

"""

import heapq

class MedianOfAStream:

    def __init__(self):
        self.smaller = []
        self.larger = []

    def insert_num(self, num):
        if len(self.larger) == 0 or num >= self.larger[0]:
            heapq.heappush(self.larger, num)
        else:
            heapq.heappush(self.smaller, -num)
        self.balance_heaps()

    def find_median(self):
        if len(self.larger) > len(self.smaller):
            return self.larger[0]
        else:
            return (self.larger[0] + -self.smaller[0]) / 2

    def balance_heaps(self):
        while len(self.larger) > len(self.smaller) + 1:
            heapq.heappush(self.smaller, -heapq.heappop(self.larger))
        while len(self.larger) < len(self.smaller):
            heapq.heappush(self.larger, -heapq.heappop(self.smaller))

Find the original version of this page (with additional content) on Notion here.

Ended: Heap Tricks e3f1996b84f54cc7a09f289d0d74f0cb

Pointers c5f2aa24da174319aec737993acf4e6a ↵

Find cycle in list

Find the original version of this page (with additional content) on Notion here.

Hare & Tortoise Algorithm

Fast & Slow pointers introduction

The Fast & Slow pointer approach, also known as the Hare & Tortoise algorithm, is a pointer algorithm that uses two pointers which move through the array (or sequence/LinkedList) at different speeds. This approach is quite useful when dealing with cyclic LinkedLists or arrays.

By moving at different speeds (say, in a cyclic LinkedList), the algorithm proves that the two pointers are bound to meet. The fast pointer should catch the slow pointer once both the pointers are in a cyclic loop.

One of the famous problems solved using this technique was Finding a cycle in a LinkedList.

Untitled

Simple problems

LinkedList Cycle

Given the head of a Singly LinkedList, write a function to determine if the LinkedList has a cycle in it or not.

Screenshot 2021-08-15 at 06.48.17.png

Imagine two racers running on a circular racing track. If one racer is faster than the other, the faster racer is bound to catch up and cross the slower racer from behind. We can use this fact to devise an algorithm to determine if a LinkedList has a cycle in it or not.

Imagine we have a slow and a fast pointer to traverse the LinkedList. In each iteration, the slow pointer moves one step and the fast pointer moves two steps. This gives us two conclusions:

If the LinkedList doesn’t have a cycle in it, the fast pointer will reach the end of the LinkedList before the slow pointer to reveal that there is no cycle in the LinkedList.
The slow pointer will never be able to catch up to the fast pointer if there is no cycle in the LinkedList.

If the LinkedList has a cycle, the fast pointer enters the cycle first, followed by the slow pointer. After this, both pointers will keep moving in the cycle infinitely. If at any stage both of these pointers meet, we can conclude that the LinkedList has a cycle in it.

why will they meet?

https://youtu.be/gBTe7lFR3vc?t=446

""" 
Linked List Cycle:

Given head, the head of a linked list, determine if the linked list has a cycle in it
There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer. 
Internally, pos is used to denote the index of the node that tail's next pointer is connected to. 
Note that pos is not passed as a parameter.
Return true if there is a cycle in the linked list. Otherwise, return false.

https://leetcode.com/problems/linked-list-cycle
https://www.notion.so/paulonteri/Hare-Tortoise-Algorithm-1020d217ffb54e47b7aea3c175d75618#0f0930e961414b1e90871b4efbe3d1b6
"""

# Definition for singly-linked list.
class ListNode:
    def __init__(self, x):
        self.val = x
        self.next = None

class Solution:
    def hasCycle(self, head: ListNode):
        if head is None:
            return False

                 # move to initial positions
        slow = head
        fast = head.next
        if fast is None:
            return False
        fast = fast.next

        while fast != None:
            if fast == slow:
                return True

            slow = slow.next
            fast = fast.next
            if fast:
                fast = fast.next

        return False

Length of LinkedList Cycle

Given the head of a LinkedList with a cycle, find the length of the cycle.

"""
Once the fast and slow pointers meet,
 we can save the slow pointer and iterate the whole cycle with another pointer
 until we see the slow pointer again to find the length of the cycle.
"""

class Node:
    def __init__(self, value, next=None):
        self.value = value
        self.next = next

def find_cycle_length(head):
    slow, fast = head, head
    while fast is not None and fast.next is not None:
        fast = fast.next.next
        slow = slow.next
        if slow == fast:  # found the cycle
            return calculate_cycle_length(slow)

    return 0

def calculate_cycle_length(slow):
    current = slow
    cycle_length = 0
    while True:
        current = current.next
        cycle_length += 1
        if current == slow:
            break
    return cycle_length

Start of LinkedList Cycle

Problem

Given the head of a Singly LinkedList that contains a cycle, write a function to find the starting node of the cycle.

Screenshot 2021-08-15 at 06.55.16.png

Solution

If we know the length of the LinkedList cycle, we can find the start of the cycle through the following steps:

Take two pointers. Let’s call them pointer1 and pointer2.
Initialize both pointers to point to the start of the LinkedList.
We can find the length of the LinkedList cycle using the approach discussed in Length of LinkedList Cycle. Let’s assume that the length of the cycle is ‘K’ nodes.
Move pointer2 ahead by ‘K’ nodes.
Now, keep incrementing pointer1 and pointer2 until they both meet.
Imagine the cycle as a circular track: As pointer2 is ‘K’ nodes ahead of pointer1, which means, pointer2 must have completed one loop in the cycle when both pointers meet. Their meeting point will be the start of the cycle.
- if pointer2 is ‘K’ nodes ahead of pointer1, it means that when pointer1 will be at the start of the cycle, pointer2 two will be at the end - they are the same node

Screenshot 2021-08-15 at 07.11.11.png

Code

""" 
Find start of linked list cycle:

Given the head of a Singly LinkedList that contains a cycle, write a function to find the starting node of the cycle.
https://www.educative.io/courses/grokking-the-coding-interview/N7pvEn86YrN
https://www.notion.so/paulonteri/Hare-Tortoise-Algorithm-1020d217ffb54e47b7aea3c175d75618#0f0930e961414b1e90871b4efbe3d1b6
"""

"""
Linked List Cycle II

Given a linked list, return the node where the cycle begins. If there is no cycle, return null.
There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer.
Internally, pos is used to denote the index of the node that tail's next pointer is connected to. Note that pos is not passed as a parameter.
Notice that you should not modify the linked list
https://leetcode.com/problems/linked-list-cycle-ii/
https://www.algoexpert.io/questions/Find%20Loop
https://www.notion.so/paulonteri/Hare-Tortoise-Algorithm-1020d217ffb54e47b7aea3c175d75618#0f0930e961414b1e90871b4efbe3d1b6
"""

class Node:
    def __init__(self, value, next=None):
        self.value = value
        self.next = next

def find_cycle_start(head):
    cycle_length = 0
    # find the LinkedList cycle
    slow, fast = head, head
    while (fast is not None and fast.next is not None):
        fast = fast.next.next
        slow = slow.next
        if slow == fast:  # found the cycle
            cycle_length = calculate_cycle_length(slow)
            break
    return find_start(head, cycle_length)

def calculate_cycle_length(slow):
    current = slow
    cycle_length = 0
    while True:
        current = current.next
        cycle_length += 1
        if current == slow:
            break
    return cycle_length

def find_start(head, cycle_length):
    pointer1 = head
    pointer2 = head

    # move pointer2 ahead 'cycle_length' nodes
    while cycle_length > 0:
        pointer2 = pointer2.next
        cycle_length -= 1

    # increment both pointers until they meet at the start of the cycle
    while pointer1 != pointer2:
        pointer1 = pointer1.next
        pointer2 = pointer2.next

    return pointer1

class Solution:
    def detectCycle(self, head):
        if not head:
            return None

        # # find cycle
        fast = head
        slow = head
        while True:
            if fast is None or fast.next is None:  # find invalid
                return None

            slow = slow.next
            fast = fast.next.next
            if slow == fast:
                break

        # # find start of cycle
        # the (dist) head to the start of the cycle ==
        #   the (dist) meeting point to the start of the cycle
        one = head
        two = fast
        while one != two:
            one = one.next
            two = two.next
        return one

"""
Find Loop:
Write a function that takes in the head of a Singly Linked List that contains a loop 
(in other words, the list's tail node points to some node in the list instead of None / null). 
The function should return the node (the actual node--not just its value) from which the loop originates in constant space.
Each LinkedList node has an integer value as well as a next node pointing to the next node in the list.

Sample Input
    head = 0 -> 1 -> 2 -> 3 -> 4 -> 5 -> 6 // the head node with value 0
                            ^         v
                            9 <- 8 <- 7
Sample Output
    4 -> 5 -> 6 // the node with value 4
    ^         v
    9 <- 8 <- 7
https://www.algoexpert.io/questions/Find%20Loop
"""

# This is an input class. Do not edit.
class LinkedList:
    def __init__(self, value):
        self.value = value
        self.next = None

def findLoop(head):
    # .next to allow the first loop to work
    p_one = head.next
    p_two = head.next.next

    # find meeting point
    while p_two != p_one:
        p_one = p_one.next
        p_two = p_two.next.next

    # # find start of cycle
    # the (dist) head to the start of the cycle ==
    #   the (dist) meeting point to the start of the cycle
    p_one = head
    while p_two != p_one:
        p_one = p_one.next
        p_two = p_two.next

    return p_one

Time & Space complexity

As we know, finding the cycle in a LinkedList with ‘N’ nodes and also finding the length of the cycle requires O(N). Also, as we saw in the above algorithm, we will need O(N) to find the start of the cycle. Therefore, the overall time complexity of our algorithm will be O(N).

Happy Number

Problem

Try doing it in constant space

"""
Happy Number:

Any number will be called a happy number if,
after repeatedly replacing it with a number equal to the sum of the square of all of its digits, leads us to number ‘1’.
All other (not-happy) numbers will never reach ‘1’. Instead, they will be stuck in a cycle of numbers which does not include ‘1’.

Example 1:
    Input: n = 19
    Output: true
    Explanation:
        12 + 92 = 82
        82 + 22 = 68
        62 + 82 = 100
        12 + 02 + 02 = 1
Example 2:
    Input: n = 2
    Output: false
Example 3:
    Input: 23
    Output: true (23 is a happy number)
    Explanations: Here are the steps to find out that 23 is a happy number:
Example 4:
    Input: 12
    Output: false (12 is not a happy number)
    Explanations: Here are the steps to find out that 12 is not a happy number:

"""

Solution

The process, defined above, to find out if a number is a happy number or not, always ends in a cycle. If the number is a happy number, the process will be stuck in a cycle on number ‘1,’ and if the number is not a happy number then the process will be stuck in a cycle with a set of numbers.

We saw in the LinkedList Cycle problem that we can use the Fast & Slow pointers method to find a cycle among a set of elements. As we have described above, each number will definitely have a cycle. Therefore, we will use the same fast & slow pointer strategy to find the cycle and once the cycle is found, we will see if the cycle is stuck on number ‘1’ to find out if the number is happy or not.

Brute force

def square_of_digits(num):
    res = 0
    while num > 0:
        res += (num % 10) * (num % 10)
        num = num // 10
    return res

# using memory
def find_happy_number_01(num):
    store = set()
    store.add(num)
    while num != 1:
        num = square_of_digits(num)
        if num in store:
            return False
        store.add(num)

    return True

Optimal

def square_of_digits(num):
    res = 0
    while num > 0:
        res += (num % 10) * (num % 10)
        num = num // 10
    return res

def find_happy_number(num):
    fast = num
    slow = num
    loop_started = False
    while slow != fast or not loop_started:
        loop_started = True
        fast = square_of_digits(square_of_digits(fast))
        slow = square_of_digits(slow)
        if slow == 1 or fast == 1:
            return True

    return False

Find the original version of this page (with additional content) on Notion here.

Sliding Window

Introduction

Sliding Window algorithm template to solve all the Leetcode substring search problem. - LeetCode Discuss

Basic concept

Your window represents the current section of the string/array that you are “looking at” and usually there is some information stored along with it in the form of constants. At the very least it will have 2 pointers, one indicating the index corresponding beginning of the window, and one indicating the end of the window.

In many problems dealing with an array (or a LinkedList), we are asked to find or calculate something among all the contiguous subarrays of a given size.

Given an array, find the average of all contiguous subarrays of size ‘K’ in it.

Let’s understand this problem with a real input:

Array: [1, 3, 2, 6, -1, 4, 1, 8, 2], K=5

Here is the final output containing the averages of all contiguous subarrays of size 5:

Output: [2.2, 2.8, 2.4, 3.6, 2.8]

A brute-force algorithm will calculate the sum of every 5-element contiguous subarray of the given array and divide the sum by ‘5’ to find the average. Since for every element of the input array, we are calculating the sum of its next ‘K’ elements, the time complexity of the above algorithm will be O(N*K) where ‘N’ is the number of elements in the input array.

Do you see any inefficiency? The inefficiency is that for any two consecutive subarrays of size ‘5’, the overlapping part (four elements) will be evaluated twice. For example, take the above-mentioned input: As you can see, there are four overlapping elements between the subarray (indexed from 0-4) and the subarray (indexed from 1-5).

Sliding%20Window%20f6685a15f97a4ca2bb40111e2b264fb2/Screenshot_2021-08-06_at_02.03.16.png

Can we somehow reuse the sum we have calculated for the overlapping elements?

Can we somehow reuse the sum we have calculated for the overlapping elements?

The efficient way to solve this problem would be to visualize each contiguous subarray as a sliding window of ‘5’ elements. This means that we will slide the window by one element when we move on to the next subarray. To reuse the sum from the previous subarray, we will subtract the element going out of the window and add the element now being included in the sliding window. This will save us from going through the whole subarray to find the sum and, as a result, the algorithm complexity will reduce to O(N).

How do you identify them?

There are some common giveaways:

The problem will involve a data structure that is ordered and iterable like an array or a string
You are looking for some subrange in that array/string, like a longest, shortest or target value.
There is an apparent naive or brute force solution that runs in O(N²), O(2^N) or some other large time complexity.

Why is this dynamic programming?

They are a subset of dynamic programming problems, though the approach to solving them is quite different from the one used in solving tabulation or memoization problems. So different in fact, that to a lot of engineers it isn’t immediately clear that there even is a connection between the two at all.

Not that important btw...

This search for an optimum hints at the relationship between sliding window problems and other dynamic problems. You are using the optimal substructure property of the problem to guarantee that an optimal solution to a subproblem can be reused to help you find the optimal solution to a larger problem.

You are also using the fact that there are overlapping subproblems in the naive approach, to reduce the amount of work you have to do. Take the Minimum Window Substring problem. You are given a string, and a set of characters you need to look for in that string. There might be multiple overlapping substrings that contain all the characters you are looking for, but you only want the shortest one. These characters can also be in any order.

Implementation

One amazing thing about sliding window problems is that most of the time they can be solved in O(N) time and O(1) space complexity.

Example:

# find characters in string
String = 'ADOBECODEBANC'
Characters = 'ABC'

The naive way to approach this would be to first, scan through the string, looking at ALL the substrings of length 3, and check to see if they contain the characters you’re looking for. If you can’t find any of length 3, then try all substrings of length 4, and 5, and 6, and 7 and so on until you reach the length of the string. If you reach that point, you know that those characters are not in there.

This is really inefficient and runs in O(N²) time. And what’s happening is that you are missing out a lot of good information on each pass by constraining yourself to look at fixed length windows, and you’re re-examining a lot of parts of the string that don’t need to be re-examined.

You’re throwing out a lot of good work, and you’re redoing a lot of useless work.

Different Kinds of Windows

There are several kinds of sliding window problems.

1st pointer/2nd pointer

1) Fast/Slow

These ones have a fast pointer that grows your window under a certain condition. So for Minimum Window Substring, you want to grow your window until you have a window that contains all the characters you’re looking for. It will also have a slow pointer, that shrinks the window. Once you find a valid window with the fast pointer, you want to start sliding the slow pointer up until you no longer have a valid window.

For example, in the Minimum Window Substring problem, once you have a substring that contains all the characters you’re looking for, then you want to start shrinking it by moving the slow pointer up until you no longer have a valid substring (meaning you no longer have all the characters you’re looking for)

2) Fast/Catchup

This is very similar to the first kind, except, instead of incrementing the slow pointer up, you simply move it up the fast pointer’s location and then keep moving the fast pointer up. It sort of jumps or catches up to the index of the fast pointer when a certain condition is met.

This is apparent in the Max Consecutive Sum problem. Here you’re given a list of integers, positive and negative, and you are looking for a consecutive sequence that sums to the largest amount. Key insight: The slow pointer “jumps” to the fast pointer’s index when the current sum ends up being negative. More on how this works later.

For example, in the array: [1, 2, 3, -7, 7, 2, -12, 6] the result would be: 9 (7 + 2)

Again, you’re looking for some kind of optimum (ie the maximum sum).

3) Fast/Lagging

This one is a little different, but essentially the slow pointer is simply referencing one or two indices behind the fast pointer and it’s keeping track of some choice you’ve made.

For example, in the House Robber problem you are trying to see what the maximum amount of gold you can steal from houses that are not next door to each other. Here the choice is whether or not you should steal from the current house, given that you could instead have stolen from the previous house.The optimum you are looking for is the maximum amount of gold you can steal.

4) Front/Back

These ones are different because instead of having both pointers traveling from the front, you have one from the front, and the other from the back. An example of this is the Rainwater Problem where you are calculating the maximum amount of rainwater you can capture in a given terrain. Again, you are looking for a maximum value, though the logic is slightly different, you are still optimizing a brute force O(N²) solution.

These four patterns should come as no surprise. After all, there are only so many ways you can move two pointers through an array or string in linear time.

Look for “Key Insights”

One final thing to think about with these problems is the key insight that “unlocks” the problem. It usually involves deducing some fact based on the constraints of the problem that helps you look at it in a different way.

For example, in the House Robber problem, you can’t rob adjacent houses, but all houses have a positive amount of gold (meaning you can’t rob a house and have less gold after robbing it). The key insight here is that the maximum distance between any two houses you rob will be two. If you had three houses between robberies, you could just rob the one in the center of the three and you will be guaranteed to increase the amount of gold you steal.

For the Bit Flip problem, you don’t need to actually mutate the array in the problem, you just need to keep track of how many flips you have remaining. As you grow your window, you subtract from that number until you’ve exhausted all your flips, and then you shrink your window until you encounter a zero and gain a flip back.

Maximum Sum Subarray of Size K

""" 
Maximum Sum Subarray of Size K (easy):

Given an array of positive numbers and a positive number ‘k,’ find the maximum sum of any contiguous subarray of size ‘k’.

Example 1:
    Input: [2, 1, 5, 1, 3, 2], k=3 
    Output: 9
    Explanation: Subarray with maximum sum is [5, 1, 3].
Example 2:
    Input: [2, 3, 4, 1, 5], k=2 
    Output: 7
    Explanation: Subarray with maximum sum is [3, 4].
https://www.educative.io/courses/grokking-the-coding-interview/JPKr0kqLGNP
"""

Solution

If has negative numbers:

A basic brute force solution will be to calculate the sum of all ‘k’ sized subarrays of the given array to find the subarray with the highest sum. We can start from every index of the given array and add the next ‘k’ elements to find the subarray’s sum.

If you observe closely, you will realize that to calculate the sum of a contiguous subarray, we can utilize the sum of the previous subarray. For this, consider each subarray as a Sliding Window of size ‘k.’ To calculate the sum of the next subarray, we need to slide the window ahead by one element. So to slide the window forward and calculate the sum of the new position of the sliding window, we need to do two things:

Subtract the element going out of the sliding window, i.e., subtract the first element of the window.
Add the new element getting included in the sliding window, i.e., the element coming right after the end of the window.

This approach will save us from re-calculating the sum of the overlapping part of the sliding window. Here is what our algorithm will look like:

Code

""" 
Maximum Sum Subarray of Size K (easy):

Given an array of positive numbers and a positive number ‘k,’ 
find the maximum sum of any contiguous subarray of size ‘k’.

Example 1:
    Input: [2, 1, 5, 1, 3, 2], k=3 
    Output: 9
    Explanation: Subarray with maximum sum is [5, 1, 3].
Example 2:
    Input: [2, 3, 4, 1, 5], k=2 
    Output: 7
    Explanation: Subarray with maximum sum is [3, 4].
https://www.educative.io/courses/grokking-the-coding-interview/JPKr0kqLGNP
"""

""" 
## Q
Given array, find the max contiguous array of size k
"""

""" 
## SOLUTION

# Brute force
- create all contiguous subarrays of size k possible & find each of their sums then return the max 
    - this can be done by iterating k-1 steps forward at each point in the array

# Optimal
- create a window of size k, and record its sum
- iterate through the array, 
    adding the next element to the window (adding it to the sum), & at the same time
    remove the 1st element in the window (remove its value from the sum),
    record the sum if it is larger than the prev recorded sum
- repeat the step above till each subarray is considered

[0,1,2,3,4], k=3 +> 9
"""

# l=0, r=2 c=6, m=3
# l=1, r=3, c=6, m=6
# l=2, r=4, c=9, m=9

def max_sub_array_of_size_k(k, arr):
    if len(arr) < k:
        return -1

    curr_sum = 0
    maximum = -1

    # first subarray -> create window
    for idx in range(k):
        curr_sum += arr[idx]
    maximum = curr_sum

    # other subarrays
    for idx in range(1, len(arr)-(k-1)):
        curr_sum -= arr[idx-1]  # remove from window
        curr_sum += arr[idx+(k-1)]  # add to window
        maximum = max(curr_sum, maximum)

    return maximum

Time & space complexity

O(N) time | O(1) space

Smallest Subarray with a given sum

Problem

"""
Smallest Subarray with a given sum:

Given an array of positive numbers and a positive number ‘S,’
find the length of the smallest contiguous subarray whose sum is greater than or equal to ‘S’.
Return 0 if no such subarray exists.

Example 1:
    Input: [2, 1, 5, 2, 3, 2], S=7
    Output: 2
    Explanation: The smallest subarray with a sum greater than or equal to '7' is [5, 2].
Example 2:
    Input: [2, 1, 5, 2, 8], S=7
    Output: 1
    Explanation: The smallest subarray with a sum greater than or equal to '7' is [8].
Example 3:
    Input: [3, 4, 1, 1, 6], S=8
    Output: 3
    Explanation: Smallest subarrays with a sum greater than or equal to '8' are [3, 4, 1]
    or [1, 1, 6].

https://www.educative.io/courses/grokking-the-coding-interview/7XMlMEQPnnQ
"""

Solution

if has negative numbers

Other

Solution 1

def decrease_window(curr_sum, arr, left):
    curr_sum -= arr[left]
    left += 1
    return left, curr_sum

def increase_window(curr_sum, arr, right):
    right += 1
    curr_sum += arr[right]
    return right, curr_sum

def smallest_subarray_with_given_sum_01(s, arr):
    if not arr or len(arr) < 1:
        return -1
    smallest_len = float('inf')

    # window boundary
    left = 0
    right = 0
    curr_sum = arr[0]

    while left < len(arr):
        if curr_sum >= s:
            smallest_len = min(smallest_len, (right-left)+1)

        # cannot increase window
        if right >= len(arr)-1:
            left, curr_sum = decrease_window(curr_sum, arr, left)

        # cannot decrease window
        elif right == left:
            right, curr_sum = increase_window(curr_sum, arr, right)

        elif curr_sum >= s:
            left, curr_sum = decrease_window(curr_sum, arr, left)
        else:
            right, curr_sum = increase_window(curr_sum, arr, right)

    if smallest_len == float('inf'):
        return -1
    return smallest_len

Solution 2

"""
Explanation 2:

---

- first, we sum up elements from the beginning of the array until their sum becomes >= s
    These elements will constitute our sliding window.
    We will remember the length of this window as the smallest window so far.
- after this we keep adding one element to the window at every loop
- at each step, we try to shrink the window, 
    we shrink the window till its sum is < s to find the smallest window
    - as we do this we try to keep updating the smallest length we have seen soo far

---

- increase the window till you get a sum >= s
- then decrease the window till your sum becomes < s (while keeping track of the smallest lengths)
- repeat till the end of the array

"""

def smallest_subarray_with_given_sum(s, arr):
    if not arr or len(arr) < 1:
        return -1
    smallest_len = float('inf')

    left = 0
    curr_sum = 0
    for right in range(len(arr)):
        curr_sum += arr[right]

        while left <= right and curr_sum >= s:
            smallest_len = min(smallest_len, (right-left)+1)

            # decrease window
            curr_sum -= arr[left]
            left += 1

    if smallest_len == float('inf'):
        return -1
    return smallest_len

Sliding%20Window%20f6685a15f97a4ca2bb40111e2b264fb2/Screenshot_2021-08-08_at_07.07.27.png

Longest Substring with K Distinct Characters

Problem

""" 
Longest Substring with K Distinct Characters:

Given a string, find the length of the longest substring in it with no more than K distinct characters.
You can assume that K is less than or equal to the length of the given string.

Example 1:
    Input: String="araaci", K=2
    Output: 4
    Explanation: The longest substring with no more than '2' distinct characters is "araa".
Example 2:
    Input: String="araaci", K=1
    Output: 2
    Explanation: The longest substring with no more than '1' distinct characters is "aa".
Example 3:
    Input: String="cbbebi", K=3
    Output: 5
    Explanation: The longest substrings with no more than '3' distinct characters are "cbbeb" & "bbebi".
"""

Solution

""" 
Solution:

- Basics
    we'll have a left, right pointer that will mark the current substring we are looking at
    we'll have a store (a HashMap), that stores the characters in the substring with their count
- we will iterate through the string with the right pointer till we have a string with k distinct characters
- while we have a string with k distinct characters:
    - then we we try to increase the substring length, by checking if the next char is in the store, then increase
    - if we cannot increase, we decrease it by removing the first character in the substring

012345
araaci K=2
l,r,max,store
l=0,r=0,0,{a:1,}
# have to increase
l=0,r=1,2,{a:1,r:1}
# can increase
l=0,r=2,3,{a:2,r:1}
l=0,r=3,4,{a:3,r:1}
# have to decrease
l=1,r=3,4,{a:2,r:1}
l=2,r=3,4,{a:2,}
# have to increase
l=2,r=4,4,{a:2,c:1}
# have to decrease
l=3,r=4,4,{a:1,c:1}
l=4,r=4,4,{c:1,}
# have to increase
l=4,r=4,4,{c:1,}
l=4,r=5,4,{c:1,r:5}

"""
from collections import defaultdict

# O(N+N) time | O(K) space ==
# O(N) time | O(K) space
def longest_substring_with_k_distinct(str1, k):
    if len(str1) <= 0:
        return -1
    longest = float('-inf')

    left = 0
    right = 0
    store = defaultdict(int)
    store[str1[0]] = 1
    while right < len(str1)-1:
        if len(store) < k:
            right += 1
            store[str1[right]] += 1
            continue

        # # we have k dist characters
        longest = max(longest, (right-left)+1)

        # can increase length of substring
        if right < len(str1)-1 and str1[right+1] in store:
            right += 1
            store[str1[right]] += 1

        # cannot increase length
        else:
            store[str1[left]] -= 1
            if store[str1[left]] <= 0:
                store.pop(str1[left])
            left += 1

    if longest == float('-inf'):
        return -1
    return longest

Fruits into Baskets

Problem

""" 
Fruits into Baskets:

Given an array of characters where each character represents a fruit tree,
 you are given two baskets, and your goal is to put maximum number of fruits in each basket. 
The only restriction is that each basket can have only one type of fruit.

You can start with any tree, but you can’t skip a tree once you have started. 
You will pick one fruit from each tree until you cannot, i.e., you will stop when you have to pick from a third fruit type.

Write a function to return the maximum number of fruits in both baskets.

Example 1:
    Input: Fruit=['A', 'B', 'C', 'A', 'C']
    Output: 3
    Explanation: We can put 2 'C' in one basket and one 'A' in the other from the subarray ['C', 'A', 'C']
Example 2:
    Input: Fruit=['A', 'B', 'C', 'B', 'B', 'C']
    Output: 5
    Explanation: We can put 3 'B' in one basket and two 'C' in the other basket. 
        This can be done if we start with the second letter: ['B', 'C', 'B', 'B', 'C']

https://www.educative.io/courses/grokking-the-coding-interview/Bn2KLlOR0lQ
"""

Solution

""" 
Solution:

- we need to find the longest subarray with a max of two distinct characters

- create a subarray with two distinct characters & once we have this,
    - check if lengthening the array will not break the 2 dist char rule, if so, increase the length otherwise,
    - decrease the subarray length by removing the first character in the subarray

['0', '1', '2', '3', '4', '5'] 6
['A', 'B', 'C', 'B', 'B', 'C']

left,right,store
l=0,r=0,{A:1,}
# increase size: we need to have a subarray with two distinct characters
l=0,r=1,{A:1,B:1}
# decrease size: we cannot increase, adding c will break the 2 dist characters rule
l=1,r=1,{B:1,}
# increase size
l=1,r=2,{B:1,C:1}
l=1,r=3,{B:2,C:1}
l=1,r=4,{B:3,C:1}
l=1,r=5,{B:3,C:2}

res = 3 # => {B:3,C:2}

"""

# from collections import defaultdict

def fruits_into_baskets(fruits):
    if not fruits or len(fruits) < 2:
        return -1

    most_fruits = float('-inf')

    left = right = 0
    store = defaultdict(int)
    store[fruits[0]] = 1
    while right < len(fruits):
        if len(store) < 2:
            right += 1
            if right < len(fruits) - 1:
                store[fruits[right]] += 1
            continue

        most_fruits = max(most_fruits, (right-left)+1)

        # can add one more
        if right < len(fruits) - 1 and fruits[right+1] in store:
            right += 1
            store[fruits[right]] += 1

        # can add: so remove one
        else:
            store[fruits[left]] -= 1
            if store[fruits[left]] <= 0:
                store.pop(fruits[left])
            left += 1

    if most_fruits == float('-inf'):
        return -1
    return most_fruits

Dutch National Flag Problem

Problem

""" 
Dutch National Flag Problem/Three Number Sort:

Given an array containing 0s, 1s and 2s, sort the array in-place. 
You should treat numbers of the array as objects, hence, we can’t count 0s, 1s, and 2s to recreate the array.

The flag of the Netherlands consists of three colors: red, white and blue; 
    and since our input array also consists of three different numbers that is why it is called Dutch National Flag problem.

Example 1:
    Input: [1, 0, 2, 1, 0]
    Output: [0 0 1 1 2]
Example 2:
    Input: [2, 2, 0, 1, 2, 0]
    Output: [0 0 1 2 2 2 ]
"""

Solution

def dutch_flag_sort(arr):

    next_zero = 0
    next_two = len(arr)-1
    idx = 0
    while idx < (len(arr)):

        # swap values to their correct place
        if arr[idx] == 0 and idx >= next_zero:
            arr[idx], arr[next_zero] = arr[next_zero], arr[idx]
            next_zero += 1
        elif arr[idx] == 2 and idx <= next_two:
            arr[idx], arr[next_two] = arr[next_two], arr[idx]
            next_two -= 1

        # only leave idx if value is in correct place
        else:
            idx += 1

Find All Anagrams in a String *

Permutation in String

""" 
Permutation in String

Given two strings s1 and s2, return true if s2 contains a permutation of s1, or false otherwise.
In other words, return true if one of s1's permutations is the substring of s2.

Example 1:
    Input: s1 = "ab", s2 = "eidbaooo"
    Output: true
    Explanation: s2 contains one permutation of s1 ("ba").
Example 2:
    Input: s1 = "ab", s2 = "eidboaoo"
    Output: false

Constraints:
    1 <= s1.length, s2.length <= 104
    s1 and s2 consist of lowercase English letters

https://leetcode.com/problems/permutation-in-string

Do after this: 
- https://leetcode.com/problems/find-all-anagrams-in-a-string/
"""

from collections import Counter

# Note: we can compare p_count and window_count in constant time because they are both at most size 26
# Space complexity: O(1) because p_count and window_count contain not more than 26 elements.
class Solution:
    def checkInclusion(self, s1: str, s2: str):

        # # create counters
        window_counter = [0] * 26
        s1_counter = [0] * 26
        for char, count in Counter(s1).items():
            s1_counter[self.char_idx(char)] = count

        # # look for permutations using a sliding window pattern
        for idx in range(len(s2)):

            # # create first window
            if idx < (len(s1)):
                window_counter[self.char_idx(s2[idx])] += 1

            # # move window forward
            else:
                window_counter[self.char_idx(s2[idx-len(s1)])] -= 1
                window_counter[self.char_idx(s2[idx])] += 1

            # # check for result
            if s1_counter == window_counter:
                return True

    def char_idx(self, char):
        return ord(char) - ord('a')

Find All Anagrams in a String *

""" 
Find All Anagrams in a String

Given two strings s and p, return an array of all the start indices of p's anagrams in s. 
You may return the answer in any order.
An Anagram is a word or phrase formed by rearranging the letters of a different word or phrase, 
    typically using all the original letters exactly once.

Example 1:
    Input: s = "cbaebabacd", p = "abc"
    Output: [0,6]
    Explanation:
        The substring with start index = 0 is "cba", which is an anagram of "abc".
        The substring with start index = 6 is "bac", which is an anagram of "abc".
Example 2:
    Input: s = "abab", p = "ab"
    Output: [0,1,2]
    Explanation:
        The substring with start index = 0 is "ab", which is an anagram of "ab".
        The substring with start index = 1 is "ba", which is an anagram of "ab".
        The substring with start index = 2 is "ab", which is an anagram of "ab".


Constraints:
    1 <= s.length, p.length <= 3 * 104
    s and p consist of lowercase English letters.

https://leetcode.com/problems/find-all-anagrams-in-a-string/
Prerequisite: 
- https://leetcode.com/problems/permutation-in-string
"""
import collections

# Time complexity: O(S) + O(P) since it's one pass along both strings.
# Note: we can compare p_count and window_count in constant time because they are both at most size 26
# Space complexity: O(1) because p_count and window_count contain not more than 26 elements.
class Solution:
    def findAnagrams(self, s: str, p: str):
        if len(p) > len(s):
            return[]
        anagrams = []

        # an array of length 26 can be used instead (with the ASCII values of the chracters)
        p_count = collections.Counter(p)
        window_count = collections.Counter()
        for idx, char in enumerate(s):
            # # create window
            if idx < len(p):
                window_count[char] += 1

            # # move window forward
            else:
                # remove char at left end
                left_end_char = s[idx-(len(p))]
                window_count[left_end_char] -= 1
                if window_count[left_end_char] == 0:
                    window_count.pop(left_end_char)
                # add char to right end
                window_count[char] += 1

            # # check if anagrams
            if p_count == window_count:
                anagrams.append(idx-(len(p)-1))

        return anagrams

Permutation in String

""" 
Permutation in String

Given two strings s1 and s2, return true if s2 contains a permutation of s1, or false otherwise.
In other words, return true if one of s1's permutations is the substring of s2.

Example 1:
    Input: s1 = "ab", s2 = "eidbaooo"
    Output: true
    Explanation: s2 contains one permutation of s1 ("ba").
Example 2:
    Input: s1 = "ab", s2 = "eidboaoo"
    Output: false

Constraints:
    1 <= s1.length, s2.length <= 104
    s1 and s2 consist of lowercase English letters

https://leetcode.com/problems/permutation-in-string

Do after this: 
- https://leetcode.com/problems/find-all-anagrams-in-a-string/
"""

from collections import Counter

# Note: we can compare p_count and window_count in constant time because they are both at most size 26
# Space complexity: O(1) because p_count and window_count contain not more than 26 elements.
class Solution:
    def checkInclusion(self, s1: str, s2: str):

        # # create counters
        window_counter = [0] * 26
        s1_counter = [0] * 26
        for char, count in Counter(s1).items():
            s1_counter[self.char_idx(char)] = count

        # # look for permutations using a sliding window pattern
        for idx in range(len(s2)):

            # # create first window
            if idx < (len(s1)):
                window_counter[self.char_idx(s2[idx])] += 1

            # # move window forward
            else:
                window_counter[self.char_idx(s2[idx-len(s1)])] -= 1
                window_counter[self.char_idx(s2[idx])] += 1

            # # check for result
            if s1_counter == window_counter:
                return True

    def char_idx(self, char):
        return ord(char) - ord('a')

Find All Anagrams in a String *

""" 
Find All Anagrams in a String

Given two strings s and p, return an array of all the start indices of p's anagrams in s. 
You may return the answer in any order.
An Anagram is a word or phrase formed by rearranging the letters of a different word or phrase, 
    typically using all the original letters exactly once.

Example 1:
    Input: s = "cbaebabacd", p = "abc"
    Output: [0,6]
    Explanation:
        The substring with start index = 0 is "cba", which is an anagram of "abc".
        The substring with start index = 6 is "bac", which is an anagram of "abc".
Example 2:
    Input: s = "abab", p = "ab"
    Output: [0,1,2]
    Explanation:
        The substring with start index = 0 is "ab", which is an anagram of "ab".
        The substring with start index = 1 is "ba", which is an anagram of "ab".
        The substring with start index = 2 is "ab", which is an anagram of "ab".


Constraints:
    1 <= s.length, p.length <= 3 * 104
    s and p consist of lowercase English letters.

https://leetcode.com/problems/find-all-anagrams-in-a-string/
Prerequisite: 
- https://leetcode.com/problems/permutation-in-string
"""
import collections

# Time complexity: O(S) + O(P) since it's one pass along both strings.
# Note: we can compare p_count and window_count in constant time because they are both at most size 26
# Space complexity: O(1) because p_count and window_count contain not more than 26 elements.
class Solution:
    def findAnagrams(self, s: str, p: str):
        if len(p) > len(s):
            return[]
        anagrams = []

        # an array of length 26 can be used instead (with the ASCII values of the chracters)
        p_count = collections.Counter(p)
        window_count = collections.Counter()
        for idx, char in enumerate(s):
            # # create window
            if idx < len(p):
                window_count[char] += 1

            # # move window forward
            else:
                # remove char at left end
                left_end_char = s[idx-(len(p))]
                window_count[left_end_char] -= 1
                if window_count[left_end_char] == 0:
                    window_count.pop(left_end_char)
                # add char to right end
                window_count[char] += 1

            # # check if anagrams
            if p_count == window_count:
                anagrams.append(idx-(len(p)-1))

        return anagrams

Minimum Window Substring *

Continuous Subarray Sum **

Trapping rain water

Sliding Window Maximum

More examples

Facebook | SWE New Grad | London | January 2019 [Reject] - LeetCode Discuss

Max Consecutive Ones III - LeetCode

Find the original version of this page (with additional content) on Notion here.

Two Pointers

Introduction

Two Pointers - InterviewBit

Introduction - Grokking the Coding Interview: Patterns for Coding Questions

Sum MegaPost - Python3 Solution with a detailed explanation - LeetCode Discuss

In problems where we deal with sorted arrays (or LinkedLists) and need to find a set of elements that fulfill certain constraints, the Two Pointers approach becomes quite useful. The set of elements could be a pair, a triplet or even a subarray. For example, take a look at the following problem:

Given an array of sorted numbers and a target sum, find a pair in the array whose sum is equal to the given target.

To solve this problem, we can consider each element one by one (pointed out by the first pointer) and iterate through the remaining elements (pointed out by the second pointer) to find a pair with the given sum. The time complexity of this algorithm will be O(N^2) where ‘N’ is the number of elements in the input array.

Given that the input array is sorted, an efficient way would be to start with one pointer in the beginning and another pointer at the end. At every step, we will see if the numbers pointed by the two pointers add up to the target sum. If they do not, we will do one of two things:

Untitled

If the sum of the two numbers pointed by the two pointers is smaller than the target sum, this means that we need a pair with a larger sum. So, to try more pairs, we can increment the start-pointer.
If the sum of the two numbers pointed by the two pointers is greater than the target sum, this means that we need a pair with a smaller sum. So, to try more pairs, we can decrement the end-pointer.

The time complexity of the above algorithm will be O(N).

Two pointers are needed because with just pointer, you would have to continually loop back through the array to find the answer. This back and forth with a single iterator is inefficient for time and space complexity. While the brute force or naive solution with 1 pointer would work, it will produce something along the lines of O(n²). In many cases, two pointers can help you find a solution with better space or runtime complexity.

Simple problems

Two sum

For differences:

""" 
Pair with Target Sum;

Given an array of sorted numbers and a target sum, find a pair in the array whose sum is equal to the given target.
https://www.educative.io/courses/grokking-the-coding-interview/xog6q15W9GP
"""

""" 
- we need to search for two numbers

- we can have two pointers, one at the beginning and one at the end then check how their sum compares to the target
    - if equal, return them
    - if less than, increase the total sum by moving the left pointer forward
    - if greater than, decrease the total sum by moving the right pointer backward

[1, 2, 3, 4, 6], target=6
l=1,r=6
l=1,r=4
l=2,r=4
"""

# O(1) space | O(n) time
def pair_with_targetsum(arr, target_sum):

    left = 0
    right = len(arr)-1
    while left < right:
        total = arr[left]+arr[right]

        if total < target_sum:
            left += 1
        elif total > target_sum:
            right -= 1
        else:
            return [arr[left], arr[right]]
    return [-1, -1]

Two%20Pointers%2078c9f1659ca14bbbadace29a5d252a41/Screenshot_2021-08-11_at_08.09.57.png

Check if number the current in the past using complements

Remove Duplicates

""" 
Remove Duplicates;

Given an array of sorted numbers, remove all duplicates from it. 
You should not use any extra space; after removing the duplicates in-place return the length of the subarray that has no duplicate in it.

"""

""" 
Solution 1;

- have a res_length variable that will be initialised as 1
- have two pointers both at the start of the array: left & right
- move the right pointer one step forward:
    - if its value is not equal to left's value, increment the value of res_length & move the left pointer to right's position
    - if equal, repeat this step (move the right pointer one step forward)

[2, 3, 3, 3, 6, 9, 9]
l=2,r=2,res=1
l=3,r=3,res=2
l=3,r=3,res=2
l=3,r=3,res=2
l=6,r=6,res=3
l=9,r=9,res=4
l=9,r=9,res=4
"""

def remove_duplicates(arr):

    res_length = 1
    last_non_dup = 0
    for idx in range(1, len(arr)):
        if arr[last_non_dup] != arr[idx]:
            res_length += 1
            last_non_dup = idx
    return res_length

""" 
Solution 2:

In this problem, we need to remove the duplicates in-place such that the resultant length of the array remains sorted. 
As the input array is sorted, therefore, one way to do this is to shift the elements left whenever we encounter duplicates. 
In other words, we will keep one pointer for iterating the array and one pointer for placing the next non-duplicate number. 
So our algorithm will be to iterate the array and whenever we see a non-duplicate number we move it next to the last non-duplicate number we’ve seen.
"""

def remove_duplicates2(arr):
    next_non_duplicate = 1

    for i in range(1, len(arr)):
        if arr[next_non_duplicate - 1] != arr[i]:
            arr[next_non_duplicate] = arr[i]
            next_non_duplicate += 1
        i += 1

    return next_non_duplicate

Squaring a Sorted Array *

""" 
Squaring a Sorted Array:

Given a sorted array, create a new array containing squares of all the numbers of the input array in the sorted order.
"""

""" 
(arrange from largest to smallest then reverse)
- beacause our input array contains negative numbers, 
    the largest square can be either on the far right or far left
- so we need to iterate inwards (from outward):
    - have a left & right pointer at both ends of the array and consider the largest square 

Use two pointers starting at both ends of the input array. 
At any step, whichever pointer gives us the bigger square, 
we add it to the result array and move to the next/previous number according to the pointer.
"""

def make_squares(arr):
    squares = []

    left = 0
    right = len(arr)-1
    while left <= right:
        left_s = arr[left] * arr[left]
        right_s = arr[right] * arr[right]
        if left_s > right_s:
            squares.append(left_s)
            left += 1
        else:
            squares.append(right_s)
            right -= 1

    squares.reverse()
    return squares

Pairs with Specific Difference *

Three Sum

Problem

"""
Three Sum. (3Sum):
Triplet Sum to Zero:

Given an array nums of n integers, are there elements a, b, c in nums such that a + b + c = 0? 
Find all unique triplets in the array which gives the sum of zero.

The solution set must not contain duplicate triplets.

Example 1:

    Input: nums = [-1,0,1,2,-1,-4]
    Output: [[-1,-1,2],[-1,0,1]]
Example 2:

    Input: nums = []
    Output: []
Example 3:

    Input: nums = [0]
    Output: []

https://www.educative.io/courses/grokking-the-coding-interview/gxk639mrr5r
"""

Solution

.

def search_triplets(nums):

    nums.sort()  # will make spotting of duplicates easy

    triplets = []
    length = len(nums)

    for i in range(length-2):  # ignore last two

        # check if element is a duplicate. the first cannot be a duplicate
        if i > 0 and nums[i] == nums[i-1]:
            # skip handling an element if it's similar to the one before it
            # because it is sorted, we effectively skip duplicates
            continue

        # TWO SUM for a sorted array
        # 1. find elements that will add up to 0
        # 2. check inner elements
        left = i + 1
        right = length - 1
        while left < right:

            total = nums[i] + nums[left] + nums[right]

            if total < 0:
                left += 1

            elif total > 0:
                right -= 1

            # 1. add list of elements to triplets
            # 2. move to inner elements
                                # 3. skip similar elements
            else:
                # add elements to triplets
                triplets.append([nums[i], nums[left], nums[right]])

                # skip:
                # no need to continue with an element with the same value as l/r
                # Skip all similar to the current left and right so that,
                # when we are moving to the next element, we dont move to an element with the same value
                while left < right and nums[left] == nums[left+1]:
                    left += 1
                while left < right and nums[right] == nums[right-1]:
                    right -= 1

                # move to inner elements
                left += 1
                right -= 1

    return triplets

Time complexity

Sorting the array will take O(N log(N)). The searchPair/twoSum() function will take O(N).

As we are calling searchPair() for every number in the input array, this means that overall searchTriplets() will take O(N log(N) + N^2),which is asymptotically equivalent to O(N^2)

Four sum

Similar to three sum

""" 
4Sum:

Given an array nums of n integers, return an array of all the unique quadruplets [nums[a], nums[b], nums[c], nums[d]] such that:
    0 <= a, b, c, d < n
    a, b, c, and d are distinct.
    nums[a] + nums[b] + nums[c] + nums[d] == target
You may return the answer in any order.

Example 1:
    Input: nums = [1,0,-1,0,-2,2], target = 0
    Output: [[-2,-1,1,2],[-2,0,0,2],[-1,0,0,1]]
Example 2:
    Input: nums = [2,2,2,2,2], target = 8
    Output: [[2,2,2,2]]
"""

""" 
[1,0,-1,0,-2,2]

[-2, -1, 0, 0, 1, 2]

- four sum is a combination of two two_sums

- sort the input array so that we can skip duplicates

- have two loops with to iterate through all the possible two number combinations:
    - for the rest of the numbers: find a two sum that = target - (arr[idx_loop_one] + arr[idx_loop_two])

"""

class Solution:

    def fourSum(self, nums, target):
        res = []
        nums.sort()

        for one in range(len(nums)):
            if one > 0 and nums[one] == nums[one-1]:
                continue  # skip duplicates
            for two in range(one+1, len(nums)):
                if two > one+1 and nums[two] == nums[two-1]:
                    continue  # skip duplicates

                # # two sum
                needed = target - (nums[one] + nums[two])
                left = two + 1
                right = len(nums)-1
                while left < right:
                    # skip duplicates
                    if left > two + 1 and nums[left] == nums[left-1]:
                        left += 1
                        continue
                    if right < len(nums)-1 and nums[right] == nums[right+1]:
                        right -= 1
                        continue

                    total = nums[left] + nums[right]
                    if total < needed:
                        left += 1
                    elif total > needed:
                        right -= 1
                    else:
                        res.append(
                            [nums[one], nums[two], nums[left], nums[right]])
                        left += 1
                        right -= 1

        return res

Subarrays with Product Less than a Target *

Problem

""" 
Subarrays with Product Less than a Target:

Given an array with positive numbers and a positive target number,
 find all of its contiguous subarrays whose product is less than the target number.

Example 1:
    Input: [2, 5, 3, 10], target=30 
    Output: [2], [5], [2, 5], [3], [5, 3], [10]
    Explanation: There are six contiguous subarrays whose product is less than the target.
Example 2:
    Input: [8, 2, 6, 5], target=50 
    Output: [8], [2], [8, 2], [6], [2, 6], [5], [6, 5] 
    Explanation: There are seven contiguous subarrays whose product is less than the target.
"""

Solution

""" 

[2, 5, 2, 2, 3, 10], target=30 

2=>2 [    [2],]
2,5=>10[[2],     [2,5],[5]]
2,5,2=>20[[2],[2,5],[5],  [2,5,2],[5,2],[2],]
# Add 2
2,5,2,2=>40
5,2,2=>20 -[[2],[2,5],[5],[2,5,2],[5,2],[2],  [5,2,2],[2,2],[2],]
# Add 3
5,2,2,3=>60
2,2,3=>12 - [[2],[2,5],[5],[2,5,2],[5,2],[2],  [5,2,2],[2,2],[2],]
# Add 10
2,2,3,10=>120
2,3,10=>60
3,10=>30 - [[2],[2,5],[5],[2,5,2],[5,2],[2],[5,2,2],[2,2],[2],   [3,10], [10]]
# 

"""

# O(n^3) time | O(n^3) space in the worst case
def find_subarrays(arr, target):
    result = []

    prod = 1
    left = 0
    for right in range(len(arr)):

        # create window that has a prod < target
        prod *= arr[right]  # add right
        while left <= right and prod >= target:
            prod /= arr[left]
            left += 1

        # since the product of all numbers from left to right is less than the target therefore,
        #   all subarrays from left to right will have a product less than the target too;
        # to avoid duplicates, we will start with a subarray containing only arr[right] and then extend it - done it the other way around here

        # record result (all the subarrays of the current window ending with right)
        # O(n^2) time | O(n^2) space in the worst case
        for i in range(left, right+1):
            result.append(arr[i:right+1])

    return result

Time & Space complexity

Time

The main for-loop managing the sliding window takes O(N) but creating subarrays can take up to O(N^2) in the worst case. Therefore overall, our algorithm will take O(N^3)

Space

At most, we need space for O(n^2) output lists. At worst, each subarray can take O(n) space, so overall, our algorithm’s space complexity will be O(n^3)

Insert Intervals

Screenshot 2021-10-24 at 19.17.41.png

""" 
Insert Interval

You are given an array of non-overlapping intervals intervals where intervals[i] = [starti, endi] represent the start and the end of the ith interval 
    and intervals is sorted in ascending order by starti. 
You are also given an interval newInterval = [start, end] that represents the start and end of another interval.
Insert newInterval into intervals such that intervals is still sorted in ascending order by starti and intervals still does not have any overlapping intervals (merge overlapping intervals if necessary).
Return intervals after the insertion.

Example 1:
    Input: intervals = [[1,3],[6,9]], newInterval = [2,5]
    Output: [[1,5],[6,9]]
Example 2:
    Input: intervals = [[1,2],[3,5],[6,7],[8,10],[12,16]], newInterval = [4,8]
    Output: [[1,2],[3,10],[12,16]]
Explanation: Because the new interval [4,8] overlaps with [3,5],[6,7],[8,10].
Example 3:
    Input: intervals = [], newInterval = [5,7]
    Output: [[5,7]]
Example 4:
    Input: intervals = [[1,5]], newInterval = [2,3]
    Output: [[1,5]]
Example 5:
    Input: intervals = [[1,5]], newInterval = [2,7]
    Output: [[1,7]]

https://leetcode.com/problems/insert-interval
"""

""" 
intervals = [[1,2],[3,5],[6,7],[8,10],[12,16]], newInterval = [4,8]

1 2 3 4 5 6 7 8 9 10 11 12 13
####
1-2 3---5 6-7 8---10    12----
      4-------8
####
1---3     6-----9
      4-------8
####
     3---5 6-7 8---10
1-2
####
     3---5 6-7 8---10
                      11-12 
###


- res = []    
- find the insert position (first interval with ending greater than newInterval's start)
    - if None, add newInterval to the end
    - else:
        - add all before the start to res (Add to the output all the intervals starting before newInterval)
        - add all overlaping intervals
          while the current index's start < newInterval's end:
            - update the newInterval's end to be the max of both ends
            - skip it (interval at current index)(move index forward)
"""

from typing import List
class Solution__:
    def insert(self, intervals: List[List[int]], newInterval: List[int]):

        # - Find the insert position (first interval with ending greater than newInterval's start)
        start_idx = -1
        for idx, interval in enumerate(intervals):
            if interval[1] >= newInterval[0]:
                start_idx = idx
                break
        # if None, add newInterval to the end
        if start_idx == -1:
            return intervals + [newInterval]

        # - Add to the output all the intervals starting before newInterval
        before_start = intervals[:start_idx]

        # - Add all overlaping intervals to inserted_interval
        inserted_interval = [
            min(newInterval[0], intervals[start_idx][0]), newInterval[1]
        ]
        idx = start_idx
        while idx < len(intervals) and inserted_interval[1] >= intervals[idx][0]:
            inserted_interval[1] = max(intervals[idx][1], inserted_interval[1])
            idx += 1

        return before_start + [inserted_interval] + intervals[idx:]

""" 

"""

class Solution_:
    def insert(self, intervals: List[List[int]], newInterval: List[int]):

        # - Find the insert position (first interval with ending greater than newInterval's start)
        start_idx = -1
        for idx, interval in enumerate(intervals):
            if interval[1] >= newInterval[0]:
                start_idx = idx
                break
        # if None, add newInterval to the end
        if start_idx == -1:
            return intervals + [newInterval]

        # - Add to the output all the intervals starting before newInterval
        merged = intervals[:start_idx]
        # - Add newInterval to output
        if len(merged) > 0 and newInterval[0] <= merged[-1][1]:
            merged[-1] = self.merge_intervals(newInterval, merged[-1])
        else:
            merged.append(newInterval)

        # - Add to the output all the intervals starting after newInterval
        for idx in range(start_idx, len(intervals)):
            # Merge it with the last added interval if newInterval starts before the last added interval.
            if intervals[idx][0] <= merged[-1][1]:
                merged[-1] = self.merge_intervals(intervals[idx], merged[-1])
            else:
                merged.append(intervals[idx])

        return merged

    def merge_intervals(self, one, two):
        return [min(one[0], two[0]), max(one[1], two[1])]

Container With Most Water

Best Time to Buy and Sell Stock

Best Time to Buy and Sell Stock II

Trapping Rain Water

Best Time to Buy and Sell Stock *

Screenshot 2021-10-16 at 19.44.06.png

Screenshot 2021-10-16 at 19.48.14.png

min & max gives maximum profit

"""
Best Time to Buy and Sell Stock: (do Container With Most Water first)

Say you have an array for which the ith element is the price of a given stock on day i.
If you were only permitted to complete at most one transaction (i.e., buy one and sell one share of the stock),
 design an algorithm to find the maximum profit.
Note that you cannot sell a stock before you buy one.

Example 1:
    Input: [7,1,5,3,6,4]
    Output: 5
    Explanation: Buy on day 2 (price = 1) and sell on day 5 (price = 6), profit = 6-1 = 5.
                Not 7-1 = 6, as selling price needs to be larger than buying price.
Example 2:
    Input: [7,6,4,3,1]
    Output: 0
    Explanation: In this case, no transaction is done, i.e. max profit = 0.

https://leetcode.com/problems/best-time-to-buy-and-sell-stock/
"""

class Solution_:
    def maxProfit(self, prices):
        min_price, max_profit = float('inf'), 0

        for price in prices:
            profit = price - min_price

            max_profit = max(max_profit, profit)
            min_price = min(min_price, price)

        return max_profit

class Solution:

    def maxProfit(self, prices):
        if len(prices) < 2:
            return 0

        left = 0
        right = 1
        max_profit = 0
        # we need to find the smallest valley following the largest peak -> try to continue increasing the slope
        while right < len(prices):
            max_profit = max(max_profit,  prices[right] - prices[left])

            # try out all values that are larger than left b4 we get a smaller value left
            # increase slope length
            if prices[right] > prices[left] or right == left:
                right += 1

            # # if we find a point that is equal or lower than left (if lower **we might make more profit**)
            # reset slope
            else:
                left = right  # move left to the smaller value
                right += 1

        return max_profit

Best Time to Buy and Sell Stock II

Screenshot 2021-10-16 at 20.39.38.png

Screenshot 2021-10-16 at 20.37.29.png

Screenshot 2021-10-16 at 20.36.18.png

Screenshot 2021-10-16 at 20.37.06.png

Screenshot 2021-10-16 at 20.38.34.png

""" 
Best Time to Buy and Sell Stock II

You are given an integer array prices where prices[i] is the price of a given stock on the ith day.
On each day, you may decide to buy and/or sell the stock. 
You can only hold at most one share of the stock at any time. However, you can buy it then immediately sell it on the same day.
Find and return the maximum profit you can achieve.

Example 1:
    Input: prices = [7,1,5,3,6,4]
    Output: 7
    Explanation: Buy on day 2 (price = 1) and sell on day 3 (price = 5), profit = 5-1 = 4.
        Then buy on day 4 (price = 3) and sell on day 5 (price = 6), profit = 6-3 = 3.
        Total profit is 4 + 3 = 7.
Example 2:
    Input: prices = [1,2,3,4,5]
    Output: 4
    Explanation: Buy on day 1 (price = 1) and sell on day 5 (price = 5), profit = 5-1 = 4.
        Total profit is 4.
Example 3:
    Input: prices = [7,6,4,3,1]
    Output: 0
    Explanation: There is no way to make a positive profit, so we never buy the stock to achieve the maximum profit of 0.

https://leetcode.com/problems/best-time-to-buy-and-sell-stock-ii
"""

class Solution:
    def maxProfit(self, prices):
        """
        If we analyze the graph, we notice that the points of interest are the consecutive valleys and peaks.
        Add every upward slope (valley->peak)
        https://www.notion.so/paulonteri/Two-Pointers-78c9f1659ca14bbbadace29a5d252a41#ca35efcb515445a091c0a0dfcefed057
        """
        result = 0

        prev_min = prices[0]
        prev_max = prices[0]
        for idx in range(1, len(prices)):

            if prices[idx] < prev_max:
                # add prev slope we were on
                result += prev_max-prev_min
                # reset slope
                prev_max = prices[idx]
                prev_min = prices[idx]

            else:
                # increase slope
                prev_max = prices[idx]

        # add prev slope we were on
        result += prev_max-prev_min

        return result

""" 

"""

class Solution_:
    def maxProfit(self, prices):
        """
        go on crawling over every slope and 
        keep on adding the profit obtained from every consecutive transaction
        """
        result = 0

        for idx in range(1, len(prices)):
            if prices[idx] > prices[idx-1]:
                result += prices[idx] - prices[idx-1]

        return result

Container With Most Water *

Trapping Rain Water (but not considering the water lost by the area/volume of bars)

Screenshot 2021-10-16 at 19.42.02.png

Screen Recording 2021-09-21 at 18.50.42.mov

Screenshot 2021-10-16 at 19.41.47.png

"""
Container With Most Water: (do Best Time to Buy and Sell Stock next)

Given n non-negative integers a1, a2, ..., an , where each represents a point at coordinate (i, ai).
n vertical lines are drawn such that the two endpoints of the line i is at (i, ai) and (i, 0).
Find two lines, which, together with the x-axis forms a container, such that the container contains the most water.
Notice that you may not slant the container.

https://leetcode.com/problems/container-with-most-water/

Trapping Rain Water (but not considering the water lost by the area/volume of bars)
"""

class SolutionBF:
    def maxArea(self, height):

        max_area = 0

        for idx in range(len(height)):

            for idx_two in range(idx+1, len(height)):

                h = min(height[idx], height[idx_two])
                w = idx_two - idx

                max_area = max(max_area, w*h)

        return max_area

""" 
The intuition behind this approach is that the area formed between the lines will always be limited by the height of the shorter line. 
Further, the farther the lines, the more will be the area obtained.

We take two pointers, one at the beginning and one at the end of the array constituting the length of the lines. 
Futher, we maintain a variable maxarea to store the maximum area obtained till now. 
At every step, we find out the area formed between them, update maxarea and move the pointer pointing to the shorter line towards the other end by one step.
"""

class Solution:
    def maxArea(self, height):

        max_area = 0
        left, right = 0, len(height) - 1
        while left < right:

            # calculate area
            h = min(height[left], height[right])
            w = right - left
            max_area = max(max_area, h*w)

            # move pointer
            if height[left] > height[right]:
                right -= 1
            else:
                left += 1

        return max_area

Trapping Rain Water *

Trapping Rain Water - Google Interview Question - Leetcode 42

Trapping Rainwater Problem | Leetcode #42

Container With Most Water (but considering the water lost by the area/volume of bars)

Screen Recording 2021-10-27 at 14.33.50.mov

""" 
Trapping Rain Water

Given n non-negative integers representing an elevation map where the width of each bar is 1,
compute how much water it can trap after raining.

Example 1:
    Input: height = [0,1,0,2,1,0,1,3,2,1,2,1]
    Output: 6
    Explanation: The above elevation map (black section) is represented by array [0,1,0,2,1,0,1,3,2,1,2,1]. In this case, 6 units of rain water (blue section) are being trapped.
Example 2:
    Input: height = [4,2,0,3,2,5]
    Output: 9

https://leetcode.com/problems/trapping-rain-water

Container With Most Water (but considering the water lost by the area/volume of bars)
"""
from typing import List

"""

3               |
2        |      | |   |
1   |    ||   | | | | | |
0 0,1,0,2,1,0,1,3,2,1,2,1

5           |
4 |         |
3 |     |   |
2 | |   | | |
1 | |   | | |
 [4,2,0,3,2,5]

"""

# O(N) space | O(N) time
class Solution:
    def trap(self, height: List[int]):
        """
        - the water stored at a particular height is
            - min(max_left, max_right) - height  # negatives are ignored
        - the max of the furthest ends are the furthest ends heights
        """
        total_water = 0

        # calculate max heights
        max_left = height[:]
        max_right = height[:]
        for idx in range(1, len(height)):
            max_left[idx] = max(height[idx], max_left[idx-1])
        for idx in reversed(range(len(height)-1)):
            max_right[idx] = max(height[idx], max_right[idx+1])

        # calculate water above
        for idx, curr_height in enumerate(height):
            water = min(max_left[idx], max_right[idx]) - curr_height
            if water > 0:
                total_water += water

        return total_water

"""

"""

# O(1) space | O(N) time
class Solution_:
    def trap(self, height: List[int]):
        """
        - maintain max left & right on the go:
            - https://youtu.be/ZI2z5pq0TqA?t=663
            - https://youtu.be/C8UjlJZsHBw?t=1413

        - have a left and right pointer at each end of the array
        - if one pointer (small_pointer) has a value less than the other:
            * the water on small_pointer's next will be most affected by small_pointer as we consider min(max_left, max_height)
            * another way we can think about this is that we can try to increase the small_pointer's value
            - move that pointer forward
            - and record (where we have moved to)'s water
        """
        total_water = 0

        max_left, max_right = height[0],  height[-1]
        left, right = 0, len(height)-1
        while left < right:
            # # left smaller
            if height[left] < height[right]:
                max_left = max(height[left], max_left)
                # calculate water at next position - remember that we know that the water at the right is greater than this
                water_at_next = max_left - height[left+1]
                if water_at_next > 0:
                    total_water += water_at_next
                # move forward
                left += 1

            # # right smaller
            else:
                max_right = max(height[right], max_right)
                # calculate water at next position - remember that we know that the water at the right is equal to/greater than this
                water_at_next = max_right - height[right-1]
                if water_at_next > 0:
                    total_water += water_at_next
                # move forward
                right -= 1

        return total_water

Strobogrammatic Number II *

More examples

Intervals Intersection
'K' Closest Numbers

Longest Substring with At Most K Distinct Characters

""" 
340. Longest Substring with At Most K Distinct Characters:

Given a string s and an integer k, 
return the length of the longest substring of s that contains at most k distinct characters.

Example 1:
    Input: s = "eceba", k = 2
    Output: 3
    Explanation: The substring is "ece" with length 3.
Example 2:
    Input: s = "aa", k = 1
    Output: 2
    Explanation: The substring is "aa" with length 2.

https://leetcode.com/problems/longest-substring-with-at-most-k-distinct-characters
"""

import collections

class Solution:
    def lengthOfLongestSubstringKDistinct(self, s: str, k: int):
        if len(s) <= 0 or k == 0:
            return 0
        store = collections.defaultdict(int)

        idx = 0
        while idx < len(s) and len(store) < k:
            store[s[idx]] += 1
            idx += 1
        longest = idx

        left = 0
        for right in range(idx, len(s)):
            store[s[right]] += 1

            while len(store) > k:
                store[s[left]] -= 1
                if store[s[left]] == 0:
                    store.pop(s[left])
                left += 1

            longest = max(longest, (right-left)+1)

        return longest

Find the original version of this page (with additional content) on Notion here.

Ended: Pointers c5f2aa24da174319aec737993acf4e6a

Trees & Graphs (Additional content) 0fcf8228f7574bfc90076f33e9e274e0 ↵

Bipartite graph/Look for even cycle using graph coloring

Dijkstra's Algorithm

Iterative traversals on Trees

Leetcode Pattern 0 | Iterative traversals on Trees

Find the original version of this page (with additional content) on Notion here.

Less than, Greater than in BST

Find the original version of this page (with additional content) on Notion here.

Prim's Minimum Spanning Tree Algorithm

Segment Trees: Range queries and Updates

Find the original version of this page (with additional content) on Notion here.

Topological Sort (for graphs) *

Introduction

Introduction to Topological Sort - LeetCode Discuss

Topological Sort Algorithm | Graph Theory

Screenshot 2021-08-21 at 10.13.52.png

Untitled

Topological Sort is used to find a linear ordering of elements that have dependencies on each other. For example, if event ‘B’ is dependent on event ‘A’, ‘A’ comes before ‘B’ in topological ordering.

This pattern defines an easy way to understand the technique for performing topological sorting of a set of elements and then solves a few problems using it.

A topological ordering is an ordering of nodes where for each edge from node A to node B, node A appears before node B in the ordering. If it helps, this is a fancy way of saying that we can align all the nodes in line and have all the edges pointing to the right. An important note to make about topological orderings is that they are not unique. As you can imagine there are multiple valid ways to enrol in courses and still graduate.

Sadly not every type of graph can have a topological ordering. For example, any graph which contains a directed cycle cannot have a valid ordering. Think of why this might be true, there cannot be an order if there is a cyclic dependency since there is nowhere to start. Every node in the cycle depends on another. So any graph with a directed cycle is forbidden. The only graphs that have valid topological orderings are Directed Acyclic Graphs, that is graphs with directed edges and no cycles.

The basic idea behind the topological sort is to provide a partial ordering among the vertices of the graph such that if there is an edge from U to V then U≤V i.e., U comes before V in the ordering. Here are a few fundamental concepts related to topological sort:

Source: Any node that has no incoming edge and has only outgoing edges is called a source.
Sink: Any node that has only incoming edges and no outgoing edge is called a sink.
Indegree: count of incoming edges of each vertex/node or how many parents it has (used to determine sources)
So, we can say that a topological ordering starts with one of the sources and ends at one of the sinks.
A topological ordering is possible only when the graph has no directed cycles, i.e. if the graph is a Directed Acyclic Graph (DAG). If the graph has a cycle, some vertices will have cyclic dependencies which makes it impossible to find a linear ordering among vertices.

https://youtu.be/eL-KzMXSXXI

Topological sort

Problem

""" 
Topological Sort:

Topological Sort of a directed graph (a graph with unidirectional edges) is a linear ordering of its vertices
 such that for every directed edge (U, V) from vertex U to vertex V, U comes before V in the ordering.

Given a directed graph, find the topological ordering of its vertices.

Example 1:
    Input: Vertices=4, Edges=[3, 2], [3, 0], [2, 0], [2, 1]
    Output: Following are the two valid topological sorts for the given graph:
    1) 3, 2, 0, 1
    2) 3, 2, 1, 0

Example 2:
    Input: Vertices=5, Edges=[4, 2], [4, 3], [2, 0], [2, 1], [3, 1]
    Output: Following are all valid topological sorts for the given graph:
    1) 4, 2, 3, 0, 1
    2) 4, 3, 2, 0, 1
    3) 4, 3, 2, 1, 0
    4) 4, 2, 3, 1, 0
    5) 4, 2, 0, 3, 1

Example 3:
    Input: Vertices=7, Edges=[6, 4], [6, 2], [5, 3], [5, 4], [3, 0], [3, 1], [3, 2], [4, 1]
    Output: Following are all valid topological sorts for the given graph:
    1) 5, 6, 3, 4, 0, 1, 2
    2) 6, 5, 3, 4, 0, 1, 2
    3) 5, 6, 4, 3, 0, 2, 1
    4) 6, 5, 4, 3, 0, 1, 2
    5) 5, 6, 3, 4, 0, 2, 1
    6) 5, 6, 3, 4, 1, 2, 0

    There are other valid topological ordering of the graph too.

https://www.educative.io/courses/grokking-the-coding-interview/m25rBmwLV00
"""

Screenshot 2021-08-21 at 06.24.22.png

Screenshot 2021-08-21 at 06.23.20.png

Solution

Solution one using sources → most optimal and can be used in many cases

Introduction to Topological Sort - LeetCode Discuss

Screenshot 2021-08-21 at 06.38.00.png

To find the topological sort of a graph we can traverse the graph in a Breadth-First Search (BFS) way. We will start with all the sources, and in a stepwise fashion, save all sources to a sorted list. We will then remove all sources and their edges from the graph. After the removal of the edges, we will have new sources, so we will repeat the above process until all vertices are visited.

This is how we can implement this algorithm:

Initialization
1. We will store the graph in Adjacency Lists, which means each parent vertex will have a list containing all of its children. We will do this using a HashMap where the ‘key’ will be the parent vertex number and the value will be a List containing children vertices.
2. To find the sources, we will keep a HashMap to count the in-degrees i.e., count of incoming edges of each vertex. Any vertex with ‘0’ in-degree will be a source.
Build the graph and find in-degrees of all vertices
1. We will build the graph from the input and populate the in-degrees HashMap.
Find all sources
1. All vertices with ‘0’ in-degrees will be our sources and we will store them in a Queue.
Sort
1. For each source, do the following things:
  - Add it to the sorted list.
  - Get all of its children from the graph.
  - Decrement the in-degree of each child by 1.
  - If a child’s in-degree becomes ‘0’, add it to the sources Queue.
2. Repeat step 1, until the source Queue is empty.

""" 
Solution:

To find the **topological sort of a graph we can traverse the graph in a Breadth-First Search (BFS) way**. 
We will start with all the sources, and in a stepwise fashion, save all sources to a sorted list. 
We will then remove all sources and their edges from the graph. After the removal of the edges, we will have new sources, so we will repeat the above process until all vertices are visited.
This is how we can implement this algorithm:

1. Initialization
    - We will store the graph in Adjacency Lists, which means each parent vertex will have a list containing all of its children. 
        We will do this using a HashMap where the ‘key’ will be the parent vertex number and the value will be a List containing children vertices.
    - To find the sources, we will keep a HashMap to count the in-degrees 
        i.e., count of incoming edges of each vertex. Any vertex with ‘0’ in-degree will be a source.
2. Build the graph and find in-degrees of all vertices
    - We will build the graph from the input and populate the in-degrees HashMap.
3. Find all sources
    - All vertices with ‘0’ in-degrees will be our sources and we will store them in a Queue.
4. Sort
    - For each source, do the following things:
        - Add it to the sorted list.
        - Get all of its children from the graph.
        - Decrement the in-degree of each child by 1.
        - If a child’s in-degree becomes ‘0’, add it to the sources Queue.
    - Repeat the step above, until the source Queue is empty.
"""

import collections

def topological_sort(vertices, edge_list):
    sorted_order = []

    # # convert edge list to an adjacency list & record the edge depths
    # graph
    adjacency_list = collections.defaultdict(list)
    # count of incoming edges of each vertex/node or how many parents it has (used to determine sources)
    in_degree = collections.defaultdict(int)
    for edge in edge_list:
        parent, child = edge[0], edge[1]
        adjacency_list[parent].append(child)
        in_degree[child] += 1  # increment child's in_degree

    # # find all sources (have no parents)
    queue = []
    for key in adjacency_list:
        if in_degree[key] == 0:
            queue.append(key)

    # # add into sorted_order each source
    while len(queue) > 0:
        vertex = queue.pop(0)
        sorted_order.append(vertex)
        # decrement the in-degree of each child by 1 & if a child’s in-degree becomes ‘0’, add it to the sources Queue.
        for child in adjacency_list[vertex]:
            in_degree[child] -= 1
            if in_degree[child] == 0:
                queue.append(child)

    return sorted_order

Solution two using sinks (reverse of solution one) → crashes if a cycle is there

not recommended as one can be used for many other problems

Topological Sort Algorithm | Graph Theory

Algorithms/topsort.txt at 80a2593fca238d47636b44bb08c2323d8b4e5a9d · williamfiset/Algorithms

An easy way to find a topological ordering with trees is to iteratively pick off the leaf nodes. It's like you're cherry-picking from the bottom, it doesn't matter the order you do it. This procedure continues until no more nodes are left...

First find an unvisited node, it doesn't matter which.
From this node do a Depth First Search exploring only reachable unvisited nodes.
On recursive callbacks add the current node to the topological ordering in reverse order.

import collections

def dfs(graph, visited, vertex, sorted_order):
    if visited[vertex]:
        return

    for child in graph[vertex]:
        dfs(graph, visited, child, sorted_order)

    visited[vertex] = True
    sorted_order.append(vertex)

def topological_sort(vertices, edge_list):
    sorted_order = []

    # # convert edge list to an adjacency list
    adjacency_list = collections.defaultdict(list)
    for edge in edge_list:
        adjacency_list[edge[0]].append(edge[1])

    visited = collections.defaultdict(bool)

    for edge in edge_list:
        dfs(adjacency_list, visited, edge[0], sorted_order)

    sorted_order.reverse()
    return sorted_order

Course Schedule II

"""
Course Schedule II:

There are a total of numCourses courses you have to take, labeled from 0 to numCourses - 1. 
You are given an array prerequisites where prerequisites[i] = [ai, bi] indicates that you must take course bi first if you want to take course ai.

For example, the pair [0, 1], indicates that to take course 0 you have to first take course 1.
Return the ordering of courses you should take to finish all courses. 
If there are many valid answers, return any of them. 
If it is impossible to finish all courses, return an empty array.

Example 1:
    Input: numCourses = 2, prerequisites = [[1,0]]
    Output: [0,1]
    Explanation: There are a total of 2 courses to take. To take course 1 you should have finished course 0. So the correct course order is [0,1].
Example 2:
    Input: numCourses = 4, prerequisites = [[1,0],[2,0],[3,1],[3,2]]
    Output: [0,2,1,3]
    Explanation: There are a total of 4 courses to take. To take course 3 you should have finished both courses 1 and 2. Both courses 1 and 2 should be taken after you finished course 0.
    So one correct course order is [0,1,2,3]. Another correct ordering is [0,2,1,3].
Example 3:
    Input: numCourses = 1, prerequisites = []
    Output: [0]

https://leetcode.com/problems/course-schedule-ii/
"""

"""
# indegree = count of incoming edges of each vertex/node or how many parents it has (used to determine sources)
# source: Any node that has no incoming edge and has only outgoing edges is called a source (indegree==0)

- top_sort = []
- get the topological sort of the courses
    - initialization:
        - create an adjacency list from the edge list given
        - while doing so, create an indegree record for each vertex/node
        - add all the sources into a queue
    - while queue:
        - get the element at the top of the queue (curr)
            - add it to the output
            - reduce the indegree for all of its children by one
                - if any child has an indegree of one after that, add it to the queue

- if the length of the sorted list == numCourses, it is possible to complete the courses, it is an asyclic graph 
"""

import collections

class Solution:

    def findOrder(self, numCourses, prerequisites):

        top_sort = []

        # # create an adjacency list from the edge list given
        # while doing so, create an indegree record for each vertex/node
        adjacency_list = collections.defaultdict(list)
        indegrees = collections.defaultdict(int)
        for arr in prerequisites:
            child, parent = arr[0], arr[1]

            adjacency_list[parent].append(child)
            indegrees[child] += 1

        # # add all the sources into a queue
        queue = []
        for vertex in range(numCourses):
            if indegrees[vertex] == 0:
                queue.append(vertex)

        # # build top_sort list
        while queue:
            vertex = queue.pop(0)
            top_sort.append(vertex)
            for child in adjacency_list[vertex]:
                indegrees[child] -= 1
                if indegrees[child] == 0:
                    queue.append(child)

        # if the length of the sorted list == numCourses, it is possible to complete the courses
        if len(top_sort) == numCourses:
            return top_sort
        return []

Course Schedule/Tasks Scheduling

Problem

"""
Course Schedule/Tasks Scheduling:
Course Schedule II is a prerequisite to this.

There are a total of numCourses courses you have to take, labeled from 0 to numCourses - 1. 
You are given an array prerequisites where prerequisites[i] = [ai, bi] indicates that you must take course bi first if you want to take course ai.
For example, the pair [0, 1], indicates that to take course 0 you have to first take course 1.
Return true if you can finish all courses. Otherwise, return false.

Example 1:
    Input: numCourses = 2, prerequisites = [[1,0]]
    Output: true
    Explanation: There are a total of 2 courses to take. 
    To take course 1 you should have finished course 0. So it is possible.
Example 2:
    Input: numCourses = 2, prerequisites = [[1,0],[0,1]]
    Output: false
    Explanation: There are a total of 2 courses to take. 
    To take course 1 you should have finished course 0, and to take course 0 you should also have finished course 1. So it is impossible.
Example 3:
    Input: numCourses = 3, prerequisites=[0, 1], [1, 2]
    Output: true
    Explanation: To execute task '1', task '0' needs to finish first. Similarly, task '1' needs 
            to finish before '2' can be scheduled. One possible scheduling of tasks is: [0, 1, 2] 
Example 4:
    Input: numCourses = 3, prerequisites=[0, 1], [1, 2], [2, 0]
    Output: false
    Explanation: The tasks have a cyclic dependency, therefore they cannot be scheduled.
Example 5:
    Input: numCourses = 6, prerequisites=[2, 5], [0, 5], [0, 4], [1, 4], [3, 2], [1, 3]
    Output: true
    Explanation: A possible scheduling of tasks is: [0 1 4 3 2 5]

https://leetcode.com/problems/course-schedule/
"""

Solution

Topological sort

"""
SOLUTION:
https://leetcode.com/discuss/general-discussion/1078072/introduction-to-topological-sort

# indegree = count of incoming edges of each vertex/node or how many parents it has (used to determine sources)
# source: Any node that has no incoming edge and has only outgoing edges is called a source (indegree==0)

- top_sort = []
- get the topological sort of the courses
    - initialization:
        - create an adjacency list from the edge list given
        - while doing so, create an indegree record for each vertex/node
        - add all the sources into a queue
    - while queue:
        - get the element at the top of the queue (curr)
            - add it to the output
            - reduce the indegree for all of its children by one
                - if any child has an indegree of one after that, add it to the queue

- return len(top_sort) == len(adjacency_list)
    - if len(top_sort) == len(adjacency_list), it means the graph is acyclic
"""

import collections

class Solution:
    def topSort(self, edge_list):
        top_sort = []

        # # create an adjacency list from the edge list given
        # while doing so, create an indegree record for each vertex/node
        adjacency_list = collections.defaultdict(list)
        indegrees = collections.defaultdict(int)
        for arr in edge_list:
            child, parent = arr[0], arr[1]

            adjacency_list[parent].append(child)
            indegrees[child] += 1

        # # add all the sources into a queue
        queue = []
        for vertex in adjacency_list:
            if indegrees[vertex] == 0:
                queue.append(vertex)

        # # build top_sort list
        while queue:
            vertex = queue.pop(0)
            top_sort.append(vertex)
            for child in adjacency_list[vertex]:
                indegrees[child] -= 1
                if indegrees[child] == 0:
                    queue.append(child)

        # if len(top_sort) == len(adjacency_list), it means the graph is acyclic
        return len(top_sort) == len(adjacency_list)

    def canFinish(self, numCourses, prerequisites):
        return self.topSort(prerequisites)

DFS

class SolutionDFS:
    def dfs(self, adjacency_list, visited_cache, vertex, curr_visiting):
        if vertex in visited_cache:
            return True
        if vertex in curr_visiting:
            return False

        curr_visiting.add(vertex)
        for child in adjacency_list[vertex]:
            if not self.dfs(adjacency_list, visited_cache, child, curr_visiting):
                return False
        curr_visiting.remove(vertex)

        visited_cache.add(vertex)
        return True

    def canFinish(self, numCourses, prerequisites):

        # # create an adjacency list from the edge list given
        adjacency_list = collections.defaultdict(list)
        for arr in prerequisites:
            child, parent = arr[0], arr[1]
            adjacency_list[parent].append(child)

        visited_cache = set()
        for vertex in list(adjacency_list.keys()):
            if not self.dfs(adjacency_list, visited_cache, vertex, set()):
                return False

        return True

Alien Dictionary

Problem

Screenshot 2021-10-09 at 12.09.14.png

Solution

Screenshot 2021-10-09 at 12.10.34.png

Screenshot 2021-10-09 at 12.11.37.png

""" 
269. Alien Dictionary:

There is a new alien language that uses the English alphabet. 
However, the order among the letters is unknown to you.

You are given a list of strings words from the alien language's dictionary, where the strings in words are sorted lexicographically by the rules of this new language.

Return a string of the unique letters in the new alien language sorted in lexicographically increasing order by the new language's rules. 
If there is no solution, return "". If there are multiple solutions, return any of them.

A string s is lexicographically smaller than a string t if at the first letter where they differ, 
    the letter in s comes before the letter in t in the alien language. 
If the first min(s.length, t.length) letters are the same, then s is smaller if and only if s.length < t.length.

Test cases:
    ["wrt", "wrf", "er", "ett", "rftt"]
    ["z", "x"]
    ["z", "x", "z"]
    ["ab", "adc"]
    ["z", "z"]
    ["abc", "ab"]
    ["z", "x", "a", "zb", "zx"]
    ["w", "wnlb"]
    ["wnlb"]
    ["aba"]

Results:
    "wertf"
    "zx"
    ""
    "abcd"
    "z"
    ""
    ""
    "wnlb"
    "wnlb"
    "ab"

['f', 't', 'r', 'e', 'w']
['x', 'z']
['x', 'z']
['a', 'd', 'b', 'c']
['z']
['a', 'x', 'z', 'b']
['w', 'n', 'l', 'b']
['w', 'n', 'l', 'b']
['a', 'b']

https://leetcode.com/problems/alien-dictionary/
"""
import collections

""" 
A few things to keep in mind:
    - The letters within a word don't tell us anything about the relative order. 
        For example, the presence of the word kitten in the list does not tell us that the letter k is before the letter i.
    - The input can contain words followed by their prefix, for example, abcd and then ab. 
        These cases will never result in a valid alphabet (because in a valid alphabet, prefixes are always first). 
        You'll need to make sure your solution detects these cases correctly.
    - There can be more than one valid alphabet ordering. It is fine for your algorithm to return any one of them.
    - Your output string must contain all unique letters that were within the input list, including those that could be in any position within the ordering. 
        It should not contain any additional letters that were not in the input.

All approaches break the problem into three steps:
    - Extracting dependency rules from the input. 
        For example "A must be before C", "X must be before D", or "E must be before B".
    - Putting the dependency rules into a graph with letters as nodes and dependencies as edges (an adjacency list is best).
    - Topologically sorting the graph nodes

"""

class Solution:
    def alienOrder(self, words):
        graph = collections.defaultdict(set)  # Adjacency list

        # build graph
        for idx in range(len(words)):
            self.add_word_letters(graph, words[idx])

            # if not at end
            if idx < len(words)-1:
                self.add_word_letters(graph, words[idx+1])
                if not self.compare_two_words(graph, words[idx], words[idx+1]):
                    return ""

        return "".join(self.top_sort(graph))

    def top_sort(self, graph):
        """ 
        Topological sort

        Remember that: 
            If the number of nodes in the the top sort result is
            less than the number of nodes in the graph, we have a cycle.
            Which means that we cannot have a valid ordering. Return []
        """
        res = []

        queue = []
        indegrees = collections.defaultdict(int)

        # calculate indegrees
        for node in graph:
            for child in graph[node]:
                indegrees[child] += 1

        # get sources
        for node in graph:
            if indegrees[node] == 0:
                queue.append(node)

        # sort
        while queue:
            node = queue.pop(0)
            res.append(node)  # Add to result

            for child in graph[node]:
                indegrees[child] -= 1
                if indegrees[child] == 0:  # Has become a source
                    queue.append(child)

        # check if has_cycle
        if len(res) != len(graph):
            return []
        return res

    def compare_two_words(self, graph, one, two):
        """
        Where two words are adjacent, we need to look for the first difference between them. 
        That difference tells us the relative order between two letters.

        Handle edge cases like:
            ab, a => error(a should be before ab)
        """

        idx = 0
        while idx < len(one) and idx < len(two) and one[idx] == two[idx]:
            idx += 1

        if idx < len(one) and idx < len(two):
            graph[one[idx]].add(two[idx])
        elif idx < len(one):
            return False  # Invalid

        return True

    def add_word_letters(self, graph, word):
        for idx in range(len(word)):
            graph[word[idx]]  # Add letter to graph.

"""  

DFS / reveese of Topological sort

"""

class SolutionDFS:
    def alienOrder(self, words):
        graph = collections.defaultdict(set)  # Adjacency list

        # build graph
        for idx in range(len(words)):
            self.add_word_letters(graph, words[idx])

            # if not at end
            if idx < len(words)-1:
                self.add_word_letters(graph, words[idx+1])
                if not self.compare_two_words(graph, words[idx], words[idx+1]):
                    return ""

        if self.has_cycle(graph):
            return ""
        return "".join(reversed(self.dfs(graph)))

    def compare_two_words(self, graph, one, two):
        """
        Where two words are adjacent, we need to look for the first difference between them. 
        That difference tells us the relative order between two letters.

        Handle edge cases like:
            ab, a => error(a should be before ab)
        """

        idx = 0
        while idx < len(one) and idx < len(two) and one[idx] == two[idx]:
            idx += 1

        if idx < len(one) and idx < len(two):
            graph[one[idx]].add(two[idx])
        elif idx < len(one):
            return False  # Invalid

        return True

    def add_word_letters(self, graph, word):
        for idx in range(len(word)):
            graph[word[idx]]  # Add letter to graph.

    def dfs(self, graph):
        """ 
        DFS => reveese of Topological sort

        Remember that: 
            If the number of nodes in the the top sort result is
            less than the number of nodes in the graph, we have a cycle.
            Which means that we cannot have a valid ordering. Return []
        """
        res = []
        visited = set()
        for node in graph:
            self.dfs_helper(graph, visited, node, res)

        # check if has_cycle
        if len(res) != len(graph):
            return []
        return res

    def dfs_helper(self, graph, visited,  curr, res):
        if curr in visited:
            return

        visited.add(curr)
        for node in graph[curr]:
            self.dfs_helper(graph, visited, node, res)

        res.append(curr)

    def has_cycle(self, graph):
        checked = {}

        for node in graph:
            if self._has_cycle_helper(graph, checked, set(), node):
                return True
        return False

    def _has_cycle_helper(self, graph, checked, visiting, node):
        if node in visiting:
            return True
        if node in checked:
            return checked[node]

        visiting.add(node)

        result = False
        for child in graph[node]:
            result = result or self._has_cycle_helper(
                graph, checked, visiting, child)

        # remember to add this!
        #   because it is a directed graph
        #   we might reach the node several times but it doesn't mean it is is a cycle
        #   eg: https://www.notion.so/paulonteri/Searching-733ff84c808c4c9cb5c40787b2df7b98#c7458268f05e4e2db359f9990366a411
        visiting.discard(node)

        checked[node] = result
        return checked[node]

Find the original version of this page (with additional content) on Notion here.

Union find (disjoint set)

Based on:

Find the original version of this page (with additional content) on Notion here.

Ended: Trees & Graphs (Additional content) 0fcf8228f7574bfc90076f33e9e274e0

Other 40309fe5fdb74185b00fd1848a50054c ↵

Divide and Conquer

Introduction to Divide and Conquer With Binary Search - Algorithms for Coding Interviews in Python

DAA Divide and Conquer Introduction - javatpoint

Divide%20and%20Conquer%2032431685f49e4580aea1cb1a41f417a7/Untitled.png

In divide and conquer approach, a problem is divided into smaller problems, then the smaller problems are solved independently, and finally the solutions of smaller problems are combined into a solution for the large problem.

Divide and conquer is an algorithmic paradigm in which the problem is repeatedly divided into subproblems until we reach a point where each problem is similar and atomic, i.e., can’t be further divided. At this point, we start solving these atomic problems and combining (merging) the solutions.

Generally, divide-and-conquer algorithms have three parts:

Divide the problem into a number of sub-problems that are smaller instances of the same problem.
Conquer the sub-problems by solving them recursively. If they are small enough, solve the sub-problems as base cases.
Combine the solutions to the sub-problems into the solution for the original problem.

Examples

Binary Search
Quicksort: It is the most efficient sorting algorithm, which is also known as partition-exchange sort. It starts by selecting a pivot value from an array followed by dividing the rest of the array elements into two sub-arrays. The partition is made by comparing each of the elements with the pivot value. It compares whether the element holds a greater value or lesser value than the pivot and then sort the arrays recursively.
Merge Sort: It is a sorting algorithm that sorts an array by making comparisons. It starts by dividing an array into sub-array and then recursively sorts each of them. After the sorting is done, it merges them back.
Tower of Hanoi problem

Find the original version of this page (with additional content) on Notion here.

More

Convert recursion to iteration

In-place reversal of linked list

Find the original version of this page (with additional content) on Notion here.

Recursive iteration

Find the original version of this page (with additional content) on Notion here.

Reservoir sampling

Find the original version of this page (with additional content) on Notion here.

More 96929a3286bd4c8db1d462e581c566e0 ↵

Convert recursion to iteration

Binary tree traversal

Find the original version of this page (with additional content) on Notion here.

In-place reversal of linked list

In a lot of problems, you may be asked to reverse the links between a set of nodes of a linked list. Often, the constraint is that you need to do this in-place, i.e., using the existing node objects and without using extra memory. This is where the above mentioned pattern is useful.

This pattern reverses one node at a time starting with one variable (current) pointing to the head of the linked list, and one variable (previous) will point to the previous node that you have processed. In a lock-step manner, you will reverse the current node by pointing it to the previous before moving on to the next node. Also, you will update the variable “previous” to always point to the previous node that you have processed.

Untitled

Examples:

Honourable mentions

Find the original version of this page (with additional content) on Notion here.

Ended: More 96929a3286bd4c8db1d462e581c566e0

Ended: Other 40309fe5fdb74185b00fd1848a50054c

Ended: Patterns for Coding Questions e3f5361611c147ebb2fb3eff37a743fd

Ended: Data Structures and Algorithms 16913c6fbd244de481b6b1705cbfa6be

Data Structures and Algorithms

Data Structures and Algorithms

SubPages

Data Structures and Algorithms

Tools:

Tips:

How to approach problems

More reading

Data Structures and Algorithms 16913c6fbd244de481b6b1705cbfa6be ↵

Complexity Analysis & Big O

Important rules to know with Big O

1. Different steps get added

2. Drop constants

3. Different inputs ⇒ Different variables

4. Drop non-dominant terms

5. Multi-Part Algorithms: Add vs. Multiply

6. Recursive Runtimes

Memory

Constant time/space complexity:

A Wrinkle (finite character set)

Examples

Logarithm

2n (2^n) - whenever the algorithm's input increases in size, the number of operations needed to complete the algorithm doubles**.

Factorial - N * (N-1) * (N-2) * (N-3) * ... * 2 * 1 == N!

Not factorial 😂 - (N-1) + (N-2) + (N-3) + ... + 2 + 1 ~= N^2

Two loops but on different arrays O(a.b) instead of O(n^2)

An algorithm that took in an array of strings, sorted each string and then sorted the full array

O(squareroot n) time.

Common

Graph DFS & BFS

Greedy Algorithms

Introduction

Examples

Honourable mentions

Hashtables & Hashsets

Examples

How to store an class in a hashtable

Sorting by keys/value

hashtable vs hashset vs hashmap python

You can compare hashtables

Examples:

Hash table libraries

collections.defaultdict

collections.OrderedDict

sortedcontainers.SortedDict

set

Examples

collections.Counter

Heaps & Priority Queues

Heaps

Representation as an array

Time complexity

Examples:

Heap sort

Priority Queue

heapq

heapq.heapify(a)

heapq.heappop(a)

heapq.heappush(a, 4)

With miltidementional arrays

🌳 Prim's Minimum Spanning Tree Algorithm *

Math Tricks

Introduction

Tips & Tricks

How to multiply matrices

Examples

One of those

Python basics

Integers

Examples

Power

Square root *

Modulus(%) vs Floor(//)

math.ceil() & math.floor()

Infinity (can be used for math.max)

.isalpha() .isnumeric() & .isalnum()

chr() & ord()

Other

Lambda functions

Sort

`collections.defaultdict`

`collections.OrderedDict`

`sortedcontainers.SortedDict`

`set`

`collections.Counter`

`heapq`

`heapq.heapify(a)`

`heapq.heappop(a)`

`heapq.heappush(a, 4)`

`collections.deque()` *

`collections.defaultdict`

`collections.OrderedDict`

`sortedcontainers.SortedDict`

`collections.OrderedDict`