Top/Smallest/Frequent K elements *
Introduction
14 Patterns to Ace Any Coding Interview Question | Hacker Noon
When to use
Any problem that asks us to find the top/smallest/frequent ‘K’ elements among a given set falls under this pattern.
The best data structure that comes to mind to keep track of ‘K’ elements is Heap. This pattern will make use of the Heap to solve multiple problems dealing with ‘K’ elements at a time from a set of given elements.
Simple examples
Top 'K' Numbers
Problem
"""
Top 'K' Numbers:
Given an unsorted array of numbers, find the ‘K’ largest numbers in it.
Example 1:
Input: [3, 1, 5, 12, 2, 11], K = 3
Output: [5, 12, 11]
Example 2:
Input: [5, 12, 11, -1, 12], K = 3
Output: [12, 11, 12]
"""
Solution
"""
Solution:
get rid of all smaller numbers
A brute force solution could be to sort the array and return the largest K numbers.
The time complexity of such an algorithm will be O(N*logN) as we need to use a sorting algorithm.
If we iterate through the array one element at a time and keep ‘K’ largest numbers in a heap such that
each time we find a larger number than the smallest number in the heap, we do two things:
- Take out the smallest number from the heap, and
- Insert the larger number into the heap.
This will ensure that we always have ‘K’ largest numbers in the heap.
As discussed above,
it will take us O(logK) to extract the minimum number from the min-heap.
So the overall time complexity of our algorithm will be O(K*logK+(N-K)*logK) since,
first, we insert ‘K’ numbers in the heap and then iterate through the remaining numbers and at every step,
in the worst case, we need to extract the minimum number and insert a new number in the heap.
This algorithm is better than O(N*logN).
"""
the time complexity of this algorithm is O(K*logK+(N-K)*logK)O(K∗logK+(N−K)∗logK), which is asymptotically equal to O(N*logK)O(N∗logK)import heapq
def find_k_largest_numbers(nums, k):
res = []
for num in nums:
heapq.heappush(res, num)
while len(res) > k:
heapq.heappop(res)
return res
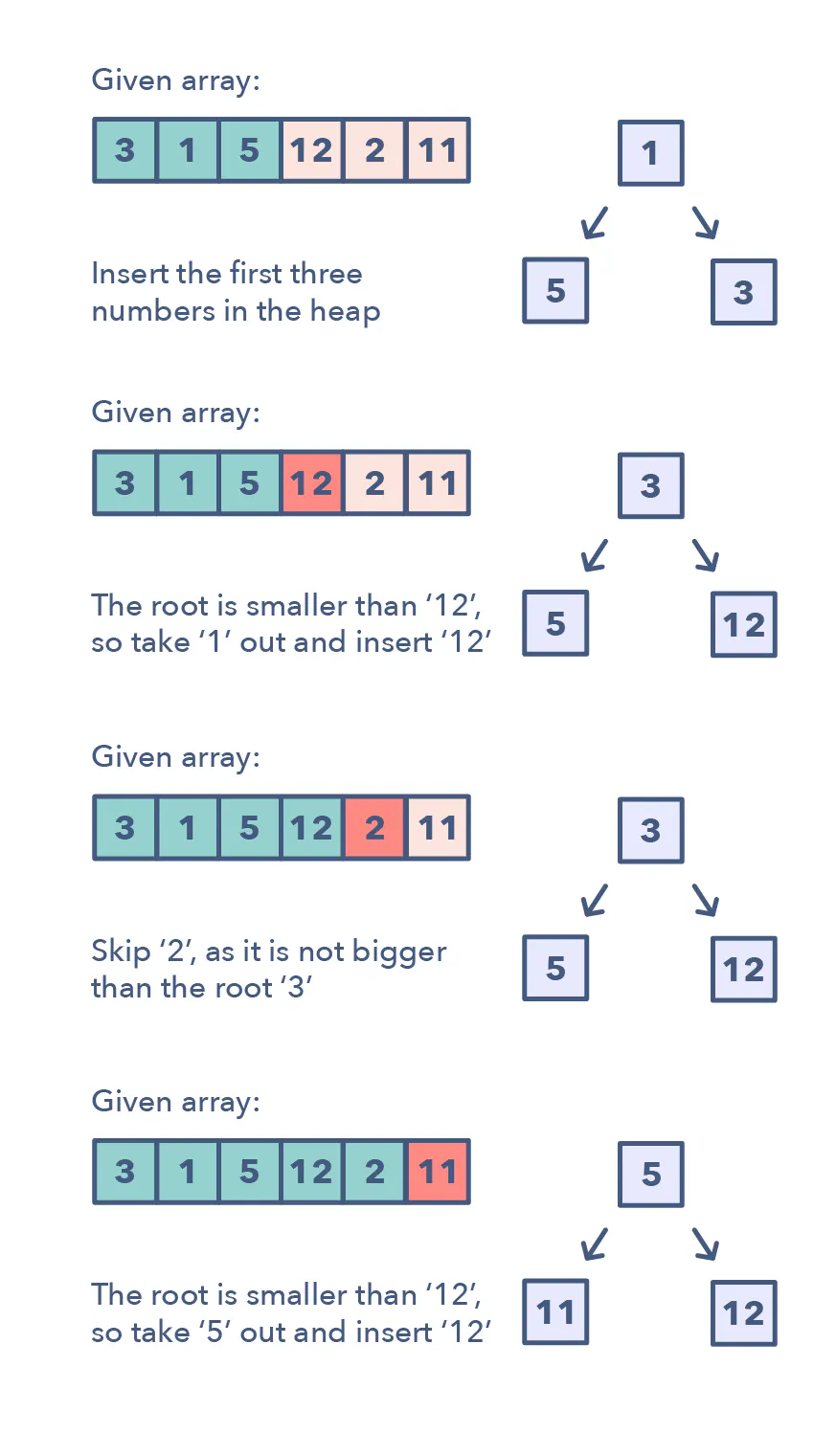
Given array: [3, 1, 5, 12, 2, 11], and K=3
- First, let’s insert ‘K’ elements in the min-heap.
- After the insertion, the heap will have three numbers [3, 1, 5] with ‘1’ being the root as it is the smallest element.
- We’ll iterate through the remaining numbers and perform the above-mentioned two steps if we find a number larger than the root of the heap.
- The 4th number is ‘12’ which is larger than the root (which is ‘1’), so let’s take out ‘1’ and insert ‘12’. Now the heap will have [3, 5, 12] with ‘3’ being the root as it is the smallest element.
- The 5th number is ‘2’ which is not bigger than the root of the heap (‘3’), so we can skip this as we already have top three numbers in the heap.
- The last number is ‘11’ which is bigger than the root (which is ‘3’), so let’s take out ‘3’ and insert ‘11’. Finally, the heap has the largest three numbers: [5, 12, 11]
Screen Recording 2021-08-17 at 05.40.47.mov
Time & Space complexity
The time complexity of this algorithm is O(K*logK+(N-K)logK), which is asymptotically equal to O(N∗logK) and is better than normal sorting O(N∗logN)
The space complexity will be O(K) since we need to store the top ‘K’ numbers in the heap.
Kth Smallest Number
This problem follows the Top ‘K’ Numbers pattern but has two differences:
- Here we need to find the Kth
smallestnumber, whereas in Top ‘K’ Numbers we were dealing with ‘K’largestnumbers. - In this problem, we need to find only one number (Kth smallest) compared to finding all ‘K’ largest numbers.
We can follow the same approach as discussed in the ‘Top K Elements’ problem. To handle the first difference mentioned above, we can use a max-heap instead of a min-heap. As we know, the root is the biggest element in the max heap. So, since we want to keep track of the ‘K’ smallest numbers, we can compare every number with the root while iterating through all numbers, and if it is smaller than the root, we’ll take the root out and insert the smaller number.
'K' Closest Points to the Origin
Problem
"""
'K' Closest Points to the Origin:
Given an array of points in a 2D2D plane, find ‘K’ closest points to the origin.
Example 1:
Input: points = [[1,2],[1,3]], K = 1
Output: [[1,2]]
Explanation: The Euclidean distance between (1, 2) and the origin is sqrt(5).
The Euclidean distance between (1, 3) and the origin is sqrt(10).
Since sqrt(5) < sqrt(10), therefore (1, 2) is closer to the origin.
Example 2:
Input: point = [[1, 3], [3, 4], [2, -1]], K = 2
Output: [[1, 3], [2, -1]]
https://leetcode.com/problems/k-closest-points-to-origin/
https://www.educative.io/courses/grokking-the-coding-interview/3YxNVYwNR5p
"""
The Euclidean distance of a point P(x,y) from the origin can be calculated through the following formula:
\(\sqrt{x^2 + y^2}\)
Solution
This solution uses the Top 'K' Numbers pattern
import heapq
import math
class Point:
def __init__(self, x, y):
self.x = x
self.y = y
# used for max-heap sorting
# can also use less than __lt__
def __gt__(self, other: 'Point'):
# return self.distance_from_origin() > other.distance_from_origin()
# we sort this way to ensure we have the k closest/smallest
return self.distance_from_origin() < other.distance_from_origin()
def distance_from_origin(self):
return math.sqrt((self.x * self.x) + (self.y * self.y))
def find_closest_points(points, k):
result = []
for point in points:
heapq.heappush(result, point)
while len(result) > k:
heapq.heappop(result)
return result
Connect Ropes
"""
Connect Ropes;
Example 1:
Input: [1, 3, 11, 5]
Output: 33
Explanation: First connect 1+3(=4), then 4+5(=9), and then 9+11(=20). So the total cost is 33 (4+9+20)
Example 2:
Input: [3, 4, 5, 6] *
Output: 36
Explanation: First connect 3+4(=7), then 5+6(=11), 7+11(=18). Total cost is 36 (7+11+18)
Example 3:
Input: [1, 3, 11, 5, 2]
Output: 42
Explanation: First connect 1+2(=3), then 3+3(=6), 6+5(=11), 11+11(=22). Total cost is 42 (3+6+11+22)
"""
Solution
"""
Solution:
In this problem, following a greedy approach to connect the smallest ropes first will ensure the lowest cost.
We can use a Min Heap to find the smallest ropes following a similar approach as discussed in Kth Smallest Number.
Once we connect two ropes, we need to insert the resultant rope back in the Min Heap so that we can connect it with the remaining ropes.
"""
import heapq
def minimum_cost_to_connect_ropes(ropeLengths):
minHeap = []
# add all ropes to the min heap
for i in ropeLengths:
heapq.heappush(minHeap, i)
# go through the values of the heap, in each step take top (lowest) rope lengths from the min heap
# connect them and push the result back to the min heap.
# keep doing this until the heap is left with only one rope
result = 0
while len(minHeap) > 1:
temp = heapq.heappop(minHeap) + heapq.heappop(minHeap)
result += temp
heapq.heappush(minHeap, temp)
return result
Time & space complexity
Time complexity
Given ‘N’ ropes, we need O(NlogN) to insert all the ropes in the heap. In each step, while processing the heap, we take out two elements from the heap and insert one. This means we will have a total of ‘N’ steps, having a total time complexity of O(NlogN).
Space complexity
The space complexity will be O(N) because we need to store all the ropes in the heap.
Top 'K' Frequent Numbers
"""
Top 'K' Frequent Numbers:
Given an unsorted array of numbers, find the top ‘K’ frequently occurring numbers in it.
Example 1:
Input: [1, 3, 5, 12, 11, 12, 11], K = 2
Output: [12, 11]
Explanation: Both '11' and '12' appeared twice.
Example 2:
Input: [5, 12, 11, 3, 11], K = 2
Output: [11, 5] or [11, 12] or [11, 3]
Explanation: Only '11' appeared twice, all other numbers appeared once.
"""
from typing import List
from collections import Counter
from heapq import heappop, heappush
"""
- have a min heap (smallest number at the top)
- get the count of all nums in the array
- all the counts plus corresponding numbers to the heap
- the heap will contain a max of k elements
- return the numbers in the heap
"""
# O(N∗logK) time | O(N) space
class Solution:
def topKFrequent(self, nums: List[int], k: int):
min_heap = []
for number, count in Counter(nums).items():
heappush(min_heap, (count, number))
if len(min_heap) > k:
heappop(min_heap)
return [item[1] for item in min_heap]
Frequency Sort
Similar to Top 'K' Frequent Numbers
"""
Given a string, sort it based on the decreasing frequency of its characters.
Example 1:
Input: "Programming"
Output: "rrggmmPiano"
Explanation: 'r', 'g', and 'm' appeared twice, so they need to appear before any other character.
Example 2:
Input: "abcbab"
Output: "bbbaac"
Explanation: 'b' appeared three times, 'a' appeared twice, and 'c' appeared only once.
"""
"""
- get the character count of each character
- sort the characters by count (using a heap)
- build a new string following the sorted charcters and filling it up with the count
"""
Kth Largest Number in a Stream
"""
Kth Largest Number in a Stream:
Design a class to efficiently find the Kth largest element in a stream of numbers.
The class should have the following two things:
The constructor of the class should accept an integer array containing initial numbers from the stream and an integer ‘K’.
The class should expose a function add(int num) which will store the given number and return the Kth largest number.
Example 1:
Input: [3, 1, 5, 12, 2, 11], K = 4
1. Calling add(6) should return '5'.
2. Calling add(13) should return '6'.
2. Calling add(4) should still return '6'.
"""
"""
Input: [3, 1, 5, 12, 2, 11], K = 4
sorted_input => [1,2,3,5,11,12]
1. Calling add(6) should return '5'.
[1,2,3,5,6,11,12]
2. Calling add(13) should return '6'.
[1,2,3,5,6,11,12,13]
2. Calling add(4) should still return '6'.
[1,2,3,4,5,6,11,12,13]
- if we find a way to store the k largest numbers,
we can be knowing the kth largest easily
- we can use a heap for this
"""
import heapq
class KthLargestNumberInStream:
def __init__(self, nums, k):
self.nums = nums
self.k = k
def add(self, num):
heapq.heappush(self.nums, num)
while len(self.nums) > self.k:
heapq.heappop(self.nums)
return self.nums[0]
'K' Closest Numbers
Problem
"""
'K' Closest Numbers:
Given a sorted number array and two integers ‘K’ and ‘X’, find ‘K’ closest numbers to ‘X’ in the array.
Return the numbers in the sorted order. ‘X’ is not necessarily present in the array.
Example 1:
Input: [5, 6, 7, 8, 9], K = 3, X = 7
Output: [6, 7, 8]
Example 2:
Input: [2, 4, 5, 6, 9], K = 3, X = 6
Output: [4, 5, 6]
Example 3:
Input: [2, 4, 5, 6, 9], K = 3, X = 10
Output: [5, 6, 9]
"""
Solution
"""
SOLUTION:
O(N∗logK):
- for each number in the array, calculate its abolute difference with X
- store the difference in a max-heap(largest on top) maintaining K numbers in the heap
- return the heap
O(logN + KlogK)
- Since the array is sorted, we can first find the number closest to ‘X’ through Binary Search. Let’s say that number is ‘Y’.
- The ‘K’ closest numbers to ‘Y’ will be adjacent to ‘Y’ in the array. We can search in both directions of ‘Y’ to find the closest numbers.
- We can use a heap to efficiently search for the closest numbers. We will take ‘K’ numbers in both directions of ‘Y’
and push them in a Min Heap sorted by their absolute difference from ‘X’.
This will ensure that the numbers with the smallest difference from ‘X’ (i.e., closest to ‘X’) can be extracted easily from the Min Heap.
- Finally, we will extract the top ‘K’ numbers from the Min Heap to find the required numbers.
"""
import heapq
# O(logN + KlogK) time | O(K) space
def find_closest_elements(arr, K, X):
closest_idx = binary_search(arr, X)
close = []
for idx in range(max(0, closest_idx-K), min(len(arr), closest_idx+K+1)):
num = arr[idx]
heapq.heappush(close, [-abs(X-num), num])
if len(close) > K:
heapq.heappop(close)
result = []
for item in close:
result.append(item[1])
return result
def binary_search(arr, num):
left = 0
right = len(arr)-1
while left < right:
mid = (left+right) // 2
if arr[mid] == num:
return mid
elif arr[mid] > num:
right = mid-1
else:
left = mid+1
return left
Alternate Solution using Two Pointers
After finding the number closest to ‘X’ through Binary Search, we can use the Two Pointers approach to find the ‘K’ closest numbers. Let’s say the closest number is ‘Y’. We can have a left pointer to move back from ‘Y’ and a right pointer to move forward from ‘Y’. At any stage, whichever number pointed out by the left or the right pointer gives the smaller difference from ‘X’ will be added to our result list.
To keep the resultant list sorted we can use a Queue. So whenever we take the number pointed out by the left pointer, we will append it at the beginning of the list and whenever we take the number pointed out by the right pointer we will append it at the end of the list.
Time & Space complexity
The time complexity of the above algorithm is O(logN + KlogK). We need O(logN) for Binary Search and O(KlogK) to insert the numbers in the Min Heap, as well as to sort the output array.
The space complexity will be O(K), as we need to put a maximum of K numbers in the heap.
Top K Frequent Words
-
Top K Frequent Words
from typing import List import collections import heapq class Word: def __init__(self, word, count): self.word = word self.count = count def __gt__(self, other): if self.count == other.count: return self.word < other.word return self.count > other.count class Solution: def topKFrequent(self, words: List[str], k: int): word_count = collections.Counter(words) heap = [] for word, count in word_count.items(): heapq.heappush(heap, Word(word, count)) if len(heap) > k: heapq.heappop(heap) top_k_words = [] while heap: top_k_words.append(heapq.heappop(heap).word) top_k_words.reverse() return top_k_words
Others
-
Sort K-Sorted Array
""" Sort K-Sorted Array: Write a function that takes in a non-negative integer k and a k-sorted array of integers and returns the sorted version of the array. Your function can either sort the array in place or create an entirely new array. A k-sorted array is a partially sorted array in which all elements are at most k positions away from their sorted position. For example, the array [3, 1, 2, 2] is k-sorted with k = 3, because each element in the array is at most 3 positions away from its sorted position. Note that you're expected to come up with an algorithm that can sort the k-sorted array faster than in O(nlog(n)) time. Sample Input array = [3, 2, 1, 5, 4, 7, 6, 5] k = 3 Sample Output [1, 2, 3, 4, 5, 5, 6, 7] https://www.algoexpert.io/questions/Sort%20K-Sorted%20Array """ import heapq """ - have a min-heap with k elements - iterate through the input array and at each index: - remove and record the value at the top of the heap at the index - add the element at index + k to the heap """ # O(nlog(k)) time | O(k) space def sortKSortedArray(array, k): # have a min-heap with k elements heap = array[:k+1] heapq.heapify(heap) for idx in range(len(array)): # remove and record the value at the top of the heap at the index array[idx] = heapq.heappop(heap) # add the element at index + k+1 to the heap if idx+k+1 < len(array): heapq.heappush(heap, array[idx+k+1]) return array
Find the original version of this page (with additional content) on Notion here.
Created: December 13, 2021 16:05:48